Калькулятор частные производные: Найти частные производные | Онлайн калькулятор

Калькулятор Частичных Производных — Mathcracker.Com

Инструкции: Используйте этот калькулятор частичных производных для нахождения производной функции более чем одной переменной, которую вы задаете относительно конкретной переменной, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже.

О частичной производной

Этот калькулятор позволит вам вычислить частную производную любой действительной дифференцируемой функции, которую вы предоставите, относительно заданной переменной.

Функция, которую вы предоставляете, должна сопровождаться определением функции, например f(x, y) = x^3 + y^2. 2 без полного определения, будет считаться, что предоставлена функция двух переменных x и y.

Как только вы зададите действительную дифференцируемую функцию и действительную переменную, следующим шагом будет нажатие на кнопку «Вычислить», после чего будут показаны все этапы процесса, со всеми используемые производные правила , прямо указано.

Деривативы и их естественное расширение до частных производных по нескольким переменным являются одними из самых важных предметов изучения в математике. Это связано с тем, что они имеют дело со скоростью изменения и течением многих моделей, которые часто появляются в приложениях.

Что такое частичная производная?

Проще говоря, частичная производная состоит в том, чтобы провести то же самое, что и обычное дифференцирование относительно одной переменной, предполагая, что остальные переменные постоянны.

Если бы мы хотели формально определить частичную производную, давайте упростим задачу и сделаем это для функции двух переменных, \(x\) и \(y\). Частная производная по отношению к \(x\) в точке \((x_0, y_0)\) имеет вид

\[\frac{\partial f}{\partial x}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h, y_0) — f(x_0, y_0)}{h} \]

Итак, как мы видим, по сути это то же самое, что и определение обычной производной, только здесь есть еще одна переменная, но она остается постоянной в процессе вычисления.

Аналогично, частная производная по отношению к \(y\) в точке \((x_0, y_0)\) равна

\[\frac{\partial f}{\partial y}(x_0, y_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0, y_0 + h) — f(x_0, y_0)}{h} \]

Вектор всех частных производных называется градиентом. Если вам нужно действительно получить все частные производные, вы можете использовать следующее градиентный калькулятор .

Шаги для вычисления частных производных

• Шаг 1: Определите функцию, частную производную которой вы хотите вычислить. Не забудьте сначала упростить ее
• Шаг 2:
  Обратите внимание, что не все функции дифференцируемы, поэтому вам нужно убедиться, что функция, о которой идет речь, действительно дифференцируема
• Шаг 3: Используйте все соответствующие правила производной для функции и дифференцируйте функцию, как обычно, по дифференцируемой переменной, а любую другую переменную считайте постоянной

Таким образом, когда мы выполняем частичную производную по x для чего-то вроде ‘x^2+y^2’, в процессе частичного дифференцирования по x переменная y рассматривается как константа. 2)}{\partial x} = 0\), поскольку y предполагается постоянным относительно x.

Зачем использовать калькулятор частных производных

Вычисление частных производных может быть относительно простым упражнением, но это не значит, что оно обязательно будет легким. Важно быть очень систематичным во время применения соответствующего Правила производных .

Использование калькулятора частичных производных с шагами может помочь вам, по крайней мере, проверить результат и точно увидеть, какие шаги являются правильными и какие правила вычисления производных необходимо использовать.

Особенно в сложных задачах, с алгебраически сложными выражениями калькулятор действительно может пригодиться.

Каковы правила производных для частичных производных?

Они точно такие же, как и для обычных производных. Для частных производных у нас есть линейность, а также Правило Продукта , Правило цепи и Правило квоты . Как правило, для более сложных примеров производных вы в конечном итоге будете использовать комбинацию всех этих правил.

Что такое неявная дифференциация

Существует ситуация, когда задействовано более одной переменной, в которой мы не предполагаем, например, что y изменяется с x, как это делается в частных производных. В некоторых случаях, когда есть уравнение, связывающее переменные, мы предполагаем наличие неявной зависимости между y и x, и пишем y = y(x).

Это контекст неявное дифференцирование это своего рода гибрид между частичной и обычной дифференциацией.

И есть одна вещь, которую невозможно переоценить: Частичные производные действительно являются одним из основных инструментов, используемых в инженерии, физике и экономике.

Пример: вычисление частичной производной

Вычислите частную производную \(\frac{\partial f}{\partial y}\) для: \(f(x,y) = \sin(xy)\)

Решение:

чем завершается расчет. 2}\)

Другие калькуляторы calculus

Понятие производной находится в центре Calculus, а использование производный калькулятор может значительно помочь вам во многих различных приложениях Calculus, включая оптимизацию, одну из самых «больших».

Идея производной естественно распространяется на случай функции со многими переменными, где a Калькулятор частичных производных будет делать то же самое, что и обычная производная, но теперь предполагается, что изменяется только одна переменная, в то время как другие переменные принимаются фиксированными.

Часто бывает так, что известно, что \(y\) зависит от \(x\), но не явно, а скорее неявно, с помощью уравнения связи, в этом случае можно использовать неявное дифференцирование использовать правила производных, чтобы получить выражение, для которого затем можно решить производную \(\frac{d f}{d x}\) .

x y производная по x

Вы искали x y производная по x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление частных производных онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x y производная по x».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x y производная по x,вычисление частных производных онлайн,как найти частную производную,как найти частные производные,калькулятор производных нескольких переменных онлайн,калькулятор производных онлайн нескольких переменных,калькулятор функции нескольких переменных онлайн,калькулятор частной производной онлайн,калькулятор частные производные,калькулятор частных производных,калькулятор частных производных онлайн,матпрофи частные производные,найти частную производную,найти частную производную онлайн,найти частные производные,найти частные производные второго порядка онлайн,найти частные производные второго порядка онлайн калькулятор,найти частные производные онлайн,найти частные производные онлайн с решением,найти частные производные первого порядка,найти частные производные первого порядка онлайн с решением,найти частные производные функции,найти частные производные функции онлайн с решением,нахождение частной производной онлайн,нахождение частных производных,нахождение частных производных онлайн,онлайн вычисление частных производных,онлайн калькулятор производные высших порядков,онлайн калькулятор производных нескольких переменных,онлайн калькулятор функции нескольких переменных,онлайн калькулятор частной производной,онлайн калькулятор частные производные,онлайн калькулятор частных производных,онлайн нахождение частных производных,онлайн решение частных производных,онлайн частные производные функции,по x по y,примеры частная производная,примеры частные производные,производная x y по y,производная двух переменных,производная двух переменных онлайн,производная нескольких переменных,производная онлайн двух переменных,производная онлайн от двух переменных,производная онлайн по x и y,производная от двух переменных,производная от двух переменных онлайн,производная по x и y онлайн,производная функции двух переменных,производная функции двух переменных онлайн,производное частное,производные частные примеры,решение онлайн частных производных,решение частных производных,решение частных производных онлайн,таблица частных производных,функции нескольких переменных калькулятор онлайн,функции нескольких переменных онлайн калькулятор,функции нескольких переменных частные производные,частная производная,частная производная онлайн,частная производная онлайн калькулятор,частная производная функции,частная производная что такое,частная производная это,частное производное,частные производные,частные производные 2 порядка,частные производные второго порядка,частные производные второго порядка онлайн,частные производные второго порядка онлайн калькулятор,частные производные для чайников,частные производные калькулятор,частные производные калькулятор онлайн,частные производные матпрофи,частные производные онлайн,частные производные онлайн калькулятор,частные производные онлайн калькулятор с подробным решением,частные производные первого и второго порядка,частные производные первого порядка,частные производные первого порядка калькулятор онлайн,частные производные первого порядка онлайн калькулятор,частные производные примеры,частные производные примеры с решением,частные производные функции,частные производные функции двух переменных,частные производные функции нескольких переменных,частные производные функции онлайн,частные производные функции с тремя неизвестными,что такое частная производная.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x y производная по x. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти частную производную).

Решить задачу x y производная по x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор частных производных с шагами онлайн

Введение в калькулятор частных производных

Калькулятор частных производных с шагами находит производную кривой с многочисленными переменными онлайн. Этот калькулятор частных производных имеет возможность многократно дифференцировать функцию.

Измерение скорости изменения функции по отношению к одной переменной известно в математике как частные производные. Он обрабатывает такие переменные, как x и y, такие функции, как f(x), и модификации переменных x и y.

С калькулятором частных производных вы можете узнать о частных производных по цепному правилу и многое другое. Чтобы легко получить производные, можно воспользоваться бесплатным онлайн-калькулятором частичного дифференцирования.

Связанный: Вы также можете найти калькулятор неявного дифференцирования и калькулятор производных второго порядка, чтобы еще больше закрепить свои представления о производных и их вычислениях.

Процесс использования калькулятора частных производных второго порядка

Калькулятор частных производных вычисляет частную производную функции путем деления функции на части. Ниже приведен процесс использования калькулятора частичного дифференцирования с пошаговыми инструкциями.

Как вводить:

• Сначала напишите функцию дифференцирования или выберите из примеров.
• Теперь из выпадающего списка выберите производную переменную.
• Затем решите, сколько раз нужно дифференцировать данную функцию.
• Нажмите кнопку расчета, чтобы увидеть результаты.

Калькулятор второй частной производной мгновенно покажет вам пошаговые результаты и другие полезные показатели.

Вы также можете найти калькулятор производной по направлению для расчета производных по направлению.

Как калькулятор частичной дифференциации показывает выходные данные?

Первый калькулятор частных производных использует правила производных и формулы для вычисления частной производной этой функции.

В результатах он показывает вам производную (только для вычисления производной функции используйте калькулятор производной функции на домашней странице. Помимо этого калькулятор второй частной производной показывает вам возможные промежуточные шаги, трехмерные графики, альтернативные формы, правила, расширение ряда и неопределенный интеграл.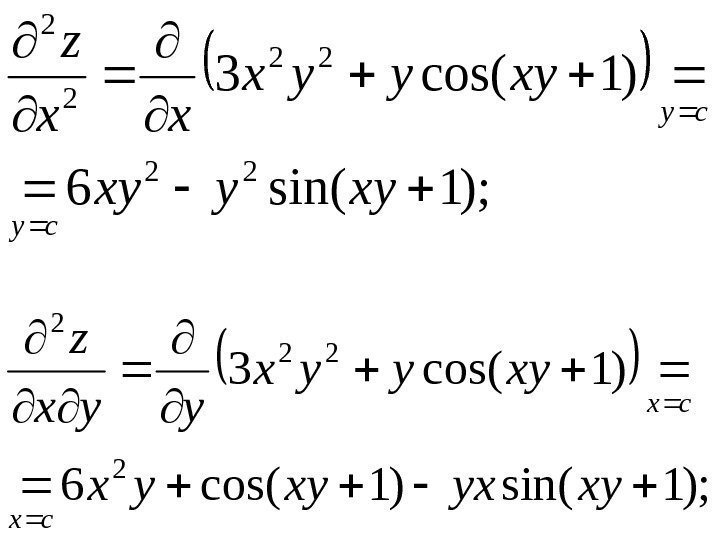 Вы также можете использовать неопределенный интеграл с шагами для большего обучения и практики.0007

Формулы, используемые калькулятором частных производных

Частная производная функции f(x,y) частично зависит от «x» и «y». Таким образом, формула для частной производной функции f(x,y) по x:

$$ \frac{∂f}{∂x} = \frac{∂f}{∂u}\frac{∂ u}{∂x} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂x} $$

Аналогично, частная производная функции f(x,y) по y:

$$ \frac{∂ f}{∂y} = \frac{∂f}{∂u}\frac{∂u}{∂y} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂y} $$ 94) $$

Заключение:

Калькулятор частичного дифференцирования представляет собой веб-инструмент, который работает с математическими функциями и несколькими переменными. Благодаря этому становится легко решать и вычислять функции частичного дифференцирования. Решатель частичного дифференцирования показывает вам различные метрики и детали, необходимые для изучения этой концепции.

Связанный: На этом веб-сайте вы также можете найти калькулятор локальной линеаризации для нахождения линейной аппроксимации.

Кроме того, изучите различные способы нахождения производной функции из этих руководств.

Часто задаваемые вопросы

Каковы преимущества использования калькулятора первой частной производной?

Одним из основных преимуществ этого калькулятора является точность. Если вы находите производные вручную, возможно, вы застрянете посреди математической задачи и не сможете избавиться от нее в течение часа. Если вы используете инструмент частной производной, он дает точный результат одним щелчком мыши.

Что такое цепное правило в дифференциальных уравнениях?

Согласно цепному правилу производная f (g (x)) равна f'(g (x)) g’ (x). Частные производные Калькулятор использует цепное правило для дифференциации составных функций.

Также на этом веб-сайте можно найти калькулятор цепного правила с несколькими переменными, чтобы найти производную от композиции двух дифференцируемых функций.

Чем полезен тест частной производной второго порядка?

Вы можете использовать частные производные второго порядка, чтобы определить, является ли местоположение локальным максимумом, минимумом или седловой точкой.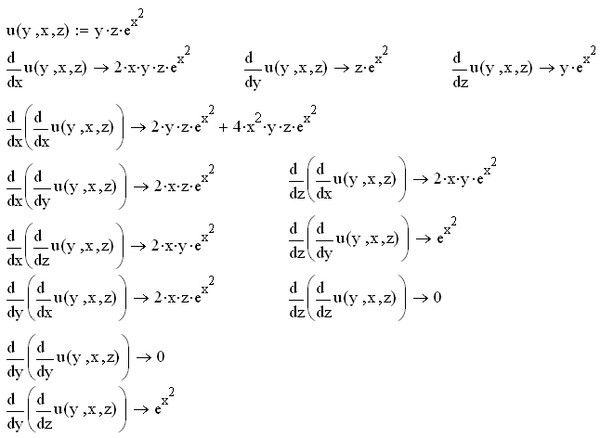 Как только вы нашли нулевой наклон вектора многомерной функции, это указывает на то, что касательная плоскость графика в этой точке гладкая.

Мы надеемся, что приведенный выше калькулятор поможет вам в ваших расчетах. Существуют и другие связанные инструменты, такие как решатель правил продукта и калькулятор производных частных, которые вы можете использовать для большей практики и обучения.

Уравнения в частных производных сложные?

Да, уравнения в частных производных решить сложно. Но когда эти уравнения преобразуются в обыкновенные дифференциальные уравнения, мы можем вычислять их другими методами или с помощью калькулятора в частных производных.

В чем разница между обыкновенными дифференциальными уравнениями и уравнениями в частных производных?

Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, в которых производные берутся по одной независимой переменной. Принимая во внимание, что дифференциальные уравнения в частных производных (УЧП) — это те уравнения, в которых производные берутся по более чем одной переменной.

Что такое частные производные первого порядка?

Производная функции многих переменных по независимой переменной один раз известна как частная производная первого порядка. В частной производной мы дифференцируем функцию с одной переменной, рассматривая другую как константу. Мы можем использовать калькулятор частных производных первого порядка, чтобы решить их онлайн.

Что такое непрерывные частные производные первого порядка?

Частная производная непрерывной функции известна как непрерывная частная производная, если производная также является непрерывной. Но для непрерывной функции вовсе не обязательно, чтобы ее производная также была непрерывной.

Что такое эллиптические уравнения в частных производных?

Уравнение в частных производных второго порядка (УЧП)

Au _xx +2Bu _xy +Cu _yy +Du _x +Fu _y +G=0 считается эллиптическим, если B ² −AC < 0. Эллиптические уравнения в частных производных не имеют вещественных характеристических поверхностей.

Вы можете использовать приведенный выше калькулятор уравнений в частных производных, чтобы решить свои уравнения онлайн.

Что такое цепное правило частичной дифференциации?

Частичное дифференцирование по цепному правилу — это метод, в котором мы дифференцируем функцию одновременно по двум или трем переменным.

Для функции f=f(u,v), u=u(x,y) и v=v(x,y) цепное правило

$$ \frac{df}{dx} \;= \; \frac{df}{du}\frac{du}{dx} \;+\; \frac{df}{dv}\frac{dv}{dx} $$

А,

$$ \frac{df}{dy} \;=\; \frac{df}{du}\frac{du}{dy} \;+\; \frac{df}{dv}\frac{dv}{dy} $$

Используйте калькулятор частных производных по цепному правилу, чтобы шаг за шагом дифференцировать частное дифференцирование по цепному правилу онлайн.

Калькулятор производных с шагами | Калькулятор дифференцирования

Знакомство с калькулятором производных с шагами

Исчисление — это раздел математики, который имеет дело с двумя основными понятиями: интегрированием и дифференцированием. Дифференцирование — это процесс нахождения скорости изменения функции по отношению к ее входной переменной. Это процесс, обратный интегрированию, то есть нахождению площади под кривой.

Расчет деривативов может быть техническим и требует надлежащего внимания и внимания. К счастью, калькулятор производных — это онлайн-инструмент, который предоставляет полное решение для дифференцирования. Калькулятор дифференциации с пошаговыми инструкциями помогает пользователям быстро и легко рассчитывать деривативы всего за несколько кликов.

Онлайн-калькулятор производной предоставляет полезные результаты в виде шагов, которые помогают пользователям и особенно студентам подробно изучить эту концепцию. Пошаговые решения, предоставляемые калькулятором производных, также могут помочь пользователям понять правила и формулы, используемые при дифференцировании.

Помимо калькулятора дифференцирования, существуют и другие инструменты, такие как калькулятор второй производной, калькулятор третьей производной, калькулятор неявной дифференцировки и многие другие.

С помощью калькулятора производных и других связанных инструментов и ресурсов, доступных на нашем веб-сайте, пользователи могут глубже понять исчисление и то, как оно используется в реальных приложениях. Итак, будь вы студентом, профессионалом или просто любителем математики, на нашем сайте есть, что вам предложить.

Чтобы максимально эффективно использовать наш веб-сайт и его инструменты, мы рекомендуем вам изучить все доступные ресурсы и узнать как можно больше об исчислении и дифференцировании.

Формулы, используемые онлайн-калькулятором производных

Калькулятор производных обратных функций использует приведенную ниже формулу для нахождения производных функции. Формула производной:

$$ \frac{dy}{dx} = \lim\limits_{Δx \to 0} \frac{f(x+Δx) — f(x)}{Δx} $$

Помимо стандартной формулы производной, существует множество других формул, с помощью которых можно найти производные функции. Эти расчетные формулы таковы:

$$ \frac{d}{dx}(Sin x) = Cos x $$ $$ \frac{d}{dx}(Cos x) = -Sin x $$ $$ \frac {d}{dx}(tan x) = Sec^2 x $$ $$ \frac{d}{dx}(Csx x) = -Csc x Cot x $$ $$ \frac{d}{dx}( Sec x) = Sec x Tan x $$ $$ \frac{d}{dx}(Cot x) = -Csc^2 x $$

Правила производных, используемые калькулятором дифференцирования

С помощью производной мы можем найти наклон функции в любой заданной точке. Правила дифференцирования используются для вычисления производной функции. Наиболее важные правила дифференцирования:

$$ \frac{d}{dx} (f(x) \pm g(x)) = \frac{d}{dx}f(x) \pm \frac{d }{dx}g(x) $$

• Производная константы:
• $$ \frac{d}{dx}(константа) = 0 $$
• Силовое правило: 9{n-1} $$
• Постоянное множественное правило:
• $$ \frac{d}{dx}[cf(x)] = c. \frac{d}{dx}f(x) $$

  Здесь c = реальное число

• Правило суммы и разности:
• Правило продукта:
• $$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x) \frac{d}{dx}[g(x)] + g(x) \frac{ d}{dx}[f(x)] $$

  или

  $$ \frac{d}{dx}[f(x) \cdot g(x)] = f(x)g'(x) + g(x)f'(x) $$

  Вы также можете использовать калькулятор производных правил произведения для обучения и практики. 92} $$

  Также найдите калькулятор производной частного правила для более точных вычислений.

Этот веб-сайт предоставляет полное решение для дифференцирования и всех расчетов, связанных с деривативами. Найдите калькулятор частичной дифференцировки и калькулятор производной по направлению на этом веб-сайте, чтобы еще больше укрепить свои представления о дифференцировании.

Как работает калькулятор производных?

Калькулятор производных — это онлайн-инструмент, который использует формулы и правила производных для вычисления точных результатов. Инструмент позволяет пользователям вводить данные в виде уравнения, которое можно вводить в различных форматах, включая стандартную алгебраическую запись, запись функции или даже графическое представление.

После ввода уравнения калькулятор производной применяет различные правила или формулы производных для его решения и вычисления производной. Эти правила и формулы могут включать правило мощности, правило произведения, правило частного и многие другие.

Калькулятор производных также предоставляет пошаговые решения, которые могут помочь пользователям понять процесс расчета производных. Это может быть особенно полезно для студентов, изучающих исчисление и нуждающихся в практике решения задач и понимания правил и формул, используемых при дифференцировании.

В целом, калькулятор производных является простым в использовании и эффективным инструментом, который поможет вам быстро и точно рассчитать производные. Используя этот инструмент, вы можете сэкономить время и сосредоточиться на понимании концепций, лежащих в основе дифференцирования, вместо того, чтобы тратить часы на вычисление производных вручную.

Как найти калькулятор производной с шагами?

Онлайн-калькулятор производных найти несложно. Вы можете либо ввести полный URL-адрес этого калькулятора дифференцирования в вашей поисковой системе или вы можете выполнить поиск в Google по его имени. Вы можете выполнить поиск в Google с помощью «калькулятора производной» или «калькулятора обратной производной», и вы найдете наш новейший и точный онлайн-инструмент.

Связанный: На этой платформе вы также можете найти аппроксимацию касательной с помощью калькулятора линеаризации. Вы также можете получить большую помощь от бесплатного онлайн-калькулятора производных цепного правила.

Как использовать калькулятор производных с шагами?

Наша 9Калькулятор дифференциации 0005 очень прост в использовании, так как вам необходимо следовать приведенной ниже процедуре:

1. Напишите свое уравнение в первом поле ввода или загрузите любое уравнение, нажав на кнопку.
2. Выберите переменную, которую хотите дифференцировать.
3. Выберите, сколько раз вы хотите различать.
4. Нажмите кнопку «РАССЧИТАТЬ».

Сразу после нажатия на кнопку расчета наш калькулятор дифференцирования решит ваше уравнение и предоставит подробные результаты. Эти результаты помогут вам понять и изучить концепцию, практикуясь во время выполнения.

Для того, чтобы закрепить ваши расчеты относительно нормальной линии уравнения, вам нужно попробовать калькулятор уравнения нормальной линии, предлагаемый этим веб-сайтом.

Связанные калькуляторы

Существует множество других калькуляторов, связанных с дифференциальным калькулятором, которые вы можете использовать на этом веб-сайте бесплатно. Эти инструменты:

• Калькулятор производной в точке
• Калькулятор крайних точек
• Калькулятор уклона криволинейной линии
• Калькулятор производных графиков
• Калькулятор производной касательной прямой
• Калькулятор второго неявного дифференцирования
• Определение калькулятора производной

Часто задаваемые вопросы

Как дифференцировать функцию f(x)=5,4x+2,4?

Данная функция:

$$ f(x) \;=\; 5.4x+2.4 $$

Дифференцирование с обеих сторон по ‘x’

$$f'(x) \;=\; d/dx(5.4x+2.4)$$

Имеем,

$$ f'(x) \;=\; d/dx(5.4x)+d/dx(2.4) $$ $$ f'(x) \;=\; 5.4(1)+0 \;=\; 5.4 $$

Таким образом, мы можем различать эту простую функцию вручную. Кроме того, мы также можем использовать дифференциальный калькулятор функций для онлайн-расчетов.

Как вычислить производную функции?

Чтобы вычислить производную функции, необходимо выполнить следующие шаги:

1. Помните, что производная – это вычисление скорости изменения функции.
2. Применить производную к функции по независимой переменной, входящей в функцию.
3. Упростите функцию, чтобы получить точное значение производной.

Та же процедура использовалась калькулятором производных для расчета скорости изменения функции в режиме онлайн.

Что такое производная x?

Производная x равна 1. Она относится к результату, полученному дифференцированием x различными способами. Нахождение скорости изменения функции включает в себя процесс дифференцирования. Таким образом, вы можете найти калькулятор производной для этого процесса. 9⁡2x $$

Производная от cos ² x является производной тригнометрической функции, которая несколько сложна для студентов, которые не могут запомнить тригнометрические тождества. Для таких студентов решатель производных является отличным инструментом для вычисления производной тригонометрической функции.

Как отличить e

^x ?

Поскольку производная экспоненциальной функции с основанием «e» равна e ^x , дифференцирование e в степени x эквивалентно самому e в степени x.