СРОЧНО!!построить график: y=3sinx-2 — Знания.site
Ответы 6
Всё дошло
ну сейчас можно
ну что получается?
Красный график — 3*sin(x), синий график — искомый.
Знаешь ответ? Добавь его сюда!
Последние вопросы
- Геометрия
46 минут назад
Помогите пожалуйста с геометрией срочно
- Математика
13 часов назад
84 баллов в скайсмарте ,это 5 или 4? - Геометрия
15 часов назад
Из вершины развернутого угла АВС проведен луч ВК и проведена биссектриса ВМ угла АВК. Найдите угол АВМ, если угол СВК равен 54о
- Геометрия
17 часов назад
Посогите пожалуйста с геометрией срочно
- ОБЖ
18 часов назад
8.
Наиболее частые заболевания, связанные с сосудосуживающим действием никотина:a) Инфаркт миокарда б) Переживающая хромота или гангрена конечности
b) Кровоточивость из носа и ушей г) Расширение вен нижних конечностей д) Гипотония
- Математика
20 часов назад
20.000 — 282 x 750 / 47 + 989 пожалуйста помогите мне
- Химия
22 часов назад
определить массу 5,6 л. Аргона при давлении 202,6 кПа и t27 градусов Цельсия . Решить задачу двумя способами
- Физика
23 часов назад
Металлическое тело кубической формы со стороной 10 см плавает в резервуаре с ртутью. В резервуар налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью тела.
Рассчитай высоту столба налитой в резервуар жидкости.Справочные данные: плотность металла — 11350 кг/м³, плотность ртути — 13600 кг/м³, плотность жидкости — 1030 кг/м³. (Ответ округли до десятых.)
- Физика
1 день назад
Металлический предмет кубической формы со стороной 40 см плавает в сосуде с ртутью. В сосуд налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью предмета. Рассчитай высоту столба налитой в сосуд жидкости. Справочные данные: плотность металла 7800 кг/м³, плотность ртути 13600 кг/м³, плотность жидкости — 1000 кг/м³.
(Ответ округли до десятых.)
- Математика
1 день назад
Маша кормит собачек
У Маши три собачки Диди, Мими и Фифи. Диди весит 3 кг, Фифи 3,5 кг, а Мими 4,5 кг.
Всего у Маши 33 кг корма на месяц для собачек. Она хочет пересыпать корм в коробки пропорционально весу каждой собаки. Сколько корма в какую коробку она должна пересыпать? Ответы дайте в килограммах.
- Физика
1 день назад
Металлический предмет кубической формы со стороной 30 см. плавает в резервуаре с ртутью. В резервуар налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью предмета. Найди высоту столба налитой в резервуар жидкости. Справочные данные: плотность металла 2700 кг/м², плотность ртути — 13600 кг/м³, плотность жидкости — 1000 кг/м³.
(Ответ округли до десятых.)
- Другие предметы
1 день назад
Что это означает?
- Математика
2 дня назад
сторона правильной треугольной пирамиды равна 8 найдите площадь полной поверхности пирамиды если ее апофема равна корень 8 из 3
- Математика
2 дня назад
сторона правильной треугольной пирамиды равна 8 найдите объем пирамиды если ее апофема равна 13
2 дня назад
два ребра прямоугольного паралепипеда выходящие из одной вершины равны 72 и 18 найти объем
Наиболее частые заболевания, связанные с сосудосуживающим действием никотина:
Рассчитай высоту столба налитой в резервуар жидкости.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | cos(45 градусов) | ||
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | 30 | ||
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Производная от 3 sin x: формула, доказательство, примеры, решение
Введение в производную от 3sin x
Производные находят широкое применение практически во всех областях техники и науки.
Производную от 3sin x можно вычислить, следуя правилам дифференцирования. Или мы можем напрямую найти производную 3sinx, применив первый принцип дифференцирования. В этой статье вы узнаете, что такое производная от 3sin x и как вычислить дифференцирование 3sin x, используя различные подходы.
Что является производным от 3sinx?
Производную 3sin x по переменной x можно рассчитать по формуле d/dx (3sin x) = 3cos x. Эта формула представляет скорость изменения тригонометрической функции sin x, которая широко используется в геометрии и математике. На самом деле sin x представляет собой отношение противоположной стороны треугольника к его гипотенузе, что делает его фундаментальным понятием в тригонометрии. Поняв, как дифференцировать 3sin x, вы сможете лучше понять, как изменения переменной x влияют на значение функции.
Производная формулы 3 sin x
Формула производной 3sinx:
d/dx(3sinx) = 3cosx.
Это означает, что скорость изменения функции 3sinx по переменной x равна функции косинуса x, умноженной на 3.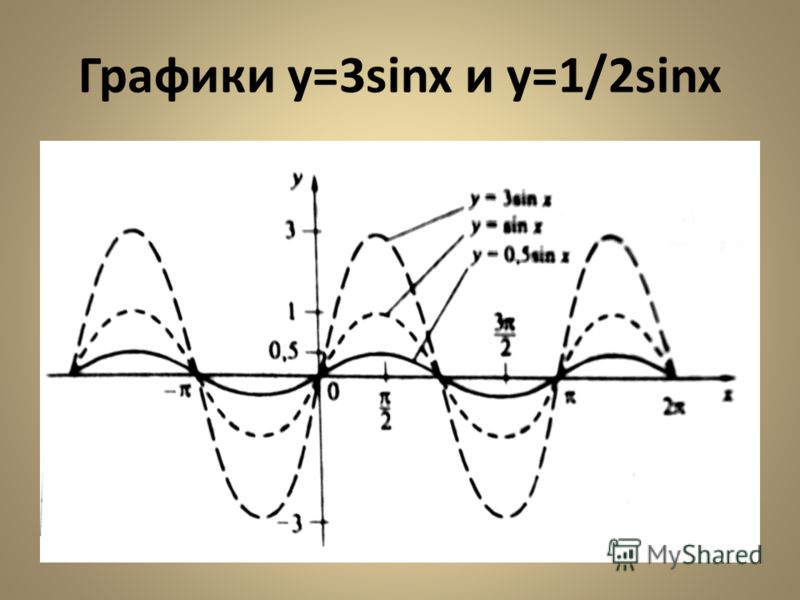
Зная эту формулу, вы можете легко вычислить производную 3sinx, что полезно при решении много математических задач.
Связанный: Найдите больше концепций исчисления и узнайте больше.
Как доказать производную от 3 sinx?
Существуют различные способы доказательства дифференцирования 3sin x. Это;
Первый принцип
Цепное правило
Частное правило
Каждый метод предлагает свой способ вычисления дифференцирования 3sin x. Используя эти методы, мы можем математически доказать формулу нахождения дифференциала 3sin x.
Производная 3sin x по первому принципу
Согласно первому принципу производной производная 3sin x равна 3cos x. Производная функции по первому принципу относится к нахождению общего выражения для наклона кривой с помощью алгебры. Он также известен как дельта-метод. Производная является мерой мгновенной скорости изменения, которая равна
f(x) = lim f(x+h)-f(x) / h
Эта формула позволяет определить скорость изменения функции в определенной точке с помощью предельного определения производной.
Доказательство производной 3 sin x по первому принципу
Чтобы доказать производную 3sin(x) по первому принципу, замените f(x) на 3sin x.
f(x) = lim h→0 f(x+h) — f(x) / h
f(x) = lim 3sin (x+h) — 3sin x / h
Кроме того, вы можно заменить f(x) на sin(2x) для вычисления производной от sin(2x). Следовательно,
f(x) = lim 3[sin(x+h) — sin x] / h
Теперь по тригонометрической формуле sin A cos B + cos A sin B = sin (A + B)
f(x) = lim 3[sin x cos h + cos x sin h — sin x] / h
f(x) = lim 3[-sin x(1 — cos h) + cos x sin h] / h
Теперь, используя формулу половинного угла, 1- cos h = 2 sin 2 (h / 2), приведенное выше уравнение записывается как:
f(x) = (- sin x) { lim [(2 sin 2 (h / 2))] / h} + (cos x) {lim (sin h) / h}
f(x) = (-sin x) [lim (sin(h /2))/(ч/2). Lim sin (h/2)] + (cos x) {lim (sin h)/h}
Как известно,
Lim (sin x/x) = 1, получаем
f(x) = — sin x (1.
sin (0 / 2)) + cos x (1)
f(x) = — sin x(0) + cos x
f(x) = cos x
Производная 3sin(x) по цепному правилу
Чтобы вычислить дифференциацию 3sin x, мы можем использовать цепное правило, поскольку функция косинуса может быть выражена как комбинация двух функций. Цепное правило производных гласит, что производная сложной функции равна производной внешней функции, умноженной на производную внутренней функции. Цепное правило производных определяется как;
dy / dx = dy / du x du / dx
Где u=g(x), y=f(u), dy/du — производная от f(u) по u и du/dx является производной от g(x) по x.
Доказательство производной 3sin x по цепному правилу
Чтобы доказать производную 3sin x по цепному правилу, предположим, что sin x можно записать как sin x = cos (π / 2 — x). Используя это, найдем дифференцирование 3sinx.
Мы можем дифференцировать 3 sin x, используя цепное правило,
y = — 3sin(π / 2 — x) . д/дх (π/2 — х)
= — 3sin(π / 2 — x) .
(-1)
= 3sin(π / 2 — x)
= 3cos x
Таким образом, мы получили формулу производной 3sin x по цепному правилу.
Вы также можете использовать калькулятор цепных правил с шагами и получать пошаговые результаты.
Производная 3sin x с использованием правила отношения
Другой метод нахождения производной 3sin x — использование правила отношения, которое представляет собой формулу для нахождения производной отношения двух функций. Поскольку функция sin является обратной величиной косеканса, производная 3sin x может быть также рассчитана с использованием правила отношения. Частное правило определяется как:
d / dx (f / g) = f(x). g(x) -g(x).f(x) / {g(x)} 2
Доказательство производной 3sin x по правилу частных
Чтобы доказать производную 3sin x, мы можем написать это,
f(x) = 3sin x = 3 / cocec x = u / v
Предположим, что u = 31 и v = 3cosec x. Теперь по правилу частных
f(x) = (vu — uv) / v 2
f(x) = [ccosec x d / dx(3) — 3.
d / dx(cosec x)] / ( cosec x) 2
= [tan x (0) — 1 (-3cosec x cot x)] / cosec 2 x
= (3cosec x.cot x) / cosec 2 x
= 3cos x
Следовательно, мы получили производную от 3sin x, используя частное правило дифференцирования.
С калькулятором частных правил вы можете мгновенно выполнять расчеты.
Как найти дифференцирование 3sinx с помощью калькулятора?
Самый простой способ вычислить производную от 3sin x — использовать онлайн-инструмент. Вы можете использовать наш производный калькулятор с бесплатными шагами для этого. Здесь мы предлагаем вам пошаговый способ расчета производных с помощью этого инструмента.
Запишите функцию как 3sin x в поле ввода функции. На этом шаге вам нужно предоставить входное значение в виде функции, так как вы должны вычислить производную от 3sin x.
Теперь выберите переменную, по которой вы хотите дифференцировать 3sin x. Здесь вы должны выбрать х.
Выберите, сколько раз вы хотите различать 3sin x. На этом шаге вы можете выбрать 2 для второй производной, 3 для третьей производной и так далее.
Нажмите кнопку расчета. После этого шага вы получите производную от 3sinx в течение нескольких секунд.
После выполнения этих шагов вы получите дифференцирование 3sin x в течение нескольких секунд. Использование онлайн-инструментов может значительно упростить и ускорить расчет производных, особенно для сложных функций.
Часто задаваемые вопросы
Что такое первая производная греха?
Производная из первого принципа является мерой скорости изменения функции. Производная от sin x обозначается как d/dx (sin x) = cos x.
Как доказать производную sinx?
Производную sinx можно доказать, используя первый принцип дифференцирования. Первый принцип дифференцирования измеряет мгновенную скорость изменения так, что;
f(x) = lim f(x+h) — f(x) / h
Что такое первые принципы математики?
Аксиомы или постулаты — термины, используемые в математике для описания первых принципов.