Разложить функцию в ряд фурье онлайн с решением: Ряд Фурье онлайн

Разложение в ряд Фурье онлайн

Разложение некоторой функции в тригонометрический ряд Фурье на отрезке имеет вид:

где

Наш онлайн калькулятор находит разложение в ряд Фурье заданной функции с описанием подробного хода решения.

Разложение в ряд Фурье

Переменная функции: xyztupqnms

Порядок разложения: 123456789101112131415161718192021222324252627282930

Тип разложения: по общей формулепо косинусампо синусам

Отрезок разложения: [ , ]

Разложить функцию fxx2в ряд Фурье на отрезке [0,3]по косинусам.Порядок разложения равен 10.

Установить калькулятор на свой сайт

В качестве примера найдём разложение в ряд Фурье для функции на отрезке . В этом случае длина отрезка разложения и коэффициенты , , вычисляются по формулам:

Таким образом, разложение функции в ряд Фурье на отрезке имеет вид:

На рисунке ниже приведено два графика: (красным цветом) и , (синим цветом) для которого мы взяли порядок разложения равным .

Стоит отметить, что в приведенном выше примере, коэффициенты и равны нулю не случайно. Дело в том, что функция является нечётной.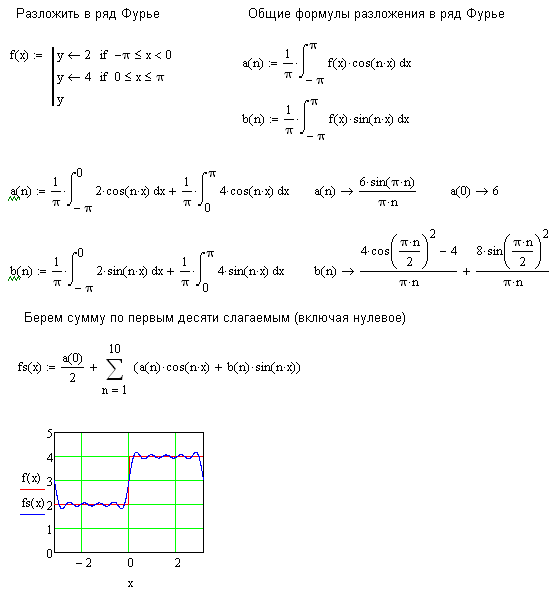

Функция — напротив является чётной. Произведение чётной функции на нечётную является нечётной функцией, поэтому согласно свойствам, определённый интеграл от нечётной функции на симметричном интервале равен нулю.

В случае, если бы мы раскладывали в ряд Фурье на симметричном интервале какую-нибудь чётную функцию, например , коэффициенты равнялись бы нулю, поскольку в этом случае, подынтегральное выражение являлось бы нечётной функцией.

Исходя из приведённых выше рассуждений можно сделать следующие выводы:

Разложение в ряд Фурье нечётной функции на симметричном отрезке будет содержать только слагаемые с синусами.

Разложение в ряд Фурье чётной функции на симметричном отрезке будет содержать только слагаемые с косинусами.

Если нам необходимо получить разложение в ряд Фурье некоторой произвольной функции на отрезке , то у нас есть две возможности. Мы можем продлить эту функцию на отрезок нечётным образом и тогда в разложении получим только синусы. Или же мы можем продлить её на указанный отрезок чётным образом и тогда получим в разложении только косинусы.

Разработанный нами онлайн калькулятор позволяет получать разложение заданной функции в ряд Фурье в общем виде или только по синусам/косинусам, на любом заданном отрезке.

Другие полезные разделы:

Калькулятор сходимости рядов
Обратное преобразование Лапласа онлайн
Преобразование Лапласа онлайн

Оставить свой комментарий:

---

Разложить в ряд Фурье online

‘) window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: rtb_id, blockId: ‘R-A-1616620-2’ }) })

на отрезке

Ввести:

{ кусочно-заданную функцию можно здесь

График:

от до

Приближения:

от до

Примеры разложения в ряд Фурье

• Кусочно-заданные и кусочно-непрерывные функции

• 1 - x при -pi < x < 0
  0 при 0 <= x < pi

• x при -2 <= x < 0
  pi - x при 0 <= x <= 2

• Элементарные функции

• log(1 + x)

• exp(x)

Что умеет калькулятор ряда Фурье?

Вы вводите функцию и период.

• Выполняет преобразование Фурье
• Различные формы и записи ряда:
  • Тригонометрический ряд Фурье
  • Комлексный ряд Фурье
• Находит:
  • Коэффициенты Фурье функции f: $a_0$, $a_n$, $b_n$
  • Амплитуда n-го гармонического колебания $A_n$
  • Комплексный спектр периодического сигнала $\dot A_n$
  • Начальная фаза n-го колебания $θ_n$
  • Угловая частота первой или основной гармоники $ω$
• Строит графики:
  • Самой функции
  • Частичные суммы Фурье

Подробнее про Ряд Фурье.

Указанные выше примеры содержат также:

• модуль или абсолютное значение: absolute(x) или |x|
• квадратные корни sqrt(x),
  кубические корни cbrt(x)
• тригонометрические функции:
  синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
• показательные функции и экспоненты exp(x)
• обратные тригонометрические функции:
  
  арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
• натуральные логарифмы ln(x),
  десятичные логарифмы log(x)
• гиперболические функции:
  гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
• обратные гиперболические функции:
  гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
• другие тригонометрические и гиперболические функции:
  секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x)
• функции округления:
  в меньшую сторону floor(x), в большую сторону ceiling(x)
• знак числа:
  sign(x)
• для теории вероятности:
  функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x)
• Факториал от x:
  x! или factorial(x)
• Гамма-функция gamma(x)
• Функция Ламберта LambertW(x)
• Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)

Правила ввода

Можно делать следующие операции

2*x

— умножение

3/x

— деление

x^2

— возведение в квадрат

x^3

— возведение в куб

x^5

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

Действительные числа

вводить в виде 7. 5, не 7,5

Постоянные

pi

— число Пи

e

— основание натурального логарифма

i

— комплексное число

oo

— символ бесконечности

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Калькулятор ряда Фурье

Этот бесплатный калькулятор ряда Фурье предназначен исключительно для вычисления ряда Фурье заданной периодической функции. Теперь мы решили начать с некоторой базовой теории!

Что такое ряд Фурье?

В математике

« Разложение периодической функции по бесконечным суммам синусов и косинусов называется рядом Фурье».

Формула ряда Фурье:

Взгляните на данную формулу, которая показывает периодическую функцию f(x) в интервале \(-L\le \:x\le \:L\:\) 9Lf\left(x\right)\sin \left(\frac{n\pi x}{L}\right)dx,\:\quad \:n>0 $$

С помощью калькулятора коэффициентов Фурье , вы можете легко найти значения этих коэффициентов.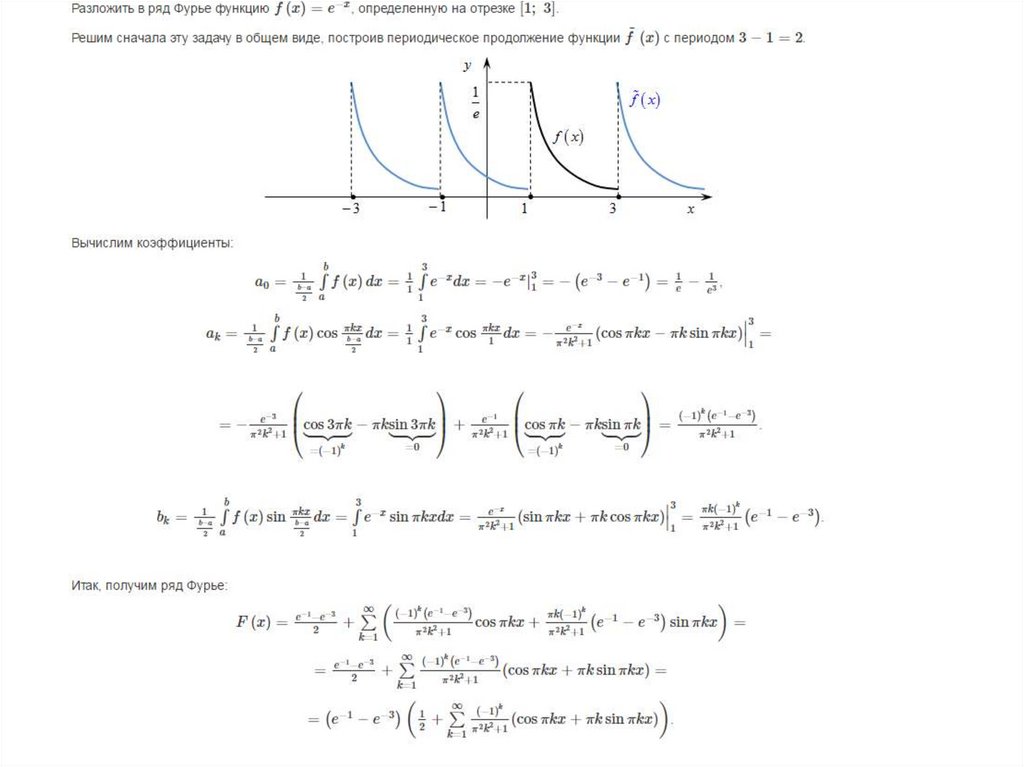 {{\,L}}{{f\ влево( х \вправо)\,dx}} $$ 9{n} \sin{\left(n x \right)}}{n} $$

Даже в этом случае калькулятор коэффициента Фурье поможет вам выполнить определенные расчеты.

Как работает калькулятор рядов Фурье?

Всякий раз, когда вы сталкиваетесь со сложными функциями, наш бесплатный онлайн-калькулятор рядов Фурье поможет вам определить точные результаты. Воспользовавшись нашим калькулятором, вы получите правильный сценарий расчетов.

Введите:

• Сначала напишите свою функцию в выпадающем списке
• После этого выберите переменную, по которой необходимо определить разложение в ряд Фурье
• Ввод нижнего и верхнего пределов
• Нажмите «Рассчитать»

Вывод:

Калькулятор разложения Фурье вычисляет:

• Ряд Фурье заданной функции
• Коэффициенты Фурье функции f: a_{0}, a_{n} и b_{n}
• Пошаговые расчеты, задействованные в процессе

Литература:

Из источника Википедии: Сходимость, Ряды Фурье на квадрате, Интерпретация гильбертова пространства, Свойства, лемма Римана–Лебега, лемма Римана–Лебега.

Разброс Фурье онлайн

на сегменте

Введите:

{ кусочно-определенная функция здесь

График:

из до

Приблизительно:

от до

Примеры разложения в ряды Фурье

• Кусочно-определенные и кусочно-непрерывные функции

•  1 - х при -пи < х < 0
  0 в 0 <= х < пи 

•  х при -2 <= х < 0
  пи - х в 0 <= х <= 2 

• Элементарные функции

•  журнал(1 + х) 

•  ехр(х) 

Что умеет калькулятор рядов Фурье?

Вы вводите функцию и период.

• Преобразование Фурье (FT)
• Различные виды и записи серии:
  • Тригонометрический ряд Фурье
  • Комплексный ряд Фурье
• Находки:
  • Коэффициенты Фурье функции f : $a_0$, $a_n$, $b_n$
  • Амплитуда n-го гармонического колебания $A_n$
  • Комплексный спектр периодического сигнала $\dot A_n$
  • Начальная фаза n-го колебания $θ_n$
  • Угловая частота первой (или основной) гармоники $ω$
• Графики:
  • Функция
  • Частичные суммы Фурье

Узнайте больше о серии Фурье .