Разложение по строкам при нахождении определителя
Задание №1. Вычислить определитель третьего порядка разложением по строкам.Решение.
Перейти к онлайн решению своего примера
Пример. Рассмотрим все виды разложений по строкам: по первой, по второй и по третьей. Запишем матрицу в виде:
| A = |
|
Минор для (1,1):
Вычеркиваем из матрицы 1-ю строку и 1-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 1,1 = |
Найдем определитель для этого минора.

∆1,1 = (2 • 3-0 • 1) = 6
Минор для (1,2):
Вычеркиваем из матрицы 1-ю строку и 2-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 2,1 = |
Найдем определитель для этого минора.
∆1,2 = (3 • 3-(-2 • 1)) = 11
Минор для (1,3):
Вычеркиваем из матрицы 1-ю строку и 3-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 3,1 = |
Найдем определитель для этого минора.

∆1,3 = (3 • 0-(-2 • 2)) = 4
Определитель исходной матрицы равен
∆ = (2 • 6-3 • 11+(-1 • 4)) = -25
Теперь разложим матрицу по второй строке. Значение определителя матрицы не должно измениться.
Минор для (2,1):
Вычеркиваем из матрицы 2-ю строку и 1-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 1,1 = |
Найдем определитель для этого минора.
Минор для (2,2):
Вычеркиваем из матрицы 2-ю строку и 2-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 2,1 = |
|
Найдем определитель для этого минора.

∆2,2 = (2 • 3-(-2 • (-1))) = 4
Минор для (2,3):
Вычеркиваем из матрицы 2-ю строку и 3-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 3,1 = |
Найдем определитель для этого минора.
∆2,3 = (2 • 0-(-2 • 3)) = 6
Главный определитель:
∆ = (3 • 9-2 • 4+1 • 6) = -25
Скачать решение
Покажем, как происходит разложение по третьей строке. Значение определителя матрицы не должно измениться. Итак, минор для (3,1):
Вычеркиваем из матрицы 3-ю строку и 1-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 1,1 = |
Найдем определитель для этого минора.

∆3,1 = (3 • 1-2 • (-1)) = 5
Минор для (3,2):
Вычеркиваем из матрицы 3-ю строку и 2-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 2,1 = |
Найдем определитель для этого минора.
∆3,2 = (2 • 1-3 • (-1)) = 5
Минор для (3,3):
Вычеркиваем из матрицы 3-ю строку и 3-й столбец.
| 2 | 3 | -1 |
| 3 | 2 | 1 |
| -2 | 0 | 3 |
Получаем:
| ∆ 3,1 = |
Найдем определитель для этого минора.

∆3,3 = (2 • 2-3 • 3) = -5
В итоге, главный определитель матрицы равен
∆ = (-2 • 5-0 • 5+3 • (-5)) = -25
Выводы. Как видим, значение определителя матрицы не зависит от способа его вычисления.
Пример №2. Является ли система арифметических векторов e1=(9;6;0),e2=(6;16;18),e3=(0;-10;-15) линейно независимой? Ответ обоснуйте.
Решение. Находим определитель матрицы. Если он отличен от нуля, то система, составленная из векторов, линейно независима. Если определитель равен нулю, система является линейно зависимой.
Матрицы и определители — презентация онлайн
Похожие презентации:
Определители. Свойства определителей
Определители. Свойства определителей
Линейная алгебра. Матрицы и действия над ними
Матрицы и определители
Обратная матрица
Определитель и его свойства. Обратная матрица
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Матрицы и определители
Матрицы и определители
Матрицы, определители, Формулы Крамера
1. Матрицы и определители
Преподаватель:Мокляк Денис Сергеевич
Матрицей размера m x n называется
прямоугольная таблица чисел,
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются
элементами матрицы.
Обозначение:
A
— матрица размерности m x n
a ij
— элемент матрицы i –ой строки и j -го
столбца,
m n
где
i=1,2…m
j=1,2…n
a11
a21
A ( aij )
m n
…
a
m1
a12
a22
…
am 2
… a1n
… a2 n
… …
… amn
Две матрицы называются равными, если
у них одинаковая размерность и
совпадают строки и столбцы.
Если число строк матрицы равно числу ее
столбцов, то такая матрица называется
квадратной.
0 2
1
A 2 4
5
0 3 1
— квадратная матрица размерности 3х3
Элементы матрицы aij , у которых номер
столбца совпадает с номером строки,
называются диагональными.

Если в квадратной матрице все
диагональные элементы равны 1, а
остальные элементы равны 0, то
она называется единичной.
1
0
E
…
0
0 … 0
1 … 0
… … …
0 … 1
Матрица любого размера называется
нулевой, если все ее элементы равны 0.
0
0
…
0
0 … 0
0 … 0
… … …
0 … 0
Матрица, состоящая из одной строки,
называется матрицей-строкой или
вектором-строкой.
A (a11 a12 … a1n )
Матрица, состоящая из одного столбца,
называется матрицей-столбцом или
вектором-столбцом.
b11
b21
B
b
n1
С
помощью матриц удобно
различного рода зависимости.
Например:
Распределение
экономики:
ресурсов
по
описывать
отраслям
Ресурсы
Промышленность
с/хозяйство
Эл.
энергия
Труд.
ресурсы
Водные
ресурсы
8
7.2
5
3
4.5
5.5
Эту зависимость можно представить в виде
матрицы:
8 7 .
 2
2 A 5
3
3 2
4 . 5 5 .5
Где элемент aij показывает сколько i – го
ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды
потребляет сельское хозяйство.
Чтобы умножить матрицу на число, надо
каждый элемент матрицы умножить на
это число.
Полученные
произведения
итоговую матрицу.
образуют
Пусть дана матрица
A (aij )
m n
Умножаем ее на число λ:
A B
Где каждый элемент матрицы В:
bij aij
Где:
i 1,2…m
j 1,2…n
Например:
Умножая матрицу
2 3 0
A
1 0 4
на число 2, получим:
2 2 3 2 0 2 4 6 0
A 2
1 2 0 2 4 2 2 0 8
Складываются матрицы одинаковой
размерности. Получается матрица той же
размерности, каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.
Пусть даны матрицы
Складываем их:
A (aij )
B (bij )
A B C
Где каждый элемент матрицы С:
cij aij bij
Аналогично проводится вычитание матриц.

Найти сумму и разность матриц:
2 3 0
A
1 0 4
0 2 3
B
1 5 2
2 1 3
A B
2 5 6
2 5 3
A B
0 5 2
Умножение матриц возможно, если число
столбцов первой матрицы равно числу строк
второй.
Тогда каждый элемент полученной матрицы
равен сумме произведений элементов i – ой
строки
первой
матрицы
на
соответствующие элементы j-го столбца
второй.
Пусть даны матрицы
A (aij )
m k
B (bij )
k n
Умножаем их:
A B C
m k k n
m n
Где каждый элемент матрицы С:
cij ai1b1 j ai 2b2 j … aik bkj
i 1,2…m
j 1,2…n
Найти произведение матриц:
2 3 0
A
1 0 4
1 0
B 1 4
0 2
Число столбцов первой матрицы равно
числу строк второй, следовательно их
произведение существует:
2 1 3 1 0 0 2 0 3 4 0 2 5 12
A B
2 3 3 2
1 1 0 1 4 0 1 0 0 4 4 2 1 8
Теперь перемножим матрицы в обратном
порядке:
1 2 0 1 1 3 0 0 1 0 0 4 2 3 0
B A 1 2 4 1 1 3 4 0 1 0 4 4 6 3 16
3 2 2 3
0 2 2 1 0 3 4 0 0 0 2 4 2 0 8
Умножение
матриц
некоммутативно:
в
A B B A
общем
случае
Перечисленные операции над матрицами
обладают следующими свойствами:
1
А+В=В+А
2
(А+В)+С=А+(В+С)
3
λ(А+В)= λА+λВ
4
А(В+С)=АВ+АС
5
А(ВС)=(АВ)С
Матрица АТ называется
транспонированной к матрице А, если
в ней поменяли местами строки
и столбцы.

a11
a21
A
m n
…
a
m1
a12
a22
…
am 2
… a1n
… a2 n
… …
… amn
a11 a21
a12 a22
T
A
n m
… …
a1n a2 n
… am1
… am 2
… …
… amn
1
(АТ)Т=А
2
(А+В)Т=АТ+ВТ
3
(λА)Т= λАТ
4
(АВ)Т=ВТАТ
Транспонировать матрицу:
1 2 3
A 4 5 6
7 8 9
1 4 7
T
A 2 5 8
3 6 9
33. Определители. Свойства определителей.
• Определителем(детерминантом)
матрицы n-го порядка называется число:
n det A
a11
a12
… a1n
a 21
a 22
… a 2 n
…
…
…
a n1
an2
… a nn
…
2
a11
a12
a21 a22
2
a11a22 a12a21
a11
a12
a13
3 a 21
a 22
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a31
a32
a33
a13 a22 a31 a32 a23 a11 a21a12 a33
• Правило Сарруса:
a11
a12
a13
a11
a21 a22
a23
a21 a22
a31
a32
a33
a31
a12
a32
a11a22a33 a12a23a31 a13a21a32
a13a22a31 a11a23a32 a12a21a33
a11
a12
a13
3 a 21
a 22
a 23 a11a 22 a33 a 21a32 a13 a12 a 23 a31
a31
a32
a33
a13a22a31 a32a23a11 a21a12a33
• Правило треугольника:
«+»
«-»
Примеры:
1)
2)
3)
3 2
1
5
3 5 2 1 15 ( 2) 17
cos x sin x
sin x
cos x
cos 2 x sin 2 x cos 2 x
cos x sin x
sin x
cos x
cos x sin x 1
2
2
Примеры:
4)
log 2 32
log 3 27
log 4 16 log 5 125
5 3
2 3
15 6 9
Примеры:
2 4 7
3 1 5 3 1
5 0
7 5 0
4
5)
7
4 ( 1) 7
7 5 5 ( 2) 3 0
5 ( 1) ( 2) 0 5 4 7 3 7
28 175 0 10 0 147 10
42.
 Свойства определителей.1.Определитель не изменится, если его
Свойства определителей.1.Определитель не изменится, если егоT
транспонировать:
det A det A
det A
3
2 4
det A
T
5
12 10 22
3 2
5
4
12 10 22
2.При перестановке двух строк или
столбцов определитель изменит свой
знак на противоположный.
3
5
2 4
2 4
3
5
12 10 22
10 12 22
3. Общий множитель всех элементов
строки или столбца можно вынести за
знак определителя.
a11
ka12
a21 ka22
k
a11
a12
a21 a22
1
2
36 12
1
3
2
1
2
2
1
2
1
24 12 3
1
2 12 2 3
1
1
4
1 3 4
1 3 2
24 2 9 2 1 12 3 24 15 360
4. Определитель с двумя одинаковыми
строками или столбцами равен нулю.
1
1
3
1
1
3
2 1 4
4 3 6 6 3 4 0
5. Если все элементы двух строк (или
столбцов) определителя пропорциональны,
то определитель равен нулю.
3 7
1
2 3
1 2 2 3 1 2 0 0
4 6 2
3 7
1
2 3 1
6.
 Если каждый элемент какого-либо ряда
Если каждый элемент какого-либо рядаопределителя представляет собой сумму
двух слагаемых, то такой определитель
равен сумме двух определителей, в первом
из которых соответствующий ряд состоит из
первых слагаемых, а во втором- из вторых
слагаемых.
a1 j b1 j
… a1n
a21 … a2 j b2 j
… a2 n
…
…
a11 …
…
…
anj bnj
an1 …
…
… ann
a11 … a1 j
… a1n
a11 … b1 j
… a1n
a21 … a2 j
… a2 n
a21 … b2 j
… a2 n
…
…
…
…
…
…
an1 … anj
…
… ann
…
…
an1 … bnj
…
… ann
2 1 4
2
7 2 3 7
7 5 5
60
2 1 4
2 2 4
2 1 4
3 1 3 7 3 3 7 1 3
7 2 3 5
7 2 5
7 3 5
38
98
7. Если к какой-либо строке (или столбцу)
определителя прибавить соответствующие
элементы другой строки (или столбца) ,
умноженные на одно и то же число, то
определитель не изменится.

a11
a12
a21 a22
к
×
a11
a12
ka11 a21 ka12 a22
5 1
0
2
10 0 10
5 1 ×2
0
2
+
5
1
10
0
0 10 10
8.
Треугольный
произведению
диагонали.
a11
0
a21
a22
a31
a32
0
определитель
равен
элементов
главной
a11
a12
a13
0 0
a 22
a 23 a11 a 22 a33
a33
0
0
a33
54. Привести определитель к треугольному виду и вычислить его:
2 1 41 2 4
×(-2) ×(-5)
7 2 3 2 7 3
7 5 5
5 7 5
1
2
4
0
3
5
0 3 15
=
1 2
+
4
5 60
0 0 20
0 3
55. Разложение определителя по элементам строки или столбца.
• Минором Mij элемента aij det Dназывается такой новый определитель,
который
получается
из
данного
вычеркиванием i-ой строки и j-го
столбца содержащих данный элемент.
a11
a12
a13
det D a 21
a 22
a 23
a31
a32
a33
a11
a12
a13
det D a 21
a 22
a 23
a31
a32
a33
M12
M 23
a21 a23
a31 a33
a11
a12
a31 a32
57.
 Для данного определителя найти миноры: М22, М31,М431
Для данного определителя найти миноры: М22, М31,М4312
3
4
0 1
5
2
3
2
1 4
1
1
3 2
2
M 31 1
1
3
4
5
2 36
3 2
1
3
4
M 22 3 1 4 28
1 3 2
1
2
4
M 43 0 1 2 16
3
2
4
• Алгебраическим
дополнением
Aij
элемента aij det D называется минор Mij
этого элемента, взятый со знаком 1 i j
т.е.
Aij 1
i j
M ij
Aij 1
i j
a11
a12
a13
det D a 21
a 22
a 23
a31
a32
a33
A12 1
1 2
M 12 1
A22 1
2 2
M 22
M ij
a21 a23
a31
a33
a11
a13
a31 a33
• Сумма произведений элементов любой
строки (или столбца) определителя на их
алгебраические дополнения равна этому
определителю.
разложение по i-ой строке:
n
det D ai1 Ai1 ai 2 Ai 2 … ain Ain aik Aik , i 1,…, n
k 1
разложение по j-му столбцу:
n
det D a1 j A1 j a2 j A2 j .
 .. anj Anj akj Akj ,
.. anj Anj akj Akj ,k 1
j 1,…, n
62. Разложить данный определитель по элементам: 1) 3-ей строки; 2) 1-го столбца.
12
3
4
0 1
5
2
3
2
1 4
1
1
3 2
63. 1) Разложим данный определитель по элементам 3-ей строки:
1) Разложим данныйэлементам 3-ей строки:
определитель
по
det D a31 A31 a32 A32 a33 A33 a34 A34
a31 1 M 31 a32 1 M 32
4
5
a33 1 M 33 a34 1 M 34
6
7
2
3 1 1
4
3
5
4
1
2 2 1 0
5
3 2
1
1
2
3
4
5
2
1 3 2
4
1
2
1 1 0 1 2 4 1 0 1
6
7
1
1
2
3 36 2 2 4 4 11 56
1
1
3
5
3
65. 2) Разложим данный определитель по элементам 1-го столбца:
2) Разложим данныйэлементам 1-го столбца:
определитель
по
det D a11 A11 a21 A21 a31 A31 a41 A41
a11 1 M 11 a21 1 M 21
2
3
a31 1 M 31 a41 1 M 41
4
5
1
1 1 2
2
1
2
3 1 1
4
1
5
2
2
1 4 0 1 2
3
3 2
3
5
2
2 1 1 1
20 0 3 36 32 56
4
1 4
1 3 2
4
3 2
3
5
2
3
4
5
2
1 4
67.
 Основные методы вычисления определителя.1. разложение определителя по
Основные методы вычисления определителя.1. разложение определителя поэлементам строки или столбца;
2. метод эффективного понижения
порядка;
3. приведение определителя к
треугольному виду.
Метод эффективного понижения порядка:
Вычисление определителя n-го порядка
сводится
к
вычислению
одного
определителя (n-1)-го порядка, сделав в
каком-либо ряду все элементы, кроме
одного, равными нулю.
1
2
3
4 ×(-3) ×(-1)
2
0 1
5
3
2
1 4
1
1
3 2
1
2
3
4
0
1
5
2
0 4 10 8
0
1
6
2
1
2
2
3
4
1
0 1
5
2
0 1 5 1
0
5
4
2
2 2 1
0 1 6 2
4 1 1 2
1
2
5 2
0
1
6 1
5 2 4 14 56
6 1
3 2
0
1 5 1
2
2
71. Вычислить определитель приведением его к треугольному виду.
12
3
4 ×(-3) ×(-1)
2
0 1
5
3
2
1 4
1
1
3 2
1
2
3
4
0
1
5
2
0 4 10 8
0
1
6
2
1
2
2
3
4
1
0 1
5
2
0 1 5 1
0
5
4
2
2 2 1
2
3 2
0 1 5 1 ×2
4
0 2 5 2
+
0 1 6 1
2
5 2
0
1
6 1
2
3
2
0 1
5
1
0
0
15 4
0
0
11 2
1
4
3 2
0
0 1 6 2
1
2
1
4
2
3
1
2
3
0 1 1
5
0 1 1
5
0
0
4 15
0
0
2 11
1
4
2
2
2
3
0 1 1
5
0
0
2
11
0
0
0 7
4
2
0
0
0
0
4 14 56
2 11 ×(-2)
4 15
74.
 Обратная Матрица
Обратная Матрица75. Определение. Матрица называется о б р а т н о й к квадратной матрице , если
A B B A EОбратная матрица обозначается символом
1
1
A
1
A A A A E
Примечание. Операция деления для матриц не
определена. Вместо этого предусмотрена операция
обращения (нахождения обратной) матрицы.
76. Определение. Матрица, составленная из алгебраических дополнений для элементов исходной матрицы , называется с о ю з н о й м а т
Определение. Матрица, составленная изалгебраических дополнений для элементов
исходной матрицы , называется
союзной матрицей.
A11
A A21
A
31
A12
A22
A32
A13
A23
A33
77. Формула для нахождения обратной матрицы
11
T
A
A
det A
A11 A21 A31
1
1
A
A12 A22 A32
det A
A
A
A
13 23 33
79. Алгоритм нахождения
• 1. Находим определительматрицы А. Он должен быть
отличен от нуля.

• 2. Находим алгебраические
дополнения для каждого
элемента матрицы А.
• 3. Составляем союзную
матрицу и транспонируем ее.
• 4. Подставляем результаты
п.1 и п.4 в формулу обратной
матрицы.
A
1
80. Пример. Найти матрицу, обратную к матрице:
1 2A
4
3
Р е ш е н и е. Действуем по алгоритму:
1. Находим определитель матрицы:
1 2
det A =
3 4
= 4- 6 = — 2
Определитель отличен от нуля det A № 0 ,
следовательно, обратная матрица существует.
2. Находим алгебраические дополнения:
A11 = 4
A21 = — 2
A12 = — 3
A22 = 1
3. Составляем союзную матрицу:
~ 4 3
A
2 1
4. Записываем обратную матрицу по
формуле
1
T
1 4
A
A
2 3
det A
1
2
1
86. 5. Проверка
• Воспользуемся определением обратнойматрицы и найдем произведение
1
A A
1 4 2 1 2
2 3 1 3 4
1 4 1 2 3 4 2 2 4 1 2 0 1 0
2 0 2 0 1
2 3 1 1 3 3 2 1 4
87.
 Задача. Найти матрицу, обратную к данной2 1 1
Задача. Найти матрицу, обратную к данной2 1 1 A 3 2 1
1 2 1
88. 1. Находим определитель
2 1 1det A 3 2 1 2 2 1 3 2 1 1 1 1
1 2 1
1 2 1 1 2 2 3 1 1
4 6 1 2 4 3 3 5 2 0.
89. 2. Алгебраические дополнения для первой строки:
2 1A11
2 2 4,
2 1
3 1
A12
3 1 2,
1 1
3 2
A13
6 2 8,
1 2
90. Алгебраические дополнения для второй строки:
1 1A21
1 2 1,
2 1
2 1
A22
2 1 1,
1 1
2 1
A23
4 1 3,
1 2
91. Алгебраические дополнения для третьей строки:
1 1A31
1 2 3,
2 1
2 1
A32
2 3 1,
3 1
2 1
A33
4 3 7.
3 2
92. Обратная матрица:
4 1 31
1
A 2 1 1
2
8
3
7
93. Элементарные преобразования матриц
• перестановка строк (столбцов) местами;• исключение из матрицы строк (столбцов),
состоящих из нулей;
• умножение всех элементов какой-либо строки
(столбца) матрицы на любое число, отличное от
нуля;
• прибавление к одной строке (столбцу) другой,
предварительно умноженной на любое число,
отличное от нуля.

Определение. Э к в и в а л е н т н ы м и называются
матрицы, полученные одна из другой путем элементарных
преобразований.
Важным понятием для матриц является понятие РАНГА.
Существует несколько определений этого понятия. Мы
остановимся на одном из них, основанном на элементарных
преобразованиях.
Определение. Р а н г о м м а т р и ц ы называется
число ненулевых строк в матрице, после приведения ее к
ступенчатому виду (путем элементарных преобразований).
Обозначение. Ранг матрицы будем обозначать r ( A)
или
rang ( A)
.
Теорема. Ранг матрицы не меняется при элементарных
преобразованиях.
English Русский Правила
03. Пример решения Заданий из раздела №1
Задание 1. Для данного определителя найти миноры и алгебраические дополнения элементов . Вычислить определитель : а) разложив его по элементам I-ой строки; б) разложив его по элементам
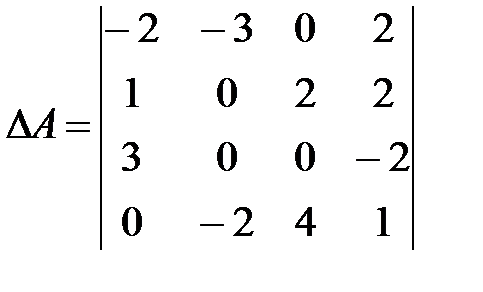
I = 1, J = 2
Решение: 1. Находим миноры к элементам :
Алгебраические дополнения элементов соответственно равны:
2. а). Вычислим определитель, разложив его по элементам первой строки:
Б) Вычислим определитель, разложив его по элементам второго столбца:
В) Вычисли определитель , Получив предварительно нули в первой строке. Используем свойство определителей: определитель Не ИЗмеНиТся, ЕСлИ ко всЕМ эЛеМентам кАКой-либо строки (столбца) прибавить СоотВЕтстВУющие эЛеМЕНтЫ другой строки (столбца), умноженНЫе на одно И то же произвольное число. Умножим третий столбец определителя на 3 и прибавим к первому, затем умножим на (-2) и прибавим ко второму. Тогда в первой строке все элементы, кроме одного, будут нулями. Разложим полученный таким образом опредЕЛитель по элемЕНтам первой строки и вычислим его:
В опрЕДЕЛитЕЛе трЕТьЕГо порядка получили нули в ПеРвом столбце по свойству тому же свойству определителей.
Задание 2.
Даны две матрицы A и B. Найти: а) AB; б) BA; в) ; г) .
Решение: а) Произведение АВ имеет смысл, так как число столбцов матрицы А равно числу строк матрицы В. Находим матрицу С=АВ, элементы которой определяются по формуле . ИмеЕМ:
Б) Вычислим
ОчЕВидНО, что ;
В) Обратная матрица матрицы А имеет виД
,
Где — алгебраическое дополнение, -минор, т. е. определитель полученный из основного определителя вычёркивание i-строки, j-столбца.
,
Т. е. матрица
Тогда
;
Г) Проверка
;
Задание 3. Проверить совместность линейной системы уравнений и в случае совместности решить ее а) по формулам Крамера б) методом Гаусса.
Решение: Совместность данной системы проверим по теореме Кронекера — Капелли. С помощью элементарных преобразований найдем ранг матрицы
С помощью элементарных преобразований найдем ранг матрицы
Данной системы и ранг расширенной матрицы
Для этого умножим первую строку матрицы В на (-2) и сложим со второй, затем умножим первую строку на (-3) и сложим с третьей, поменяем местами второй и третий столбцы. Получим
.
Следовательно, (т. е. числу неизвестных). Значит, исходная система совместна и имеет единственное решение.
А) По формулам Крамера
,
Где -главный определитель, который мы посчитаем, например, по правилу треугольника
,
Аналогично найдем
,
,
,
Находим: .
Б) Решим систему методом Гаусса. Исключим из второго и третьего уравнений. Для этого первое уравнение умножим на 2 и вычтем из второго, затем первое уравнение умножим на 3 и вычтем из третьего:
Из полученной системы находим .
Задание 4
Решить матричное уравнение
Пусть ,
решение матричного уравнения находим по формуле
Х=А -1В, где А -1 обратная матрица
— алгебраическое дополнение, где
— определитель, полученный из основного вычеркивание i-строки, j-столбца, — определитель матрицы.
Найдем обратную матрицу.
(-1)1+14=4
А12=(-1)1+23=-3
А21= (-1)2+12=-2
А22=(-1)2+21=1
DetA==1*4-2*3=4-6=-2
Итак,
Задание 5
Предприятие выпускает три вида продукции, используя сырье трёх видов: . Необходимые характеристики указаны в таблице .
Вид сырья | Нормы расхода сырья на изготовление одного вида продукции, усл. ед. | Расход сырья за один день, усл. ед. | ||
Сапог | Кроссовок | Ботинок | ||
S1 S2 S3 | 5 2 3 | 3 1 2 | 4 1 2 | 2700 900 1600 |
Найти ежедневный объем выпуска каждого вида продукции.
Решение: Пусть ежедневно фабрика выпускает x1 – единиц продукции первого вида, x2 — единиц продукции второго вида, x3 — единиц продукции третьего вида. Тогда в соответствии с расходом сырья каждого вида имеем систему.
Тогда в соответствии с расходом сырья каждого вида имеем систему.
Решаем систему линейных уравнений любым способом. Решим данную систему, например, методом Гаусса. Составим матрицу из коэффициентов стоящих перед неизвестными и из свободных членов.
Обнуляем первый столбец, кроме первого элемента
1. Первую строчку оставляем без изменения
2. Вместо второй записываем сумму первой, умноженной на -2 и второй, умноженной на 5
3. Вместо третьей записываем сумму первой, умноженной на -3 и третьей, умноженной на 5
Аналогично обнуляем второй столбец под элементом второй строки второго столбца
˜˜
Вернемся к системе
Т. е. фабрика выпускает 200- единиц продукции первого вида, 300- единиц продукции второго вида и 200- единиц продукции третьего вида.
Задание 6. Решить однородную систему линейных алгебраических
Уравнений.
Решение: Так как определитель системы
,
То система ИМЕЕт бЕСчисленное множество решений. Поскольку , , возьмем любые два уравнения системы (наПРИМЕР, ПЕрвое И второе) и найдем ее рЕШение. ИмЕеМ:
Поскольку , , возьмем любые два уравнения системы (наПРИМЕР, ПЕрвое И второе) и найдем ее рЕШение. ИмЕеМ:
Так как определитель из коэффициентов при неизвестных и не равен нулю, то в качестве базисных нЕИзвестных ВОзьмЕМ и (хотя можно брать и другие пары нЕИзвЕСтных) И ПеРЕМЕСтим члЕНы с в правые частИ УравнЕНИЙ:
РЕШаЕМ пОСлЕдНюю систЕМу по формулам КрамЕРа :
Где
,
,
.
Отсюда находим, что Полагая , где K—Произвольный коэффициент пропорциональности (произвольная постоянная), получаем решение исходной сИСтЕМы: .
| < Предыдущая | Следующая > |
|---|
Что такое NMF и что с ним можно делать? – От данных к решениям
Что такое NMF?
NMF расшифровывается как неотрицательная матричная факторизация, метод получения низкорангового представления матриц с неотрицательными или положительными элементами. Такие матрицы распространены в различных приложениях, представляющих интерес. Например, изображения — это не что иное, как матрицы положительных целых чисел, представляющих интенсивность пикселей. В информационном поиске и анализе текста мы полагаемся на матрицы терминов-документов для представления коллекций документов. В рекомендательных системах у нас есть матрицы полезности, показывающие предпочтения клиентов в отношении товаров.
Такие матрицы распространены в различных приложениях, представляющих интерес. Например, изображения — это не что иное, как матрицы положительных целых чисел, представляющих интенсивность пикселей. В информационном поиске и анализе текста мы полагаемся на матрицы терминов-документов для представления коллекций документов. В рекомендательных системах у нас есть матрицы полезности, показывающие предпочтения клиентов в отношении товаров.
Given a data matrix A of m rows and n columns with each and every element a ij ≥ 0, NMF seeks matrices W and H of размер m строк и k столбцов, и k строк и n столбцов соответственно, так что A ≈ WH 2 элементов каждой матрицы, и0012 и H либо нулевой, либо положительный. Количество k задается пользователем и должно быть меньше или равно наименьшему из m и n . Матрица W обычно называется словарной матрицей или базисной матрицей , а H известна как расширение или матрица коэффициентов . Основная идея этой терминологии состоит в том, что заданная матрица данных A можно выразить как сумму k базисных векторов (столбцы W ), умноженные на соответствующие коэффициенты (столбцы H ).
Матрица W обычно называется словарной матрицей или базисной матрицей , а H известна как расширение или матрица коэффициентов . Основная идея этой терминологии состоит в том, что заданная матрица данных A можно выразить как сумму k базисных векторов (столбцы W ), умноженные на соответствующие коэффициенты (столбцы H ).
Матрицы W и H определяются минимизацией нормы Фробениуса:
|| А – WH || 2
Минимизация осуществляется некоторым подходящим итерационным процессом поиска и решения, т.е. матрицы W и H не уникальны. Существует много вариантов базового подхода NMF, в которых на результирующее решение накладываются дополнительные ограничения, например разреженность, чтобы ограничить пространство решения для W и H .
В качестве примера рассмотрим изображение уровня серого размером 128 x 128 в качестве нашей матрицы данных A . Я провел факторизацию NMF в Matlab, используя код, доступный на http://www.csie.ntu.edu.tw/~cjlin/nmf. Matlab также имеет встроенную функцию для выполнения такой факторизации; однако я обнаружил, что факторизация cjlin работает лучше. Если у вас нет Matlab, вы можете попробовать версии с открытым исходным кодом на сайте scikit-learn или R of NMF. Я получил три аппроксимации низкого ранга A для k = 32, 16 и 8 соответственно. Эти приближения вместе с исходным изображением приведены ниже. Вы можете видеть, что качество аппроксимаций, особенно для k = 32 и 16, превосходно.
NMF и SVDРазложение по сингулярным числам (SVD) — еще один и более известный метод матричной факторизации для получения аппроксимаций низкого ранга. В SVD вещественная матрица A of size m x n is factorized as
A = U D V t
where U is an orthogonal matrix of size m x m левых сингулярных векторов и V — ортогональная матрица размера n x n правых сингулярных векторов. Матрица D представляет собой диагональную матрицу размера m x n сингулярных значений. Приближение низкого ранга к A может быть получено с использованием только подмножества сингулярных значений и соответствующих левого и правого сингулярных векторов.
Матрица D представляет собой диагональную матрицу размера m x n сингулярных значений. Приближение низкого ранга к A может быть получено с использованием только подмножества сингулярных значений и соответствующих левого и правого сингулярных векторов.
Чтобы сравнить аппроксимации, полученные с помощью NMF и SVD, я использовал одно и то же изображение мандрилла для выполнения разложения по сингулярным значениям и реконструкции изображения с использованием 32, 16 и 8 верхних сингулярных значений. Результаты этой реконструкции вместе с исходным изображением показаны ниже.
Как вы можете заметить, и NMF, и SVD дают почти идентичные результаты, что приводит к вопросу о том, что NMF предлагает по сравнению с SVD. Одно большое различие между двумя методами факторизации заключается в том, что SVD не накладывает ограничения на положительность факторизованных матриц, в то время как NMF накладывает это ограничение. Следствием этого ограничения является то, что факторизация на основе NMF предлагает лучшую интерпретацию исходной матрицы данных, поскольку она представлена/аппроксимирована как сумма положительных матриц/векторов. С другой стороны, представление на основе SVD приводит к базовым изображениям положительных и отрицательных элементов, что затрудняет интерпретацию. Позвольте мне проиллюстрировать это на простом примере семисегментного дисплея. Такие дисплеи обычно используются для отображения чисел в различных электронных устройствах. Как показано ниже, различные комбинации цифр могут быть получены путем выборочного включения/выключения сегментов дисплея, расположенных определенным образом.
Следствием этого ограничения является то, что факторизация на основе NMF предлагает лучшую интерпретацию исходной матрицы данных, поскольку она представлена/аппроксимирована как сумма положительных матриц/векторов. С другой стороны, представление на основе SVD приводит к базовым изображениям положительных и отрицательных элементов, что затрудняет интерпретацию. Позвольте мне проиллюстрировать это на простом примере семисегментного дисплея. Такие дисплеи обычно используются для отображения чисел в различных электронных устройствах. Как показано ниже, различные комбинации цифр могут быть получены путем выборочного включения/выключения сегментов дисплея, расположенных определенным образом.
I создал следующую матрицу A из 7 строк и 10 столбцов для описания цифров 0-9. «1» означает, что соответствующий сегмент включен, а «0» означает, что сегмент выключен.
Используя приведенную выше матрицу A , я выполнил факторизацию NMF с k = 4. Столбцы полученного W 9Матрица 0005 представляет собой четыре базисных вектора, которые при объединении в соответствии с коэффициентами матрицы H дают образы цифр. Визуальное представление четырех базисных векторов матрицы W показано ниже. Легко представить, что различные комбинации базовых изображений, сложенные вместе с подходящими весами, будут воспроизводить паттерны из 0-9 цифр.
Столбцы полученного W 9Матрица 0005 представляет собой четыре базисных вектора, которые при объединении в соответствии с коэффициентами матрицы H дают образы цифр. Визуальное представление четырех базисных векторов матрицы W показано ниже. Легко представить, что различные комбинации базовых изображений, сложенные вместе с подходящими весами, будут воспроизводить паттерны из 0-9 цифр.
Чтобы увидеть, как будут выглядеть базисные векторы на основе SVD, матрица A также был разложен с помощью SVD. При этом в обеих матрицах U и V были обнаружены положительные и отрицательные элементы. Визуальное представление первых четырех векторов-столбцов матрицы U , образующих базисные векторы, оказалось таким, как показано ниже. В этом случае я включил шкалу серого, используемую при визуализации, рядом с каждым изображением, чтобы выделить наличие положительных и отрицательных компонентов. [Затенение в центре изображений связано с масштабированием фона] Нетрудно заметить, что интерпретация различных рисунков цифр как комбинации разных базисных векторов в этом случае затруднена, поскольку включает сложение и вычитание сегментов с разными множителями. .
[Затенение в центре изображений связано с масштабированием фона] Нетрудно заметить, что интерпретация различных рисунков цифр как комбинации разных базисных векторов в этом случае затруднена, поскольку включает сложение и вычитание сегментов с разными множителями. .
Чтобы суммировать основное различие между NMF и SVD, достаточно сказать, что NMF-разложение делает упор на представлении по частям , что помогает лучше понять результаты факторизации. Другой связанный с этим результат заключается в том, что результирующие факторизованные матрицы имеют тенденцию быть разреженными.
Приложения NMF NMF используется для кластеризации документов, предоставления рекомендаций, распознавания визуальных образов, таких как распознавание лиц, анализ экспрессии генов, извлечение признаков, разделение источников и т. д. матрица A не имеет отрицательных элементов.
Я собираюсь использовать небольшой пример, чтобы продемонстрировать, как можно использовать NMF для кластеризации. Рассмотрим матрицу 7 x 9, показывающую некоторые питательные компоненты девяти различных видов продуктов питания.
Применяя NMF-факторизацию к этой матрице с k = 3, мы получаем матрицу W в виде: Я выделил самую высокую запись в каждой строке, используя другой цвет. Выделенные записи в каждом столбце обозначают функции, подчеркнутые соответствующими кластерами. Давайте посмотрим на 3 x 9 H матрица, полученная в результате факторизации.
Интерпретация этой матрицы заключается в том, что индекс строки самой высокой записи в каждом столбце указывает принадлежность этого столбца к кластеру. Я выделил самую высокую запись в каждом столбце одним из трех цветов, используемых в матрице W . Таким образом, факторизация NMF показывает, что яблоко, банан и груша образуют один (желтый) кластер, синий краб и креветка — второй (красный) кластер, а сладкий перец, брокколи и морковь — третий (зеленый) кластер.
Таким образом, на вопрос «что вы можете делать с NMF?» ответ заключается в том, что NMF можно использовать для выполнения различных задач машинного обучения, пока у нас есть положительная матрица данных. Мало того, факторизацию NMF можно расширить до факторизации тензоров (наборов матриц) для выполнения таких задач, как сегментация видео и распознавание активности.
Нравится:
Нравится Загрузка…
Опубликовано Krishan
Я профессионал с многолетним опытом работы в области компьютерного зрения, интеллектуального анализа данных, машинного обучения, нейронных сетей и распознавания образов. Я предоставляю консультационные и обучающие услуги через свою компанию Integrated Knowledge Solutions. Просмотреть все сообщения Кришана
Опубликовано
Разложение по сингулярным значениям (SVD) в рекомендательной системе .
 Эта популярность связана с его применением в разработке рекомендательных систем. Существует множество онлайн-приложений, ориентированных на пользователя, таких как видеоплееры, музыкальные плееры, приложения для электронной коммерции и т. д., где пользователям рекомендуются дополнительные элементы для взаимодействия.
Эта популярность связана с его применением в разработке рекомендательных систем. Существует множество онлайн-приложений, ориентированных на пользователя, таких как видеоплееры, музыкальные плееры, приложения для электронной коммерции и т. д., где пользователям рекомендуются дополнительные элементы для взаимодействия.Найти и порекомендовать множество подходящих товаров, которые понравились бы пользователям и которые они выбрали бы, всегда сложно. Для этой задачи используется множество методов, и SVD является одним из таких методов. В этой статье представлено краткое введение в рекомендательные системы, введение в декомпозицию по сингулярным значениям и ее реализацию в рекомендациях фильмов.
Что такое рекомендательная система?
Рекомендательная система — это интеллектуальная система, которая прогнозирует рейтинг и предпочтения пользователей в отношении продуктов. Основное применение рекомендательных систем — найти взаимосвязь между пользователем и продуктом, чтобы максимизировать взаимодействие пользователя с продуктом. Основное применение рекомендательных систем заключается в предложении связанного видео или музыки для создания списка воспроизведения для пользователя, когда он занимается связанным элементом.
Основное применение рекомендательных систем заключается в предложении связанного видео или музыки для создания списка воспроизведения для пользователя, когда он занимается связанным элементом.
Аналогичное приложение используется в сфере электронной коммерции, где покупателям рекомендуются сопутствующие товары, но в этом приложении используются другие методы, такие как изучение правил ассоциации. Он также используется для рекомендации контента на основе поведения пользователей на платформах социальных сетей и новостных сайтах.
Существует два популярных подхода, используемых в рекомендательных системах для предложения товаров пользователям:
- Совместная фильтрация: Предполагается, что этот подход заключается в том, что людям, которым понравился товар в прошлом, он понравится и в будущем. . Этот подход строит модель на основе прошлого поведения пользователей. Поведение пользователя может включать ранее просмотренные видео, приобретенные товары, присвоенные оценки товарам.
 Таким образом, модель находит связь между пользователями и элементами. Затем модель используется для прогнозирования элемента или рейтинга элемента, который может заинтересовать пользователя. Разложение по сингулярным значениям используется в качестве подхода к совместной фильтрации в рекомендательных системах.
Таким образом, модель находит связь между пользователями и элементами. Затем модель используется для прогнозирования элемента или рейтинга элемента, который может заинтересовать пользователя. Разложение по сингулярным значениям используется в качестве подхода к совместной фильтрации в рекомендательных системах. - Фильтрация на основе содержимого: Этот подход основан на описании элемента и записи предпочтений пользователя. Он использует последовательность дискретных, предварительно помеченных характеристик элемента, чтобы рекомендовать дополнительные элементы с аналогичными свойствами. Этот подход лучше всего подходит, когда имеется достаточно информации об элементах, но не о пользователях. Рекомендательные системы на основе контента также включают рекомендательную систему на основе мнений.
Помимо двух вышеупомянутых подходов, существует еще несколько подходов к созданию рекомендательных систем, таких как многокритериальные рекомендательные системы, рекомендательные системы с учетом рисков, мобильные рекомендательные системы и гибридные рекомендательные системы (сочетающие совместную фильтрацию и фильтрацию на основе контента). ).
).
Разложение по сингулярным значениям
Разложение по сингулярным значениям (SVD) — метод линейной алгебры, который обычно используется в качестве метода уменьшения размерности в машинном обучении. SVD — это метод матричной факторизации, который уменьшает количество признаков в наборе данных за счет уменьшения размерности пространства с N-размерности до K-размерности (где K Разложение этой матрицы на множители осуществляется с помощью разложения по сингулярным числам. Он находит факторы матриц из факторизации матрицы высокого уровня (рейтинга пользователя). Разложение по сингулярным числам — это метод разложения матрицы на три другие матрицы, как указано ниже: где A — матрица полезности m x n , U — m x r ортогональная левая сингулярная матрица, которая представляет отношения между пользователями. Пусть каждый элемент представлен вектором x i , а каждый пользователь представлен вектором y u . Ожидаемая оценка пользователем элемента может быть представлена следующим образом: Здесь является формой факторизации в разложении по сингулярным числам. x i и y u можно получить таким образом, чтобы разница квадратичной ошибки между их скалярным произведением и ожидаемым рейтингом в матрице пользовательских элементов была минимальной. Приведенное выше уравнение является основным компонентом алгоритма, который работает для системы рекомендаций, основанной на разложении по сингулярным значениям. Ниже представлена реализация разложения по сингулярным значениям (SVD) на основе совместной фильтрации в задаче рекомендации фильмов. Импорт необходимых библиотек Python: Прочитать набор данных, откуда он загружен в системе. Он состоит из двух файлов «ratings.dat» и «movies.dat», которые необходимо прочитать. movie_data = pd.io.parsers.read_csv('data/movies.dat', Создайте матрицу оценок со строками в виде фильмов и столбцами в виде пользователей. Нормализация матрицы. Вычислить разложение по сингулярным числам (SVD). Определите функцию для вычисления сходства косинусов. Отсортируйте по наиболее похожим и верните первые N результатов. Определите функцию для вывода первых N похожих фильмов. Инициализировать значение k основных компонентов, идентификатор фильма, указанный в наборе данных, и количество верхних элементов для печати. Print топ N похожих фильмов. Связывание всех вместе: Набор данных #Reading (набор данных рейтингов фильмов MovieLens 1M: загружен с https://grouplens. #Создание матрицы оценок (строки как фильмы, столбцы как пользователи) # Нормализация матрицы (вычесть среднее значение) #Вычисление разложения по сингулярным числам (SVD) # Функция для вычисления косинусного сходства (сортировка по наибольшему сходству и возврат наибольшего N) # Функция для печати первых N похожих фильмов #k-главных компонентов для представления фильмов, movie_id для поиска рекомендаций, top_n вывести n результатов # Печать первых N похожих фильмов примеры выходных данных приведены ниже: Чтобы создать матричную модель факторизации в BigQuery, используйте
Оператор BigQuery ML Для получения информации о поддерживаемых типах моделей каждого оператора SQL и функции,
и все поддерживаемые операторы SQL и функции для каждого типа модели, прочитайте
Сквозной путь пользователя для каждой модели. Создает новую модель машинного обучения BigQuery в указанном наборе данных. Создает новую модель BigQuery ML, только если модель в настоящее время не существует.
существуют в указанном наборе данных. Создает новую модель BigQuery ML и заменяет любую существующую модель новой
то же имя в указанном наборе данных. Если у вас нет настроенного проекта по умолчанию, добавьте идентификатор проекта перед
имя модели в следующем формате, включая обратные кавычки: `[PROJECT_ID].[DATASET].[MODEL]` Например: `myproject.mydataset.mymodel` Синтаксис Описание Указывает тип модели. Чтобы создать матричную модель факторизации, установите В Модели матричной факторизации поддерживают следующие параметры: Синтаксис Описание Указывает тип обратной связи для матричных моделей факторизации. Существует два типа оценок (отзывы пользователей): Если пользователь явно поставил рейтинг (например, 1–5) элементу
например рекомендации фильмов, затем укажите Большинство проблем, связанных с рекомендацией продукта, не имеют явной обратной связи с пользователем.
Вместо этого значение рейтинга должно быть искусственно сконструировано на основе пользовательского
взаимодействие с элементом (например, клики, просмотры страниц и покупки).
В этой ситуации укажите Для получения дополнительной информации о различиях между двумя типами обратной связи и
когда использовать какой тип, см.
Дополнительная информация о типах обратной связи. Аргументы Значение по умолчанию: Синтаксис Описание Указывает количество скрытых факторов для использования в матричных моделях факторизации. Аргументы Синтаксис Описание Имя пользовательского столбца для матричных моделей факторизации. Аргументы Синтаксис Описание Имя столбца фактора факторизации для матрицы. Аргументы Синтаксис Описание 9000 Имя столбца факторизации для моделей рейтинга. Аргументы Синтаксис Описание AIRPARATER для Для получения дополнительной информации см.
Дополнительная информация о типах обратной связи Аргументы Синтаксис Описание Сумма Применена регуляризация L2. Аргументы Синтаксис Описание Максимальное количество итераций или шагов обучения. Аргументы Синтаксис Описание Следует ли останавливать обучение после первой итерации, в которой
снижение потерь меньше, чем значение, указанное для
MIN_REL_PROGRESS. Аргументы Значение Синтаксис Описание Минимальное улучшение относительных потерь, необходимое для продолжения обучения, когда Аргументы Синтаксис Описание Метод разделения входных данных на наборы для обучения и оценки. Тренировочные данные
используется для обучения модели. Данные оценки используются, чтобы избежать переоснащение через раннюю остановку. Аргументы Принимает следующие значения: Синтаксис Описание Этот вариант используется с Аргументы Синтаксис Описание используется для разделения данных 9000 Этот столбец нельзя использовать в качестве
характеристика или метка и будет автоматически исключена из характеристик. Когда значение Когда значением Информацию о поддерживаемых типах ввода см. в разделе Поддерживаемые
типы ввода для Аргументы Предложение Для матричных моделей факторизации ожидается, что query_statement будет содержать
ровно 3 столбца ( Оператор BigQuery ML поддерживает различные стандартные типы данных SQL для входных данных
столбцы для матричной факторизации. Важная часть создания хорошей матричной модели факторизации для
рекомендации, чтобы убедиться, что данные обучены алгоритму, который
лучше всего подходит для этого. Оценки, которые пользователь должен ввести и установить, считаются явными
Обратная связь. Низкий явный рейтинг, как правило, означает, что пользователь чувствовал себя очень негативно.
о предмете, в то время как высокий явный рейтинг, как правило, подразумевает, что пользователю понравилось
вещь. Сайты потокового кино, на которых пользователи выставляют оценки, являются примерами явно
помеченные наборы данных. Для задач с явной обратной связью мы используем знакопеременный наименьший
алгоритм квадратов, обычно называемый ALS. БАС стремится свести к минимуму
следующая функция потерь: 92)$$ Где \(r_{ui} = \) оценка, которую пользователь \(u\) дал элементу \(i\) Однако в большинстве случаев данные редко помечаются пользователями. Зачастую единственным
метрики, которые есть у компании относительно того, понравился ли пользователю товар или фильм.
по рейтингу кликов или времени взаимодействия. Его часто можно использовать в качестве прокси-рейтинга,
но это не обязательно является окончательным указанием на то, является ли пользователь
нравится или не нравится что-то. Данные в этих наборах данных считаются
неявная обратная связь. Для задач с неявной обратной связью мы используем вариант этого
алгоритм взвешенных чередующихся наименьших квадратов или WALS, который описан
в http://yifanhu.net/PUB/cf.pdf. Этот подход
использует эти прокси-рейтинги и рассматривает их как достоверность наблюдения, которое
пользователь отдает за товар. WALS стремится минимизировать следующую функцию потерь: 92) $$ Где, помимо переменных, определенных выше, функция также вводит
следующие переменные: \(p_{ui} = 1\), когда \(r_{ui} > 0\), и \(p_{ui} = 0\), когда \(r_{ui}
\(c_{ui} = 1 + \alpha r_{ui}\) известный фиксированный диапазон. Если возникает ошибка "Модель слишком велика (>100 МБ)", проверьте ввод
данные. Это вызвано наличием слишком большого количества оценок для одного пользователя или одного
вещь. Хэширование столбцов пользователя или элемента в значение Где num_rated_user — максимальный рейтинг элемента, который имеет один пользователь. В следующем примере создаются модели с именем В этом примере создается явная модель факторизации матрицы обратной связи. В этом примере создается модель факторизации матрицы неявной обратной связи. и латентные факторы, S представляет собой диагональную матрицу r x r , которая описывает силу каждого скрытого фактора, а V представляет собой диагональную правую сингулярную матрицу r x n , которая указывает на сходство между элементами и скрытыми факторами. Скрытыми факторами здесь являются характеристики предметов, например, жанр музыки. SVD уменьшает размерность матрицы полезности A , извлекая ее скрытые факторы. Он отображает каждого пользователя и каждый элемент в r — мерное скрытое пространство. Это сопоставление облегчает четкое представление взаимосвязей между пользователями и элементами.
и латентные факторы, S представляет собой диагональную матрицу r x r , которая описывает силу каждого скрытого фактора, а V представляет собой диагональную правую сингулярную матрицу r x n , которая указывает на сходство между элементами и скрытыми факторами. Скрытыми факторами здесь являются характеристики предметов, например, жанр музыки. SVD уменьшает размерность матрицы полезности A , извлекая ее скрытые факторы. Он отображает каждого пользователя и каждый элемент в r — мерное скрытое пространство. Это сопоставление облегчает четкое представление взаимосвязей между пользователями и элементами. Это можно выразить так: чтобы модель хорошо обобщалась и не соответствовала обучающим данным, в приведенную выше формулу в качестве штрафа добавляется член регуляризации. Чтобы уменьшить ошибку между значением, предсказанным моделью, и фактическим значением, алгоритм использует член смещения. Пусть для пары пользователь-элемент (u, i) , μ — средний рейтинг всех элементов, b i — средний рейтинг элемента i минус μ и b u 0 — средний рейтинг, заданный 0 . пользователем u минус μ , окончательное уравнение после добавления члена регуляризации и смещения может быть дано как:
Это можно выразить так: чтобы модель хорошо обобщалась и не соответствовала обучающим данным, в приведенную выше формулу в качестве штрафа добавляется член регуляризации. Чтобы уменьшить ошибку между значением, предсказанным моделью, и фактическим значением, алгоритм использует член смещения. Пусть для пары пользователь-элемент (u, i) , μ — средний рейтинг всех элементов, b i — средний рейтинг элемента i минус μ и b u 0 — средний рейтинг, заданный 0 . пользователем u минус μ , окончательное уравнение после добавления члена регуляризации и смещения может быть дано как: Разложение по сингулярным значениям (SVD) на основе рекомендации фильмов
 Эта задача реализована на Python. Для простоты использовался набор данных MovieLens 1M. Этот набор данных был выбран потому, что он не требует предварительной обработки, поскольку основное внимание в этой статье уделяется SVD и рекомендательным системам.
Эта задача реализована на Python. Для простоты использовался набор данных MovieLens 1M. Этот набор данных был выбран потому, что он не требует предварительной обработки, поскольку основное внимание в этой статье уделяется SVD и рекомендательным системам. импортировать numpy как np
импортировать pandas как pd data = pd.io.parsers.read_csv('data/ratings.dat',
names=['user_id', 'movie_id', 'rating', 'time'],
engine='python', delimiter= '::')
names=['movie_id', 'название', 'жанр'],
engine='python', delimiter= '::') ratings_mat = np.ndarray(
shape=(np.max(data. movie_id.values), np.max(data.user_id.values)),
movie_id.values), np.max(data.user_id.values)),
dtype=np.uint8)
ratings_mat[data.movie_id.values -1, data.user_id.values-1] = data.rating.values normalized_mat = ratings_mat - np.asarray([(np.mean(ratings_mat, 1))]).T
A = normalized_mat.T / np.sqrt(ratings_mat.shape[0] - 1)
U, S, V = np.linalg.svd(A) def top_cosine_similarity(data, movie_id, top_n=10):
index = movie_id - 1 # Идентификатор фильма начинается с 1 в наборе данных
movie_row = data[index, :]
величина = np.sqrt(np.einsum(' ij, ij -> i', data, data))
подобие = np.dot(movie_row, data.T) / (величина[индекс] * величина)
sort_indexes = np.argsort(-simiarity)
return sort_indexes[:top_n] 
def print_similar_movies(movie_data, movie_id, top_indexes):
print('Рекомендации для {0}: \n'.format(
movie_data[movie_data.movie_id == movie_id].title.values[0]))
для id in top_indexes + 1:
print(movie_data[movie_data.movie_id == id].title.values[0]) k = 50
movie_id = 10 # (получение идентификатора из movie.dat)
top_n = 10
sliced = V.T[:, :k] # репрезентативные данные
indexes = top_cosine_similarity(sliced, movie_id, top_n) print_similar_movies (movie_data, movie_id, indexes)
# Импорт библиотек
import numpy as np
import pandas as pd  org/datasets/movielens/1m/)
org/datasets/movielens/1m/)
data = pd.io.parsers.read_csv('data/ratings.dat ',
names=['user_id', 'movie_id', 'рейтинг', 'время'],
engine='python', delimiter='::')
movie_data = pd.io.parsers.read_csv('data /movies.dat',
names=['movie_id', 'title', 'genre'],
engine='python', delimiter='::')
ratings_mat = np.ndarray(
shape=(np.max(data.movie_id.values), np.max(data.user_id.values)),
dtype=np.uint8)
ratings_mat[data.movie_id.values- 1, data.user_id.values-1] = data.rating.values
normalized_mat = ratings_mat - np.asarray([(np.mean(ratings_mat, 1))]). T
A = normalized_mat.T / np.sqrt(ratings_mat.shape[0] - 1)
U, S, V = np.linalg.svd(A)
def top_cosine_similarity(data, movie_id, top_n=10):
index = movie_id - 1 # Идентификатор фильма начинается с 1 в наборе данных
movie_row = данные [индекс,:]
величина = np. sqrt(np.einsum('ij, ij -> i', данные, данные))
sqrt(np.einsum('ij, ij -> i', данные, данные))
сходство = np.dot(movie_row, data.T) / (величина [индекс ] * величина)
sort_indexes = np.argsort(-подобие)
возврат sort_indexes[:top_n]
def print_similar_movies(movie_data, movie_id, top_indexes):
print('Рекомендации для {0}: \n'.format(
movie_data[movie_data.movie_id == movie_id].title. values[0]))
для id в top_indexes + 1:
print(movie_data[movie_data.movie_id == id].title.values[0])
k = 50
movie_id = 10 # (получение идентификатора из movie.dat)
top_n = 10
sliced = V.T[:, :k] # репрезентативные данные
indexes = top_cosine_similarity(sliced, movie_id, top_n) Оператор CREATE MODEL для матричной факторизации | BigQuery ML
Примечание. Матричные модели факторизации доступны только клиентам с фиксированной ставкой или
клиентов с резервированием. На лету
клиентам рекомендуется использовать гибкие слоты
использовать матричную факторизацию.
Матричные модели факторизации доступны только клиентам с фиксированной ставкой или
клиентов с резервированием. На лету
клиентам рекомендуется использовать гибкие слоты
использовать матричную факторизацию. CREATE MODEL и укажите MODEL_TYPE как 'MATRIX_FACTORIZATION' .
СОЗДАТЬ МОДЕЛЬ синтаксис
{СОЗДАТЬ МОДЕЛЬ | СОЗДАТЬ МОДЕЛЬ, ЕСЛИ НЕ СУЩЕСТВУЕТ | СОЗДАТЬ ИЛИ ЗАМЕНИТЬ МОДЕЛЬ}
имя_модели
ОПЦИИ (MODEL_TYPE = 'MATRIX_FACTORIZATION'
FEEDBACK_TYPE = {'EXPLICIT' | 'СКРЫТЫЙ'},
NUM_FACTORS = int64_value ,
USER_COL = строковое_значение ,
ITEM_COL = строковое_значение ,
RATING_COL = string_value ,
WALS_ALPHA = float64_value ,
L2_REG = float64_value ,
MAX_ITERATIONS = int64_value ,
EARLY_STOP = {ИСТИНА | ЛОЖНЫЙ },
МИН_РЕЛ_ПРОГРЕСС = float64_value ,
DATA_SPLIT_METHOD = { 'AUTO_SPLIT' | 'СЛУЧАЙНЫЙ' | 'ПЕРСОНАЛ' | 'ПОСЛЕДОВАТЕЛЬНОСТЬ' | 'NO_SPLIT'},
DATA_SPLIT_EVAL_FRACTION = float64_value ,
DATA_SPLIT_COL = строковое_значение )
AS запрос_оператор
CREATE MODEL
 Если модель
имя существует,
Если модель
имя существует, CREATE MODEL возвращает ошибку. СОЗДАТЬ МОДЕЛЬ, ЕСЛИ НЕ СУЩЕСТВУЕТ
СОЗДАТЬ ИЛИ ЗАМЕНИТЬ МОДЕЛЬ
имя_модели
имя_модели — это имя модели машинного обучения BigQuery, которую вы создаете или
замена. Имя модели должно быть уникальным для каждого набора данных: никакая другая модель или таблица
может иметь одно и то же имя. Имя модели должно соответствовать тем же правилам именования, что и
Таблица BigQuery. Название модели может содержать следующее: имя_модели регистр не учитывается.
CREATE MODEL поддерживает следующие параметры: МОДЕЛЬ_ТИП
MODEL_TYPE = 'MATRIX_FACTORIZATION'
model_type до 'MATRIX_FACTORIZATION' . model_option_list
model_option_list требуется параметр model_type . Все остальные
являются необязательными. FEEDBACK_TYPE
FEEDBACK_TYPE = { 'EXPLICIT' | 'СКРЫТЫЙ' }
 Тип обратной связи
определяет алгоритм, который используется во время обучения.
Тип обратной связи
определяет алгоритм, который используется во время обучения. 'ЯВНАЯ' и 'ЯВНАЯ' .
Используйте нужный тип обратной связи в параметрах создания модели в зависимости от ваших
вариант использования. FEEDBACK_TYPE='EXPLICIT' .
Это обучит модель, используя
Чередование наименьших квадратов
алгоритм. ОБРАТНАЯ СВЯЗЬ_TYPE='НЕЯВНАЯ' . Это позволит обучить
модель с использованием
Алгоритм взвешенных чередующихся наименьших квадратов.
Это позволит обучить
модель с использованием
Алгоритм взвешенных чередующихся наименьших квадратов. 'ЯВНОЕ' . NUM_FACTORS
NUM_FACTORS = int64_value int64_value является 'INT64' . Допустимые значения: 2-200.
Значение по умолчанию: log 2 (n) , где n — число
обучающих примеров.
USER_COL
USER_COL = string_value string_value является 'STRING' . Значение по умолчанию 'пользователь' . ITEM_COL
ITEM_COL = string_value string_value является 'STRING' . Значение по умолчанию
Значение по умолчанию 'предмет' . RATING_COL
RATING_COL = string_value string_value является 'STRING' . Значение по умолчанию 'рейтинг' . WALS_ALPHA
WALS_ALPHA = FLOAT64_VALUE 7 . float64_value — это 'FLOAT64' . Значение по умолчанию — 40.
Значение по умолчанию — 40. L2_REG
L2_REG = float64_value float64_value - это FLOAT64 . Значение по умолчанию — 1,0. MAX_ITERATIONS
МАКСИМАЛЬНЫЕ ИТЕРАЦИИ = int64_value int64_value является INT64 . Значение по умолчанию — 20.
EARLY_STOP
EARLY_STOP = { TRUE | ЛОЖНЫЙ }
BOOL . Значение по умолчанию — ИСТИНА . MIN_REL_PROGRESS
MIN_REL_PROGRESS = float64_value EARLY_STOP имеет значение true. Например, значение 0,01 указывает
что каждая итерация должна уменьшать потери на 1% для продолжения обучения.
float64_value — это FLOAT64 . Значение по умолчанию — 0,01. DATA_SPLIT_METHOD
DATA_SPLIT_METHOD = { 'AUTO_SPLIT' | 'СЛУЧАЙНЫЙ' | 'ПЕРСОНАЛ' | 'ПОСЛЕДОВАТЕЛЬНОСТЬ' | 'NO_SPLIT' }
'AUTO_SPLIT' Стратегия автоматического разделения следующая: RANDOM .
СЛУЧАЙНЫЙ разделить. 'СЛУЧАЙНЫЙ' Случайное разделение данных. Случайное разделение является детерминированным: разные
тренировочные прогоны дают одинаковые результаты разделения, если базовое обучение
данные остаются прежними. 'CUSTOM' Разделить данные, используя предоставленный пользователем столбец типа BOOL . Ряды
со значением TRUE используются в качестве данных оценки. Строки со значением FALSE используются в качестве обучающих данных. 'ПОСЛ.' Последовательное разделение данных с использованием предоставленного пользователем столбца. Колонка может
иметь любой упорядоченный тип данных: NUMERIC , BIGNUMERIC , STRING или ОТМЕТКА ВРЕМЕНИ . Все строки со значениями разделения меньше порогового значения используются как
данные тренировки. Остальные строки, включая
Все строки со значениями разделения меньше порогового значения используются как
данные тренировки. Остальные строки, включая значений NULL , используются в качестве данных оценки. 'NO_SPLIT' Использовать все данные для обучения. DATA_SPLIT_EVAL_FRACTION
DATA_SPLIT_EVAL_FRACTION = float64_value 'СЛУЧАЙНЫЙ' и 'ПОСЛЕДОВАТЕЛЬНОСТЬ' разделяются. В нем указывается
часть данных, используемых для оценки, с точностью до двух знаков после запятой.
В нем указывается
часть данных, используемых для оценки, с точностью до двух знаков после запятой. float64_value - это FLOAT64 . Значение по умолчанию — 0,2. DATA_SPLIT_COL
DATA_SPLIT_COL = string_value DATA_SPLIT_METHOD равно 'CUSTOM' , соответствующий столбец
должен быть типа BOOL . Строки со значениями TRUE или NULL используются как
данные оценки. Строки с
Строки с значениями FALSE используются в качестве обучающих данных. DATA_SPLIT_METHOD является 'SEQ' , последний n Используется строк от наименьшего к наибольшему в соответствующем столбце
в качестве оценочных данных, где n — значение, указанное для DATA_SPLIT_EVAL_FRACTION . Первые ряды используются
как обучающие данные. DATA_SPLIT_COL . string_value является STRING . query_statement
AS query_statement указывает стандартный SQL-запрос, который используется для
генерировать обучающие данные. Для получения информации о поддерживаемом синтаксисе SQL
Для получения информации о поддерживаемом синтаксисе SQL query_statement пункт, см.
Стандартный синтаксис SQL-запроса. пользователь , элемент и рейтинг ), если пользователь не укажет DATA_SPLIT_METHOD , который требует использования DATA_SPLIT_COL . Поддерживаемые входные данные
CREATE MODEL поддерживает следующие типы данных для пользователя,
элемент и столбцы рейтинга. Поддерживаемые типы данных для входных данных модели матричной факторизации
 Поддерживаемые типы данных для каждого
столбец включает:
Поддерживаемые типы данных для каждого
столбец включает: Входной столбец матричной факторизации Поддерживаемые типы пользователь Любой группируемый тип данных позиция Любой группируемый тип данных рейтинг INT64
NUMERIC
BIGNUMERIC
FLOAT64 Дополнительная информация о типах обратной связи
 Для моделей матричной факторизации существуют два разных
способы получить рейтинг для пары пользователь-элемент.
Для моделей матричной факторизации существуют два разных
способы получить рейтинг для пары пользователь-элемент.
\(x_u = \) вектор скрытых факторных весов для пользователя \(u\). Длина ЧИСЛО_ФАКТОРОВ .
\(y_i = \) вектор скрытых весов факторов для элемента \(i\).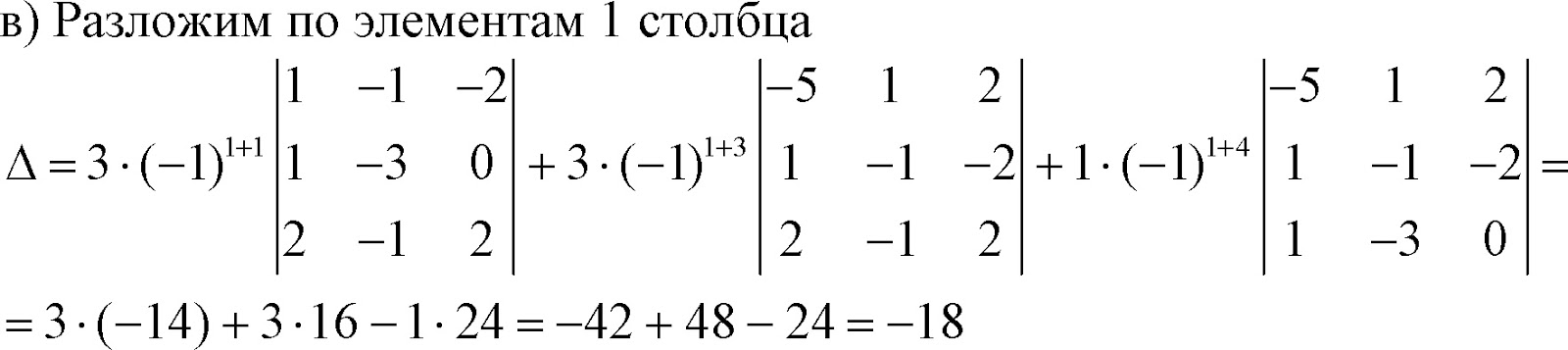 Длина
Длина ЧИСЛО_ФАКТОРОВ .
\(\lambda = \) L2_REG
\(\alpha = \) WALS_ALPHA  Для неявной матричной факторизации входные рейтинги могут
быть двойными или целыми числами, которые охватывают более широкий диапазон. Рекомендуем вам убедиться
во входных оценках нет никаких выбросов, и вы масштабируете входные данные
оценки, если модель работает плохо.
Для неявной матричной факторизации входные рейтинги могут
быть двойными или целыми числами, которые охватывают более широкий диапазон. Рекомендуем вам убедиться
во входных оценках нет никаких выбросов, и вы масштабируете входные данные
оценки, если модель работает плохо. Известные ограничения
CREATE MODEL Операторы для моделей матричной факторизации должны соответствовать
следующие правила: INT64 или уменьшение
размер данных может помочь. Общая формула для определения того, произойдет ли это:
следующее: макс(num_rated_user, num_rated_item) < 100 миллионов  введено, а num_rated_items — максимальный рейтинг пользователя для данного элемента.
введено, а num_rated_items — максимальный рейтинг пользователя для данного элемента. СОЗДАТЬ МОДЕЛЬ примеры mymodel в mydataset в вашем
проект по умолчанию. Обучение модели матричной факторизации с явной обратной связью
СОЗДАТЬ МОДЕЛЬ `project_id.mydataset.mymodel`
ОПЦИИ (MODEL_TYPE = 'MATRIX_FACTORIZATION') КАК
ВЫБРАТЬ
пользователь,
вещь,
рейтинг
ИЗ
`mydataset.mytable`
Обучение модели факторизации матрицы с неявной обратной связью
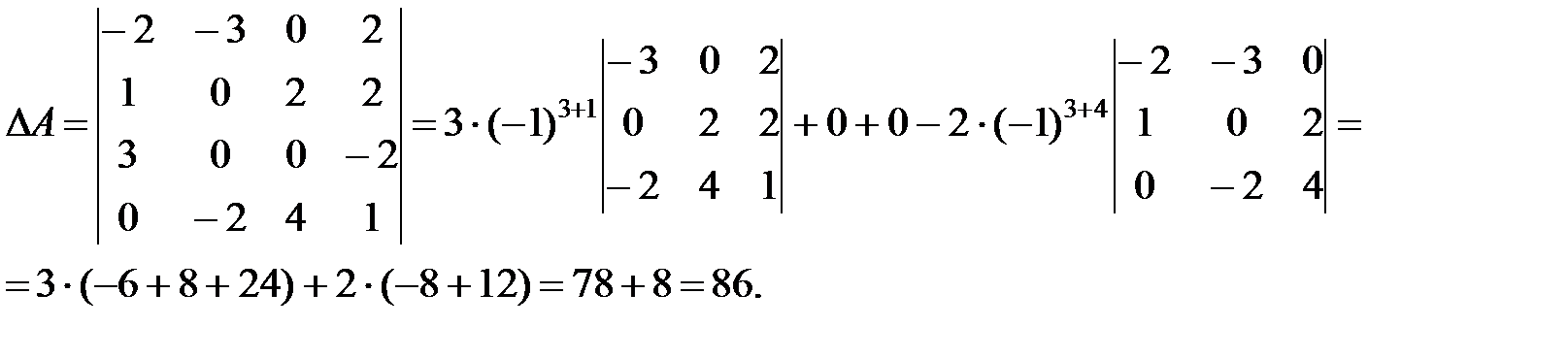

 Таким образом, модель находит связь между пользователями и элементами. Затем модель используется для прогнозирования элемента или рейтинга элемента, который может заинтересовать пользователя. Разложение по сингулярным значениям используется в качестве подхода к совместной фильтрации в рекомендательных системах.
Таким образом, модель находит связь между пользователями и элементами. Затем модель используется для прогнозирования элемента или рейтинга элемента, который может заинтересовать пользователя. Разложение по сингулярным значениям используется в качестве подхода к совместной фильтрации в рекомендательных системах.