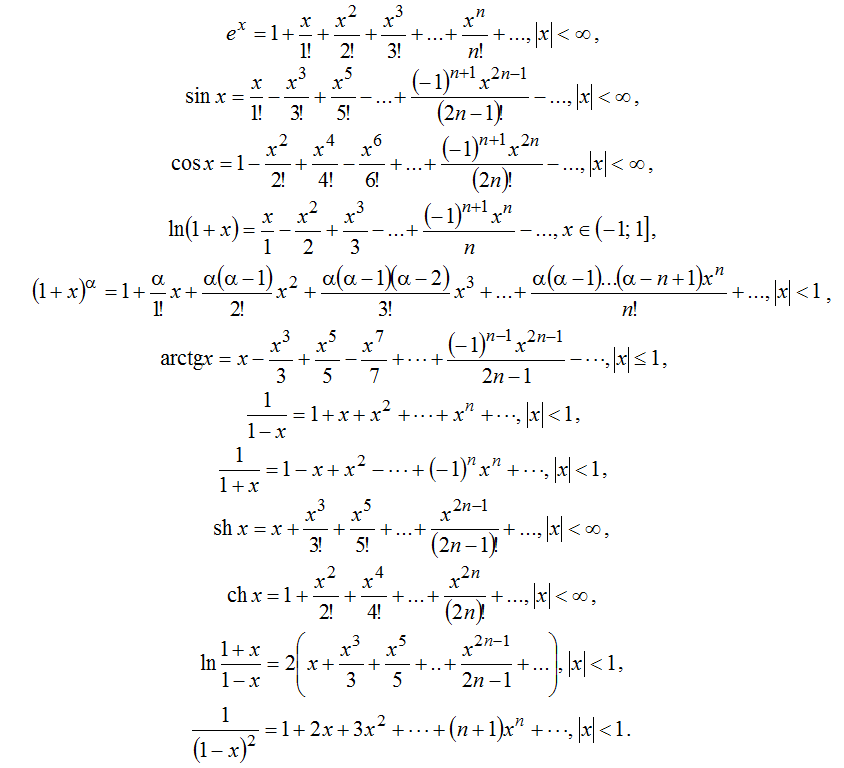Разложить в ряд тейлора с решением онлайн: Ряд Тейлора онлайн

Содержание

Ряд Тейлора онлайн

Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
,
где r_n – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
, где число x заключено между х и а.

Решение онлайн
Видеоинструкция

f(x)=

в точке x₀= Количество элементов ряда34567

Использовать разложение элементарных функций e^x, cos(x), sin(x), ln(1+x), (1+x)^m

Правила ввода функций:

Если для некоторого значения х r_n→0 при n→∞, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если:

она имеет производные всех порядков;
построенный ряд сходится в этой точке.

При а=0 получаем ряд, называемый рядом Маклорена:

Разложение простейших (элементарных) функций в ряд Маклорена:

Показательные функции
, R=∞
Тригонометрические функции
, R=∞
, R=∞
, (-π/2 < x < π/2), R=π/2
Функция actgx не разлагается по степеням x, т.к. ctg0=∞
Гиперболические функции

Логарифмические функции
, -1<x<1, R = 1

Биномиальные ряды
.

Пример №1. Разложить в степенной ряд функцию f(x)=2

x.
Решение. Найдем значения функции и ее производных при х=0
f(x) = 2^x, f(0) = 2⁰=1;
f'(x) = 2^xln2, f'(0) = 2⁰ ln2= ln2;
f»(x) = 2^x ln²2, f»(0) = 2⁰ ln²2= ln²2;
…
f⁽ⁿ⁾(x) = 2^x lnⁿ2, f⁽ⁿ⁾(0) = 2⁰ lnⁿ2= lnⁿ2.

Подставляя полученные значения производных в формулу ряда Тейлора, получим:

Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -∞<x<+∞.

Пример №2. Написать ряд Тейлора по степеням (

х+4) для функции f(x)=e^x.
Решение. Находим производные функции e^x и их значения в точке х=-4.
f(x) = е^x, f(-4) = е^-4;
f'(x) = е^x, f'(-4) = е^-4;
f»(x) = е^x, f»(-4) = е^-4;
…
f⁽ⁿ⁾(x) = е^x, f⁽ⁿ⁾( -4) = е^-4.

Следовательно, искомый ряд Тейлора функции имеет вид:

Данное разложение также справедливо для -∞<x<+∞.

Пример №3. Разложить функцию f(x)=lnx в ряд по степеням (х-1),

( т.е. в ряд Тейлора в окрестности точки х=1).
Решение. Находим производные данной функции.
f(x)=lnx, , , ,

f(1)=ln1=0, f'(1)=1, f»(1)=-1, f»'(1)=1*2,…, f⁽ⁿ⁾=(-1)^n-1(n-1)!
Подставляя эти значения в формулу, получим искомый ряд Тейлора:

С помощью признака Даламбера можно убедиться, что ряд сходится при ½х-1½<1. Действительно, Ряд сходится, если ½х-1½<1, т.е. при 0<x<2. При х=2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х=0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].

Пример №4. Разложить в степенной ряд функцию .
Решение. В разложении (1) заменяем х на -х², получаем:

, -∞<x<∞

Пример №5. Разложить в ряд Маклорена функцию .
Решение. Имеем
Пользуясь формулой (4), можем записать:

подставляя вместо х в формулу –х, получим:

Отсюда находим: ln(1+x)-ln(1-x) = —
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
. Этот ряд сходится в интервале (-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.

Замечание.
Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо

х стоит k(х-а)^m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t=х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

Этот метод основан на теореме о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.

Пример №5а. Разложить в ряд Маклорена функцию , указать область сходимости.
Решение. Сначала найдем 1-x-6x²=(1-3x)(1+2x), далее разложим дробь с помощью сервиса.
на элементарные:

Дробь 3/(1-3x) можно рассматривать как сумму бесконечно убывающей геометрической прогрессии знаменателем 3x, если |3x| < 1. Аналогично, дробь 2/(1+2x) как сумму бесконечно убывающей геометрической прогрессии знаменателем -2x, если |-2x| < 1. В результате получим разложение в степенной ряд

с областью сходимости |x| < 1/3.

Пример №6. Разложить функцию в ряд Тейлора в окрестности точки х=3.
Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х=3. Однако проще будет воспользоваться имеющимся разложением (5):

Полученный ряд сходится при или –3<x-3<3, 0<x< 6 и является искомым рядом Тейлора для данной функции.

Пример №7. Написать ряд Тейлора по степеням (х-1) функции ln(x+2).

Решение.

Ряд сходится при , или -2 < x < 5.

Пример №8. Разложить функцию f(x)=sin(πx/4) в ряд Тейлора в окрестности точки x=2.
Решение. Сделаем замену t=х-2:

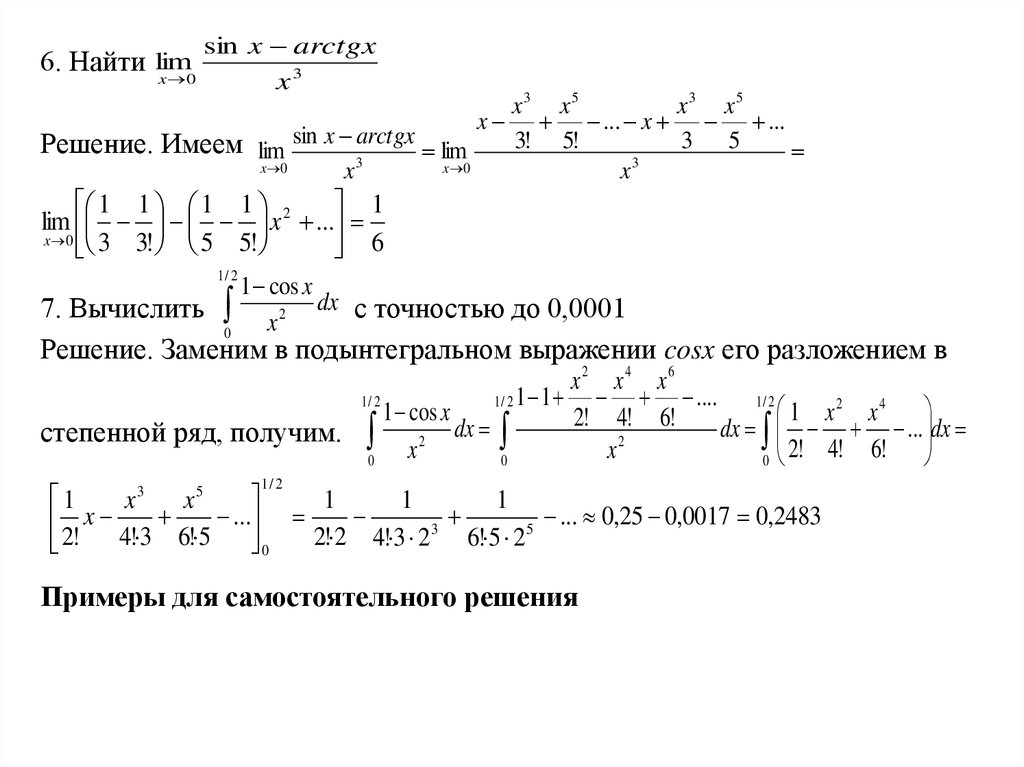Воспользовавшись разложением (3), в котором на место х подставим ^π/₄t, получим: Полученный ряд сходится к заданной функции при -∞<^π/₄t<+∞, т.

е. при (-∞<x<+∞).
Таким образом,

, (-∞<x<+∞)

Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Рассмотрим разложение функции в степенной ряд: Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают: Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток r_n(x). Для этого применяют следующие приемы:

если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена.
если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией.

в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа: a<c<x (или x<c<a).

Пример №1. Вычислить ln(3) с точностью до 0,01.
Решение. Воспользуемся разложением , где x=1/2 (см. пример 5 в предыдущей теме):

Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии: Таким образом, мы можем отбросить этот остаток и получаем

Пример №2. Вычислить с точностью до 0,0001.
Решение. Воспользуемся биномиальным рядом. Так как 5³ является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=5³+5.

так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
, поэтому его и следующие за ним члены можно отбросить.

Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подынтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Пример №3. Вычислить интеграл ∫014sin(x)x с точностью до 10^-5.
Решение. Соответствующий неопределенный интеграл не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
Разделив почленно ряд для sinx на x , получим:

Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:

Так как полученный ряд удовлетворяет условиям Лейбница и достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.

Таким образом, находим

Пример №4. Вычислить интеграл ∫014ex2 с точностью до 0,001.
Решение.

Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.

≈0.0001<0.001

Следовательно, .

Разложить в ряд Тейлора online

‘) window.yaContextCb.push(()=>{ Ya.Context.AdvManager.render({ renderTo: rtb_id, blockId: ‘R-A-1616620-2’ }) })

В точке до степени

Ввести:

{ кусочно-заданную функцию можно здесь

График:

от до

Приближения:

от до

Примеры разложения в ряд Тейлора

С кубическим корнем
```
cbrt(27 - x)
```
С квадратным корнем
```
sqrt(1 - x)
```
```
sqrt(1 + x)
```
С экспонентой
```
exp(-x^2)
```
С параметром
```
(1 + x)^a
```
Элементарные функции
```
log(1 + x)
```
```
cos(x)
```
```
tan(x)
```
```
exp(x)
```
Ряд Маклорена
```
sin(x)*exp(-x)
```
Ряд Ньютона — Меркатора
```
ln(1 + x)
```
```
ln((1 + x)/(1 - x))
```
Геометрический ряд
```
1/(1-x)
```

Что умеет калькулятор ряда Тейлора?

Вы вводите функцию, точку, в которой надо разложить соотвествующую функцию и количество членов в разложении. k$

Строит графики:

Самой функции
Частичные суммы ряда Тейлора

Подробнее про Ряд Тейлора.

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)

Правила ввода

Можно делать следующие операции

2*x: — умножение
3/x: — деление
x^2: — возведение в квадрат
x^3: — возведение в куб
x^5: — возведение в степень
x + 7: — сложение
x — 6: — вычитание
Действительные числа: вводить в виде 7. 5, не 7,5

Постоянные

pi: — число Пи
e: — основание натурального логарифма
i: — комплексное число
oo: — символ бесконечности

Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:

Калькулятор ряда Тейлора

Калькулятор ряда Тейлора вычисляет все коэффициенты разложения в ряд Тейлора для функции с центром в точке n. Кроме того, вы можете установить точку n равной нулю (0), чтобы получить представление ряда Маклорена.

Что такое серия Тейлора?

В математике ряд Тейлора определяется как представление заданной функции. Это бесконечный ряд, представляющий значение производной функции в определенной точке. 93 / 125 $$

Как работает наш калькулятор?

Ввод:

Во-первых, подставьте функцию относительно определенной переменной.
Теперь введите конкретную точку, чтобы вычислить ряд функций Тейлора вокруг этой точки.
Затем добавьте порядок n для аппроксимации.
С помощью калькулятора ошибок серии Тейлора найдите серию и определите ошибку в заданной точке. (опционально)
Нажмите кнопку расчета для дальнейшего решения.

Вывод:

Калькулятор суммы ряда Тейлора с шагами показывает ряд после упрощения.
Вычисляет ряд введенных функций вокруг заданного порядкового номера n.
Калькулятор полиномов Тейлора третьей степени берет производную для получения полиномов и помещает результаты в формулу ряда Тейлора.
Отображает результаты после упрощения полиномов.

Ссылка:

Из источника Википедии: Аналитические функции, Ошибка приближения и сходимость, Обобщение, Список рядов Маклорена некоторых общих функций, Показательная функция, Натуральный логарифм, Геометрический ряд, Биномиальный ряд.