Разложить вектор c по векторам a и b: Разложение вектора по векторам

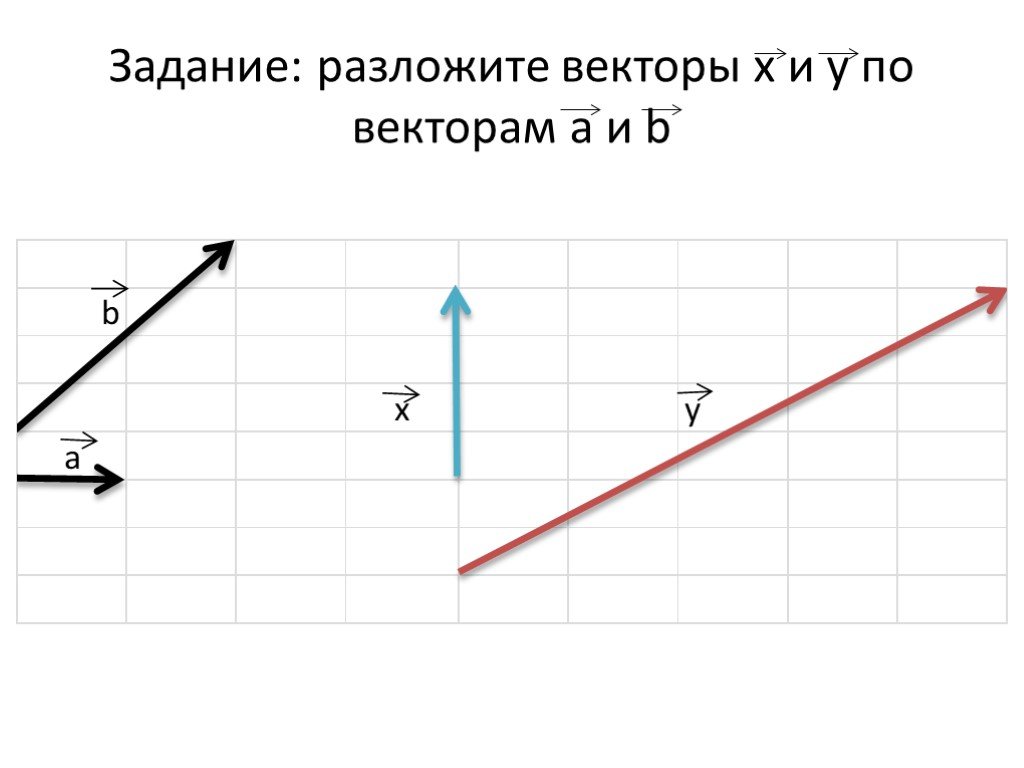
Разложение вектора по трём некомпланарным векторам

В пространстве, как и на плоскости, можно использовать вектора. Правила работы с ними похожи на уже известные нам действия с плоскими векторами.

Напомним, что в курсе планиметрии мы уже подробно изучали вектора и действия с ними. При этом предполагалось, что все вектора располагаются в одной плоскости. Однако можно расширить понятие вектора так, чтобы они использовались и в стереометрии. В таком случае вектора уже могут располагаться в различных плоскостях.

Начнем с определения вектора:

Вектором называется направленный отрезок, он имеет направление и величину.

Длина вектора соответствует длине отрезка, задающего этот вектор.

Вектор – это направленный отрезок прямой. Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например:

 →

  a . Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так:

 →

 AB.

А теперь — обратите внимание на следующую схему (она представлена ниже).

Конец вектора обозначают с помощью стрелки.

Здесь показаны сразу три вектора: У вектора АВ начало находится в точке А, а конец – в точке В. Аналогично у вектора СD точка С – это начало, а D – это конец. В обоих случаях начало и конец – это различные точки, поэтому АВ и CD именуют ненулевыми векторами. Если же начало и конец находятся в одной точке, например в Т, то получается нулевой вектор ТТ.

Всякую точку в пространстве можно рассматривать как нулевой вектор:

Нулевой вектор — это вектор, у которого начало и конец находится в одной и той же точке.

Длина вектора АВ — это длина соответствующего ему отрезка АВ. Для обозначения длины используют квадратные скобки.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Естественно, что нулевой вектор имеет нулевую длину. Далее напомним понятие коллинеарных векторов:

Коллинеарные вектора — это вектора, лежащие на одной прямой или на параллельных прямых.

Коллинеарные вектора могут быть либо сонаправленными, либо противоположно направленными. Сонаправленные вектора находятся на сонаправленных лучах.

Компланарные векторы — векторы, лежащие в одной плоскости или в параллельных плоскостях.

Если вектор с можно разложить по векторам а и b, то есть, представить в виде с=ха+yb, где x и y – некоторые числа, то векторы а, b и с компланарны.

Правило параллелепипеда — правило сложения трёх некомпланарных векторов, состоящее в том, что все три вектора откладывают из одной точки и строят параллелепипед таким образом, чтобы данные векторы были его рёбрами. Тогда вектор, отложенный из той же точки и совпадающий с диагональю параллелепипед, будет суммой трёх данных векторов.

          →                                                                          →  → → 

Вектор р разложен по трём некомпланарным векторам а, b и с, если его можно представить в виде

→  → → →

 р = ха + yb + zc,

где x, y и z — коэффициенты разложения.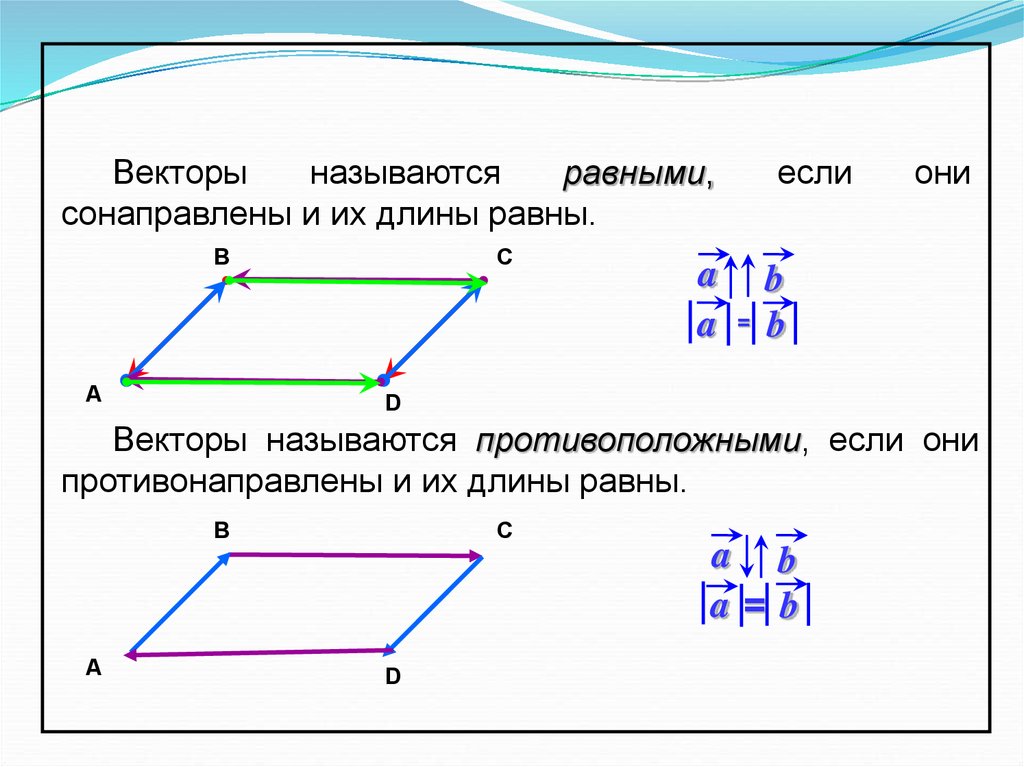

Теорема о разложении вектора по трём некомпланарным векторам. Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.

Прямоугольная система координат в пространстве — три взаимно перпендикулярные прямые x, y, z, на которых выбраны направление и единица измерения отрезков, которые лежат в трёх разных плоскостях xy, yz, xz и имеют общую точку пересечения O.

Оси координат — прямые x, y, z с выбранными на них направлениями.

Начало координат — точка их пересечения О.

Оси координат в пространстве обозначают Ox, Oy, Oz (соответственно ось абсцисс, ось ординат, ось аппликат).

Координатные векторы — единичные векторы, направление которых совпадает с положительным направлением координатных осей.

        →                                                                                    →

Вектор i совпадает по направлению с осью абсцисс, вектор j совпадает по

                                                            →

направлению с осью ординат, вектор k– с осью аппликант.

                            → 

Любой вектор с можно разложить по координатным векторам:

   →   →   → → 

     с = xi + yj + zk

                                → 

Координаты вектора с в данной системе координат — коэффициенты разложения x, y и k, которые определяются единственным образом:

→ 

c (x ; y ; z).

Разложение вектора на некомпланарные вектора

Иногда вектор можно разложить не на два, а на три вектора. Выглядит такое разложение так:

 →   →   → →

  p = xa + yb + zc 

Здесь p, a, b, c — это некоторые сектора, а x, y, z — это какие-то действительные числа. Оказывается, что справедлива следующая теорема.

Теорема. Любой вектор в пространстве можно разложить по трем заранее заданным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.

Пример решения задачи на разложение вектора по трем некомпланарным

Задача: дан куб  с ребром m.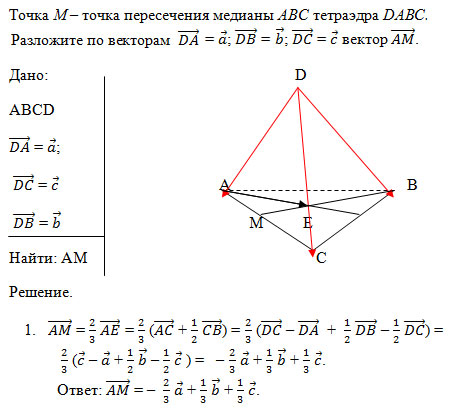 Точка К – середина ребра . Разложить вектор по векторам и найти его длину.

Решение: построим заданный куб

Векторами и задается плоскость квадрата . Третий вектор не лежит в этой плоскости, отсюда заключаем, что три заданных вектора , и некомпланарны, и мы можем выразить через них искомый вектор . Найдем вектор по правилу многоугольника. Очевидно, что в данной задаче для этого есть множество способов, но мы выбираем самый короткий путь: . вектор мы по условию обозначили как вектор . Вектор согласно свойствам куба равен вектору , обозначенному за вектор .

Вектор составляет половину вектора , так как точка К – середина ребра по условию: . Вектор согласно свойствам куба, равен вектору , обозначенному как вектор . Имеем:

Так, заданный вектор выражен через три некомпланарных вектора. Осталось найти его длину. Здесь нужно применить теорему Пифагора. Рассмотрим прямоугольный треугольник . Он прямоугольный потому, что ребро перпендикулярно всей плоскости основания , значит и любой прямой в этой плоскости, значит прямой . Один из катетов равен m как ребро куба. Катет найдем из другого прямоугольного треугольника – , где он уже является гипотенузой. Здесь катет равен m как ребро куба. Катет равен , так как точка К – середина ребра . Имеем:

Для закрепления нового материала повторите новые для себя определения, правила, теоремы. Также запомните Признак компланарности трёх векторов. Это пригодится вам в дальнейшей изучении материала.

Даны векторы cba    , , . Показать, что векторы a  и образуют … — Учеба и наука

Лучший ответ по мнению автора

08. 03.21 Лучший ответ по мнению автора

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше

На окружности с центром в точке О по порядку отмечены 4 точки: D, H, L, P. Найди вторую сторону получившегося четырехугольника, если угол D=90

Периметр правильного треугольника, вписанного в окружность, равен 6√3 дм. Найдите периметр правильного шестиугольника описанного около той же окружности.

Решено

Начертите треугольник АВС. Постройте вектор: 1) АС+СВ 2)ВА-ВС 3)АС+АВ

Прямоугольник со сторонами 2 см и 11см вращается около прямой, находящейся на расстоянии 2см от большей стороны. Вычислить объем полученного

Пользуйтесь нашим приложением

2.3 Создание векторов с шаблонами

Теперь вы знакомы с числовым вектором, вектором символов и логическим вектором и можете создавать их с нуля, используя функцию c() . Однако во многих приложениях нам может понадобиться создать векторы со значениями определенных шаблонов . В этом разделе мы представим несколько часто используемых функций для генерации векторов с шаблонами.

2.3.1 Создание равноотстоящих числовых векторов через

:

Одним из часто используемых шаблонов, связанных с числовыми векторами, являются числовые векторы, состоящие из равноотстоящих целых чисел, где все различия между соседними значениями в векторах равны \(1\) или \(-1\).

Предположим, мы хотим создать вектор с последовательными целыми числами от 1 до 5. Первый способ — записать все числа в c() ,

 pattern1 <- c(1, 2, 3, 4, 5) 

Как видите, перечислить все 5 целых чисел при создании 9 не так уж и сложно.0003 шаблон1 . Давайте представим, что мы хотим создать вектор, содержащий 100 последовательных целых чисел. Есть ли у нас более быстрый способ, чем запись всех 100 целых чисел? Ответ: Да!

Вы можете использовать оператор двоеточия : , который часто используется в повседневном программировании. (Обратите внимание, что вам не нужно использовать c() вместе с : )

 pattern2 <- 1:5 #последовательные целые числа от 1 до 5 

В дополнение к созданию векторов с последовательными целыми числами, которые возрастают, : также можно использовать для создания векторов с целыми числами в убывающей последовательности.

 pattern3 <- 6:2 # убывающая последовательность от 6 до 2
pattern4 <- 3:-3 #убывающая последовательность от 3 до -3 

Мощный оператор : , он может генерировать только равноотстоящие числовые векторы с приращением 1 или -1. Если вы хотите генерировать равноотстоящие числовые векторы с разными приращениями, вы можете использовать более мощную функцию

seq() .

2.3.2 Создание равноотстоящих числовых векторов с помощью

seq()

Очень эффективный способ создать равноотстоящих числовых векторов — использовать функцию seq() , сокращенно от sequence.

а. Создание последовательности с аргументом на

Чтобы использовать функцию seq() , вы можете указать начальное значение последовательности в аргументе из , предельное конечное значение в аргументе от до и увеличить аргумент на .

 seq(from = 1, to = 5, by = 1) 

Здесь вектор начинается с 1, увеличивается на 1 на каждом шаге и заканчивается на 5. Обратите внимание, что от и по аргументы необязательно в seq() . Если вы не укажете их значения, seq() будет использовать значение по умолчанию 1 для обоих аргументов.

 seq(to = 5) 

Далее давайте изменим приращение на 2, и вы получите числовой вектор со значениями 1 3 5 .

 посл(от = 1, до = 5, по = 2)
#> [1] 1 3 5 

Обратите внимание, что конечное значение последовательности не всегда равно аргументу от до .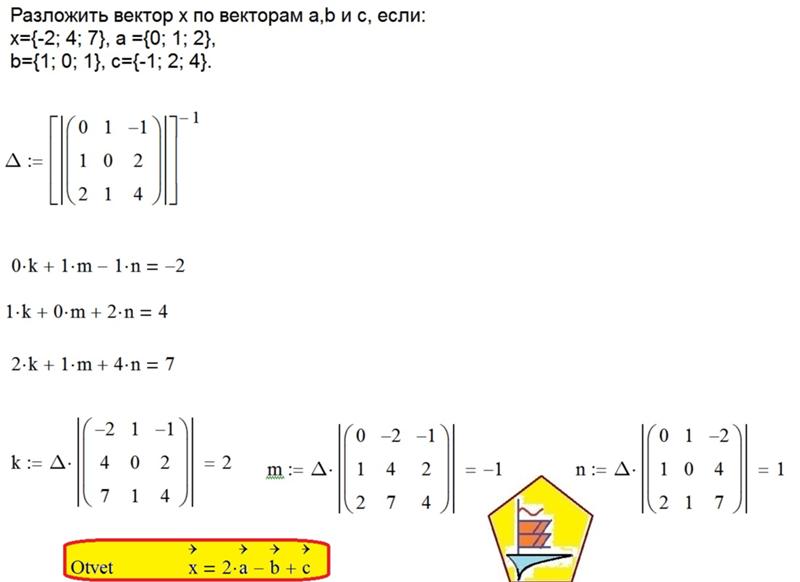 Если вы измените предельное конечное значение на 6, вы все равно получите ту же последовательность, поскольку следующим значением в последовательности будет 7, что больше, чем предельное конечное значение 6. Это причина, по которой от до называется ограниченным концом. значение, а не конечное значение.

 посл(от = 1, до = 6, по = 2)
#> [1] 1 3 5 

В отличие от : , вы можете установить значения трех аргументов в seq() в виде десятичных чисел.

 сл(от = 1,1, до = 6,2, по = 0,7)
#>
  [1] 1.1 1.8 2.5 3.2 3.9 4.6 5.3 6.0 

Здесь вы получите последовательность, которая начинается с 1.1 и каждый раз увеличивается на 0,7, пока не превысит 6,2.

Вы также можете создать убывающую последовательность, используя меньшее значение от до , чем значение из , в сочетании с отрицательным значением в аргументе на .

 сл(от = 1,5, до = -1, по = -0,5) 

Если в аргументе на используется положительное значение в убывающей последовательности, вы увидите сообщение об ошибке.

 сл(от = 1,5, до = -1, по = 0,5)
#> Ошибка в seq.default(from = 1.5, to = -1, by = 0.5): неверный знак в аргументе by 

b. Создание последовательностей с аргументом length.out

Вместо установки приращения вы также можете указать аргумент

length.out , который создает последовательность с равным пробелом в указанной длине. R автоматически рассчитает интервал между двумя соседними числами по значениям трех аргументов в последовательность() .

 seq(from = 1, to = 5, length.out = 9) 

Здесь вы получите равноотстоящую последовательность длины 9 от 1 до 5.

Вы также можете создать убывающую последовательность, используя аргумент length.out .

 seq(from = 5, to = -5, length.out = 9) 

В отличие от создания последовательностей с аргументом на , если вы укажете аргумент length.out в seq() , начальное значение и конечное значение последовательности, которую вы получите, будет точно соответствовать входным аргументам.

в. Создайте последовательности с аргументами на и length.out

. С одним фиксированным значением (начальное значение или предельное конечное значение) seq() создаст вектор с указанным приращением и длиной.

Если у вас есть только аргумент из , вы получите последовательность, начинающуюся со значения, которое вы установили, с приращением в на , пока не получите последовательность указанной длины.

 seq(from = 1, by = 2, length.out = 5) 

Если у вас есть только аргумент от до , вы получите конец последовательности со значением, которое вы установили с приращением в аргументе на , пока не получите последовательность заданной длины.

 seq(to = 1, by = 2, length.out = 5) 

Последнее, что касается seq() , заключается в том, что вы можете максимум предоставить три аргумента. Например, вы увидите ошибку при выполнении следующего примера, поскольку указаны все четыре аргумента.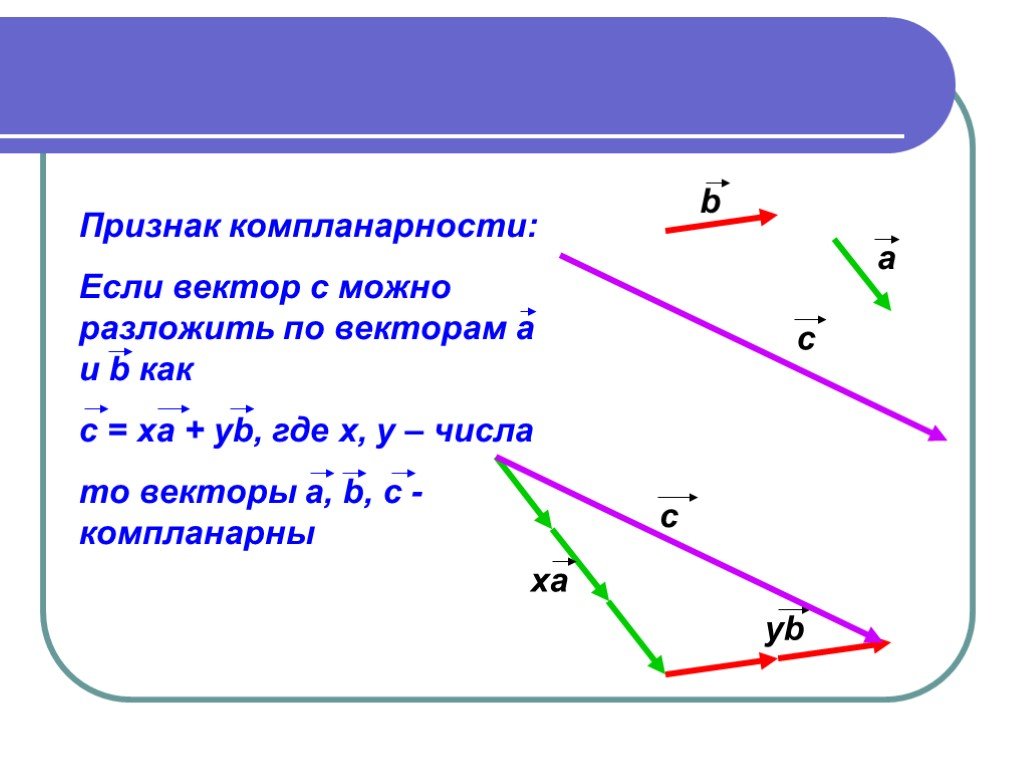

 seq(от = 1, до = 3, по = 1, length.out = 3)
#> Ошибка в seq.default(from = 1, to = 3, by = 1, length.out = 3): слишком много аргументов 

2.3.3 Создать совпадающие числовые векторы с помощью

seq_along()

Теперь мы представит одну функцию, связанную с seq() . Давайте сначала создадим числовой вектор,

 extend <- seq(from = 2, to = 8, length.out = 9) 

Из приведенного выше seq() вы знаете, что длина этого вектора равна 9. Затем поместим этот числовой вектор в seq_along() .

 seq_along (расширить)
#> [1] 1 2 3 4 5 6 7 8 9 

seq_along() принимает вектор в качестве аргумента и генерирует последовательные целые числа от 1 до длины входного вектора. Функция seq_along() обычно используется при написании циклов, которые будут рассмотрены позже.

2.3.4 Создание числовых векторов с помощью

sequence()

Иногда вам может понадобиться объединить несколько целочисленных последовательностей с равными интервалами в один вектор. Для этого можно использовать функцию последовательность() . Чаще всего функция sequence() используется для подачи вектора целых чисел в качестве входных данных.

 comp_seq1 <- последовательность (с (2, 3, 5))
comp_seq1
#> [1] 1 2 1 2 3 1 2 3 4 5 

Из результата видно, что сначала создаются равноотстоящие векторы 1:2 , 1:3 и 1:5 , затем объедините все векторы в один. Это позволяет избежать проблем с записью чего-то вроде c(1:2, 1:3, 1:5) .

2.3.5 Создание числовых, символьных и логических векторов с повторением

Другим часто используемым шаблоном, связанным с векторами, является повторение . Обратите внимание, что в то время как шаблон с равными интервалами имеет смысл только для числовых векторов, шаблон повторения работает для всех трех типов векторов.

Чтобы выполнить повторение, вы можете использовать функцию rep() , которая работает, повторяя первый аргумент столько раз, сколько указано во втором аргументе.

Во-первых, давайте создадим числовой вектор с повторением.

 num1 <- rep(2, 4)
число1
#> [1] 2 2 2 2 

Поскольку первый аргумент равен 2 , а второй аргумент равен 4 , 2 повторяется 4 раза, в результате получается вектор длины 4 со всеми элементами со значением 2.

Первый аргумент также может быть числовым вектором с несколькими значениями.

 num2 <- rep(c(1, 4, 2), 3)
число2
#> [1] 1 4 2 1 4 2 1 4 2 

Здесь rep() будет повторять весь вектор c(1, 4, 2) три раза. Обратите внимание, что вектор равен повторяет целиком, а не поэлементно.

Вам может быть интересно, что происходит, когда второй аргумент также имеет несколько чисел? Давайте попробуем вместе.

 num3 <- rep(c(1,5,7), c(3,2,1))
число3
#> [1] 1 1 1 5 5 7 

Когда второй аргумент также является вектором, R выполнит операцию повторения элементов , повторив каждый элемент в первом аргументе количество раз, указанное в соответствующем месте второй аргумент и объединить повторяющиеся векторы в один вектор.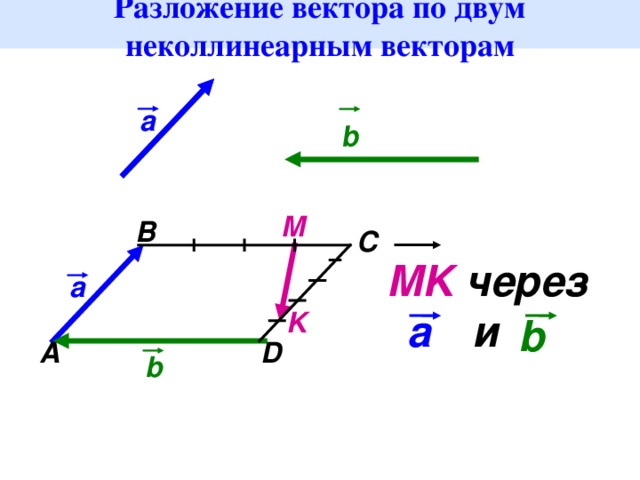 В этом примере 1 повторяется 3 раза, 4 повторяется дважды, а 7 повторяется один раз. Это эквивалентно

 c(rep(1,3), rep(4,2), rep(7,1)) 

Функция rep() работает так же, если первый аргумент является вектором символов.

 animals1 <- rep(c("овца", "свинья", "обезьяна"), 2)
животные1
животные2 <- rep(c("овца", "свинья", "обезьяна"), c(3, 2, 1))
animals2 

Вы также можете использовать логические векторы в первом аргументе.

 логика <- rep(c(ИСТИНА, ЛОЖЬ), c(3,2))
логика 

2.3.6 Получение уникальных элементов и их частот

Итак, вы узнали, как создавать векторы с различными шаблонами. Иногда вам может понадобиться получить уникальные элементы (элементы с разными значениями) вектора и соответствующие им частоты. Давайте использовать num3 в качестве примера. (не забудьте использовать ls() или проверьте панель среды, чтобы найти все определенные вами объекты) ,

 num3 #проверьте значения
#> [1] 1 1 1 5 5 7 

Вы можете использовать unique() для отображения всех уникальных элементов в векторах.

 unique(num3) #получить уникальные элементы
#> [1] 1 5 7 

Из результата вы знаете, что уникальными элементами в num3 являются 1 , 5 и 7 . Чтобы получить частоту каждого элемента, вы можете использовать функцию table() .

 table(num3) #получить таблицу частот
#> число3
#> 1 5 7
#> 3 2 1 

Здесь первая строка — это имя объекта, вторая строка показывает все уникальные элементы, а третья строка — соответствующая частота каждого элемента в том же столбце. В num3 есть три 1 s, два 5 s и один 7 .

уникальный() и table() работают одинаково для векторов символов и логических векторов. Вы можете попробовать следующие коды.

 животных
уникальные (животные)
стол(животные)
логика
уникальный (логика)
table(logic) 

2.3.7 Упражнения

1. Используйте пять различных способов для создания равноотстоящей последовательности с 2 4 6 8 10 в результате.

2. Используйте два разных способа для создания числового вектора с результатом 1 2 3 1 2 3 4 5 1 2 3 4 5 6 7 . Покажите уникальные элементы и их соответствующую частоту.

3. Напишите код R, используя функцию rep() для создания вектора символов с тем же результатом, что и c("овца","свинья", "кошка","овца","свинья", "кошка"," овца", "свинья", "кошка")

4. Напишите код R, используя функцию rep() для создания вектора символов с тем же результатом, что и c("овца","овца","свинья","свинья","свинья","свинья","кошка ","кошка","кошка")

numpy.reshape — Руководство NumPy v1.24

numpy.reshape ( a , newshape , order='C' ) [источник]

Придает новую форму массиву без изменения его данных.

Параметры:

a array_like

Массив для изменения формы.

newshape int или кортеж int

Новая форма должна быть совместима с исходной формой. Если целое число, то результатом будет одномерный массив этой длины. Один размер формы может быть -1. В этом случае значение равно выводится из длины массива и оставшихся измерений.

порядок {‘C’, ‘F’, ‘A’}, необязательный

Считать элементы a , используя этот индексный порядок, и разместить элементы в измененный массив, используя этот порядок индексов. «С» означает чтение/запись элементов с использованием C-подобного порядка индексов, с последним индексом оси, изменяющимся быстрее всего, обратно к первому индекс оси меняется медленнее всего. «F» означает читать/писать элементы, использующие порядок индексов, подобный Fortran, с первым индексом изменяется быстрее всего, а последний индекс изменяется медленнее всего. Обратите внимание, что опции «C» и «F» не учитывают структуру памяти базовый массив и ссылаться только на порядок индексации. «A» означает чтение/запись элементов в Фортран-подобном индексе. заказать если a - это Fortran смежные в памяти, C-подобный порядок в противном случае.

Возвратов:

reshed_array ndarray

Если возможно, это будет новый объект просмотра; иначе будет быть копией. Обратите внимание, что не гарантируется макет памяти (C- или Fortran-contiguous) возвращаемого массива.

См. также

ndarray.reshape

Эквивалентный метод.

Примечания

Не всегда возможно изменить форму массива без копирование данных. Если вы хотите, чтобы при копировании данных возникала ошибка, вы должны назначить новую форму атрибуту формы массива:

 >>> a = np.zeros((10, 2))
# Транспонирование делает массив несмежным
>>> б = а.Т
# Просмотр позволяет изменить форму без изменения
# исходный объект. 
>>> c = b.view()
>>> c.shape = (20)
Traceback (последний последний вызов):
   ...
AttributeError: Несовместимая форма для модификации на месте. Использовать
`.reshape()`, чтобы сделать копию нужной формы.
 

Ключевое слово order задает порядок индекса как для , так и для выборки значений. из в , а затем помещая значений в выходной массив. Например, допустим, у вас есть массив:

.

 >>> a = np.arange(6).reshape((3, 2))
>>> а
массив([[0, 1],
       [2, 3],
       [4, 5]])
 

Вы можете думать об изменении формы как о первом распутывании массива (используя заданный порядок индекса), затем вставка элементов из распутанного массива в новый массив, использующий тот же порядок индексов, что и для распутывать.

 >>> np.reshape(a, (2, 3)) # C-подобный порядок индексов
массив([[0, 1, 2],
 [3, 4, 5]])
>>> np.reshape(np.ravel(a), (2, 3)) # эквивалентно C ravel then C reshape
массив([[0, 1, 2],
 [3, 4, 5]])
>>> np.
No related posts.