Разность комплексных чисел: Вычитание комплексных чисел | Математика

Алгебраические действия с комплексными числами: сумма, разность

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Сложение и вычитание комплексных чисел

В данной публикации мы рассмотрим формулы, с помощью которых можно найти сумму или разность двух комплексных чисел, представленных в алгебраической форме. Также приведены примеры для лучшего понимания теоретического материала.

• Сложение комплексных чисел
• Вычитание комплексных чисел

Сложение комплексных чисел

Если сложить два комплексных числа x = a₁ + b₁i и y = a₂ + b₂i, то получится тоже комплексное число z:

z = x + y = (a₁ + a₂) + (b₁ + b₂) ⋅ i

Таким образом, мы отдельно складываем действительные и мнимые части суммируемых чисел.

Пример 1
Найдем сумму комплексных чисел: x = 8 + 3i и y = 5 – i.

Решение:
x + y = (8 + 5) + (3i – i) = 13 + 2i.

Вычитание комплексных чисел

Разность двух комплексных чисел x = a₁ + b₁i и y = a₂ + b₂i вычисляется по формуле:

z = x – y = (a₁ – a₂) + (b₁ – b₂) ⋅ i

То есть получится комплексное число, действительная и мнимая части которого равны разности соответствующих частей

x и y.

Пример 2
Вычтем из x = 12 – 7i число y = -8 + 4i.

Решение:
x – y = (12 – (-8)) + (-7i – 4i) = 20 – 11i.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Курс высшей математики, Т.

1 Курс высшей математики, Т.1

В.И.Смирнов Курс высшей математики, Т.1.: Изд-во «Наука». 1974. — 479 с. Фундаментальный учебник по высшей математике, выдержавший более двадцати изданий, переведенный на множество языков мира, отличается, с одной стороны, систематичностью и строгостью изложения, а с другой – простым языком, подробными пояснениями и многочисленными примерами. Книга состоит из пяти томов. Тома третий и четвертый – каждый из двух частей. Для студентов университетов и технических вузов. Оглавление ПРЕДИСЛОВИЕ К ВОСЬМОМУ ИЗДАНИЮ ГЛАВА I. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ И ТЕОРИЯ ПРЕДЕЛОВ 1. Величина и ее измерение. 2. Число. 3. Величины постоянные и переменные. 4. Промежуток. 5. Понятие о функции. 6. Аналитический способ задания функциональной зависимости. 7. Неявные функции. 8. Табличный способ. 9. Графический способ изображения чисел. 10. Координаты. 11. График и уравнение кривой. 12. Линейная функция. 13. Приращение. Основное свойство линейной функции. 14. График равномерного движения. 15. Эмпирические формулы. 16. Парабола второй степени. 17. Парабола третьей степени. 18. Закон обратной пропорциональности. 19. Степенная функция. 20. Обратные функции. 21. Многозначность функции. 22. Показательная и логарифмическая функции. 23. Тригонометрические функции. 24. Обратные тригонометрические, или круговые, функции. § 2. ТЕОРИЯ ПРЕДЕЛОВ. НЕПРЕРЫВНЫЕ ФУНКЦИИ 25. Упорядоченное переменное. 26. Величины бесконечно малые. 27. Предел переменной величины. 28. Основные теоремы. 29. Величины бесконечно большие. 30. Монотонные переменные. 31. 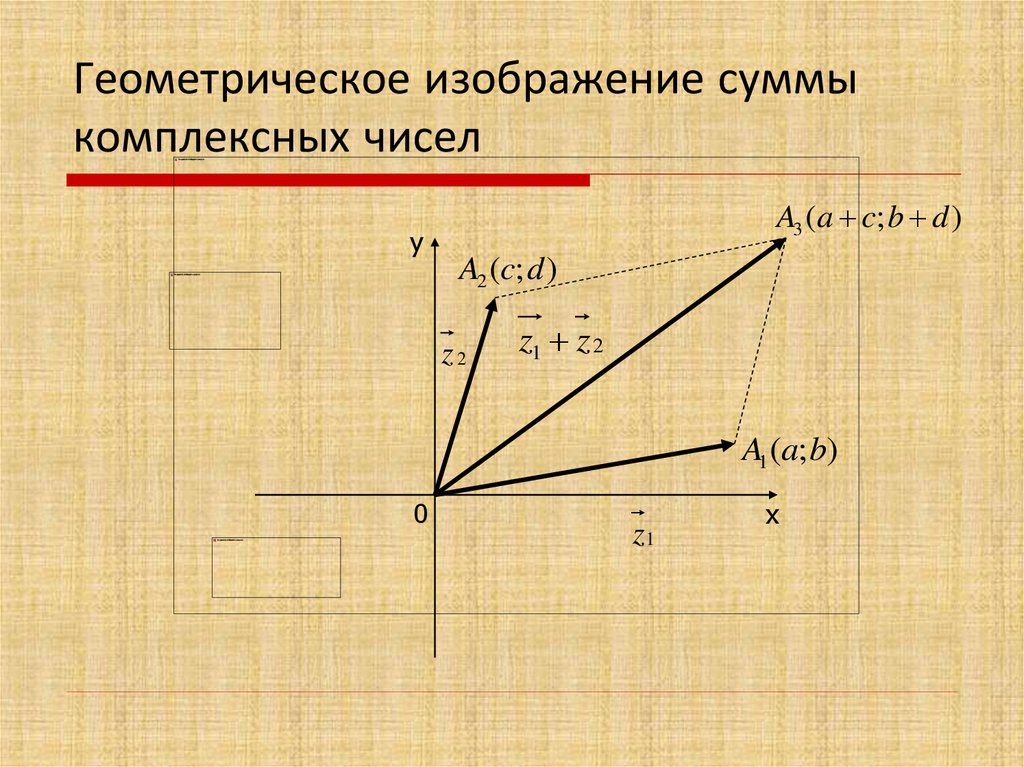Признак Коши существования предела. 32. Одновременное изменение двух переменных величин, связанных функциональной зависимостью. 33. Примеры. 34. Непрерывность функции. 35. Свойства непрерывных функций. 36. Сравнение бесконечно малых и бесконечно больших величин. 37. Примеры. 38. Число е. 39. Недоказанные предложения. 40. Вещественные числа. 41. Действия над вещественными числами. 42. Точные границы числовых множеств. Признаки существования предела. 43. Свойства непрерывных функций. 44. Непрерывность элементарных функций. ГЛАВА II. ПОНЯТИЕ О ПРОИЗВОДНОЙ И ЕГО ПРИЛОЖЕНИЯ 45. Понятие о производной. 46. Геометрическое значение производной. 47. Производные простейших функций. 48. Производные сложных и обратных функций. 49. Таблица производных и примеры. 50. Понятие о дифференциале. 51. Некоторые дифференциальные уравнения. 52. Оценка погрешностей. § 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ 53. Производные высших порядков. 54. Механическое значение второй производной. 55. Дифференциалы высших порядков. 56. Разности функций. § 5. ПРИЛОЖЕНИЕ ПОНЯТИЯ О ПРОИЗВОДНОЙ К ИЗУЧЕНИЮ ФУНКЦИЙ 57. Признаки возрастания и убывания функций. 58. Максимумы и минимумы функций. 59. Построение графиков. 60. Наибольшее и наименьшее значения функций. 61. Теорема Ферма. 62. Теорема Ролля. 63. Формула Лагранжа. 64. Формула Коши. 65. Раскрытие неопределенностей. 66. Различные виды неопределенностей. § 6. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ 68. Частные производные и полный дифференциал функции двух независимых переменных. 69. Производные сложных и неявных функций. § 7. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОНЯТИЯ О ПРОИЗВОДНЫХ 70. Дифференциал дуги. 71. Выпуклость, вогнутость и кривизна. 72. Асимптоты. 73. Построение графиков. 74. Параметрическое задание кривой. 75. Уравнение Ван-дер-Ваальса. 76. Особые точки кривых. 77. Элементы кривой. 78. Цепная линия. 79. Циклоида. 80. Эпициклоиды и гипоциклоиды. 81. Развертка круга. 82. Кривые в полярных координатах. 83. Спирали. 85. Овалы Кассини и лемниската. ГЛАВА III. ПОНЯТИЕ ОБ ИНТЕГРАЛЕ И ЕГО ПРИЛОЖЕНИЯ 86. Понятие о неопределенном интеграле. 87. Определенный интеграл как предел суммы. 88. Связь определенного и неопределенного интегралов. 89. Свойства неопределенного интеграла. 90. Таблица простейших интегралов. 91. Правило интегрирования по частям. 92. Правило замены переменных. Примеры. 93. Примеры дифференциальных уравнений первого порядка. § 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 94. Основные свойства определенного интеграла. 95. Теорема о среднем. 96. Существование первообразной функции. 97. Разрыв подынтегральной функции. 98. Бесконечные пределы. 99. Замена переменной под знаком определенного интеграла. 100. Интегрирование по частям. § 10. ПРИЛОЖЕНИЯ ПОНЯТИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 101. Вычисление площадей. 102. Площадь сектора. 103. Длина дуги. 104. Вычисление объемов тел по их поперечным сечениям. 105. Объем тела вращения. 106. Поверхность тела вращения. 107. Определение центров тяжести. Теоремы Гульдина. 108. Приближенное вычисление определенных интегралов; формулы прямоугольников и трапеций. 109. Формула касательных и формула Понселе. 110. Формула Симпсона. 111. Вычисление определенного интеграла с переменным верхним пределом. 112. Графические способы. 113. Площади быстро колеблющихся кривых. § 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ОБ ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ 115. Разбиение промежутка на части и образование различных сумм. 116. Интегрируемые функции. 117. Свойства интегрируемых функций. ГЛАВА IV. РЯДЫ И ИХ ПРИЛОЖЕНИЯ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 118. Понятие о бесконечном ряде. 119. Основные свойства бесконечных рядов. 120. Ряды с положительными членами. Признаки сходимости. 121. Признаки Коши и Даламбера. 122. Интегральный признак сходимости Коши. 123. Знакопеременные ряды. 124. Абсолютно сходящиеся ряды. 125. Общий признак сходимости. § 13. ФОРМУЛА ТЕЙЛОРА И ЕЕ ПРИЛОЖЕНИЯ 126. Формула Тейлора. 127. Различные виды формулы Тейлора. 128. Ряды Тейлора и Маклорена. 129. Разложение exp(x). 130. Разложение sin x и cos x. 131. Бином Ньютона. 132. Разложение log(1+x). 133. Разложение arctg x. 134. Приближенные формулы. 135. Максимумы, минимумы и точки перегиба. 136. Раскрытие неопределенностей. § 14. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ РЯДОВ 137. Свойства абсолютно сходящихся рядов. 138. Умножение абсолютно сходящихся рядов. 139. Признак Куммера. 140. Признак Гаусса. 141. Гипергеометрический ряд. 142. Двойные ряды. 143. Ряды с переменными членами. Равномерно сходящиеся ряды. 144. Равномерно сходящиеся последовательности функций. 145. Свойства равномерно сходящихся последовательностей. 146. Свойства равномерно сходящихся рядов. 147. Признаки равномерной сходимости. 148. Степенные ряды. Радиус сходимости. 149. Вторая теорема Абеля. 150. Дифференцирование и интегрирование степенного ряда. ГЛАВА V. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 15. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ФУНКЦИИ 152. О предельном переходе. 153. Частные производные и полный дифференциал первого порядка. 154. Однородные функции. 155. Частные производные высших порядков. 156. Дифференциалы высших порядков. 157. Неявные функции. 158. Пример. 159. Существование неявных функций. 160. Кривые в пространстве и поверхности. § 16. ФОРМУЛА ТЕЙЛОРА. МАКСИМУМЫ И МИНИМУМЫ ФУНКЦИИ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 161. Распространение формулы Тейлора на случай функции от нескольких независимых переменных. 162. Необходимые условия максимума и минимума функции. 163. Исследование максимума и минимума функции двух независимых переменных. 164. Примеры. 165. Дополнительные замечания о нахождении максимумов и минимумов функции. 166. Наибольшее и наименьшее значения функции. 167. Относительные максимумы и минимумы. 168. Дополнительные замечания. 169. Примеры. ГЛАВА VI. КОМПЛЕКСНЫЕ ЧИСЛА, НАЧАЛА ВЫСШЕЙ АЛГЕБРЫ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ 170. Комплексные числа. 171. Сложение и вычитание комплексных чисел. 172. Умножение комплексных чисел. 173. Деление комплексных чисел. 174. Возвышение в степень. 175. Извлечение корня. 176. Показательная функция. 177. Тригонометрические и гиперболические функции. 178. Цепная линия. 179. Логарифмирование. 180. Синусоидальные величины и векторные диаграммы. 181. Примеры. 182. Кривые в комплексной форме. 183. Представление гармонического колебания в комплексной форме. § 18. ОСНОВНЫЕ СВОЙСТВА ЦЕЛЫХ МНОГОЧЛЕНОВ И ВЫЧИСЛЕНИЕ ИХ КОРНЕЙ 185. Разложение многочлена на множители. 186. Кратные корни. 187. Правило Горнера. 188. Общий наибольший делитель. 189. Вещественные многочлены. 190. Зависимость между корнями уравнения и его коэффициентами. 191. Уравнение третьей степени. 192. Решение кубического уравнения в тригонометрической форме. 193. Способ итерации. 194. Способ Ньютона. 195. Способ простого интерполирования. § 19. ИНТЕГРИРОВАНИЕ ФУНКЦИИ 196. Разложение рациональной дроби на простейшие. 197. Интегрирование рациональной дроби. 198. Интеграл от выражений, содержащих радикалы. 199. Интегралы вида… 200. Интегралы вида… 201. Интегралы вида…

Сложение и вычитание комплексных чисел

Сложение и вычитание комплексных чисел — математические операции над комплексными числами. Прежде чем вдаваться в подробности сложения и вычитания комплексных чисел, давайте вспомним значение комплексных чисел. Комплексное число — это комбинация действительного числа и мнимого числа. Он имеет вид a + ib и обычно обозначается буквой z. Действительная и мнимая части комплексного числа складываются отдельно при сложении комплексных чисел. Точно так же для вычитания комплексных чисел мы вычитаем действительную и мнимую части комплексных чисел отдельно.

В этой статье мы рассмотрим концепцию сложения и вычитания комплексных чисел вместе с их правилами и шагами с помощью примеров. Мы также изучим концепцию сложения и вычитания комплексных чисел в полярной форме.

1.	Что такое сложение и вычитание комплексных чисел?
2.	Добавление комплексных чисел
3.	Вычитание комплексных чисел
4.	Шаги и правила сложения и вычитания комплексных чисел
5.	Свойства сложения и вычитания комплексных чисел
6.	Часто задаваемые вопросы о сложении и вычитании комплексных чисел

Что такое сложение и вычитание комплексных чисел?

Сложение и вычитание комплексных чисел являются фундаментальными операциями, применяемыми к комплексным числам. Точно так же, как когда мы складываем или вычитаем многочлены, мы комбинируем одинаковые члены. Точно так же для сложения и вычитания комплексных чисел мы объединяем действительные части и мнимые части комплексных чисел, а затем применяем операцию. Давайте посмотрим формулу сложения и вычитания комплексных чисел z ₁ = a + ib и z ₂ = c + id, где a, b, c, d — действительные числа:

Добавление комплексных чисел

При выполнении операции сложения комплексных чисел мы соединяем действительные и мнимые части комплексных чисел и складываем их. Формула сложения комплексных чисел:

z ₁ + z ₂ = a + ib + c + id

= (a + c) + (ib + id)

= (a + c ) + i(b + d)

Отсюда имеем (a + ib) + (c + id) = (a + c) + i(b + d)

Вычитание комплексных чисел

Для вычитания комплексных чисел мы рассматриваем действительную и мнимую части комплексных чисел отдельно и вычитаем действительную и мнимую части одного комплексного числа из действительной и мнимой частей соответственно другого комплексного числа. Формула вычитания комплексных чисел:

z ₁ — z ₂ = (a + ib) — (c + id)

= a + ib — c — id

= (a — c) + (ib — id)

= (a — c) + i(b — г)

Отсюда имеем (а + ib) — (с + id) = (а — с) + i(b — d)

Шаги и правила сложения и вычитания комплексных чисел

Теперь мы знаем формулы сложения и вычитания комплексных чисел. Далее мы будем понимать процесс для того же пошагово. Ниже приведены шаги для сложения и вычитания комплексных чисел:

• Шаг 1: Разделите действительные и мнимые части комплексных чисел.
• Шаг 2: Сложите (вычтите) действительные части комплексных чисел.
• Шаг 3: Сложите (вычтите) мнимые части комплексных чисел.
• Шаг 4: Дайте окончательный ответ в формате + ib.

Свойства сложения и вычитания комплексных чисел

Ниже приведен список свойств сложения и вычитания комплексных чисел:

• Свойство замыкания: сумма и разность комплексных чисел также являются комплексными числами. Следовательно, он обладает свойством замыкания.
• Коммутативное свойство: сложение комплексных чисел коммутативно, но вычитание комплексных чисел не коммутативно.
• Ассоциативное свойство: сложение комплексных чисел является ассоциативным, но вычитание комплексных чисел не является ассоциативным.
• Аддитивное тождество: 0 — это аддитивное тождество комплексных чисел, т. е. для комплексного числа z мы имеем z + 0 = 0 + z = z.
• Обратное сложение: для комплексного числа z обратным сложением в комплексных числах является -z, т. е. z + (-z) = 0

Важные замечания по сложению и вычитанию комплексных чисел

• Сложение и вычитание комплексных чисел аналогично сложению и вычитанию двух двучленов. т. е. нам нужно просто скомбинировать подобные термы.
• Все действительные числа являются комплексными числами, но не все комплексные числа должны быть действительными числами.
• Вычитание комплексных чисел не соблюдает коммутативный закон.
• Для сложения и вычитания комплексных чисел в полярной форме мы сначала преобразуем комплексные числа в прямоугольную форму, а затем выполняем операцию. Затем мы преобразуем окончательный ответ в полярную форму.

Связанные темы

• Комплексные числа
• Деление комплексных чисел
• Умножение комплексных чисел

Часто задаваемые вопросы о сложении и вычитании комплексных чисел

Что такое сложение и вычитание комплексных чисел в математике?

Сложение и вычитание комплексных чисел — это основные операции, применяемые к комплексным числам. Точно так же, как когда мы складываем или вычитаем многочлены, мы комбинируем одинаковые члены. Точно так же для сложения и вычитания комплексных чисел мы объединяем действительные части и мнимые части комплексных чисел, а затем применяем операцию.

Что такое сложение комплексных чисел?

При выполнении операции сложения комплексных чисел мы соединяем действительные и мнимые части комплексных чисел и складываем их.

Что такое вычитание комплексных чисел?

Для вычитания комплексных чисел мы рассматриваем действительную и мнимую части комплексных чисел отдельно и вычитаем действительную и мнимую части одного комплексного числа из действительной и мнимой частей соответственно другого комплексного числа.

Как складывать и вычитать комплексные числа?

Действительная и мнимая части комплексного числа складываются отдельно при сложении комплексных чисел. Точно так же для вычитания комплексных чисел мы вычитаем действительную и мнимую части комплексных чисел отдельно.

Каковы свойства сложения и вычитания комплексных чисел?

Некоторые из важных свойств сложения и вычитания комплексных чисел :

• Сумма и разность комплексных чисел также являются комплексными числами.
• Сложение комплексных чисел ассоциативно, но вычитание комплексных чисел не ассоциативно.
• Сложение комплексных чисел коммутативно, но вычитание комплексных чисел не коммутативно.

Как найти сумму и разность двух комплексных чисел?

Чтобы найти сумму двух комплексных чисел, мы объединяем действительные части и мнимые части комплексных чисел, а затем складываем их и даем окончательный ответ в формате a + bi. Мы следуем тому же процессу, чтобы найти разность двух комплексных чисел. Единственное отличие состоит в том, что здесь мы вычитаем действительные и мнимые части, а не складываем их.

Какие формулы для сложения и вычитания комплексных чисел?

Для вычитания комплексных чисел мы используем формулу (a + ib) — (c + id) = (a — c) + i(b — d), а для сложения комплексных чисел используем формулу (a + ib) + (с + id) = (а + с) + i(b + d).

комплексная плоскость, сложение и вычитание

Комплексные числа: комплексная плоскость, сложение и вычитание Поскольку Гаусс доказал основную теорему алгебры, мы знаем, что все комплексные числа имеют вид x  +  yi, , где x и y — действительные числа, действительные числа — все те числа, которые являются положительными, отрицательными или нулевыми. Следовательно, мы можем использовать плоскость xy для отображения комплексных чисел. Мы даже назовем ее комплексной плоскостью , когда используем таким образом плоскость xy . Это дает нам второй путь к комплексным числам, первый путь — алгебраический, как в выражении x  +  yi.

Обозначение.

Стандартный символ для набора всех комплексных чисел — C , и мы также будем называть комплексную плоскость C .

Мы попробуем использовать x и y для действительных переменных, а z и w для комплексных переменных. Например, уравнение z  =  x  +  yi следует понимать как говорящее, что комплексное число z — это сумма действительного числа х и действительного числа y , умноженного на i. В целом, x Часть комплексного числа z = x + Yi называется Реальная часть из Z , в то время как Y называется воображаемая часть из y . . (Иногда и называют мнимой частью.)

Когда мы используем xy -плоскость для комплексной плоскости C , мы будем называть ось x реальной осью , ось и ось y мы будем называть мнимой осью.

Вещественные числа следует рассматривать как частные случаи комплексных чисел; это просто цифры x  +  yi , когда y равно 0, то есть это числа на действительной оси. Например, действительное число 2 равно 2 + 0 , т.е. Числа на мнимой оси иногда называют чисто мнимые числа.

Арифметические операции на

C Операции сложения и вычитания понятны. Чтобы сложить или вычесть два комплексных числа, просто сложите или вычтите соответствующие действительные и мнимые части. Например, сумма 5 + 3 i и 4 + 2 i равна 9 + 5 i. Во-вторых, сумма 3 +  i и 1 + 2 i равна 2 + 3 i.

Дополнение может быть представлено графически на комплексной плоскости C . Возьмем последний пример. Комплексное число z  = 3 +  i расположено на 3 единицы правее мнимой оси и на 1 единицу выше действительной оси, а w  = 1 + 2 i расположено на 1 единицу левее и 2 единиц вверх. Таким образом, сумма z + w  = 2 + 3 i равна 2 единицам вправо и 3 единицам вверх.

Правило параллелограмма.

Обратите внимание, что в последнем примере четыре комплексных числа 0, z  = 3 +  i, w  = 1 + 2 i, и z  + 7 w i 3 = 902 + 06 равны 902 06. углы параллелограмма. В целом это правда. Чтобы найти, где в плоскости C находится сумма z + w двух комплексных чисел z и w , на графике z и w, провести прямые от 0 до каждого из них, и завершите параллелограмм. Четвертая вершина будет с  +  с.

Дополнение в виде перевода.

Используя правило параллелограмма, можно интерпретировать сложение w как преобразование плоскости C . Добавление w к 0 дает w, , конечно, поэтому в этом преобразовании 0 перемещается в w . Любая другая точка z перемещается в z  +  w, , поэтому z перемещается в том же направлении на то же расстояние. Другими словами, каждая точка в C перемещается в том же направлении и на то же расстояние, когда к нему добавляется w . Можно сказать, что сложение w дает перевод плоскости C в направлении и на расстояние от 0 до w. Термин «вектор» обычно используется в описании: «плоскость переводится по вектору 0 w.

Отрицание и вычитание.

Есть и хорошая геометрическая интерпретация отрицания. Конечно, отрицание x  +  yi равно x    yi, , поэтому отрицание комплексного числа будет расположено прямо напротив 0 и на таком же расстоянии от него. Например, z  = 2 +  i расположено на 2 единицы вправо и на одну единицу вверх, поэтому его отрицание z  = 2   i расположено на 2 единицы влево и на одну единицу вниз.