Что такое прямой угол описания. Виды углов
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов.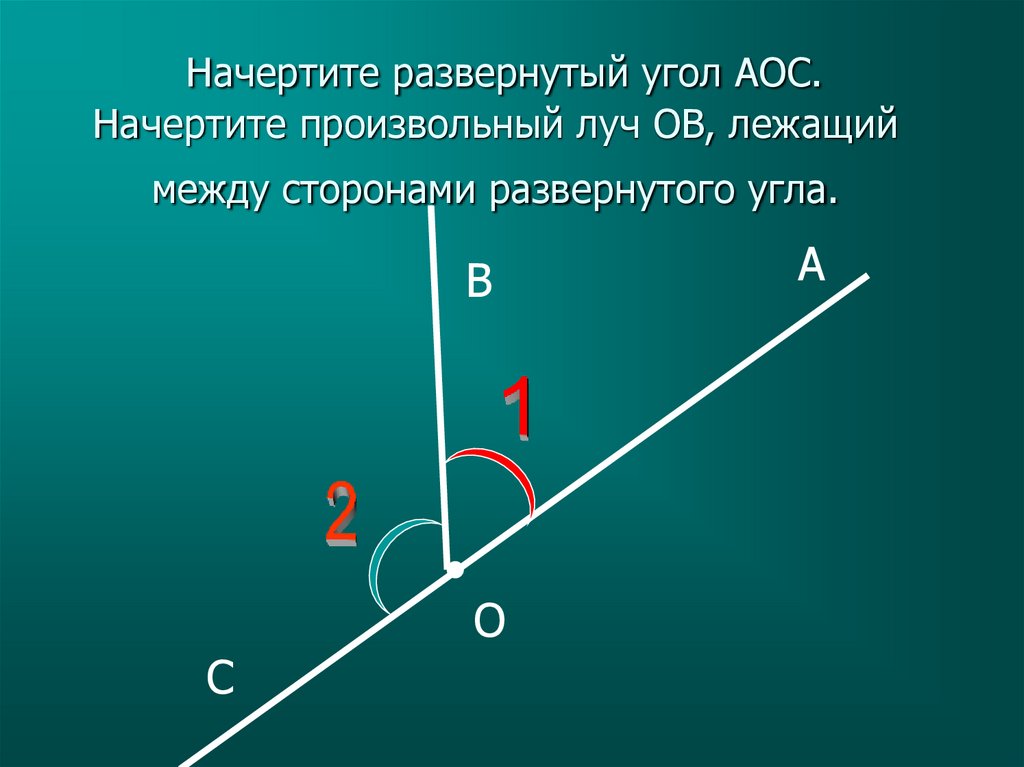
Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Посмотрите на картинку. (Рис. 1)
Рис. 1. Иллюстрация к примеру
Из каких знакомых вам геометрических фигур она состоит?
Конечно, вы увидели, что картинка состоит из треугольников и прямоугольников. Какое слово спряталось в названии обеих этих фигур? Это слово — угол (рис. 2).
Рис. 2. Определение угла
Сегодня мы будем учиться чертить прямой угол.
В названии этого угла уже есть слово «прямой». Чтобы правильно изобразить прямой угол, нам понадобится угольник. (Рис. 3)
Рис. 3. Угольник
В самом угольнике уже есть прямой угол. (Рис. 4)
Рис. 4. Прямой угол
Он и поможет нам изобразить эту геометрическую фигуру.
Чтобы правильно изобразить фигуру, мы должны приложить угольник к плоскости (1), обвести его стороны (2), назвать вершину угла (3) и лучи (4).
1.
2.
3.
4.
Давайте определим, есть ли среди имеющихся углов прямые (Рис.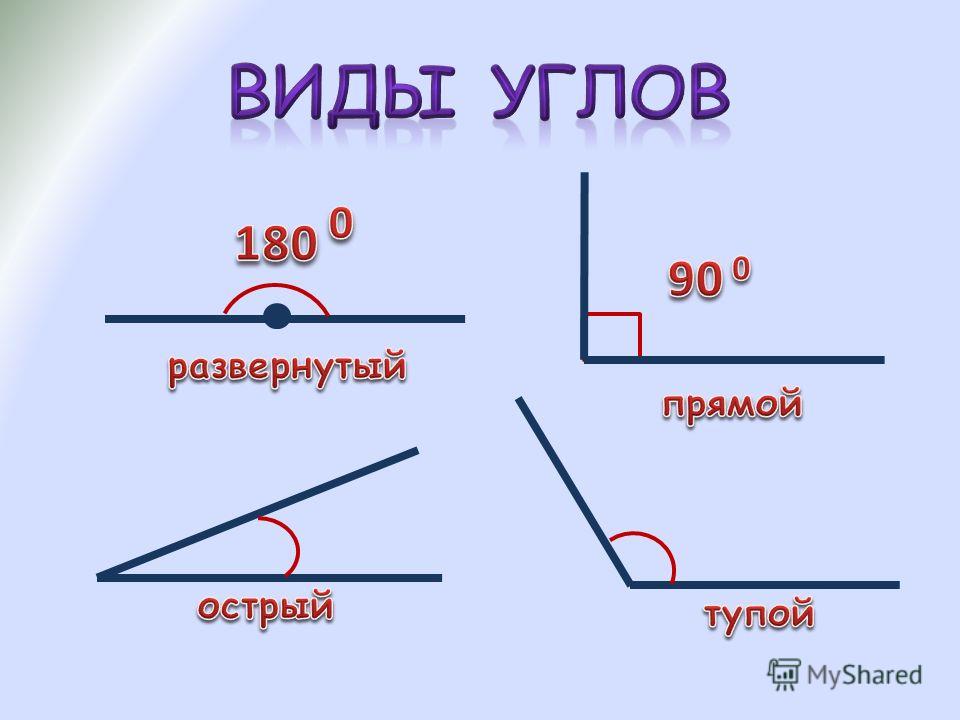
5). В этом нам поможет угольник.
Рис. 5. Иллюстрация к примеру
Найдем прямой угол угольника и приложим его к имеющимся углам (рис. 6).
Рис. 6. Иллюстрация к примеру
Мы видим, что прямой угол совпал с углом ВОМ. Это значит, что угол ВОМ прямой. Проделаем эту же операцию еще раз. (Рис. 7)
Рис. 7. Иллюстрация к примеру
Мы видим, что прямой угол нашего угольника не совпал с углом СOD. Это значит, что угол COD не прямой. Еще раз приложим прямой угол угольника к углу АОТ. (Рис. 8)
Рис. 8. Иллюстрация к примеру
Мы видим, что угол АОТ гораздо больше, чем прямой угол. Это значит, что угол АОТ не является прямым.
На этом уроке мы учились строить прямой угол с помощью угольника.
Слово «угол» дало название многим вещам, а также геометрическим фигурам: прямоугольник, треугольник, угольнику, с помощью которого можно начертить прямой угол.
Треугольник — это геометрическая фигура, которая состоит из трех сторон и трех углов.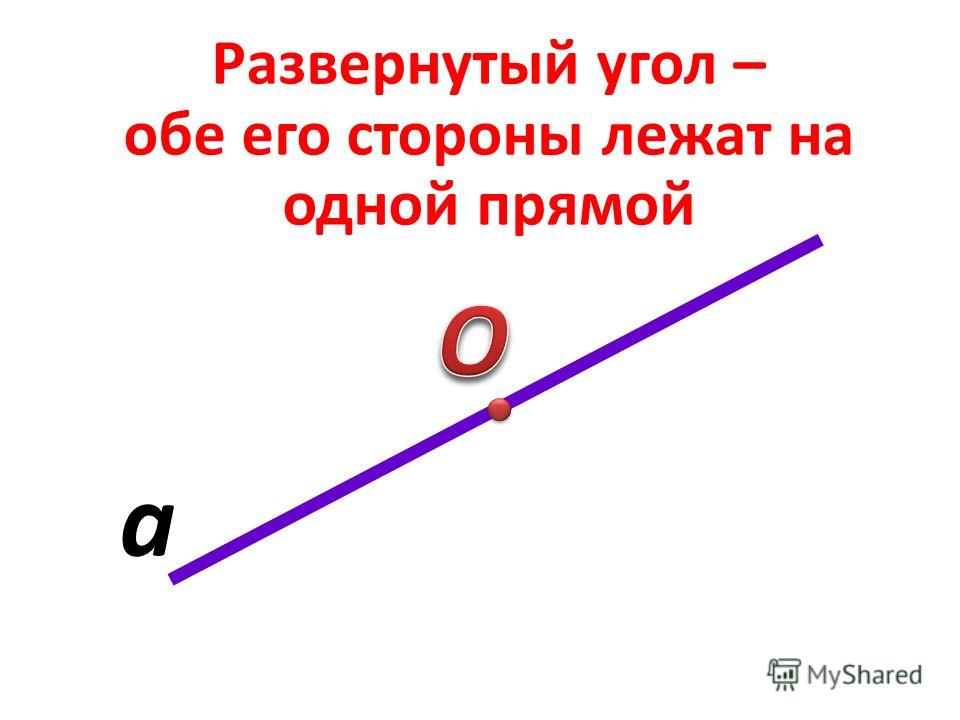
Треугольник, у которого есть прямой угол, называется прямоугольным треугольником.
Каждый угол, в зависимости от его величины, имеет своё название:
| Вид угла | Размер в градусах | Пример |
|---|---|---|
| Острый | Меньше 90° | |
| Прямой | Равен 90°. На чертеже прямой угол, обычно обозначают символом , проведённым от одной стороны угла до другой. | |
| Больше 90°, но меньше 180° | ||
| Развёрнутый | Равен 180° Развёрнутый угол равен сумме двух прямых углов, а прямой угол составляет половину развёрнутого угла. | |
| Выпуклый | Больше 180°, но меньше 360° | |
| Полный | Равен 360° |
Два угла называются смежными , если у них одна сторона общая, а две другие стороны составляют прямую линию:
Углы MOP и PON смежные, так как луч OP — общая сторона, а две другие стороны — OM и ON составляют прямую.
Общая сторона смежных углов называется наклонной к прямой , на которой лежат две другие стороны, только в том случае, когда смежные углы не равны между собой. Если смежные углы равны, то их общая сторона будет перпендикуляром
.Сумма смежных углов равна 180°.
Два угла называются вертикальными , если стороны одного угла дополняют до прямых линий стороны другого угла:
Углы 1 и 3, а также углы 2 и 4 — вертикальные.
Вертикальные углы равны.
Докажем, что вертикальные углы равны:
Сумма ∠1 и ∠2 составляет развёрнутый угол. И сумма ∠3 и ∠2 составляет развёрнутый угол. Значит, эти две суммы равны:
∠1 + ∠2 = ∠3 + ∠2.
В этом равенстве слева и справа есть по одинаковому слагаемому — ∠2. Равенство не нарушится, если это слагаемое в левой и в правой части опустить. Тогда мы получаем.
Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла.
В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).
Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.
Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.
Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.
Прямой
Он выглядит так:
Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.
Тупой
Он имеет такой вид:
Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.
Острый
Он выглядит так:
Градусная мера острого угла всегда меньше 90 о.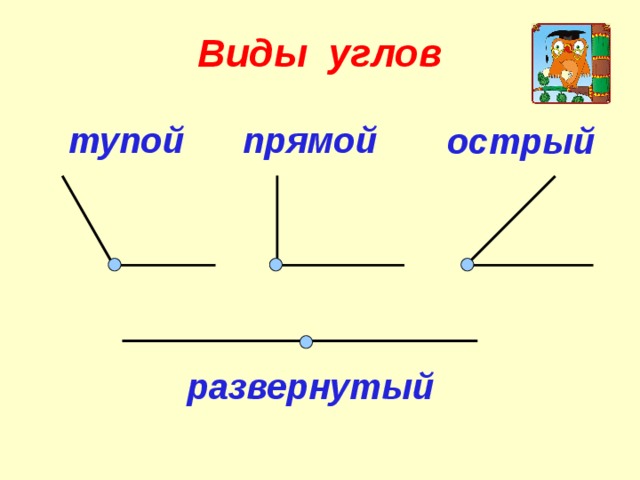
Развернутый
Развернутый угол имеет такой вид:
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях.
Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:
1. Нулевой
Он выглядит так:
Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке.
2. Косой
Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о.
3. Выпуклый
Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы.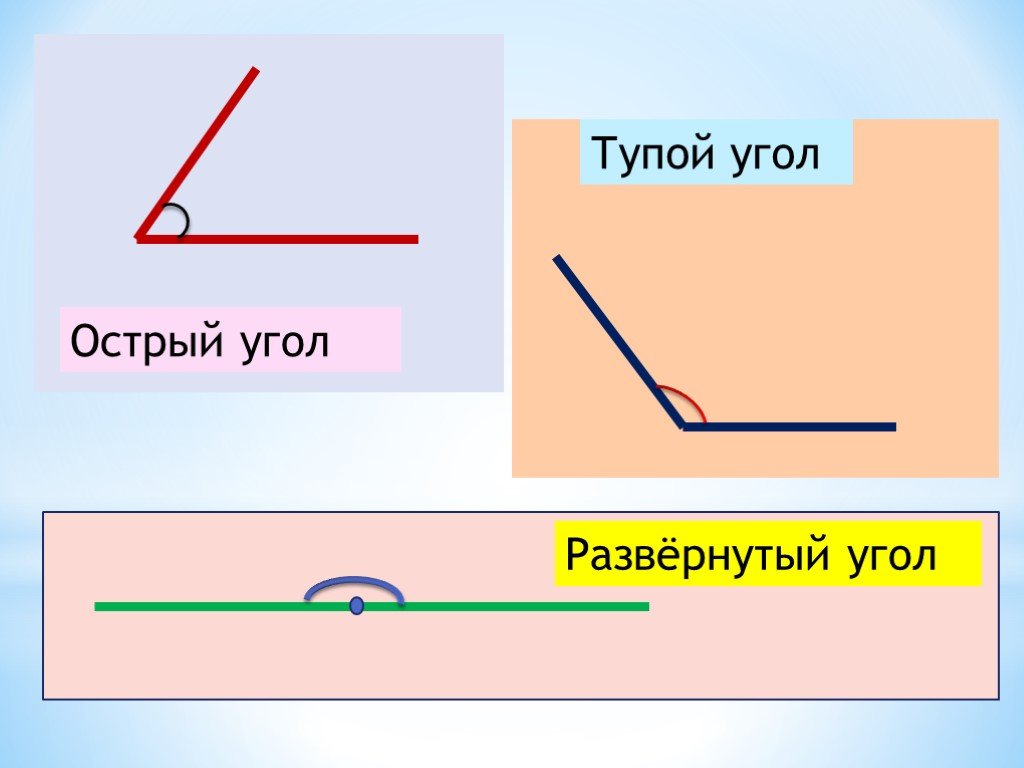
Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о.
4. Невыпуклый
Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно.
5. Полный
Полным является угол с градусной мерой 360 о.
Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.
1. Дополнительные
Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о.
2. Смежные
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о.
3. Вертикальные
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.
Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.
1. Центральный
Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.
2. Вписанный
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.
Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение 1
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения .
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Определение 2
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча .
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
Определение 3
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.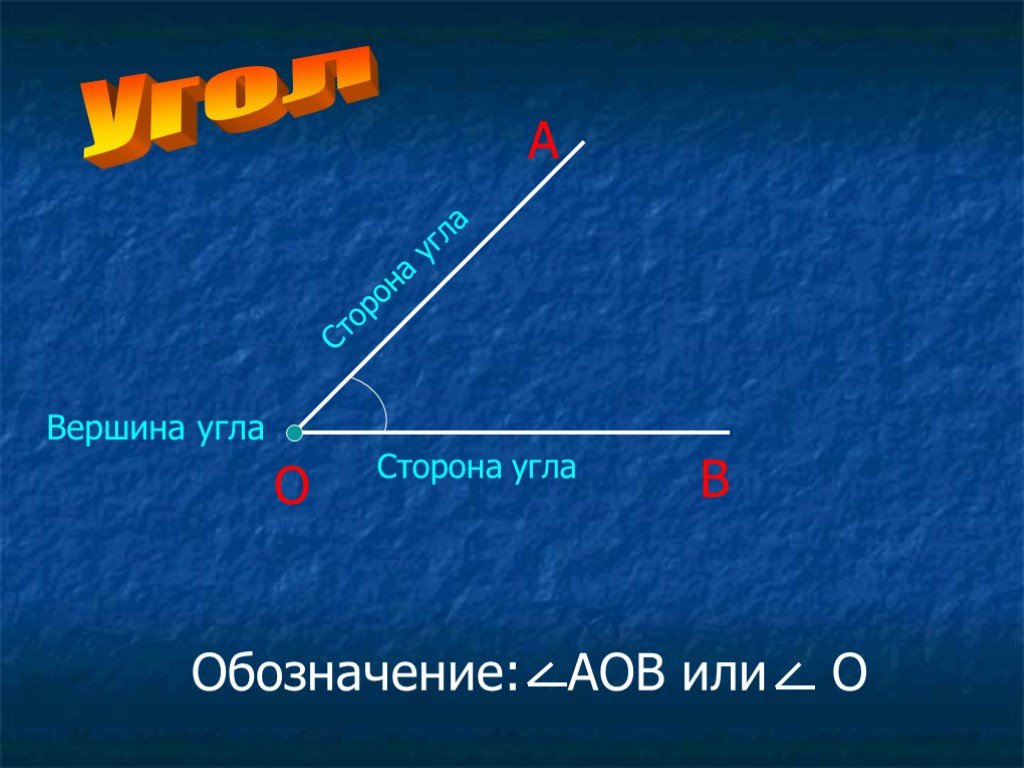
Определение 4
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым .
На рисунке ниже изображен развернутый угол.
Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Определение 5
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.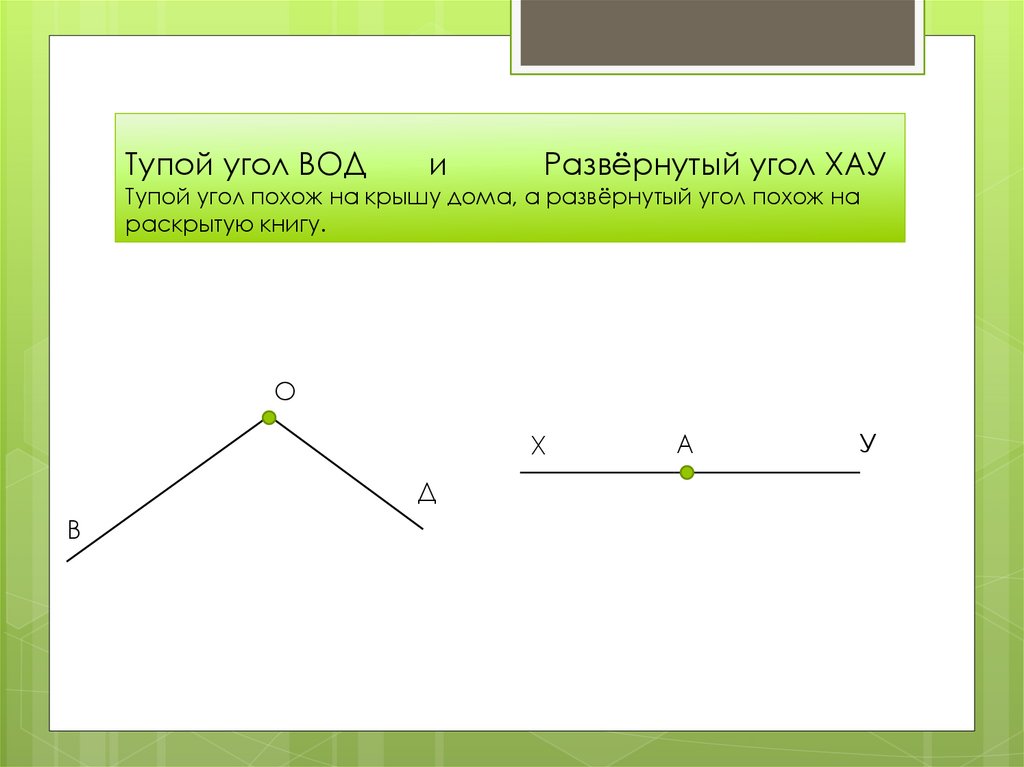
Определение 6
Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
Определение 7
Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус .
Определение 8
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты.
Определение 9
Минутой называют одну шестидесятую часть градуса.
Определение 10
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». Имеет место обозначение:
1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» .
Определение 11
Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Ниже наглядно изображены три вида углов.
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными.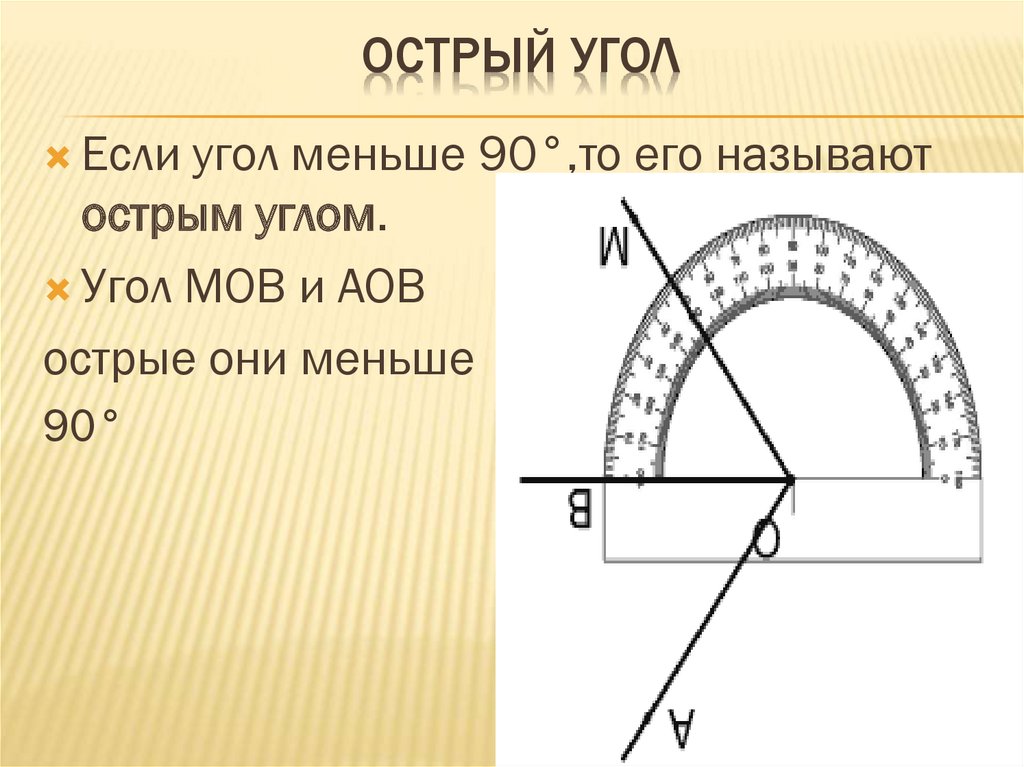
Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
Определение 12
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла.
Они считаются подобными.
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.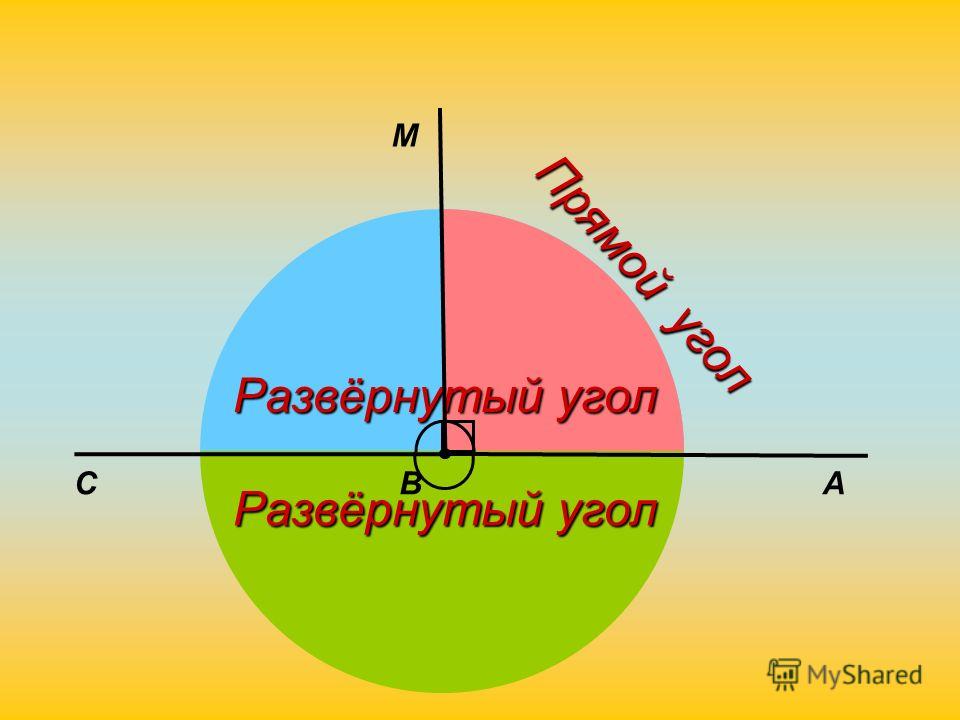
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Про Actions, или до чего доводит лень!: awo_onyshchenko — LiveJournal
Все фотографии в моём ЖЖ оформлены одинаково:
А именно: черная рамка шириной в 1 пиксел, тень, «отрывающая» картинку от белого фона моего журнала, и копирайт, который с некоторых пор располагается вертикально в правом нижнем углу фотографии.
Смотрится достаточно интересно, однако подобное оформление весьма трудоёмко, особенно, когда пост включает 30 — 40 фотографий.
Поскольку лень родилась раньше меня, то я наваял нехитрый action, который создавал тонкую чёрную рамку, белый фон, тень и текст копирайта в вертикальной ориентации, где-то близко к середине фотографии.
Таким образом, вручную мне оставалось только расположить этот копирайт в нужном месте, и задать его непрозрачность.
Эти операции не подлежали автоматизации, т.к. размер картинок, как и соотношение их сторон, были совершенно разными.
Так же непредсказуема была и яркость в нужном мне месте.
Больше всего меня доставало ручное позиционирование копирайта.
Сначала тащишь его мышом в угол, а затем ещё стрелочками позиционируешь окончательно.
Желание автоматизировать этот процесс стало навязчивой идеей.
Поиск дал кучу ссылок на actions с копирайтами, но все они тоже не включали в себя точное позиционирование.
На второй день поисков решения, я обратился к Андрею Журавлёву, которого Павел Косенко не зря окрестил «Маргулисом всея Руси».
Андрей помыслил с минутку, и посоветовал покурить команды выравнивания слоёв.
Как только он это сказал, я вспомнил, что достаточно давно, когда деревья были большими я только знакомился с фотошопом, то уже пробовал эти команды.
Но потом, за ненадобностью, они были забыты.
Дальнейшее было уже делом техники и некоторого времени.
На примере заглавного снимка поста, (на котором изображён, пожалуй, самый активный слушатель киевского интенсива Андрея Журавлёва по наложениям слоёв — Саша Маслюченко),
я покажу, как заставить action позиционировать копирайт, либо логотип, в нужное место картинки.
Итак, вот обработанный оригинал снимка, приведенный к стандартной для горизонтальных снимков ширине — 950 пикселов:
После нажатия клавиши F7, которую я назначил этому action, менее, чем за 1 секунду, картинка приобретает желаемый вид (см верхний снимок).
Вот как при этом выглядит палитра Layers:
Снизу — белый фон, длина и ширина которого на 20 пикселов превосходят длину и ширину снимка.
Затем — сам снимок, отбрасывающий тень, которая достигается применением эффектов наложения слоёв (Drop Shadow).
И сверху — прозрачный слой, содержащий собственно, мой копирайт, написанный белым.
Моя палитра Actions, с показанным в развёрнутом виде action «with Shadow to WEB»:
Тут я позволю себе немного позанудствовать.
И повторить то, что и я, и Андрей Журавлёв не устаём повторять на всех семинарах: давайте своим действиям информативные и осмысленные названия!
В противном случае, если некоторое время активно ими не пользовались, будете смотреть на свои же творения, как баран на новые ворота.
Проверено электричеством!
В правой части скриншота видно, что некоторым, наиболее часто применяемым actions, назначены служебные клавиши.
Первая часть action отвечает за создание белого фона, тонкой чёрной окантовки картинки и тени от неё.
Ничего интересного.
А красными цифрами обозначены шаги, отвечающие за создание и точное позиционирование копирайта.
Вот их и рассмотрим подробнее.
1. «Make text layer».
Как понятно из названия, этот шаг action создаёт текстовую надпись.
В моём случае только один нюанс: символ © набран иным шрифтом, чем остальной текст, ибо в том шрифте он выглядит некрасиво.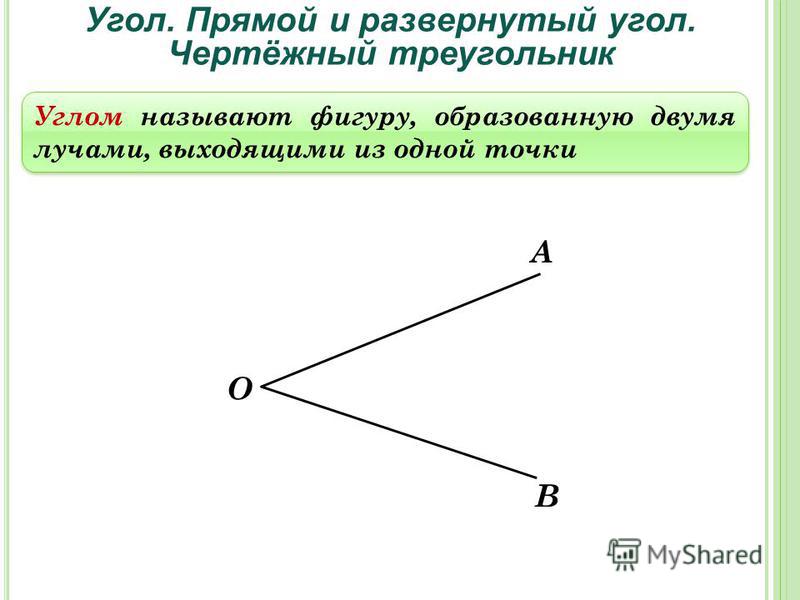
Цвет надписи по умолчанию — белый.
2. «Rotate current layer».
Этот шаг action поворачивает копирайт на 90 градусов против часовой стрелки.
3. » Select layer «Layer 1″».
На этом этапе следует, помимо активного слоя с копирайтом, выбрать дополнительно и нижний слой с картинкой.
Делается это так: при активном верхнем слое нажимаем Shift, и, удерживая его нажатым, щёлкаем левым кликом по слою «Layer 1».
Это необходимо, т.к. далее мы будем позиционировать копирайт относительно нижележащего изображения.
4 и 5. «Align current layer» — выравниваем слои.
На этапе 4 — по нижней границе («bottom edges»).
На этапе 5 — по правой границе («right edges»).
Вот как это делается:
В результате этих этапов, наш, развёрнутый вертикально, копирайт, оказывается помещён точно в правый нижний угол картинки.
Комбинируя различные варианты выравнивания, его можно разместить в любом из 4-ёх углов.
6. «Move current layer» — смещаем копирайт на 15 пикселов вверх и на 6 влево.
Всё, он занял желаемое положение.
Причем так будет всегда, для картинок с любым размером и соотношением сторон.
7. Растеризация текстового слоя.
В результате текстовый слой превращается в обычный, растровый, прозрачный.
Который содержит только белую надпись — копирайт.
Вот как это делается:
Для чего нужна растеризация?
Иногда изображение имеет настолько светлый правый нижний угол, что белый копирайт на нём совершенно теряется.
Если сам копирайт растрирован, то активировав слой с ним, и нажав Ctrl — I, мы инвертируем его, получая вместо белого — чёрный.
В обоих случаях остаётся сделать вручную только одно действие — задать подходящую непрозрачность слоя с копирайтом, чтобы он не слишком бросался в глаза.
И ещё один момент: внимательные, наверное, обратили внимание на то, что первой командой action значится «Image Size», назначение которой непонятно.
Причина появления этой команды достаточно любопытна.
Когда я создавал action, то пользовался картинками из интернета.
И всё работало на ура.
Однако после я загрузил из Lightroom реальную картинку (которая и показана в данном посте), обработал ее , уменьшил до 950 пикселов по длинной, запустил action, и очень удивился.
Т.к. мой копирайт попал в нужный угол, но был, почему-то, написан большими буквами.
Заметно бОльшими, чем те, которые я хотел, и которые вы можете видеть на заглавном снимке.
Через некоторое время пришло озарение: разница между картинками из интернета, и моей, была только в одном: количество точек на дюйм.
В интернете — 72 ppi, а в картинке из Lightroom — 300 ppi (такая у меня настройка).
А размер шрифта указан в неких пунктах (pt), реальный размер которых (и снова: спасибо Андрей!) привязан к разрешению.
Для того, чтобы исключить этот фактор, и был добавлен первый шаг action — «Image Size», со следующими параметрами:
Важно 2 момента:
1. в графе Resolution значится 72, дабы все картинки имели одинаковое разрешение, под которое я подбирал размер шрифта (16 pt) при разработке.
2. галочка Resample Image сброшена, дабы происходило только изменение разрешения без всяких ресайзов.
Теперь работа action никак не зависит от разрешения картинки.
Продолжение статьи здесь:
Про Actions, продолжение (часть 2).
Про Actions, продолжение (часть 3).
Про Actions, с подарком под ёлочку! (часть 4)
Повернуть изображение или фигуру
Вставка таблиц, изображений и водяных знаков
Справка и обучение Word
Вставка таблиц, изображений и водяных знаков
Вставка таблиц, изображений и водяных знаков
Поворот изображения или фигуры
- Вставить таблицу
Статья - Вставить картинки
Статья - Вставить значки
Статья - Вставить объект WordArt
Статья - Вставить водяной знак
Статья - Показать линейку
Статья - Поворот изображения или фигуры
Статья - Обтекание изображения текстом
Статья
Следующий: Сохранить и распечатать
Word для Microsoft 365 Word 2021 Word 2019 Word 2016 Дополнительно.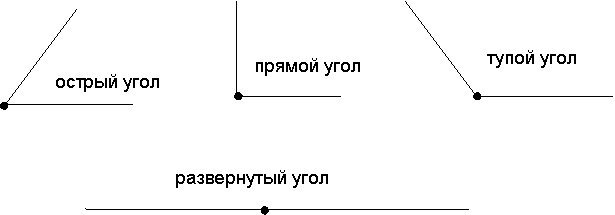
..Меньше
Попробуйте!
Ручной поворот изображения или фигуры
Выберите изображение или фигуру.
Поверните текстовое поле вручную, выбрав маркер поворота фигуры или изображения и перетащив его в нужном направлении. Чтобы угол поворота оставался равным 15 градусам, нажмите и удерживайте клавишу Shift при перетаскивании маркера поворота.
Повернуть изображение или изменить форму на определенную величину
Выбрать Повернуть . Используйте любую команду поворота из списка, например Flip Horizontal .
Выберите «Дополнительные параметры поворота» и введите точную величину в поле «Поворот ».
org/ListItem»>Выберите изображение или фигуру. Откроется 9Лента 0063 Shape Format или Picture Format .
Хотите больше?
Повернуть и отразить текст
Повернуть текст в Word
Добавить фигуры
Как повернуть изображение в Photoshop (шаг за шагом)
Дженн МишраА- А+
Скачать как PDF
Подпишитесь ниже, чтобы скачать статью немедленно
Вы также можете выбрать свои интересы для бесплатного доступа к нашему обучению премиум-класса:
Основы бизнеса
Шпаргалки
Детская фотография
Красочные городские пейзажи
Состав
Творческая фотография
Креативные концепции портрета
Цифровые фотоколлажи
Сказочная портретная фотография
Фотография еды
Интерьерная фотография
Редактирование ландшафта
Пейзажная фотография
Обработка Lightroom
Пресеты Lightroom
Длинная выдержка
Макрофотография
Фотография Млечного Пути
Моя камера и фотография
Органический маркетинг
Домашние животные
Фотография продукта
Фотография неба
Социальные сети
Натюрморт
Интервальная съемка
Туристическая фотография
Городская фотография
Фотография дикой природы
Ваша конфиденциальность в безопасности.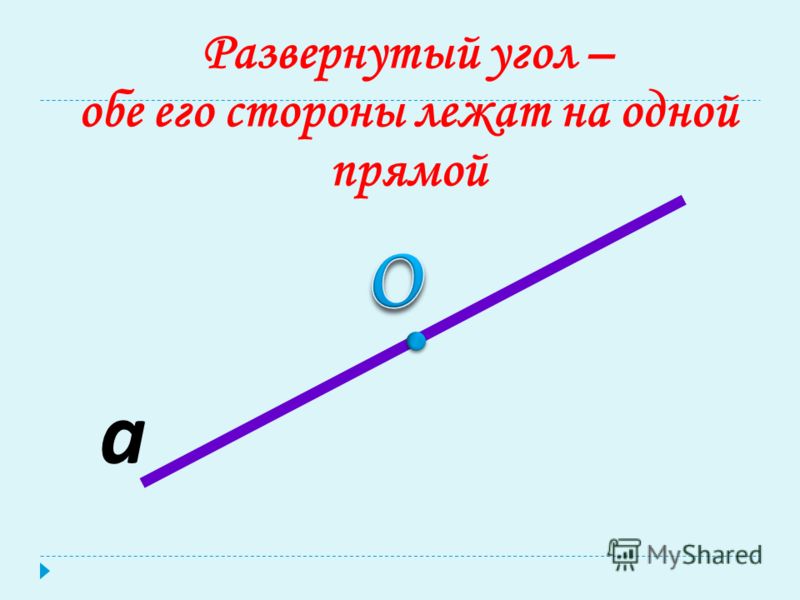
Я никогда не поделюсь вашей информацией.Повернуть фотографию в Adobe Photoshop очень просто. Иногда я поворачиваюсь, чтобы исправить наклон камеры. В других случаях я поворачиваю изображение, чтобы изменить перспективу, или добавляю диагональную линию для динамического интереса.
Я даже могу вращать выбранные части моей фотографии.
В этой статье я покажу вам несколько способов поворота изображения в Photoshop.
Как повернуть объект в Photoshop, используя различные параметры?
Параметр поворота изображения
Поворот фотографии — полезная функция Adobe Photoshop. К счастью, это очень простое действие.
Этот снимок был сделан с целью повернуть изображение, чтобы творчески использовать перспективу.
Сначала щелкните раскрывающееся меню «Изображение» в строке меню. Затем перейдите к Поворот изображения>90° против часовой стрелки . Это повернет фотографию влево.
Если вы хотите повернуть фотографию вправо, выберите Изображение Поворот>90° по часовой стрелке .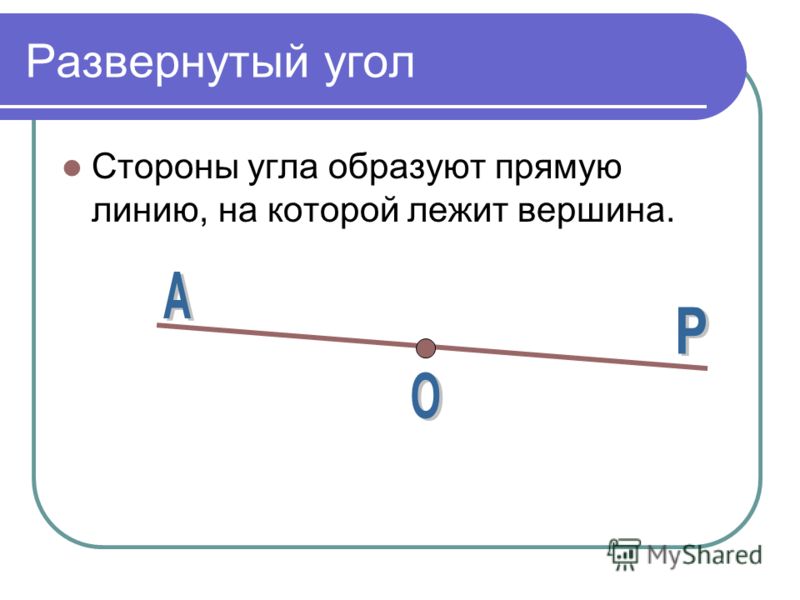
У вас также есть возможность повернуть изображение на 180°. Фотошоп перевернет картинку вверх ногами.
Это окончательное изображение после поворота влево или против часовой стрелки.
Вариант преобразования
Другой вариант — использовать инструмент преобразования. Чтобы это работало, сначала вам нужно выбрать слой. Перейдите на панель «Слои» в правом нижнем углу и нажмите на слой. Если он заблокирован, нажмите на значок замка справа. Это разблокирует слой.
Затем перейдите в раскрывающееся меню «Правка» на верхней панели инструментов. Найти Преобразование>Повернуть на 90° против часовой стрелки . Photoshop повернет фотографию влево.
Некоторые изображения приобретают совершенно другой вид при повороте. Я повернул это изображение на 90°, чтобы увидеть, какая версия мне больше нравится. В конечном итоге мне нравится версия с перилами, входящими из нижнего левого угла.
Иногда поворот фотографии может буквально перевернуть мир с ног на голову.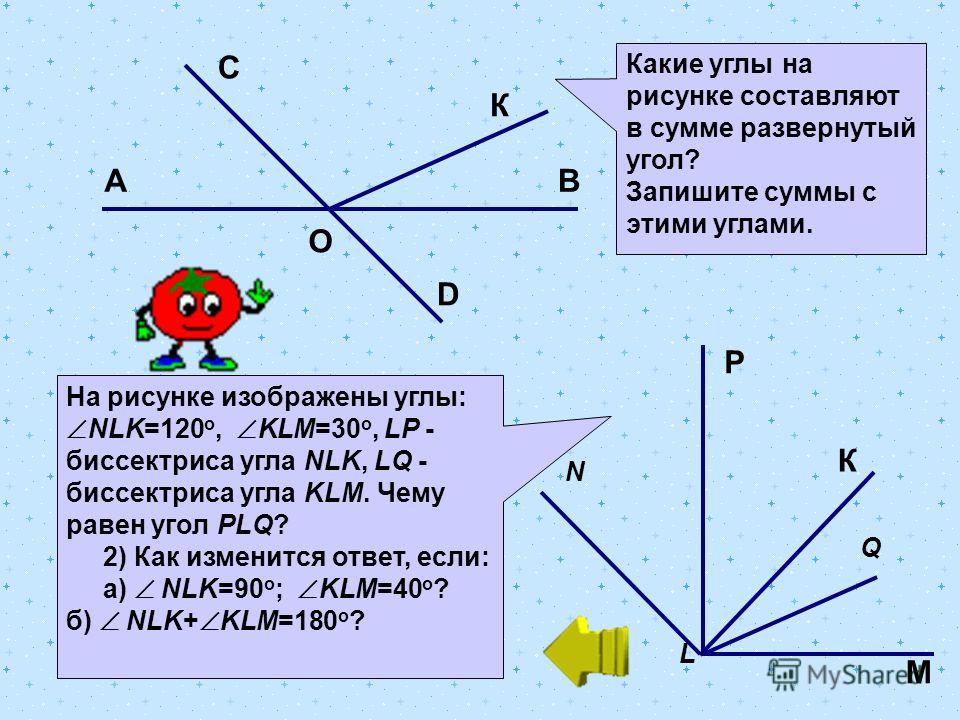
Поверните эту танцовщицу на 180°, и теперь она будет падать или летать по воздуху.
Я поворачиваю фотографии, чтобы создать визуальный эффект или поиграть с перспективой. Параметры поворота в Photoshop также полезны для выпрямления наклоненного изображения.
Как наклонить изображение в Photoshop?
Вот очень плохо наклоненная фотография, которую я сделал в Индии. Честно говоря, я был на движущейся лодке и с трудом стабилизировал камеру. Наклон еще более выражен из-за графических линий на окрашенной лестнице.
У меня есть несколько вариантов выпрямления этой фотографии:
- Произвольный поворот изображения
- Свободное преобразование
- Выпрямление инструмента для обрезки
Произвольный поворот изображения
Произвольный поворот изображения на самом деле вовсе не произвольный.
Этот выбор позволяет мне точно настроить величину вращения, которую я хочу.
В раскрывающемся меню «Изображение» выберите «Поворот изображения» > «Произвольно». Параметр «Произвольно» позволяет мне выбрать число градусов для поворота моей фотографии.
Если мне не нравится количество поворотов, я всегда могу отменить изменение ( Правка>Отменить или нажмите Ctrl или ⌘+Z).
Используя этот простой инструмент, вы можете повернуть изображение на любое количество градусов. Я использую инструмент «Обрезка», чтобы удалить лишнее белое пространство вокруг изображения.
Free Transform Rotation
Инструмент Free Transform — это еще один вариант управления степенью вращения.
В раскрывающемся меню «Правка» выберите параметр «Свободное преобразование» (Ctrl или ⌘T). Вокруг изображения появится ограничивающая рамка. Когда я навожу курсор возле угла, я получаю инструмент со стрелкой. Я могу перетаскивать изображение по часовой стрелке или против часовой стрелки.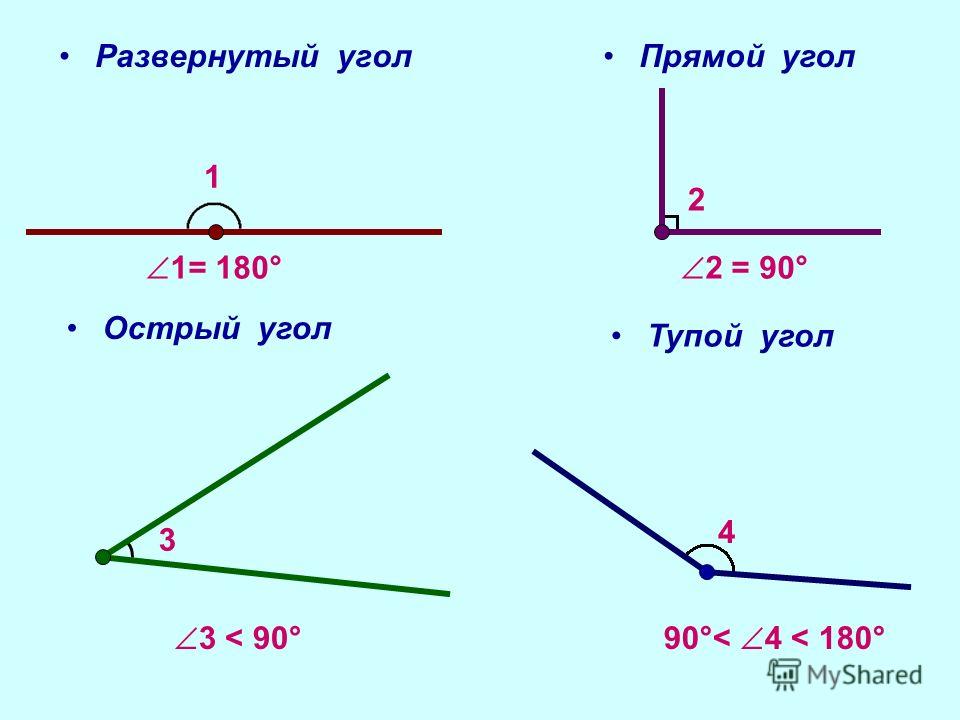
Чем больше я тяну, тем больше вращение.
Та же опция доступна в инструменте Transform. Инструмент «Обрезка» также позволит вам перетаскивать углы изображения для поворота.
Вместо перетаскивания я могу ввести количество градусов на панели инструментов «Свободное преобразование». Когда меня устраивает поворот, я нажимаю Enter или ставлю галочку на верхней панели инструментов. И я готов идти.
Опция выпрямления в инструменте обрезки
Начиная с версии Photoshop CS6 имеется простая встроенная опция для выпрямления горизонта.
Выберите инструмент кадрирования (или нажмите C). На панели инструментов «Обрезка». Нажмите на маленький значок уровня на панели инструментов с надписью «Выпрямить».
Нарисуйте линию через изображение вдоль линии горизонта. Затем Photoshop повернет все изображение, чтобы сделать эту линию прямой. Photoshop также автоматически обрежет ваше изображение, чтобы удалить пустое пространство в углах.
Вращение слоев
Параметры поворота в раскрывающемся меню «Изображение» влияют на все слои.
Параметры поворота в раскрывающемся меню «Правка» влияют только на выбранные слои. Сюда входят инструменты Transform и Free Transform.
Если вы хотите повернуть часть изображения, используйте инструмент «Быстрое выделение», чтобы выделить этот элемент. Выберите раскрывающееся меню «Слой», затем «Создать»> «Слой через копирование» (Ctrl или ⌘J).
Выберите только те слои, которые вы хотите повернуть, и используйте инструмент «Свободное преобразование».
Для этого изображения я наслаил 20 изображений полного солнечного затмения 2017 года. Я повернул каждый слой с помощью инструмента «Свободное преобразование» на несколько градусов, чтобы создать спиральный узор.
Вывод
Независимо от того, настраиваете ли вы технический элемент или вносите творческие изменения, Photoshop предоставляет множество возможностей для поворота изображения.
Инструменты поворота в раскрывающемся меню «Изображение» влияют на все изображение.