Треугольник Паскаля. Свойства треугольника Паскаля
Прогресс человечества во многом связан с открытиями, сделанными гениями. Одним из них является Блез Паскаль. Его творческая биография еще раз подтверждает истинность выражения Лиона Фейхтвангера «Талантливый человек, талантлив во всем». Все научные достижения этого великого ученого трудно перечесть. К их числу относится одно из самых элегантных изобретений в мире математики — треугольник Паскаля.
Несколько слов о гении
Блез Паскаль по современным меркам умер рано, в возрасте 39 лет. Однако за свою короткую жизнь он проявил себя как выдающийся физик, математик, философ и писатель. Благодарные потомки назвали в его честь единицу давления и популярный язык программирования Pascal. Он уже почти 60 лет используется для обучения написания различных кодов. Например, с его помощью каждый школьник может написать программу для вычисления площади треугольника на «Паскале», а также исследовать свойства схемы, о которой речь пойдет ниже.
Деятельность этого ученого с экстраординарным мышлением охватывает самые разные области науки. В частности, Блез Паскаль является одним из основателей гидростатики математического анализа, некоторых направлений геометрии и теории вероятностей. Кроме того, он:
- создал механический калькулятор, известный под названием Паскалева колеса;
- представил экспериментальное доказательство того, что воздух обладает упругостью и имеет вес;
- установил, что барометр можно использовать для предсказания погоды;
- изобрел тачку;
- придумал омнибус — конные экипажи с фиксированными маршрутами, ставшие впоследствии первым видом регулярного общественного транспорта и пр.
Арифметический треугольник Паскаля
Как уже было сказано, этот великий французский ученый внес огромный вклад в математическую науку. Одним из его безусловных научных шедевров является «Трактат об арифметическом треугольнике», который состоит из биномиальных коэффициентов, расставленных в определенном порядке. Свойства этой схемы поражают своим разнообразием, а сама она подтверждает пословицу «Все гениальное — просто!».
Свойства этой схемы поражают своим разнообразием, а сама она подтверждает пословицу «Все гениальное — просто!».
Немного истории
Справедливости ради нужно сказать, что на самом деле треугольник Паскаля был известен в Европе еще в начале 16 века. В частности, его изображение можно увидеть на обложке учебника арифметики известного астронома Петра Апиана из Ингольтштадского университета. Похожий треугольник представлен и в качестве иллюстрации в книге китайского математика Ян Хуэй, изданной в 1303 году. О его свойствах было известно также и замечательному персидскому поэту и философу Омару Хайяму еще в начале 12 века. Причем считается, что он познакомился с ним из трактатов арабских и индийских ученых, написанных ранее.
Описание
Прежде чем исследовать интереснейшие свойства треугольника Паскаля, прекрасного в своем совершенстве и простоте, стоит узнать, что он из себя представляет.
Говоря научным языком, эта числовая схема — бесконечная таблица треугольной формы, образованная из биномиальных коэффициентов, расположенных в определенном порядке. В его вершине и по бокам находятся цифры 1. Остальные позиции занимают числа, равные сумме двух чисел, расположенных над ними рядом выше. При этом все строки треугольника Паскаля симметричны относительно его вертикальной оси.
В его вершине и по бокам находятся цифры 1. Остальные позиции занимают числа, равные сумме двух чисел, расположенных над ними рядом выше. При этом все строки треугольника Паскаля симметричны относительно его вертикальной оси.
Основные свойства
Треугольник Паскаля поражает своим совершенством. Для любой строки под номером n (n = 0, 1, 2…) верно:
- первое и последнее числа — 1;
- второе и предпоследнее — n;
- третье число равно треугольному числу (количеству кружков, которые можно расставить в виде равностороннего треугольника, т. е. 1, 3, 6, 10): Tn-1 = n (n — 1) / 2.
- четвертое число является тетраэдрическим, т. е. представляет собой пирамиду с треугольником в основании.
Кроме того, сравнительно недавно, в 1972 году, было установлено еще одно свойство треугольника Паскаля. Для того чтобы его обнаружить, нужно записать элементы этой схемы в виде таблицы со сдвигом строк на 2 позиции. Затем отмечают числа, делящиеся на номер строки. Оказывается, что номер столбца, в котором выделены все числа, является простым числом.
Оказывается, что номер столбца, в котором выделены все числа, является простым числом.
Тот же трюк можно осуществить и по-другому. Для этого в треугольнике Паскаля заменяют числа на остатки от их деления на номер строки в таблице. Затем располагают строки в полученном треугольнике так, чтобы следующая из них начиналась правее на 2 колонки от первого элемента предыдущей. Тогда столбцы, имеющие номера, являющиеся простыми числами, будут состоять только из нулей, а в тех, у которых они составные, будет присутствовать хотя бы один ноль.
Связь с биномом Ньютона
Как известно, так называется формула для разложения на слагаемые целой неотрицательной степени суммы двух переменных, которая имеет вид:
Присутствующие в них коэффициенты равны Cnm = n! / (m! (n — m)!), где m, представляет собой порядковый номер числа в строке n треугольника Паскаля. Иными словами, имея под рукой эту таблицу, можно легко возводить в степень любые числа, предварительно разложив их на два слагаемых.
Таким образом, треугольник Паскаля и бином Ньютона взаимосвязаны самым тесным образом.
Математические чудеса
При внимательном изучении треугольника Паскаля можно обнаружить, что:
- сумма всех чисел в строке с порядковым номером n (отсчет ведется с 0) равна 2n;
- если строки выровнять по левому краю, то суммы чисел, которые расположены вдоль диагоналей треугольника Паскаля, идущих снизу вверх и слева направо, равны числам Фибоначчи;
- первая «диагональ» состоит из натуральных чисел, идущих по порядку;
- любой элемент из треугольника Паскаля, уменьшенный на единицу, равен сумме всех чисел, расположенных внутри параллелограмма, который ограничен левыми и правыми диагоналями, пересекающимися на этом числе;
- в каждой строке схемы сумма чисел на четных местах равна сумме элементов на нечетных местах.
Треугольник Серпинского
Такая интересная математическая схема, достаточно перспективная с точки зрения решения сложных задач, получается, если раскрасить четные числа Паскалевого изображения в один цвет, а нечетные — в другой.
Треугольник Серпинского можно выстроить и другим образом:
- в закрашенной схеме Паскаля перекрашивают в другой цвет серединный треугольник, который образован путем соединения середин сторон исходного;
- точно также поступают с тремя незакрашенными, расположеными в углах;
- если процедуру продолжать бесконечно, то в итоге должна получиться двухцветная фигура.
Самое интересное свойство треугольника Серпинского — его самоподобие, так как он состоит из 3-х своих копий, которые уменьшены в 2 раза. Оно позволяет отнести эту схему к фрактальным кривым, а они, как показывают новейшие исследования лучше всего подходят для математического моделирования облаков, растений, дельт рек, да и самой Вселенной.
Несколько интересных задач
Где используется треугольник Паскаля? Примеры задач, которые можно решать с его помощью, достаточно разнообразны и относятся к различным областям науки. Рассмотрим некоторые, наиболее интересные из них.
Задача 1. У некоторого большого города, обнесенного крепостной стеной, только одни входные ворота. На первом перекрестке основная дорога расходится на две. То же происходит и на любом другом. В город заходят 210 человек. На каждом из встречающихся перекрестков они делятся пополам. Сколько человек будет находить на каждом перекрестке, когда делиться будет уже невозможно. Ее ответом является 10 строка треугольника Паскаля (формула коэффициентов представлена выше), где по обе стороны от вертикальной оси расположены числа 210.
У некоторого большого города, обнесенного крепостной стеной, только одни входные ворота. На первом перекрестке основная дорога расходится на две. То же происходит и на любом другом. В город заходят 210 человек. На каждом из встречающихся перекрестков они делятся пополам. Сколько человек будет находить на каждом перекрестке, когда делиться будет уже невозможно. Ее ответом является 10 строка треугольника Паскаля (формула коэффициентов представлена выше), где по обе стороны от вертикальной оси расположены числа 210.
Задача 2. Имеется 7 наименований цветов. Нужно составить букет из 3 цветков. Требуется выяснить, сколькими различными способами это можно сделать. Эта задача из области комбинаторики. Для ее решения опять же используем треугольник Паскаля и получаем на 7 строке на третьей позиции (нумерация в обоих случаях с 0) число 35.
Теперь вы знаете, что изобрел великий французский философ и ученый Блез Паскаль. Его знаменитый треугольник при правильном использовании может стать настоящей палочкой-выручалочкой для решения множества задач, особенно из области комбинаторики. 2
2
Треугольник Паскаля | Определение и факты
Треугольник Ян Хуэя
Просмотреть все СМИ
- Ключевые люди:
- Блез Паскаль
- Похожие темы:
- биномиальная теорема Последовательность Фибоначчи биномиальный коэффициент фигурное число треугольник
Просмотреть все связанные материалы →
Треугольник Паскаля , в алгебре треугольное расположение чисел, которое дает коэффициенты в разложении любого биномиального выражения, например ( x + y ) n . Он назван в честь французского математика 17-го века Блеза Паскаля, но он намного старше. Китайский математик Цзя Сянь разработал треугольное представление коэффициентов в 11 веке. Его треугольник в дальнейшем изучал и популяризировал китайский математик Ян Хуэй в 13 веке, по этой причине в Китае его часто называют треугольником Ян Хуэй.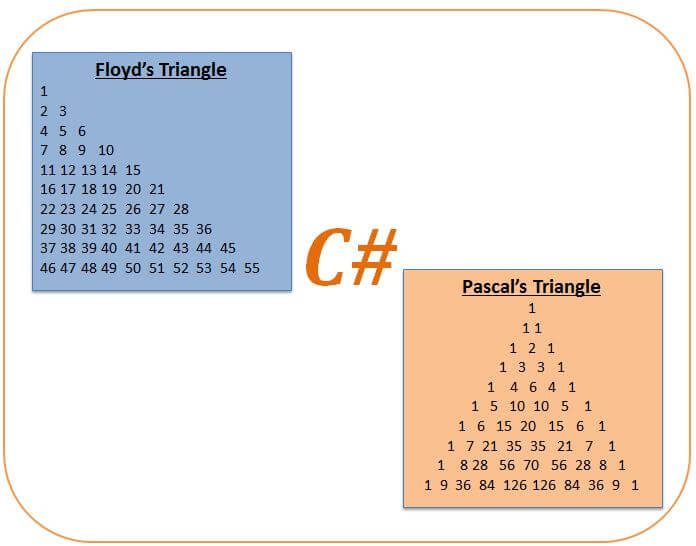 Он был включен в качестве иллюстрации в книгу китайского математика Чжу Шицзе «9».0023 Сиюань юйцзянь (1303; «Драгоценное зеркало четырех элементов»), где его уже называли «Старым методом». Замечательная закономерность коэффициентов была также изучена в XI веке персидским математиком, астрономом и поэтом Омаром Хайямом.
Он был включен в качестве иллюстрации в книгу китайского математика Чжу Шицзе «9».0023 Сиюань юйцзянь (1303; «Драгоценное зеркало четырех элементов»), где его уже называли «Старым методом». Замечательная закономерность коэффициентов была также изучена в XI веке персидским математиком, астрономом и поэтом Омаром Хайямом.
Треугольник можно построить, сначала поставив 1 (китайский «-») вдоль левого и правого краев. Затем треугольник можно заполнить сверху, сложив вместе два числа чуть выше слева и справа от каждой позиции в треугольнике. Таким образом, второй ряд индийско-арабскими цифрами равен 1 1, третий ряд – 1 2 1, четвертый ряд – 1 3 3 1, пятый ряд – 1 4 6 4 1, шестой ряд – 1 5 10. 10 5 1 и так далее. Первая строка, или просто 1, дает коэффициент для разложения ( x + y ) 0 = 1; вторая строка, или 1 1, дает коэффициенты для ( x + y ) 1 = x + y ; Третий ряд, или 1 2 1, дает коэффициенты для ( x + Y ) 2 = x 2 +2 x Y + Y 2 ; и так далее.
Britannica Quiz
Числа и математика
A-B-C, 1-2-3… Если вы считаете, что считать числа — это то же самое, что читать алфавит, проверьте, насколько свободно вы владеете языком математики в этом тесте.
В треугольнике много интересных узоров. Например, рисование параллельных «неглубоких диагоналей» и сложение чисел на каждой линии вместе дает последовательность Фибоначчи (1, 1, 2, 3, 5, 8, 13, 21,…,), которая была впервые отмечена средневековым итальянцем. математик Леонардо Пизано («Фибоначчи») в своей книге Liber abaci (1202; «Книга счетов»).
Еще одно интересное свойство треугольника состоит в том, что если все позиции, содержащие нечетные числа, закрасить черным цветом, а все позиции, содержащие четные числа, закрасить белым, то фрактал, известный как прокладка Серпинского в честь польского математика 20-го века Вацлава Серпинского, будет сформировался.
Уильям Л. Хош
Треугольник Паскаля | Brilliant Math & Science Wiki
Энди Хейс, Мохаммад Фархат, Хуа Чжи Ви, а также
способствовал
Содержимое
- Построение треугольника Паскаля.

- Обозначение треугольника Паскаля
- Закономерности в треугольнике Паскаля
Начните с размещения 111 в центре верхней части листа бумаги. Следующая строка треугольника строится путем суммирования соседних элементов в предыдущей строке. Поскольку рядом с 111 в верхней строке нет ничего, соседние элементы считаются равными 0:0:0:
.
Этот процесс повторяется для получения каждой последующей строки: 9\text{th}-я строка треугольника Паскаля, где 0≤j≤i0\le j\le i0≤j≤i. Тогда
xi,j=(ij).x_{i,j}=\binom{i}{j}.xi,j=(ji).
Это свойство треугольника Паскаля является следствием того, как он построен, и следующего тождества:
Пусть nnn и kkk — целые числа такие, что 1≤k≤n1\le k\le n1≤k≤n. Тогда
(nk)=(n−1k−1)+(n−1k).
\binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k }.(kn)=(k−1n−1)+(kn−1).
Используя треугольник Паскаля, чему равно (62)\binom{6}{2}(26)? 9\text{th}5-я строка:
1+3+6+10=20,1+3+6+10=20,1+3+6+10=20.
Или просто посмотрите на следующий элемент по диагонали в противоположном направлении, то есть на 202020. □_\square□
111121133114641⋮⋮⋮⋮⋮125300230012650⋯126325260014950⋯1000
\begin{массив}{c} 1 \end{массив} \\
\begin{массив}{cc} 1 и 1 \end{массив} \\
\begin{массив}{ccc} 1 и 2 & \color{#D61F06}{1}\end{массив} \\
\begin{массив}{cccc} 1 и 3 & \color{#D61F06}{3} & 1\end{массив} \\
\begin{массив}{ccccc} 1 & 4 & \color{#D61F06}{6} & 4 & 1\end{массив} \\
\begin{массив}{cccccc} \vdots & \hphantom{\vdots} & \vdots & \hphantom{\vdots} & \vdots \end{массив}\\
\begin{array}{cccccc} 1 & 25 & \color{#D61F06}{300} & 2300 & 12650 & \cdots \end{массив} \\
\begin{массив}{ccccccc} 1 и 26 и 325 и 2600 и 149n.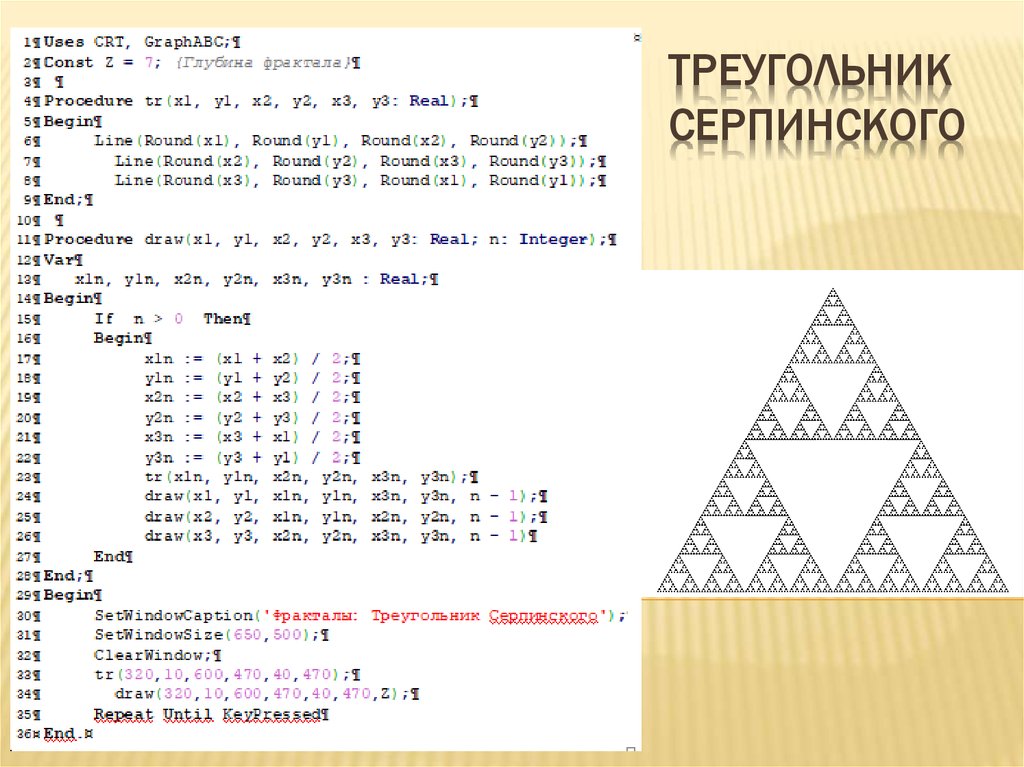


 \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k }.(kn)=(k−1n−1)+(kn−1).
\binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k }.(kn)=(k−1n−1)+(kn−1).