Рациональные числа —
числа, которые можно записать в виде отношения а/n, где а — целое, а n — натуральное число.
Любое рациональное число можно записать:
в виде десятичной дроби: 1/4 = 0,25; 4/2 =2,0 или
в виде периодической дроби: 1/3 =0,333…=0,(3).
СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
Рис. 3. Опорный конспект по теме «Рациональные числа».
В
процессе формирования математических
представлений существенную роль играет
специфика математических знаний, умений,
навыков и методов. Математика оперирует
с объектами уже представляющими
абстрагирование от действительного
мира и, как правило, обобщающими
разнообразные реальные и идеальные
ситуации: интеграл как обобщение и
абстрагирование понятий площади, длины,
объема, но в то же время абсолютно
непрерывная функция; производная как
обобщение и абстрагирование понятий
касательной, скорости, плотности, но в
то же время переменная площадь, заключенная
под непрерывной кривой.
2.3 Технология проблемного обучения
Не
обходится технология обучения В.Ф.
Шаталова и без проблемного обучения,
которое реализуется
в том случае, если учителю удается
создавать проблемные ситуации, ища
выход из которых, школьники осваивают
неизвестные ранее знания или способы
деятельности. Однако учитель работает
одновременно с группой учащихся, каждый
из которых имеет определенный запас
знаний, отличный от других. Тогда учитель
вынужден создавать проблемную ситуацию,
ориентируясь на какой-то конкретный
“слой” учащихся, чаще всего на
“середняков”. В этом случае для “сильных”
учащиеся, которые сразу видят путь
решения, и для “слабых”, даже и не
понимающих, что есть проблема, проблемной
ситуации не будет.
Таким образом, чтобы организовать проблемную ситуацию для всех (в смысле для каждого), надо чтобы, по крайней мере “уже известное” для них было одинаковым, и одинаково хорошо понятым. Применение технологического приема «доводящих карточек» позволит уравнять «стартовые возможности» членов учебной группы.
2.4 Спортивные и игровые приемы
Важнейшим
компонентом технологии интенсивного
обучения В.Ф. Шаталова является спортивные
и игровые приемы,
с помощью которых решается задача
поддержания высокого рабочего тонуса,
бодрого, оптимистического настроя.
Шаталов
утверждает, что слишком рано угасает
педагогический интерес к играм, которые
верой и правдой призваны служить развитию
смекалки и познавательных интересов
детей на всех без исключения уровнях
возрастного развития. Таких
возможностей, которые раскрывает игра
в плане оценки творческих задатков
детей, их находчивости, изобретательности,
инициативности, не может дать никакой,
даже самый лучший в методическом
отношении урок.
Система
В.Ф.Шаталова предусматривает вторичное
воспроизведение изучаемого преподавателем. Цель такого
изложения – сконцентрировать внимание
учащихся на самом существенном, главном
в новом материале, подчеркнуть важнейшие
связи между его компонентами, сходство
и различие между близкими понятиями.
Учитель лишь очень кратко упоминает о
приведенных при объяснении фактах,
примерах, опыта и других средствах
конкретизации. В процессе вторичного
воспроизведения материала учитель
способствует установлению связи между
излагаемым материалом и знаками опорных
сигналов.
Реализация
принципа быстрого движения вперед может
быть осуществлена только при условии
внедрения таких форм повторения, которые
обеспечивают надежность усвоения
программного материала всеми, без
каких-либо исключений, учащимися.
Достижению этой цели служит методика
обучения по листам группового контроля,
которая может быть эффективно использована
и в традиционных условиях. Можно сказать,
что именно этот первый лист при правильной
постановке работы с ним может стать тем
ядром конденсации, вокруг которого
образуется устойчивое поле основных
знаний. Работа по листу группового
контроля начинается без промежутка, и
в таком темпе заложен свой смысл: потерям
времени в течение года места не будет.
Сразу же раздаются брошюры, открывается
первая страница, и учитель начинает
давать ответы на все вопросы. Без суеты,
без спешки, обстоятельно проговаривая
все тонкости ответов, расставляя
смысловые интонации на каждом фрагменте
правил. Каждое правило подкрепляется
одним или несколькими примерами.
Реферат на тему «Развитие понятия о числе»
Развитие понятия о числе
План
1 Введение
2 Число как основное понятие математики
3 Рациональные числа
4 Дробные числа.
О происхождении дробей
5 Дроби в Древнем Египте
6 Отрицательные числа.
7 Действительные рациональные и иррациональные числа
8 Комплексные и мнимые числа
9 Заключение
10 Список использованной литературы
1Введение .
Числа — это неотъемлемое орудие современной цивилизации, используемое для упорядочения сферы ее деятельности.
Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и неудивительно: более 10 тыс. лет прошло с тех пор, как люди всерьёз занялись земледелием, скотоводством и производством простейших товаров. Назвать же имя гения, впервые задавшегося вопросом «сколько?», тем более, невозможно.
В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счёте возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в 1937 г. в Вестонице (Моравия) на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Позже в других местах учёные находили столь же древние каменные предметы с точками и чёрточками, сгруппированными по три или по пять.
Такая
система записи чисел называется единичной, так как любое число в ней образуется
путём повторения одного знака, символизирующего единицу.
Любопытно отметить, что у многих народов для обозначения числа 1 применялся один и тот же символ — вертикальная чёрточка. Это самое древнее число в истории человечества. Оно возникло из простой черты на земле, из зарубки на дереве или кости.
Поштучно считать предметы удобно тогда, когда их не очень много. Пересчитывать же таким образом большие совокупности скучно и утомительно, поэтому возникла идея объединять единицы в группы. Появился счёт пятёрками, десятками, пальцев рук и ног «счетовода».
Единичная система счисления первобытных людей, рисовавших палочки на стенах пещеры или делавших зарубки на костях животных и ветках деревьев, не забыта и в наши дни.
2 Число как основное понятие математики.
Число
является одним из основных понятий математики. Понятие числа развивалось в
тесной связи с изучением величин; эта связь сохраняется и теперь.
Первое научное определение числа дал Эвклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 – около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.).
Еще
раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое
измеряется с помощью единиц». Со слов греческого философа Ямвлиха, еще Фалес
Милетский – родоначальник греческой стихийно-материалистической философии –
учил, что «число есть система единиц». Это определение было известно и
Пифагору.В своей «Общей арифметике» (1707 г) великий английский физик, механик,
астроном и математик Исаак Ньютон пишет: «Под числом мы подразумеваем не
столько множество единиц, сколько абстрактное отношение какой-нибудь величины к
другой величине такого же рода, взятой за единицу.
3. Рациональные числа.
Числа целые, дробные (положительные и отрицательные) и нуль получили общее название рациональных чисел. Совокупность рациональных чисел обладает свойством замкнутости по отношению к четырем арифметическим действиям. Это значит, что сумма, разность, произведение и частное (кроме частного при делении на нуль, которое не имеет смысла) любых двух рациональных чисел является снова рациональным числом.
Совокупность
рациональных чисел упорядочена в отношении понятий «больше» и «меньше». Далее,
совокупность рациональных чисел обладает свойством плотности: между любыми
двумя различными рациональными числами находится бесконечно много рациональных
чисел. Это даёт возможность при помощи рациональных чисел осуществлять
измерение (например, длины отрезка в выбранной единице масштаба) с любой
степенью точности.
Таким образом, совокупность рациональных чисел оказывается достаточной для удовлетворения многих практических потребностей. Формальное обоснование понятий дробного и отрицательного числа было осуществлено в 19 в. и не представило, в отличие от обоснования натурального числа, принципиальных затруднений.
Совокупность рациональных чисел оказалась недостаточной для изучения непрерывно изменяющихся переменных величин. Здесь оказалось необходимым новое расширение понятий числа, заключающееся в переходе от множества рациональных чисел к множеству действительных (вещественных) чисел. Этот переход состоит в присоединении к рациональным числам т.н. иррациональных чисел. [1]
4. Дробные числа.
О происхождении дробей.
Необходимость
в дробных числах возникла в результате практической деятельности человека.
Потребность в нахождении долей единицы появилась у наших предков при дележе
добычи после охоты. Второй существенной причиной появления дробных чисел
следует считать измерение величин при помощи выбранной единицы измерения.
Так возникли дроби.
В истории развития дробного числа мы встречаем дроби трёх видов:
1) доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число;
2) дроби систематические, у которых числителями могут быть любые числа, знаменателями же – только числа некоторого частного вида, например степени десяти или шестидесяти;
3) дроби общего вида, у которых числители и знаменатели могут быть любыми числами.
Изобретение этих трёх различных видов дробей представляло для человечества разные степени трудности, поэтому разные виды дробей появлялись в разные эпохи.
Знакомство человека с дробными числами началось с единичных дробей с малыми знаменателями.
Понятия «половина», «треть», «четверть», «осьмушка» употребляются часто людьми, которые арифметике дробных чисел никогда не обучались. Эти простейшие дроби изобрёл каждый народ самостоятельно в ходе своего развития.
Первой
дробью, с которой познакомились люди, была половина.
Хотя названия всех
следующих дробей связаны с названиями их знаменателей (три – «треть», четыре –
«четверть» и т. д.), для половины это не так – ее название во всех языках не
имеет ничего общего со словом «два». Следующей дробью была треть.
Таким образом, первые дроби, с которыми нас знакомит история, это дроби вида – – так называемые единичные дроби или аликвотные (от лат. aliquot – «несколько»).
Единичные дроби встречаются в древнейших дошедших до нас математических текстах, составленных более 5000 лет тому назад, – древнеегипетских папирусах и вавилонских клинописных табличках.
В
древности наибольшего развития обыкновенные дроби достигли в Индии. В
рукописях, относящихся к 4 веку до нашей эры, встречаются уже не только
единичные дроби, но и дроби с произвольными числителями. В начале VII столетия
индийцы знали и формулировали правила действий над обыкновенными дробями. В
Западной Европе окончательно установленную и ясную теорию обыкновенных дробей
дал в 1585 году фламандский инженер Симон Стевин.
[5]
5. Дроби в Древнем Египте.
В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику. Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную (но не позиционную) систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела. На протяжении многих веков египтяне именовали дроби “ломаным числом”, а первая дробь с которой они познакомились была 1/2. За ней последовали 1/4, 1/8, 1/16, …, затем 1/3, 1/6, …, т.е. самые простые дроби называемые единичными. У них числитель всегда единица.
Египтяне
все дроби старались записать как суммы единичных дробей (долей). Например,
вместо они
писали . Дробь
записывали в виде долей: .
Производить арифметические действия над числами, всякий раз раскладывая их в
сумму долей единицы, очень неудобно.
Имеет ли пристрастие египтян к аликвотным
дробям какое-либо объяснение?
Поясним это примером. Рассмотрим такую задачу: «Разделить 7 хлебов между 8 людьми».
Вот как эта задача решена на папирусе Райнда – это древнеегипетский математический текст, переписанный около 1650 г. до н.э. писцом Ахмесом.
Поскольку . Следовательно, каждому человеку нужно дать по половине, четверти и восьмушке хлеба. Теперь ясно, что надо 4 хлеба разрезать пополам, 2 хлеба на 4 части и только один хлеб – на 8 частей.
Для разложения неединичных дробей на сумму единичных существовали готовые таблицы, которыми и пользовались египетские писцы для необходимых вычислений.
Можно показать, что каждое положительное рациональное число может быть представлено в виде египетской дроби. Сумма такого типа использовалась математиками как определение для дробей начиная со времён древнего Египта до средневековья. В современной математике вместо египетских дробей используются простые и десятичные дроби, однако египетские дроби продолжают изучаться в теории чисел и истории древней математик
6 Отрицательные
числа.
Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные.
Впервые отрицательные числа были узаконены в Китае в III веке, но использовались лишь для исключительных случаев, так как считались, в общем, бесмыссленными. Чуть позднее отрицательные числа стали использоваться в Индии для обозначения долгов, или признавались как промежуточный этап, полезный для вычисления окончательного, положительного результата, но западнее они не прижились.
Знаменитый Диофант Александрийский утверждал, что уравнение 4x+20=0 – абсурдно. В Европе отрицательные числа появились благодаря Леонардо Пизанскому (Фибоначчи), который тоже ввёл его для решения финансовых задач с долгами — в 1202 году он впервые использовал отрицательные числа для подсчёта своих убытков.
Правда, умножение и деление для отрицательных чисел тогда ещё не были определены.
Диофант
в III веке уже знал правило знаков и умел умножать отрицательные числа.
Однако
и он рассматривал их лишь как временные значения.
Полезность и законность отрицательных чисел утверждались постепенно. Индийский математики Брахмагупта (VII век) уже рассматривал их наравне с положительными. В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Даже Паскаль считал, что 0 − 4 = 0, так как ничто не может быть меньше, чем ничто. Бомбелли и Жирар, напротив, считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения недостачи чего-либо. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия.
В
XVII веке, с появлением аналитической геометрии, отрицательные числа получили
наглядное геометрическое представление на числовой оси. С этого момента
наступает их полное равноправие. Тем не менее теория отрицательных чисел долго
находилась в стадии становления.
Оживлённо обсуждалась, например, странная
пропорция 1:(-1) = (-1):1 — в ней первый член слева больше второго, а справа —
наоборот, и получается, что большее равно меньшему («парадокс Арно»). Непонятно
было также, какой смысл имеет умножение отрицательных чисел, и почему
произведение отрицательных положительно; на эту тему проходили жаркие
дискуссии.
Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Грассман).
7 Действительные рациональные и иррациональные числа.
Рациональные
и иррациональные числа составляют вместе множество действительных чисел.
Каждому действительному числу соответствует единственная точка координатной
прямой. Каждая точка координатной прямой соответствует единственному
действительному числу (достаточно найти расстояние до этой точки от начала
отсчета и поставить перед найденным числом знак + или – в зависимости от того,
справа или слева от начала отсчете находится заданная точка). Для краткости
обычно вместо фразы “точка координатной прямой, соответствующая действительному
числу a” пишут и говорят “точка a”, а, употребляя термин “число a”, имеют в
виду ”действительное число a”.
Множество действительных чисел называют также
числовой прямой. Геометрической моделью числовой прямой служит координатная
прямая.
Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.
Древнегреческие
математики классической эпохи пользовались только рациональными числами (вернее
целыми, дробными и положительными).
В своих «Началах» Евклид излагает учение об
иррациональностях чисто геометрически. [4]
Математики
Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и
астрономию, не могли обойтись без иррациональных величин, которые, однако,
длительное время не признавали за числа. Греки называли иррациональную
величину, например, корень из квадратного числа, «алогос» – невыразимое
словами, а позже европейские переводчики с арабского на латынь перевели это
слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые
появился в середине XII в. у Герарда Кремонского, известного переводчика
математических прозведений с арабского на латынь, затем у итальянского
математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII
в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик
Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие
иррационального числа равноправным с понятием рационального числа. Стевин
писал: «Мы приходим к выводу, что не существует никаких абсурдных,
иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел
существует такое совершенство и согласие, что нам надо размышлять дни и ночи
над их удивительной закономерностью.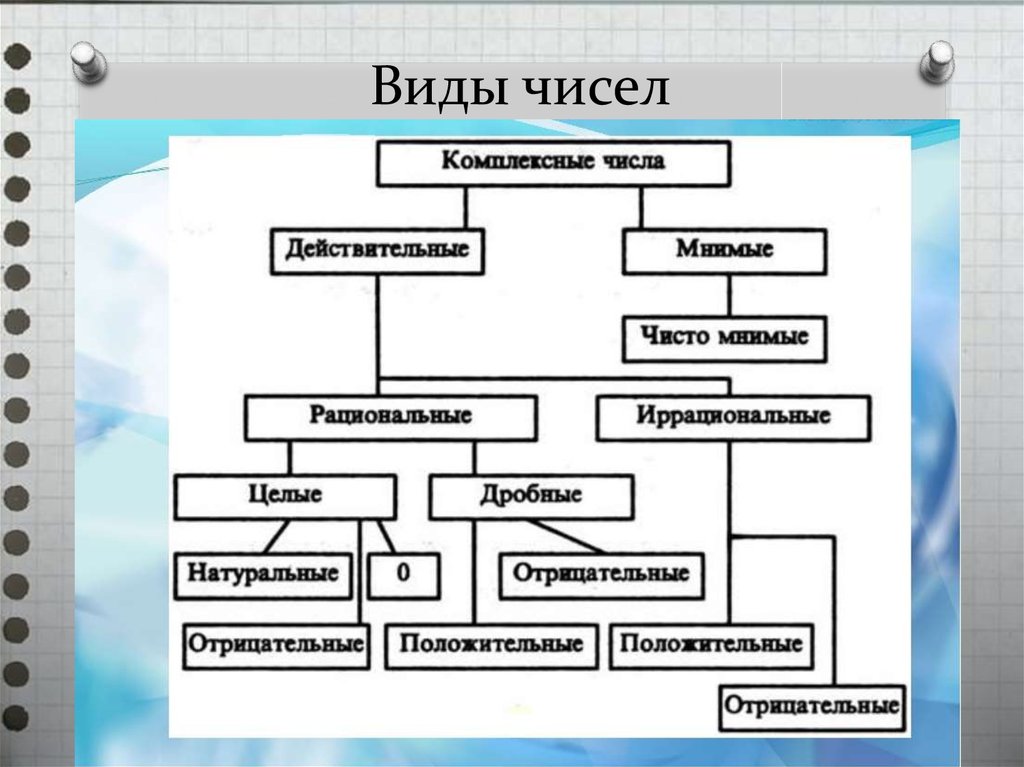
»
8 Комплексные и мнимые числа.
Комплексные
числа были введены в математику для того, чтобы сделать возможной операцию
извлечения квадратного корня из любого действительного числа. Это, однако, не
является достаточным основанием для того, чтобы вводить в математику новые
числа. Оказалось, что если производить вычисления по обычным правилам над
выражениями, в которых встречаются квадратный корень из отрицательного числа,
то можно прийти к результату, уже не содержащему квадратный корень из
отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического
уравнения. Оказалось, когда кубическое уравнение имеет три действительных
корня, в формуле Кардано встречается квадратный корень из отрицательного числа.
Поэтому квадратные корни из отрицательных чисел стали употреблять в математике
и назвали их мнимыми числами – тем самым они как бы приобрели право на
нелегальное существование. Полные гражданские права мнимым числам дал Гаусс,
который назвал их комплексными числами, дал геометрическую интерпретацию и
доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя
бы один действительный корень.
Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.
Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.
На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A· X+B=0 (A0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2 =2, X3 =5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.
9 Заключение.
Число
является одним из основных понятий математики, оно зародилось в глубокой
древности.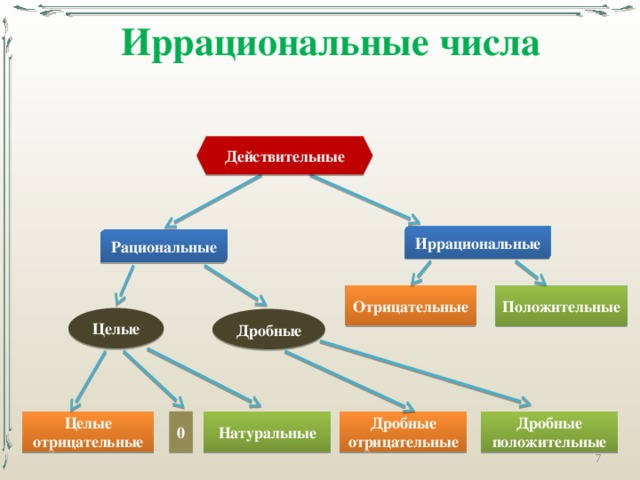
Понятие числа развивалось в тесной связи с изучением величин; эта
связь сохраняется и теперь.
Любопытно отметить, что у многих народов для обозначения числа 1 применялся один и тот же символ — вертикальная чёрточка. Это самое древнее число в истории человечества. Оно возникло из простой черты на земле, из зарубки на дереве или кости.
Около 3 — 2,5 тыс. лет до новой эры древние египтяне придумали свою числовую систему. В ней ключевые числа: 1, 10, 100 и т. д. — изображались специальными значками — иероглифами. Египтяне высекали их на стенах погребальных камер, писали тростниковым пером на свитках папируса.
Величина числа, записанного в иероглифической системе, не зависит от того, в каком порядке расположены составляющие его знаки. Даже если записать их справа налево, один под другим или вперемешку — число от этого не изменится.
В
результате упрощений и стилизаций от иероглифов позднее произошли условные
знаки, облегчающие письмо от руки. Они легли в основу так называемого
иератического письма (от греч.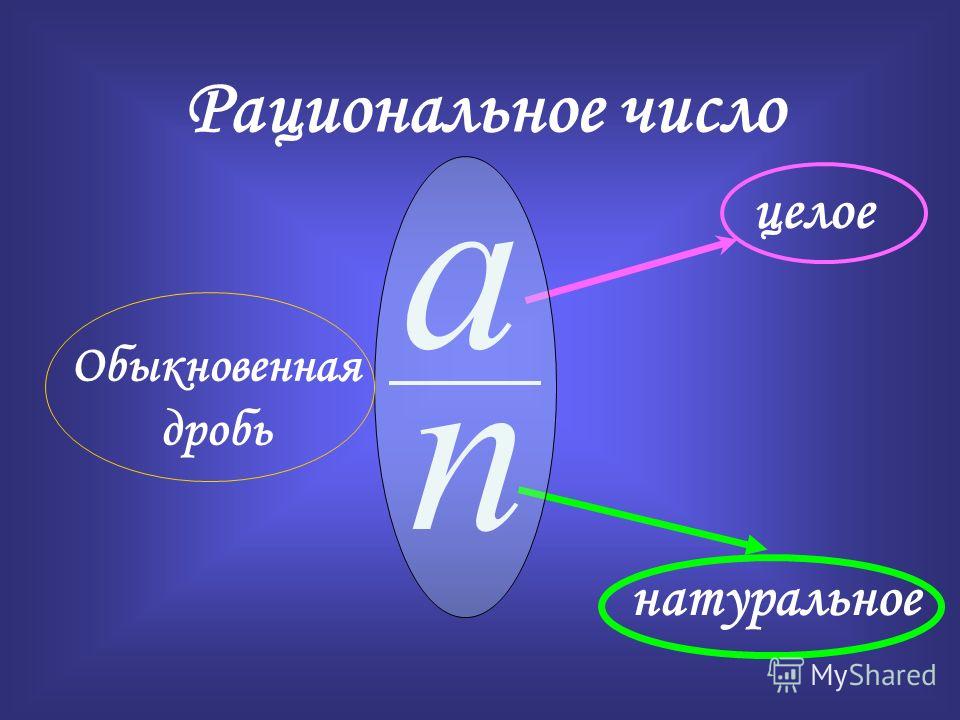
«иератикос» — «священный»).
Эту систему записи чисел можно обнаружить в более поздних египетских папирусах.
С развитием алгебры, уже при решении линейных уравнений с одним неизвестным, возникает необходимость в отрицательных числах. Еще до нашей эры их стали употреблять китайские математики. Широко использовали отрицательные числа и индийские математики (Брахмагупта, VII в.). Замечательным достижением индийских математиков было введение понятия нуля и знака для него, что позволило им создать десятичную систему записи натуральных чисел и разработать правила операций над записанными так числами. Эту запись чисел стали применять математики многих восточных стран, откуда она попала в Европу.
10 Список использованной литературы.
1. Андронов И.К. Математика действительных и комплексных чисел.– М.: Просвещение, 1975 г.
2. Андронов И.К., Окунев А.К. Арифметика рациональных чисел. – М.: Просвещение, 1971 г.
3.
Архангельская В.М. Элементарная теория чисел: учебное пособие.
Издательство
саратовского университета, 1962 г.
4. Выгодский М.Я. Справочник по высшей математике. – М.:Физмат, 1963г.
5. Выгодский М.Я. Справочник по элементарной математике. — Москва: Государственное издательство физико-математической литературы, 1960 г. — 368 с.
6. Гейзер Г.И. История математики в школе. Пособие для учителей. — М.: Просвещение, 1981. — 239 с.
7. Клюйков С.Ф. Числа и познание мира. — Мариуполь: Полиграфический центр газеты «ИнформМеню». 1997г. — 112 с.
Рациональные числа — 856 слов
Колледж математики
Общественный колледж Мохаве
Келси Улес
3 мая 2014 г.
В математике мы должны уметь классифицировать различные числа. Числа можно разделить на группы, которые после небольшого изучения легко понять с течением времени. Термины в математике легко перебрасываются, и если вы не понимаете терминов, математика внезапно станет намного сложнее. Термины и группы, о которых я говорю, — это те, где разные числа попадают в разные группы.
Этими группами являются натуральные числа, целые числа, целые числа, рациональные числа, действительные числа и иррациональные числа.
Первые натуральные числа, которые мы используем и видим в качестве наших счетных чисел. Эти числа состоят из этих простых чисел 1, 2, 3, 4… и так далее. Целые числа — это следующие числа, которые включают в себя все натуральные числа вместе с числом ноль, что означает, что они, например, 0, 1, 2, 3, 4… и так далее. Целые числа также могут быть целыми числами, но также могут быть целыми числами со знаком минус перед ними. Целые числа — это отдельные числа, такие как -4, -3, -2, -1, 0, 1, 2, 3, 4… и так далее. Рациональные числа включают целые числа вместе с дробями и десятичными знаками. Примеры рациональных чисел включают ¼, -¾, 7,82, 2, 123/25, 0,3333. Иррациональные числа не включают целые числа или дроби. Хотя иррациональные числа — единственная группа, которая классифицируется с числами, которые могут иметь десятичное значение, которое может продолжаться сколь угодно долго без определенного шаблона, в отличие от рациональных чисел.
Примером иррационального числа может быть пи. Число Пи, которое мы обычно округляем до 3,14, на самом деле равно 3,14159.26535897932384626433832795… и это продолжается триллионы цифр. И наконец, действительные числа, которые включают в себя натуральные числа, целые числа, целые числа, рациональные числа…
… середина бумаги…
…er являются рациональными, такими как √2, мы можем перейти к следующий шаг. Если вспомнить, что это относится только к положительному квадратному корню из 2, это означает, что его можно записать как частное двух положительных целых чисел, например, √2 =a/b, где дроби в наименьших терминах. Можно считать, что a и b не имеют общих делителей. Затем мы можем использовать простую алгебру, чтобы выяснить следующий вывод: 92 — четное число. Таким образом, a/b не будет в самом низком выражении, поскольку и a, и b имеют 2 в качестве множителя, который показывает, что √2 является иррациональным числом и не может быть рациональным.
В этом эссе автор
- объясняет, что числа можно классифицировать по группам при небольшом изучении, и если вы не понимаете терминов, математика становится намного сложнее.
- Объясняет натуральные и целые числа. рациональные числа включают целые числа, дроби и десятичные числа, а иррациональные числа — нет.
- Объясняет, что иррациональные числа отличаются от других чисел, потому что они отделены от других. теория человека заключается в том, что они были впервые обнаружены в Древней Греции, но Пифагор считал, что все числа рациональны.
- Объясняет, что Пифагор мог открыть иррациональные числа примерно в то же время, когда определял стороны пентаграммы.
- Объясняет, что Пифагор родился в 570 г. до н.э. на Самосе, что в Греции. он считал, что все числа можно выразить в виде дроби или повторяющейся десятичной дроби 9.0022
- Анализирует, как Пифагор был в ярости, когда узнал, что Гиппас был прав в том, что его нельзя записать в виде дроби и что существуют иррациональные числа.
- Объясняет, что одно из самых популярных иррациональных чисел — 2, которое нельзя выразить как частное двух целых чисел.
- Объясняет, что 2 — иррациональное число и не может быть рациональным.
Получить доступ
Проверить качество записи
- Реальный номер
- Номер
- Рациональное число
- Целое число
- Множество
- Иррациональное число
Это не обязательно отражает взгляды, выраженные в Заявлении о миссии RationalWiki, но мы приветствуем обсуждение широкого круга идей.
Если не указано иное, это исходный контент, выпущенный под лицензией CC-BY-SA 3.0 или любой более поздней версии. См. RationalWiki:Авторские права.
Не стесняйтесь оставлять комментарии на странице обсуждения, которые, вероятно, будут намного интереснее и могут отражать более широкий круг мыслей редакторов RationalWiki.
Это развлекательно-образовательное эссе основано на материале, удаленном из статьи Innumeracy. Не стесняйтесь помочь заполнить любые пробелы.
В зависимости от того, как давно вы посещали курс математики, вы можете помнить или не помнить, что существуют разные типы чисел, и в зависимости от того, на каком уровне вы занимаетесь математикой, существует множество типов чисел, но есть несколько основных.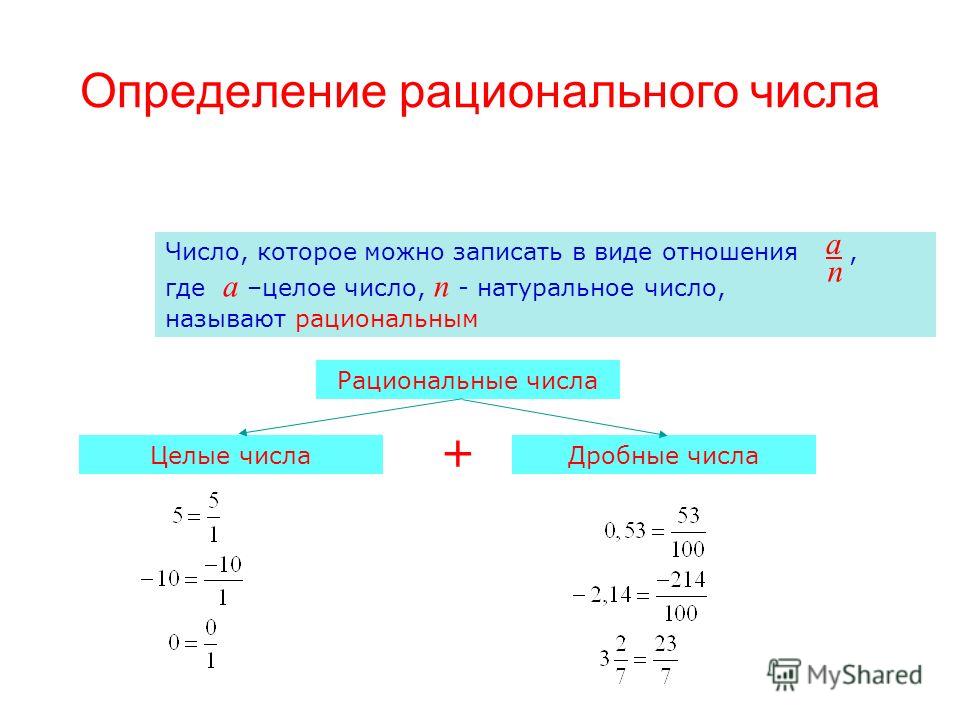
Содержание
- 1 Натуральные числа
- 2 целых числа
- 3 Рациональные числа, действительные числа и иррациональные числа
- 4 Мнимое число и комплексные числа
- 5 сносок
Натуральные числа[править]
Первый тип, о котором трудно спорить, называется Натуральные числа , которые представляют собой целые числа (не десятичные или дробные), которые являются положительными (справа от 0). Иногда 0 считается натуральным числом, а иногда нет, но пока давайте поступим так, как есть. Трудно, а может и невозможно, действительно отрицать или не понимать концепцию натурального числа или 0. Однако существует широко распространенный миф о том, что концепция 0 была изобретена (открыта?) майя. Это миф в том смысле, что он также был придуман (открыт?) индийцами примерно в то же время, и несколько других обществ имели по крайней мере заполнитель для 0 в своих системах счета 9.0099 [1] .
Целые числа[править]
Целые числа просто добавляет идею отрицательных чисел к натуральным числам.
Если число является натуральным числом, оно также является целым числом. Вы могли бы подумать, что идея отрицательных чисел довольно проста, но, к сожалению, это не так. Всеми любимый математик утверждает, что отрицательные числа — это зло [2] или что-то в этом роде. Также всегда есть небольшая путаница в том, как выполнять операции с отрицательными числами. Например, для умножения и деления отрицательных чисел результат будет отрицательным, только если одно число отрицательное, а другое положительное, и если отрицательное число возводится в степень, оно будет положительным, если степень четная. Знание того, как работают негативы, очень важно, потому что они используются для многих вещей, не только для понимания того, что в электронике отрицательный поток означает, что он движется в противоположном направлении, но и для понимания того, насколько далеко кто-то залез в долги.
Путаница с отрицательными числами может впервые появиться в начальной школе, главным образом потому, что учителя ограничивают математику подсчетом чисел и настаивают на том, что это все области математики.
В некоторых случаях есть законная причина для исключения отрицательных чисел (например, вы формулируете вопросы с точки зрения подсчета яблок, и, очевидно, нет возможности получить -3 яблока).
Рассмотрим следующую простую математическую задачу «5 — 8 = ?». Хотя правильный ответ — -3, путаница привела к следующему:
- Простой ответ о том, что это невозможно. Тем не менее, учителя, использующие этот метод, обычно не ограничиваются подсчетом чисел и рассматривают это как вопрос с подвохом.
- Переключение между 5 и 8 для решения задачи «8 — 5 = ?». Если следовать этой логике, «у Бобби Тейблса 5 яблок, а после того, как вы уберете 8, у него останется 3».
Вот почему математика так сложна для некоторых людей.
А иногда люди просто не понимают, что -1 больше, чем -2 [3]
Рациональные числа, действительные числа и иррациональные числа По сути,
Рациональное число — это число, которое можно представить в виде дроби с целым числителем и ненулевым натуральным числом в знаменателе (помните, что числитель — это верхняя часть дроби, а знаменатель — нижняя).
[4] Итак, 0,333… может быть выражено как «1/3», так что это рациональное число. Проблема может возникнуть при выяснении, является ли число рациональным или нет, если оно выглядит так: 0,30769.230769…, то есть 12/39. По сути, число может быть кучей мусора, но если его можно выразить в виде дроби без нуля внизу, оно рационально.Если у вас есть число, которое нельзя представить в виде дроби, это иррациональное число. Достаточно просто. Если у меня есть 123,456, я могу сделать это дробью, положив на 1, и то же самое можно сделать с 0,3845784758944132475. Но поскольку √2 дает бесконечное число, его нельзя представить в виде дроби, поэтому оно нерационально. Это иррационально. Помните, с иррациональным числом: десятичная дробь продолжается вечно, не повторяясь. [5]
A Реальный номер — это практически любой номер, попадающий в одну из этих категорий. Число, которое не является реальным, называется мнимым числом , а мнимое число i создается с помощью √-1.
Теперь, когда мы знаем, что это такое, есть несколько ключевых иррациональных чисел. Первая — это греческая буква ϕ или фи, если вы не говорите по-гречески. Далее идет «e», математическая константа, используемая, среди прочего, для определения сложных процентов. Итак, да, эта большая куча мусора, которую я только что заставил вас прочитать, важна для вас, если вы хотите понять, как накапливаются проценты по вашему банковскому счету и по вашей ипотеке. Некоторые нетехнические места, где можно узнать об e, можно найти здесь [6] [7]
Наконец-то Пи. В Пи не так уж много бессмыслицы, но в ней есть кое-что забавное. Например, в Библии есть ссылка на то, что для нахождения потребуется число Пи, и указано, что число Пи равно 3. Краткое описание этого можно найти здесь, а более подробное обсуждение — здесь [8] . Ответ от всеми любимого фонда смотрите здесь. Однажды кто-то попытался (к счастью, потерпел неудачу) дать библейское определение числа Пи как 3 9.
0099 [9] . Для настоящего головокружения есть этот парень, доказывающий, что значение Пи равно 4 [10]
А теперь кое-что совершенно другое!
Мнимое число и комплексные числа
Некоторое время у математиков возникала проблема: что делать с −1{\displaystyle {\sqrt {-1}}}? Решение, которое в конце концов было найдено, заключалось в том, чтобы просто изобрести число, а именно мнимое число i . При обучении понятию «если я» некоторые предпочитают говорить «я — это число, разберись с ним», в то время как другие говорят, что это просто сокращенная версия выражения «квадратный корень отрицательный один». В конечном счете, пока концепция понята, это не имеет большого значения. Комплексные числа — это числа, состоящие из «действительной» части и «мнимой» части. Хотя это может показаться глупым любому, кто раньше не сталкивался с мнимыми числами, это очень мощная область математики, и только потому, что что-то воображаемое, не означает, что оно не существует.