Регрессия в excel: Основы регрессионного анализа для инвесторов. Построение модели в Excel

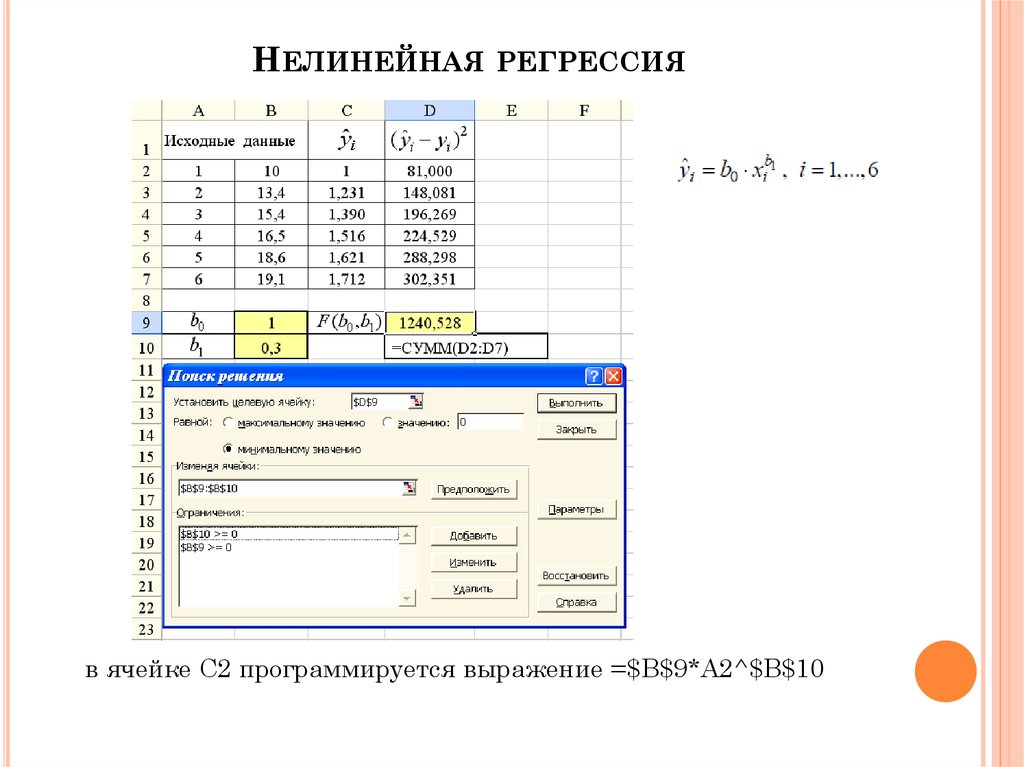
Основы регрессионного анализа для инвесторов. Построение модели в Excel

Представляем вашему вниманию статистический метод расчета справедливой стоимости акций. Речь идет о регрессионном анализе. Незаменимую помощь в процессе исследования окажет обычный Excel.

Что такое регрессия

Регрессионный анализ является статистическим методом исследования. Он позволяет оценить зависимость одной (зависимой) переменной от других (независимых) переменных. Самой простой является линейная регрессия. Ее формула такова:

Y = a0 + a1x1 + … + anxn

где Y — зависимая переменная,
x — независимые переменные, влияющие на нее,
a — коэффициенты регрессии.

Зависимой переменной может выступать цена актива. Возможные влияющие факторы — цены других активов, финансовые и макропоказатели и т.д. В нашем случае считать будем теоретическую (расчетную) условно справедливую стоимость акций, зависящую от цен на другие активы.

Важно, чтобы независимых переменных было не слишком мало, но и не слишком много. Влияющие переменные стоит отбирать из экономических соображений, руководствуясь здравым смыслом. В идеале их нужно тестировать на мультиколлинеарность и т.д., но наш обзор посвящен базовым принципам регрессионного анализа. Статистическую значимость модели поможет оценить показатель R2 (R — квадрат), о нем речь пойдет дальше.

Если фактическая цена бумаги заметно отклоняется от расчетной, появляется повод для дополнительного анализа. Стоит также смотреть на техническую картину, мультипликаторы, общерыночную ситуацию. Существуют также методы финансового моделирования, носящие фундаментальный подход, в частности, модели дисконтирования денежных потоков (DCF) и модели дисконтирования дивидендов (DDM).

Пример расчетов в Excel и выводы

В качестве примера возьмем акции американского нефтегазового гиганта Exxon Mobil (XOM). Модель будет упрощенной и учебной и не является рекомендацией для осуществления операций с бумагами, ситуацию нужно смотреть в комплексе.

Независимыми переменными у нас выступят фьючерсы на американскую нефть WTI (склеенные фронтальные контракты) и индекс S&P 500. Логика проста — бизнес компании зависит от цен на нефть, а поведение акций в теории должно быть связано в общерыночной ситуацией.

Шаг 1. Выкачиваем в Excel котировки XOM, SPX и CL1. Данные возьмем за пять лет. Так как на более длительных периодах наблюдалась разная структурная ситуация на нефтяном рынке. Возьмем статистику в недельной разбивке, будет 262 наблюдения.

Шаг 2. Активируем настройку регрессионного анализа. Открываем раздел Файл. Переходим на вкладку Параметры Excel — Надстройки. Внизу появившегося окна будет вкладка Управление, где стоит параметр Надстройки Excel, жмем — Перейти.

Выбираем опцию Пакет анализа.

Готово. Результат появится в разделе Данные — Анализ данных.

Шаг 3. Строим регрессию. При клике на Анализ данных появится меню с опциями функционала для анализа.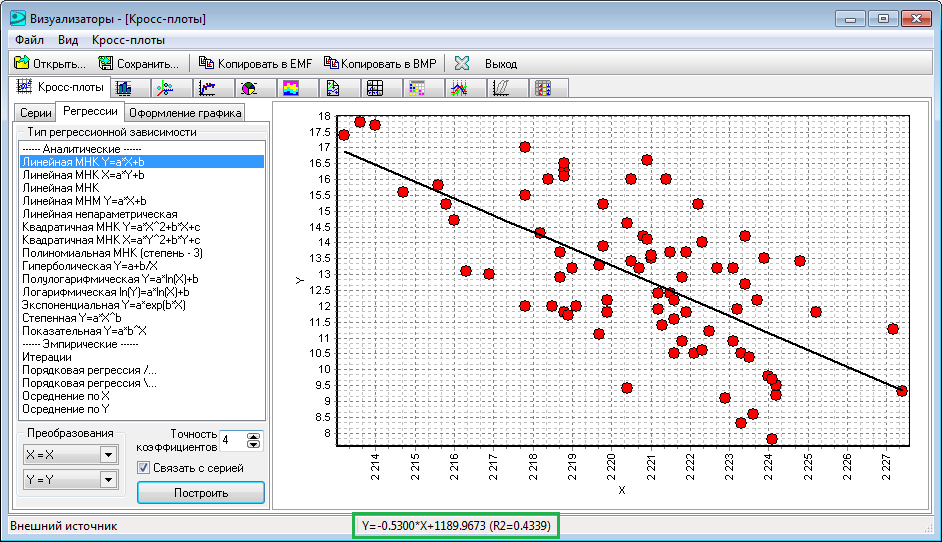 Выбираем Регрессия.

Заполняем окна по аналогии со схемой, используя ранее выгруженные данные по активам.

На выходе получаем вот такие данные.

Шаг 4. Интерпретация. Статистических показателей много. Не вдаваясь в теорию, наиболее интересными являются значения коэффициентов регрессии и показатель R2.

Наша модель будет иметь следующий вид:

Цена акций Exxon Mobil = $96,2 + 0,28*WTI — 0,01*S&P 500

R — квадрат равен 0,61. Показатель показывает, насколько значение зависимой переменной определяется значениями независимых переменных. Речь идет о статистической значимости модели. Модель является очень хорошей, если R2 превышает 0,8, и при этом сама модель имеет экономическое обоснование. В нашем случае все не настолько идеально, но все же выше 0,5, поэтому модель можно использовать.

Отмечу, что в процессе подготовки материала делались расчеты не только за пять лет, но и за 10, и за три года, также WTI заменялась на Brent. Итоговый вариант был выбран в связи с наибольшим значением R2.

Шаг 5. Применение. Рассчитаем в Excel теоретические значения акций Exxon за весь использовавшийся для построения модели период (5 лет).

Построим линейную диаграмму, на которой будут представлены динамика фактической цены и расчетной цены акций. Заметно, что расхождения между двумя величинами редко носили слишком серьезный характер. По состоянию на 06.06.2019 фактическая цена акций составила $74,2, а теоретическая — $76,7. Исходя из этого, критерия бумаги вполне справедливо оценены рынком. Однако это только один, причем упрощенный подход. Ситуацию нужно рассматривать в комплексе. К примеру, медианный таргет аналитиков на 12 месяцев равен $84. Это усредненный показатель результатов моделей фундаментальной оценки, предполагающий заметный потенциал роста.

Корреляционный анализ

Дополним нашу регрессию корреляционным анализом. Корреляция означает зависимость одного показателя от другого. Коэффициент корреляции — показатель взаимосвязи (в нашем случае финансовых активов).

Строим корреляционную матрицу. В том же разделе Анализ данных выбираем опцию Корреляция. Заполняем окно, как показано ниже, с учетом котировок наших активов.

На выходе получаем корреляционную матрицу. На ней видно, что цена Exxon положительно связана с WTI (коэффициент корреляции = 0,55) и отрицательно зависит от динамики индекса S&P 500 (коэффициент корреляции = -0,48).

Так что Exxon — это преимущественно нефтяная история, зачастую не совпадающая по динамике с широким рынком. Это можно заметить на графике трех активов с 2010 г. Ситуация стала такой с 2014 г., когда рынок нефти обвалился из-за структурных сдвигов. На нашей выборке за 5 лет корреляция между WTI и S&P 500 равна 0,13, то есть несущественна.

Построение графика простой регрессии

Расскажем об еще одном регрессионном функционале Excel. Программа позволяет построить график линейной регрессии. Правда доступно это лишь при наличии одной независимой переменной. В нашем случае ею будет нефть, так как она в большей мере объясняет движения акций Exxon — коэффициент регрессии равен 0,28 против (-0,01) у S&P 500.

Строим точечную диаграмму по XOM и WTI за 5 лет. Получаем поле корреляции. Щелкаем по любой из точек на диаграмме и меню левой кнопки мыши выбираем Добавить линию тренда.

В окне выбираем линейную линию тренда, ставим галочки напротив Показывать уравнение и Поместить на диаграмму R2.

В итоге получим такую схему зависимости Exxon (y) от WTI (x). В нашем случае модель не является статистически значимой — R-квадрат равен лишь 0,3.

Как еще использовать корреляционно-регрессионный анализ

В архивах раздела Обучение БКС Экспресс есть материалы на эту тему.

1) Корреляционная икселька — «Составление инвестиционного портфеля по Марковицу для чайников»

2) Оценка коэффициентов альфа и бета. Теория — «Коэффициенты альфа и бета. Выбираем акции в портфель «по науке», практика — «Как коэффициент бета помогает портфельному инвестору».

Отмечу, что наш материал носил ознакомительный характер.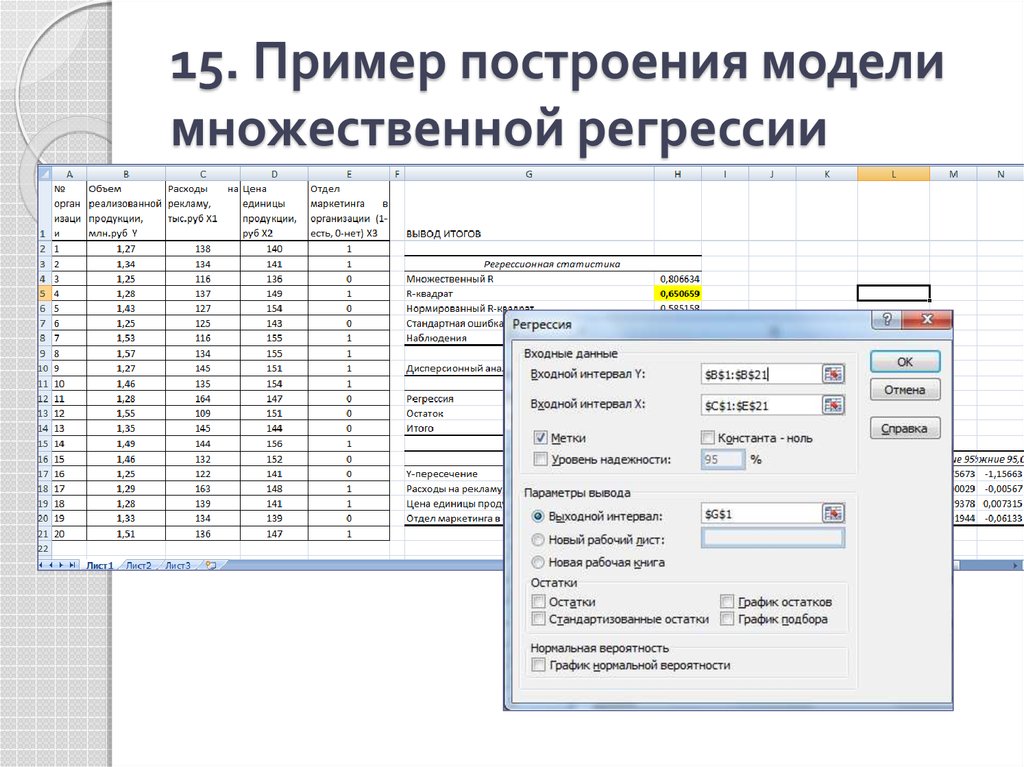 В регрессионные модели можно вносить макроэкономические, финансовые и прочие показатели. В идеале, независимые переменные нужно тестировать на ряд факторов. Наш обзор — это пример «мгновенной и грубой» оценки. В любом случае, выводы, полученные в результате регрессионного моделирования, стоит комбинировать с другими подходами к инвестиционному анализу.

Начать инвестировать

БКС Брокер

При использовании функции линейная регрессия (ЛИНЕЙН) в Excel возвращается неверный результат

Проблемы

При использовании функции ЛИНЕЙН на листе в Microsoft Excel результаты статистического вывода могут возвращать неверные значения. Средство регрессия в окне «пакет анализа» может также возвращать неверные значения.

Причина

Результат, возвращаемый функцией ЛИНЕЙН, может быть неправильным, если выполняется одно или несколько из указанных ниже условий.

• Диапазон значений x перекрывает диапазон значений y.

• Количество строк в диапазоне входных данных меньше числа столбцов в общем диапазоне (x-value + y-Value).

• Вы задаете нулевую константу (для третьего аргумента функции ЛИНЕЙН установите значение истина).

Обходное решение

Случай 1: диапазоны x-value и y перекрываются

Если диапазоны x-value и y перекрываются, функция ЛИНЕЙН возвращает неверные значения во всех ячейках результата. Нормальная статистическая вероятность запрещает значения в диапазонах x и y для перекрытия (повторяющиеся друг друга). Не перекрывают диапазоны x и y при ссылке на ячейки в формуле.Примечание. Средство регрессия предупреждает об этой проблеме и не продолжает работу. Вы можете использовать средство регрессия вместо функции ЛИНЕЙН. В Microsoft Office Excel 2007 вы можете найти инструмент регрессия, щелкнув

анализ данных в группе анализ на вкладке данные . В Microsoft Office Excel 2003 и более ранних версиях Excel можно найти инструмент регрессия, выбрав пункт анализ данных в меню Сервис .

Случай 2: количество строк меньше числа столбцов x-Columns.

Статистические функции не действительны, так как количество строк должно быть меньше числа столбцов x (переменных). Количество строк данных должно быть больше количества столбцов данных (столбцов x и y).

Случай 3: указывается нулевая константа

Не указывайте нулевые константы (b = 0) в функции.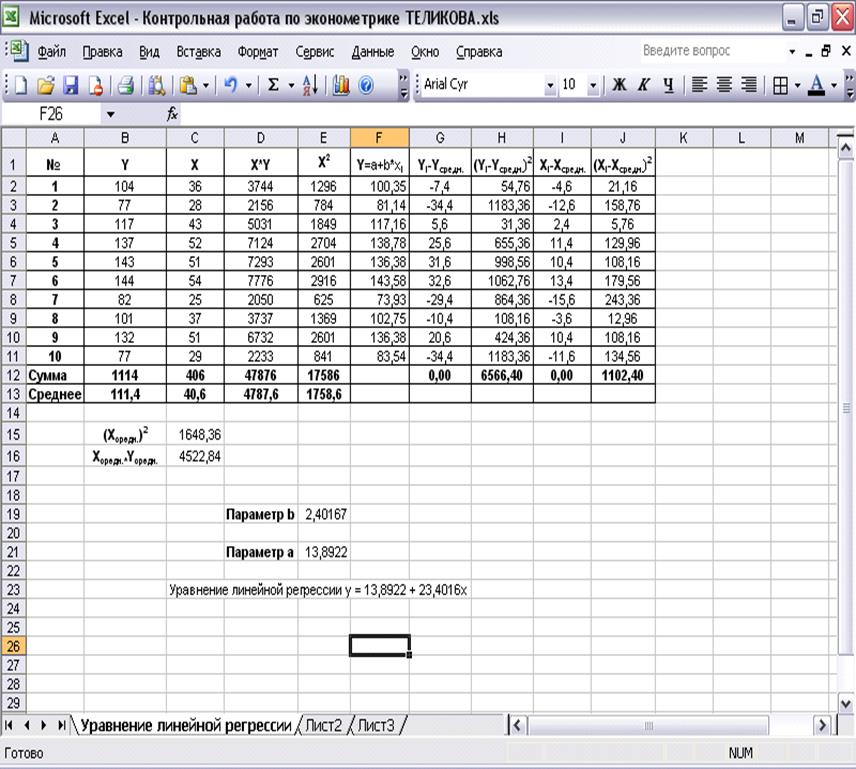

Дополнительная информация

Средство регрессия входит в пакет анализа. Пакет анализа — это программа надстройки Excel. Оно доступно при установке Microsoft Office или Excel. Прежде чем использовать средство регрессия в Excel, вы должны загрузить анализ ToolPak.To в Excel 2007, выполнив указанные ниже действия.

1. Нажмите кнопку Microsoft Office, затем нажмите кнопку Параметры Excel.

2. Выберите пункт надстройки, а затем в поле Управление выберите пункт надстройки Excel .

3. org/ListItem»>

   Нажмите кнопку Перейти.

4. В окне Доступные надстройки установите флажок Пакет анализа , а затем нажмите кнопку ОК.Примечание. Если в списке Доступные надстройки не указан Пакет анализа , нажмите кнопку Обзор , чтобы найти его.

Чтобы сделать это в Excel 2003 и более ранних версиях Excel, выполните указанные ниже действия.

1. В меню Сервисвыберите пунктнадстройки.

2. В диалоговом окне надстройки выберите Пакет анализаи нажмите кнопку ОК,Обратите внимание на то, что

   Пакет анализа не указан в поле Доступные надстройки, нажмите кнопку Обзор , чтобы найти его.

Ссылки

Статистические вычисления на цифровом компьютере. Уильям J. Hemmerle. Blaisdell компания публикации: 1967. Глава 3, «вычисления с несколькими регрессиями» и раздел 3.2.1, «теория для предварительной регрессии».

Регрессионный анализ в Excel с примером

Регрессионный анализ представляет собой набор статистических методов, используемых для оценки отношений между зависимой переменной и независимыми переменными. Мы можем использовать его для оценки силы взаимосвязи между переменными и для моделирования будущих взаимосвязей между ними.

Пакет инструментов для анализа данных

Data Analysis ToolPak — это надстройка Excel, предоставляющая инструменты анализа данных для финансового, статистического и инженерного анализа данных

• Перейдите на вкладку «Файл», щелкните «Параметры» и выберите категорию «Надстройки».
• Выберите пакет инструментов анализа и нажмите кнопку «Перейти».
• Проверьте пакет инструментов анализа и нажмите OK.

• На вкладке «Данные» в группе «Анализ» теперь можно нажать «Анализ данных».

Запустить регрессионный анализ

В Excel мы используем регрессионный анализ для оценки отношений между двумя или более переменными. Вам необходимо знать два основных термина:

Зависимая переменная — это фактор, который вы пытаетесь предсказать.

Независимая переменная — это фактор, который может повлиять на зависимую переменную.

Рассмотрим следующие данные, где у нас есть количество случаев COVID и масок, проданных в определенном месяце.

• Перейдите на вкладку Данные > группа Анализ > Анализ данных.
• Выберите «Регрессия» и нажмите «ОК».

Откроется следующее окно аргументов.

Выберите входной диапазон Y в качестве количества проданных масок и входной диапазон X в качестве случаев COVID.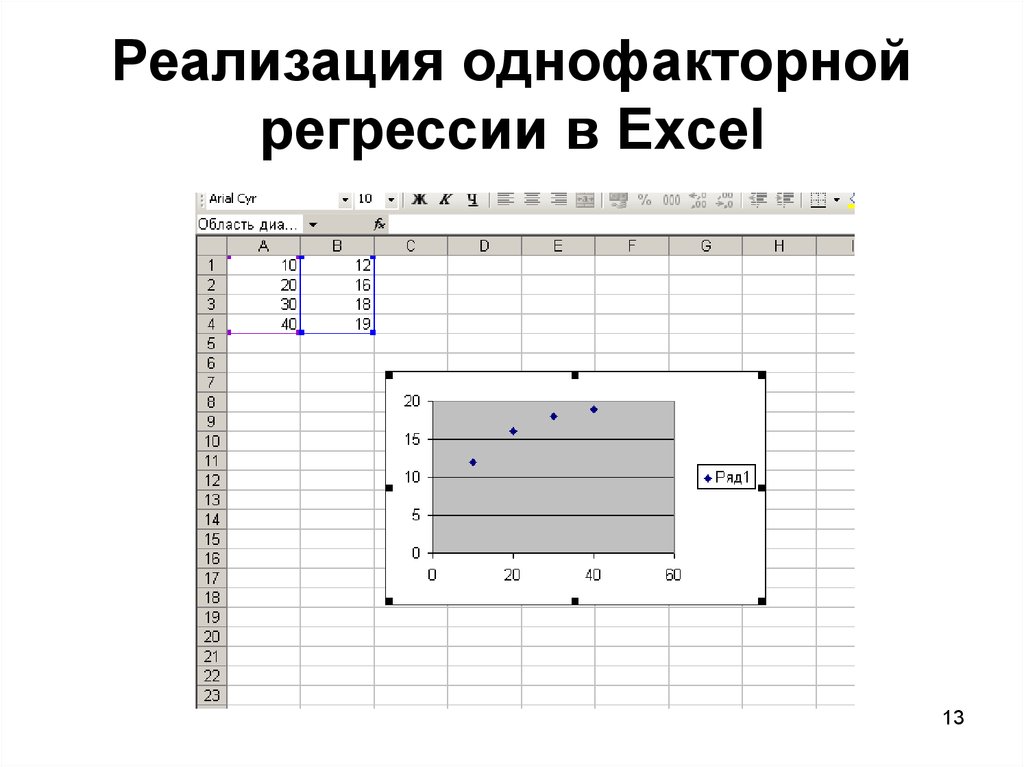 Проверьте остатки и нажмите OK.

Вы получите следующий вывод:

Интерпретация выходных данных регрессионного анализа

Давайте теперь разберемся со значением каждого термина в выводе. Мы разделим вывод на четыре основные части для нашего понимания.

Суммарный вывод

Итоговый вывод показывает, насколько хорошо рассчитанное уравнение линейной регрессии соответствует вашему источнику данных.

Множитель R — это коэффициент корреляции, который измеряет силу линейной зависимости между двумя переменными. Чем больше абсолютное значение, тем сильнее связь.

• 1 означает сильную положительную связь
• -1 означает сильную отрицательную связь
• 0 означает полное отсутствие связи

R Квадрат означает коэффициент детерминации, который показывает качество подгонки. Он показывает, сколько точек приходится на линию регрессии. В нашем примере значение R в квадрате равно 0,9.6, который отлично подходит. Другими словами, 96% зависимых переменных (значений y) объясняются независимыми переменными (значениями x).

Скорректированный квадрат R — это модифицированная версия квадрата R, которая корректирует предикторы, не являющиеся значимыми для регрессионной модели.

Стандартная ошибка

— это еще одна мера согласия, которая показывает точность вашего регрессионного анализа.

Анализ

ANOVA расшифровывается как дисперсионный анализ. Он дает информацию об уровнях изменчивости в вашей регрессионной модели.

• Df — число степеней свободы, связанных с источниками дисперсии.
• СС — сумма квадратов. Чем меньше Residual SS, а именно Total SS, тем лучше ваша модель соответствует данным.
• мс — среднеквадратичное значение.
• F — это F-статистика или F-тест для нулевой гипотезы. Он очень эффективно используется для проверки общей значимости модели.
• Значимость F представляет собой P-значение F.

График регрессии в Excel

Вы можете быстро визуализировать взаимосвязь между двумя переменными, создав график. Чтобы создать график линейной регрессии, выполните следующие действия:

• Выберите два переменных столбца ваших данных, включая заголовки.
• Перейдите на вкладку «Вставка» > группу «Диаграммы» > «Точечная диаграмма».

На вашем рабочем листе появится точечная диаграмма.

• Теперь, чтобы добавить линию тренда, щелкните правой кнопкой мыши любую точку и выберите Добавить линию тренда.

Получите опыт работы с новейшими инструментами и методами бизнес-аналитики с помощью магистерской программы для бизнес-аналитиков. Зарегистрируйтесь сейчас!

Заключение

Вот как вы делаете регрессионный анализ в Excel. Вы также должны знать тот факт, что Microsoft Excel не является статистической программой.

Повысьте свою карьеру в области аналитики с помощью новых мощных навыков работы с Microsoft Excel, пройдя курс Business Analytics with Excel, который включает обучение работе с Power BI.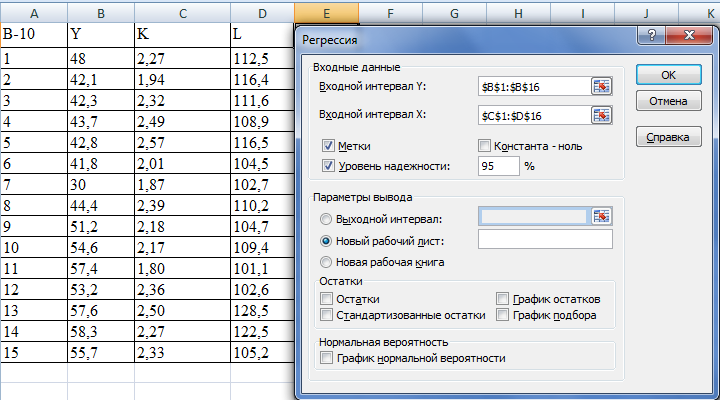

Этот курс бизнес-аналитики знакомит вас с основными понятиями анализа данных и статистики, чтобы помочь вам принимать решения на основе данных. Это обучение знакомит вас с Power BI и углубляется в статистические концепции, которые помогут вам извлекать ценные сведения из доступных данных для представления результатов с помощью панелей мониторинга на уровне руководителей.

У вас есть к нам вопросы? Не стесняйтесь задавать их в разделе комментариев к этой статье, и наши специалисты оперативно ответят на них!

Линейный регрессионный анализ в Excel

В этом учебном пособии объясняются основы регрессионного анализа и показаны несколько различных способов выполнения линейной регрессии в Excel.

Представьте себе: вам предоставляется множество различных данных, и вас просят спрогнозировать объемы продаж вашей компании на следующий год. Вы обнаружили десятки, а то и сотни факторов, которые могут повлиять на цифры. Но как узнать, какие из них действительно важны? Запустите регрессионный анализ в Excel.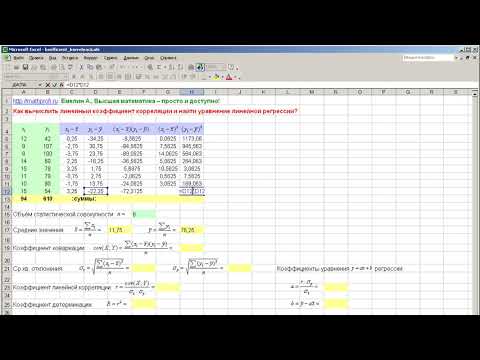 Это даст вам ответ на этот и многие другие вопросы: какие факторы имеют значение, а какими можно пренебречь? Насколько тесно связаны между собой эти факторы? И насколько вы можете быть уверены в предсказаниях?

• Регрессионный анализ в Excel
• Линейная регрессия в Excel с помощью Analysis ToolPak
• Нарисуйте график линейной регрессии
• Регрессионный анализ в Excel с формулами

Регрессионный анализ в Excel — основы

В статистическом моделировании регрессионный анализ используется для оценки отношений между двумя или более переменными: пытаясь понять и предсказать.

Независимые переменные (также известные как объясняющие переменные или предикторы ) — это факторы, которые могут влиять на зависимую переменную.

Регрессионный анализ помогает понять, как изменяется зависимая переменная при изменении одной из независимых переменных, и позволяет математически определить, какая из этих переменных действительно оказывает влияние.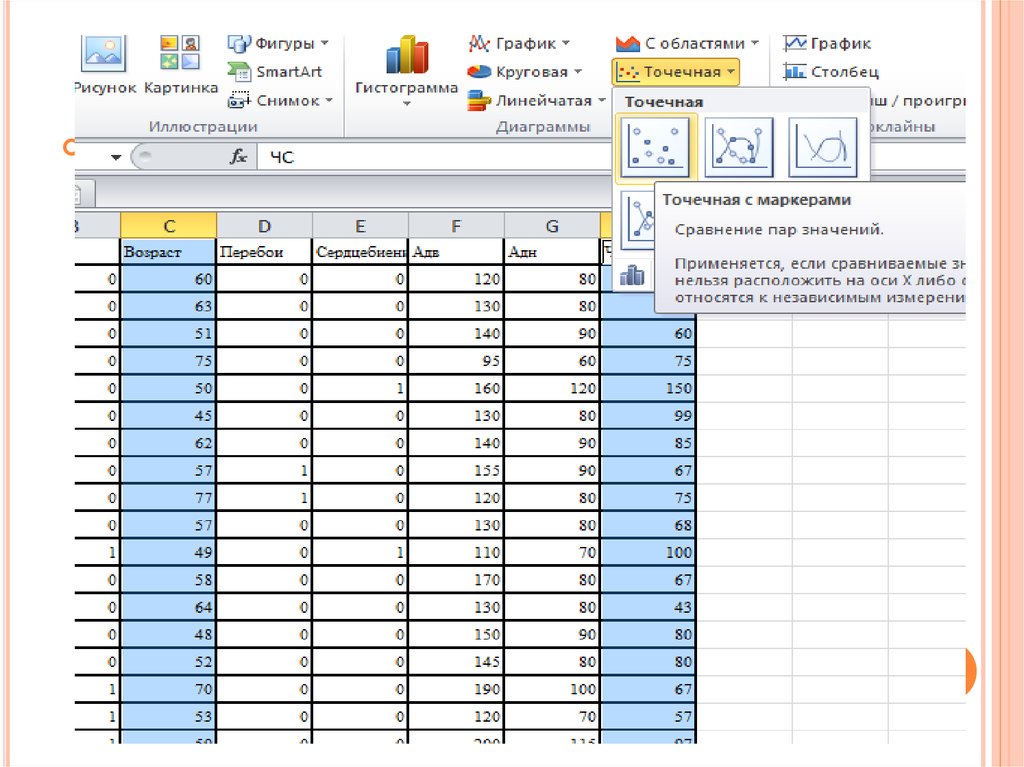

Технически модель регрессионного анализа основана на сумме квадратов , что представляет собой математический способ найти разброс точек данных. Цель модели — получить наименьшую возможную сумму квадратов и нарисовать линию, наиболее близкую к данным.

В статистике различают простую и множественную линейную регрессию. Простая линейная регрессия моделирует взаимосвязь между зависимой переменной и одной независимой переменной с помощью линейной функции. Если вы используете две или более независимых переменных для прогнозирования зависимой переменной, вы имеете дело с множественной линейной регрессией . Если зависимая переменная моделируется как нелинейная функция, потому что отношения данных не следуют прямой линии, используйте нелинейная регрессия вместо . Основное внимание в этом руководстве будет уделено простой линейной регрессии.

В качестве примера возьмем данные о продажах зонтов за последние 24 месяца и узнаем среднемесячное количество осадков за тот же период. Нанесите эту информацию на график, и линия регрессии продемонстрирует взаимосвязь между независимой переменной (осадки) и зависимой переменной (продажи зонтиков):

Уравнение линейной регрессии

Математически линейная регрессия определяется следующим уравнением:

y = bx + a + ε

Где:

• x — независимая переменная.
• y — зависимая переменная.
• a — это Y-пересечение , которое является ожидаемым средним значением y , когда все переменные x равны 0. На графике регрессии это точка пересечения прямой с осью Y.
• b — это наклон линии регрессии, которая представляет собой скорость изменения для y при изменении x .
• ε — член случайной ошибки, представляющий собой разницу между фактическим значением зависимой переменной и ее прогнозируемым значением.

Уравнение линейной регрессии всегда содержит погрешность, потому что в реальной жизни предикторы никогда не бывают идеально точными.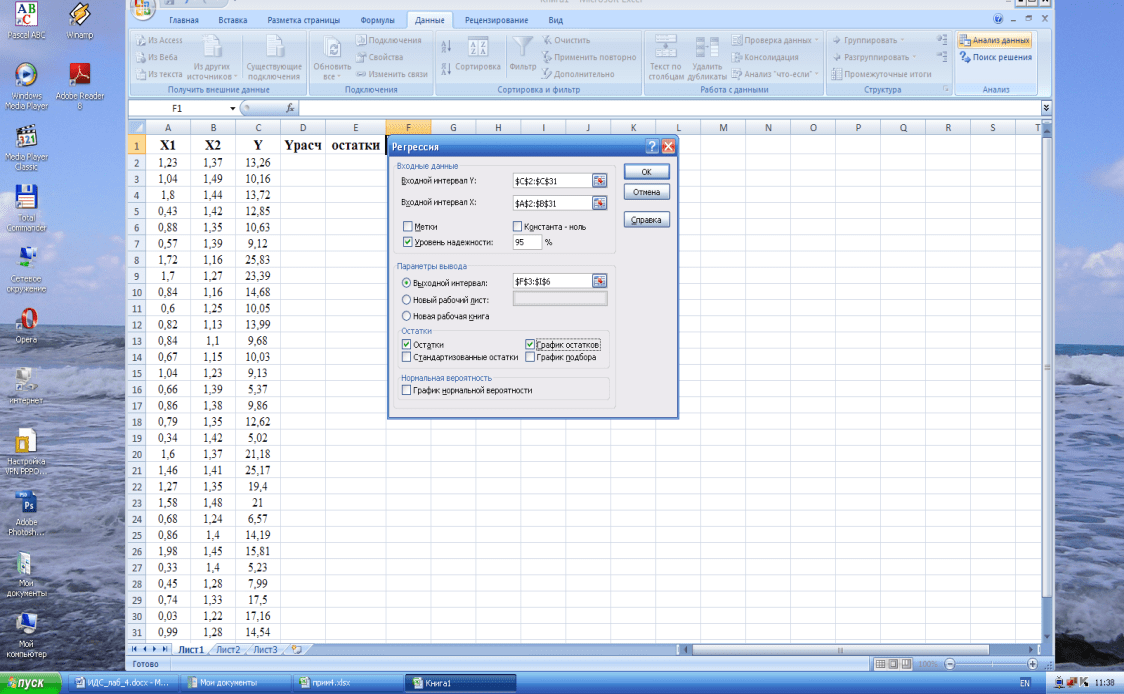 Однако некоторые программы, в том числе Excel, выполняют вычисление члена ошибки за кулисами. Итак, в Excel вы выполняете линейную регрессию, используя метод наименьших квадратов 90 151 90 152, и ищете коэффициенты a и b такие, что:

y = bx + a

Для нашего примера уравнение линейной регрессии принимает следующий вид: различных способов найти a и b . Три основных метода выполнения линейного регрессионного анализа в Excel:

Точечная диаграмма с линией тренда

Формула линейной регрессии

Ниже вы найдете подробные инструкции по использованию каждого метода.

Как выполнить линейную регрессию в Excel с помощью Analysis ToolPak

В этом примере показано, как выполнить регрессию в Excel с помощью специального инструмента, включенного в надстройку Analysis ToolPak.

Включить надстройку Analysis ToolPak

Analysis ToolPak доступен во всех версиях Excel 365 до 2003, но не включен по умолчанию. Итак, вам нужно включить его вручную. Вот как:

1. В Excel щелкните Файл > Параметры .
2. В диалоговом окне Параметры Excel выберите Надстройки на левой боковой панели, убедитесь, что Надстройки Excel выбраны в поле Управление , и нажмите Перейти .
3. В диалоговом окне Надстройки отметьте Analysis Toolpak и нажмите OK :

Это добавит инструменты Data Analysis к Data на вкладке ленты Excel.

Запустить регрессионный анализ

В этом примере мы собираемся выполнить простую линейную регрессию в Excel. У нас есть список среднемесячных осадков за последние 24 месяца в столбце B, который является нашей независимой переменной (предиктор), и количество проданных зонтов в столбце C, который является зависимой переменной. Конечно, есть много других факторов, которые могут повлиять на продажи, но пока мы сосредоточимся только на этих двух переменных:

При включенном пакете инструментов анализа выполните следующие действия для выполнения регрессионного анализа в Excel:

1. На вкладке Данные в группе Анализ нажмите кнопку Анализ данных .
2. Выберите Регрессия и нажмите OK .
3. В диалоговом окне Регрессия настройте следующие параметры:
   • Выберите Input Y Range , который является вашей зависимой переменной . В нашем случае это зонтичные продажи (C1:C25).
   • Выберите Input X Range , то есть вашу независимую переменную . В этом примере это среднемесячное количество осадков (B1:B25).

   Если вы строите модель множественной регрессии, выберите два или более смежных столбца с разными независимыми переменными.

   • Установите флажок Labels , если в верхней части диапазонов X и Y есть заголовки.
   • Выберите нужный Параметр вывода, новый рабочий лист в нашем случае.
   • При необходимости установите флажок Остатки , чтобы получить разницу между прогнозируемыми и фактическими значениями.
4. Щелкните OK и просмотрите результаты регрессионного анализа, созданные Excel.

Интерпретация выходных данных регрессионного анализа

Как вы только что видели, запустить регрессию в Excel легко, поскольку все расчеты выполняются автоматически. Интерпретация результатов немного сложнее, потому что вам нужно знать, что стоит за каждым числом. Ниже вы найдете разбивку по 4 основным частям результатов регрессионного анализа.

Выходные данные регрессионного анализа: итоговые выходные данные

В этой части сообщается, насколько хорошо рассчитанное уравнение линейной регрессии соответствует вашим исходным данным.

Вот что означает каждая часть информации:

Несколько R . Именно C или Коэффициент связи измеряет силу линейной зависимости между двумя переменными. Коэффициент корреляции может принимать любое значение от -1 до 1, а его абсолютное значение указывает на силу связи. Чем больше абсолютное значение, тем сильнее связь:

• 1 означает сильную положительную связь
• -1 означает сильную отрицательную связь
• 0 означает полное отсутствие связи

Квадрат R . Это Коэффициент детерминации , который используется в качестве индикатора качества подгонки. Он показывает, сколько точек приходится на линию регрессии. Значение R ² вычисляется из общей суммы квадратов, точнее, это сумма квадратов отклонений исходных данных от среднего.

В нашем примере R ² равно 0,91 (округлено до 2 цифр), что очень хорошо. Это означает, что 91% наших значений соответствуют модели регрессионного анализа. Другими словами, 91% зависимых переменных (значений y) объясняется независимыми переменными (значениями x). Как правило, хорошим соответствием считается значение R в квадрате, равное 95% или более.

Скорректированный квадрат R . Это R-квадрат с поправкой на количество независимых переменных в модели. Вы захотите использовать это значение вместо R квадрат для множественного регрессионного анализа.

Стандартная ошибка . Это еще одна мера согласия, показывающая точность вашего регрессионного анализа: чем меньше число, тем больше вы можете быть уверены в своем регрессионном уравнении. В то время как R ² представляет собой процент дисперсии зависимых переменных, который объясняется моделью, стандартная ошибка является абсолютной мерой, которая показывает среднее расстояние, на которое точки данных отходят от линии регрессии.

Наблюдения . Это просто количество наблюдений в вашей модели.

Выходные данные регрессионного анализа: ANOVA

Вторая часть выходных данных — это дисперсионный анализ (ANOVA):

По сути, он разбивает сумму квадратов на отдельные компоненты, которые дают информацию об уровнях изменчивости в вашей регрессионной модели:

• df — это число степеней свободы, связанных с источниками дисперсии.
• SS сумма квадратов. Чем меньше Residual SS по сравнению с Total SS, тем лучше ваша модель соответствует данным.
• MS среднеквадратичное значение.
• F — это F-статистика или F-тест для нулевой гипотезы. Он используется для проверки общей значимости модели.
• Значение F представляет собой P-значение F.

Часть ANOVA редко используется для простого линейного регрессионного анализа в Excel, но вам определенно следует внимательно изучить последний компонент. Значимость Значение F дает представление о том, насколько надежны (статистически значимы) ваши результаты. Если значимость F меньше 0,05 (5%), ваша модель в порядке. Если оно больше 0,05, вам, вероятно, лучше выбрать другую независимую переменную.

Выходные данные регрессионного анализа: коэффициенты

В этом разделе содержится конкретная информация о компонентах вашего анализа:

Наиболее полезным компонентом в этом разделе является Коэффициенты . Это позволяет вам построить уравнение линейной регрессии в Excel:

y = bx + a

Для нашего набора данных, где y — количество проданных зонтов, а x — среднемесячное количество осадков, наша формула линейной регрессии выглядит следующим образом:

Y = Коэффициент осадков * x + Пересечение

Если значения a и b округлить до трех знаков после запятой, получится:

Y=0,45*x-19,074

Например, при среднемесячном количестве осадков, равном 82 мм, продажи зонтов будут быть примерно 17,8:

0,45*82-19,074=17,8

Аналогичным образом вы можете узнать, сколько зонтов будет продано с любым другим указанным вами месячным количеством осадков (переменная x).

Выходные данные регрессионного анализа: остатки

Если вы сравните расчетное и фактическое количество проданных зонтов, соответствующих месячному количеству осадков 82 мм, вы увидите, что эти цифры немного отличаются:

Факт: 15 (строка 2 исходных данных)

В чем разница? Потому что независимые переменные никогда не являются идеальными предикторами зависимых переменных. А остатки могут помочь вам понять, насколько далеки фактические значения от прогнозируемых значений:

Для первой точки данных (осадки 82 мм) невязка составляет примерно -2,8. Итак, прибавляем это число к прогнозируемому значению, и получаем фактическое значение: 17,8 — 2,8 = 15.

Как построить график линейной регрессии в Excel

Если вам нужно быстро визуализировать взаимосвязь между двумя переменными, нарисуйте график линейной регрессии. Это очень легко! Вот как:

1. Выберите два столбца с вашими данными, включая заголовки.
2. На вкладке Вставка в группе Чаты щелкните значок Точечная диаграмма и выберите миниатюру Точечная (первая):

   Это добавит в ваш рабочий лист точечную диаграмму, которая будет похожа на эту:

3. Теперь нам нужно провести линию регрессии методом наименьших квадратов. Для этого щелкните правой кнопкой мыши любую точку и выберите Добавить линию тренда… из контекстного меню.
4. На правой панели выберите форму линии тренда Linear и, при необходимости, отметьте Display Equation on Chart , чтобы получить формулу регрессии:

   Как вы могли заметить, уравнение регрессии, созданное для нас в Excel, совпадает с формулой линейной регрессии, которую мы построили на основе выходных данных Коэффициенты.

5. Перейдите на вкладку Fill & Line и настройте линию по своему вкусу. Например, вы можете выбрать другой цвет линии и использовать сплошную линию вместо пунктирной (выберите Сплошная линия в Тире типа коробка):

На данный момент ваша диаграмма уже выглядит как приличный график регрессии:

Тем не менее, вы можете сделать еще несколько улучшений:

• Перетащите уравнение туда, куда считаете нужным.
• Добавить заголовки осей (кнопка Элементы диаграммы > Заголовки осей ).
• Если ваши точки данных начинаются в середине горизонтальной и/или вертикальной оси, как в этом примере, вы можете избавиться от лишнего пробела. Следующий совет объясняет, как это сделать: Масштабируйте оси диаграммы, чтобы уменьшить пустое пространство.

  А вот так выглядит наш улучшенный график регрессии:

  Важное примечание! На графике регрессии независимая переменная всегда должна располагаться на оси X, а зависимая переменная — на оси Y. Если ваш график построен в обратном порядке, поменяйте местами столбцы на листе, а затем нарисуйте диаграмму заново. Если вам не разрешено переупорядочивать исходные данные, вы можете переключить оси X и Y прямо на диаграмме.

Как сделать регрессию в Excel с помощью формул

Microsoft Excel имеет несколько статистических функций, которые могут помочь вам в проведении линейного регрессионного анализа, таких как ЛИНЕЙН, НАКЛОН, ОТРЕЗОК и КОРРЕЛ.

Функция ЛИНЕЙН использует метод регрессии наименьших квадратов для вычисления прямой линии, которая лучше всего объясняет взаимосвязь между вашими переменными, и возвращает массив, описывающий эту линию.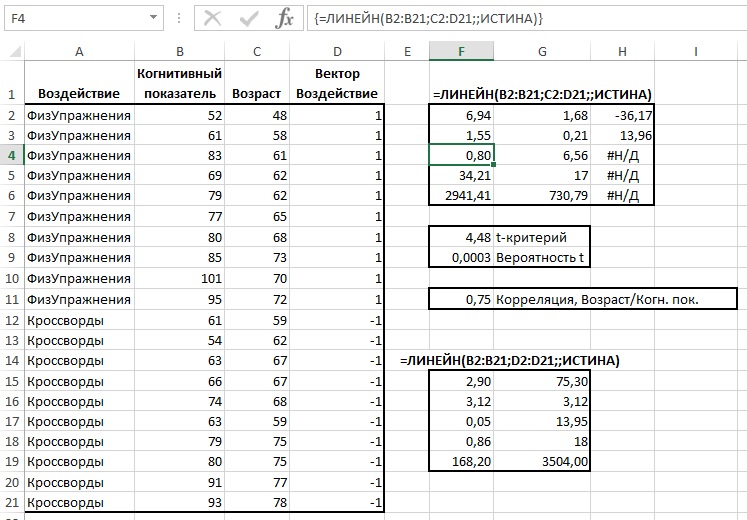 Вы можете найти подробное объяснение синтаксиса функции в этом руководстве. А пока давайте просто составим формулу для нашего примера набора данных:

=ЛИНЕЙН(C2:C25, B2:B25)

Поскольку функция ЛИНЕЙН возвращает массив значений, вы должны ввести ее как формулу массива. Выберите две соседние ячейки в одной строке, в нашем случае E2:F2, введите формулу и нажмите Ctrl + Shift + Enter, чтобы завершить ее.

Формула возвращает коэффициент b (E1) и константу a (F1) для уже знакомого уравнения линейной регрессии:

y = bx + a

Если вы избегаете использования формул массива в своих рабочих листах, вы можете вычислить a и b по отдельности с помощью обычных формул:

Получить точку пересечения Y (a):

=INTERCEPT(C2:C25, B2:B25)

Получить наклон (b):

2 =НАКЛОН(C2:C25, B2:B25)

Кроме того, вы можете найти коэффициент корреляции ( Multiple R в итоговых результатах регрессионного анализа), который показывает, насколько сильно две переменные связаны друг с другом:

=КОРРЕЛ(B2:B25,C2:C25)

На следующем снимке экрана показаны все эти формулы регрессии Excel в действии:

Совет.