Решение задач по математическому анализу
Математический анализ, он же матан, — бесспорно, самый пугающий предмет на первом курсе. Особенно для студентов-технарей (ибо студентам-математикам он нужен безусловно, а к гуманитариям требования ниже). В головах многих что-то в роде: «Мы пришли научиться конструировать самолеты, а не доказывать расходимость несобственного интеграла».
Зачем же нужен мат. анализ нематематикам?
Все слышали, что это основы и что без них дальше будет сложно. Но почему?
Приведем простой пример: мы узнаем после прохождения курса математического анализа — производные, их вычисление, что это такое и т.п. Без производных мы не поймем дифференциальные уравнения, уравнения математической физики. Без этих знаний мы просто-напросто не сможем решить задачу распределения тепла в комнате.
Таких примеров — банальных и не очень — много.
Как учить матан?
Данная статья не является учебным пособием, ее цель показать, что не нужно бояться сложного, нужно преодолевать сложности, впрочем, как и в жизни.
Матан — наша жизнь!
Итак, как же разобраться в этой куче бесконечно малых и бесконечно больших величин?
Ответ очевиден — читать литературу и решать задачи. Учебник, ставший классикой для технических вузов, конечно же «Основы Математического Анализа», авторы которого Ильин В.А. и Позняк Э.Г. Есть еще множество хороших книг. В общем, мы не будем осуждать программу вашего университета и возьмем книгу, которая рекомендована для вашей специальности. В качестве сборника задач лучше всего взять проверенного временем Демидовича или Кудрявцева. Так же стоит обратить внимание на очень известное пособие-решебник «Анти Демидович».
Итак, мы снарядились. Пора в бой!
Изучение теории
Как правило, манат «начинается» с последовательностей. На примере этой темы мы и рассмотрим порядок изучения.
Читаем теорию постепенно. По одному параграфу. Разбираемся, «проникаемся». Вследствие чего мы узнаем о ББП, БМП, предельным переходом в неравенствах, монотонными последовательностями, необходимыми и достаточными условиями сходимости и еще много интересного.
Решение задач
Изучив параграф, приступаем к самому главному — решению задач. Первым делом внимательно смотрим примеры по теме. Затем закрепляем знания с помощью решения нескольких задач на последовательности.
Практика решения задач в анализе — самое важное и самое сложное. Естественно, начинаем с простых задачек, которые решаются «по шаблону». Но и здесь не забываем, почему мы так делаем и какая теорема лежит в основе.
Например:
Пользуясь критерием Коши, доказать сходимость последовательности:
Вспоминаем критерий Коши, вспоминаем что такое фундаментальная последовательность и решаем, поначалу основываясь на примерах.
Разобравшись с простыми задачами, переходим к задачам, где нужно думать более глубже. Что-то вроде такого:
Выяснить, вытекает или нет сходимость последовательности {xn} из условия, что для любого натурального p существует предел
Вооружившись своими новыми знаниями и немного подумав мы решим и эти задачи, и докажем все, что от нас требует учебник.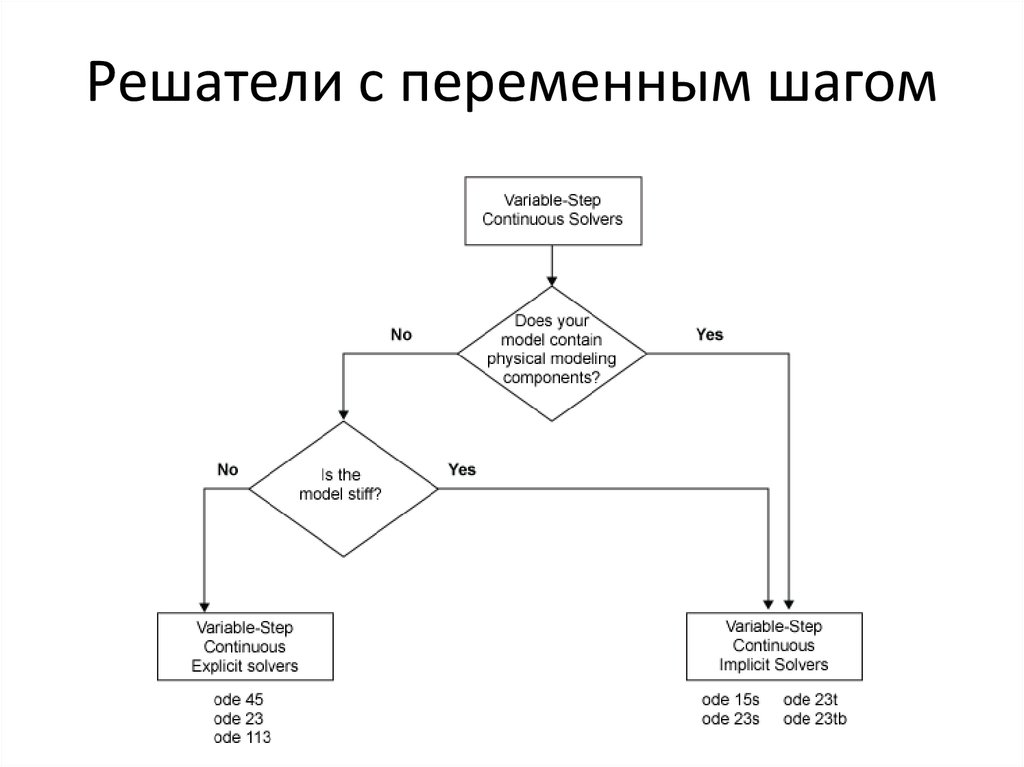
Далее параграф за параграфом, тему за темой мы усвоим основы замечательной дисциплины математический анализ. Мы научим наш мозг думать логически, основываясь на фактах. Это нам очень поможет в дальнейшей жизни.
Решение задач по матану является очень увлекательным занятием. Попробуйте, вам понравится!
Желаем успехов!
Также советуем обратить внимание на статью «Задачи с пределами и интегралами».
Решение математического анализа на заказ
Наши специалисты могут помочь решить задачи по матану любой степени сложности. Заказать работу можно у нас на сайте.
Обновление исследований и решателей — обзор версии COMSOL® 5.3
В программный пакет COMSOL Multiphysics® версии 5.3 включен новый решатель для моделирования CFD, а также новый решатель для моделирования электромагнитных и коррозионных процессов методом граничных элементов. Просмотрите все обновления версии 5.3 программного продукта COMSOL Multiphysics®, относящиеся к исследованиям и решателям.
Алгебраический многосеточный (AMG) решатель для вычислительной гидродинамики
Алгебраический многосеточный метод сглаженной агрегации (SA-AMG) расширили для работы с особыми сглаживающими алгоритмами вычислительной гидродинамики в программном пакете COMSOL Multiphysics®: сглаживающими алгоритмами SCGS, Vanka и SOR.
Использование альтернативного геометрического многосеточного (GMG) решателя требует создания трех уровней сетки, что может привести к проблемам при попытке построения сетки и решения моделей с изменяющейся геометрической формой на разных масштабах. Для решателя SA-AMG (Алгебраический многосеточный метод сглаженной агрегации) требуется только один уровень сетки, что значительно облегчает построение сетки, а процесс решения значительно более устойчив к крупным проблемам и «трудным» геометриям.
Например, в модели взаимодействия жидкости и конструкции в солнечной панели (на изображении), стойки и балки, поддерживающие панели, малы по сравнению с окружающей воздушной областью.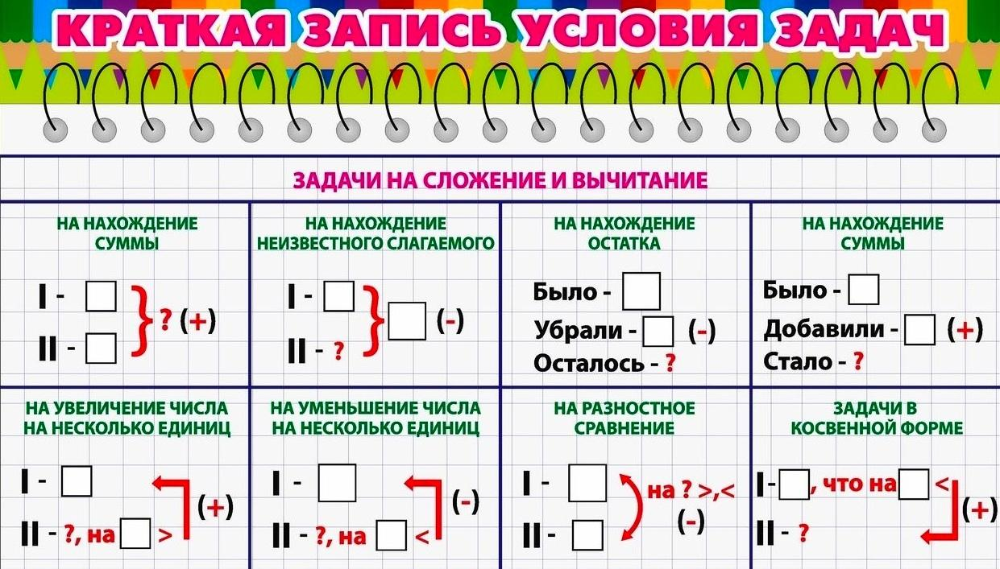
Путь к Библиотеке приложений с примером, использующим алгебраический многосеточный решатель:
CFD_Module/Single-Phase_Tutorials/solar_panel
Адаптивная сетка
H-адаптационный алгоритм для стационарных задач, параметрических задач и задач на собственные значения был пересмотрен, чтобы можно было сохранять промежуточные решения и сетки. Кроме того, адаптированные сетки теперь основаны на функциях построения сетки, которые позволяют плавно перейти от автоматизированного процесса решения к ручной адаптации, когда это необходимо.
Для этого были введены две новые опции для построения сетки: Adapt (Адаптация) и Size Expression (Выражение для размера сетки).
С помощью узла Adapt (Адаптация) сетку можно улучшить либо на основании выражения для ошибки в решении, либо на основании выражения для желаемого размера элемента сетки. Кроме этого, узел Size Expression (Выражение для размера сетки) можно добавить в последовательность операций построения сетки в Построителе моделей, чтобы изменить размер элемента во всем пространстве моделирования, используя выражения. Подробности на странице Mesh Updates (обновления Сетки).Функции адаптации и оценки ошибки были объединены. Оценки ошибок, используемые методом адаптации, теперь доступны как зависимые переменные; их можно использовать для постобработки результатов. Более того, оценка ошибки по норме L2 (невязки уравнения в частных производных) теперь также доступна для постобработки.
Усовершенствования также привели к тому, что метод Mesh initialization (Инициализация сетки) теперь может выполнять адаптацию не только на треугольных и тетраэдрических сетках. Это стало возможно благодаря адаптированным сеткам, построенным с помощью функции Reference (Ссылка), которая сохраняет исходную последовательность сетки, и новой функции построения сетки Size Expression (Выражение для размера сетки).
Методы Regular refinement (Регулярное уточнение) и Longest refinement (Самое длительное уточнение) теперь при необходимости автоматически преобразуют сетку в треугольную или тетраэдрическую. Это означает, что пользователю нет нужды добавлять какие-либо опции типа Convert (Преобразовать) в последовательность построения сетки.
В тестовой модели Euler Bump (Выступ Эйлера) пакета COMSOL Multiphysics® используется новая функция адаптивного измельчения расчетной сетки. В тестовой модели Euler Bump (Выступ Эйлера) пакета COMSOL Multiphysics® используется новая функция адаптивного измельчения расчетной сетки.
Путь к Библиотеке приложений для приложения, использующее новое адаптивное измельчение сетки.
CFD_Module/High_Mach_Number_Flow/euler_bump
Быстрый итерационный решатель для решения задач методом граничных элементов
Добавлен прямой решатель для решения задач методом граничных элементов (BEM).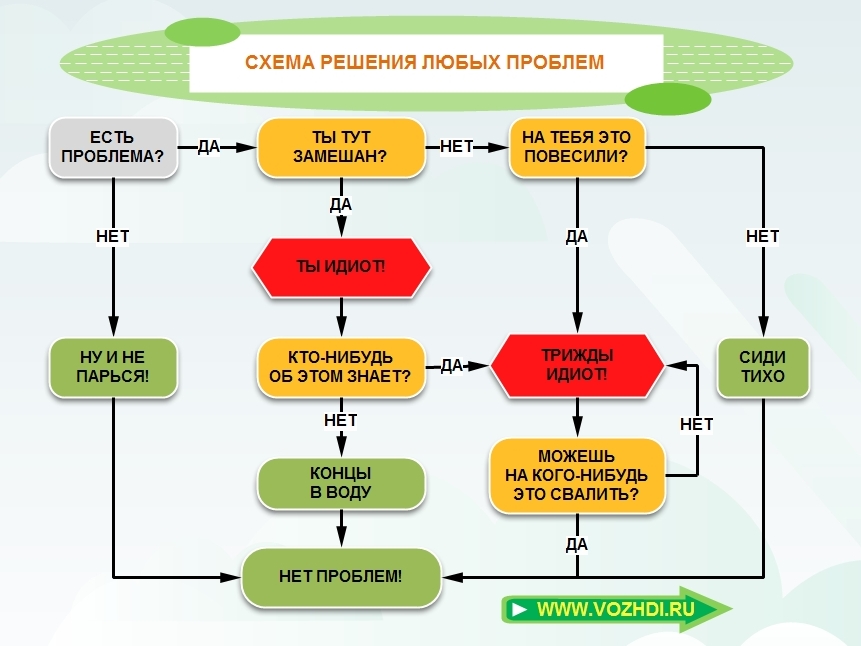
Это полезно для задач, в которых метод конечных элементов (FEM) не слишком эффективен.
Время решения для этого прямого решателя приблизительно пропорционально кубу числа степеней свободы данной задачи. Другими словами, время решения значительно увеличивается с ростом размера задачи. Чтобы облегчить задачу, поддерживаются итеративные решатели на основе быстрого матрично-векторного перемножения. Это дает возможность выполнить сжатие матриц с использованием так называемого сжатия
Предусмотрены два типа предобуславливателя: Sparse Approximate Inverse (Разреженная приблизительная обратная матрица, SAI) _ и _Direct Preconditioner (Прямой предобуславливатель). Оба они подвергаются воздействию так называемой ближнепольной части матрицы. Ближнепольная часть матрицы является разреженной и требует гораздо меньше памяти для хранения и решения, чем полная матрица.
Предобуславливатель SAI — это пример явной предварительной подготовки, когда аппроксимируют обратную матрицу, а не саму матрицу. В прямом предобуславливателе используется метод LU (нижняя-верхняя триангуляция) матрицы.
Метод граничных элементов был реализован в общем физическом интерфейсе для решения уравнений в частных производных, в интерфейсе модуля AC/DC для решения задач электростатики, а также в модуле Коррозия и в [модуле Электроосаждение](/release /5.3/electrodeposition-module) для решения задач электрохимической плотности тока.
Моделирование электростатических свойств буровой установки в морской воде с использованием метода граничных элементов (BEM). Размер конструкции, количество составных частей и сложность геометрии, а также открытое пространство, в котором находится платформа, делают метод граничных элементов оптимальным средством моделирования в этой и подобных задачах. Моделирование электростатических свойств буровой установки в морской воде с использованием метода граничных элементов (BEM).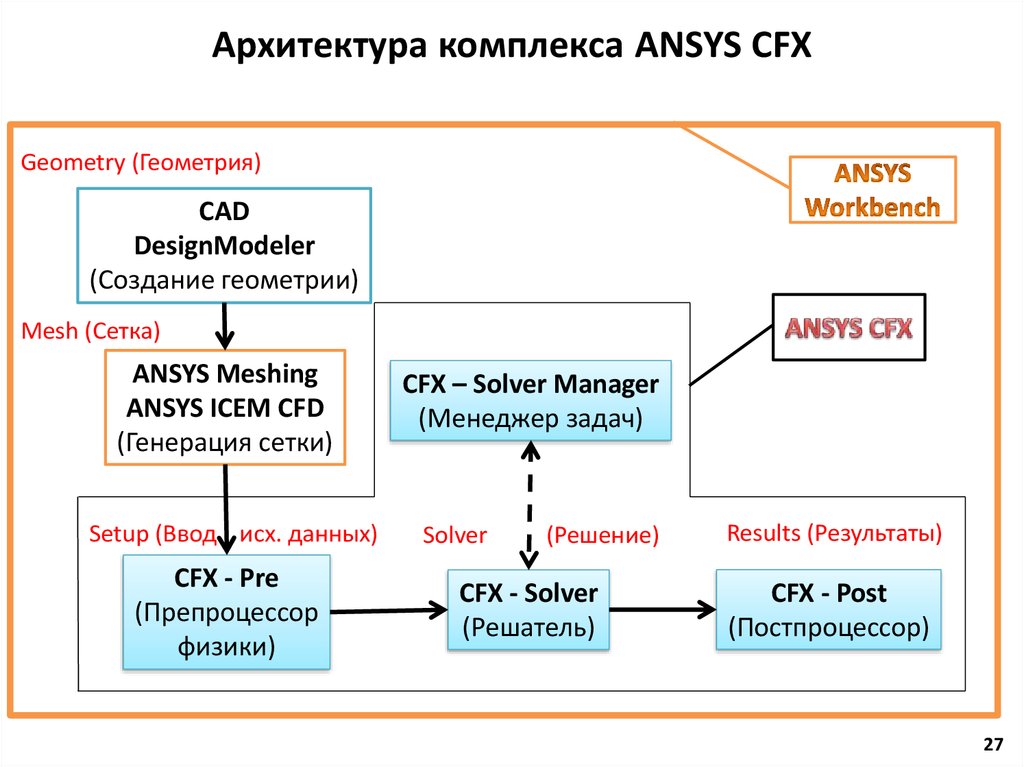
Путь к Библиотеке приложений для примеров, использующих BEM (Метод граничных элементов):
ACDC_Module/Capacitive_Devices/capacitor_tunable
ACDC_Module/Applications/touchscreen_simulator
ACDC_Module/Tutorials/capacitive_pressure_sensor_bem
Поддержка решателя для гибридных задач BEM/FEM
Иногда задачи мультифизического моделирования решаются с помощью одного численного метода, но оптимально их можно решить с использованием различных численных методов: BEM (метода граничных элементов) и FEM (метода конечных элементов) для различных физик. Гибридные модели BEM/FEM могут использоваться там, где матрица хранится в оптимальном разреженном формате для части FEM и в плотном или в безматричном формате для части BEM.
Тогда становится возможным использовать отдельно предобуславливатель или сглаживатель для отдельных FEM (метод конечных элементов) и BEM (метод граничных элементов) частей матрицы.
Например, можно использовать эффективный итеративный решатель с гибридным предобуславливателем. Часть FEM (метод конечных элементов) можно предварительно обусловить как обычно, а для части BEM (метод граничных элементов) подойдет один из ранее упомянутых предобуславливателей для матриц ближнего поля. Итерационный метод вычисляет невязку с помощью гибридного метода матричных и безматричных вычислений, оптимально используя различные виды быстрых матрично-векторных произведений.
Чувствительность для точных переменных граничного потока
Теперь можно получить вклад чувствительности из переменных Boundary Flux (Граничный поток) с помощью метода Forward sensitivity (Прямая чувствительность). Это точные переменные граничного потока, которые имеются в некоторых физических интерфейсах, таких как интерфейс тепломассообмена.
В соответствующих разделах Discretization (Дискретизация) этих интерфейсов можно выбрать флажок Compute boundary fluxes (Рассчитать граничные потоки), чтобы получить доступ к этим переменным и использовать их.
Объединение решений
Теперь можно объединить два решения в единое решение или набор данных. Это полезно, когда для постобработки нужно одно решение или один набор данных, а также когда одно решение используется как входные данные для нового этапа моделирования. Нестационарные решения, параметрические решения и собственные значения частот можно объединить, их можно либо связать последовательно, либо суммировать.
Посмотреть скриншот
Улучшения производительности на основе сеток в разрывном методе Галеркина
Было реализовано несколько улучшений как для ускорения разрывного метода Галеркина (dG), так и для уменьшения требуемого объема памяти. Одно из улучшений касается новой метрики сетки, которая используется для расчета устойчивого временного интервала для метода явной дискретизации по времени.
Метрика на треугольной сетке — диаметр наибольшей вписанной в треугольник окружности, а на тетраэдрической — диаметр наибольшей сферы, вписанной в тетраэдр. С помощью этой метрики можно лучше определять шаг времени, необходимый для устойчивого интегрирования во времени, и лучше описывать элементы сетки в модели.
Другое улучшение связано с новым методом оптимизации качества сетки. Этот метод нужно использовать вместе с методом Галеркина (dG), чтобы еще больше увеличить устойчивый временной интервал метода явной дискретизации по времени. В этом методе сетка строится таким образом, чтобы не создавать слишком маленькие ячейки и не ограничивать устойчивый временной интервал. Можно использовать новую опцию сетки
Посмотреть скриншот
В качестве примера рассмотрим учебную модель Ultrasound Flow Meter with Generic Time-of-Flight Configuration (Ультразвуковой расходомер с обобщенной настройкой времени полета), который содержит 7,5 миллиона степеней свободы.
В тестовом прогоне в версии 5.3 программного пакета COMSOL Multiphysics® на настольном компьютере (процессор Intel® Core™ i7, частота 3,60 ГГц, 4 ядра и 32 ГБайт оперативной памяти) акустическая задача решена за 7 часов и 5 минут; при этом использовалось 6,0 ГБайт оперативной памяти. В версии 5.3 с новым методом разреженной сборки на то же самое исследование требуется 5 часов и 1 минута и 5,8 ГБайт оперативной памяти. Это означает ускорение примерно на 30% и небольшое уменьшение использования памяти.
Улучшение производительности многоядерных процессоров в разрывном методе Галеркина (dG)
Уменьшение требований к памяти достигнуто при расчете моделей на многоядерных системах. Здесь для вектора невязки использовали новый метод разреженной сборки. Требования к памяти уменьшились и не зависят от числа используемых процессорных ядер. Кроме того, используемый объем памяти во время инициализации значительно снижен. Это усовершенствование ускоряет метод, поскольку удается избежать излишнего выделения памяти.
В последующем исследовании оптимизации использования памяти при расчете решений на многоядерных системах, помимо рассмотрения преимуществ, достигнутых благодаря сеточному разбиению и метрическим параметрам сетки, можно сравнить модели, вычисленные как в версии 5.2а пакета COMSOL Multiphysics
| Size | Version 5.2a | Version 5.3 | Improvement |
|---|---|---|---|
Medium (6.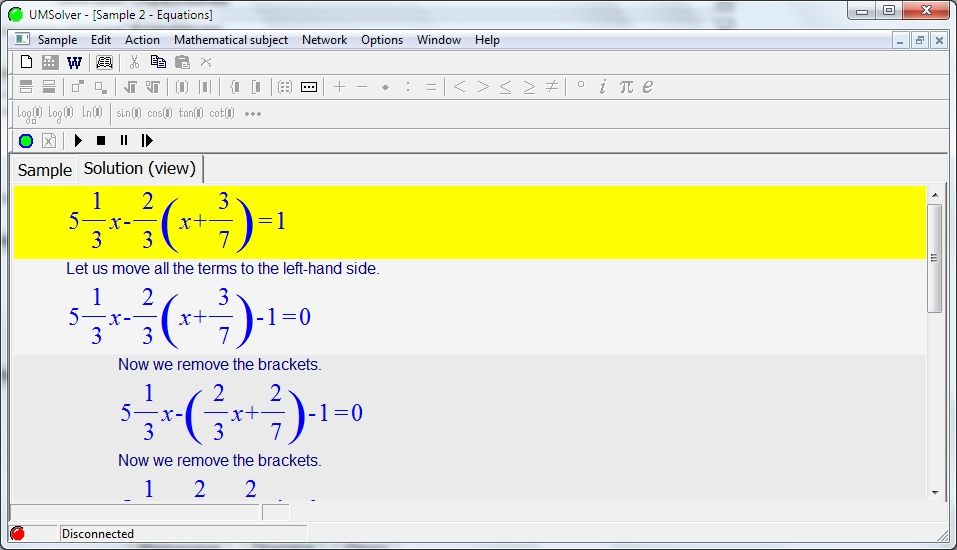 7 MDOF/t = 0.05) | 74 sec./4.1 GB | 61 sec./3.2 GB | 18%/22% |
| Large (20 MDOF/t = 0.05) | 307 sec./10 GB | 250 sec./7.3 GB | 19%/27% |
Intel, Intel Core и Xenon являются товарными знаками корпорации Intel или ее дочерних компаний в США и/или других странах.
Учебное пособие по Решателю Excel с пошаговыми примерами
В этом учебном пособии объясняется, как добавить и где найти Решатель в различных версиях Excel с 2016 по 2003 год. В пошаговых примерах показано, как использовать Решатель Excel для поиска оптимальных решения для линейного программирования и других видов задач.
Всем известно, что Microsoft Excel содержит множество полезных функций и мощных инструментов, которые могут сэкономить часы вычислений. Но знаете ли вы, что у него также есть инструмент, который может помочь вам найти оптимальные решения для проблем принятия решений?
В этом руководстве мы рассмотрим все основные аспекты надстройки Excel Solver и предоставим пошаговое руководство по ее наиболее эффективному использованию.
- Что такое Solver в Excel?
- Как добавить решатель в Excel
- Как использовать Solver в Excel
- Примеры решения Excel
- Как сохранить и загрузить модели Excel Solver
- Алгоритмы Excel Solver
Что такое решатель Excel?
Решатель Excel принадлежит к специальному набору команд, часто называемых инструментами анализа «что, если». Он в первую очередь предназначен для моделирования и оптимизации различных бизнес-моделей и инженерных моделей.
Надстройка Excel Solver особенно полезна для решения задач линейного программирования, также называемых задачами линейной оптимизации, и поэтому иногда называется решателем линейного программирования . Кроме того, он может решать гладкие нелинейные и негладкие задачи. Дополнительные сведения см. в разделе Алгоритмы Excel Solver.
Хотя Solver не может решить каждую возможную проблему, он действительно полезен при работе со всевозможными проблемами оптимизации, когда вам нужно принять наилучшее решение. Например, он может помочь вам максимизировать возврат инвестиций, подобрать оптимальный бюджет для вашей рекламной кампании, составить оптимальный график работы ваших сотрудников, минимизировать затраты на доставку и так далее.
Как добавить Solver в Excel
Надстройка Solver включена во все версии Microsoft Excel, начиная с 2003, но по умолчанию она не включена.
Чтобы добавить Solver в Excel, выполните следующие действия:
- В Excel 2010 — Excel 365 щелкните Файл > Параметры .
В Excel 2007 нажмите кнопку Microsoft Office , а затем щелкните Параметры Excel . - В диалоговом окне Параметры Excel нажмите Надстройки на левой боковой панели, убедитесь, что Надстройки Excel выбраны в поле Управление в нижней части окна, и нажмите Перейти .
- В диалоговом окне Add-Ins установите флажок Надстройка Solver и нажмите OK :
Чтобы получить Solver для Excel 2003 , перейдите в меню Инструменты и щелкните Надстройки . В списке надстроек доступных установите флажок надстройка Solver и нажмите OK .
Примечание. Если Excel отображает сообщение о том, что надстройка Solver в настоящее время не установлена на вашем компьютере, нажмите Да для установки.
Где находится Solver в Excel?
В современных версиях Excel кнопка Solver появляется на вкладке Data , в группе Analysis :
Где находится Solver в Excel 2003?
После того, как надстройка Solver загружена в Excel 2003, ее команда добавляется в меню Tools :
Теперь, когда вы знаете, где найти Solver в Excel, откройте новый рабочий лист и приступим!
Примечание. В примерах, обсуждаемых в этом руководстве, используется Solver в Excel 2013. Если у вас есть другая версия Excel, снимки экрана могут не точно соответствовать вашей версии, хотя функциональность Solver в основном такая же.
Как использовать Solver в Excel
Перед запуском надстройки Excel Solver сформулируйте модель, которую вы хотите решить, на листе. В этом примере давайте найдем решение следующей простой задачи оптимизации.
Проблема . Предположим, вы владелец салона красоты и планируете предоставлять своим клиентам новую услугу. Для этого вам необходимо купить новое оборудование стоимостью 40 000 долларов США, которое необходимо оплатить в рассрочку в течение 12 месяцев.
Цель : Рассчитать минимальную стоимость услуги, которая позволит вам оплатить новое оборудование в указанные сроки.
Для этой задачи я создал следующую модель:
А теперь давайте посмотрим, как Excel Solver может найти решение этой проблемы.
1. Запустите Excel Solver
На вкладке Data в группе Analysis нажмите кнопку Solver .
2. Определите проблему
Solver Parameters откроется окно, в котором вы должны настроить 3 основных компонента:
- Целевая ячейка
- Переменные ячейки
- Ограничения
Что именно делает Excel Solver с указанными выше параметрами? Он находит оптимальное значение (максимальное, минимальное или заданное) для формулы в ячейке Цель путем изменения значений в ячейках Переменная и с учетом ограничений в ячейках Ограничения .
Цель
Ячейка Цель (ячейка Цель в более ранних версиях Excel) — это ячейка , содержащая формулу , которая представляет задачу или цель проблемы. Целью может быть максимизация, минимизация или достижение некоторого целевого значения.
В этом примере целевой ячейкой является B7, которая рассчитывает срок платежа по формуле =B3/(B4*B5) , и результат формулы должен быть равен 12:
Переменные ячейки
Переменные ячейки ( Изменяющиеся ячейки или Настраиваемые ячейки в более ранних версиях) — это ячейки, содержащие переменные данные, которые можно изменить для достижения цели. Excel Solver позволяет указать до 200 переменных ячеек.
В этом примере у нас есть пара ячеек, значения которых можно изменить:
- Прогнозируемое количество клиентов в месяц (B4), которое должно быть меньше или равно 50; и
- Стоимость услуги (B5), которую должен рассчитать Excel Solver.
Совет. Если переменные ячейки или диапазоны в вашей модели несмежные , выберите первую ячейку или диапазон, а затем нажмите и удерживайте клавишу Ctrl при выборе других ячеек и/или диапазонов. Или введите диапазоны вручную, разделив их запятыми.
Ограничения
Решатель Excel Ограничения — это ограничения или пределы возможных решений проблемы. Другими словами, ограничения — это условия, которые должны быть соблюдены.
Чтобы добавить ограничения, выполните следующие действия:
- Нажмите кнопку Добавить справа от поля « С учетом ограничений ».
- В окне Constraint введите ограничение.
- Нажмите кнопку Добавить , чтобы добавить ограничение в список.
- Продолжайте вводить другие ограничения.
- После того, как вы ввели окончательное ограничение, нажмите OK для возврата в главное окно Solver Параметры .
Excel Solver позволяет указать следующие отношения между указанной ячейкой и ограничением.
- Меньше или равно , равно и больше или равно . Вы устанавливаете эти отношения, выбирая ячейку в поле Ссылка на ячейку , выбирая один из следующих знаков: <= , =, или >= , а затем введите число, ссылку на ячейку/имя ячейки или формулу в поле Constraint (см. скриншот выше).
- Целое число . Если указанная ячейка должна быть целым числом, выберите int , и слово integer появится в поле Constraint .
- Различные значения . Если каждая ячейка в указанном диапазоне должна содержать другое значение, выберите dif и слово AllDifferent появится в поле Constraint .
- Двоичный . Если вы хотите ограничить ссылочную ячейку значением 0 или 1, выберите bin , и слово binary появится в поле Constraint .
Примечание. Отношения int , bin и dif можно использовать только для ограничений переменных ячеек.
Чтобы отредактировать или удалить существующее ограничение, выполните следующие действия:
- В диалоговом окне Solver Parameters щелкните ограничение.
- Чтобы изменить выбранное ограничение, нажмите Изменить и внесите необходимые изменения.
- Чтобы удалить ограничение, нажмите кнопку Удалить .
В этом примере ограничения таковы:
- B3=40000 — стоимость нового оборудования 40000 долларов.
- B4<=50 - прогнозируемое количество пациентов в месяц в возрасте до 50 лет.
3. Решить задачу
После настройки всех параметров нажмите кнопку Решить в нижней части окна Параметры решателя (см. скриншот выше) и дайте надстройке Excel Solver найти оптимальное решение вашей проблемы.
В зависимости от сложности модели, памяти компьютера и скорости процессора это может занять несколько секунд, несколько минут или даже несколько часов.
Когда Solver закончит обработку, он отобразит 9 OK :
Окно Solver Result закроется, и решение сразу же появится на листе.
В этом примере в ячейке B5 отображается 66,67 доллара США, что является минимальной стоимостью за услугу, которая позволит вам оплатить новое оборудование через 12 месяцев при условии, что количество клиентов в месяц составляет не менее 50:
Чаевые:
- Если Excel Solver слишком долго обрабатывал определенную проблему, вы можете прервать процесс, нажав клавишу Esc. Excel пересчитает рабочий лист с последними значениями, найденными для ячеек Variable .
- Чтобы получить дополнительные сведения о решенной проблеме, щелкните тип отчета в поле Reports , а затем щелкните OK . Отчет будет создан на новом листе: .
Теперь, когда вы получили общее представление о том, как использовать Solver в Excel, давайте подробнее рассмотрим еще пару примеров, которые могут помочь вам лучше понять.
Примеры Excel Solver
Ниже вы найдете еще два примера использования надстройки Excel Solver. Сначала мы найдем решение известной головоломки, а затем решим реальную задачу линейного программирования.
Решатель Excel, пример 1 (магический квадрат)
Я думаю, все знакомы с головоломками «магический квадрат», где вы должны поместить набор чисел в квадрат так, чтобы все строки, столбцы и диагонали в сумме давали определенное число.
Например, знаете ли вы решение для квадрата 3×3, содержащего числа от 1 до 9?где каждая строка, столбец и диагональ в сумме дают 15?
Вероятно, решить эту головоломку методом проб и ошибок не составит большого труда, но держу пари, что Решатель найдет решение быстрее. Наша часть работы состоит в том, чтобы правильно определить проблему.
Для начала введите числа от 1 до 9 в таблицу, состоящую из 3-х строк и 3-х столбцов. Решателю Excel на самом деле не нужны эти числа, но они помогут нам визуализировать проблему. Что действительно нужно надстройке Excel Solver, так это формулы SUM, которые суммируют каждую строку, столбец и 2 диагонали:
Со всеми формулами запустите Solver и настройте следующие параметры:
- Set Objective . В этом примере нам не нужно устанавливать какую-либо цель, поэтому оставьте это поле пустым.
- Переменные ячейки . Мы хотим заполнить числами ячейки от B2 до D4, поэтому выберите диапазон B2:D4.
- Ограничения . Должны быть соблюдены следующие условия:
- $B$2:$D$4 = AllDifferent — все ячейки переменных должны содержать разные значения.
- $B$2:$D$4 = целое число — все ячейки переменных должны быть целыми числами.
- $B$5:$D$5 = 15 — сумма значений в каждом столбце должна быть равна 15.
- $E$2:$E$4 = 15 — сумма значений в каждой строке должна быть равна 15.
- $B$7:$B$8 = 15 — сумма обеих диагоналей должна быть равна 15.
Наконец, нажмите кнопку Решить , и решение уже готово!
Excel Solver, пример 2 (задача линейного программирования)
Это пример простой задачи оптимизации транспортировки с линейной целью. Более сложные модели оптимизации такого рода используются многими компаниями для ежегодной экономии тысяч долларов.
Проблема : Вы хотите минимизировать стоимость доставки товаров с 2 разных складов 4 различным клиентам. Каждый склад имеет ограниченное предложение, и у каждого клиента есть определенный спрос.
Цель : Минимизировать общую стоимость доставки, не превышая количество, доступное на каждом складе, и удовлетворить спрос каждого клиента.
Исходные данные
Вот как выглядит наша задача оптимизации транспортировки:
Формулировка модели
Чтобы определить нашу задачу линейного программирования для Excel Solver, давайте ответим на 3 основных вопроса:
- Какие решения должны быть сделанный? Мы хотим рассчитать оптимальное количество товара для доставки каждому покупателю с каждого склада. Это переменных ячеек (B7:E8).
- Какие ограничения? Запасы, доступные на каждом складе (I7:I8), не могут быть превышены, и должно быть доставлено количество, заказанное каждым клиентом (B10:E10). это Ограничено ячеек.
- Какова цель? Минимальная общая стоимость доставки. А это наша ячейка Objective (C12).
Следующее, что вам нужно сделать, это рассчитать общее количество товаров, отгруженных с каждого склада (G7:G8), и общее количество товаров, полученных каждым клиентом (B9:E9). Вы можете сделать это с помощью простых формул суммы, показанных на снимке экрана ниже. Кроме того, вставьте формулу СУММПРОИЗВ в C12 для расчета общей стоимости доставки:
Чтобы облегчить понимание нашей модели оптимизации транспортировки, создайте следующие именованные диапазоны:
| Имя диапазона | Клетки | Параметр решающей программы |
| Отгруженные товары | В7:Е8 | Переменные ячейки |
| В наличии | И7:И8 | Ограничение |
| Всего отправлено | G7:G8 | Ограничение |
| Заказано | В10:Е10 | Ограничение |
| Всего_получено | В9:Е9 | Ограничение |
| Стоимость доставки | С12 | Цель |
Последнее, что вам осталось сделать, это настроить параметры Excel Solver:
- Цель: Shipping_cost установить на Min
- Переменные ячейки: Products_shipped
- Ограничения: Всего_получено = Заказано и Всего_отгружено <= Доступно
Обратите внимание, что в данном примере мы выбрали метод решения Simplex LP , потому что мы имеем дело с задачей линейного программирования. Если вы не уверены, какая у вас проблема, вы можете оставить метод решения GRG Nonlinear по умолчанию. Для получения дополнительной информации см. Алгоритмы Excel Solver.
Решение
Нажмите кнопку Решить в нижней части окна Параметры решателя , и вы получите ответ. В этом примере надстройка Excel Solver рассчитала оптимальное количество товаров для доставки каждому покупателю с каждого склада с минимальной общей стоимостью доставки:
Как сохранить и загрузить сценарии Excel Solver
При решении определенной модели может потребоваться сохранить значения ячеек Variable в качестве сценария, который можно просмотреть или повторно использовать позже.
Например, при расчете минимальной стоимости обслуживания в самом первом примере, обсуждаемом в этом руководстве, вы можете попробовать различное количество предполагаемых клиентов в месяц и посмотреть, как это повлияет на стоимость обслуживания. При этом вы можете захотеть сохранить уже просчитанный вами наиболее вероятный сценарий и восстановить его в любой момент.
Сохранение Сценарий решателя Excel сводится к выбору диапазона ячеек для сохранения данных. Загрузка модели решателя — это просто предоставление Excel диапазона ячеек, в которых сохраняется ваша модель. Подробные шаги следуют ниже.
Сохранение модели
Чтобы сохранить сценарий решателя Excel, выполните следующие действия:
- Откройте рабочий лист с рассчитанной моделью и запустите решатель Excel.
- В параметрах решателя , нажмите кнопку Загрузить/Сохранить .
- Excel Solver сообщит вам, сколько ячеек необходимо для сохранения вашего сценария. Выберите столько пустых ячеек и нажмите Сохранить :
- Excel сохранит вашу текущую модель, которая может выглядеть примерно так:
В то же время появится окно Solver Parameters , где вы можете изменить свои ограничения и попробовать различные варианты «что, если».
Загрузка сохраненной модели
Если вы решили восстановить сохраненный сценарий, сделайте следующее:
- В окне Параметры решателя нажмите кнопку Загрузить/Сохранить .
- На рабочем листе выберите диапазон ячеек, содержащих сохраненную модель, и нажмите Загрузить :
- В диалоговом окне Загрузить модель нажмите кнопку Заменить :
- Откроется главное окно Excel Solver с параметрами ранее сохраненной модели. Все, что вам нужно сделать, это нажать на Кнопка «Решить » для пересчета.
Алгоритмы решателя Excel
При определении задачи для решателя Excel вы можете выбрать один из следующих методов в раскрывающемся списке Выберите метод решения :
- GRG Нелинейный. Обобщенный редуцированный градиентный нелинейный алгоритм используется для задач, которые являются гладкими нелинейными, т.е. в которых хотя бы одно из ограничений является гладкой нелинейной функцией переменных решения. Более подробную информацию можно найти здесь.
- LP Симплекс . Метод Simplex LP Solving основан на алгоритме Simplex, созданном американским ученым-математиком Джорджем Данцигом. Он используется для решения так называемых задач линейного программирования — математических моделей, требования к которым характеризуются линейными отношениями, т.е. состоят из одной цели, представленной линейным уравнением, которое необходимо максимизировать или минимизировать. Для получения дополнительной информации, пожалуйста, посетите эту страницу.
- Эволюционный . Он используется для негладких задач, которые представляют собой наиболее сложный тип задач оптимизации, потому что некоторые функции не являются гладкими или даже прерывистыми, и поэтому трудно определить направление, в котором функция увеличивается или уменьшается. Для получения дополнительной информации см. эту страницу.
Чтобы изменить способ поиска решения Solver, нажмите кнопку Options в диалоговом окне Solver Parameters и настройте любые или все параметры в GRG Нелинейный , Все методы и Эволюционный вкладки.
Вот как вы можете использовать Solver в Excel, чтобы найти лучшие решения для ваших проблем принятия решений. А теперь вы можете загрузить примеры Excel Solver, обсуждаемые в этом руководстве, и перепроектировать их для лучшего понимания. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе.
Вас также может заинтересовать
Использование Solver для определения оптимального ассортимента продукции
В этой статье обсуждается использование Solver, надстройки Microsoft Excel, которую можно использовать для анализа возможных вариантов, чтобы определить оптимальный набор продуктов.
Как определить ежемесячную номенклатуру продуктов, обеспечивающую максимальную рентабельность?
Компаниям часто необходимо определить количество каждого продукта, которое необходимо производить ежемесячно. В своей простейшей форме задача о наборе продуктов заключается в том, как определить количество каждого продукта, которое должно быть произведено в течение месяца, чтобы максимизировать прибыль. Ассортимент продукции обычно должен соответствовать следующим ограничениям:
На каждый товар существует ограниченный спрос. Мы не можем произвести в месяц больше продукта, чем диктует спрос, потому что лишнее производство тратится впустую (например, скоропортящийся препарат).
Набор продуктов не может использовать больше ресурсов, чем доступно.
Теперь давайте решим следующий пример задачи о наборе продуктов. Вы можете найти решение этой проблемы в файле Prodmix.xlsx, показанном на рисунке 27-1.
Допустим, мы работаем в фармацевтической компании, которая производит шесть различных продуктов на своем заводе. Производство каждого продукта требует рабочей силы и сырья. В строке 4 на рис. 27.1 показаны часы труда, необходимые для производства фунта каждого продукта, а в строке 5 показаны фунты сырья, необходимые для производства фунта каждого продукта. Например, для производства фунта Продукта 1 требуется шесть часов труда и 3,2 фунта сырья. Для каждого лекарства цена за фунт указана в строке 6, удельная стоимость за фунт указана в строке 7, а доля прибыли в расчете на фунт указана в строке 9.. Например, Продукт 2 продается по цене 11,00 долларов за фунт, имеет удельную стоимость 5,70 долларов за фунт и приносит прибыль 5,30 долларов за фунт. Месячный спрос на каждое лекарство указан в строке 8. Например, спрос на продукт 3 составляет 1041 фунт. В этом месяце доступно 4500 часов труда и 1600 фунтов сырья. Как эта компания может максимизировать свою ежемесячную прибыль?
Если бы мы ничего не знали о Excel Solver, мы бы решили эту проблему, создав рабочий лист для отслеживания прибыли и использования ресурсов, связанных с набором продуктов. Затем мы будем использовать метод проб и ошибок, чтобы варьировать ассортимент продукции для оптимизации прибыли, не используя больше рабочей силы или сырья, чем доступно, и не производя никаких лекарств сверх спроса. Мы используем Солвер в этом процессе только на этапе проб и ошибок. По сути, Solver — это механизм оптимизации, который безупречно выполняет поиск методом проб и ошибок.
Ключом к решению проблемы ассортимента продукции является эффективное вычисление использования ресурсов и прибыли, связанной с любым набором продуктов. Важным инструментом, который мы можем использовать для выполнения этих вычислений, является функция СУММПРОИЗВ. Функция СУММПРОИЗВ умножает соответствующие значения в диапазонах ячеек и возвращает сумму этих значений. Каждый диапазон ячеек, используемый в оценке СУММПРОИЗВ, должен иметь одинаковые размеры, что означает, что вы можете использовать СУММПРОИЗВ с двумя строками или двумя столбцами, но не с одним столбцом и одной строкой.
В качестве примера того, как мы можем использовать функцию СУММПРОИЗВ в нашем примере с набором продуктов, давайте попробуем вычислить использование наших ресурсов. Наше использование рабочей силы рассчитывается на
(Затраты труда на фунт наркотика 1)*(Произведенный фунт наркотика 1)+
(Затраты труда на фунт наркотика 2)*(Произведено 2 фунта наркотика) + . ..
(Затраты труда на фунт наркотика 6)*(Произведено 6 фунтов наркотика)
Мы могли бы вычислить использование рабочей силы более утомительным способом: D2*D4+E2*E4+F2*F4+G2*G4+h3*h5+I2*I4 . Точно так же использование сырья можно рассчитать как D2*D5+E2* E5+F2*F5+G2*G5+h3*H5+I2*I5 . Однако ввод этих формул в рабочую таблицу для шести продуктов занимает много времени. Представьте, сколько времени это заняло бы, если бы вы работали с компанией, которая произвела, например, 50 продуктов на своем заводе. Гораздо проще вычислить использование труда и сырья, скопировав из D14 в D15 формулу 9.0684 СУММПРОИЗВ($D$2:$I$2,D4:I4) . Эта формула вычисляет D2*D4+E2*E4+F2*F4+G2*G4+h3*h5+I2*I4 (это наше использование труда), но ее гораздо проще ввести! Обратите внимание, что я использую знак $ с диапазоном D2:I2, поэтому при копировании формулы я по-прежнему получаю набор продуктов из строки 2. Формула в ячейке D15 вычисляет использование сырья.
Аналогичным образом наша прибыль определяется
(Прибыль препарата 1 на фунт)*(Произведено фунта препарата 1) +
(Прибыль препарата 2 на фунт)*(Производство препарата 2 фунта) + …
(Прибыль препарата 6 на фунт)*(Производство препарата 6 фунтов)
Прибыль легко вычислить в ячейке D12 по формуле СУММПРОИЗВ(D9:I9,$D$2:$I$2) .
Теперь мы можем определить три компонента нашей модели Solver для набора продуктов.
Целевая ячейка. Наша цель — максимизировать прибыль (вычисляется в ячейке D12).
Изменение ячеек. Количество произведенных фунтов каждого продукта (указано в диапазоне ячеек D2:I2)
Не используйте больше рабочей силы или сырья, чем доступно. То есть значения в ячейках D14:D15 (используемые ресурсы) должны быть меньше или равны значениям в ячейках F14:F15 (доступные ресурсы).
Не производить больше препарата, чем требуется. То есть значения в ячейках D2:I2 (фунты, произведенные каждым наркотиком) должны быть меньше или равны спросу на каждый наркотик (указанному в ячейках D8:I8).
Мы не можем произвести отрицательное количество любого лекарства.
Ограничения. У нас есть следующие ограничения:
Я покажу вам, как ввести целевую ячейку, изменить ячейки и ограничения в Солвере. Тогда все, что вам нужно сделать, это нажать кнопку «Решить», чтобы найти сочетание продуктов, максимизирующее прибыль!
Для начала щелкните вкладку Данные и в группе Анализ щелкните Решатель.
Примечание. Как объяснялось в главе 26 «Введение в оптимизацию с помощью Excel Solver», Solver устанавливается нажатием кнопки Microsoft Office, затем «Параметры Excel» и «Надстройки». В списке «Управление» выберите «Надстройки Excel», установите флажок «Надстройка решения», а затем нажмите «ОК».
Появится диалоговое окно Solver Parameters, как показано на рисунке 27-2.
Щелкните поле «Установить целевую ячейку», а затем выберите нашу ячейку прибыли (ячейка D12). Щелкните поле «Изменение ячеек», а затем укажите диапазон D2:I2, который содержит количество фунтов, произведенных каждым лекарством. Теперь диалоговое окно должно выглядеть, как показано на рис. 27-3.
Теперь мы готовы добавить в модель ограничения. Нажмите кнопку «Добавить». Вы увидите диалоговое окно Add Constraint, показанное на рисунке 27-4.
Чтобы добавить ограничения на использование ресурсов, щелкните поле Ссылка на ячейку и выберите диапазон D14:D15. Выберите <= из среднего списка. Щелкните поле Ограничение и выберите диапазон ячеек F14:F15. Диалоговое окно Add Constraint теперь должно выглядеть так, как показано на рис. 27-5.
Теперь мы добились того, что когда Решатель пробует разные значения для меняющихся ячеек, только те комбинации, которые удовлетворяют обоим D14<=F14 (затраченная рабочая сила меньше или равна доступной рабочей силе) и D15<=F15 (использованное сырье меньше или равно доступному сырью). Щелкните Добавить, чтобы ввести ограничения спроса. Заполните диалоговое окно Add Constraint, как показано на рисунке 27-6.
Добавление этих ограничений гарантирует, что когда Решатель пробует разные комбинации для меняющихся значений ячеек, будут рассматриваться только комбинации, которые удовлетворяют следующим параметрам:
E2<=E8 (количество произведенного Лекарства 2 меньше или равно спросу на Лекарство 2)
F2<=F8 (количество производимого Лекарства 3 меньше или равно спросу на Лекарство 3)
G2<=G8 (количество произведенного лекарства 4 меньше или равно спросу на лекарство 4)
h3<=H8 (количество произведенного лекарства 5 меньше или равно спросу на лекарство 5)
D2<=D8 (количество произведенного Лекарства 1 меньше или равно спросу на Лекарство 1)
I2<=I8 (количество производимого Лекарства 6 меньше или равно спросу на Лекарство 6)
Нажмите кнопку «ОК» в диалоговом окне «Добавить ограничение». Окно Solver должно выглядеть так, как показано на рис. 27-7.
Мы вводим ограничение, согласно которому изменение ячеек должно быть неотрицательным, в диалоговом окне «Параметры решения». Нажмите кнопку «Параметры» в диалоговом окне «Параметры решателя». Установите флажок «Предполагать линейную модель» и поле «Предполагать неотрицательное», как показано на рис. 27-8 на следующей странице. Нажмите «ОК».
Установка флажка «Предполагать неотрицательное» гарантирует, что «Поиск решения» будет учитывать только комбинации изменяющихся ячеек, в которых каждая изменяющаяся ячейка принимает неотрицательное значение. Мы установили флажок «Предполагать линейную модель», поскольку задача о наборе продуктов представляет собой особый тип задачи «Решатель», называемый линейной моделью . По сути, модель Solver является линейной при следующих условиях:
Целевая ячейка вычисляется путем сложения членов формы (изменяющаяся ячейка)*(константа) .
Каждое ограничение удовлетворяет «требованиям линейной модели». Это означает, что каждое ограничение оценивается путем сложения членов формы (изменяющаяся ячейка) * (константа) и сравнения сумм с константой.
Почему эта задача Решателя является линейной? Наша целевая ячейка (прибыль) вычисляется как
. (Прибыль препарата 1 на фунт)*(Произведено фунта препарата 1) +
(Прибыль препарата 2 на фунт)*(Производство препарата 2 фунта) + …
(Прибыль препарата 6 на фунт)*(Производство препарата 6 фунтов)
Это вычисление следует шаблону, в котором значение целевой ячейки получается путем сложения членов формы (изменяющаяся ячейка) * (константа) .
Наше трудовое ограничение оценивается путем сравнения значения, полученного из (Труд, затраченный на фунт лекарства 1)*(Произведенный фунт лекарства 1) + (Затраченный труд на фунт произведенного лекарства 2)*(Произведенный фунт лекарства 2)+ …(Затраты труда ед на фунт лекарства 6)*( Препарат 6 фунтов произведен) в наличии.
Таким образом, трудовое ограничение оценивается путем сложения членов формы (изменяющаяся ячейка) * (константа) и сравнения сумм с константой. И ограничение по труду, и ограничение по сырью удовлетворяют требованиям линейной модели.
Наши ограничения спроса принимают форму
(Лекарство 1 произведено) <= (Спрос на лекарство 1)
(Произведено лекарство 2)<=(Спрос на лекарство 2)
§
(Произведено лекарство 6)<=(Спрос на лекарство 6)
Каждое ограничение спроса также удовлетворяет требованию линейной модели, поскольку каждое оценивается путем сложения членов формы (изменяющаяся ячейка)*(постоянная) и сравнивая суммы с константой.
Показав, что наша модель ассортимента продукции является линейной моделью, почему нас это должно волновать?
Если модель Решателя является линейной и мы выбираем Предполагать линейную модель, Решатель гарантированно найдет оптимальное решение для модели Решателя. Если модель Solver не является линейной, Solver может найти или не найти оптимальное решение.
Если модель Решателя является линейной и мы выбираем Предполагать линейную модель, Решатель использует очень эффективный алгоритм (симплексный метод) для нахождения оптимального решения модели. Если модель Solver является линейной и мы не выбираем Assume Linear Model, Solver использует очень неэффективный алгоритм (метод GRG2) и может столкнуться с трудностями при поиске оптимального решения модели.
После нажатия OK в диалоговом окне Solver Options мы возвращаемся к основному диалоговому окну Solver, показанному ранее на рис. 27-7. Когда мы нажимаем «Решить», Solver вычисляет оптимальное решение (если оно существует) для нашей модели ассортимента продуктов. Как я говорил в главе 26, оптимальным решением для модели ассортимента продуктов будет набор изменяющихся значений ячеек (фунтов, произведенных каждым лекарством), который максимизирует прибыль по сравнению с набором всех возможных решений. Опять же, допустимое решение — это набор изменяющихся значений ячеек, удовлетворяющих всем ограничениям. Изменение значений ячеек показано на рис. 27-9.являются допустимым решением, потому что все уровни производства неотрицательны, уровни производства не превышают потребности, а использование ресурсов не превышает доступных ресурсов.
Изменение значений ячеек, показанное на рис. 27-10 на следующей странице, представляет собой недопустимое решение по следующим причинам:
Мы используем больше рабочей силы, чем доступно.
Мы используем больше сырья, чем доступно.
Мы производим больше Лекарства 5, чем требуется.
После нажатия кнопки «Решить» Solver быстро находит оптимальное решение, показанное на рис. 27-11. Вам нужно выбрать Keep Solver Solution, чтобы сохранить оптимальные значения решения на листе.
Наша фармацевтическая компания может максимизировать свою ежемесячную прибыль на уровне 6 625,20 долларов США, производя 596,67 фунта Наркотика 4, 1084 фунта Наркотика 5 и ни одного другого наркотика! Мы не можем определить, сможем ли мы достичь максимальной прибыли в размере 6 625,20 долларов США другими способами. Все, в чем мы можем быть уверены, так это в том, что с нашими ограниченными ресурсами и спросом мы не сможем заработать больше $6 627,20 в этом месяце.
Предположим, что спрос на каждый продукт должен быть удовлетворен . (См. рабочий лист No Feasible Solution в файле Prodmix.xlsx.) Затем мы должны изменить наши ограничения спроса с D2:I2<=D8:I8 от до D2:I2>=D8:I8 . Для этого откройте Solver, выберите зависимость D2:I2<=D8:I8, а затем нажмите кнопку «Изменить». Появится диалоговое окно «Изменить ограничение», показанное на рис. 27-12.
Выберите >= и нажмите OK. Теперь мы уверены, что Solver рассмотрит возможность изменения только тех значений ячеек, которые соответствуют всем требованиям. Когда вы нажмете «Решить», вы увидите сообщение «Решатель не смог найти подходящее решение». Это сообщение не означает, что мы допустили ошибку в нашей модели, а скорее то, что с нашими ограниченными ресурсами мы не можем удовлетворить спрос на все продукты. Solver просто говорит нам, что если мы хотим удовлетворить спрос на каждый продукт, нам нужно добавить больше труда, больше сырья или больше того и другого.
Давайте посмотрим, что произойдет, если мы допустим неограниченный спрос на каждый продукт и позволим производить отрицательное количество каждого лекарства. (Вы можете увидеть эту проблему Решателя на рабочем листе Set Values Do Not Converge в файле Prodmix.xlsx.) Чтобы найти оптимальное решение для этой ситуации, откройте Решатель, нажмите кнопку «Параметры» и снимите флажок «Предполагать неотрицательное». . В диалоговом окне «Параметры решателя» выберите ограничение потребности D2:I2<=D8:I8, а затем нажмите «Удалить», чтобы удалить ограничение. Когда вы нажимаете «Решить», «Поиск решения» возвращает сообщение «Установить значения ячеек не сходятся». Это сообщение означает, что если целевая ячейка должна быть максимизирована (как в нашем примере), существуют допустимые решения с произвольно большими значениями целевой ячейки. (Если целевая ячейка должна быть минимизирована, сообщение «Установить значения ячеек не сходятся» означает, что существуют допустимые решения с произвольно малыми значениями целевых ячеек.) В нашей ситуации, допуская отрицательное производство лекарства, мы фактически «создаем ресурсы, которые можно использовать для производства сколь угодно больших количеств других наркотиков. Учитывая наш неограниченный спрос, это позволяет нам получать неограниченную прибыль. В реальной ситуации мы не можем заработать бесконечное количество денег. Короче говоря, если вы видите «Установленные значения не сходятся», в вашей модели действительно есть ошибка.
Предположим, что наша фармацевтическая компания может купить до 500 часов рабочей силы по цене на 1 доллар в час больше, чем текущая стоимость рабочей силы.
Как мы можем максимизировать прибыль?На заводе по производству микросхем четыре техника (A, B, C и D) производят три продукта (Продукты 1, 2 и 3). В этом месяце производитель чипов может продать 80 единиц продукта 1, 50 единиц продукта 2 и не более 50 единиц продукта 3. Техник А может производить только продукты 1 и 3. Техник Б может производить только продукты 1 и 2. Техник C может производить только Продукт 3. Техник D может производить только Продукт 2. Каждая произведенная единица продукции приносит следующую прибыль: Продукт 1 — 6 долларов; Продукт 2, 7 долларов; и Продукт 3, 10 долларов. Время (в часах), необходимое каждому специалисту для производства продукта, составляет:
Продукт
Техник А
Техник Б
Техник С
Техник Д
1
2
2,5
Не могу
Не могу сделать
2
Не могу
3
Не могу
3,5
3
3
Не могу
4
Не могу
Завод по производству компьютеров производит мыши, клавиатуры и джойстики для видеоигр. Прибыль на единицу, использование труда на единицу, месячный спрос и использование машинного времени на единицу приведены в следующей таблице:
Мыши
Клавиатуры
Джойстики
Прибыль/единица
$8
11 долларов
$9
Использование труда/единица
.
2 часа.3 часа
.24 часа
Машинное время/ед.
.04 часа
.055 час
.04 часа
Ежемесячная потребность
15 000
27 000
11 000
Решите наш пример с лекарством, предполагая, что минимальный спрос на каждое лекарство должен составлять 200 единиц.
Джейсон делает бриллиантовые браслеты, ожерелья и серьги. Он хочет работать максимум 160 часов в месяц. У него 800 унций бриллиантов. Прибыль, рабочее время и унции алмазов, необходимые для производства каждого продукта, приведены ниже. Если спрос на каждый продукт неограничен, как Джейсон может максимизировать свою прибыль?
Продукт
Удельная прибыль
Рабочее время на единицу
Унций алмазов на единицу
Браслет
$300
.
Каждый техник может работать до 120 часов в месяц. Как производитель микросхем может максимизировать свою ежемесячную прибыль? Предположим, что можно произвести дробное количество единиц.
Каждый месяц доступно 13 000 рабочих часов и 3 000 часов машинного времени. Как производитель может максимизировать свой ежемесячный вклад в прибыль от завода?