|
В предыдущей главе мы решали уравнения и неравенства аналитически, и сейчас вдохнём в эти
задачи геометрический смысл. И это вас вдохновит! – это будет просто, это будет круто и это будет красиво! А, главное, чрезвычайно полезно. Решением неравенства являются те промежутки, на которых график выше оси , Соответственно, решением неравенства является интервал . В случае нестрогих неравенств к решениям нужно добавить пограничные точки: и соответственно. А если вам не хочется возиться с нахождением опорных точек, «тыкая в них наугад» (ведь параболы бывают большие, размашистые), то есть общий случай: Чтобы решить уравнение , нужно построить графики и найти их точки пересечения. «Иксовые» координаты этих точек и будут решениями. Если графики не пересекаются, то действительных решений нет. Таким образом, вместо решения уравнения с вычерчиванием параболы,
представим его в виде и изобразим элементарные графики: Решением неравенства являются те промежутки, на которых график выше графика , и, наоборот: – там, где график ниже графика . Так, решением неравенства являются промежутки – поскольку на них парабола расположена выше прямой. И, наоборот, решением неравенства является промежуток , так как здесь парабола расположена ниже прямой. Аналогично для нестрогих неравенств. Кстати, всем ли понятно, как из общих правил получаются частные правила для и ? Элементарно. Это тот случай, когда , а эта функция задаёт ось . Когда удобно использовать графический метод? Прежде всего, в простых случаях. Так, при решении неравенства проще мысленно представить гиперболу, нежели использовать метод интервалов. Где гипербола Графический способ спасёт в экстремальных ситуациях, например, когда вы позабыли, как решать квадратное уравнение, а помощи ждать неоткуда. Используйте приём, описанный выше – вместо уравнения рассмотрИте с двумя простыми графиками, не построить которые – эт нужно постараться 🙂 Иногда графика эффективна в уравнениях «разнородными» функциями. Так, для решения уравнения не существует стандартных аналитических методов, но это не беда. Мысленно представляем график и график синуса (о котором позже), после чего сразу понятно, что уравнение имеет единственный корень . Кстати, в некоторых задачах нужно просто определить количество корней и / или их приблизительное расположение, и на этот вопрос зачастую легко ответит чертёж! Разумеется, графики должны быть простыми – это важнейшее условие применения графического метода. И после этого невероятно полезного параграфа возвращается к нашим функциям: 3.6. Показательная функция 3.4. СтепеннАя функция | Оглавление | |
Показательные неравенства — как решать? Примеры, методы решения и свойства
Поможем понять и полюбить математику
Начать учиться
Как правило, показательные неравенства начинают изучать после того, как уже познакомились с показательными уравнениями. Если знакомство прошло успешно и уравнения вам теперь как родные, этот материал будет во многом повторением пройденного. Но это не значит, что вы не увидите ничего нового — в решении показательных неравенств есть свои фишки.
Определение показательных неравенств
Показательными считаются неравенства, которые включают в себя переменную, стоящую в показателе степени: . Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании. |
Для изучения этой темы стоит повторить:
показательные уравнения;
метод интервалов;
разложение многочлена на множители;
свойства степенной функции.
И, конечно, для решения смешанных неравенств, включающих в себя тригонометрические и логарифмические, также придется вспомнить формулы соответствующих разделов алгебры.
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции.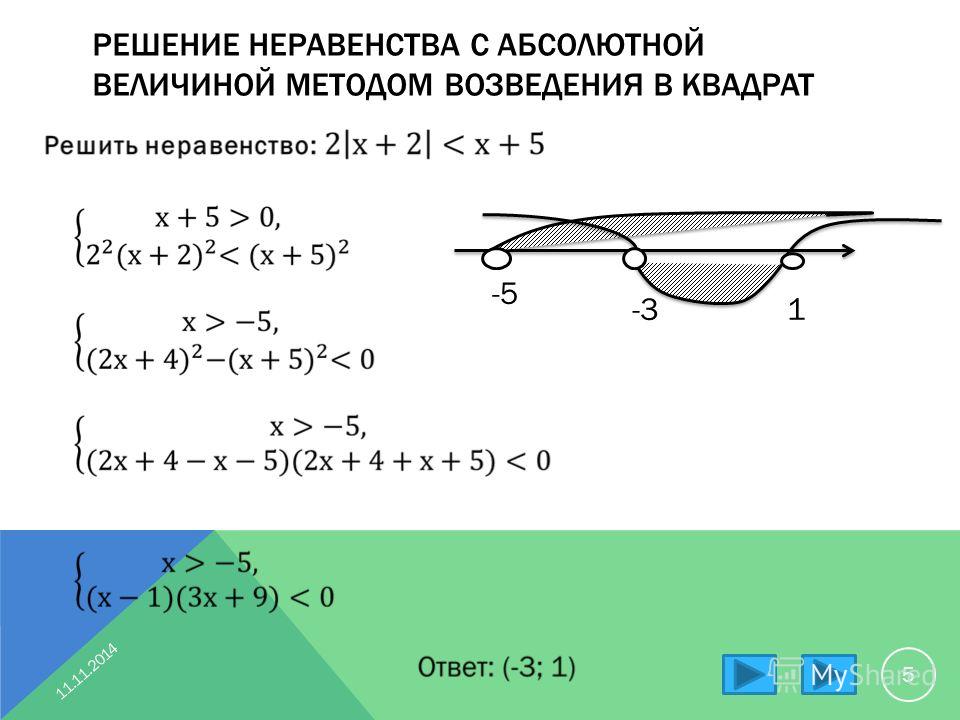 Напомним, что она выглядит так: y = ax, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а положительно, но не равно единице. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
Напомним, что она выглядит так: y = ax, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а положительно, но не равно единице. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения функции всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число (большее нуля) во всевозможные степени, включая отрицательные. Например: 2-2 = 4, 2-4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.
Для любых а и х верно неравенство ax > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
, когда функция возрастает, т.
 е. ;
е. ;, когда функция убывает, т. е. .
На этом свойстве показательных неравенств так или иначе основываются все методы решения, и сейчас мы разберемся, как им пользоваться.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…
Допустим, у нас есть простейшее показательное неравенство:
3х > 9
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
3х > 32
х > 2
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
0,5х > 0,52
Проверим, верно ли в таком случае х > 2.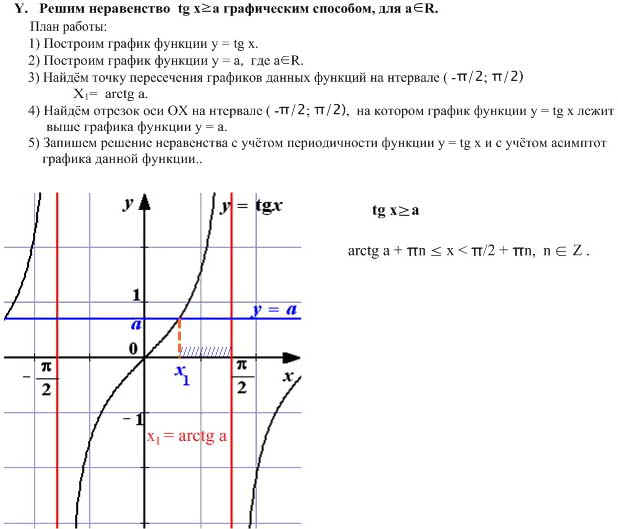
0,52 = 0,25;
0,53 = 0, 125 и т. д.
Как видите, на самом деле в этом случае х < 2. Неудивительно, если вспомнить, о чем мы писали в самом начале, когда рисовали графики возрастающей и убывающей показательной функции.
Если а > 1, то , и при решении неравенства можно просто убрать одинаковые основания степени. Если 0 < а < 1, то , т. е. одинаковые основания по-прежнему можно убрать, но при этом необходимо поменять знак неравенства. |
Для ясности всегда предполагается, что основание степени — положительное число.
Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Показательные неравенства, сводящиеся к простейшим
Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. 😎
Попробуем на примере несложного показательного неравенства с разными основаниями.
Пример 1
3х < 243
3х < 35
Поскольку 3 больше 1, знак не меняем:
х < 5
Ответ: х ∈ (−∞; 5).
Пример 2
, обратите внимание — мы поменяли знак, поскольку .
Ответ: .
Показательные неравенства, сводящиеся к квадратным
Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям.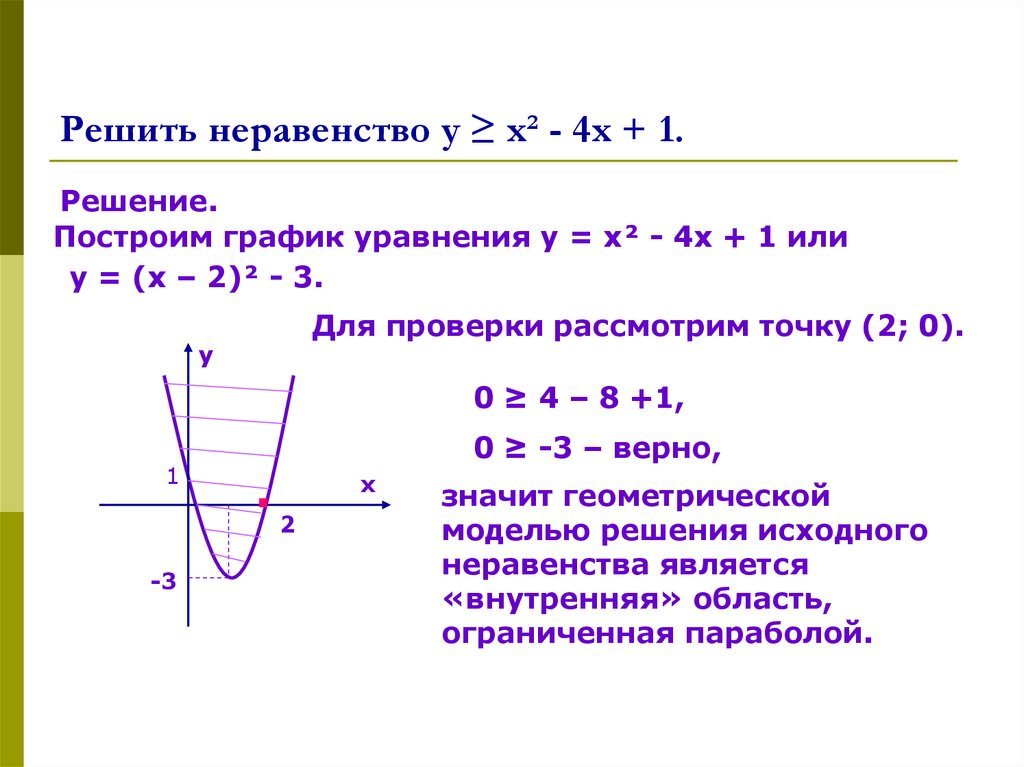 Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Пример 1
9х + 27 < 12 × 3х
Наименьший общий множитель в данном случае будет 3х, обозначим его новой переменной у и перенесем все слагаемые в левую сторону.
9х + 27 < 12 × 3х
(3х)2— 12 × 3х + 27 < 0
3х = у при y > 0
y2 — 12y + 27 < 0
3 < y < 9
Пришло время выполнить обратную замену.
3 < 3х < 9
31 < 3х < 32
Поскольку 3 > 1, мы не меняем знак.
1 < х < 2
Ответ: х ∈ (1;2).
Показательные неравенства, сводящиеся к рациональным
Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).
Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.
Пример 1
Преобразуем неравенство:
(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).
Поскольку выражение 2х + 2 всегда больше нуля, мы можем домножить на него все неравенство и сократить.
и
Ответ:
Пример 2
Обозначим 3х через новую переменную y:
3х = y, при условии что y > 0.
Применим метод интервалов и получим:
Произведем обратную замену:
Поскольку 3 больше 1, знаки не меняем:
Ответ: .
Однородные показательные неравенства
Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова. |
Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.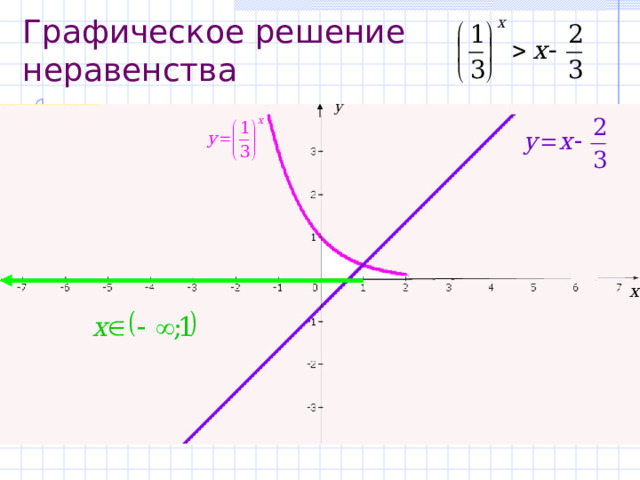
Пример 1
В левой части неравенства мы видим однородные функции относительно 2х и 5х. Следовательно, можно разделить обе части на 22х или 52х. Выберем 52х, т. е. 25х. В итоге у нас получится:
Если обозначить новой переменной y (при условии, что y > 0), получим квадратное неравенство:
y2— y — 2 > 0
y1 > 2
y2 < -1
Исходя из этого, у нас образуется следующее неравенство:
Поскольку меньше 1, функция убывающая и мы должны поменять знак:
Ответ: .
Пример 2
Но где здесь одинаковая сумма степеней? Сейчас будет:
Ответ:
Неравенства, решаемые графическим методом
Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Но для использования данного метода точки пересечения должны быть целыми числами. Если бы мы имели дело с уравнением, такие точки стали бы его корнями.
Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Но для использования данного метода точки пересечения должны быть целыми числами. Если бы мы имели дело с уравнением, такие точки стали бы его корнями.
Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.
Пример 1
Итак, нам нужны графики двух функций: и , а также точка их пересечения.
Очевидно, что абсциссой точки пересечения является х = 1, при этом график функции ниже в области .
Ответ: .
Пример 2
Начертим графики этих двух функций, чтобы найти точку пересечения.
Искомой точкой будет х = -1, а областью, где функция находится выше — диапазон значений х от -∞ до -1.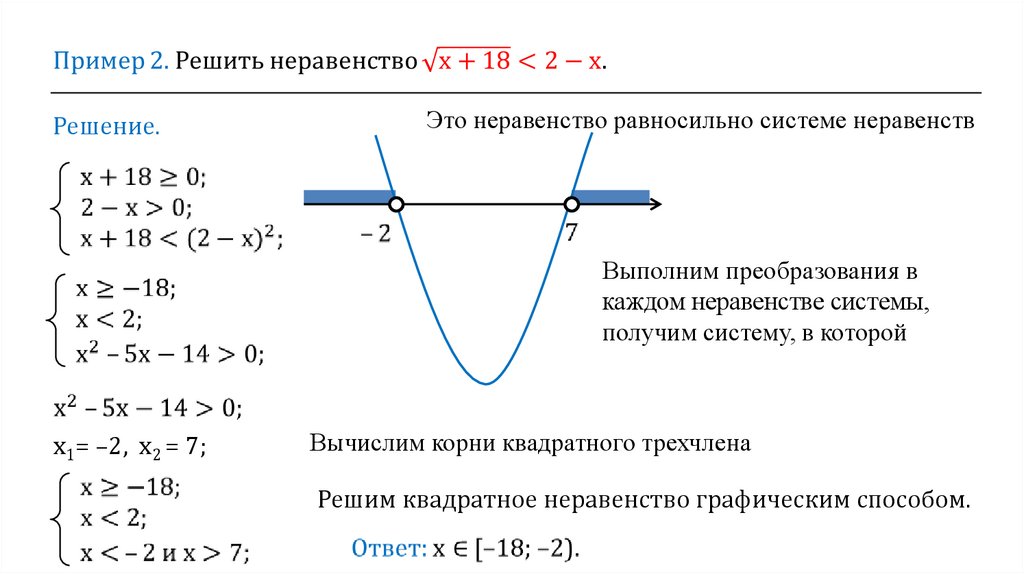
Ответ: .
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Яна Кононенко
К предыдущей статье
158.2K
Касательная к окружности
К следующей статье
138.5K
Показательные уравнения
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
графических неравенств | Начальная алгебра
Цели обучения
- Определение графиков и решений уравнений и неравенств
- Определите сходства и различия между решениями линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
- Определите сходства и различия между графиками линейных уравнений с двумя переменными и линейных неравенств с двумя переменными
- График неравенства двух переменных
- Определите и выполните шаги для построения графика линейного неравенства с двумя переменными
Определите разницу между графиком линейного уравнения и линейным неравенством
Вспомните, что решениями линейных неравенств являются целые наборы чисел, а не одно число, как вы находите с решениями равенств (уравнений).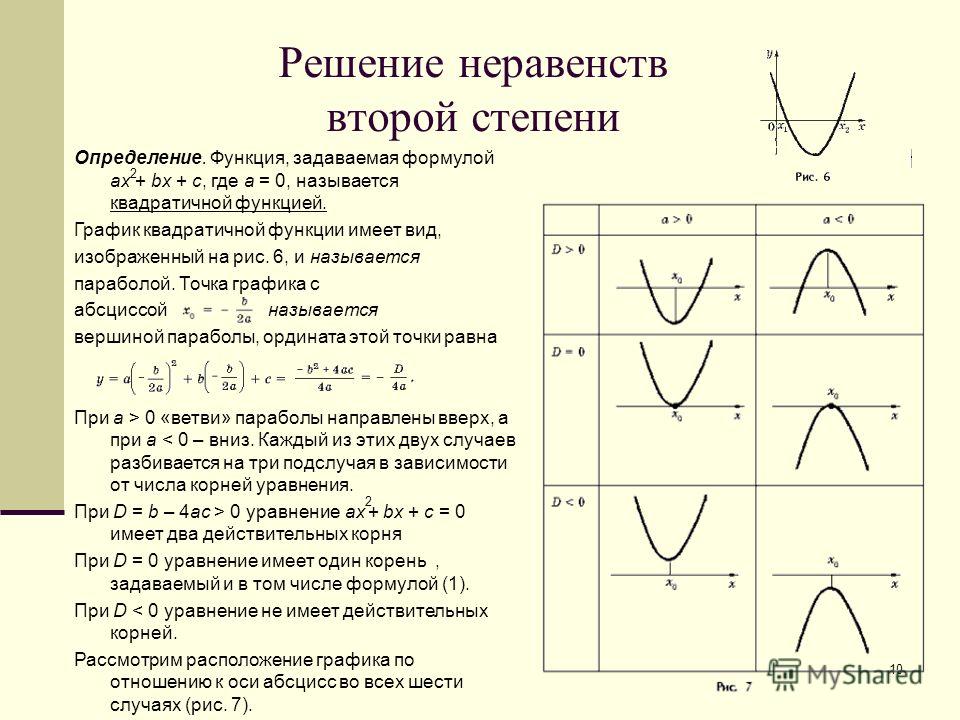
Вот пример из раздела о решении линейных неравенств:
Решить для p . [латекс]4p+5<29[/латекс]
[латекс] \displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\ ,\,-5\,\,\,\,\,\,\,-5}\\\подчеркивание{4p}\,\,\,\,\,\,\,\,<\,\, \подчеркнуть{24}\,\,\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,4\\\,\,\,\,\,\,\,\,\,\,\,p<6\end{array}[/latex]
Вы можете интерпретировать решение как p может быть любым числом меньше шести. Теперь вспомните, что мы можем построить уравнения линий, определив выходные данные y и входные данные x и написав уравнение.
Ранее мы показали, как изобразить линию, описываемую этим уравнением: [latex]y=2x+3[/latex] , и обнаружили, что можно построить бесконечную таблицу значений, которые образуют точки на линия — это некоторые решения уравнения [латекс]у=2х+3[/латекс].
| x значения | [латекс]2x+3[/латекс] | y значения |
|---|---|---|
| 0 | [латекс]2(0)+3[/латекс] | 3 |
| 1 | [латекс]2(1)+3[/латекс] | 5 |
| 2 | [латекс]2(2)+3[/латекс] | 7 |
| 3 | [латекс]2(3)+3[/латекс] | 9 |
Кроме того, мы узнали, как изобразить линию, представляющую все точки, которые делают [латекс]у=2х+3[/латекс] верным утверждением.
Что, если мы объединим эти две идеи — линейные неравенства и графики линий? Сначала переведите строку [latex]y=2x+3[/latex] в слова:
Вы получите и , умножив x на два и прибавив три. [latex]y=2x+3[/latex]
Как бы вы перевели это неравенство словами? [latex]y<2x+3[/latex]
Для каких значений x вы получите результат y, который на меньше, чем 2 умножить на x плюс три?
ВАУ, это может показаться запутанным, но продолжайте читать, мы поможем вам разобраться.
Линейные неравенства отличаются от линейных уравнений, хотя вы можете применить свои знания об уравнениях, чтобы понять неравенства. Неравенства и уравнения — это математические операторы, которые сравнивают два значения. В уравнениях используется символ = ; помните, что неравенства представлены символами < , ≤ , > и ≥.
Один из способов визуализировать неравенства с двумя переменными — нанести их на координатную плоскость. Вот как выглядит неравенство [latex]x>y[/latex] .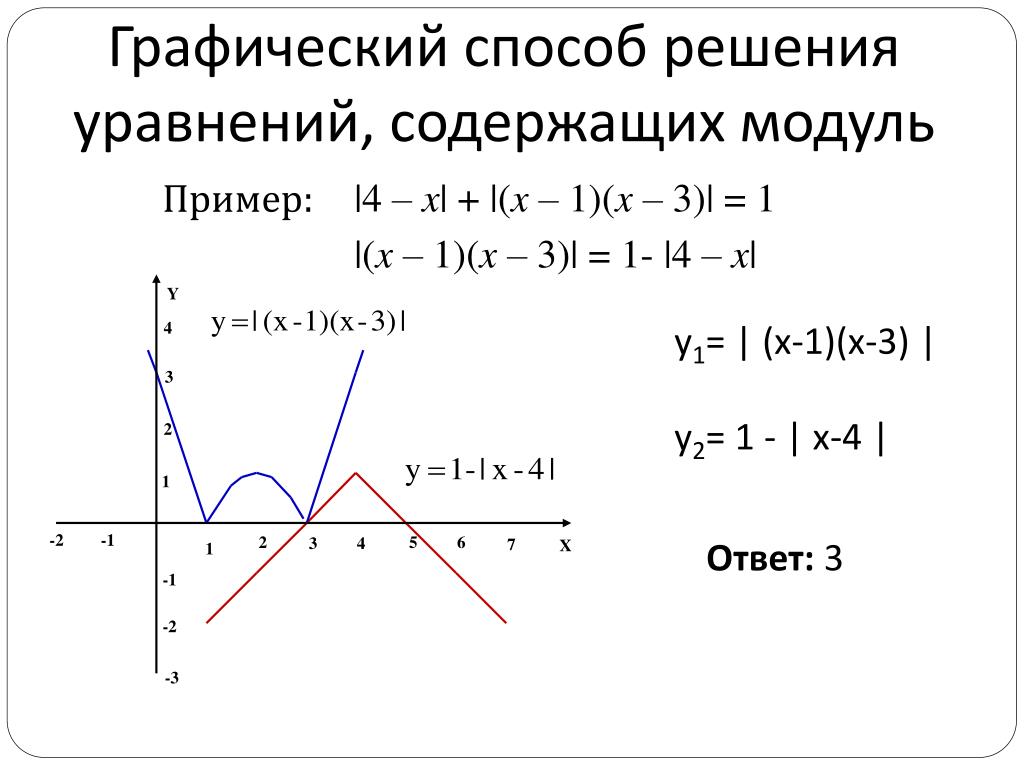 Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.
Решение представляет собой область, которая заштрихована. Эта область состоит из множества упорядоченных пар, каждая из которых делает утверждение [latex]x>y[/latex] верным.
Здесь следует отметить несколько моментов. Во-первых, посмотрите на пунктирную красную граничную линию: это график соответствующего линейного уравнения [latex]x=y[/latex]. Затем посмотрите на светло-красную область справа от линии. Эта область (за исключением строки [latex]x=y[/latex]) представляет собой все множество решений неравенства [latex]x>y[/latex]. Помните, как все точки на строки решения линейного уравнения линии? Итак, все точки в области являются решениями линейного неравенства , представляющего эту область.
Давайте задумаемся об этом на мгновение — если [латекс]x>y[/латекс], то график [латекс]х>у[/латекс] покажет все упорядоченные пары [латекс](х,у)[ /latex], для которого координата x- больше, чем координата y-.
На приведенном ниже графике показана область [латекс]x>y[/латекс], а также некоторые упорядоченные пары на координатной плоскости. Посмотрите на каждую заказанную пару. 9Координата 0027 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?
Посмотрите на каждую заказанную пару. 9Координата 0027 x- больше, чем координата y-? Находится ли упорядоченная пара внутри или снаружи заштрихованной области?
Упорядоченные пары [латекс](4,0)[/латекс] и [латекс](0,−3)[/латекс] лежат внутри заштрихованной области. В этих упорядоченных парах координата x- больше, чем координата y-. Эти упорядоченные пары входят в набор решений уравнения [латекс]х>у[/латекс].
Упорядоченные пары [латекс](−3,3)[/латекс] и [латекс](2,3)[/латекс] находятся за пределами заштрихованной области. В этих упорядоченных парах 9Координата 0027 x- на меньше , чем координата y-, поэтому они не включены в набор решений неравенства.
Упорядоченная пара [латекс](−2,−2)[/латекс] находится на граничной линии. Это не решение, так как [латекс]-2[/латекс] не больше, чем [латекс]-2[/латекс]. Однако если бы неравенство было [латекс]x\geq y[/латекс] (читается как « x больше или равно y »), то [латекс](−2,−2)[/латекс ] был бы включен (и линия была бы представлена сплошной, а не пунктирной линией).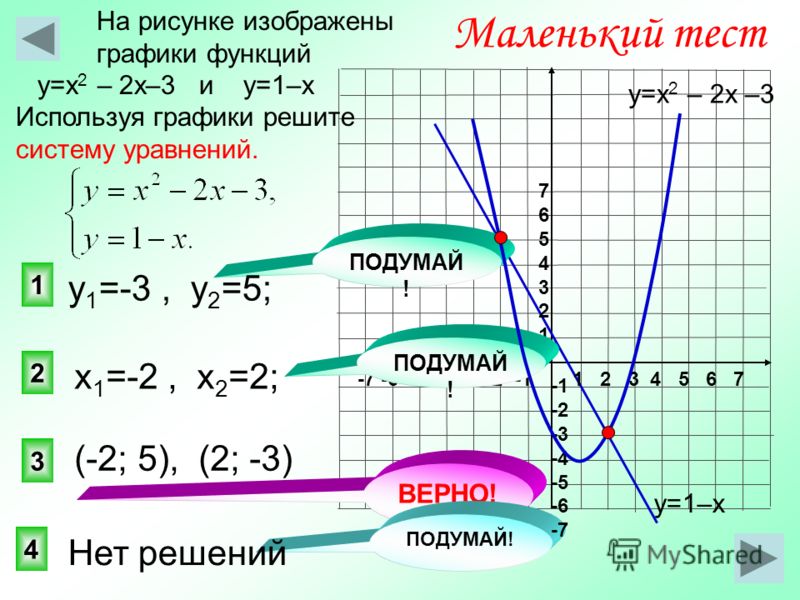
Разница между линейным уравнением и линейным неравенством (две переменные)
Рассмотрим еще один пример: неравенство [latex]3x+2y\leq6[/latex]. На приведенном ниже графике показана область значений, которая делает это неравенство верным (заштрихована красным), граничная линия [латекс]3x+2y=6[/латекс], а также несколько упорядоченных пар. Граничная линия на этот раз сплошная, потому что точки на граничной линии [latex]3x+2y=6[/latex] делают неравенство [latex]3x+2y\leq6[/latex] истинным.
Как и в предыдущем примере, вы можете подставить значения x- и y- в каждую из упорядоченных пар [latex](x,y)[/latex] в неравенство, чтобы найти решения . Хотя вы, возможно, смогли сделать это в уме для неравенства [latex]x>y[/latex], иногда создание таблицы значений имеет смысл для более сложных неравенств.
| Заказная пара | Делает неравенство [латекс]3x+2y\leq6[/латекс] верное утверждение | Делает неравенство [латекс]3x+2y\leq6[/латекс] ложное заявление |
|---|---|---|
| [латекс](−5, 5)[/латекс] | [латекс]\begin{array}{r}3\left(-5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array }[/латекс] | |
| [латекс](−2,−2)[/латекс] | [латекс]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\ –10\leq6\end{массив}[/латекс] | |
| [латекс](2,3)[/латекс] | [латекс]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/ латекс] | |
| [латекс](2,0)[/латекс] | [латекс]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/ латекс] | |
| [латекс](4,−1)[/латекс] | [латекс]\begin{массив}{r}3\влево(4\вправо)+2\влево(-1\вправо)\leq6\\12+\влево(-2\вправо)\leq6\\10\ leq6\end{массив}[/латекс] |
Если подстановка [latex](x,y)[/latex] в неравенство дает верное утверждение, то упорядоченная пара является решением неравенства, и точка будет нанесена на график в заштрихованной области или в точке будет частью сплошной граничной линии.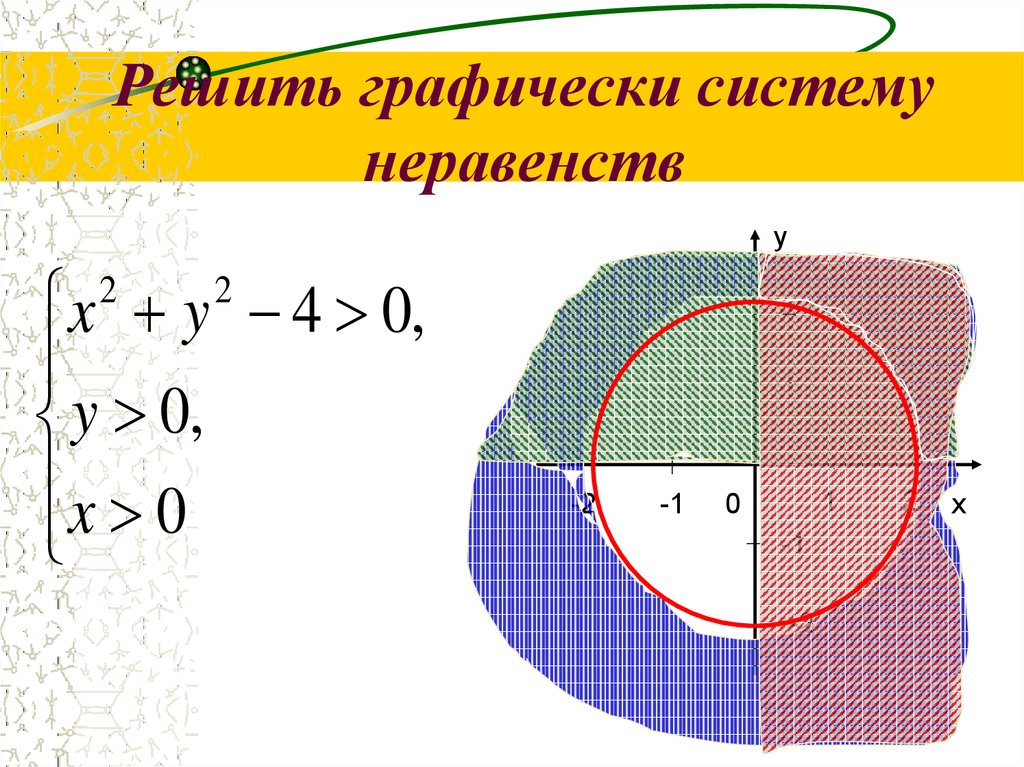 Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет находиться вне заштрихованной области или будет частью пунктирной граничной линии.
Определите, удовлетворяют ли упорядоченные пары линейному неравенству
Использование графика Определение упорядоченных пар решений линейного неравенства с двумя переменными
Определение того, удовлетворяют ли упорядоченные пары линейному неравенству
Небольшое примечание к описанной выше проблеме: обратите внимание, что вы можете использовать точки [латекс](0,−3)[/латекс] и [латекс](2,1)[/латекс] для построения граничной линии, но это эти точки не входят в область решений, так как область не включает граничную линию!
Графики линейных неравенств с двумя переменными (форма пересечения наклона)
Резюме
Когда неравенства изображаются на координатной плоскости, решения располагаются в области координатной плоскости, которая представлена в виде заштрихованной области на самолет.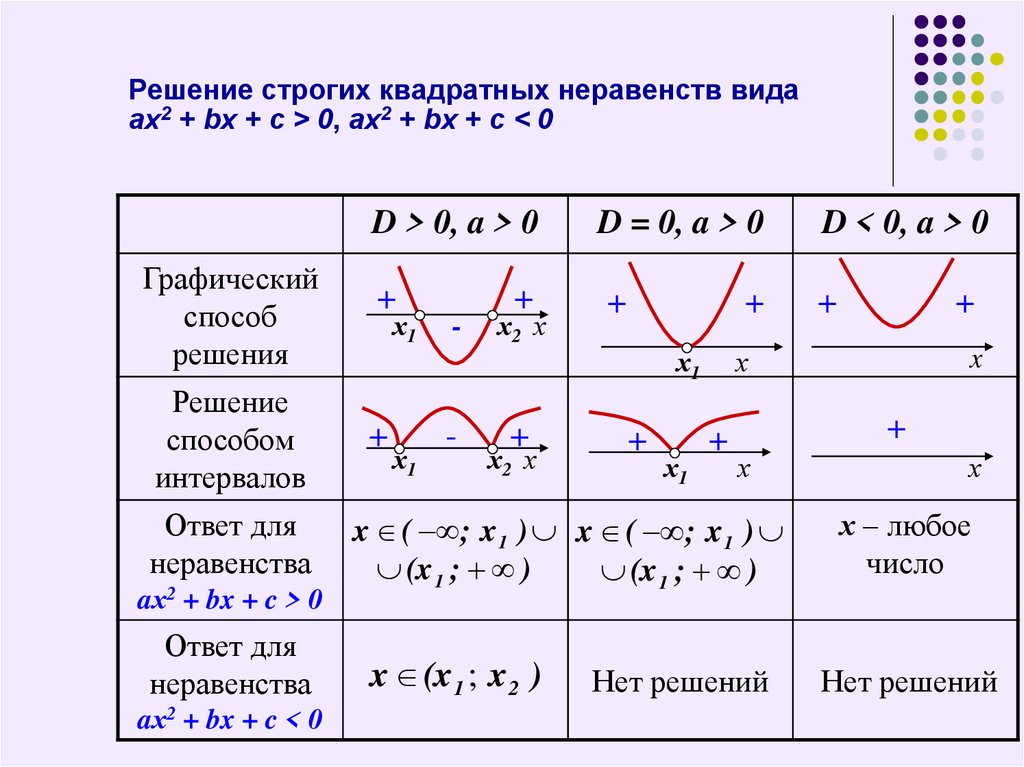 Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.
Граница неравенства рисуется сплошной линией, если точки на самой линии удовлетворяют неравенству, как в случаях ≤ и ≥. Она рисуется штриховой линией, если точки на прямой не удовлетворяют неравенству, как в случаях < и >. Вы можете сказать, какую область закрасить, проверив некоторые точки в неравенстве. Использование координатной плоскости особенно полезно для визуализации области решений неравенств с двумя переменными.
Графическое решение линейных неравенств с двумя переменными
Мы умеем составлять уравнения разной степени, и это очень много используется в реальной жизни, но возникает вопрос, всегда ли можно преобразовать ситуацию в уравнение? Иногда мы получаем заявления о том, что число случаев Covid в день в Дели достигло более 10 000. Это фразы «Меньше чем», «Больше чем», «меньше или равно» и т.д. Такие фразы сложно перевести в уравнения. Для таких случаев нам нужно научиться составлять уравнения с неравенствами в них. Давайте посмотрим на это подробно.
Что такое неравенство?
Давайте рассмотрим пример. Анил хочет купить прохладительные напитки. Каждый холодный напиток стоит 20 рупий, а всего у него с собой 190 рупий. Предположим, он покупает x холодных напитков. Каким может быть максимальное значение x? Его можно представить в виде уравнения, приведенного ниже,
Анил хочет купить прохладительные напитки. Каждый холодный напиток стоит 20 рупий, а всего у него с собой 190 рупий. Предположим, он покупает x холодных напитков. Каким может быть максимальное значение x? Его можно представить в виде уравнения, приведенного ниже,
20x < 190
Два действительных выражения или действительные числа, связанные символами «<», «>», «≤» или «≥», называются неравенствами. Приведенное выше утверждение является неравенством. Существует два типа неравенства:
- Числовые неравенства: 3 < 5 или 7 > 5.
- Буквенные неравенства: x > 5 и y < 7.
Некоторые общие примеры неравенств:
ax + by + c > 0 …. (1)
ax + by + c < 0 ….(2)
ax + by + c ≥ 0 ….(3)
ax + by + c ≤ 0 ….(4)
Из приведенного выше уравнений, уравнения (1) и (2) называются строгими неравенствами, а (3) и (4) – слабыми неравенствами.
Решения неравенств
Любое решение неравенства — это значение той переменной, которая делает неравенство истинным утверждением.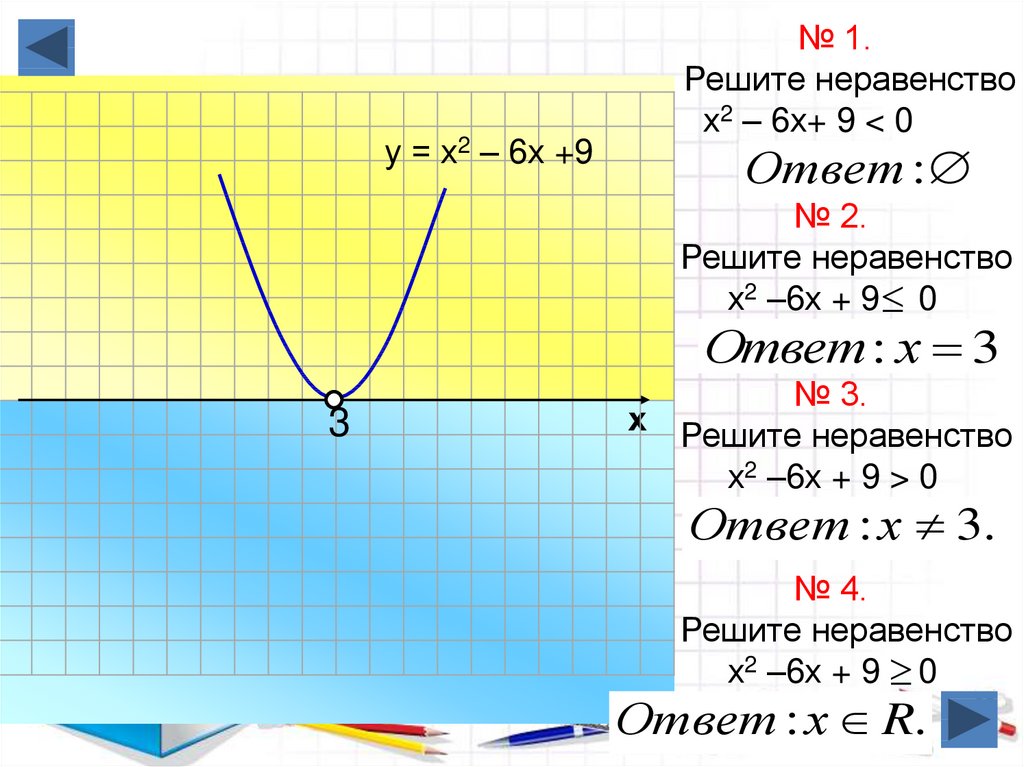 Например, предположим, что у нас есть неравенство x < 5. В таком случае все значения x, которые меньше 5, делают это неравенство истинным неравенством. При решении неравенств необходимо помнить о некоторых правилах:
Например, предположим, что у нас есть неравенство x < 5. В таком случае все значения x, которые меньше 5, делают это неравенство истинным неравенством. При решении неравенств необходимо помнить о некоторых правилах:
- К обеим частям неравенства можно прибавлять или вычитать одинаковые числа.
- Обе части неравенства можно умножить (или разделить) на одно и то же положительное число. Но когда обе части умножаются или делятся на отрицательное число, то знак неравенства меняется на противоположный.
Эти операции не влияют на неравенство и могут быть использованы для упрощения неравенства для нас.
Вопрос: Решите неравенство 20x < 80 и покажите его решения на графике.
Решение:
Нам дано,
20x < 80
Мы знаем, что деление неравенства на положительное число ничего не меняет. Разделим неравенство на 20.
x < 4.
Теперь все значения меньше 10 являются решениями этого неравенства.
На рисунке ниже это решение представлено на графике.
Графическое представление неравенства с двумя переменными
Мы видели график линейного неравенства с одной переменной. Линейное уравнение с двумя переменными представляет собой линию, которая делит плоскость на две части. Назовем каждую часть полуплоскостью. Если линия вертикальна, то она разделит плоскость на левую полуплоскость и правую полуплоскость, а невертикальная линия разделит плоскость на верхнюю левую полуплоскость и нижнюю полуплоскость.
Любая точка декартовой плоскости будет лежать либо на прямой, либо на любой из полуплоскостей I и II.
Допустим, у нас есть линия,
ax + by = c
Здесь a ≠ 0 и b ≠ 0.
Теперь, когда мы помещаем любую точку (x, y) в уравнение, есть три возможные случаи:
- ax + by > c
- ax + by < c
- ax + by = c
Рассмотрим все случаи
Случай (i): ax + by > c
Допустим, b > 0.
Рассмотрим точку (h, k), которая удовлетворяет уравнению. Тогда
ah + bk = c
Возьмем другую произвольную точку (h, l). На рисунке ниже представлены две точки вместе с линией. Мы знаем, что
l > k
bl > bk
ah + bl > ah +bk
ah + bl > c
Таким образом, точки (h, l) удовлетворяют свойству ax + by > c. Таким образом, все точки, лежащие в полуплоскости II, удовлетворяют этому неравенству. Аналогично можно доказать и для b < 0.
Случай (ii): ax + by = c
Все точки, удовлетворяющие прямой, лежащей на прямой, удовлетворяют этому уравнению.
Случай (iii): ax + by < c
Все остальные точки, то есть точки, лежащие в полуплоскости, удовлетворяют этому неравенству.
Давайте рассмотрим некоторые проблемы с этими концепциями.
Примеры задач
Вопрос 1. Решите уравнение 5x + 3y > 6 графически.
Решите уравнение 5x + 3y > 6 графически.
Решение:
Сначала нам нужно нарисовать график для 5x + 3y = 6. Это можно сделать, представив уравнение в форме пересечения наклона или в форме пересечения.
Теперь произвольно выберите точку для проверки. Возьмем (0,0).
Подставляя эту точку (0,0) в уравнение,
5(0) + 3(0) = 0 < 6.
Таким образом, точки в нижней половине будут удовлетворять 5x + 3y < 6. Таким образом, все точки, удовлетворяющие данному уравнению, будут лежать на верхней полуплоскости.
Вопрос 2: Решите уравнение 6x + 2y > 3 графически.
Решение:
Сначала нам нужно нарисовать график для 6x + 2y = 3. Это можно сделать, представив уравнение в форме пересечения наклона или в форме пересечения.
Подставляя (0,0) в уравнение,
6(0) + 2(0) = 0 < 3. Таким образом, точки верхней полуплоскости удовлетворяют данному уравнению.
6x + 2y > 3
Вопрос 3: Решите уравнение x + y < 2 графически.
Решение:
Приведенное уравнение: x + y < 2.
Подставив (0, 0) в уравнение,
0 < 2.
Эта точка удовлетворяет заданному уравнению. Таким образом, график будет таким:
Вопрос 4: Решите уравнение 3x – 5y < 20 графически.
Решение:
Как обычно, мы возьмем (0, 0) в качестве точки, которую мы хотим протестировать.
3(0) – 5(0) < 20.
Эта точка удовлетворяет заданному неравенству. Таким образом, верхняя левая полуплоскость удовлетворяет неравенству.
Вопрос 5: Составьте неравенство из приведенного ниже графика.
Решение:
Мы видим, что эта линия параллельна одной из осей. Уравнение прямой:
x = 4
Теперь мы хотим сформировать линейное неравенство для заштрихованной области.



 И ещё этот метод хорош для лучшего понимания математики.
И ещё этот метод хорош для лучшего понимания математики. Ибо строить для решения –
затея как-то не очень 🙂 Уж лучше метод интервалов.
Ибо строить для решения –
затея как-то не очень 🙂 Уж лучше метод интервалов.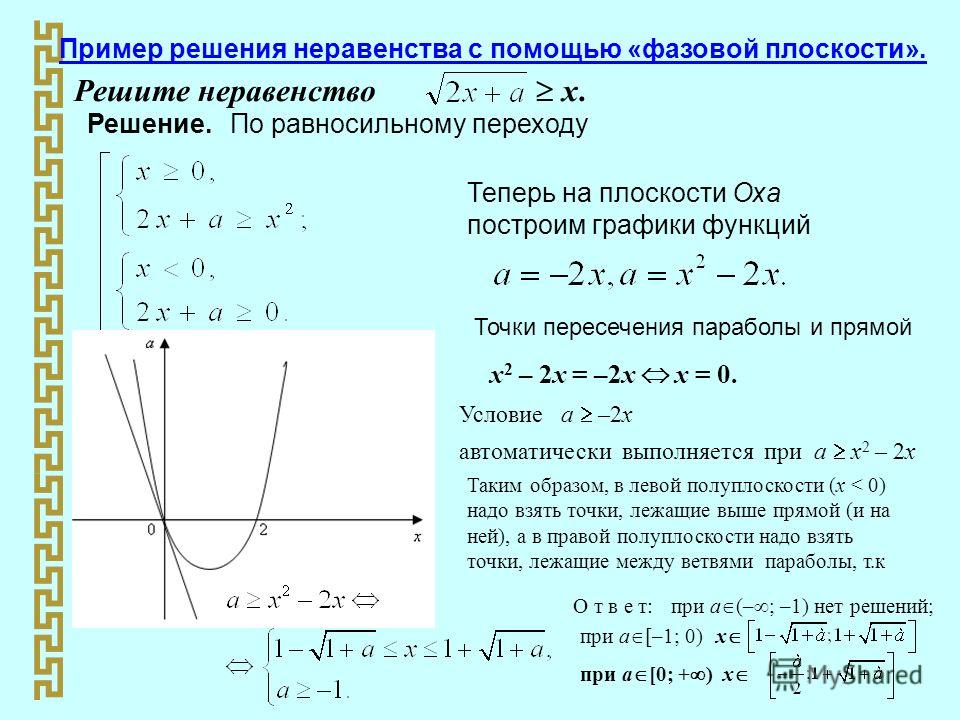
 е. ;
е. ; На рисунке ниже это решение представлено на графике.
На рисунке ниже это решение представлено на графике.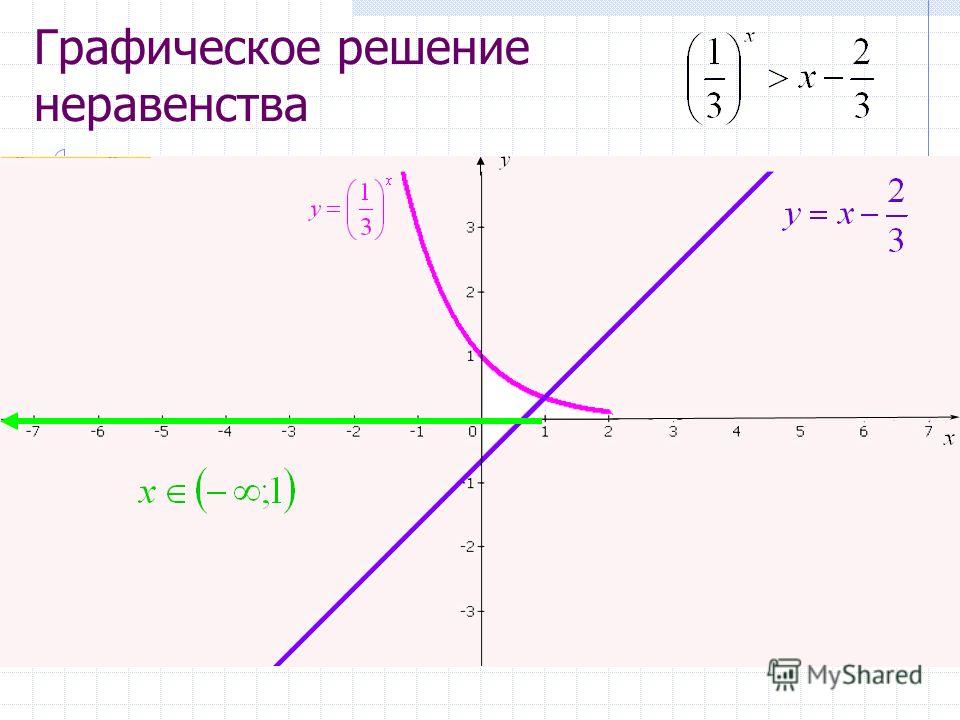 Рассмотрим точку (h, k), которая удовлетворяет уравнению. Тогда
Рассмотрим точку (h, k), которая удовлетворяет уравнению. Тогда