§ Квадратные уравнения. Формула для корней квадратного уравнения
Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения
В предыдущих уроках мы разбирали «Как решать линейные уравнения», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.
Что называют квадратным уравнением
Важно!
Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.
Если максимальная степень, в которой стоит неизвестное — «2», значит, перед вами квадратное уравнение.
Примеры квадратных уравнений
- 5x2 − 14x + 17 = 0
- −x2 + x + = 0
- x2 + 0,25x = 0
- x2 − 8 = 0
Важно! Общий вид квадратного уравнения выглядит так:
ax2 + bx + c = 0
«a», «b» и «c» — заданные числа.
- «a» — первый или старший коэффициент;
- «b» — второй коэффициент;
- «c» — свободный член.
Чтобы найти «a», «b» и «c» нужно сравнить свое уравнение с общим видом квадратного уравнения «ax2 + bx + c = 0».
Давайте потренируемся определять коэффициенты «a», «b» и «c» в квадратных уравнениях.
| Уравнение | Коэффициенты |
|---|---|
| 5x2 − 14x + 17 = 0 |
|
| −7x2 − 13x + 8 = 0 |
|
| −x2 + x + = 0 |
|
| x2 + 0,25x = 0 |
|
| x2 − 8 = 0 |
|
Как решать квадратные уравнения
В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней.
Запомните!
Чтобы решить квадратное уравнение нужно:
- привести квадратное уравнение к общему виду «ax2 + bx + c = 0». То есть в правой части должен остаться только «0»;
- использовать формулу для корней:
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.
x2 − 3x − 4 = 0
Уравнение « x2 − 3x − 4 = 0 » уже приведено к общему виду «ax2 + bx + c = 0» и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения.
Определим коэффициенты «a», «b» и «c» для этого уравнения.
| Уравнение | Коэффициенты |
|---|---|
| x2 − 3x − 4 = 0 |
|
Подставим их в формулу и найдем корни.
x2 − 3x − 4 = 0
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
x1;2 =
| −(−3) ± √(−3)2 − 4 · 1· (−4) |
| 2 · 1 |
x1;2 =
| 3 ± √9 + 16 |
| 2 |
x1;2 =
| 3 ± √25 |
| 2 |
x1;2 =
| 3 ± 5 |
| 2 |
x1 =
| x2 =
| ||||
| x1 = | x2 = | ||||
| x1 = 4 | x2 = −1 |
Ответ: x1 = 4; x2 = −1
Важно!
Обязательно выучите наизусть формулу для нахождения корней.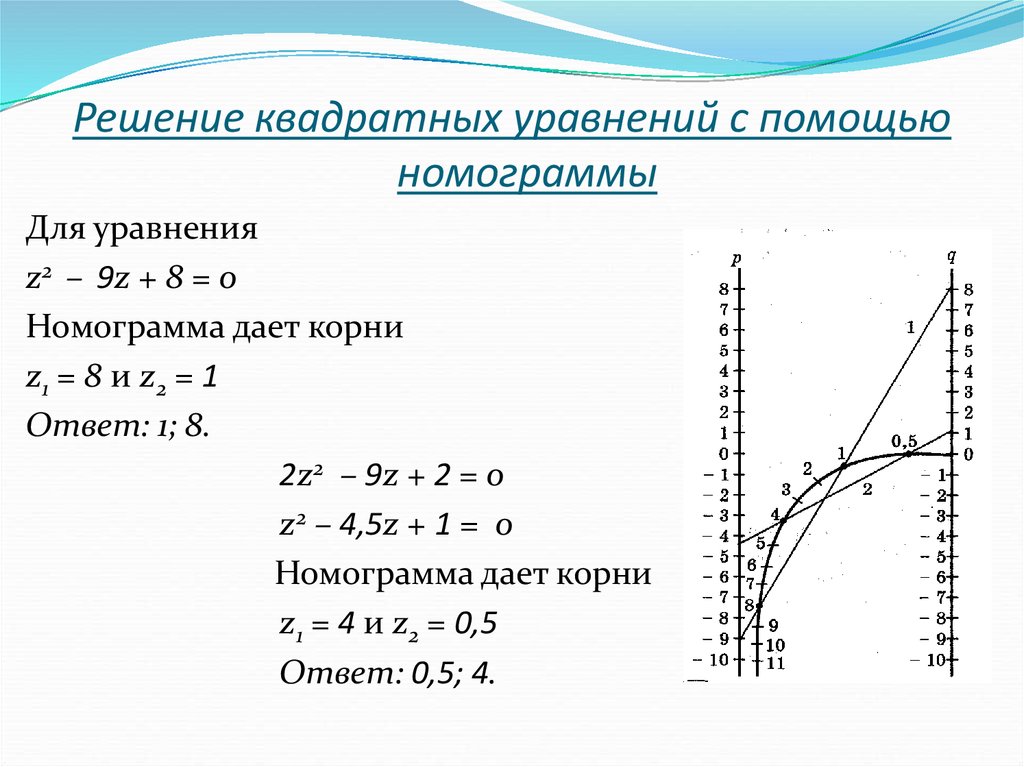
x1;2 =
| −b ± √b2 − 4ac |
| 2a |
С её помощью решается любое квадратное уравнение.
В формуле «x1;2 =
| −b ± √b2 − 4ac |
| 2a |
» часто заменяют подкоренное выражение
«b 2 − 4ac» на букву «D» и называют
дискриминантом. Более подробно понятие дискриминанта рассматривается в уроке
«Что такое дискриминант».
Рассмотрим другой пример квадратного уравнения.
x2 + 9 + x = 7x
В данном виде определить коэффициенты «a», «b» и «c» довольно сложно. Давайте вначале приведем уравнение к общему виду «ax2 + bx + c = 0».
Используем правило переноса и упростим подобные члены.
x2 + 9 + x = 7x
x2 + 9 + x − 7x = 0
x2 + 9 − 6x = 0
x2 − 6x + 9 = 0
Теперь можно использовать формулу для корней.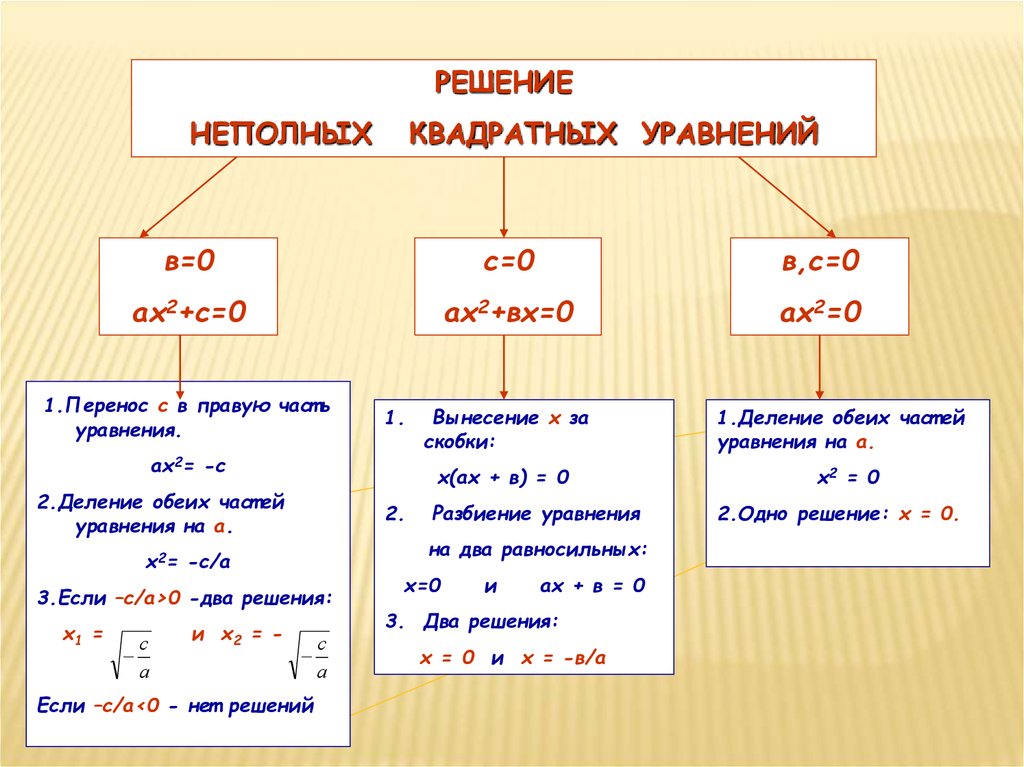
x1;2 =
| −(−6) ± √(−6)2 − 4 · 1 · 9 |
| 2 · 1 |
x1;2 =
| 6 ± √36 − 36 |
x1;2 =
| 6 ± √0 |
| 2 |
x1;2 =
| 6 ± 0 |
| 2 |
x =
x = 3
Ответ: x = 3
Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.
Мы помним из определения квадратного корня о том, что извлекать квадратный корень из отрицательного числа нельзя.
Рассмотрим пример квадратного уравнения, у которого нет корней.
5x2 + 2x = − 3
5x2 + 2x + 3 = 0
x1;2 =
| −2 ± √22 − 4 · 3 · 5 |
| 2 · 5 |
x1;2 =
| −2 ± √4 − 60 |
| 10 |
x1;2 =
| −2 ± √−56 |
| 10 |
Ответ: нет действительных корней.
Итак, мы получили ситуацию, когда под корнем стоит отрицательное число. Это означает, что в уравнении нет корней. Поэтому в ответ мы так и записали «Нет действительных корней».
Важно!
Что означают слова «нет действительных корней»? Почему нельзя просто написать «нет корней»?
На самом деле корни в таких случаях есть, но в рамках школьной программы они не проходятся, поэтому и в ответ мы записываем, что среди действительных чисел корней нет. Другими словами «Нет действительных корней».
Неполные квадратные уравнения
Иногда встречаются квадратные уравнения, в которых отсутсвуют в явном виде коэффициенты «b» и/или «c». Как например, в таком уравнении:
4x2 − 64 = 0
Такие уравнения называют неполными квадратными уравнениями. Как их решать рассмотрено в уроке «Неполные квадратные уравнения».
Как решать квадратные уравнения Дискриминант Неполные квадратные уравнения
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
Решение квадратных уравнений через производные / Хабр
Здравствуйте, уважаемые читатели. После прочтения статьи у вас, вероятно, возникнет закономерный вопрос: «А зачем, собственно, это надо?». В силу этого сперва считаю необходимым заблаговременно сообщить, что искомый метод решения квадратных уравнений представлен скорее с морально-эстетической стороны математики, нежели со стороны практического сухого применения. Также заранее извиняюсь перед теми читателями, которые посчитают мои дилетантские изречения неприемлемыми. Итак, начнем забивать гвозди микроскопом.
Имеем алгебраическое уравнение второй степени (оно же квадратное) в общем виде:
Перейдем от квадратного уравнения к квадратичной функции:
Где, очевидно, необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль.
Кажется, нужно просто решить квадратное уравнение с помощью теоремы Виета или через дискриминант. Но мы ведь собрались здесь не для этого. Давайте-ка лучше возьмем производную!
Исходя из определения физического смысла производной первого порядка ясно, что подставляя аргумент в получившуюся выше функцию мы (в частности) получим скорость изменения функции в заданной этим аргументом точке.
Что же дальше делать? Непонятно. А в любом непонятном случае нужно брать производную ещё раз:
На этот раз мы получили «скорость скорости» изменения функции (то бишь ускорение) в конкретной точке. Немного проанализировав полученное, можно сделать вывод, что «ускорением» является константа, которая не зависит от аргумента функции — запомним это.
Сейчас вспомним немного физику и равноускоренное движение (РУД). Что у нас есть в арсенале? Верно, имеется формула для определения координаты перемещения по оси при искомом движении:
Где — время, — начальная скорость, — ускорение.
Нетрудно заметить, что наша изначальная функция как раз представляет из себя РУД.
Разве формула перемещения для РУД не является следствием решения квадратного уравнения?
Нет. Формула для РУД выше по факту есть результат взятия интеграла от формулы скорости при ПРУД. Или из графика можно найти площадь фигуры. Там вылезет трапеция.
Формула перемещения при РУД не вытекает из решения каких-либо квадратных уравнений. Это очень важно, иначе не было бы смысла статьи.
Теперь осталось разобраться что есть что, и чего нам не хватает.
«Ускорение» у нас уже есть — им является производная второго порядка , выведенная выше. А вот чтобы получить начальную скорость , нам нужно взять в общем-то любой (обозначим его как ) и подставить его в производную теперь уже первого порядка — ибо она и будет искомым.
В таком случае возникает вопрос, какой же нужно взять? Очевидно, такой, чтобы начальная скорость была равна нулю, чтобы формула «перемещения при РУД» стала иметь вид:
В таком случае составим уравнение для поиска :
[подставили в производную первого порядка ]
Корнем такого уравнения относительно будет:
А значением исходной функции при таком аргументе будет:
Вспомним, какой целью мы задались в самом начале: «необходимо найти такие значения аргумента функции, в которых оная возвратила бы ноль».
Иными словами, нам от положения необходимо «дойти до нуля».
Так как теперь нам известна начальная скорость, ускорение и какой путь необходимо пройти, то настало время отметить следующее:
, также как и
Тогда, подставив все известные величины, получим:
Поделим все на :
Теперь становится очевидно, что:
Соединим все «детали пазла» воедино:
Вот мы и получили окончательное решение поставленной задачи. Вообще Америку мы не открыли — мы просто пришли к формуле решения квадратного уравнения через дискриминант окольными путями. Практического смысла это не несет (примерно таким же образом можно решать уравнения первой/второй степени любого (не обязательно общего) вида).
Целью этой статьи является, в частности, подогрев интереса к анализу мат. функций и вообще к математике.
С вами был Петр, спасибо за внимание!
2} + bx + c = 0, потому что трехчлен в левой части нельзя легко разложить на множители. Это не значит, что квадратное уравнение не имеет решения.
На этом этапе нам нужно обратиться к прямому подходу квадратной формулы, чтобы найти решения квадратного уравнения или, проще говоря, определить значения x, которые могут удовлетворять уравнению.Чтобы использовать квадратную формулу, квадратное уравнение, которое мы решаем, должно быть приведено к «стандартной форме», иначе все последующие шаги не будут работать. Цель состоит в том, чтобы преобразовать квадратное уравнение так, чтобы квадратное выражение было изолировано на одной стороне уравнения, а противоположная сторона содержала только число ноль, 0,9.2} + bx + c = 0.
Притормози, если нужно. Будьте осторожны с каждым шагом, упрощая выражения. Именно здесь обычно случаются распространенные ошибки, потому что учащиеся склонны «расслабляться», что приводит к ошибкам, которые можно было бы предотвратить, например, при сложении, вычитании, умножении и/или делении действительных чисел.
Примеры решения квадратных уравнений с помощью квадратной формулы
Пример 1 : Решите приведенное ниже квадратное уравнение с помощью квадратной формулы.
При осмотре становится очевидным, что квадратное уравнение имеет стандартную форму, поскольку правая часть равна нулю, а остальные члены остаются в левой части. Другими словами, у нас есть что-то вроде этого
Это здорово! Что нам нужно сделать, так это просто определить значения a, b и c, а затем подставить их в квадратичную формулу.
Вот оно! Сделайте привычкой всегда проверять решенные значения x обратно в исходное уравнение для проверки.
Пример 2 : Решите приведенное ниже квадратное уравнение, используя квадратную формулу.
Это квадратное уравнение абсолютно не в той форме, которую мы хотим, потому что правая часть НЕ ноль. Мне нужно исключить 7 справа, вычитая обе стороны на 7. Это решит нашу проблему. После этого найдите x как обычно.
Окончательные ответы: {x_1} = 1 и {x_2} = — {2 \over 3}.
Пример 3 : Решите приведенное ниже квадратное уравнение, используя квадратную формулу.
Это квадратное уравнение выглядит как «каша». У меня есть переменные x и константы с обеих сторон уравнения. Если мы сталкиваемся с чем-то подобным, всегда придерживаемся того, что знаем. Да, это все о стандартной форме. Мы должны заставить правую часть быть равной нулю. Мы можем сделать это в два этапа.
Сначала я вычту обе части в 5 раз, а затем прибавлю 8.
Значения, которые нам нужны:
a = — 1, b = — \,8 и c = 2
Пример 4 : Решите приведенное ниже квадратное уравнение, используя квадратную формулу.
Что ж, если вы думаете, что пример 3 — это «беспорядок», то этот должен быть еще «беспорядок». Однако вскоре вы поймете, что они действительно очень похожи.
Сначала нам нужно выполнить некоторую очистку, преобразовав это квадратное уравнение в стандартную форму. Звучит знакомо? Поверьте мне, эта проблема не так серьезна, как кажется, если мы знаем, что делать.
Напоминаем, что нам нужно нечто подобное 92} член с правой стороны.
- Удалите член x с правой стороны.
- Удалите константу с правой стороны.
После получения правильной стандартной формы на предыдущем шаге пришло время подставить значения a, b и c в квадратичную формулу, чтобы найти x.
- Из преобразованной стандартной формы извлеките необходимые значения.
a = 1, b = — \,4 и c = — \,14
- Затем вычислите эти значения по квадратичной формуле.
Вас также могут заинтересовать:
Решение квадратных уравнений методом квадратного корня
Решение квадратных уравнений методом факторинга
Решение квадратных уравнений методом возведения в квадрат
Как решать квадратные уравнения? Решение квадратных уравнений
Прежде чем перейти к решению квадратных уравнений, давайте вспомним несколько фактов о квадратных уравнениях. Слово «квадратный» произошло от слова «квадрат» и означает «квадрат». Это означает, что в квадратном уравнении есть переменная, возведенная в степень 2 как член наибольшей степени.
Стандартная форма квадратного уравнения задается уравнением ax 2 + bx + c = 0, где a ≠ 0. Мы знаем, что любое значение (значения) x, удовлетворяющее уравнению, известно как решение (или) корень уравнения, и процесс нахождения значений x которые удовлетворяют уравнению ax 2 + bx + c = 0, называется решением квадратных уравнений.
Существуют различные методы решения квадратных уравнений. Но самым популярным методом является решение квадратных уравнений методом факторизации. Давайте подробно изучим все методы здесь вместе с несколькими решенными примерами.
| 1. | Как решать квадратные уравнения? |
| 2. | Решение квадратичных уравнений с помощью факторинга |
| 3. | Решение квадратных уравнений путем заполнения квадрата |
| 4. | Решение квадратичных уравнений с помощью графика |
5. | Решение квадратных уравнений по квадратичной формуле |
| 6. | Часто задаваемые вопросы о решении квадратных уравнений |
Как решать квадратные уравнения?
Решение квадратных уравнений означает нахождение значения (или) значений переменной, которые удовлетворяют уравнению. Значение (я), которые удовлетворяют квадратному уравнению, известны как его корни (или) решения (или) нули. Поскольку степень квадратного уравнения равна 2, оно может иметь максимум 2 корня. Например, легко видеть, что x = 1 и x = 2 удовлетворяют квадратному уравнению x 2 — 3x + 2 = 0 (можно подставить каждое из значений в это уравнение и проверить). Таким образом, x = 1 и x = 2 являются корнями x 2 — 3x + 2 = 0. Но как их найти, если они не заданы? Существуют различные способы решения квадратных уравнений.
- Решение квадратных уравнений методом факторизации
- Решение квадратных уравнений путем заполнения квадрата
- Решение квадратных уравнений с помощью графика
- Решение квадратных уравнений по квадратной формуле
Помимо этих методов, существуют и другие методы, которые используются только в особых случаях (когда в квадратном уравнении отсутствуют члены), как описано ниже.
Решение квадратных уравнений отсутствует b
В квадратном уравнении ax 2 + bx + c = 0, если член с b отсутствует, уравнение принимает вид ax 2 + c = 0. Это можно решить, взяв квадратный корень с обеих сторон. Процесс поясняется примерами ниже.
- x 2 — 4 = 0 ⇒ x 2 = 4 ⇒ x = ±√4 ⇒ x = ± 2
Таким образом, корни уравнения равны 2 и -2. - x 2 + 49 = 0 ⇒ x 2 = -49 ⇒ x = ±√(-49) ⇒ x = ± 7i
Таким образом, корни уравнения равны 7i и -7i.
(обратите внимание, что это мнимые (или) комплексные числа).
Решение квадратных уравнений отсутствует c
В квадратном уравнении ax 2 + bx + c = 0, если член с c отсутствует, уравнение становится ax 2 + bx = 0. Чтобы решить уравнение этого типа, мы просто выносим x из левой части, устанавливаем каждый из множителей равным нулю и решаем. Процесс поясняется примерами ниже.
- х 2 — 5х = 0 ⇒ х (х — 5) = 0 ⇒ х = 0; х — 5 = 0 ⇒ х = 0; х = 5
Таким образом, корни уравнения равны 0 и 5.
- х 2 + 21х = 0 ⇒ х (х + 21) = 0 ⇒ х = 0; х + 21 = 0 ⇒ х = 0; х = -21
Таким образом, корни уравнения равны 0 и -11.
Теперь мы изучим методы решения квадратных уравнений в каждом из вышеупомянутых методов.
Решение квадратичных уравнений с помощью факторинга
Решение квадратичных уравнений с помощью факторизации — один из известных методов, используемых для решения квадратных уравнений. Пошаговый процесс решения квадратных уравнений факторингом объясняется вместе с примером.
- Шаг — 1: Приведите уравнение к стандартной форме. т. е. получить все члены с одной стороны (обычно с левой стороны) уравнения так, что другая сторона равна 0,
- Шаг — 2: Фактор квадратного выражения. Если вы хотите узнать, как разложить квадратное выражение на множители, нажмите здесь.
- Шаг — 3: По нулевому свойству продукта установите каждый из коэффициентов равным нулю.
- Шаг — 4: Решите каждое из приведенных выше уравнений.
Пример: Решите квадратное уравнение x 2 — 3x + 2 = 0, разложив его на множители.
Решение:
Разлагая на множители левую часть, получаем (x — 1) (x — 2) = 0,
Тогда x — 1 = 0 (или) x — 2 = 0
что дает x = 1 (или) x = 2.
Таким образом, решения квадратного уравнения x 2 — 3x + 2 = 0 равны 1 и 2. Этот метод применим только тогда, когда квадратное выражение факторизуемо. Если это НЕ факторизуемо, то мы можем использовать один из других методов, как описано ниже. Подобно квадратным уравнениям, у нас есть решения для линейных уравнений, которые используются для решения задач линейного программирования.
Решение квадратных уравнений путем заполнения квадрата
Завершение квадрата означает запись квадратного выражения ax 2 + bx + c в форме a (x — h) 2 + k (которая также известна как вершинная форма), где h = -b/2a и «k» можно получить, подставив x = h в ax 2 + bx + c.
Пошаговый процесс решения квадратных уравнений путем заполнения квадрата объясняется вместе с примером.
- Шаг — 1: Приведите уравнение к стандартной форме.
- Шаг — 2: Заполните квадрат с левой стороны. Если вы хотите узнать, как заполнить квадрат, нажмите здесь.
- Шаг — 3: Решите это для x (Нам нужно будет извлечь квадратный корень с обеих сторон по пути).
Пример: Решите 2x 2 + 8x = -3, заполнив квадрат.
Решение:
Данное уравнение в стандартной форме имеет вид 2x 2 + 8x + 3 = 0. Заполнив квадрат слева, получим 2 (x + 2) 2 — 5 = 0. Теперь решим это для x,
Прибавив 5 с обеих сторон,
2 (х + 2) 2 = 5
Разделив обе части на 2,
(х + 2) 2 = 5/2
Извлекая квадратный корень с обеих сторон,
х + 2 = √(5/2) = √5/√2 · √2/√2 = √10/2
Вычитание 2 с обеих сторон,
x = -2 ± (√10/2) = (-4 ± √10) / 2
Таким образом, корни квадратного уравнения 2x 2 + 8x = -3 равны (-4 + √10)/2 и (-4 — √10)/2.
Решение квадратичных уравнений с помощью графика
Для решения квадратного уравнения путем построения графика сначала нужно построить квадратное выражение (когда уравнение имеет стандартную форму) либо вручную, либо с помощью графического калькулятора. Тогда точки пересечения графика (точки, в которых график пересекает ось x) являются не чем иным, как корнями квадратного уравнения. Вот шаги, чтобы решить квадратные уравнения с помощью графика.
- Шаг — 1: Войдите в стандартную форму.
- Шаг — 2: Нарисуйте квадратное выражение (которое находится слева).
- Шаг — 3: Идентифицируйте точки пересечения.
- Шаг — 4: Координаты абсцисс точек пересечения абсцисс являются не чем иным, как корнями квадратного уравнения.
Пример: Решите квадратное уравнение 3x 2 + 5 = 11x с помощью графика.
Решение:
Преобразование данного уравнения в стандартный вид, вычитание 11x с обеих сторон, 3x 2 — 11x + 5 = 0. Теперь нарисуйте квадратное выражение. Нарисуйте квадратную функцию y = 3x 2 — 11x + 5 либо вручную или с помощью графического калькулятора (GDC) и определите точки пересечения по оси x. Его график равен
Таким образом, решения квадратного уравнения 3x 2 + 5 = 11x равны 0,532 и 3,135.
Из приведенного выше примера видно, что графический метод решения квадратных уравнений может не давать точных решений (т. е. давать только десятичные приближения корней, если они иррациональны). т. е., если мы решим то же уравнение с помощью дополнения квадрата, мы получим x = (11 + √61) / 6 и x = (11 — √61) / 6. Но мы не можем получить эти точные корни графическим методом.
Что делать, если график вообще не пересекает ось X? Это означает, что квадратное уравнение имеет два комплексных корня.
т. е. метод построения графика НЕ помогает найти корни, если они являются комплексными числами. Мы можем использовать квадратичную формулу (которая объясняется в следующем разделе), чтобы найти любой тип корней.
Решение квадратных уравнений по формуле квадратов
Как мы уже видели, предыдущие методы решения квадратных уравнений имеют некоторые ограничения, такие как метод факторизации полезен только тогда, когда квадратное выражение факторизуемо, метод построения графиков полезен только тогда, когда квадратное уравнение имеет действительные корни и т. д. Но решение квадратных уравнений по квадратной формуле преодолевает все эти ограничения и полезно для решения любого типа квадратных уравнений. Вот пошаговое объяснение решения квадратного уравнения по формуле квадратного уравнения.
- Шаг — 1: Входим в стандартную форму.
- Шаг — 2: Сравните уравнение с ax 2 + bx + c = 0 и найдите значения a, b и c.
- Шаг — 3: Подставьте значения в квадратную формулу, которая говорит x = [-b ± √(b² — 4ac)] / (2a). Тогда мы получим
- Шаг — 4: Упрощение.
Пример: Решите квадратное уравнение 2x 2 = 3x — 5 по квадратной формуле.
Решение:
Приведенное выше уравнение в стандартной форме 2x 2 — 3x + 5 = 0.
Сравнивая уравнение с ax 2 + bx + c = 0, получаем a = 2, b = -3. и c = 5.
Подставляем значения в квадратную формулу
x = [-(-3) ± √((-3)² — 4(2)(5))] / (2(2))
= [ 3 ± √(9 — 40) ] / 4
= [ 3 ± √(-31) ] / 4
= [ 3 ± i√(31) ] / 4
Таким образом, корнями квадратного уравнения 2x 2 = 3x — 5 являются [ 3 + i√(31) ] / 4 и [ 3 — i√(31) ) ] / 4. В квадратичной формуле выражение b² — 4ac называется дискриминантом (обозначается буквой D). т. е. D = b² — 4ac. Это используется для определения природы корней квадратного уравнения.
Природа корней с использованием дискриминанта
- Если D > 0, то уравнение ax 2 + bx + c = 0 имеет два действительных и различных корня.
- Если D = 0, то уравнение ax 2 + bx + c = 0 имеет только один действительный корень.
- Если D < 0, то уравнение ax 2 + bx + c = 0 имеет два различных комплексных корня.
Таким образом, используя дискриминант, мы можем найти количество решений квадратных уравнений, фактически не решая его.
Важные замечания по решению квадратных уравнений:
- Метод факторизации нельзя применять, если квадратное выражение НЕ факторизуемо.
- Графический метод не может дать комплексные корни, а также не может дать точные корни в случае, если квадратное уравнение имеет иррациональные корни.
- Завершение метода квадратов и метода квадратичных формул может быть применено для решения любого типа квадратного уравнения.
- Корни квадратного уравнения также известны как «решения» или «нули».
- Для любого квадратного уравнения ax 2 + bx + c = 0,
сумма корней = -b/a
произведение корней = с/а.
☛Связанные темы:
- Решение квадратных уравнений с помощью калькулятора квадратных формул
- Решение квадратных уравнений с помощью квадратного калькулятора
- Калькулятор корней квадратного уравнения
- Решение квадратных уравнений с помощью калькулятора факторинга
Часто задаваемые вопросы о решении квадратных уравнений
В чем смысл решения квадратных уравнений?
Решение квадратных уравнений означает нахождение их решений или корней. т. е. это процесс нахождения значений переменной, удовлетворяющих уравнению.
Какие самые популярные способы решения квадратных уравнений?
Существуют разные способы решения квадратичных уравнений. Но самыми популярными способами являются «решение квадратных уравнений факторингом» и «решение квадратных уравнений по квадратной формуле».
Каковы этапы решения квадратных уравнений с помощью графика?
Чтобы решить квадратное уравнение с помощью графика, сначала приведите к стандартной форме ax 2 + bx + c = 0. Затем начертите квадратное выражение ax 2 + bx + c. Найдите, где график пересекает ось x. X-координата x-перехвата (ов) — это не что иное, как решения квадратного уравнения.
Какие 4 способа решения квадратичных уравнений?
Существует 4 способа решения квадратных уравнений.
- по факторингу
- , заполнив квадрат
- по графику
- по квадратичной формуле
Как решать квадратные уравнения по квадратным формулам?
Решения квадратного уравнения ax 2 + bx + c = 0 находятся по квадратной формуле x = [-b ± √(b² — 4ac)] / (2a). Таким образом, чтобы решить квадратное уравнение с помощью квадратичной формулы, просто приведите уравнение к стандартной форме: ax 2 + bx + c = 0 и примените квадратную формулу.
Как узнать, какой метод использовать при решении квадратных уравнений?
Мы можем решать квадратные уравнения любого типа, дополняя квадрат или квадратную формулу. Но если квадратное выражение факторизуемо, то проще всего применить метод факторинга. Мы можем решить его и графическим методом, но он дает только аппроксимированные вещественные корни (т.е. комплексные корни не могут быть найдены в этом методе).
Какой самый простой способ решения квадратных уравнений?
Самым простым способом решения квадратных уравнений является метод факторинга. Но не всегда квадратные выражения факторизуемы. В этом случае мы можем либо использовать квадратичную формулу, либо использовать метод завершения квадрата.
Какие этапы решения квадратичных уравнений путем заполнения квадрата?
Чтобы решить квадратное уравнение ax 2 + bx + c = 0 путем завершения квадрата, преобразуйте ax 2 + bx + c в вершинную форму a (x — h) 2 + k, где h = -b /2a и k получается подстановкой x = h в ax 2 + бх + в.
Тогда мы можем легко решить (x — h) 2 + k = 0, изолируя x. В этом процессе нам придется извлекать квадратный корень с обеих сторон.
Как решать квадратные уравнения с помощью факторинга?
Для решения квадратных уравнений методом факторизации сначала приведите его к стандартной форме (ax 2 + bx + c = 0). Затем разложите левую часть на множители, используя методы факторизации квадратных выражений, установите каждый из множителей равными нулю, что приведет к двум линейным уравнениям, и, наконец, решите линейные уравнения.
Как факторизованная форма помогает решать квадратные уравнения?
Если квадратное выражение в стандартной форме квадратного выражения в нем факторизуемо, то мы можем просто установить каждый множитель равным нулю и решить их. Решения — это не что иное, как корни квадратного уравнения.
Как найти корни квадратных уравнений?
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти с помощью квадратной формулы, которая гласит: x = [-b ± √(b² — 4ac)] / (2a).