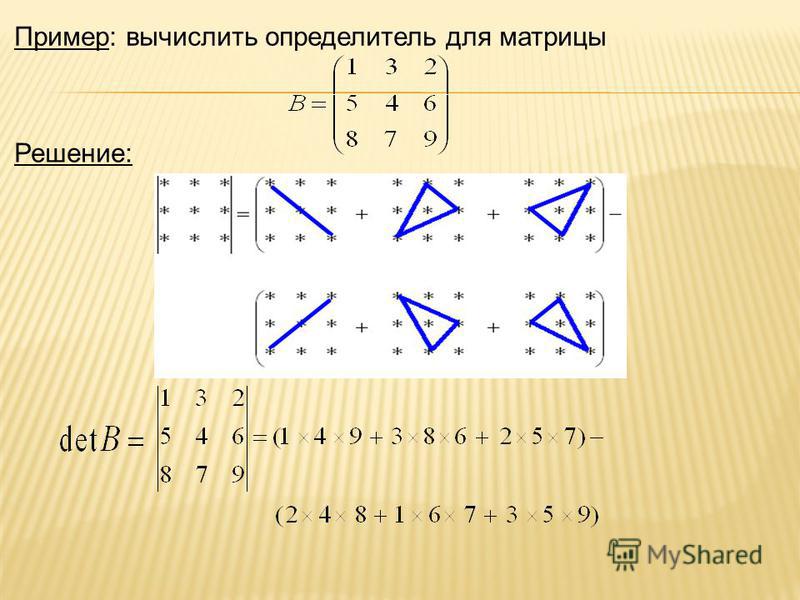
решаем системы линейных алгебраических уравнений (слау)
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод,
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т. е. имеет вид
е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A — 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:
14) слева на A — 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = — 3 + 2t
x 2 = — 1 — 3t
x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений:
$x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.

Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя.
 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. - При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Рассмотрим систему 3-х уравнений с тремя неизвестными
Используя
определители 3-го порядка, решение такой
системы можно записать в таком же виде,
как и для системы двух уравнений, т. е.
е.
(2.4)
если 0. Здесь
Это есть правило Крамера решения системы трех линейных уравнений с тремя неизвестными .
Пример 2.3. Решить систему линейных уравнений при помощи правила Крамера:
Решение . Находим определитель основной матрицы системы
Поскольку 0, то для нахождения решения системы можно применить правило Крамера, но предварительно вычислим еще три определителя:
Проверка:
Следовательно, решение найдено правильно.
Правила Крамера, полученные для линейных систем 2-го и 3-го порядка, наводят на мысль, что такие же правила можно сформулировать и для линейных систем любого порядка. Действительно имеет место
Теорема Крамера. Квадратная система линейных уравнений с отличным от нуля определителем основной матрицы системы (0) имеет одно и только одно решение и это решение вычисляется по формулам
(2.5)
где
– определитель
основной матрицы ,
i – определитель
матрицы , полученной
из основной, заменой i -го
столбца столбцом свободных членов .
Отметим, что если =0, то правило Крамера не применимо. Это означает, что система либо не имеет вообще решений, либо имеет бесконечно много решений.
Сформулировав теорему Крамера, естественно возникает вопрос о вычислении определителей высших порядков.
2.4. Определители n-го порядка
Дополнительным минором M ij элемента a ij называется определитель, получаемый из данного путем вычеркивания i -й строки и j -го столбца. Алгебраическим дополнением A ij элемента a ij называется минор этого элемента, взятого со знаком (–1) i + j , т.е. A ij = (–1) i + j M ij .
Например, найдем миноры и алгебраические дополнения элементов a 23 и a 31 определителя
Получаем
Используя
понятие алгебраического дополнения
можно сформулировать теорему
о разложении определителя n -го
порядка по строке или столбцу .
Теорема 2.1. Определитель матрицы A равен сумме произведений всех элементов некоторой строки (или столбца) на их алгебраические дополнения:
(2.6)
Данная теорема лежит в основе одного из основных методов вычисления определителей, т.н. метода понижения порядка . В результате разложения определителя n -го порядка по какой-либо строке или столбцу, получается n определителей (n –1)-го порядка. Чтобы таких определителей было меньше, целесообразно выбирать ту строку или столбец, в которой больше всего нулей. На практике формулу разложения определителя обычно записывают в виде:
т.е. алгебраические дополнения записывают в явном виде через миноры.
Примеры 2.4. Вычислить определители, предварительно разложив их по какой-либо строке или столбцу. Обычно в таких случаях выбирают такой столбец или строку, в которой больше всего нулей. Выбранную строку или столбец будем обозначать стрелкой.
2.
 5. Основные свойства определителей
5. Основные свойства определителейРазлагая определитель по какой-либо строке или столбцу, мы получим n определителей (n –1)-го порядка. Затем каждый из этих определителей (n –1)-го порядка также можно разложить в сумму определителей (n –2)-го порядка. Продолжая этот процесс, можно дойти до определителей 1-го порядка, т.е. до элементов матрицы, определитель которой вычисляется. Так, для вычисления определителей 2-го порядка придется вычислить сумму двух слагаемых, для определителей 3-го порядка – сумму 6 слагаемых, для определителей 4-го порядка – 24 слагаемых. Число слагаемых будет резко возрастать по мере увеличения порядка определителя. Это означает, что вычисление определителей очень высоких порядков становится довольно трудоемкой задачей, непосильной даже для ЭВМ. Однако вычислять определители можно и по-другому, используя свойства определителей.
Свойство
1 . Определитель
не изменится, если в нем поменять местами
строки и столбцы, т. е. при транспонировании
матрицы :
е. при транспонировании
матрицы :
.
Данное свойство свидетельствует о равноправии строк и столбцов определителя. Иначе говоря, любое утверждение о столбцах определителя справедливо и для его строк и наоборот.
Свойство 2 . Определитель меняет знак при перестановке двух строк (столбцов).
Следствие . Если определитель имеет две одинаковые строки (столбца), то он равен нулю.
Свойство 3 . Общий множитель всех элементов в какой-либо строке (столбце) можно вынести за знак определителя .
Например,
Следствие . Если все элементы некоторой строки (столбца) определителя равны нулю, то и сам определитель равен нулю .
Свойство
4 . Определитель
не изменится, если к элементам одной
строки (столбца), прибавить элементы
другой строки (столбца), умноженной на
какое-либо число .
Например,
Свойство 5 . Определитель произведения матриц равен произведению определителей матриц:
Лекция 3 СЛУ Метод Крамера
6
Лекция 3. Системы линейных уравнений.
метод Крамера
Содержание
Основные определения.
Метод Крамера (определителей) решения систем линейных уравнений.
1. Основные определения
где числа — коэффициенты при неизвестных, — номер уравнения, — номер неизвестной, — свободные члены.
,
который при подстановке в каждое уравнение системы вместо неизвестных соответственно обращает их в верные равенства.
Система линейных уравнений называется:
а) совместной, если она имеет хотя бы одно решение;
б) несовместной, если она не имеет решений;
в) определенной, если она имеет единственное решение;
г) неопределенной, если она имеет бесконечное множество решений;
д) однородной, если все свободные члены равны нулю ;
е) неоднородной,
если есть
.
2. Метод Крамера (определителей) решения систем линейных уравнений
Правило (метод) Крамера применяется к системам, у которых число уравнений равно числу неизвестных. Этот метод использует определители.
2.1. Число уравнений и неизвестных равно 2
Рассмотрим систему линейных уравнений
Вычисляются определители:
, , .
Здесь
— определитель системы, составленный из коэффициентов при неизвестных;
— это определитель, полученный из определителя заменой столбца коэффициентов при на столбец свободных членов;
— это определитель, полученный из определителя заменой столбца коэффициентов при на столбец свободных членов.
1. Если , то система совместная и определенная, то есть имеет единственное решение, которое находится по формулам Крамера:
.
2. Если , а хотя бы один из определителей , отличен от нуля, то система не имеет решений (несовместная).
3. Если , то система имеет бесконечно много решений (совместная и неопределенная).
Пример 1. Решить с помощью метода Крамера систему уравнений
Решение
, поэтому СЛУ имеет единственное решение.
, .
Тогда ; .
Ответ: система уравнений совместна и определенна, ее единственное решение .
Пример 2. Решить с помощью метода Крамера систему уравнений
.
Решение
Определитель системы равен нулю: , однако один из вспомогательных определителей не равен нулю: , значит, СЛУ не имеет решений, то есть СЛУ несовместная.
Пример
3. Решить с
помощью метода Крамера систему уравнений
Решить с
помощью метода Крамера систему уравнений
Решение
, , .
Поэтому система имеет бесконечно много решений.
Разделив коэффициенты 2-го уравнения на 3, получим: Оставим только одно из этих уравнений: .
Выразим через : , значение — любое действительное число. Это и есть выражение для общего решения СЛУ. Ответ можно записать так: , где .
Придавая различные значения, будем получать бесконечное множество частных решений. Например, при получим и первое частное решение . При получим и второе частное решение , и так далее.
2.2. Число уравнений и неизвестных равно 3
Рассмотрим СЛУ
Вычисляются определители:
, ,
, .
1. Если
,
то система имеет единственное
решение, которое находится по формулам
Крамера:
Если
,
то система имеет единственное
решение, которое находится по формулам
Крамера:
, .
2. Если , а хотя бы один из определителей , , отличен от нуля, то система не имеет решений.
3.Если , то система имеет бесконечно много решений.
Пример 4. Решить систему линейных уравнений .
Составим определитель из коэффициентов при неизвестных и вычислим его: ,
значит, СЛУ имеет единственное решение.
Найдем вспомогательные определители и значения неизвестных.
Ответ: Система совместная и определенная, единственное решение .
Рассмотрим пример, в котором СЛУ имеет бесконечное множество решений, и они будут найдены с применением формул Крамера.
Пример
5. Решить СЛУ
Решить СЛУ
Решение
Вычислим определитель системы:
Заметим, что третье уравнение системы равно сумме первых двух уравнений, т.е. зависит от первых двух уравнений.
Отбросив третье уравнение, получим равносильную систему двух уравнений с тремя неизвестными:
Оставим в левой части системы те неизвестные, коэффициенты при которых образуют определитель, не равный нулю.
Например, коэффициенты при и образуют определитель . Поэтому оставим в левой части уравнений слагаемые с и , а слагаемые с перенесем в правую часть с противоположным знаком.
Неизвестное назовем свободным, а неизвестные и — базисными неизвестными.
Запишем систему в виде и применим к ней правило Крамера:
;
Выражение
—
общее
решение неопределенной
СЛУ, где — любое действительное число.
Из общего решения можно получить частные решения, если придать свободной неизвестной какое-то конкретное значение.
Например, пусть , тогда ; тогда частное решение . И так далее.
Контрольные вопросы
Запишите общий вид системы 2 линейных уравнений с тремя неизвестными.
Что называется решением СЛУ?
Что значит «решить систему линейных уравнений»?
Какие системы линейных уравнений называются совместными и несовместными?
При каком условии система линейных уравнений с неизвестными имеет единственное решение?
Напишите формулы Крамера для решения системы линейных уравнений. В каком случае они применимы?
Как, зная общее решение, записать частное решение неопределенной системы?
Глава 99. Приложение В.
 Применение MathCad для решения математических задач
Применение MathCad для решения математических задачРешение системы линейных алгебраических уравнений методом Гаусса:
1. Вводите матрицу системы и матрицу-столбец правых частей.
2. Сформируйте расширенную матрицу системы.
3. Приведите расширенную матрицу системы к ступенчатому виду.
4. Сформируйте столбец решения системы.
Пример
Пусть A — матрица системы, B — матрица-столбец правых частей, Ar — расширенная матрица системы, Ag — расширенная матрица системы в ступенчатом виде, X — столбец решения системы.
Примечание
ORIGIN := 1 — установка нумерации элементов матриц с единицы.
Augment – функция объединения матриц.
Rref – функция прямого и обратного хода Гаусса.
Submatrix – функция выделения подматрицы с указанными диапазонами из большей матрицы.
Решение системы линейных алгебраических уравнений по формулам Крамера:
1. Вводите матрицу системы и матрицу-столбец правых частей.
2. Вычислите определитель матрицы системы. Если определитель отличен от нуля, то система имеет единственное решение.
3. Вычислите определители матриц, полученных заменой соответствующего столбца столбцом правых частей.
4. Найдите решение системы по формулам Крамера.
Пример
Решение системы линейных алгебраических уравнений матричным методом:
1. Введите матрицу системы и матрицу-столбец правых частей.
2. Определите решение системы по формуле X = A-1B.
Пример
Решение неоднородной системы линейных алгебраических уравнений:
1. Введите матрицу системы и расширенную матрицу системы для правой части.
2. Вычислите ранги основной матрицы и ранги расширенной матрицы системы.
3. Приведите расширенную матрицу совместной системы к ступенчатому виду.
4. Определите базисные и свободные переменные.
5. Запишите эквивалентную систему и разрешите ее относительно базисных переменных.
6. Запишите общее решение системы.
7. Найдите частное решение системы.
Пример
Общее и частное решение системы:
Определение функций
Функция в MathCad должна иметь имя и параметры, перечисленные в скобках. Для получения значения функции в точке, вводится имя функции, указывается в скобках значение аргумента и вводится знак равенства.
Пример
Для ввода составных функций можно пользоваться кнопками панели программирования.
Пример
Построение графиков функций
Для построения графиков функции используется объект X-Y Plot. В помеченной позиции возле оси абсцисс вводится имя аргумента, а в позиции возле оси ординат – имя функции. Если нужно построить одновременно графики нескольких функций, вводятся их имена через запятую. Вместо имени функции можно ввести выражение для ее вычисления. Параметры изображения проще всего изменить, щелкнув дважды по полю графика и установив настройки в соответствующих окнах диалога.
Пример
Графики функций, заданных в параметрической форме, строятся аналогично. Отличие состоит в том, что позициях аргумента и функции вводятся выражения или имена соответствующих функций параметра.
Пример
Вычисление пределов
Три нижние кнопки панели Calculus(Вычисление) предназначены для вычисления пределов. Необходимо также пользоваться первой кнопкой со стрелкой на панели символьных операций Symbolic(Символьный).
Пример
Исследование функций
Порядок исследования:
1. Определите функцию f(x) и постройте ее график.
2. Найдите точку пересечения с осью ординат, вычислив f(0). Сравните с данными на графике.
3. Найдите точки пересечения с осью абсцисс, решив уравнение f(x) = 0. Сравните с данными на графике.
4. Проверить четность (нечетность, периодичность) функции.
5. Найдите точки разрыва функции, вычислите соответствующие односторонние пределы, запишите уравнения вертикальных асимптот. Сравните с данными на графике.
Сравните с данными на графике.
6. Вычислите пределы для определения вертикальных и наклонных асимптот. Изобразите наклонные асимптоты на графике.
7. Найдите нули производной, решив уравнение F’(x) = 0.
8. Вычислите и запишите координаты точек экстремума.
9. Постройте график второй производной.
10. Укажите тип точек экстремума (максимум/минимум).
11. Найдите нули второй производной, решив уравнение F’’(x) = 0.
12. Вычислите и запишите координаты точек перегиба.
13. Опишите интервалы выпуклости и вогнутости функции
Пример
Примечание
Функция root(F(X), X) решает уравнение F(X) = 0 относительно переменной X.
Вычисление интегралов
Для того чтобы вычислить неопределенный или определенный интеграл, необходимо воспользоваться соответствующими кнопками на панели Calculus(Исчисление).
Пример
Числовые ряды
Сходимость радов проверяется достаточно легко с помощью кнопки символьных вычислений.
Пример
| < Предыдущая |
|---|
Метод 1 — исключение Гаусса
Здесь мы формируем расширенную матрицу коэффициентов уравнения.
#( (1, -2, 1, |, -2), (2, -3, 2, |, 2), (4, -8, 5, |, -5) )#
Теперь мы можем выполнять элементарные операции со строками с целью получения начальных нулей в прогрессивных строках:
#( (1, -2, 1, |, -2), (2, -3, 2, |, 2), (4, -8, 5, |, -5) ) stackrel(R_2-2R_1 rarr R_2)(rarr) ( (1, -2, 1, |, -2), (0, 1, 0, |, 6), (4, -8, 5, |, -5) )#
#( (1, -2, 1, |, -2), (0, 1, 0, |, 6), (4, -8, 5, |, -5) ) stackrel(R_3-4R_1 rarr R_3)(rarr) ( (1, -2, 1, |, -2), (0, 1, 0, |, 6), (0, 0, 1, |, 3) )#
Теперь мы можем использовать обратную замену для получения значений #x#, #y# и #z#:
Ряд №3 => z=3 #
Ряд №2 => y = 6 #
Ряд №1 => x-2y+z=-2 ##:.
х-12+3=-2 => х= 7 #
Таким образом, мы имеем единственное решение:
# х=7, у=6, z=3 #
Метод 2. Инверсия матрицы
Матрица #bb(A)# обратима тогда и только тогда, когда ее определитель #abs(bb(A)) != 0#. Есть несколько способов инвертировать матрицу, наклонив поиск сопряженной, редукции строк или даже калькулятор. Я буду использовать сопряженный метод, состоящий из нескольких шагов;
- Вычисление матрицы миноров,
- Сформируйте матрицу кофакторов, #cof(bb(A))#
- Сформируйте сопряженную матрицу, #adj(bb(A))# 9-1#
В какой-то момент нам нужно вычислить #abs(bb(A))# или #det(bb(A))#, и это также можно использовать для проверки того, действительно ли матрица обратима, поэтому я предпочитаю делать это первое;
# bb(A) = ((1,-2,1), (2,-3,2), (4,-8,5)) #
Если мы расширим первую строку и «вычеркнем» строку и столбец, чтобы сформировать меньший определитель и чередующиеся знаки, мы получим;
# abs(bb(A)) = +(1)|(-3, 2), (-8, 5)| -(-2) |(2, 2), (4, 5)| +(1)|(2, -3), (4, -8)| №
# \ \ \ \ \ = {(-3)(5)-(-8)(2)} +2{(2)(5)-(4)(2)} +{(2)(-8 )-(4)(-3)} #
# \ \ \ \ \ = {-15+16} +{10-8}+{-16+12} #
# \ \ \ \ \ = 1 +4 -4#
#\\\\\=1#
Поскольку #abs(bb(A)) !=0 => bb(A) # обратимо, поэтому теперь мы вычисляем матрицу миноров, систематически перебирая каждый элемент в матрице и «вычеркивая» эту строку и столбцы и сформировать определитель остальных элементов следующим образом:
#»несовершеннолетние»(bb(A))=( ( |(-3, 2), (-8, 5)|, |(2, 2), (4, 5)|, |(2, -3), (4, -8)| ), ( |(-2, 1), (-8, 5)|, |(1, 1), (4, 5)|, |(1, -2), (4, -8)| ), ( |(-2, 1), (-3, 2)|, |(1, 1), (2, 2)|, |(1, -2), (2, -3)| ) )#
#\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \= ( (-15+16, 10-8, -16+12), (-10+8, 5-4, -8+ 8), (-4+3, 2-2, -3+4))#
#\ \\\\\\\\\\\\\\\= ((1, 2, -4), (-2, 1, 0), (-1, 0, 1))#
Теперь мы формируем матрицу кофакторов #cof(A)#, взяв вышеуказанную матрицу миноров и применив матрицу чередующихся знаков, как в
# ( (+, -, +), (-, +, -), (+, -, +))#
Где мы меняем знак тех элементов со знаком минус, чтобы получить; 9(-1) bb(ul b) # . …. #[звездочка]#
…. #[звездочка]#
#:. ( (х), (у), (г) ) = ( (1, 2, -1), (-2, 1, 0), (-4, 0, 1) ) ( (-2), (2 ), (-5) ) #
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = ( ((1)(-2)+(2)(2)+(-1)(-5 )), ((-2)(-2)+(1)(2)+(0)(2)), ((-4)(-2)+(0)(2)+(1)(- 5)) ) #
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = ( (-2+4+5), (4+2), (8-5) ) #
# \ \ \ \ \ \ \ \ \ \ \ \ \ \ = ( (7), (6), (3) ) #
Таким образом, мы имеем единственное решение:
# х=7, у=6, z=3 #
Метод 3. Теорема Кэли Гамильтона
Теорема CH утверждает, что любая квадратная матрица удовлетворяет своему собственному характеристическому уравнению. Мы можем использовать это свойство, чтобы найти обратное.
У нас есть:
# bb(A) = ((1,-2,1), (2,-3,2), (4,-8,5)) #
Таким образом, характеристическое уравнение имеет вид:
2-3bb(A) +3bb(I) ## abs(bb(A) — lamdabb(I)) = 0 => abs( (1- лямбда,-2,1), (2,-3- лямбда,2), (4,-8,5- лямда) ) = 0#
# \ \ \ \ \ \ \ \ = ( (1,-4,2), (4,-11,6), (8,-24,13) )-3( (1,-2,1), (2,-3,2), (4,-8,5))+3( (1,0,0), (0,1,0), (0,0,1) ) #
# \ \ \ \ \ \ \ = ( (1,-4,2), (4,-11,6), (8,-24,13) )-( (3,-6,3), (6,-9,6), (12,-24,15) )+( (3,0,0), (0,3,0), (0,0,3)) #
# \ \ \ \ \ \ \ \ = ( (1-3+3,-4+6,2-3), (4-6,-11+9+3,6-6), (8-12 ,-24+24,13-15+3) ) #
# \ \ \ \ \ \ \ \ = ( (1,-2,-1), (-2,1,0), (-4,0,1) ) #, как указано выше, и мы продолжаем с #[ звездочка]# в методе 2.
как найти y, используя правило Крамера с этими уравнениями? x+y+z=15 x+2y+3z=34 x+3y+4z=49 с использованием графического расчета?
Ваш ответ
1 Ответ
x=0
y=11
z=4
ответил по Расчетная мощность Пользователь 1-го уровня (740 баллов)Похожие вопросы
1 ответ
Решите эти уравнения с помощью матриц без калькулятора. x=y=z=6, 2x=y-4z=-15, 5x-3y+z=-10
спросил 30 января 2013 г. по алгебре 2 Ответы по анонимный | 617 просмотров
- решение систем уравнений
1 ответ
найти упорядоченную тройку этих уравнений x-2y+2z=-2, 2x+3y-z=0, 3x+2y+3z=-15
спросил 11 декабря 2012 г. по алгебре 2 Ответы по анонимный | 1.2k просмотров
- решение уравнений
1 ответ
Найдите упорядоченную тройку этих уравнений 2x+5y-3z=-5, 3x+2y+7z=15, 5x-4y+6z=34
спросил
14 января 2014 г. по алгебре 2 Ответы
по
анонимный
| 1.0k просмотров
по алгебре 2 Ответы
по
анонимный
| 1.0k просмотров
- решение систем уравнений
- систем уравнений с тремя переменными
- алгебра 2 помощь
1 ответ
решить трехстороннее уравнение с z. 1:3x-2y+2z=30 2:-x+3y-4z=-33 3:2x-4y+3z=42
спросил 24 сентября 2012 г. по алгебре 2 Ответы по анонимный | 902 просмотра
- системы уравнений с тремя переменными
2 ответа
2x+4y+3z=-11 4x-3y+4z=34 x+2y-4z=-33 решить систему
спросил 16 сентября 2014 г. по алгебре 1 ответы по анонимный | 610 просмотров
- системы уравнений с тремя переменными
1 ответ
решить по правилу Крамера x + y + z = 0, 2 x — y — 4 z = 15, x — 2 y — z = 7
спросил 18 апр. 2014 г. по алгебре 2 Ответы по анонимный | 499 просмотров
- правило Крамера
1 ответ
Решить x,y,z (6y+4z=-18), (3x+3y=9),(2x-3z+12), используя матрицы
спросил
11 января 2013 г.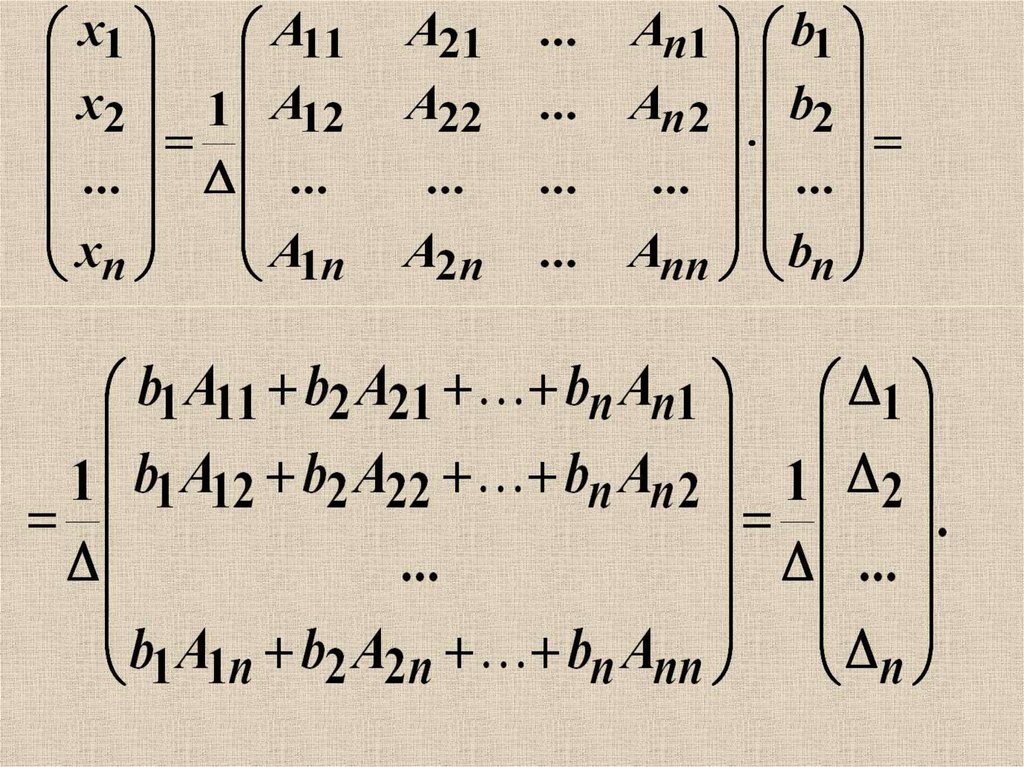 в исчислении ответы
по
анонимный
| 631 просмотр
в исчислении ответы
по
анонимный
| 631 просмотр
- системы уравнений с тремя переменными
1 ответ
Решите 2x + 3y + z = 12 с помощью матриц. 3x + y – 4z = -5, -4x – y + 3z = 6
спросил 19 февраля 2016 г. по алгебре 1 ответы по анонимный | 1.4k просмотров
- матрицы
- решение систем уравнений
1 ответ
Как решить линейную систему по правилу Крамера на графическом калькуляторе?
спросил 21 ноября 2011 г. по алгебре 2 Ответы по анонимный | 709 просмотров
- помощь с графическим калькулятором
- правило Крамера
1 ответ
решить 2x-y+z, x+y-z,3x-2y+z по правилу Крамера?
спросил 22 сентября 2013 г. по алгебре 1 ответы по Пушпарадж К. | 569 просмотров
- правило Крамера
- решение уравнений
1 ответ
решить уравнения используя (a) матричный метод (b) правило Крамера
спросил
21 февраля 2014 г.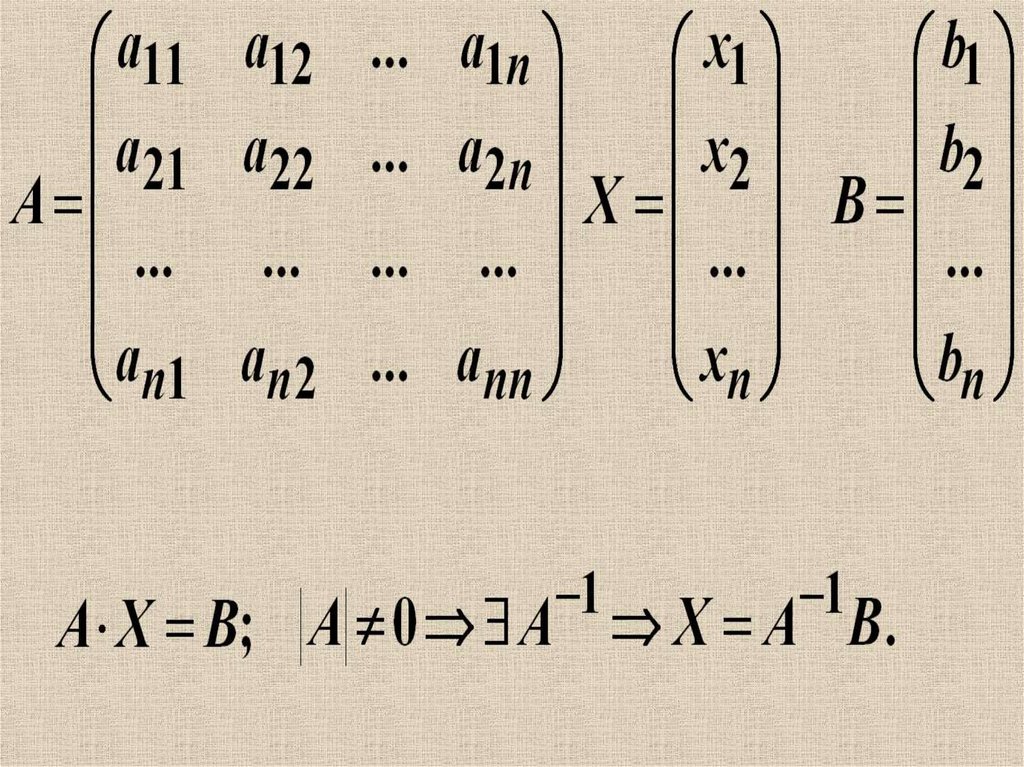 в ответы по геометрии
по
Канабеса
Пользователь 1-го уровня
(400 баллов)
| 500 просмотров
в ответы по геометрии
по
Канабеса
Пользователь 1-го уровня
(400 баллов)
| 500 просмотров
- решение уравнений
- правило Крамера
1 ответ
решить систему уравнений методом сложения 3x+4y+z=-27 5x-3y-z=14 4x+y+3z=- 21
спросил 24 апр. 2012 г. по алгебре 2 Ответы по анонимный | 625 просмотров
- метод сложения
1 ответ
какое решение системы? использовать исключение:(x+y-3Z=8)(-x-2y+z=4)(-x+y+4z=7)
спросил 13 января 2013 г. по алгебре 2 Ответы по анонимный | 528 просмотров
- системы уравнений с тремя переменными
1 ответ
Метод исключения решить 2x-y+z=1 x+2y-4z=3 4x+3y-7z=-8
спросил 10 декабря 2013 г. по алгебре 2 Ответы по Зои | 616 просмотров
- метод исключения
1 ответ
Использование исключения решить 2x-y+z=1 x+2y-4z=3 4x+3y-7z=-8
спросил
10 декабря 2013 г. по алгебре 2 Ответы
по
Зои
| 826 просмотров
по алгебре 2 Ответы
по
Зои
| 826 просмотров
- метод устранения
1 ответ
как решить: -3x-2y+4z=-15, 2x+5y-3z=3, 4x-y+7z
спросил 13 ноября 2012 г. по алгебре 1 ответы по анонимный | 515 просмотров
- системы уравнений с тремя переменными
- метод исключения
1 ответ заказал тройной
спросил 31 октября 2011 г. по алгебре 2 Ответы по анонимный | 986 просмотров
- решение уравнений
1 ответ
Каково решение приведенной ниже системы линейных уравнений? 4x+3y +2z = 1 5x-2y — z = -1 x-4y + 3z = -7
спросил 24 сент. 2021 г. в других математических темах по анонимный | 196 просмотров
1 ответ
Решить {3x-2y+2z=30, -x+3y-4z=-33, 2x-4y+3z=42}
вопрос 29 октября 2013 г. по алгебре 2 Ответы по анонимный | 497 просмотров
- решение уравнений
- набор решений
1 ответ
решить систему: 5x-10y+4z=-73; -х+2у-3г=19; 4x-3y=5z=-42
спросил
12 сентября 2012 г. по алгебре 2 Ответы
по
анонимный
| 598 просмотров
по алгебре 2 Ответы
по
анонимный
| 598 просмотров
- Системы уравнений, содержащих три переменных
Имя| Назг | . | Дата | Rating | Description | (Parent Dir) | folder | | Up to TI-83/84 Plus BASIC Math Programs | acommag.zip | 1k | 02-08-02 | | adjoint.zip | 1k | 13-09-17 | Присоединенная программа5. |  Просто введите матрицу на главном экране (она резервирует место для матриц A, B и C), а программа сделает все остальное. Наслаждаться! Просто введите матрицу на главном экране (она резервирует место для матриц A, B и C), а программа сделает все остальное. Наслаждаться! ADOTB.ZIP | 1K | 02-03-15 | ADOTBAR | . между 2 векторами, a.b, mod векторов, вектор разрешает: (a perp к b, a в направлении (параллельно) b, b perp к a, b в направлении (параллельно) a) и ALL in surd ответы. | Agreatmatrixprog.zip | 1K | 05-06-04 | Matrix, Alse Salefate, Alse Sale, Alse Alnabe 9058, Alse Sale, Alse Alt Leartes 9058, Alse Alt Leartes 9058, Alse Alt Legle 9048, | , Alse Salefate, Alse Alt Leartes 9048,. Программа AllSimultary. |  zip zip 1K | 10-03-02 | Smote Smoption . достаточно уравнений, чтобы его можно было решить математически, и что у вас достаточно памяти. Просто введите коэффициенты по горизонтали, начиная с первого уравнения, и константы по вертикали, начиная сверху. Ответ приходит в виде матрицы с первым неизвестным наверху. Всего 214 байт. | AngleWeEwneVectors2.zip | 1K | 13-10-01 | Angel Might vect 2 | . но он также выводит синус, косинус и тангенс угла. Наслаждаться! | anglebetweenvectors.zip0485 | Эта программа вычисляет угол между векторами в радианном режиме. Просто введите векторы в виде списков, а программа сделает все остальное.  Наслаждаться! Наслаждаться! aigmentedmatrices.zip | 1K | 03-11-18 | Aupmented. Ответ показан так, как он будет выглядеть, если вы выполните работу! Пример: [[1 0 -1] [0 1 2 ]] | AutoDOT.ZIP | 1K | 04-03-07 | DOT Product, Autodt Product | . Это полезно для выполнения матричных умножений, когда вам нужно найти много скалярных произведений. Пожалуйста, прочтите readme для получения инструкций, иначе вы, скорее всего, получите сообщение об ошибке. | autox.zip | 1k | 05-09-29 | Перекрестное произведение | Очень простая программа, позволяющая очень быстро вычислить перекрестное произведение двух векторов.  Пожалуйста, прочитайте readme или вы, вероятно, получите ошибку Пожалуйста, прочитайте readme или вы, вероятно, получите ошибку Basictoolbox2 дела с матрицами. Если вы хотите добавить к нему, пожалуйста, не стесняйтесь. | . Введите требуемые векторы, и программа сообщит вам необходимые коэффициенты. Наслаждаться! | bestалгебра1.zip | 2k | 12-03-22 | Лучшая программа v2.1! | Наконец-то выпущена версия 2.1 программы The Best Algebra 1. В соответствии с просьбой я обновил ключ учителя, чтобы он не содержал ошибок. Также добавлено бортовое руководство по эксплуатации. В этой версии используется совершенно новый формат с графическими клавишами и привлекательным титульным экраном (как показано на скриншоте) вместо скучного старого меню. Он выполняет те же математические функции, которые были улучшены, а также включает такие функции, как обновленный ключ учителя и файл «прочитай меня».  Эта программа не только полезна для всего в Алгебре 1, но также может быть использована для большинства тем Алгебры 2. Пожалуйста, напишите мне о любых ошибках или предложениях на мой адрес электронной почты в разделе «Прочитай меня», и я буду использовать их в следующей версии. Обязательно просмотрите файл read me, чтобы узнать, как использовать все возможности этой программы. ПОЖАЛУЙСТА, ОЦЕНИТЕ И ПРОСМОТРИТЕ ЭТУ ПРОГРАММУ, СПАСИБО!! Эта программа не только полезна для всего в Алгебре 1, но также может быть использована для большинства тем Алгебры 2. Пожалуйста, напишите мне о любых ошибках или предложениях на мой адрес электронной почты в разделе «Прочитай меня», и я буду использовать их в следующей версии. Обязательно просмотрите файл read me, чтобы узнать, как использовать все возможности этой программы. ПОЖАЛУЙСТА, ОЦЕНИТЕ И ПРОСМОТРИТЕ ЭТУ ПРОГРАММУ, СПАСИБО!! blockmatrix.zip | 2k | 15-03-07 | Block Matrix | This file contains three programs concerning block matrices, including LDU decomposition, inverse and Woodbury’s formula. Наслаждаться! Chouleskyfactorization.zip | 1K | 11-07-15 | | . |  cofactorjl.zip | 1k | 13-09-17 | Кофактор5. Просто введите матрицу на главном экране (матрицы A, B и C очищаются для ввода во время работы программы) и сообщите программе, какую строку и столбец вы хотите удалить. Программа производит подматрицу, минор и кофактор. Наслаждаться! | cofactor.zip | 1k | 03-10-05 | Cofactor | Эта программа позволяет вычислить матрицу кофакторов куалькье матрицу квадрада (в единственном числе). Collatz.zip | 1K | 15-01-19 | Collatz Methods 4011. |  положительные записи. Это итерационный метод. Отлично подходит для линейной алгебры или численного анализа. Наслаждаться! положительные записи. Это итерационный метод. Отлично подходит для линейной алгебры или численного анализа. Наслаждаться!. В основном он закончен, но я могу добавить сложные итерации в другой версии0006 Эта программа вычисляет число обусловленности матрицы. | Cramer3.zip | 1K | 10-03-04 | Ruder ATSERER ATS. Он имеет всего 97 байт, поэтому не займет много места на вашем калькуляторе. | cramersrule_jon.zip | 1k | 11-03-09 | Правило Крамера | Эта программа может решить систему линейных или плоских уравнений с использованием правила Крамера. Cramer. |  zip zip 31K | 11-10-05 | . Ax + By = C, Dx + Ey = F Программа для калькулятора TI-83 Джонатан Л. Московичи Используя материал из #Weisstein, Eric W. «Правило Крамера». Из MathWorld — веб-ресурса Wolfram. http://mathworld.wolfram.com/CramersRule.html | Crosprod.zip | 1K | 09-09-30 | , Cross Product 3D , | . z2) и получить результат векторного векторного произведения. | crossproduct.zip | 1k | 11-11-02 | | Пользователь вводит компоненты вектора перекрестного произведения. Наслаждаться! DefinetyMatrix. |  ZIP ZIP 1K | 13-11-23 | Определенность. или бессрочный. Пользователь просто вводит данные в матрицу, а программа определяет результат. Это также создаст список определителей подматриц. Отлично подходит для линейной алгебры или численного анализа. Наслаждаться! | DET.ZIP | 1K | 00-08-31 | DEGRINANTS v1.2 9040 | DEGRINANTS V1.2 9046 9066 9666 9066 9666. уравнение второго и третьего порядка и находит определители. Программа *update* на 90 байт больше, чем V1.11, но в целом экономит около 400 байт ОЗУ. | easyvect.zip | 7k | 04-05-17 | Easy Vectors | Это очень сложная программа для работы с векторами.  Он может выполнять расчеты 2D, 3D и ND векторов. Функции включают скалярное произведение, векторное произведение, преобразование между полярными и прямоугольными, нахождение углов между двумя векторами, нахождение единичных векторов и многое другое. В этом обновлении исправлена ошибка Lbl. Он может выполнять расчеты 2D, 3D и ND векторов. Функции включают скалярное произведение, векторное произведение, преобразование между полярными и прямоугольными, нахождение углов между двумя векторами, нахождение единичных векторов и многое другое. В этом обновлении исправлена ошибка Lbl. EIGEN84.ZIP | 4K | 11-11-25 | EIGEN8490 | . [А] матрица. За один прогон можно получить только одно собственное значение и соответствующий ему собственный вектор, поэтому необходимы повторные выполнения программы, если необходимо вычислить все собственные значения/собственные векторы. | Eigenvalues.zip | 1K | 14-04-17 | Eigenval | Eigenval | . |  Он также построит характеристический полином. Отлично подходит для начинающих студентов линейной алгебры. Наслаждаться! Он также построит характеристический полином. Отлично подходит для начинающих студентов линейной алгебры. Наслаждаться! Эйген.zip | 1K | 08-12-11 | eigen v1.00 | . Эта программа (если захочет) найдет собственные значения любой матрицы 2×2 или 3×3, помещенной в [A]. Он использует метод итерации, который аппроксимирует доминирующее (наибольшую величину) собственное значение для введенной матрицы. Проблема в том, что он использует случайную матрицу для предсказания таких значений, которая иногда оказывается с большим количеством ошибок, например, ошибка деления на ноль. Ну просто посмотрите сами и, пожалуйста, оцените. Если у вас есть какие-либо вопросы, не стесняйтесь, пишите мне по электронной почте. | Frobeniousnorm.zip | 1K | 12-02-17 | FROBENIL. |  Наслаждаться! Наслаждаться! gershgorindiscs.zip | 1k | 13-05-20 | Gershgorin dics | This program will compute the center and radius of Gershgorin discs used to localize eigenvalues for a matrix. Центр следует интерпретировать как место на Комплексном Плане. Вы можете использовать строки или столбцы для создания дисков. Также появится график дисков. Наслаждаться! грамммианматрикс. Наслаждаться! | Грамшмидт. | 1K | 14-04-14 | | . Пользователь вводит матрицу, и программа выводит ортонормальные векторы в столбцах матрицы. Отлично подходит для студентов линейной алгебры. | 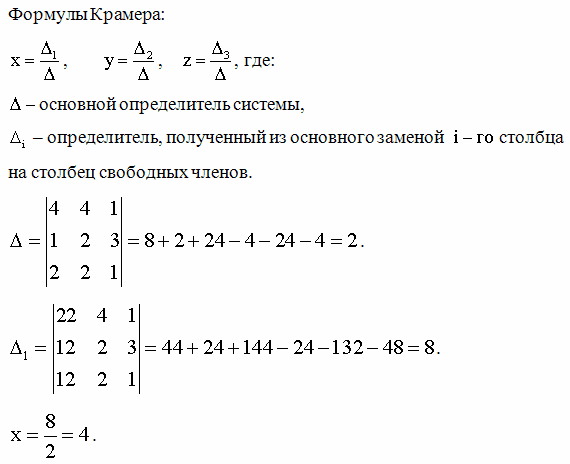 Наслаждаться! Наслаждаться! Graphtheorybasics.zip | 1K | 17-09-12 | Граф. эксцентриситет, радиус и диаметр; количество деревьев и информация о степенях. Пользователь просто предоставляет матрицу смежности. Пожалуйста, прочтите сопроводительную документацию для получения подробной информации. Наслаждаться! | inversecomplexmatrix.zip | 1k | 14-11-11 | Эта программа вычислит комплексную матрицу6. Наслаждаться! | Invmatr.zip | 1K | 12-04-19 | inverse of Matrix | inverse of Matrix | с Matrix | с Matrix | с Matrix | с Matrix | . |  матрицы с помощью сопряженного. матрицы с помощью сопряженного. IPMatrix.ZIP | 1K | 13-10-01 | IPMATRIX | . Наслаждаться! | jacobimethod.zip | 1K | 13-06-10 | jacobi Methodious . Пользователь вводит матрицу, правую часть, начальное предположение, количество итераций и допуск. Отлично подходит для классов численного анализа или линейной алгебры. Наслаждаться! | Linearcombination.zip | 1K | . Просто введите набор векторов в виде столбцов в матрицу и вектор, который вы хотите переписать, в виде списка. Программа создаст матрицу после RREF и опубликует решение. |  Наслаждаться! Наслаждаться! linearsystems.zip | 1k | 12-07-11 | Linear Systems | Решение системы уравнений. Системы типов как в учебниках. LS4.ZIP | 334K | 08-08-24 | SELVERGATION 4.0485. Использует интуитивно понятный процесс ввода уравнения. Позволяет пользователям использовать любые переменные A-Z или тета. См. Linear System Solver 4.doc для получения дополнительной информации о функциях и системных требованиях. | ludecomposition.zip | 1k | 13-06-10 | LU Decomposition 4 Программа для 65- LU Decomposition 90 Он будет размещать единицы вдоль главной диагонали нижней треугольной матрицы (по сути, это разложение Дулиттла). |  Пользователь вводит матрицу и все. Программа выведет нижнюю треугольную матрицу, а затем верхнюю треугольную матрицу. Отлично подходит для занятий по линейной алгебре или численному анализу. Наслаждаться! Пользователь вводит матрицу и все. Программа выведет нижнюю треугольную матрицу, а затем верхнюю треугольную матрицу. Отлично подходит для занятий по линейной алгебре или численному анализу. Наслаждаться! Ludecomp.zip | 1K | 10-03-14 | LU DECOPOSION .GIRIER. | markov1.zip | 1k | 12-01-25 | Markov 1 | This program will produce a steady-state vector for a transition matrix common in Markov chain problems. Наслаждаться! markov2.zip | 1k | 12-01-28 | Марков 2 9048 Эта программа работает с обычными системами Маркова 5 9048. |  Он создаст матрицы или список, отвечающий на вопросы: 1) сколько временных шагов от состояния i до состояния j ожидается до поглощения, 2) каково ожидаемое общее количество шагов от состояния i до поглощения и 3) какова вероятность окончания в каждом состоянии поглощения. Наслаждаться! Он создаст матрицы или список, отвечающий на вопросы: 1) сколько временных шагов от состояния i до состояния j ожидается до поглощения, 2) каково ожидаемое общее количество шагов от состояния i до поглощения и 3) какова вероятность окончания в каждом состоянии поглощения. Наслаждаться! Маркован3.ZIP | 1K | 12-01-28 | Markov 3 | . Пользователь вводит матрицу перехода, начальное распределение и количество шагов в системе. Программа сохранит полученное распределение в матрице [C] для просмотра. Наслаждаться! matmnor3.zip | 1k | 02-03-28 | Младшие матрицы (3×3) | Эта программа покажет вам, как работать с младшими матрицами, чтобы найти определитель.  MATMNOR4.ZIP | 1K | 02-01-16 | MATRIX MINORS MATIRIX 4X45. найти определитель. | MATRICES.ZIP | 1K | 02-03-28 | Easy Erasy 90 | . умножай и добавляй…) в удобной для пользователя среде. | matrix2.zip | 1k | 15-04-25 | Matrix 2 | This folder contains two programs, one for computing determinants of rectangular matrices (see documentation this is not a опечатка) и один для вычисления произведения Адамара. Наслаждаться! MATRIXMANIP. |  ZIP ZIP 1K | 04-01-08 | MATRIX . что ваш ответ неправильный из-за НИЧЕГО отрицательного знака или чего-то еще? Эта программа сделает всю математику, которую вы укажете правильно, тем самым исключив арифметические ошибки! | matrixrowdeletion.zip | 1k | 14-11-14 | DelRow Matrix | довольно простой. Вам нужно знать операции, но вам не нужны все эти техно-вещи, они просто делают их очень простыми.Эта программа удалит строку матрицы. Наслаждаться! Эта программа делает матрицы matrixtype.zip | 1k | 14-04-20 | Тип матрицы | Эту программу можно использовать для определения типа используемой матрицы.  Он скажет вам, есть ли у вас симметричная, кососимметричная, идемпотентная, обратимая, ортогональная или нормальная матрица. Отлично подходит для студентов линейной алгебры или студентов теории матриц. Наслаждаться! Он скажет вам, есть ли у вас симметричная, кососимметричная, идемпотентная, обратимая, ортогональная или нормальная матрица. Отлично подходит для студентов линейной алгебры или студентов теории матриц. Наслаждаться! moorepenroseinverse.zip | 1k | 14-03-09 | Обратная Мура-Пенроуза | Эта программа вычисляет левую или правую обратную Мура-Пенроуза матрицы. Mtrxops.zip | 1K | 14-08-06 | MTRXPS | 9066. | 9066. 9066 9066. | . | . |  Он упрощает работу с матрицами, отображая операции с матрицами в выбираемом пользователем меню и запрашивая у пользователя необходимые входные данные для каждой операции. Далее, если пользователь допустил ошибку, есть возможность восстановить предыдущую матрицу. MTRXOPS требует, чтобы пользователь ввел матрицу для решения в матрицу [A] перед запуском MTRXOPS. MTRXOPS использует матрицу [B] в качестве матрицы восстановления. Пожалуйста, отправьте электронное письмо, если вы заметили какие-либо ошибки. Он упрощает работу с матрицами, отображая операции с матрицами в выбираемом пользователем меню и запрашивая у пользователя необходимые входные данные для каждой операции. Далее, если пользователь допустил ошибку, есть возможность восстановить предыдущую матрицу. MTRXOPS требует, чтобы пользователь ввел матрицу для решения в матрицу [A] перед запуском MTRXOPS. MTRXOPS использует матрицу [B] в качестве матрицы восстановления. Пожалуйста, отправьте электронное письмо, если вы заметили какие-либо ошибки. NEOMATRIX.ZIP | 1K | 02-09-05 | NEO MATRIX | 902. teacher asked me to make him this so i did and here it is updates soon | nullfind.zip | 15k | 05-03-07 | Null Space (Kernel) Finder | finds the null space (kernel) if a matrix orthogonalprojection. |  zip zip 1k | 13-09-26 | Orthogonal Projection | This program will compute the orthogonal projection of a вектор U на вектор V. Это также даст U — Proj_v(U). Просто введите векторы в виде списка, а программа сделает все остальное. Наслаждаться! ортогональное подпространство.zip | 1k | 15-01-11 | Ортогональное подпространство | Эта программа будет информировать пользователя, если остовный набор ортогонален другому остовному набору. Отлично подходит для вводного линейной алгебры. Наслаждаться! Это внешнее произведение двух векторов Введите два вектора в виде списков, и программа сохранит результат в матрице [A]. Наслаждаться! ParareAandvolume. |  zip zip 1K | 13-10-04 | Pare Area и VolameLEGE AREALENGERELENGERELENGERELENGERED ALEAREL AREALENGEL AREALENGEL AREALENGELENGELENGEL AREALENGERELENGERELENGERELENGERELENGERELENGERELENGERELENGEL AREA. нужные векторы. Наслаждаться! | Pivot.zip | 1K | 00-10-01 | Simale Simale Simale Biveu. | polyfit.zip | 1k | 13-10-04 | PolyFit | 5 Эта программа будет соответствовать набору данных PolyFit5. Наслаждаться! PositionVector.ZIP | 1K | 12-02-21 | позиционирует | позиционирование 9 | позиционирование | позиционирование | позиционирование | . |  powermethod.zip | 16k | 11-07-27 | Степенной метод | Эта программа использует метод наибольшего квадрата для определения собственного значения матрицы. Пользователь вводит матрицу [A] и начальное предположение в [B], дает максимальное количество итераций и допуск (это итеративный процесс). Выход (в случае успеха) будет наибольшим собственным значением (приблизительно) и соответствующим собственным вектором (приблизительно). Наслаждаться! qrfactorization.zip | 1k | 14-04-14 | QR Factorization is small QR Factorization for Sch. Наслаждаться! | qrhouseholder.zip | 1K | 13-11-12 | QR HEATERSER 9048 4. |  SMIASTIASTIASTIASTIARIASTIASTIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIARIASTIARIASTIARIASTIARIAST. Просто введите матрицу, а программа сделает все остальное. Наслаждаться! SMIASTIASTIASTIASTIARIASTIASTIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIASTIARIASTIARIASTIARIASTIARIASTIARIAST. Просто введите матрицу, а программа сделает все остальное. Наслаждаться! QuickMatrix.zip | 1K | 03-11-19 | Quick Matrix Solver | Quick Matrix | . вместо того, чтобы нажимать 2-ю матрицу, вправо, вниз, вниз, вниз и т. еще одно простое меню, оно помогает мне летать прямо по матрицам, но при этом легко показывает мою работу, оно даже показывает шаги (*row+(3,[A],3,2)) | Rankofmatrix.ZIP | 1K | 13-10-13 | Рейн-рейтинг и MATRIX | RINGE RINGE и RINLISE THERISO SOLLINITION и RINLISE THERISO SOLLINITIOR и STUMILIS SOLLINITIOR и SOLLISIOR SOLLINITIOR 9066. |  матрица. Просто введите в матрицу, а программа сделает все остальное. Наслаждаться! матрица. Просто введите в матрицу, а программа сделает все остальное. Наслаждаться! richit.zip | 1k | 18-10-02 | Ричардсон Итерация | Эта программа использует итерацию Ричардсона для решения системы линейных уравнений. Аналогичен Якоби и Гауссу-Зейделю, за исключением того, что в качестве матрицы разделения используется матрица идентичности. Отлично подходит для численной линейной алгебры. Наслаждаться! Rowandcolumnbasis.zip | 1K | 13-10-26 | ROW COLLAD 9048. сделать все остальное. Отлично подходит для начинающих студентов линейной алгебры. Наслаждаться! | ROWECHLN.ZIP | 1K | 04-05-12 | ROW ECHEL SYSTERON. |  уравнения? Вы когда-нибудь работали с системами, которые могут иметь до 8 переменных и 99 уравнений? Если да, то вам нужен Row Echelon System Solver v1.2. Эта программа предоставляет простой интерфейс для ввода уравнений, преобразует их в форму Row Echelon и решает полученную систему. Решения отображаются в формате уравнение/ответ. Двери CS v4.0/v5.0 оптимизированы; посмотрите скриншоты! уравнения? Вы когда-нибудь работали с системами, которые могут иметь до 8 переменных и 99 уравнений? Если да, то вам нужен Row Echelon System Solver v1.2. Эта программа предоставляет простой интерфейс для ввода уравнений, преобразует их в форму Row Echelon и решает полученную систему. Решения отображаются в формате уравнение/ответ. Двери CS v4.0/v5.0 оптимизированы; посмотрите скриншоты! ROWOPS.ZIP | 1K | 07-02-18 | ROW OPS . Использование | . Поворот, умножение и т.д. Действительно полезно для конечной математики. simplex.zip | 1k | 00-10-01 | Simplex Tableau Maximizer | Input the initial simplex tableau and this program will perform all pivot operations, and display the maximum value целевой функции, а также итоговой таблицы.  SolvVect.zip | 1K | 09-04-04 | 2 и 3-х годов. 2-мерный вектор и движущийся. Он также может определить угол между двумя векторами, 2-х или 3-х мерными, и указать, пересекаются ли они, параллельны или наклонены. Также имеет дополнительную функцию решателя величины. На стадии разработки для создания дополнения, которое решает точку наибольшего сближения между двумя движущимися векторами. | SOR.ZIP | 1K | 13-06-18 | SOR | . Эта метод Solving. Отлично подходит для численного анализа или численной линейной алгебры. Наслаждаться! SPAN.ZIP | 1K | 13-10-04 | SPAN | IT SPAP SPAN OR.  Пользователь вводит векторы, как указано, и программа сообщит вам, пересекаются ли векторы или нет. Отлично подходит для вводных классов линейной алгебры. Наслаждаться! Пользователь вводит векторы, как указано, и программа сообщит вам, пересекаются ли векторы или нет. Отлично подходит для вводных классов линейной алгебры. Наслаждаться! STEEPESTDECTENCENCESTS.ZIP | 1K | 13-12-12 | STEEPEST LISES | . Наслаждаться! | SVDEC.ZIP | 90K | 05-06-28 | DEMOPTION | . матрица размера m на n. Используемый алгоритм представляет собой небольшую модификацию алгоритма, подобного Якоби, называемого алгоритмом Хестенеса-Нэша. | symmetricpowermethod.zip | 1k | 11-07-27 | Symmetric Power Method | This code is an iterative scheme used to find the largest eigenvalue and associated eigenvector for a symmetric matrix .  Матрица должна быть симметричной, чтобы использовать этот код. Наслаждаться! Матрица должна быть симметричной, чтобы использовать этот код. Наслаждаться! tableau_maximizing.zip | 7k | 04-02-17 | Симплексная таблица Максимизация 1.0 | Как следует из названия, эта программа максимизирует симплексную таблицу. Учитывая матрицу в [A], она будет отображать опорный элемент шаг за шагом. Как только пыль уляжется, на нем будет написано либо «ПОСЛЕДНЯЯ ТАБЛИЦА», либо «НЕТ РЕШЕНИЯ». Очень удобно с большими таблицами! TRACEEIGNEVALUE.ZIP | 1K | 14-08-25 | | . Он найдет наибольшее собственное значение по величине. Пожалуйста, прочтите документацию для получения дополнительной информации. |  Наслаждаться! Наслаждаться! tracematrix.zip | 1k | 13-03-15 | Эта программа будет вычислять трассировку матрицы6. Просто войдите в матрицу прямо с главного экрана, а программа сделает все остальное. Наслаждаться! | . Наслаждаться! | UNITVECTOR.ZIP | 1K | 09-10-22 | . на длину 1), сохраняя при этом то же направление. | VECADD.ZIP | 1K | 05-08-02 | ADDECTER ADDECTERS 9000. ADDECTERS ADDECTERS ADDECTERS ADDECTERS 9048S ADDECTERS 9066. | VECCONV. |  ZIP ZIP 1K | 05-08-02 | Vecter Confortion (Polar hр. (r, тета) или наоборот. | vecsub1.zip | 1k | 05-08-02 | Вычитание векторов из других векторов 906 векторов. | VECT1.ZIP | 1K | 13-05-20 | Vectors 90 | . Я использовал это для моего математического класса, надеюсь, что это поможет вам! (it is in german, working on translations) | vectcal.zip | 1k | 02-06-08 | vectcal | vecteur. |  zip zip 1k | 06-02-17 | Vecteur | Позволяет суммировать или вычитать векторы, а также производить скалярное произведение. На французском. vector3.zip | 1k | 11-04-09 | Векторы для всего v3.6 90 | vector.8xp | 1k | 03-02-03 | Вектор | Вычисляет векторы и выдает результат. — Пример: 10N, 30° и 20N, 150° = 17,32, 120° Лучшего на Рынке не найти! — Показывает графически, четко и быстро. vectoraddsub.zip | 1k | 09-10-26 | Add as Many Vectors as You Wish | enter as many individuals vectors and find the resultant vector’s magnitude and angle vectoradd. |  zip zip 1k | 04-05-09 | Сложение векторов | Эта программа очень проста, быстра и проста в использовании. Как следует из названия, он складывает два вектора и отображает результат. vectorcalc.zip | 1k | 03-12-01 | Векторный калькулятор 8 904 Эта программа будет отображать векторы на экране, а затем отображать результирующий вектор в прямоугольном и полярном формате. | вектор. вектор по величине и направлению, скалярное произведение по координатам (и указывает, параллелен он или ортогонален) и угол по координатам (в градусах). Работает для X, Y и Z. Выводит ответы в дробной форме. Посмотреть код программы можно здесь: http://pastebin.com/AcS3n32v | vectormagic. |  zip zip 1k | 02-10-23 | SS Tech. Vector Magic | Делает все, что я могу придумать с векторами. Если переменные запутались, откройте учебник по математике, чтобы решить головоломку. Попробуйте, автору нравится отзыв! Vector_mb.zip | 1K | 11-01-17 | VECTER V1.4998 | 9056 9056. Эта программа используется для нахождения компонентов и сумм векторов в двух измерениях. Его можно запустить через MirageOS, если вы хотите сохранить его в архиве. vectornorm.zip | 1k | 11-11-16 | Векторная норма5. Это может сделать бесконечность норм. |  Наслаждаться! Наслаждаться! vectorproduct2.zip | 1k | 14-11-11 | Vector Product 2 | This file contains programs to compute the vector triple product as well as cross products with the added feature знания величин и углов, а не вычисления определителя. Наслаждаться! vectors_01.zip | 1k | 10-06-10 | Vectors | Does Cross Product, Dot Product and all that good stuff vectors1.zip | 2k | 00-11-09 | Vector Solver | Эта программа будет складывать и вычитать любое количество векторов, которое вам нужно, она также умножает вектор на коэффициент, а затем складывает или вычитает его.  Необходимая вещь для всех, кто занимается предварительной каллиграфией или физикой! Необходимая вещь для всех, кто занимается предварительной каллиграфией или физикой! vectors3.zip | 1k | 01-05-31 | Векторы 90 Просто введите две конечные точки вектора, и эта программа переключит вектор в стандартную форму и даст вам величину (длину) и направление. | vectors.8xp.zip | 1к0485 | Вы вводите Xt Yt Yi Xi, и он говорит вам Y1 и Y2, а также некоторые другие вещи. Подходит для триггерного теста. vectorsdegree.zip | 1K | 02-05-11 | . | vectors_math_formula.zip | 1k | 03-03-07 | Векторная математика — на основе меню | Некоторые меню векторной математики для выполнения векторных вычислений.  vectorsolver.zip | 1k | 09-10-19 | vector solver | This program used to solve simple vectors vector_solving.zip | 22k | 09-05-20 | Векторы | С помощью этой программы вы можете решать многие векторные уравнения. В том числе: величина, форма компонента, масштабирование умножения и сложения, единичный вектор и многое другое! Эта программа также может представить ваши ответы в радианной форме (поскольку большинство учителей хотят, чтобы ваши ответы были в радикальной форме). Надеюсь, ты повеселишься! =) Vectors.zip | 1K | 00-10-20 | Vectors V1. |  09048. любые два вектора, которые вы предоставляете. Отлично подходит для отчисления 3. 09048. любые два вектора, которые вы предоставляете. Отлично подходит для отчисления 3. Vectorwizard.zip | 11K | 03-09-14 | VECTION WITER 8. Введите два вектора в прямоугольном формате (поддерживает 3 измерения), и это даст вам величину A, B и A X B, угол между двумя векторами, скалярное произведение, векторное произведение, единичные векторы A, B и A X B; Также дает вам масштабную проекцию, векторную проекцию и ортогональный компонент от А до векторной проекции! Дает вам ответы на все, что спросит ваш учитель, если он не скажет мне, и я это исправлю. Если вам нравится эта программа, посмотрите на Tools3Dv3.0 (это на самом деле ее подпрограмма). Вопросы или комментарии? [email protected] | vector.zip | 1k | 03-09-20 | Vector | Vector algebra operations vectradd. |  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы. х-12+3=-2 => х= 7 #
х-12+3=-2 => х= 7 #