Задачи на теорему косинусов
Репетитор
по физике
916 478 1032
П
Р
О
Г
Р
А
М
М
И
Р
О
В
А
Н
И
Е
Репетитор
916 478 1032
Репетитор
по физике
916 478 1032
Репетитор
по алгебре
916 478 1032
Репетитор
по физике
916 478 1032
Для любого треугольника справедливо следующее соотношение:
\( a^2=b^2+c^2-2 \cdot b \cdot c \cdot cos \;\; \alpha \)
Квадрат стороны треугольника равен сумме квадратов двух других сторон вычесть удвоенное произведение
этих сторон на косинус угла между ними.
0 \)
Теорема синусов и теорема косинусов
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусовВы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
Пусть дан треугольник АВС, ВС = — радиус его описанной окружности. Угол а может быть острым, тупым или прямым. Рассмотрим эти случаи отдельно.
1) Угол острый (рис. 152, а). Проведя диаметр BD и отрезок DC, получим прямоугольный треугольник BCD, в котором как вписанный угол, опирающийся на диаметр.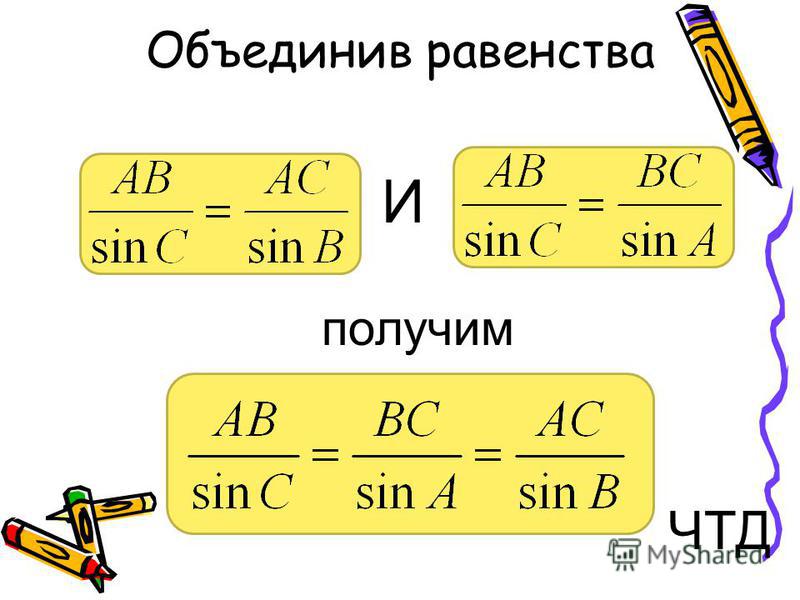
Заметим, что как вписанные углы, опирающиеся на одну и ту же дугу ВС. Из прямоугольного треугольника BCD находим т. е. откуда
2) Угол тупой (рис. 152, б). Проведем диаметр BD и отрезок DC. В четырехугольнике ABDC по свойству вписанного четырехугольника Из прямоугольного треугольника как вписанный угол, опирающийся на диаметр) Поскольку то откуда
3) Для справедливость равенства докажите самостоятельно, В силу доказанного откуда
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция позволяет решить две следующие задачи:
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы можно решить еще три задачи (рис.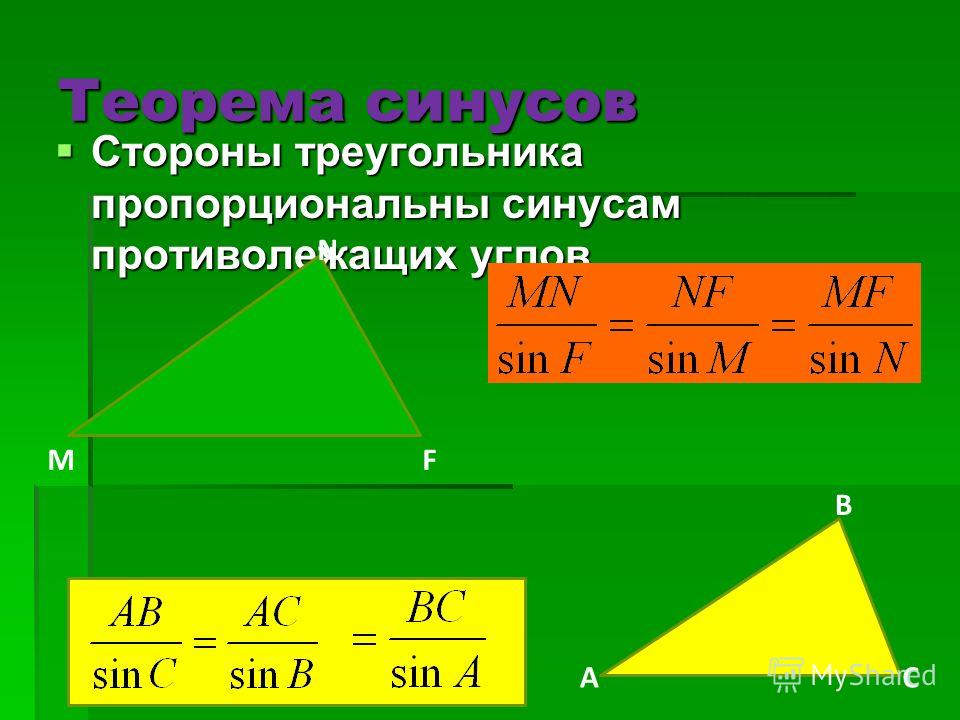
153):
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
Пример:
В остроугольном треугольнике известны стороны и угол Найти два других угла округлив их значения до 1°, и третью сторону треугольника, округлив ее длину до 0,1.
Решение:
По теореме синусов откуда При помощи калькулятора (таблиц). находим Тогда По теореме синусов откуда
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом то, зная вначале мы нашли бы острый угол А затем, используя формулу получили бы, что
Пример:
Доказать справедливость формулы площади треугольника где — его стороны, R — радиус описанной окружности.
Доказательство:
Воспользуемся известной формулой площади треугольника: По теореме синусов откуда Тогда Что и требовалось доказать.
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13
(рис. 154).Решение:
Способ 1. Из формулы следует, что Найдем . Для этого в треугольнике АВС проведем высоту ВК, которая будет и медианой, откуда Из по теореме Пифагора откуда
Тогда
Способ 2. Используем формулу из которой Так как то
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников.
Также мы могли использовать формулу где — боковая сторона, — высота, проведенная к основанию
Заменив в формуле получим — формулу радиуса описанной окружности для произвольного треугольника. Итак, мы имеем четыре формулы для нахождения радиуса
Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны треугольника АВС (рис. 165) через длины сторон ). Теорему косинусов можно назвать самой «работающей» в геометрии. Она имеет многочисленные следствия, которые часто используются при решении задач.
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис.
166).
Проведем высоту ВН к стороне АС. Из находим откуда
Из по теореме Пифагора
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда или тупой или прямой, докажите самостоятельно. Теорема доказана.
Для сторон теорема косинусов запишется так:
Замечание. Если , то по теореме Пифагора Так как то Таким образом, теорема Пифагора — частный случай теоремы косинусов.
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов).
Для углов получим:
Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы с учетом того, что следует:
- если то и угол острый;
- если то и угол тупой;
- если то и угол прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с.
Так как то угол тупой и данный треугольник тупоугольный.
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD — острый, откуда — тупой (рис. 169). По теореме косинусов из
Из Поскольку cos то
(2)
Сложив почленно равенство (1) и равенство (2), получим что и требовалось доказать.
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
Медиану треугольника со сторонами а, b и с можно найти по формуле
Доказательство:
Рассмотрим — медиана треугольника (рис. 170). Продлим медиану AM за точку М на ее длину:
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма Отсюда следует, что
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, Найти сторону с. б) Дан треугольник АВС, а = 7, с = 8, а = 60°. Найти сторону Ь.
Решение:
а) По теореме косинусов
Отсюда б) Пусть По теореме косинусов то есть Отсюда или так как для наборов длин отрезков 7, 3, 8 и 7, 5, 8 выполняется неравенство треугольника.
Ответ: а) 7; б) 3 или 5.
Пример:
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в стороны АВ = 6, ВС = 10 и (рис. 171).
Поскольку то откуда
Так как и по условию — тупой, то . Для нахождения стороны АС применим теорему косинусов:
Ответ: 14.
Пример:
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника Пусть — медиана (рис. 172).
По формуле медианы откуда По обратной теореме Пифагора данный треугольник со сторонами 6, 8 и 10 — прямоугольный, его площадь равна половине произведения катетов:
Ответ: 24.
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: а также по двум сторонам и углу между ними: Теперь мы выведем формулу нахождения площади треугольника по трем сторонам.
Теорема (формула Герона).
Площадь треугольника со сторонами можно найти по формуле где — полупериметр треугольника.
Доказательство:
(рис. 183). Из основного тригонометрического тождества следует, что Для синус положительный. Поэтому Из теоремы косинусов откуда
Тогда
Так как
Теорема доказана.
Решение треугольниковРешением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
Дано: (рис. 184).
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол находим при помощи калькулятора или таблиц.
4) Угол
Замечание. Нахождение угла по теореме синусов требует выяснения того, острый или тупой угол
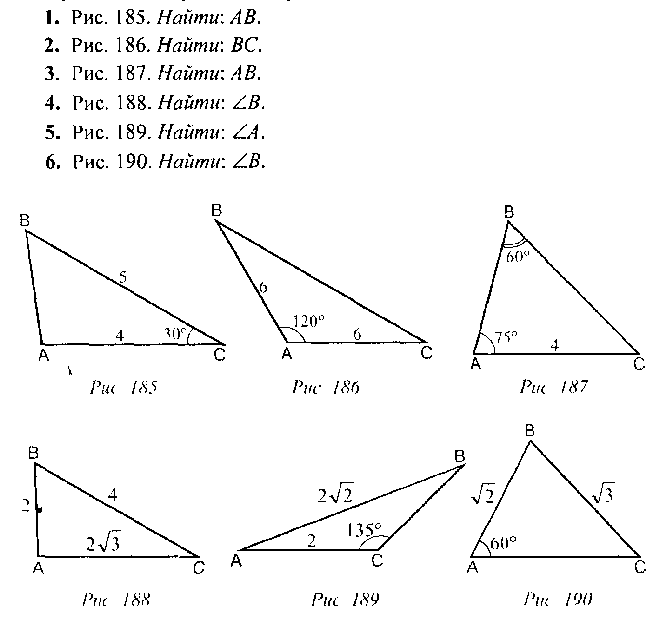
Дано: (рис. 185).
Найти:
Решение:
1) Угол
2) По теореме синусов (sin и sin находим при помощи калькулятора или таблиц).
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: или (cos и sin находим при помощи калькулятора или таблиц).
Пример №3 (решение треугольника по трем сторонам).Дано: (рис. 186).
Найти: и радиус R описанной окружности.
Решение:
1) По следствию из теоремы косинусов
2) Зная угол находим при помощи калькулятора или таблиц.
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле где
Замечание*.
Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов затем нахождение по косинусу угла его синуса и, наконец, использование теоремы синусов для нахождения R.
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
Тогда
Радиус R описанной окружности найдем из формулы Имеем:
Ответ:
Способ 2. Так как поскольку то треугольник — прямоугольный по обратной теореме Пифагора. Его площадь равна половине произведения катетов: а радиус описанной окружности равен половине гипотенузы:
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и Проведем (рис.
187). Так как АВСК — параллелограмм, то СК = АВ = 10, АК = ВС = 5, откуда KD = AD — АК = 9. Найдем высоту СН треугольника KCD, которая равна высоте трапеции. Площадь треугольника KCD найдем по формуле Герона, обозначив его стороны а = 10, b = 17, с = 9. Получим:
Так как СН = 8. Площадь трапеции
Ответ: 76.
Пример:
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть Найдем
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС , то около него можно описать окружность по признаку вписанного четырехугольника (рис.
189, б). Поскольку прямой вписанный угол опирается на диаметр, то отрезок AM — диаметр этой окружности, т. е. где R — радиус. Из по теореме косинусов Из по теореме синусов откуда
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
В прямоугольном треугольнике АВС известно: высота СН = 2 (рис. 190). Найти гипотенузу АВ.
Решение:
Построим симметричный относительно прямой АВ (см. рис. 190).
Поскольку то вокруг четырехугольника можно описать окружность, где АВ — диаметр этой окружности (прямой вписанный угол опирается на диаметр). Треугольник вписан в эту окружность, По теореме синусов откуда
Ответ: 8.
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = На гипотенузе АВ как на стороне построен квадрат ADFB (рис.
191). Найти расстояние от центра О этого квадрата до вершины С прямого угла, т. е. отрезок СО.
Решение:
Способ 1. Так как (диагонали квадрата ADFB взаимно перпендикулярны), то поэтому четырехугольник АОВС является вписанным в окружность, ее диаметр Тогда
Пусть СО = х. По теореме косинусов из находим
из находим
По свойству вписанного четырехугольника Поскольку то откуда находим Тогда .
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим до квадрата CMNK, как показано на рисунке 192. Можно показать, что центр квадрата CMNK совпадет с центром квадрата ADFB, т. е. с точкой О (точки В и D симметричны относительно центров обоих квадратов).
Тогда
Ответ:
Точка О — центр окружности, вписанной в треугольник АВС, Найти стороны треугольника (см. задачу 232*).
Решение:
Пусть и
— радиус вписанной окружности (рис. 193).
Тогда
Отсюда Применим формулу Герона:
С другой стороны, Из уравнения находим = 2. Откуда (см), (см), (см).
Ответ: 15 см; 20 см; 7 см.
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из и (см. рис. 194) следует:
(1)
(2)
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
Теорема доказана.
Следствие:
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника Разделив сторону с в отношении получим:
По теореме Стюарта
Пример №9Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, — биссектрисы, проведенные к сторонам ВС = а и АС = b соответственно, и (рис. 196). Нужно доказать, что Выразим и через и приравняем полученные выражения. Биссектриса делит противолежащую сторону на части, пропорциональные прилежащим сторонам. Поэтому откуда откуда
По формуле биссектрисы треугольника
Из условия следует: Перенеся слагаемые в одну сторону равенства и разложив на множители (проделайте это самостоятельно), получим: Отсюда (второй множитель при положительных больше нуля).
Утверждение доказано.
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е. (рис. 197).
Доказательство:
Из по теореме косинусов
Так как (по свойству вписанного четырехугольника) и откуда
Аналогично из получим Тогда Теорема доказана.
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть — стороны треугольника и с — большая сторона. Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
Если , то треугольник тупоугольный, если то треугольник остроугольный, если , то треугольник прямоугольный.Теорема косинусов для треугольника — формула, доказательство
Теорема косинусов отлично помогает в решении треугольников. Решение треугольника — это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 900.
Содержание
Теорема и доказательство
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
| Произвольный треугольник | Теорема косинусов и обозначения |
где , , — стороны треугольника, — угол треугольника, напротив стороны . |
Доказательство теоремы косинусов
Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:
Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:
.
В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:
Так как, , , а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть .
Подставим все в формулу (2):
.
Что и требовалось доказать.
Следствие теоремы косинусов
Проведем высоты :
Обратим внимание, что . То есть — это проекция стороны на сторону треугольника . Если угол А острый, то , если угол А тупой, то косинус угла А будет отрицательным и . То есть из теоремы косинусов вытекает важное следствие:
квадрат стороны треугольника равен сумме квадратов двух других сторон «» удвоенное произведение одной из них на проекцию другой на эту сторону.
Знак надо брать, если угол тупой, а знак , если угол острый.Задачи на теорему косинусов
Задача 1
Найдите , если дано: , , .
Решение: Так как нам известен угол между сторонами и и известна сторона — мы сможем найти сторону , если воспользуемся теоремой косинусов.
Из теоремы косинусов выразим сторону .
Получим:
Обозначим
Тогда
Получаем квадратное уравнение. Подставим в него значения и решим:
Находим дискриминант:
.
Тогда .
— не может быть длиной стороны треугольника.
Ответ: 12.
Задача 2
В треугольника ABC , , . Найдите
Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.
Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:
.
Так как , то из формулы (1), получим:
Сделаем замену: :
,
перенесем в правую часть равенства и получим квадратное уравнение:
,
Подставим значения:
Так как , значит, .
Ответ: 6
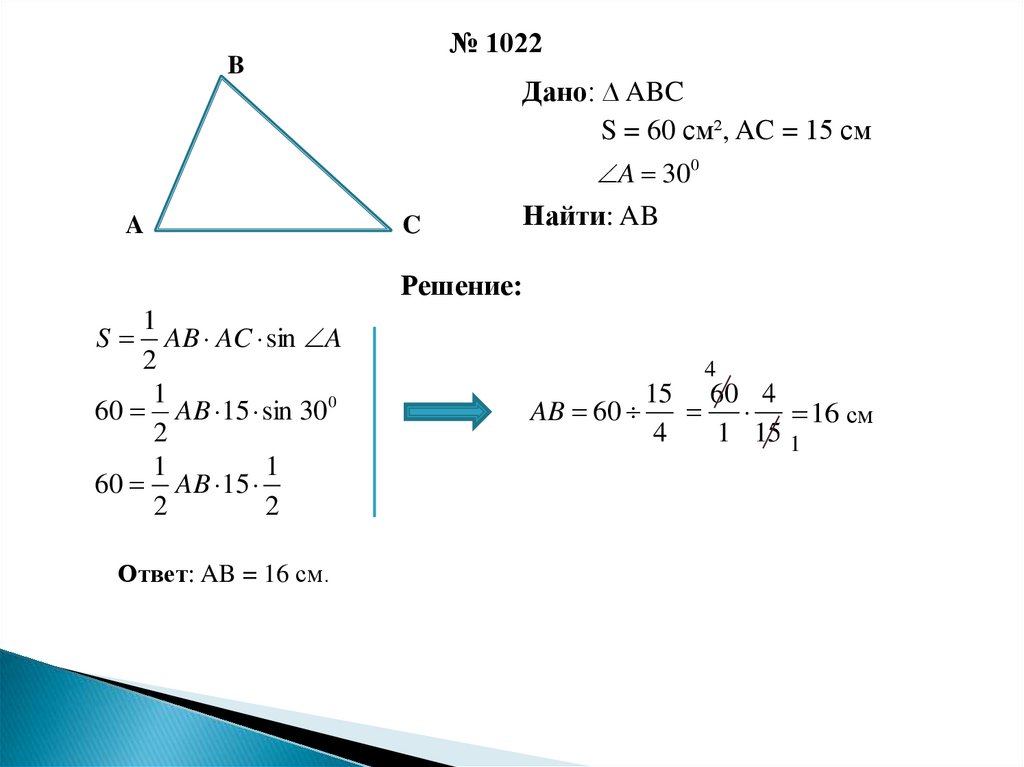
Задача 3
Решите треугольник ABC, если известно, что , , .
Решение: Решить треугольник — это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна получим:
.
Обозначим неизвестные стороны треугольника: , .
Выразим сторону треугольник по теореме косинусов:
Выразим сторону треугольника по теореме косинусов:
или
Решим уравнения (1) и (2) совместно, записав их в систему уравнений:
Преобразуем второе уравнение системы:
Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:
Из второго уравнения выразим :
Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.
, раскрываем скобки и умножим левую и правую части уравнения на 2:
Разделим левую и правую части уравнения на 2:
.
Получили квадратное уравнение. Решим его.
Находим дискриминант:
Тогда корни уравнения:
.
Оба значения подходят — они положительны. Находим, :
— отрицательное значение нам не подходит.
.
Таким образом, получаем следующие значения , .
Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.
Ответ: , .
Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему — синусов. Например, третью задачу мы могли решить гораздо проще — используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение . Теорема косинусов дает нам точный результат.
Однако, в дальнейшем, когда вы выучите две теоремы — рекомендуем решать задачи, используя их обе.
Закон косинусов и закон синусов
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 Следующая →
Тригонометрия Помощь » Треугольники » Закон косинусов и закон синусов
К какой известной теореме сводится закон косинусов для прямоугольных треугольников?
Возможные ответы:
Теорема косинуса
Isosceles Triangle Теорема
Pythagorean Теорема
Теорема среднего значения
Теорема вертикального угла
Правильный ответ:
Pythagorean. Объяснение:
Закон косинусов выглядит следующим образом:
Обратите внимание, что эти уравнения содержат Теорему Пифагора, внутри него.
Термин в конце является корректирующим термином для треугольников, которые не являются прямоугольными.
Сообщить об ошибке
Найдите значение с точностью до десятых.
Возможные ответы:
Правильный ответ:
Объяснение:
Это яркий пример случая, который требует использования закона косинусов, который гласит
, где , , и являются тремя сторонами треугольника, а является углом, противоположным стороне . Глядя на наш треугольник, принимая , мы имеем , , и . Подставив это в нашу формулу, мы получим.
Использование нашего калькулятора для приблизительного значения косинуса придает
Упрощение Далее дает
Решение путем принятия квадратного корня дает
Отчет о ошибке
Использование закона косинусов, определяйте Определение The Erry
.
периметр вышеприведенного треугольника.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы применить закон косинусов, является неизвестным, и являются соответствующими заданными сторонами, а заданный угол равен .
Следовательно, уравнение становится:
, которое дает
Добавить к двум другим данным сторонам, чтобы получить периметр,
Отчет о ошибке
Решайте для X:
Возможные ответы: .
Правильный ответ:
Объяснение:
Мы можем найти x, используя закон косинусов, где C — угол между сторонами a и b.
В данном случае:
Сообщить об ошибке
Найдите недостающие углы и стороны.
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Пояснение:
Закон косинусов принимает различные формы в зависимости от того, какой угол или сторону вы хотите найти. Одним из недостающих элементов информации о нашем треугольнике является длина стороны а. Важно найти эту сторону, потому что с длиной стороны a мы можем использовать закон синусов, чтобы легко найти меры угла. Сторона а «открывает» проблему.
Соответствующий LOC .
Теперь, когда мы знаем сторону а, мы можем использовать обратную форму закона синусов, чтобы найти остальные меры угла.
Угол B:
Чтобы найти соответствующий угол, возьмем арксинус.
Но есть два угла между 0° и 180°; есть 44,7° и . Как узнать, какой угол выбрать? Мы узнаем это, находя последний угол C с обоими нашими гипотетическими углами для угла B. Поскольку сторона c является наибольшей стороной, из этого следует, что она должна иметь наибольший угол из всех трех углов в треугольнике. Вычислите меру угла C, вычитая заданный угол (угол A) и рассчитанный угол (угол B) из 180°. Сделайте это один раз с 44,7° и один раз с 135,3°. В первом случае наибольший угол C соответствует наибольшей стороне c. Таким образом, угол B=44,7°, а угол C должен быть равен 110,3°.
Сообщить об ошибке
В треугольнике ниже , и . Найдите меру с точностью до десятых.
Возможные ответы:
Недостаточно информации.
Правильный ответ:
Пояснение:
Чтобы найти угол в косоугольном треугольнике, где известны все стороны, используйте закон косинусов:
Сообщить об ошибке
В треугольнике ниже , метры и метры.
Какова длина b с точностью до десятых долей метра?
Возможные ответы:
Недостаточно информации.
8,5 метра
5,7 метра
9,0 метра
13,0 метра
Правильный ответ:
9,0 метра
Объяснение:
Закон косинусов гласит, что .
Итак:
Сообщить об ошибке
Радиолокационная вышка обнаружила два корабля. Корабль A находится в 730 метрах к юго-западу. Корабль B находится в 525 метрах к северо-западу. Каково расстояние между двумя кораблями с точностью до метра?
Возможные ответы:
696 метров
297 метров
507 метров
899 метров
516 метров
Правильный ответ:
696 метров
Объяснение:
На схеме ниже показано, что угол между кораблями от РЛС составляет 65 градусов.
Чтобы найти расстояние между кораблями, используйте закон косинусов:
Сообщить об ошибке
В треугольнике ниже, , , и . Какова мера с точностью до десятых долей градуса?
Возможные ответы:
Недостаточно информации.
Правильный ответ:
Пояснение:
Чтобы найти , нужно сначала найти сторону c по закону косинусов:
Зная c , можно найти по закону косинусов.
Закон синусов:
Закон косинусов:
Сообщить о ошибке
, учитывая треугольник, где, и, рассчитывайте длину боковой стороны до тысячи децимальной точки.
Возможные ответы:
Правильный ответ: 9005 90144
5
Объяснение:
Вспомните закон косинусов, чтобы определить длину одной стороны треугольника, зная длины других сторон и прилежащий к ним угол:
Здесь указана неизвестная длина стороны, а указаны другие стороны и угол между ними.
Подставьте эти значения в закон косинусов и оцените квадратные корни с точностью до ближайшего тысячного десятичного знака, чтобы определить длину стороны .
Следовательно, длина оставшейся стороны треугольника примерно единиц.
Сообщить об ошибке
← Предыдущий 1 2 3 4 5 6 7 Следующий →
Уведомление об авторских правах
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Законы косинусов и синусов
Сначала опустите перпендикулярную линию AD из A вниз к основанию BC из
треугольник. Основание D этого перпендикуляра будет лежать на ребре BC треугольника, когда оба угла B и C являются острыми. Но если угол B тупой, то основание D будет лежать на BC , вытянутом в направлении B.
Но если угол C тупой, то D будет прямой г. до н.э. г. вытянулся в направлении г. н.э. г. К счастью,
Аргумент один и тот же во всех трех случаях.
Пусть h обозначает длина этой линии г. н.э., г., то есть высота (или высота) треугольника.
Если угол B острый, то sin B = h/c. Но это верно даже тогда, когда B является тупым углом, как на третьей диаграмме. Там, угол ABC тупой. Но синус тупого угла равен то же, что и синус его добавки. Это означает sin ABC совпадает с sin ABD, , то есть они оба равны ч/к.
Точно так же не имеет значения, острый угол C или тупой, sin C = h/b в любом случае.
Эти два уравнения говорят нам, что h равно c sin B и b sin C. Но из уравнения c sin B = b sin C, мы можем легко получить закон синусов:
Закон косинусов
Существуют две другие версии закона косинусов,
а также
Поскольку три версии отличаются только маркировкой треугольника, достаточно проверить только один из них. Будем рассматривать изложенную версию первый.
Чтобы понять, почему эти законы действуют, нам нужно рассмотреть три случая. Для случая 1 примем угол C тупым. В случае 2 угол C будет прямым. В случае 3 угол С будет острым.
| Случай 1. В этом случае мы принимаем угол C тупым. Этот случай имеет в нем морщина, так как косинус тупого угла отрицателен. Посмотрим, как это пойдет. | |||||||||||||
| Сначала опустите перпендикулярную линию AD от A до основания BC треугольник. В этом случае основание D этого перпендикуляра будет лежать вне
треугольник. Пусть h обозначает высоту треугольника, пусть d обозначает BD, и пусть e обозначает CD. Из рисунка можно вывести следующие уравнения:
В общем случае косинус тупого угла есть отрицание косинуса его дополнения. | |||||||||||||
В данном случае это косинус
угол C, , то есть угол ACB, есть отрицание
косинус угла ACD. Вот почему в последнем уравнении стоит знак минус.Эти уравнения и простая алгебра завершают рассуждения следующим образом:
| с 2 | = | д 2 + ч 2 |
| = | ( a + e ) 2 + h 2 | |
| = | а 2 + 2 ae + e 2 + h 2 | |
| = | а 2 + б 2 + 2 ае | |
| = | a 2 + b 2 – 2 ab cos C |
Таким образом, закон косинусов справедлив, когда C — тупой угол.
Случай 2. Теперь рассмотрим случай, когда угол C прямой. Косинус прямого угла равен 0, поэтому закон косинусы, c 2 = a 2 + b 2 2 ab cos C, упрощается до пифагорейского тождества, в 2 = а 2 + б 2 , для прямоугольных треугольников, которое, как мы знаем, справедливо.
Случай 3. В этом случае мы предполагаем, что угол C является остроугольным треугольником. Бросьте Перпендикулярная линия AD от A вниз к основанию BC треугольника. Ступня D перпендикуляра будет (1) лежать на ребре BC , если угол B острый, (2) совпадают с точкой B , если угол B прямой, или (3) лежат на стороне BC расширен, если угол B тупой.
Пусть h обозначает высоту треугольника, пусть d обозначают BD, и e обозначают CD.
Тогда мы можем прочитать следующие отношения из схемы:
| с 2 | = | д 2 + ч 2 |
| б 2 | = | е 2 + ч 2 |
| соз С | = | е/б |
| г 2 | = | ( и и ) 2 |
Последнее уравнение требует пояснений. Если точка D лежит на стороне BC, тогда d = a – e, , но если D лежит на BC расширенный, затем д = д – а. В любом случае d 2 = ( e – a ) 2 .
Эти уравнения и немного алгебры завершают доказательство следующим образом:
| в 2 | = | д 2 + ч 2 |
| = | d 2 – e 2 + b 2 | |
| = | ( д – д ) ( д + д ) + б 2 | |
| = | ( a – 2 e ) a + b 2 | |
| = | a 2 + b 2 – 2 ae | |
| = | a 2 + b 2 – 2 ab cos C |
Между прочим, Евклид включил в свои Элементы пару предложений,
II.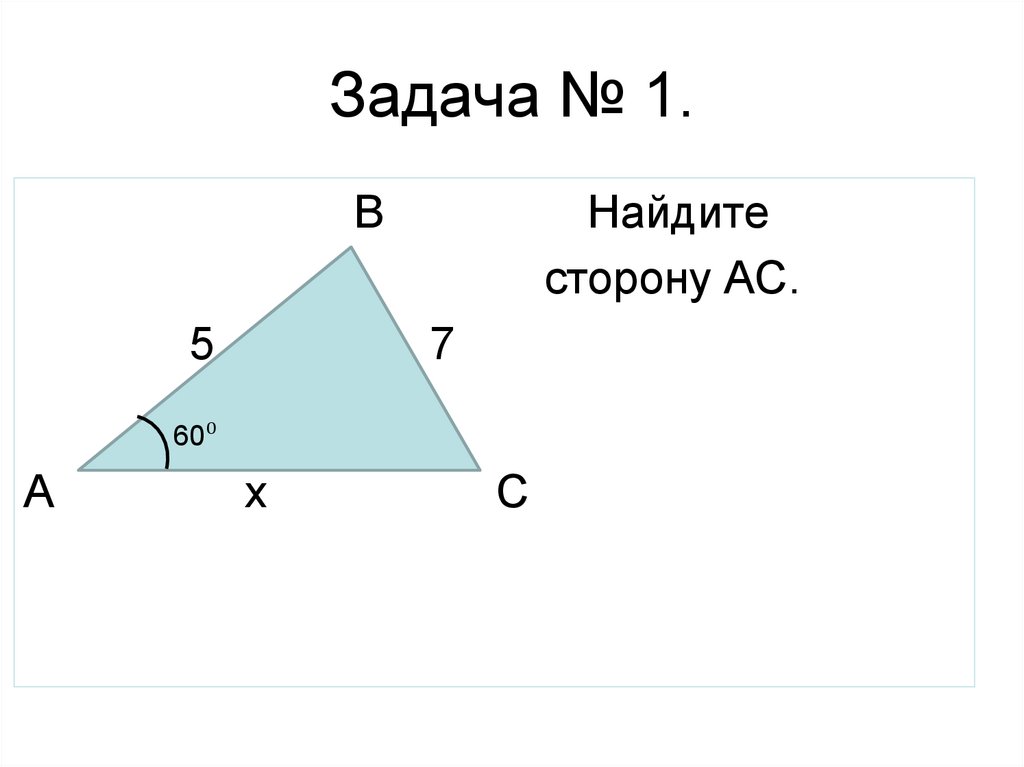
12 и
II.13,
это очень похоже на закон косинусов, но на самом деле это, конечно, не закон косинусов, поскольку тригонометрия не была развита во времена Евклида.
Объяснение урока: Применение законов синусов и косинусов
В этом объяснении мы узнаем, как использовать законы синусов и косинусов для решения реальных задач.
Применения этих двух законов очень разнообразны. Они могут быть применены к задачам в области техники для расчета расстояний или углов места, например, при строительстве мостов или телефонных столбов. В навигации пилоты или моряки могут использовать эти законы для расчета расстояния или угла направления, в котором им нужно двигаться, чтобы добраться до места назначения.
Начнем с двух законов. Рассмотрим треугольник 𝐴𝐵𝐶 с соответствующими длинами сторон 𝑎, 𝑏 и 𝑐.
Определение: Закон синусов
В треугольнике 𝐴𝐵𝐶, как описано выше, закон синусов гласит, что 𝑎𝐴=𝑏𝐵=𝑐𝐶.sinsinsin
Верно и обратное:
sinsinsin𝐴𝑎=𝐵𝑏=𝐶𝑐.
Мы можем признать необходимость закона синусов, когда данная информация состоит из противоположных пар длин сторон и мер углов в непрямоугольном треугольнике. На практике нам обычно нужно использовать в наших расчетах только две части отношения.
Определение: Закон косинусов
В треугольнике 𝐴𝐵𝐶, как описано выше, закон косинусов гласит, что 𝑎=𝑏+𝑐−2𝑏𝑐𝐴.cos
Закон косинусов можно преобразовать в cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐.
Мы можем признать необходимость закона косинусов в двух случаях:
- Мы используем первую форму, когда нам даны длины двух сторон непрямого треугольника и мера угла между ними, и мы хотим вычислить длину третьей стороны.
- Мы используем переставленную форму, когда нам известны длины всех трех сторон непрямоугольного треугольника, и мы хотим вычислить меру любого угла.
Лучше не слишком беспокоиться о самих буквах, а скорее о том, что они обозначают с точки зрения их положения относительно длины стороны или меры угла, которую мы хотим вычислить.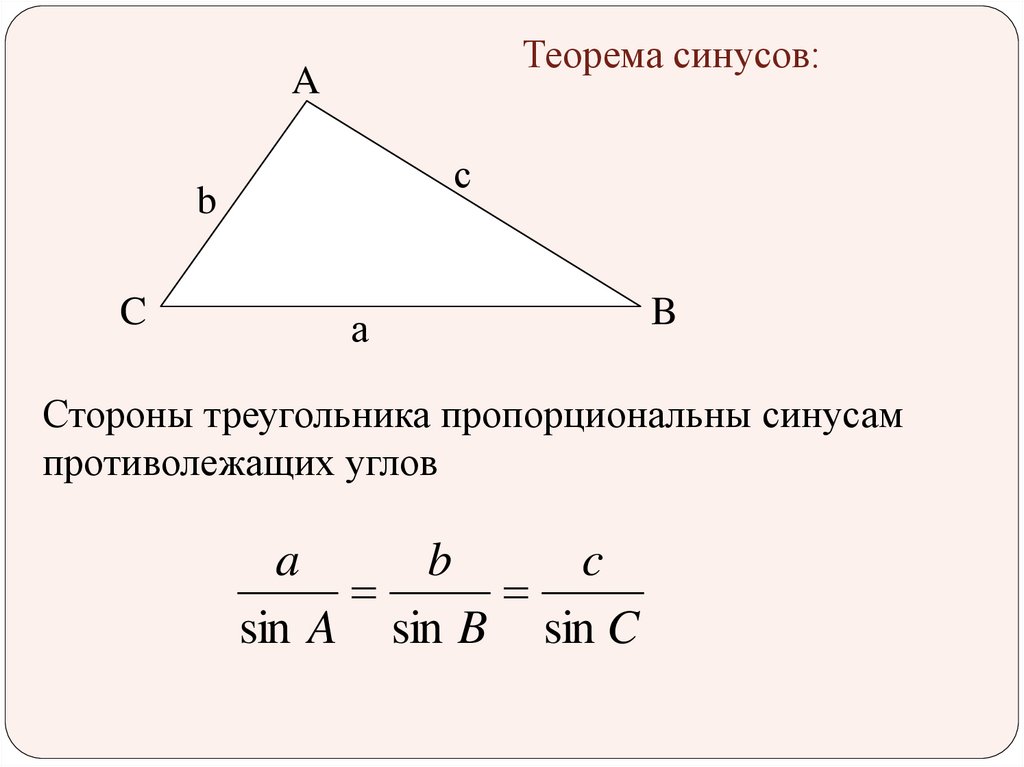
Например, во втором утверждении закона косинусов буквы 𝑏 и 𝑐 обозначают длины двух сторон, заключающих угол, меру которого мы вычисляем, а a представляет длину противоположной стороны.
Если мы помним эту структуру, мы можем подставить соответствующие значения в закон синусов и закон косинусов без необходимости вводить буквы 𝑎, 𝑏 и 𝑐 в каждой задаче.
Мы уже должны быть знакомы с применением каждого из этих законов к математическим задачам, особенно если у нас есть диаграмма. Цель этого объяснителя — использовать эти навыки для решения проблем, имеющих практическое применение. Часто нам приходится начинать с рисования схемы из словесного описания, как мы увидим в нашем первом примере.
Пример 1. Использование закона косинусов для вычисления неизвестной длины треугольника в текстовой задаче
Фермер хочет отгородить треугольный участок земли. Длины двух сторон забора 72 метра и 55 метров, а угол между ними 83∘. Найдите периметр забора, ответив на него с точностью до метра.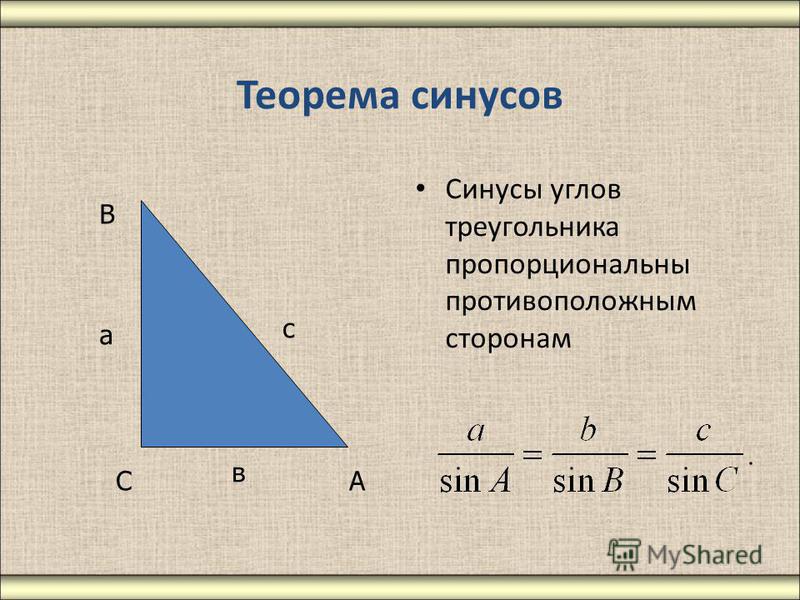
Ответ
Начнем с рисования треугольного участка земли, используя предоставленную информацию, как показано ниже (не в масштабе).
Чтобы найти периметр забора, нам нужно вычислить длину третьей стороны треугольника. Мы определяем из нашей диаграммы, что нам даны длины двух сторон и мера угла между ними. Следовательно, мы можем вычислить длину третьей стороны, применив закон косинусов: 𝑎=𝑏+𝑐−2𝑏𝑐𝐴.cos
Нам может быть полезно обозначить стороны и углы в нашем треугольнике буквами, соответствующими буквам, используемым в законе косинусов, как показано ниже.
Однако это не существенно, если мы знакомы со структурой закона косинусов. Если мы вспомним, что 𝑏 и 𝑐 представляют собой две известные длины сторон, а 𝐴 представляет собой угол между ними, то мы можем подставить данные значения непосредственно в закон косинусов без явного обозначения сторон и углов буквами.
Замена 𝑏=55, 𝑐=72 и
𝑚∠𝐴=83∘ в закон косинусов, получаем
𝑎=55+72−(2×55×72)83.
∘cos
Вычисление и упрощение дает 𝑎=3025+5184−792083=7243,794….∘cos
Находим 𝑎 методом извлечения квадратного корня. Мы можем игнорировать отрицательное решение нашего уравнения, поскольку мы решаем найти длину: 𝑎=√7243,794…=85,110….мм
Наконец, вспомним, что нас просят вычислить периметр треугольника. Суммируя три длины сторон и округляя до ближайшего метра, как того требует вопрос, мы имеем следующее: периметр=72+55+(85,110…)=212,110…≈212.
Периметр поля с точностью до метра составляет 212 метров.
Другие задачи, к которым можно применить законы синусов и косинусов, могут принимать форму задач о путешествии. Нам могут дать словесное описание, включающее движение объекта или расположение нескольких объектов относительно друг друга, и попросить вычислить расстояние или угол между двумя точками. В более сложных задачах нам может потребоваться применить как закон синусов, так и закон косинусов. Сейчас мы рассмотрим это на примере.
Пример 2.
Определение величины и направления смещения тела с помощью закона синусов и закона косинусовЧеловек проехал на велосипеде 7√2 км на восток, а затем проехал еще 21 км 45∘ на юг востока. Определить величину и направление смещения, округлив направление до ближайшей минуты.
Ответ
Мы начнем с того, что набросаем путь, пройденный этим человеком, взяв север за вертикальное направление на нашем экране. Его начальная точка обозначена на нашем эскизе буквой 𝐴, а пунктирная линия представляет собой продолжение восточного направления, чтобы помочь в проведении второй части пути. Угол 45° к югу от востока — это угол, измеренный на 45° вниз (по часовой стрелке) от этой линии.
Нас просят рассчитать величину и направление смещения. Величина — это длина линии, соединяющей начальную точку 𝐴 и конечную точку 𝐶. Направление смещения точки 𝐶 из точки 𝐴 юго-восточное, а величина этого угла является мерой угла 𝐵𝐴𝐶.
Рассмотрим треугольник 𝐴𝐵𝐶, в котором нам даны две длины сторон.
Мы можем вычислить меру их внутреннего угла, угол 𝐴𝐵𝐶, вспомнив, что сумма углов на прямой равна 180∘. Вычитание 45∘ из 180∘ дает
𝑚∠𝐴𝐵𝐶=180−45=135.∘∘∘
Теперь, когда мы знаем длины двух сторон и величину угла между ними, мы можем применить закон косинусов для вычисления длины третьей стороны: 𝐴𝐶=𝐴𝐵+𝐵𝐶−(2×𝐴𝐵×𝐵𝐶×𝐴𝐵𝐶).cos
. 𝐴𝐶=7√2+21−2×7√2×21×135=833.∘cos
Находим 𝐴𝐶 методом извлечения квадратного корня: 𝐴𝐶=√833=7√17.kmkm
Добавляем полученную информацию к нашей диаграмме.
Для вычисления меры угла 𝐵𝐴𝐶 у нас есть выбор методов:
- Мы можем применить закон косинусов, используя три известные длины сторон.
- Мы могли бы применить закон синусов, используя противоположную длину 21 км, а пара боковых углов показана красным.
Применим закон синусов, используя версию, в которой синусы углов стоят в числителе: sinsin𝐴𝑎=𝐵𝑏.
Замена 𝑎=21, 𝑏=7√17 и 𝑚∠𝐵=135∘ дает sinsin𝐴21=1357√17.∘
Умножение каждой части этого уравнения на 21 приводит к
sinsin𝐴=211357√17.
∘
Находим 𝐴, применяя функцию обратного синуса: 𝐴=211357√17=30,963….sinsin∘∘
Напомним, что нас просят дать ответ с точностью до минуты, поэтому с помощью функции калькулятора для преобразования между ответом в градусах и ответом в градусах и минут дает 30∘ 58′.
Величина смещения 7√17 км и направление с точностью до минуты 30∘ 58′ к югу от востока.
В предыдущем примере мы видели, что при наличии достаточной информации о треугольнике у нас может быть выбор методов. Применение закона синусов и закона косинусов, конечно, приведет к одному и тому же ответу, и ни один из них не является более эффективным, чем другой. Также можно применить закон синусов или закон косинусов несколько раз в одной и той же задаче.
Законы синусов и косинусов можно также применять к задачам, связанным с другими геометрическими фигурами, такими как четырехугольники, поскольку их можно разделить на треугольники. Давайте теперь рассмотрим пример этого, в котором мы дважды применяем закон косинусов для вычисления меры угла в четырехугольнике.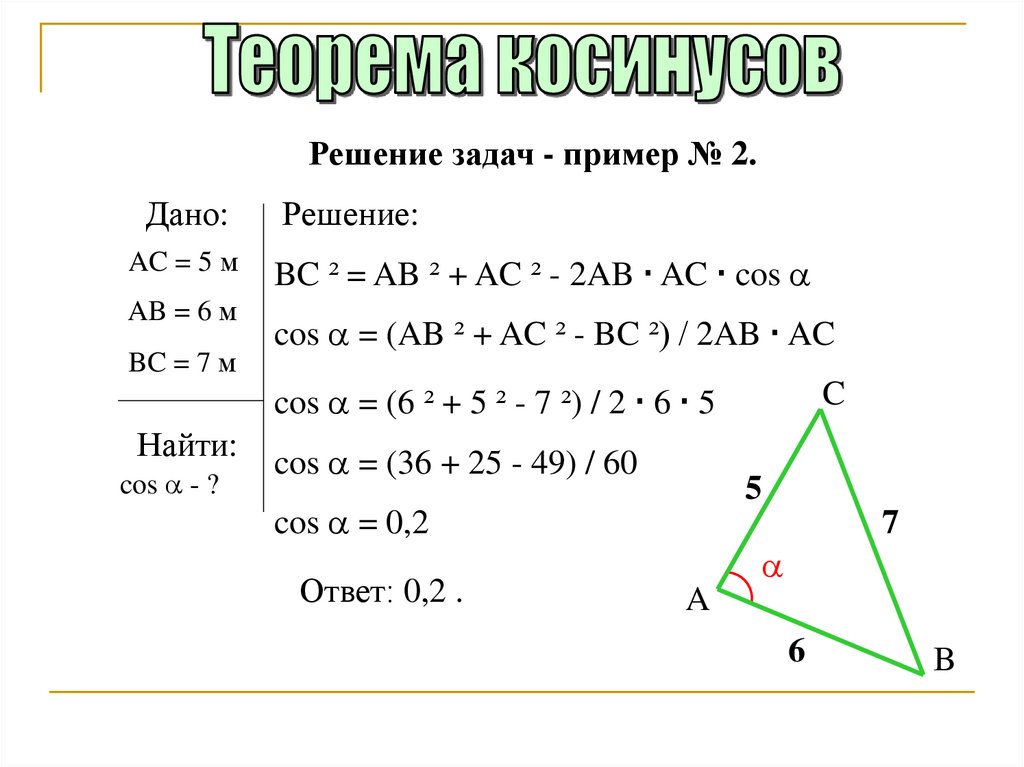
Пример 3: Использование закона косинусов для нахождения меры угла в четырехугольнике . Найдите 𝑚∠𝐶𝐵𝐷, дающий ответ с точностью до степени.
Ответ
Начнем с рисования четырехугольника 𝐴𝐵𝐶𝐷, как показано ниже (без масштаба).
Мы также можем провести диагональ 𝐵𝐷 и определить угол, меру которого нас просят вычислить, угол 𝐶𝐵𝐷.
Диагональ 𝐵𝐷 делит четырехугольник на два треугольника. Мы видим, что угол 𝐶𝐵𝐷 является одним углом в треугольнике 𝐵𝐶𝐷, в котором нам даны длины двух сторон. Если бы мы знали длину третьей стороны, 𝐵𝐷, мы могли бы применить закон косинусов для вычисления меры любого угла в этом треугольнике.
Сторона 𝐵𝐷 является общей с другим треугольником на диаграмме, треугольником 𝐴𝐵𝐷, поэтому давайте теперь рассмотрим этот треугольник. Нам даны длины двух сторон (𝐴𝐷 и 𝐴𝐵) и угол между ними, поэтому мы можем применить закон косинусов для вычисления длины третьей стороны. Для этого треугольника закон косинусов гласит, что
𝐵𝐷=𝐴𝐵+𝐴𝐷−(2×𝐴𝐵×𝐴𝐷×𝐴).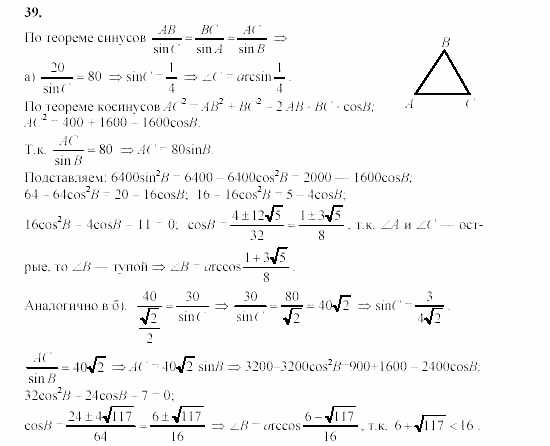
cos
Подставляя 𝐴𝐵=31, 𝐴𝐷=32, и 𝑚∠𝐴=64∘ дает 𝐵𝐷=31+32−(2×31×32×64)=1985−198464=1115,271….∘∘coscos
Находим 𝐵𝐷 методом извлечения квадратного корня, игнорируя отрицательное решение, поскольку 𝐵𝐷 представляет длину: 𝐵𝐷=√(1115,271…)=33,395….cmcm
Добавим к нашей диаграмме длину 𝐵𝐷.
Теперь мы знаем длины всех трех сторон треугольника 𝐵𝐶𝐷, поэтому можем вычислить величину любого угла. Вспомним преобразованную форму закона косинусов: cos𝐴=𝑏+𝑐−𝑎2𝑏𝑐, где 𝑏 и 𝑐 — длины сторон, заключающих угол, который мы хотим вычислить, а 𝑎 — длина противоположной стороны. На нашем рисунке стороны, окружающие угол 𝐵, имеют длины 40 см и 33,395… см, а противоположная сторона имеет длину 43 см. Подставляя эти значения в закон косинусов, имеем cos(𝐶𝐵𝐷)=40+(33,395…)−432×40×(33,395…)=0,324….
Находим угол 𝐶𝐵𝐷, применяя функцию арккосинуса: 𝑚∠𝐶𝐵𝐷=(0,324…)=71,080…≈71.cos∘
Мера угла 𝐶𝐵𝐷 с точностью до градуса равна 71∘.
Мы рассмотрели примеры вычисления как длин неизвестных сторон, так и мер неизвестных углов в задачах на треугольники и четырехугольники с использованием как закона синусов, так и закона косинусов.
Другое применение закона синусов связано с диаметром описанной окружности треугольника. Напомним, что описанная окружность треугольника — это окружность, проходящая через все три вершины треугольника, как показано на рисунке ниже.
Определение: закон синусов и связь описанной окружности
Для любого треугольника 𝐴𝐵𝐶 диаметр описанной окружности равен соотношению синусов: 𝑎𝐴=𝑏𝐵=𝑐𝐶=2𝑟.sinsinsin
Теперь мы увидим, как мы можем применить этот результат для вычисления площади описанной окружности, зная меру одного угла в треугольнике и длину его противоположной стороны.
Пример 4. Нахождение площади описанной окружности по величине угла и длине противоположной стороны
𝐴𝐵𝐶 — треугольник, где 𝑚∠𝐴=152∘ и 𝐵𝐶=11см. Найдите площадь описанной окружности с точностью до ближайшего квадратного сантиметра.
Ответ
Прежде всего вспомним, что описанная окружность треугольника — это окружность, проходящая через все три вершины треугольника. Чтобы вычислить площадь любого круга, мы используем формулу площадь=𝜋𝑟, поэтому нам нужно рассмотреть, как мы можем определить радиус этого круга.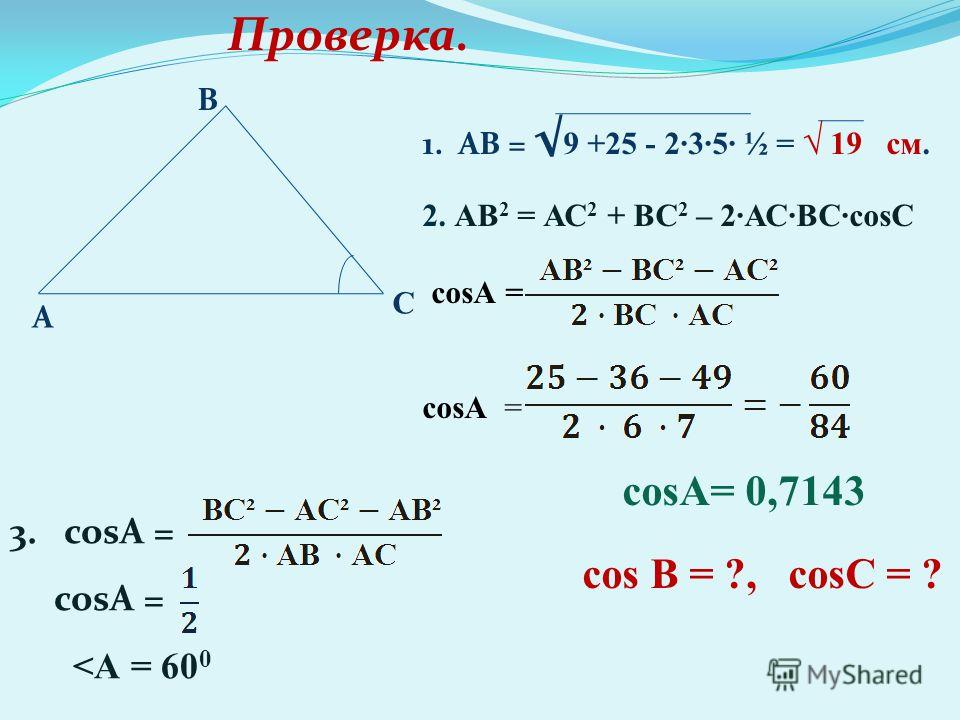
Информация, данная в вопросе, состоит из меры угла и длины его противоположной стороны. Мы знаем это, потому что указана длина стороны, соединяющей вершины 𝐵 и 𝐶, которая будет противоположна третьему углу треугольника, углу 𝐴. Альтернативный способ обозначения этой стороны — 𝑎.
Вспомним связь между законом соотношения синусов и радиусом описанной окружности: 𝑎𝐴=𝑏𝐵=𝑐𝐶=2𝑟.sinsinsin
Подставляя 𝑎=11 и 𝑚∠𝐴=152∘ в первую часть этого отношения и игнорируя две средние части, которые не требуются, мы имеем 11152=2𝑟.sin∘
Решим это уравнение, чтобы определить радиус описанной окружности: 𝑟=112152=11,715….sincm∘
Теперь мы можем вычислить площадь описанной окружности: площадь=𝜋𝑟=𝜋×(11,715…)=431,178…≈431,
Площадь описанной окружности с точностью до квадратного сантиметра равна 431 см 2 .
Мы также можем объединить наши знания о законах синусов и косинусов с другими результатами, касающимися непрямоугольных треугольников. Вспомним тригонометрическую формулу площади треугольника.
areain=12𝑎𝑏𝐶,
где 𝑎 и 𝑏 представляют собой длины двух сторон треугольника, а 𝐶 представляет собой меру прилежащего к ним угла. В нашем последнем примере мы увидим, как мы можем применить закон синусов и тригонометрическую формулу площади треугольника к задаче, связанной с площадью.
Пример 5. Использование закона синусов и тригонометрической формулы площади треугольников для вычисления площадей круговых сегментов
Найдите площадь зеленой части диаграммы, учитывая, что 57∘, а 𝐶𝐵=19см. Дайте ответ с точностью до ближайшего квадратного сантиметра.
Ответ
Начнем с добавления информации, указанной в вопросе, к диаграмме. Нам также может быть полезно обозначить стороны буквами 𝑎, 𝑏 и 𝑐.
Заштрихованную площадь можно рассчитать как площадь треугольника 𝐴𝐵𝐶, вычтенную из площади круга: затенениеплощадькругаплощадьтреугольника=−𝐴𝐵𝐶.
Вспоминаем тригонометрическую формулу площади треугольника, используя две стороны и угол между ними:
площадь треугольников = 12𝑎𝑏𝐶.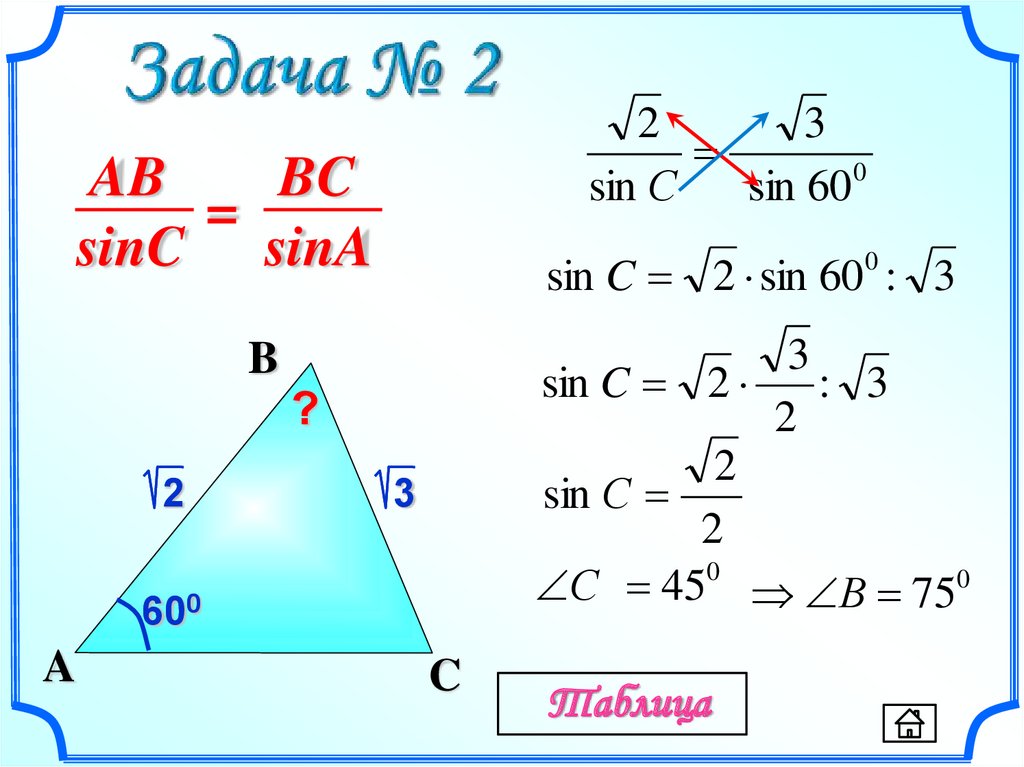
Чтобы вычислить площадь треугольника 𝐴𝐵𝐶, нам сначала нужно вычислить длину стороны 𝑏. Мы уже знаем длину стороны в этом треугольнике (сторона 𝑎) и величину противолежащего ей угла (угол 𝐴). Мы можем определить меру угла, противоположного стороне 𝑏, вычитая меры двух других углов треугольника из 180∘: 𝑚∠𝐵=180−77−57=46.∘∘∘∘
Поскольку информация, с которой мы работаем, состоит из противоположных пар длин сторон и мер углов, мы признаем необходимость закона синусов: 𝑏𝐵=𝑎𝐴.sinsin
Подставляя 𝑎=19, 𝑚∠𝐴=77∘, и 𝑚∠𝐵=46∘, имеем 𝑏46=1977.sinsin∘∘
Решим это уравнение, чтобы найти 𝑏, умножив обе части на sin46∘: 𝑏=194677=14,026….sinsincm∘∘
Теперь мы можем заменить 𝑎=19, 𝑏=14,026… и 𝑚∠𝐶=57∘ в тригонометрическую формулу площади треугольника: площадь треугольников в см𝐴𝐵𝐶=12×19×(14,026…)×57=111,758….∘
Чтобы найти площадь круга, нам нужно определить его радиус. Эта окружность на самом деле является описанной окружностью треугольника 𝐴𝐵𝐶, поскольку она проходит через все три вершины треугольника.
Напомним связь между законом отношения синусов и радиусом описанной окружности:
𝑎𝐴=𝑏𝐵=𝑐𝐶=2𝑟.sinsinsin
Используя длину стороны 𝑎 и меру угла 𝐴, мы можем составить уравнение: 1977=2𝑟.sin∘
Решение для 𝑟 дает 𝑟=19277=9,749….sincm∘
Следовательно, площадь круга равна: areaofcirclecm=𝜋×(9,749…)=298,640….
Наконец, мы вычитаем площадь треугольника 𝐴𝐵𝐶 из площади описанной окружности: затенениеплощадькругаплощадьтреугольника=−𝐴𝐵𝐶=(298,640…)−(111,758…)=186,882…≈187.
Заштрихованная площадь с точностью до квадратного сантиметра равна 187 см 2 .
Давайте закончим повторением некоторых ключевых моментов этого объяснения.
Ключевые точки
- Для треугольника 𝐴𝐵𝐶, как показано на рисунке ниже, закон синусов гласит, что 𝑎𝐴=𝑏𝐵=𝑐𝐶.sinsinsin Закон косинусов гласит, что 𝑎=𝑏+𝑐−2𝑏𝑐𝐴.cos
- Закон синусов и закон косинусов можно применять в задачах реального мира для вычисления неизвестных длин и мер углов в непрямоугольных треугольниках.
