Решение матрицы методом гаусса: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Содержание

13. Метод Гаусса

На приведении расширенной матрицы системы к ступенчатым матрицам специального вида основан метод решения систем линейных уравнений, называемый методом Гаусса или методом последовательного исключения неизвестных.

На первом этапе (прямой ход метода Гаусса) расширенная матрица Приводится к ступенчатой матрице , у которой все ненулевые строки имеют первый элемент, равный единице. Решение полученной системы уравнений с расширенной ступенчатой матрицей называется обратным ходом метода Гаусса. Обратный ход может быть выполнен как в форме последовательного определения неизвестных, начиная с последнего, так и в форме последующего преобразования матрицы к ступенчатой матрице , у которой все ненулевые строки содержат только одну единицу и позволяют в явном виде представить решение системы.

Отметим, что, выполняя прямой ход метода Гаусса, мы получаем возможность эффективного вычисления ранга матрицы и определителя. Если нас интересует ранг матрицы, то после преобразования ее к ступенчатой форме, достаточно подсчитать число ненулевых строк: это и будет ранг матрицы.

Если нас интересует определитель матрицы, то эта матрица, естественно, должна быть квадратной. После преобразования ее методом Гаусса к ступенчатой форме она примет вид верхней треугольной матрицы, то есть матрицы, у которой все элементы ниже главной диагонали равны нулю. Определитель любой верхней треугольной матрицы равен произведению всех элементов, стоящих на главной диагонали. Если на главной диагонали имеется хотя бы один нулевой элемент, то определитель треугольной матрицы равен нулю и, соответственно, определитель исходной матрицы равен нулю. Если же на главной диагонали в результате преобразований прямого хода метода Гаусса окажутся только единицы, то надо в процессе преобразований следить за перестановками строк, которые изменяют знак определителя на обратный, и за умножениями или делениями строк матрицы на числа, которые пропорционально изменяют величину определителя. Определитель исходной матрицы находится как произведение всех чисел, на которые делились строки. Знак этого произведения остается прежним, если было проведено четное число перестановок строк, и изменяется на противоположный, если число перестановок строк было нечетным.

Пример. Решим методом Гаусса следующую систему:

Выполняя прямой ход метода Гаусса, приведем расширенную матрицу этой системы к ступенчатой матрице, у которой все ненулевые строки имеют первый ненулевой элемент, равный единице. На первом этапе выполним следующие элементарные преобразования исходной расширенной матрицы: разделим первую строку на число два; сложим вторую строку с первой и результат запишем во вторую строку; из третьей строки вычтем преобразованную первую строку и результат запишем в третью строку:

Мы получили в результате, что первая строка ненулевая, имеет первым ненулевым элементом число один, а все элементы в первой колонке под числом один равны нулю. Для того чтобы, вторая строка начиналась с единицы, переставим вторую и третью строки местами:

Для того чтобы под единицей во втором столбце стоял нуль, из третьей строки полученной матрицы вычтем вторую строку, умноженную на три, и запишем в третью строку:

Наконец, чтобы третья строка имела первым ненулевым элементом число один, поделим третью строку на число пять:

На этом завершается прямой ход метода Гаусса, а преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице, равносильна исходной системе уравнений и имеет следующий вид:

В нашем примере, выполнив прямой ход метода Гаусса, мы одновременно нашли ранг матрицы коэффициентов системы (, так как число ненулевых строк преобразованной матрицы равно трем), а также ранг расширенной матрицы (, так как число ненулевых строк преобразованной матрицы равно трем).

Для вычисления определителя исходной матрицы коэффициентов необходимо обратить внимание на три обстоятельства: вид верхней треугольной матрицы, в которую преобразовалась исходная матрица; на какие числа делились или умножались строки; какое количество (четное или нечетное) перестановок было выполнено в процессе преобразований.

Так как на главной диагонали стоят только единицы, то определитель не равен нулю. Далее в процессе преобразований было использовано деление на число 2 первой строки и деление на число 5 третьей строки. Их надо перемножить и подсчитать число перестановок строк местами: была выполнена одна перестановка. Таким образом, определитель матрицы коэффициентов равен: .

Выполним обратный ход метода Гаусса сначала первым способом, то есть последовательно определим неизвестные, начиная с последнего уравнения:

Выполним обратный ход метода Гаусса вторым способом. Продолжим элементарные преобразования матрицы и приведем ее к ступенчатой матрице , у которой все ненулевые строки содержат только одну единицу. Это позволит в явном виде представить решение системы. Сложим вторую строку с третьей строкой и результат запишем во вторую строку:

Далее, чтобы заменить число два первой строки на число нуль, умножим третью строку на число (-2), сложим с первой строкой и результат запишем в первую строку:

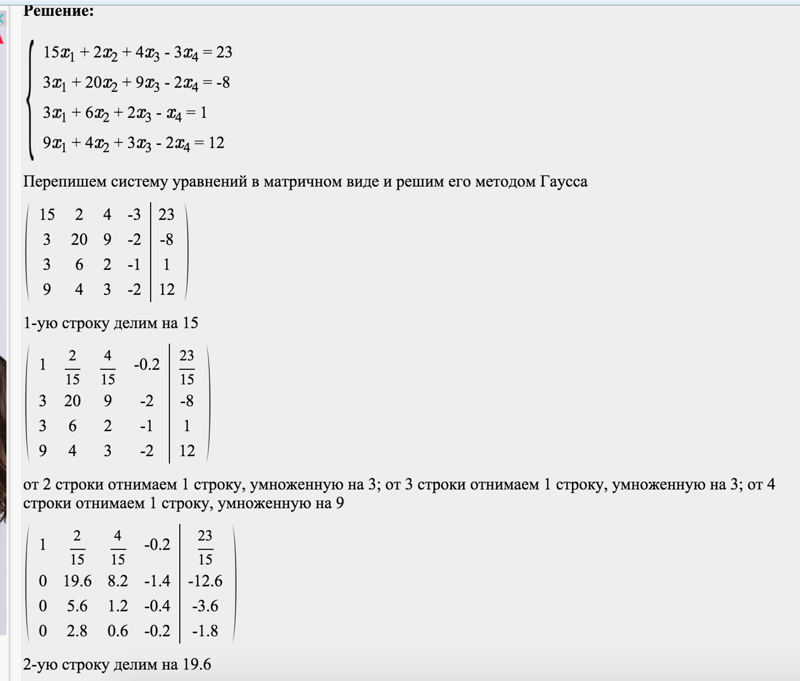
На этом заканчивается обратный ход метода Гаусса. Преобразованная система уравнений, соответствующая полученной ступенчатой расширенной матрице типа, равносильна исходной системе уравнений и имеет следующий вид

Который представляет собой запись решения системы в явной форме.

Для исследования решения систем линейных уравнений с произвольным числом уравнений и неизвестных полезна следующая теорема.

< Предыдущая		Следующая >

Алгоритм решения неопределенной системы линейных уравнений методом Гаусса » ProcMem.Ru Линейная Алгебра

Пятница, 31 января 2014 г.
Рубрика: Системы линейных уравнений
Просмотров: 25554
Подписаться на комментарии по RSS

п.10. Алгоритм решения неопределенной системы линейных уравнений методом Гаусса.

Пусть дана система .

1. Выписываем расширенную матрицу системы .

2. Пользуясь элементарными преобразованиями строк расширенной матрицы, приводим ее к ступенчатому виду.

Далее, вся работа проводится с полученной системой ступенчатого вида.

3. Убеждаемся, что базисный минор матрицы системы является базисным минором расширенной матрицы системы, т.е. . В противном случае, система несовместна, т.е. не имеет решений.

4. Вычисляем размерность пространства решений соответствующей однородной системы : .

5. Определяем, какие переменные системы будут независимыми, а какие зависимыми:

а) те переменные, коэффициенты при которых входят в базисный минор объявляем независимыми, их оставляем в левых частях уравнений системы;

б) оставшиеся переменные объявляем зависимыми, их переносим в правую часть уравнений. Зависимых переменных должно быть штук.

6. Обозначаем зависимые переменные буквами греческого алфавита: , если их не очень много; или буквой с индексами, например: .

7. Придавая зависимым переменным какие-нибудь числовые значения, находим частное решение данной системы X*.

8. Обнуляем столбец свободных членов в системе и, двигаясь от последнего уравнения системы к первому (снизу вверх), выражаем независимые переменные системы через зависимые.

9. Записываем общее решение соответствующей однородной системы.

10. Записываем общее решение данной неоднородной системы.

11. Выписываем полученную фундаментальную систему решений соответствующей однородной системы.

12. Записываем множество решений данной неоднородной системы в виде суммы линейной оболочки, натянутой на фундаментальную систему решений и частного решения Х*.

13. Записываем ответ (из пункта 10 и 12).

Пример 1. Решить систему: .

Решение.

1) Выписываем расширенную матрицу системы :

2) Пользуясь элементарными преобразованиями строк расширенной матрицы, приводим ее к ступенчатому виду:

а) умножаем первую строку на (–2) и прибавляем ко второй строке, затем умножаем первую строку на (–1) и прибавляем к третьей:

;

б) умножаем вторую строку на (–1) и прибавляем к третьей:

3) Находим базисные миноры матрицы системы и расширенной матрицы системы:

– базисный минор матрицы системы;

– базисный минор расширенной матрицы системы.

Мы видим, что , . Так как , то данная система является несовместной, т.е. не имеет решений.

Ответ. Система не имеет решений.

Пример 2. Решить систему: .

Приводим расширенную матрицу системы к ступенчатому виду:

В результате получили квадратную систему

с определителем системы . Следовательно, система имеет единственное решение:

Ответ: .

Пример 3. Решить систему: .

1) Приводим расширенную матрицу системы к ступенчатому виду:

2) Находим базисные миноры матрицы системы и расширенной матрицы системы:

– базисный минор матрицы системы и он же базисный минор расширенной матрицы системы, . Следовательно, полученная система , которая равносильна данной, имеет решения, т.е. является совместной.

3) Вычисляем размерность пространства решений соответствующей однородной системы: . Следовательно, из трех неизвестных системы, два неизвестных и объявляем независимыми, а неизвестное объявляем зависимым.

4) Обозначаем зависимую неизвестную и переносим его в правую часть уравнения:

5) Полагаем , получаем частное решение системы:

6) Обнуляем столбец свободных членов системы и получаем соответствующую однородную систему:

7) Выписываем общее решение соответствующей однородной системы:

8) Выписываем решение неоднородной системы:

9) Фундаментальная система решений соответствующей однородной системы состоит из одного столбца:

10) Множество решений данной системы:

Ответ: общее решение системы: , ;

множество решений системы: .

Пример 4. Решить систему: .

Решение. Расширенная матрица системы:

Коэффициент при , равный 1, можно принять за базисный минор, так что .

Соответствующая однородная система имеет вид:

размерность пространства ее решений:

Обозначим – три свободные переменные. Систему можно записать так:

Полагая , получаем частное решение данной системы: или

Соответствующая однородная система имеет вид:

Тогда ее общее решение имеет вид:

где .

Общее решение данной неоднородной системы:

где .

Фундаментальная система решений соответствующей однородной системы:

Множество решений данной системы:

или .

Ответ: общее решение системы

где ; множество решений системы:

п.11. Формулы Крамера.

Теорема. Пусть квадратная система линейных уравнений и . Тогда единственное решение системы можно найти по формулам:

, ,

где – определитель матрицы системы, – столбцы матрицы системы,

– определитель системы, в котором i-й столбец заменен столбцом свободных членов В. Эти формулы называются формулами Крамера.

Доказательство. Так как , то матрица А – обратимая и из равенства получаем:

откуда и следуют формулы Крамера. Проработка деталей оставляется читателю.

Теорема доказана.

MathOnWeb — исключение Гаусса

Что такое система линейных уравнений?
Некоторые уроки, которые можно извлечь из построения графика двух уравнений с двумя неизвестными

Расширенная матрица
Элементарные операции со строками
Исключение Гаусса
Резервный корпус
Противоречивый случай

Что такое система линейных уравнений?

Линейное уравнение на n неизвестных x ₁ , x ₂ , …, x _N — это уравнение формы:

A ₁ x ₁ + A ₂ X ₂ + + + … + a _n x _n = b

где a ₁ , a _{6 ₆₂ ,
… , a _n и b — константы.}

Название линейный происходит от того факта, что такое уравнение с двумя неизвестными или переменными представляет собой прямую линию. Набор таких уравнений называется системой

. Пример системы трех линейных уравнений с тремя неизвестными х , у и z это:

Некоторые уроки, которые можно извлечь из построения графика 2 уравнений с 2 неизвестными
Графический метод не очень полезен в качестве вычислительного инструмента, но полезен для визуализации такие понятия, как уникальность решения или значение противоречивых или избыточных систем. Рассмотрим следующую систему двух линейных уравнений с двумя неизвестными:
В этом методе мы просто рисуем графики уравнений, как мы делали справа. Обратите внимание, что график каждого уравнения представляет собой прямую линию. (Это отличительная черта линейной системы. Здесь нет кривых, только прямые линии.)

Любая точка на одной прямой является решением одного уравнения, а любая точка на другой прямой является решением другого уравнения. Точка пересечения линий { x =3,6, y =0,4} является решением которая удовлетворяет обоим уравнениям одновременно. Заметим, что решение единственное. Это потому что линии прямые и есть только одна точка, где они могут пересекаться.

Система линейных уравнений с единственным решением является «нормальной» ситуацией. Однако это можно иметь систему уравнений без решения. Такая система уравнений называется противоречивый . Часто это результат неточного или неправильного анализа физического состояния. система описывается системой уравнений.
Рассмотрим следующую систему двух линейных уравнений с двумя неизвестными:
Эта система уравнений несовместима, так как
x + y никак не могут равняться 2 и 4 одновременно. На рисунке справа показано, что граф этой системы состоит двух параллельных прямых, которые никогда не пересекаются. Таким образом, решения нет.

Также возможна система уравнений с бесконечным числом решений. Такая система уравнений называется избыточной . Часто это результат неполного анализ физической системы.
Рассмотрим следующую систему уравнений:
Эта система является избыточной, поскольку второе уравнение эквивалентно первому. График состоит из двух линий, лежащих одна над другой. Они «пересекаются» в бесконечном числе точек, поэтому существует бесконечное количество решений.

Подводя итог, линейная система с двумя неизвестными должна иметь как минимум два уравнения, чтобы получить единственное решение. Иметь 1 уравнение недостаточно, потому что 1 уравнение с 2 неизвестными представлено целой строкой. Достаточно двух уравнений, если они не избыточны и не противоречат друг другу. Наличие 3 (или более) уравнений — это слишком много. Третье уравнение должно быть либо избыточным, либо противоречивым.
Эти идеи можно обобщить на линейные системы уравнений с большим количеством неизвестных:
Линейное уравнение в n переменных представляет собой «гиперплоскость» в пространстве n измерений. Линейная система уравнений с n неизвестными должна иметь по крайней мере n уравнений, чтобы получить уникальное решение. Иметь меньшее количество недостаточно; решение не будет единственным. Достаточно иметь n уравнений, если они не являются избыточными или противоречивыми. Имея более n уравнений слишком много; система будет либо избыточной, либо непоследовательной.

Расширенная матрица
Мы представим систему уравнений прямоугольным массивом чисел, называемым дополненная матрица . Вот расширенная матрица для приведенного выше примера:

Немного терминологии:
Элементы расширенной матрицы называются элементами .
Строки проходят через всю матрицу.
Столбцы идут вниз по матрице.
Диагональ матрицы представляет собой набор элементов, который начинается в верхнем, левом углу и идет по диагонали вниз и вправо. Диагональ вышеуказанной матрицы состоит из чисел 4, 1 и 2.
Любые элементы в позиции a считаются лежащими на выше диагонали , а любой в позиции B на ниже диагонального :
Имейте в виду следующее:

I -THTH -ряд -ТИТ.
j -й столбец (слева от вертикальной черты) представляет собой (коэффициенты) j -я переменная или неизвестная
вертикальная линия представляет знаки равенства

Элементарные операции с строками
Напомним, что такое уравнение, как:
7( x −4)=14,
можно решить для разрешения x , применив следующие операции:
Разделив обе части уравнения на одно и то же значение, а именно на 7, получим x -4=2,
, затем прибавив одинаковое количество к обеим сторонам, а именно 4, чтобы получить х = 6.
Решение x = 6, в чем можно убедиться, подставив его обратно в исходное значение. уравнение и нахождение тождества 14=14.
Аналогично, решением системы уравнений является любой набор значений всех переменных, удовлетворяющих всем уравнениям одновременно. Например, система:
имеет решение:
{ x = 7, y = 5, z = 3}.
Это можно проверить, подставив эти значения во все три уравнения и создание трех тождеств.
Система уравнений может быть решена путем обобщения двух операций, описанных выше, и заметив, что решение системы уравнений не меняется при:
делении обеих частей уравнения на константу, или
вычитание кратного одного уравнения из другого уравнения.
Эти же операции можно применить к строкам расширенной матрицы, поскольку каждая строка просто представляет уравнение. Затем они называются Elementary Row Operations .

Элементарные операции со строками (E.R.O.):
E.R.O.#1: Выберите строку расширенной матрицы и разделите (каждый элемент) строку константой.
Пример:
Обозначение означает разделить первую строку расширенной матрицы на 2, чтобы получить новую расширенную матрицу.
E.R.O.#2: Выберите любую строку расширенной матрицы и вычтите кратное любой другую строку из него (поэлементно).
Пример:
Обозначение означает взять строку 2 и вычесть из нее 3 раза строку 1, чтобы получить новую расширенную матрицу.

Мы будем применять E.R.O. в определенной последовательности (метод исключения Гаусса, описанный ниже) преобразовать расширенную матрицу в треугольную эшелонированную форму . В этой форме расширенная матрица имеет 1 по диагонали, 0 по диагонали и любые числа по диагонали. Например, расширенная матрица:
в виде треугольного эшелона:
Эта новая расширенная матрица представляет собой систему уравнений:
Она решается обратной подстановкой. Подставляя z = 3 из третьего уравнения в второе уравнение дает y = 5, а подстановка z = 3 и y = 5 в первое уравнение дает x = 7 . Таким образом, полное решение:
{ x = 7, y = 5, z = 3}.

Исключение по Гауссу
В методе исключения по Гауссу элементарные операции со строками (E.R.O.) применяются в определенном чтобы максимально эффективно преобразовать расширенную матрицу в треугольную эшелонированную форму.
В этом суть метода: Дана система m уравнений в n переменных или неизвестных, выберите первое уравнение и вычтите подходящие множители его из оставшиеся м -1 уравнения. В каждом случае выберите кратное так, чтобы вычитание отменяет или исключает ту же самую переменную, скажем, x ₁ . В результате оставшиеся m -1 уравнения содержат только n -1 неизвестных ( x ₁ больше не появляется).
Теперь отложите первое уравнение и повторите вышеуказанный процесс с оставшимися м -1 уравнения в n -1 неизвестных.
Продолжайте повторять процесс. Каждый цикл уменьшает количество переменных и количество уравнений. Процесс останавливается, когда:
Остается одно уравнение с одной переменной. В этом случае существует единственное решение а обратная замена используется для поиска значений других переменных.
Остались переменные, но нет уравнений. В этом случае нет единственного решения.
Остались уравнения, но нет переменных (т. е. самые нижние строки расширенной матрицы содержат только нули слева от вертикальной линии). Это свидетельствует о том, что либо система уравнения противоречивы или избыточны. В случае несоответствия информации, содержащейся в уравнениях противоречиво. В случае избыточности все еще может быть уникальное решение и обратная замена может использоваться для поиска значений других переменных.
Примеры всех этих возможностей приведены ниже.

Алгоритм исключения Гаусса:
Преобразование столбцов расширенной матрицы по одному в треугольную ступенчатую форму. Столбец, который в настоящее время преобразуется, называется сводным столбцом . Продолжайте слева направо, пусть основной столбец будет первым столбцом, затем вторым столбцом, и т. д. и, наконец, последний столбец перед вертикальной чертой. Для каждого сводного столбца выполните следующие два шага, прежде чем перейти к следующему сводному столбцу:
Найдите диагональный элемент в опорном столбце. Этот элемент называется стержнем . Строка, содержащая сводную строку, называется сводной строкой . Разделите каждый элемент в своде ряд по оси (т. е. используйте E.R.O. #1), чтобы получить новую строку оси с 1 в позиции оси.
Получите 0 в каждой позиции ниже точки поворота, вычитая подходящее кратное значение точки поворота. строку из каждой из строк под ней (т. е. с помощью E.R.O. #2).
По завершении этой процедуры расширенная матрица будет иметь форму треугольного эшелона и можно решить обратной заменой.

Пример: Используйте исключение Гаусса для решения системы уравнений:
Решение: Выполните эту последовательность E. R.O. на расширенной матрице. Установите сводной столбец в столбец 1. Получите 1 в диагональной позиции (подчеркнуто):
Затем установите 0 под опорной точкой (подчеркнуто):
Теперь пусть опорная колонка = вторая колонка. Сначала получите 1 в диагональной позиции:
Затем получите 0 в позиции ниже опорной:
Теперь пусть опорная колонка = третья колонка. Получите 1 в диагональной позиции:
Эта матрица, которая теперь имеет форму треугольного эшелона, представляет:
Она решается обратной подстановкой. Замена z = 3 из третьего уравнения в второе уравнение дает y = 5, а подстановка z = 3 и y = 5 в первое уравнение дает x = 7 . Таким образом, полное решение:
{ x = 7, y = 5, z = 3}.

Пример применения исключения Гаусса к избыточной системе линейных уравнений решите, если возможно:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установить сводную колонку в столбец 1. 1 уже находится в опорной позиции, поэтому продолжайте получать 0 под опорной точкой:
Теперь установите опорную колонку на вторую колонку. Сначала получите 1 в диагональной позиции:
Затем получите 0 в позиции ниже опорной:
Теперь установите опорную колонку в третью колонку. Первое, что нужно сделать, это получить 1 в диагональное положение, но нет возможности сделать это. На самом деле эта матрица уже в виде треугольного эшелона и представляет собой:
Эта система уравнений не может быть решена обратной подстановкой, потому что у нас нет значения для z . Последнее уравнение просто утверждает, что 0=0. Единого решения не существует, потому что z могут принимать на любом значении.
Обычно одна или несколько строк нулей внизу расширенной матрицы, которая была помещена в треугольную эшелонированную форму указывает на избыточную систему уравнений.

Пример применения исключения Гаусса к противоречивой системе линейных уравнений
Используйте исключение Гаусса, чтобы привести эту систему уравнений к решите, если возможно:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установить точку опоры от столбца к столбцу 1. В опорной позиции уже есть 1, поэтому продолжайте получать 0 ниже опорной точки:
Теперь установите опорный столбец на второй столбец. В позиции поворота уже есть 1, поэтому продолжайте, чтобы получить 0 ниже опорной:
Теперь установите опорную колонку на третью колонку. Первое, что нужно сделать, это получить 1 в диагональное положение, но нет возможности сделать это. На самом деле эта матрица уже находится в имеет форму треугольного эшелона и представляет собой:
Эта система уравнений противоречива и не имеет решения. Последнее уравнение утверждает противоречие, а именно 0 = −50.
В общем, расширенная матрица, которая представлена в виде треугольного эшелона и которая содержит одну или несколько нижних строк, состоящих из всех нулей слева от вертикальной линии и ненулевое число справа указывает на противоречивую систему уравнений, не имеющую решения.
Алгоритм исключения Гаусса
Подраздел 2.5.1 Некоторые матрицы, ассоциированная система уравнений которых легко решается
Элементарные операции со строками позволяют нам изменять матрицы и связанные с ними системы линейных уравнений, не изменяя решения этих уравнений. Цель состоит в том, чтобы в конечном итоге получить матрицы, которые сделают эти общие решения очевидными. Вот несколько примеров.
Расширенная матрица
\begin{уравнение*} \left[\begin{массив}{cccc|c} 1\амп 0\амп 0\амп 0\амп 1\\ 0\амп 1\амп 0\амп 0\амп 2\\ 0\амп 0\амп 1\амп 0\амп 5\\ 0\амп 0\амп 0\амп 1\амп -1 \конец{массив}\справа] \end{уравнение*}
соответствует системе линейных уравнений
\begin{уравнение*} \begin{массив}{cccccc} x_1\ампер \amp \amp \amp =\amp 1\\ \усилитель x_2\усилитель \усилитель \усилитель =\усилитель 2\\ \усилитель \усилитель x_3\усилитель \усилитель =\усилитель 5\\ \amp \amp \amp x_4\amp =\amp -1 \конец{массив} \end{уравнение*}
Сами уравнения фактически описывают единственное решение! Обратите внимание на структуру матрицы коэффициентов, которая делает это возможным. В каждой строке есть только одна ненулевая запись, ее значение равно 1, и по мере того, как вы переходите от одной строки к другой, ненулевая запись перемещается на один столбец вправо.
Расширенная матрица
\begin{уравнение*} \left[\begin{массив}{cc|c} 1\амп 1\амп 4\\ 0\амп 2\амп 6 \конец{массив}\справа] \end{уравнение*}
соответствует системе линейных уравнений
\begin{уравнение*} \begin{массив}{rcc} x_1+x_2\усилитель =\усилитель 4\\ 2x_2\амп =\амп 6 \конец{массив} \end{уравнение*}
Последнюю строку решить легко: получаем \(x_2=3\text{. }\) Используя это значение, также легко решить \(x_1+x_2=x_1+3=4\text{,}\ ) или \(x_1=1\текст{.}\)
Расширенная матрица
\begin{уравнение*} \left[\begin{массив}{ccc|c} 1\amp 1\amp 1\amp 4\\ 0\amp 0\amp 2\amp 6 \end{массив}\right] \end{уравнение*}
соответствует системе линейных уравнений
\begin{уравнение*} \begin{массив}{rcc} x_1+x_2+x_3\amp =\amp 4\\ 2x_3\amp =\amp 6 \конец{массив} \end{уравнение*}
Как и раньше, получаем \(x_3=3\text{.}\) Две переменные остаются неопределенными: второй присваиваем параметр: \(x_2=t\text{.}\) Используя это значение, у нас есть \(x_1+x_2+x_3=x_1+t+3=4\text{,}\) или \(x_1=1-t\text{.}\) Теперь мы знаем решения: \(x_1=1 -t\text{,}\) \(x_2=t\text{,}\) \(x_3=3\), где \(t\) может быть любым вещественным числом. На самом деле мы можем проверить этот результат с помощью первого уравнения: \(x_1+x_2+x_3=(1-t) + t + 3=4\text{.}\) Компактный способ записи этого решения: \((x_1 ,x_2,x_3)=(1-t,t,3)\text{.}\)
Из приведенных примеров видно, что наличие большого количества нулей в матрице коэффициентов полезно для вычисления решений. Также ясно, что если первая ненулевая запись в строке равна единице, то вычисление упрощается. Наш план состоит в том, чтобы с помощью элементарных операций над строками преобразовать заданную матрицу коэффициентов в матрицу с этими свойствами, а затем описать все решения. Вот некоторые наблюдения, которые нам помогут:
Если в столбце есть какая-то ненулевая запись, мы всегда можем сделать верхнюю запись ненулевой, поменяв строки местами, при необходимости используя \(R_1\leftrightarrow R_i\) для некоторого \(i>1\text{.}\)
Если первая ненулевая запись строки \(R_i\) равна \(\lambda\text{,}\), мы можем преобразовать ее в 1, используя \(R_i\leftarrow \tfrac 1\lambda R_i\text{ .}\)
Если две строки \(R_i\) и \(R_j\) имеют ненулевые записи в некотором столбце \(k\text{,}\), мы можем преобразовать запись \(j,k\) в ноль, используя \( R_j \leftarrow R_j — \frac{a_{j,k}}{a_{i,k}} R_i\text{.}\)
Подраздел 2.5.2 Эшелонная форма ряда
Теперь мы хотим определить общий класс матриц, соответствующие системы линейных уравнений которых имеют решения, которые легко найти. Эти матрицы имеют особый набор нулей и единиц, и говорят, что они находятся в рядная эшелонированная форма.
Рисунок 2.5.1. Матрица в форме эшелона строк
Приведенная выше матрица дает представление о том, чего мы хотим. Обратите внимание, что линия лестницы, проведенная через матрицу, имеет все элементы под ней, равные нулю. Записи, отмеченные символом \(*\), могут принимать любое значение.
Первая ненулевая запись в строке (если она есть) называется ведущей записью. Если он равен \(1\text{,}\), то он называется ведущим.
Определение 2.5.2. Эшелонно-рядная форма.
Матрица находится в ступенчатой форме строки , если
Каждая ведущая запись является ведущей.
Каждая запись ниже первой имеет вид \(0\text{.}\)
По мере продвижения вниз по матрице ведущие перемещаются вправо.
Любые все нулевые строки находятся внизу.
КПП 2.
5.3.
Какие из следующих матриц имеют форму эшелона строк?
\(\displaystyle \begin{bmatrix} 1\amp2\amp3\amp4\\ 0\amp5\amp6\amp7\\ 0\amp0\amp8\amp9\\ 0\amp0\amp0\amp10 \end{bmatrix}\)
\(\displaystyle \begin{bmatrix} 1\amp2\amp3\amp4\\ 0\amp1\amp2\amp3\\ 0\amp0\amp0\amp0\\ 0\amp0\amp0\amp1 \end{bmatrix}\)
\(\displaystyle \begin{bmatrix} 1\amp2\amp3\amp4\\ 0\amp1\amp2\amp3\\ 0\amp0\amp0\amp1\\ 0\amp0\amp0\amp0 \end{bmatrix}\)
\(\displaystyle \begin{bmatrix} 1\amp2\amp3\amp4\\ 0\amp1\amp6\amp7\\ 0\amp0\amp1\amp1\\ 0\amp0\amp1\amp1 \end{bmatrix}\)
\(\displaystyle \begin{bmatrix} 1\amp0\amp0\amp0\\ 0\amp0\amp0\amp0\\ 0\amp0\amp0\amp0\\ 0\amp0\amp0\amp0 \end{bmatrix}\)
Решение
Не в форме эшелона строк, потому что не каждая ведущая запись является \(1\text{.}\)
Не в форме эшелона строк, потому что нулевая строка не находится внизу.
Рядная эшелонированная форма.
Не эшелонированная форма строки, потому что ведущая запись имеет ненулевую запись под ней.
Рядная эшелонированная форма.
Подраздел 2.5.3 Алгоритм исключения Гаусса
Теперь план начинается с расширенной матрицы и с помощью последовательности элементарных операций над строками изменяется на новую матрицу, в которой легко найти решения связанной системы линейных уравнений. Так как любая элементарная операция со строками оставляет решения неизменными, решения конечной системы линейных уравнений будут идентичны решениям исходной.
Работаем со столбцами матрицы слева направо и меняем матрицу следующим образом:
Начните с первого столбца. Если все записи равны нулю, перейдите к следующему столбцу справа.
Если в столбце есть ненулевые записи, при необходимости поменяйте местами строки, чтобы получить ненулевую запись сверху.
При необходимости измените верхнюю запись на \(1\text{.}\)
Для любой ненулевой записи ниже верхней используйте элементарную операцию строки, чтобы изменить ее на ноль.
Теперь рассмотрим часть матрицы ниже верхней строки и правее рассматриваемого столбца: если таких строк или столбцов нет, остановитесь, так как процедура завершена. В противном случае проделайте ту же процедуру на новой матрице .
Вот первый пример:
\begin{уравнение*} \начать{массив}{г} 3x_1-2x_2-x_3+x_4=1\\ 6x_1-8x_2+x_3+2x_4=4 \конец{массив} \end{уравнение*}
имеет дополненную матрицу
\begin{уравнение*} \begin{bmatrix} 3 \амп -2 \ампер -1 \ампер 1 \ампер 1\ 6 амп -8 амп 1 амп 2 амп 4 \end{bматрица}. \end{уравнение*}
Нам не нужно менять местами строки, чтобы сделать верхнюю запись первого столбца отличной от нуля, поэтому мы продолжаем делать верхнюю запись \(1\), используя элементарную операцию строки \(R_1\gets \frac13R_1\text{. } \) Матрица становится
\begin{уравнение*} \begin{bmatrix} 1 \amp -\frac23 \amp -\frac13 \amp\frac13 \amp\frac13 \\ 6 амп -8 амп 1 амп 2 амп 4 \end{bматрица}. \end{уравнение*}
Теперь мы должны сделать все записи ниже верхней в столбце равными нулю. Такая запись, конечно, всего одна, поэтому с помощью \(R_2\leftarrow R_2-6R_1\text{,}\) получаем
\begin{уравнение*} \begin{bmatrix} 1 \amp -\frac23 \amp -\frac13 \amp\frac13 \amp\frac13 \\ 0 \amp -4 \amp 3 \amp 0 \amp 2 \end{bmatrix}\text{.} \end{уравнение*}
Теперь мы закончили с первым столбцом, поэтому продолжим ту же процедуру с матрицей, полученной путем удаления первой строки и первого столбца:
\begin{уравнение*} \begin{bmatrix} -4 \амп 3 \ампер 0 \ампер 2 \end{bматрица}. \end{уравнение*}
Поскольку имеется только одна строка, нам нужно только изменить верхнюю запись на \(1\) с помощью деления на \(-4\text{,}\), то есть \(R_1\gets -\frac14R_1\text{. }\) Тогда мы получим
\begin{уравнение*} \begin{bmatrix} 1 \amp -\frac34 \amp 0 \amp -\frac12 \end{bматрица}. \end{уравнение*}
и, подставив обратно в исходную матрицу, получим
\begin{уравнение*} \begin{bmatrix} 1 \amp -\frac23 \amp -\frac13 \amp\frac13 \amp\frac13 \\ 0 \amp 1 \amp -\frac34 \amp 0 \amp -\frac12 \end{bmatrix} \end{уравнение*}
Матрица имеет форму эшелона строк. Теперь мы можем определить все решения исходной системы линейных уравнений. Первая ненулевая запись в первой строке находится в первом столбце, столбце, связанном с \(x_1\text{.}\). Первая ненулевая запись во второй строке аналогично связана с \(x_2\text{.} \) Мы назначаем параметры другим переменным: \(x_3=s\) и \(x_4=t\text{.}\). Затем вторая строка сообщает нам, что \(x_2-\frac34s =-\frac12 \text{ ,}\) или \(x_2=\frac34s-\frac12\text{.}\) Теперь, когда мы знаем \(x_2\text{,}\), мы можем использовать первую строку, чтобы найти \(x_1\text{: }\) получаем \(x_1-\frac23x_2-\frac13s+\frac13t=\frac13\text{.}\) Подставляем известное значение \(x_2\) в это уравнение и после некоторого упрощения получаем \ (x_1=\tfrac56s-\tfrac13t\text{. }\) Таким образом, мы имеем: Все решения задачи
\begin{уравнение*} \начать{массив}{г} 3x_1-2x_2-x_3+x_4=1\\ 6x_1-8x_2+x_3+2x_4=4 \конец{массив} \end{уравнение*}
имеют форму
\begin{уравнение*} \begin{массив}{rcl} x_1\amp =\amp\tfrac56s-\tfrac13t\\ x_2\amp =\amp -\tfrac12 +\tfrac34 с\\ x_3\амп =\ампер с\\ x_4\amp =\amp т \конец{массив} \end{уравнение*}
, где \(s\) и \(t\) — любые действительные числа. Более компактно мы запишем это как \((x_1,x_2,x_3,x_4)= \tfrac56s-\tfrac13t,-\tfrac12 +\tfrac34 s,s,t)\text{.}\) Другими словами, для любого приписывая \(s\) и \(t\text{,}\) действительные числа, мы получаем решение системы линейных уравнений.
Легко (и полезно) проверить, что подстановка \(x_1,\dots,x_4\) в два уравнения действительно дает решение.
Теперь рассмотрим другой пример с уравнениями
\begin{alignat*}{3} x_1 \amp {}+2x_2 \amp{}-2x_3 \amp{}= \amp{}-1\\ 3x_1 \amp{}- 2x_2 \amp{}-4x_3 \amp{}= \amp{}3\\ 4x_1 \amp \amp{}-2x_3 \amp{}= \amp{}-2\\ -x_1 \amp {}-x_2 \amp{}+2x_3 \amp{}= \amp{}0 \end{выравнивание*}
и соответствующая ему расширенная матрица, измененная методом исключения Гаусса:
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 3\амп -2\амп -4\амп 3\\ 4\амп 0\амп -2\амп -2\\ -1\ампер -1\ампер 2\ампер 0 \end{bmatrix} \начать{массив}{с} \\R_2 \стрелка влево R_2-3R_1\\ R_3\получает R_3-4R_1\\ R_4\получает R_4+R_1 \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 0\амп -8\амп 2\амп 6\\ 0\амп -8\амп 6\амп 2\\ 0\амп 1\амп 0\амп -1 \end{bmatrix} \начать{массив}{с} R_2\gets-\frac18 R_2\\ R_3\gets R_3+8R_2\\R_4\gets R_4-R_2 \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 0\amp 1\amp -\frac14\amp -\frac34\\ 0\амп 0\амп 4\амп -4\\ 0\amp 0\amp\tfrac14 \amp -\tfrac14 \end{bmatrix} \начать{массив}{с} R_3 \gets\frac14 R_3\\R_4\gets R_4-\frac14 R_3 \конец{массив} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 0\amp 1\amp -\frac14\amp -\frac34\\ 0\амп 0\амп 1\амп -1\\ 0\амп 0\амп 0\амп 0 \end{bmatrix} \end{уравнение*}
Последняя строка для любого выбора \(x_1, x_2, x_3\text{,}\) сводится к \(0=0,\), поэтому любое решение соответствующих первых трех уравнений также будет решением последнего один. Другими словами, последняя строка матрицы не влияет на набор решений и может быть исключена из матрицы. Третья строка дает \(x_3=-1.\) Вторая строка дает \(x_2=-1\), а первая строка дает \(x_1=-1.\) Следовательно, есть одно решение: \((x_1, х_2,х_3)=(-1,-1,-1).\)
Теперь немного изменим уравнения из последнего примера (правая часть последнего уравнения изменена с \(0\) на \(1\)):
\begin{alignat*}{3} x_1 \amp {}+2x_2 \amp{}-2x_3 \amp{}= \amp{}-1\\ 3x_1 \amp{}- 2x_2 \amp{}-4x_3 \amp{}= \amp{}3\\ 4x_1 \amp \amp{}-2x_3 \amp{}= \amp{}-2\\ -x_1 \amp {}-x_2 \amp{}+2x_3 \amp{}= \amp{}1 \end{выравнивание*}
Исключение Гаусса почти идентично
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 3\амп -2\амп -4\амп 3\\ 4\амп 0\амп -2\амп -2\\ -1\амп -1\амп 2\амп 1 \end{bmatrix} \end{уравнение*}
уменьшается до
\begin{уравнение*} \begin{bmatrix} 1\амп 2\амп -2\амп -1\ 0\amp 1\amp -\frac14\amp -\frac34\\ 0\амп 0\амп 1\амп -1\\ 0\амп 0\амп 0\амп 1 \end{bmatrix} \end{уравнение*}
Теперь в последней строке указано \(0x_1+0x_2+0x_3=1\text{,}\), что для любого выбора \(x_1\text{,}\) \(x_2\) и \(x_3\text{ ,}\) сводится к \(0=1\) и никогда не бывает истинным. Это означает, что исходная система уравнений не имеет решений, то есть система несовместна.
Здесь мы можем сделать полезное наблюдение: если строка расширенной матрицы имеет вид
\begin{уравнение*} \begin{bmatrix} 0 \amp 0 \amp 0 \amp \cdots \amp 0 \amp * \end{bmatrix} \end{уравнение*}
, где \(*\) равно нулю или отлично от нуля, происходит одно из двух:
\(*=0\) в этом случае строка может быть удалена из матрицы
\(*\not=0\) в этом случае решения нет.
Пример 2.5.4.
Рассмотрим систему линейных уравнений:
\begin{уравнение*} \begin{массив}{rcl} х+у+г\амп =\амп 1\\ 2x+y+z \amp =\amp 2\\ 3x+ay+bz\amp =\amp c \конец{массив} \end{уравнение*}
Мы хотим знать значения \(a,\) \(b\) и \(c\), для которых нет решений, одно решение или более одного решения. Чтобы решить эту проблему, мы применяем исключение Гаусса к расширенной матрице:
\begin{уравнение*} \begin{bmatrix} 1\амп 1\амп 1\амп 1\\ 2\амп 1\амп 1\амп 2\\ 3\амп а\амп б\амп с \end{bmatrix} \begin{матрица}R_2\получает R_2-2R_1\\ R_3\получает R_3-3 R_1\конец{матрица} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1\amp 1\amp 1\amp 1\\0\amp -1\amp -1\amp 0\\0\amp a-3\amp b-3\amp c-3 \end{ bматрица} \begin{matrix}R_2\gets -R_2\\R_3\gets R_3-(a-3)R_2\end{matrix} \end{уравнение*}
\begin{уравнение*} \begin{bmatrix} 1\amp 1\amp 1\amp 1\\0\amp 1\amp 1\amp 0\\0\amp 0\amp b-a\amp c-3 \end{bmatrix} \end{уравнение*}
Анализ последней строки говорит нам обо всем: если \(b-a\not=0,\), то существует ровно одно решение.
No related posts.