Решение линейных неравенств онлайн
Решение неравенств
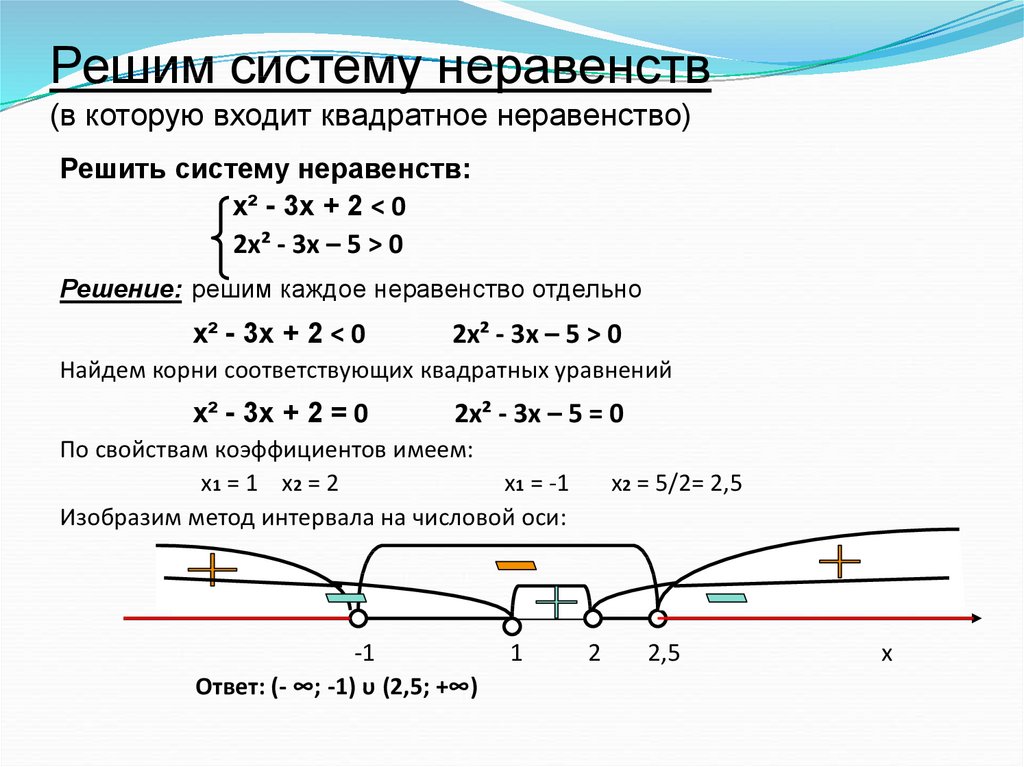
Линейными неравенствами с одной переменной х называются неравенства, в которых неизвестное находится исключительно в первой степени, вида:
ах + b
ах + b > 0;
ах + b >= 0;
ах + b
где а, b — любые действительные числа, х — переменная, число а не равно 0. В отличии от уравнения, где используется знак равенства « = », в неравенстве используют знаки сравнения: меньше , больше или равно >=, меньше или равно Правила преобразования неравенств:
— любой член неравенства можно переносить из левой части в правую и наоборот, поменяв знак на противоположный;
— если обе части неравенства умножить или разделить на одно и то же положительное число, получим равносильное ему неравенство, знак неравенства сохраняется;
— знак меняется на противоположный, если обе части неравенства умножить или разделить на отрицательное число.
Рассмотрим решение линейного неравенства ах + b
— переносим число b в другую часть неравенства, меняя при этом знак на противоположный, получим равносильное неравенство: ах
— делим обе части неравенства на число а, отличное от 0.
Если а = 0, возможны 2 варианта:
1. при b > 0 х может быть любое число;
2. при b
Решать линейные неравенства можно с использованием метода интервалов (при а не равном 0) и графическим способом.
Линейными неравенствами с 2-мя переменными являются неравенства вида:
ax + by + c > 0;
ax + by + c
ax + by + c >= 0;
ax + by + c
В отличие от неравенства с одной переменной (х) в данном неравенстве содержится еще одна переменная (у).
Решение неравенства подразумевает нахождение всех значений переменной, при подстановке которых неравенство будет верным числовым неравенством. При решении используют равносильные преобразования, чтобы заменить данное неравенство более простым. В результате преобразования в левой части неравенства должно остаться только неизвестное с коэффициентом «1».
Три правила решения линейных неравенств
При перемещении слагаемых из одной части в другую отрицательные величины становятся положительными, и наоборот.
Знак самого неравенства при этом сохраняется x – y > z => x – z > y => x > z + y.
При умножении или делении обоих частей на одинаковое положительное число неравенство останется правильным и его знак не изменится x yx x/y .
Если множитель (делитель) является отрицательным, знак неравенства необходимо заменить на противоположный x -yx > -yz => -x/y > -z/y.
| X: | |
| Y: | |
| Z: |
Предыдущая Решение интегралов
Следующая Решение СЛАУ методом LU-разложения
Линейные неравенства с двумя переменными и их системы: решение, график и примеры
- Линейное неравенство с двумя переменными и его решение
- Графическое представление линейного неравенства с двумя переменными
- Графическое решение системы линейных неравенств с двумя переменными
- Примеры
Линейное неравенство с двумя переменными и его решение
Неравенство вида ax+by $ \begin{bmatrix} \lt \\ \gt \\ \le \\ \ge \end{bmatrix} $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.
Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac{1}{2} x-8y \gt 7$
Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.
Например: для неравенства $2x+5y \lt 6$
пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина
пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь
Графическое представление линейного неравенства с двумя переменными
Например:
$2x+3y \lt 4$
$2x+3y \le 4$
$2x+3y \gt 4$
$2x+3y \ge 4$
Графическое решение системы линейных неравенств с двумя переменными
Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.
Напомним, что:
Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.
Пересечение обозначают знаком $\cap$.
Найдём графическое решение системы линейных неравенств:
$$ {\left\{ \begin{array}{c}2x+3y \ge 4 \\ 2x-y \ge -4 \\ 2x+y \le 4 \end{array} \right.}$$
Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).
Примеры
Пример 1. Найдите графическое представление линейного неравенства:
а)$ x+y \lt 4 $
Граница x+y = 4
$y \lt -x+4$
Представление – полуплоскость под границей, сама граница не входит
б) $2x-y \ge 5$
Граница 2x-y = 5
$y \le 2x-5$
Представление – полуплоскость под границей, сама граница входит
в)$ x \ge 2$
Граница x = 2
Представление – полуплоскость справа от границы, сама граница входит
г)$ y \lt 3 $
Граница y = 3
Представление – полуплоскость под границей, сама граница не входит
Пример 2*. Найдите графическое решение системы линейных неравенств:
$$ {\left\{ \begin{array}{c} |x|+y \lt 2 \\ |x|-y \lt 4 \end{array} \right.
} $$
Распишем модули:
$$ {\left\{ \begin{array}{c} y \lt -|x|+2 \\ y \gt |x|-4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} {\left\{ \begin{array}{c} y \lt -x+2, x≥0 \\ y \lt x+2, x \lt 0 \end{array} \right.} \\ {\left\{ \begin{array}{c} y \gt x-4, x \ge 0 \\ y\gt -x-4, x \lt 0 \end{array} \right.} \end{array} \right.} $$
Получаем:
Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)
Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.
Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.
Подберите состав грузовиков для выполнения заказа.
Пусть x — количество грузовиков по 3т, y – по 5т.
По условию задачи:
$$ {\left\{ \begin{array}{c} 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end{array} \right.} $$
Решением системы неравенств является заштрихованный треугольник.
Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.
Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна
Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит
Ответ: 2 грузовика по 3т и 5 грузовиков по 5т
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделюСм. подробности
Графические неравенства Определение линейного неравенства
Решение линейных неравенств Шаги решения неравенств
Пример Эскиз решения для 2x — у < 2 Раствор
Пример Эскиз решения для х + 3 года < 0 Раствор
Упражнения Зарисуйте решение следующего
Назад к математике 152A Домашняя страница электронная почта Вопросы и предложения
|
Если уравнение дает (0,0) в виде точки, начертите другую удобную
точка, например, когда x = 1.
графических неравенств на числовой прямой решить на онлайн калькуляторе
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
03.2006 
08.2005 
04.2003 
Я настоятельно рекомендую вам попробовать Algebrator.
Это действительно отличное математическое программное обеспечение. Я помню, как решал задачи с рациональными выражениями, дополнениями к углам и расчетными формулами. Я просто набирал задачу из рабочей тетради, нажимал «Решить» — и пошагово решал домашнее задание по математике. Очень рекомендую программу.