Один из подходов к изучению тригонометрии в 10-м классе
Разделы: Математика
Еще в 1905 г. русские читатели могли прочесть в книге Уильяма Джеймса “Психология” его рассуждения о том, “почему зубрение представляет такой дурной способ учения?”
“Знания, приобретенные путем простого зубрения, почти неизбежно забываются совершенно бесследно. Наоборот, умственный материал, набираемый памятью постепенно, день за днем, в связи с различными контекстами, связанный ассоциативно с другими внешними событиями и неоднократно подвергший обсуждению, образует такую систему, вступает в такую связь с остальными сторонами нашего интеллекта, легко возобновляется в памяти массою внешних поводов, что остается надолго прочным приобретением”.
С тех пор прошло более 100 лет, а слова эти поразительно остаются злободневными. В этом каждодневно убеждаешься, занимаясь со школьниками. Массовые пробелы в знаниях настолько велики, что можно утверждать: школьный курс математики в дидактическом и психологическом отношениях – не система, а некое устройство, поощряющее кратковременную память и нисколько не заботиться о памяти долговременной.
Знать школьный курс математики – значит владеть материалом каждого из направлений математики, быть в состоянии актуализировать любое из них в любое время. Чтобы достичь этого, нужно систематически обращаться каждому из них, что порой не всегда возможно из-за сильной загруженности на уроке.
Есть другой путь долговременного запоминания фактов и формул – это опорные сигналы.
Тригонометрия – один из больших разделов школьной математики, изучаемой в курсе геометрии 8, 9 классов и в курсе алгебры 9 класса, алгебры и начал анализа в 10 классе.
Самый большой объем изучаемого материала по тригонометрии приходится на долю 10 класса. Большую часть этого материала из тригонометрии можно изучить и запомнить на тригонометрическом круге (окружность единичного радиуса с центром в начале прямоугольной системы координат). Приложение1.ppt
Это следующие понятия тригонометрии:
- определения синуса, косинуса, тангенса и котангенса угла;
- радианное измерение углов;
- область определения и область значений тригонометрических функций
- значения тригонометрических функций для некоторых значений числового и углового аргумента;
- периодичность тригонометрических функций;
- четность и нечетность тригонометрических функций;
- возрастание и убывание тригонометрических функций;
- формулы приведения;
- значения обратных тригонометрических функций;
- решение простейших тригонометрических уравнений;
- решение простейших неравенств;
- основные формулы тригонометрии.
Рассмотрим изучение этих понятий на тригонометрическом круге.
1) Определение синуса, косинуса, тангенса и котангенса.
После введения понятия тригонометрического круга (окружность единичного радиуса с центром в начале координат), начального радиуса (радиус окружности по направлению оси Ох), угла поворота, учащиеся самостоятельно получают определения для синуса, косинуса, тангенса и котангенса на тригонометрическом круге, используя определения из курса геометрии, то есть, рассматривая прямоугольный треугольник с гипотенузой, равной 1.
Косинусом угла называется абсцисса точки на окружности при повороте начального радиуса на данный угол.
Синусом угла называется ордината точки на окружности при повороте начального радиуса на данный угол.
2) Радианное измерение углов на тригонометрическом круге.
После введения радианной меры угла (1 радиан – это центральный угол, которому соответствует длина дуги, равная длине радиуса окружности), учащиеся делают вывод, что радианное измерение угла – это числовое значение угла поворота на окружности, равное длине соответствующей дуги при повороте начального радиуса на заданный угол. .
Тригонометрический круг разделен на 12 равных частей диаметрами окружности. Зная, что угол радианам, можно определить радианное измерение для углов кратных .
и т.д.
А радианные измерения углов, кратных, получаются аналогично:
3) Область определения и область значений тригонометрических функций.
Будет ли соответствие углов поворота и значений координат точки на окружности функцией?
Каждому углу поворота соответствует единственная точка на окружности, значит данное соответствие – функция.
Получаем функции
На тригонометрическом круге видно, что область определения функций – множество всех действительных чисел, а область значений — .
Введем понятия линий тангенсов и котангенсов на тригонометрическом круге.
1) Пусть Введем вспомогательную прямую, параллельную оси Оу, на которой определяются тангенсы для любого числового аргумента.
2) Аналогично получаем линию котангенсов. Пусть у=1, тогда . Значит, значения котангенса определяются на прямой, параллельной оси Ох.
На тригонометрическом круге без труда можно определить область определения и область значений тригонометрических функций:
для тангенса —
для котангенса —
4) Значения тригонометрических функций на тригонометрическом круге.
Катет , противолежащий углу в равен половине гипотенузы, то есть Другой катет по теореме Пифагора:
Значит по определению синуса, косинуса, тангенса, котангенса можно определить значения для углов кратных или радианам. Значения синуса определяются по оси Оу, косинуса по оси Ох, а значения тангенса и котангенса можно определить по дополнительным осям, параллельным осям Оу и Ох соответственно.
Табличные значения синуса и косинуса расположены на соответствующих осях следующим образом:
Табличные значения тангенса и котангенса —
5) Периодичность тригонометрических функций.
На тригонометрическом круге видно, что значения синуса, косинуса повторяются через каждые радиана, а тангенса и котангенса – через радиан.
6)Четность и нечетность тригонометрических функций.
Это свойство можно получить, сравнивая значения положительных и им противоположных углов поворота тригонометрических функций. Получаем, что
Значит, косинус – четная функция, все остальные функции – нечетные.
7) Возрастание и убывание тригонометрических функций.
По тригонометрическому кругу видно, что функция синус возрастает и убывает
Аналогично рассуждая, получаем промежутки возрастания и убывания функций косинуса, тангенса и котангенса.
8) Формулы приведения.
За угол берем меньшее значение угла на тригонометрическом круге. Все формулы получаются в сравнении значений тригонометрических функций на катетах выделенных прямоугольных треугольников.Алгоритм применения формул приведения:
1) Определить знак функции при повороте на заданный угол.
При повороте на угол функция сохраняется, при повороте на угол — целое, нечетное число, получается кофункция (
9) Значения обратных тригонометрических функций.
Введем обратные функции для тригонометрических функций, пользуясь определением функции.
Каждому значению синуса, косинуса, тангенса и котангенса на тригонометрическом круге соответствует только одно значение угла поворота. Значит, для функции область определения , область значений — Для функции область определения — , область значений — . Аналогично получаем область определения и область значений обратных функций для косинуса и котангенса.
Алгоритм нахождения значений обратных тригонометрических функций:
1) нахождение на соответствующей оси значения аргумента обратной тригонометрической функции;
2) нахождение угла поворота начального радиуса с учетом области значений обратной тригонометрической функции.
Например:
10) Решение простейших уравнений на тригонометрическом круге.
Чтобы решить уравнение вида , найдем точки на окружности, ординаты которых равны и запишем соответствующие углы с учетом периода функции.
Для уравнения , найдем точки на окружности, абсциссы которых равны и запишем соответствующие углы с учетом периода функции.
Аналогично для уравнений вида Значения определяются на линиях тангенсов и котангенсов и записываются соответствующие углы поворота.
11) Решение неравенств.
Чтобы решить неравенства вида , необходимо найти точки на окружности с ординатой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точки на окружности с абсциссой и прочитать соответствующее неравенство против часовой стрелки с учетом периода функции.
Чтобы решить неравенства вида , необходимо найти точку на линии тангенсов с координатой и прочитать соответствующее неравенство против часовой стрелки с учетом области определения и периода функции.
Аналогично для неравенств с котангенсом.
Необходимо практиковать чтение промежутков на тригонометрическом круге, тогда решения неравенств определяются безошибочно.
12) Основные формулы тригонометрии.
1) Основные тригонометрические тождества.
Очевидны выводы формул которые получаются в прямоугольном треугольнике на тригонометрическом круге.
2) Формулы сложения выводятся с использованием скалярного произведения векторов начального и “конечного” радиусов.
Другие формулы сложения получаются с использованием предыдущей, формул приведения и свойств четности и нечетности тригонометрических функций.
Почти все формулы тригонометрии являются следствиями этих основных формул.
Все понятия и формулы тригонометрии получают сами ученики под четким руководством учителя с помощью тригонометрического круга. В дальнейшем этот “круг” будет служить для них опорным сигналом или внешним фактором для воспроизведения в памяти понятий и формул тригонометрии.
Выводы:
Изучение тригонометрии на тригонометрическом круге способствует:
- выбору оптимального для данного урока стиль общения, организации учебного сотрудничества;
- целевые ориентиры урока становятся личностно значимыми для каждого ученика;
- новой материал опирается на личный опыт действия, мышления, ощущения учащегося;
- урок включает в себя различные формы работы и способы получения и усвоения знаний; присутствуют элементы взаимо- и самообучения; само- и взаимоконтроля;
- имеет место быстрое реагирование на непонимание и ошибку (совместное обсуждение, опоры-подсказки, взаимоконсультации).
18.01.2008
xn--i1abbnckbmcl9fb.xn--p1ai
основные понятия, история :: SYL.ru
Синус, косинус, тангенс – при произнесении этих слов в присутствии учеников старших классов можно быть уверенным, что две трети из них потеряют интерес к дальнейшему разговору. Причина кроется в том, что основы тригонометрии в школе преподаются в полном отрыве от реальности, а потому учащиеся не видят смысла в изучении формул и теорем.
В действительности данная область знаний при ближайшем рассмотрении оказывается весьма интересной, а также прикладной – тригонометрия находит применение в астрономии, строительстве, физике, музыке и многих других областях.
Ознакомимся с основными понятиями и назовем несколько причин изучить этот раздел математической науки.
История
Неизвестно, в какой момент времени человечество начало создавать будущую тригонометрию с нуля. Однако документально зафиксировано, что уже во втором тысячелетии до нашей эры египтяне были знакомы с азами этой науки: археологами найден папирус с задачей, в которой требуется найти угол наклона пирамиды по двум известным сторонам.
Более серьезных успехов достигли ученые Древнего Вавилона. На протяжении веков занимаясь астрономией, они освоили ряд теорем, ввели особые способы измерения углов, которыми, кстати, мы пользуемся сегодня: градусы, минуты и секунды были заимствованы европейской наукой в греко-римской культуре, в которую данные единицы попали от вавилонян.Предполагается, что знаменитая теорема Пифагора, относящаяся к основам тригонометрии, была известна вавилонянам почти четыре тысячи лет назад.
Название
Дословно термин «тригонометрия» можно перевести как «измерение треугольников». Основным объектом изучения в рамках данного раздела науки на протяжении многих веков был прямоугольный треугольник, а точнее – взаимосвязь между величинами углов и длинами его сторон (сегодня с этого раздела начинается изучение тригонометрии с нуля). В жизни нередки ситуации, когда практически измерить все требуемые параметры объекта (или расстояние до объекта) невозможно, и тогда возникает необходимость недостающие данные получить посредством расчётов.
Например, в прошлом человек не мог измерить расстояние до космических объектов, а вот попытки эти расстояния рассчитать встречаются задолго до наступления нашей эры. Важнейшую роль играла тригонометрия и в навигации: обладая некоторыми знаниями, капитан всегда мог сориентироваться ночью по звездам и скорректировать курс.
Основные понятия
Для освоения тригонометрии с нуля требуется понять и запомнить несколько основных терминов.
Синус некоторого угла – это отношение противолежащего катета к гипотенузе. Уточним, что противолежащий катет – это сторона, лежащая напротив рассматриваемого нами угла. Таким образом, если угол составляет 30 градусов, синус этого угла всегда, при любом размере треугольника, будет равен ½. Косинус угла – это отношение прилежащего катета к гипотенузе.Тангенс – это отношение противолежащего катета к прилежащему (либо, что то же самое, отношение синуса к косинусу). Котангенс – это единица, деленная на тангенс.
Стоит упомянуть и знаменитое число Пи (3,14…), которое представляет собой половину длины окружности с радиусом в одну единицу.
Популярные ошибки
Люди, изучающие тригонометрию с нуля, совершают ряд ошибок – в основном по невнимательности.
Во-первых, при решении задач по геометрии необходимо помнить, что использование синусов и косинусов возможно только в прямоугольном треугольнике. Случается, что учащийся «на автомате» принимает за гипотенузу самую длинную сторону треугольника и получает неверные результаты вычислений.
Во-вторых, поначалу легко перепутать значения синуса и косинуса для выбранного угла: напомним, что синус 30 градусов численно равен косинусу 60, и наоборот. При подстановке неверного числа все дальнейшие расчёты окажутся неверными.В-третьих, пока задача полностью не решена, не стоит округлять какие бы то ни было значения, извлекать корни, записывать обыкновенную дробь в виде десятичной. Часто ученики стремятся получить в задаче по тригонометрии «красивое» число и сразу же извлекают корень из трёх, хотя ровно через одно действие этот корень можно будет сократить.
Этимология слова «синус»
История слова «синус» поистине необычна. Дело в том, что буквальный перевод этого слова с латыни означает «впадина». Всё потому, что верное понимание слова затерялось при переводе с одного языка на другой.
Названия базовых тригонометрических функций произошли из Индии, где понятие синуса обозначалось словом «тетива» на санскрите — дело в том, что отрезок вместе с дугой окружности, на которую он опирался, походил на лук. Во времена расцвета арабской цивилизации индийские достижения в области тригонометрии были заимствованы, и термин перешел в арабский язык в виде транскрипции. Случилось так, что в этом языке уже было похожее слово, обозначающее впадину, и если арабы понимали фонетическую разницу между родным и заимствованным словом, то европейцы, переводящие научные трактаты на латынь, по ошибке буквально перевели арабское слово, никакого отношения к понятию синуса не имеющее. Им мы и пользуемся по сей день.
Таблицы значений
Существуют таблицы, в которые занесены числовые значения для синусов, косинусов и тангенсов всех возможных углов. Ниже представим данные для углов в 0, 30, 45, 60 и 90 градусов, которые необходимо выучить как обязательный раздел тригонометрии для «чайников», благо запомнить их довольно легко.
Если случилось так, что числовое значение синуса или косинуса угла «вылетело из головы», есть способ вывести его самостоятельно.Геометрическое представление
Начертим круг, через его центр проведем оси абсцисс и ординат. Ось абсцисс располагается горизонтально, ось ординат – вертикально. Обычно они подписываются как «X» и «Y» соответственно. Теперь из центра окружности проведем прямую таким образом, чтобы между ней и осью X получился нужный нам угол. Наконец, из той точки, где прямая пересекает окружность, опустим перпендикуляр на ось X. Длина получившегося отрезка будет равна численному значению синуса нашего угла.
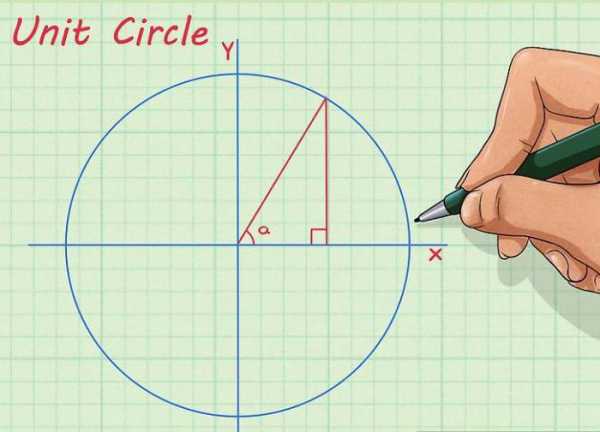Данный способ весьма актуален, если вы забыли нужное значение, например, на экзамене, и учебника по тригонометрии под рукой нет. Точной цифры вы таким образом не получите, но разницу между ½ и 1,73/2 (синус и косинус угла в 30 градусов) вы точно увидите.Применение
Одними из первых специалистов, использующих тригонометрию, были моряки, не имеющие никакого другого ориентира в открытом море, кроме неба над головой. Сегодня капитаны кораблей (самолётов и других видов транспорта) не ищут кратчайший путь по звёздам, зато активно прибегают к помощи GPS-навигации, которая без использования тригонометрии была бы невозможна.
Практически в каждом разделе физики вас ждут расчёты с использованием синусов и косинусов: будь то приложение силы в механике, расчёты пути объектов в кинематике, колебания, распространение волн, преломление света – без базовой тригонометрии в формулах просто не обойтись.
Ещё одна профессия, которая немыслима без тригонометрии – это геодезист. Используя теодолит и нивелир либо более сложный прибор – тахиометр, эти люди измеряют разницу в высоте между различными точками на земной поверхности.
Повторяемость
Тригонометрия имеет дело не только с углами и сторонами треугольника, хотя именно с этого она начинала своё существование. Во всех областях, где присутствует цикличность (биологии, медицине, физике, музыке и т. д.) вы встретитесь с графиком, название которого наверняка вам знакомо — это синусоида.
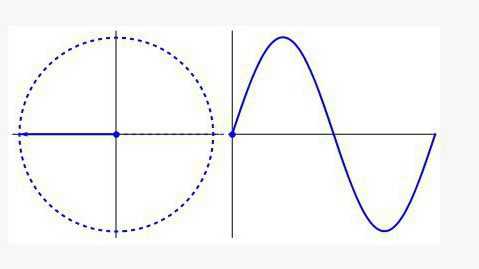Такой график представляет собой развёрнутую вдоль оси времени окружность и внешне похож на волну. Если вы когда-нибудь работали с осциллографом на занятиях по физике, вы понимаете, о чем идет речь. Как музыкальный эквалайзер, так и прибор, отображающий сердечные ритмы, используют формулы тригонометрии в своей работе.В заключение
Задумываясь о том, как выучить тригонометрию, большинство учащихся средней и старшей школы начинают считать её сложной и непрактичной наукой, поскольку знакомятся лишь со скучной информацией из учебника.
Что касается непрактичности — мы уже увидели, что в той или иной степени умение обращаться с синусами и тангенсами требуется практически в любой сфере деятельности. А что касается сложности… Подумайте: если люди пользовались этими знаниями больше двух тысяч лет назад, когда взрослый человек имел меньше знаний, чем сегодняшний старшеклассник, реально ли изучить данную область науки на базовом уровне лично вам? Несколько часов вдумчивых занятий с решением задач – и вы достигнете своей цели, изучив базовый курс, так называемую тригонометрию для «чайников».www.syl.ru
Тригонометрические функции. Алгебра, 10 класс: уроки, тесты, задания.
Вход на портал Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв- Предметы
- Алгебра
- 10 класс
-
Числовая окружность
-
Синус и косинус. Тангенс и котангенс
-
Тригонометрические функции числового аргумента
-
Тригонометрические функции углового аргумента
-
Свойства функции y = sinx и её график
-
Свойства функции y = cosx и её график
-
Периодичность тригонометрических функций, чётность, нечётность
-
График гармонического колебания (профильный)
-
Функции y = tgx, y = ctgx, их свойства и график
-
Обратные тригонометрические функции (профильный)
www.yaklass.ru
А-10 Ср-01 ВАРИАНТ 1 | А-10 Ср-01 ВАРИАНТ 2 | А-10 Ср-01 ВАРИАНТ 3 | А-10 Ср-01 ВАРИАНТ 4 |
1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: |
А-10 Ср-01 ВАРИАНТ 5 | А-10 Ср-01 ВАРИАНТ 6 | А-10 Ср-01 ВАРИАНТ 7 | А-10 Ср-01 ВАРИАНТ 8 |
1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: |
А-10 Ср-01 ВАРИАНТ 9 | А-10 Ср-01 ВАРИАНТ 10 | А-10 Ср-01 ВАРИАНТ 11 | А-10 Ср-01 ВАРИАНТ 12 |
1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: |
А-10 Ср-01 ВАРИАНТ 13 | А-10 Ср-01 ВАРИАНТ 14 | А-10 Ср-01 ВАРИАНТ 15 | А-10 Ср-01 ВАРИАНТ 16 |
1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: | 1°. Переведите в радианы: 2°. Выразите в градусах: 3. На числовой окружности отметьте точку с координатой: 4. В какой четверти координатной окружности лежит число: |
nsportal.ru
Урок на тему «Тригонометрия» 10 класс
Класс: 10
Предмет: алгебра
Дата проведения: 9.04.2014 г.
Тема урока: Тригонометрия
Цели урока:
— Обобщить и систематизировать знания учащихся по теме: «Тригонометрия».
— способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, развить математический кругозор мышление, математическую речь, внимание, память, и навыки самоконтроля;
— содействовать воспитанию интереса к математике.
Тип урока:
Урок обобщения и систематизации знаний по теме: «Тригонометрия » с использованием фронтальной, индивидуальной работы.
Оборудование:
презентация к уроку, раздаточный материал и индивидуальные задания.
Ход урока.
1 Организационный момент
Здравствуйте, садитесь! Тема сегодняшнего урока «Тригонометрия». В ходе урока мы с вами повторим и закрепим теорию по теме: «Тригонометрия», тригонометрические формулы, свойства тригонометрических функций, проверим умения преобразовывать тригонометрические выражения, решать тригонометрические уравнения и неравенства.
Что такое тригонометрия?
Скучные и никому не нужные формулы скажут почти все старшеклассники и многие из вас. Тем не менее, я хочу вас в этом разубедить. Чтобы взглянуть на тригонометрию по-новому, я предлагаю Вам поработать на уроке.
И начну я наш урок словами русского математика и академика Андрея Андреевича Маркова: «Не бойтесь формул! Учитесь владеть этим инструментом Человеческого гения! В формулах заключено величие и могущество разума…»
А теперь откройте тетради, запишите сегодняшнее число и тему урока «Тригонометрия». У каждого из вас на столе лежит лист самооценки сейчас я попрошу вас его заполнить и ознакомиться с планом урока.
«Решение кроссворда» — предлагается решить кроссворд, а затем осуществить проверку
КРОССВОРД
1
2
3
4
5
6
7
8
9
10
11
12
13
По вертикали: Название раздела математики, в переводе с греческого означает «измерение треугольников».
По горизонтали:
1.У какой функции наименьший положительный период равен π
2. От него зависит значение функции.
3. Мера измерения угла.
4. Какой функции недостает: sin x, cos x, ctg x….
5. Значение тригонометрических функций повторяется через.
6. Cos x — тригонометрическая…..
7. Как называется график функции sin x?
8. Интервал, полуинтервал, отрезок, луч, открытый луч – одним словом что это?
9. Есть в каждом слове, у растения а также есть у уравнения.
10. Утверждение, требующее доказательства.
11. Ось ОУ.
12. Ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол α.
13. Sin x — нечетная функция, а cos x -……
Верно ли что?
Да- ˄, нет- __
1. arcsin (-α) =π — arcsin α.
2. Область определения тангенса ( +πn;), где n ϵ z .
3. Котангенс в 4 четверти положительный.
4. cos(π-45°)=.
5. Если tg х =0, то х=πn, где n ϵ z.
6. Синус — функция четная.
7. График функции y=cos x — симметричен относительно начала координат.
8.Решением неравенства sin x> является промежуток (+2πn; +2πn),где
nϵz.
9. sin 279° — число отрицательное.
10. sin (arccos )=?
1 2 3 4 5 6 7 8 9 10
. . . . . . . . . . .
Баллы: 10-9 -«5», 8-7-«4», 6-5-«3», 4-0 -«2».
Оценка: «___». Молодец!!!
3. Узнай формулу и собери цифры в цепочку:
0. Разность косинусов. 0. sinx*cosy+cosx*siny
1.Уравнение касательной. 1.cosx*cosy-sinx*siny
2.Производная котангенса. 2.3sin x-4 sin³ x
3.Синус тройного аргумента. 3.
4.Косинус суммы. 4.-
5.Синус разности. 5.у=f (xₒ)+f´(xₒ)(x-xₒ)
6.Сумма синусов. 6. sinx*cosy-cosx*siny
7. Косинус разности. 7. cosx*cosy+sinx*siny
8.Производная тангенса. 8. 1-2sin²x
9.Косинус двойного аргумента. 9.
*. Синус суммы. *.
Ответы:
0* 15 24 32 41 56 63 77 89 98 *0
3.Тест
1 Упростить выражение: + cos
A) -1
B) cos
C) 1
D) sin
E) sin
2 Найти tg, если sin = – , 180 < < 270
A) 1
B)
C) 1
D)
E) 2
3 Упростить выражение:
A) cos
B) sin
C) tg
D) sin
E) cos
4 Упростить выражение:
A) — sin
B) — cos
C) tg
D) cos
E) sin
5 Вычислить : 2sin 30 — sin 60сtg 45tg 30
A)
B)
C) – ()
D)
E) –
6. Решите тригонометрическое уравнение
Не правильного ответа
7 . Отношение синуса угла к косинусу угла есть … угла .
A) котангенс
B) тангенс
C) косинус
D ) синус
E) арккостнус
8 .Если осуществить поворот точки Р(1;0) на угол , то точка будет находиться в следующей четверти:
А) I
В) II
С) III
D) IV
E) нет правильного ответа
9. Градусная мера углов равностороннего треугольника равна … градусам.
А) 60
В) 80
С) 120
D) 30
Е) 90
10. Центральный угол, опирающийся на дугу, длина которого равна радиусу окружности, называется углом в … радиан.
А) 2
В) 1
С) 2
D) 5
Е) 3
Ответы:
1-С
2-А
3-В
4-Д
5-А
6-А
7-В
8-В
9-А
10-В
4.Самостоятельная работа
Решить тригонометрические уравнения
Пример 1. Решить уравнение .
Решение. Это уравнение является квадратным относительно . Поэтому сделаем замену . В результате получим уравнение . Его корни: , то есть получаем уравнение или . Первое уравнение дает . Второе уравнение не имеет корней.
Ответ: .
Пример 2. Решить уравнение
Решение. Вместо соs2x подставим 1-sin2x, тогда исходное уравнение примет вид b 1-sin2x-2sin x+2=0
-sin2x-2sin x+3=0 *(-1)
sin2x+2sin x-3=0 поэтому сделаем замену
sin x=t,тогда уравнение примет вид t2+2t-3=0, получим корни
t1=-3. t2=1, то есть получаем уравнение
sin x=1,имеет решение х=
Пример 3. Решить уравнение 2 sin x — 3cosx=0
Решение. Разделив обе части уравнения почленно на cos x, получим 2 tg x-3=0, получим 2 tg x=3, tg x= , х= arctg +
Пример 4. Решить уравнение .
Решение. Применяя формулу синуса двойного угла, получим , . Полученное уравнение равносильно совокупности уравнений:
Решение 1-го уравнения:
Уравнение преобразуем к виду имеющему решение
5. Итог урок и выставление оценок
6.Домашнее задание
infourok.ru
Урок 7. Введение в тригонометрию. Теория. Видеоурок. Алгебра 11 Класс
На этом уроке мы познакомимся с определениями тригонометрических функций и их основными свойствами, узнаем, как работать с тригонометрической окружностью, выясним, что такое период функции и вспомним о различных способах измерения углов. Кроме этого, разберемся с применением формул приведения.
Данный урок поможет Вам подготовиться к одному из типов задания В7.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 7.Введение в тригонометрию.
Теория
Конспект урока
Сегодня мы с вами начинаем раздел, который имеет пугающее для многих название «Тригонометрия». Давайте сразу выясним, что это не отдельный предмет, похожий по названию на геометрию, как некоторые думают. Хотя в переводе с греческого слово «тригонометрия» означает «измерение треугольников» и имеет прямое отношение к геометрии. Кроме этого тригонометрические вычисления широко применяются в физике и технике. Но начнем мы с вами именно с рассмотрения того, как основные тригонометрические функции вводятся в геометрии с помощью прямоугольного треугольника.
Только что мы использовали термин «тригонометрическая функция» ‑ это означает, что мы введем целый класс определенных законов соответствия одной переменной величины от другой.
Для этого рассмотрим прямоугольный треугольник, в котором для удобства используются стандартные обозначения сторон и углов, которые вы можете видеть на рисунке:
Рассмотрим, например, угол и введем для него следующие действия:
— отношение противолежащего катета к гипотенузе назовем синусом, т.е.
— отношение прилежащего катета к гипотенузе назовем косинусом, т.е. ;
— отношение противолежащего катета к прилежащему назовем тангенсом, т.е. ;
— отношение прилежащего катета к противолежащему назовем котангенсом, т.е. .
Все эти действия с углом называют тригонометрическими функциями. Сам угол, при этом, принято называть аргументом тригонометрической функции и его можно обозначать, например, иксом, как это обыкновенно принято в алгебре.
Важно сразу понять, что тригонометрические функции зависят именно от угла в прямоугольном треугольнике, а не от его сторон. Это легко доказать, если рассмотреть треугольник, подобный данному, в нем длины сторон будут другими, а все углы и отношения сторон не изменятся, т.е. останутся неизменными и тригонометрические функции углов.
После такого определения тригонометрических функций может возникнуть вопрос: «А существует ли например ? Ведь угла в прямоугольном треугольнике быть не может». Как ни странно, но ответ на этот вопрос утвердительный, причем, значение этого выражения равно , а это еще больше удивляет, поскольку все тригонометрические функции являются отношением сторон прямоугольного треугольника, а длины сторон являются положительными числами.
Но никакого парадокса в это
interneturok.ru
Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»
Разделы: Математика
Цель урока:
- Закрепить навыки решения простейших тригонометрических уравнений.
- Сформировать понятие решения тригонометрических уравнений сводящихся к квадратным.
- Развивать умения сравнивать, выявлять закономерности, обобщать.
- Воспитывать ответственное отношение к труду.
Оборудование:
- Карточки для повторения формул решения простейших тригонометрических уравнений.
- Плакат с алгоритмом решения тригонометрических уравнений (большой на доску и каждому на стол).
Литература: Учебник Колмагорова “Алгебра и начала анализа, 10-11 класс”.
Ход урока.
I. Повторение
1. sin x = a, cos x = a, tg x = a
При каких значениях а эти уравнения имеют решения?
[sin x и cos x при /а/ 1 tg x при любом a]
2. Повторить формулы решения простейших тригонометрических уравнений (на карточках):
sin x = а х = (-1)к arc sin a+
к, к z
sin x = 0
sin x = 1
sin x = -1
cos x = a x=± arc cos a + 2 , n z
cos x = 0
cos x = 1
cos x = -1
tg x = a x = arc tg a + n, n z
arc sin (-а) = — arc sin а
arc cos (-а) = — arc cos а
arc tg а (-а) = — arc tg а
II. Проверка домашнего задания.
Игра “Поле чудес”. Правила игры несколько изменены, а название оставлено.
Правила игры.
- Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же примеров или задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.
- Каждому ученику учитель дает карточку с заданиями и ученик сразу начинает решать.
- На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.
- Ниже записаны числа по порядку (по количеству букв в высказывании).
- Ученик, выполнявший задание, называет номер своей карточки и букву, под которой записан ответ.
- Учитель под числом (…) ставит букву (…). И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.
- За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь более чем число.
Ум хорошо, а два лучше
12 3 45 67 8 9 10 11 12 13 14 15 1 6 17
| а | в | д |
| n z | , к z | , n z |
| е | л | м |
| , n z | , n z | , n z |
| о | р | у |
| , n z | , n z | , n z |
| x | ч | ш |
| , n z | , n z | , n z |
Уравнение:
| , n z | у | |
| cos x = -1 | х = +2 n, n z | м |
| , n z | x | |
| , n z | o | |
| , n z | p | |
| , n z | o | |
| , n z | ш | |
| , n z | o | |
| , n z | a | |
| , n z | д | |
| , k z | в | |
| , n x | a | |
| , n z | л | |
| , n z | у | |
| , n z | ч | |
| , n z | ш | |
| , n z | е |
Дополнительные уравнения
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , n z | |
| , k z | |
| , n z | |
| , k z | |
| , k z | |
| , n z | |
| , n z |
III. Объяснение нового.
1.
- В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a
- К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.
- Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.
2.
- На доске записаны уравнения:
а) 3х-8=х+6 (линейное уравнение)
б) х2+2х-15=0 (квадратное уравнение)
в) х4-5х2+4=0 (квадратное уравнение
относительно х2).
г) 2 cos2x-cosx-1=0 (квадратное уравнение
относительно cosx)
- Какие из них являются квадратными?
- Общий вид квадратного уравнения:
ax2+bx+c=0
,
Корни квадратного уравнения, приведенного, т.е. х2+рх+q=0 можно находить по теореме Виета:
Х1+х2=-р; х1х2=q
- х4-5х2+4=0 – квадратное уравнение относительно х2. Это уравнение назвали биквадратным. Общий вид ах4+вх2+с=0, где а± 0.
- Его легко решить методом введения новой переменной, т.е. х2=а и уравнение принимает вид: а2-5а+4=0
3. Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у2-у-1=0. Получили квадратное уравнение.
Д=1+8=9;
Следовательно:
а) cosx=1 б) cosx=
х=2p n, n z , n z
, n n
Ответ: 2 n, n z; , n z
4. Решим уравнение:
Надо привести уравнение к одной функции. Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:
Пусть xinx=у, тогда 2у2+5у-3=0
Получили квадратное уравнение
Д=25+24=49
;
Следовательно:
а) б) xinx=-3 – решение не имеет
, к z
, к z
Ответ: , к z
5.
tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgx через tgx.
пусть tgx=у, то у2+у-2=0 (дальше, как в предыдущем случае).
6. Для закрепления
4 xin2x- cosx-1=0
Заменим xin2x на 1- cos2x. Получим
4(1- cos2x)- cosx-1=0
4-4 cos2x- cosx-1=0
-4 cos2x- cosx+3=0
4 cos2x+ cosx-3=0
пусть cosx=у, то
4у2+у-3=0
Д=1-48=49 ;
Следовательно,
а) cosx=-1 б)
х= +2 n, n z , n z
Ответ: +2 n; , n z
7. №164 (в) — cамостоятельно
2 xin2x- xinx-1=0
пусть xinx=у, то
2у2-у-1=0
Д=1+8=9;
Следовательно,
а) xinx=1 б)
, n z , n z
,к z.
Ответ: , n z
, к z
№ 165(б)
2 xin2x+3 cosx=0
Заменим xin2x на 1- cos2x получим
2(1- cos2x)+3 cosx=0
2-2 cos2x+3 cosx=0
-2 cos2x+3 cosx+2=0, т.е.
2 cos2x-3 cosx-2=0
пусть cosx=у, то
2у2-3у=0
Д=9+16=25
;
Следовательно,
а) cosx=2 б)
решение не имеет , n z
, n z
, n z
Ответ: , n z
8.
Итог урока
Алгоритм решения тригонометрических уравнений.
- Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.
- Ввести новую переменную.
- Записать данное уравнение, используя эту переменную.
- Найти корни полученного квадратного уравнения.
- Перейти от новой переменной к первоначальной.
- Решить простейшие тригонометрические уравнения.
- Записать ответ.
26.02.2008
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai