Как найти производную. Таблица производных.
 Как мы знаем,
Как мы знаем,
Производной функции называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

Математический смысл этого определения понять не очень просто, поскольку в школьном курсе алгебры понятие предела функции либо не изучают совсем, либо изучают очень поверхностно. Но для того, чтобы научиться находить производные различных функций, это и не обязательно.
Тем, кто все же хочет понять, что такое предел числовой последовательности, я предлагаю посмотреть ВИДЕОУРОК:
Операция нахождения производной функции называется дифференцированием. В результате выполнения этой операции мы по определенным правилам получаем другую функцию:

В этом равенстве  — функция, от которой мы берем производную,
— функция, от которой мы берем производную,
 — функция, которая получается в результате этой операции.
— функция, которая получается в результате этой операции.
Для того, чтобы каждый раз не искать
производные элементарных функций, используя определение производной, существует таблица производных элементарных функций:1. Производная константы равна нулю:

2. Производная степенной функции:

Заметим, что  может принимать любые действительные значения.
может принимать любые действительные значения.
Примеры.
1. 
2. 
3. 
3. Производная показательной функции:

Пример.

Частный случай этой формулы:

4. Производная логарифма:

Частный случай этой формулы:

5. Производные тригонометрических функций:




6. Производные обратных тригонометрических функций:




Правила дифференцирования:
1. Производная суммы двух функций:

2. Производная произведения двух функций:

3. Производная дроби:

4. Производная произведения функции на число равна произведению числа на производную функции (число «выносится» за знак производной):

Чтобы правильно найти производную функции  , полезно придерживаться такого алгоритма:
, полезно придерживаться такого алгоритма:
1. Выделите, какие элементарные функции входят в состав уравнения функции.
2. Отделите в явном виде коэффициенты.
3. Если возможно, упростите выражение  , используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции
, используя свойства степени, свойства логарифмов или тригонометрические формулы в зависимости от того, какие элементарные функции входят в состав функции 
4. Вспомните, чему равны производные этих функций или посмотрите в таблице производных.
5. Обратите внимание на то, какими арифметическими действиями связаны между собой элементарные функции, которые входят в состав функции  и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
и вспомните правило, по которому находится производная суммы, разности, произведения или частного двух функций.
Пример 1. Найти производную функции:


Используя свойства логарифмов, упростим выражение в правой части уравнения функции:

Так как по условию  , следовательно,
, следовательно, 
Таким образом:

Пример 2. Найти производную функции:

1. Упростим каждую дробь, используя свойства степени :

Мы видим, что наша функция представляет собой сумму степенных функций.
Следовательно:

Пример 3. Найти производную функции

Сначала запишем каждое слагаемое в виде степени  и выделим в явном виде числовые коэффициенты:
и выделим в явном виде числовые коэффициенты:

Теперь легко найти производную:

Пример 4. Найти производную функции:

Мы видим, что наша функция представляет собой дробь, в числителе которой стоит степенная функция, а в знаменателе сумма косинуса и константы.
Найдем производную функции  по формуле производной дроби:
по формуле производной дроби:

В нашем случае:


Отсюда:

КАК ИСКАТЬ ПРОИЗВОДНУЮ СЛОЖНОЙ ФУНКЦИИ читайте здесь
Видеоурок «Производная сложной функции» смотрите здесь.
И.В. Фельдман, репетитор по математике.
Производная сложной функции — примеры решений
Основные формулы
Здесь мы приводим примеры вычисления производных от следующих функций:
; ; ; ; .
Если функцию можно представить как сложную функцию в следующем виде:
,
то ее производная определяется по формуле:
.
В приводимых ниже примерах, мы будем записывать эту формулу в следующем виде:
.
где .
Здесь нижние индексы или , расположенные под знаком производной, обозначают переменные, по которой выполняется дифференцирование.
Обычно, в таблицах производных, приводятся производные функций от переменной x. Однако x – это формальный параметр. Переменную x можно заменить любой другой переменной. Поэтому, при дифференцировании функции от переменной , мы просто меняем, в таблице производных, переменную x на переменную u.
Простые примеры
Пример 1
Найти производную сложной функции
.
Решение
Запишем заданную функцию в эквивалентном виде:
.
В таблице производных находим:
;
.
По формуле производной сложной функции имеем:
.
Здесь .
Ответ
.
Пример 2
Найти производную
.
Решение
Выносим постоянную 5 за знак производной и из таблицы производных находим:
.
Применяем формулу производной сложной функции:
.
Здесь .
Ответ
.
Пример 3
Найдите производную
.
Решение
Выносим постоянную –1 за знак производной и из таблицы производных находим:
;
Из таблицы производных находим:
.
Применяем формулу производной сложной функции:
.
Здесь .
Ответ
.
Более сложные примеры
В более сложных примерах мы применяем правило дифференцирования сложной функции несколько раз. При этом мы вычисляем производную с конца. То есть разбиваем функцию на составные части и находим производные самых простых частей, используя таблицу производных. Также мы применяем правила дифференцирования суммы, произведения и дроби. Затем делаем подстановки и применяем формулу производной сложной функции.
Пример 4
Найдите производную
.
Решение
Выделим самую простую часть формулы и найдем ее производную. .
Применяем правило дифференцирования сложной функции.
.
Здесь мы использовали обозначение
.
Находим производную следующей части исходной функции, применяя полученные результаты. Применяем правило дифференцирования суммы:
.
Еще раз применяем правило дифференцирования сложной функции.
.
Здесь .
Ответ
.
Пример 5
Найдите производную функции
.
Решение
Выделим самую простую часть формулы и из таблицы производных найдем ее производную. .
Применяем правило дифференцирования сложной функции.
.
Здесь
.
Дифференцируем следующую часть, применяя полученные результаты.
.
Здесь
.
Дифференцируем следующую часть.
.
Здесь
.
Теперь находим производную искомой функции.
.
Здесь
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:

Правила вычисления производных
Вычисление производных основано на применении следующих правил, которые мы будем использовать без доказательств, поскольку доказательства выходят за рамки школьного курса математики.
Правило 1 (производная от произведения числа на функцию). Справедливо равенство
(c f (x))’ = c f ‘ (x) ,
где c – любое число.
Другими словами, производная от произведения числа на функцию равна произведению этого числа на производную функции.
Правило 2 (производная суммы функций). Производная суммы функций вычисляется по формуле
(f (x) + g (x))’ = f ‘ (x) + g’ (x),
то есть производная от суммы функций равна сумме производных этих функций.
Правило 3 (производная разности функций). Производная разности функций вычисляется по формуле
(f (x) – g (x))’ = f ‘ (x) – g’ (x),
то есть производная от разности функций равна разности производных этих функций.
Правило 4 (производная произведения двух функций). Производная произведения двух функций вычисляется по формуле
(f (x) g (x))’ =
= f ‘ (x) g (x) + f (x) g’ (x),
Другими словами, производная от произведения двух функций равна производной от первой функции, умноженной на вторую функцию, плюс первая функция, умноженная на производную от второй функции.
Правило 5 (производная частного двух функций). Производная от дроби (частного двух функций) вычисляется по формуле
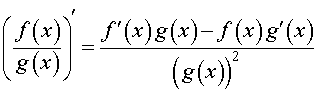
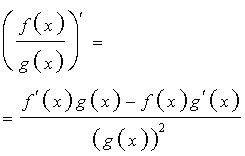
Определение. Рассмотрим функции f (x) и g (x) . Сложной функцией или «функцией от функции» называют функцию вида
f (g (x))
При этом функцию f (x) называют внешней функцией, а функцию g (x) – внутренней функцией.
Правило 6 (производная сложной функции). Производная сложной функции вычисляется по формуле
[ f (g (x))]’ = f ‘ (g (x)) g’ (x)
Другими словами, для того, чтобы найти производную от сложной функции f (g (x)) в точке x нужно умножить производную внешней функции, вычисленную в точке g (x) , на производную внутренней функции, вычисленную в точке x .
Таблица производных часто встречающихся функций
В следующей таблице приведены формулы для производных от степенных, показательных (экспоненциальных), логарифмических, тригонометрических и обратных тригонометрических функций. Доказательство большинства их этих формул выходит за рамки школьного курса математики.
| Функция | Формула для производной | Название формулы |
y = c , где c – любое число | y’ = 0 | Производная от постоянной функции |
y = x c , где c – любое число | y’ = c xc – 1 | Производная степенной функции |
| y = e x | y’ = e x | Производная от экспоненты (показательной функции с основанием e) |
y = a x где a – любое положительное число, не равное 1 | y’ = a x ln a | Производная от показательной функции с основанием a |
| y = ln x , x > 0 | 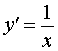 , x > 0 , x > 0 | Производная от натурального логарифма |
y = log a x , x > 0 где a – любое положительное число, не равное 1 | 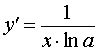 , x > 0 , x > 0 | Производная от логарифма по основанию a |
| y = sin x | y’ = cos x | Производная синуса |
| y = cos x | y’ = – sin x | Производная косинуса |
y = tg x ,
|  , , 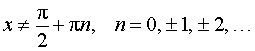 | Производная тангенса |
y = ctg x ,
| 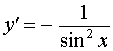 , , 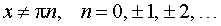 | Производная котангенса |
y = arcsin x , | 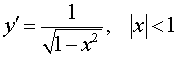 | Производная арксинуса |
y = arccos x , |  | Производная арккосинуса |
| y = arctg x | 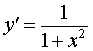 | Производная арктангенса |
| y = arcctg x | 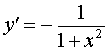 | Производная арккотангенса |
| Производная от постоянной функции |
Функция: y = c , где c – любое число Формула для производной: y’ = 0 |
| Производная степенной функции |
Функция: y = x c , где c – любое число Формула для производной: y’ = c xc – 1 |
| Производная от экспоненты (показательной функции с основанием e) |
Функция: y = e x Формула для производной: y’ = e x |
| Производная от показательной функции с основанием a |
Функция: y = a x где a – любое положительное число, не равное 1 Формула для производной: y’ = a x ln a |
| Производная от натурального логарифма |
Функция: y = ln x , x > 0 Формула для производной: 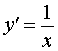 , x > 0 , x > 0 |
| Производная от логарифма по основанию a |
Функция: y = log a x , x > 0 где a – любое положительное число, не равное 1 Формула для производной: 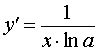 , x > 0 , x > 0 |
| Производная синуса |
Функция: y = sin x Формула для производной: y’ = cos x |
| Производная косинуса |
Функция: y = cos x Формула для производной: y’ = – sin x |
| Производная тангенса |
Функция: y = tg x , где 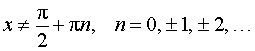 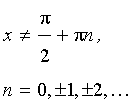 Формула для производной:  , ,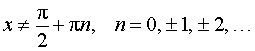 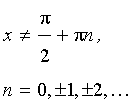 |
| Производная котангенса |
Функция: y = ctg x , где 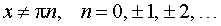 Формула для производной: 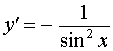 , ,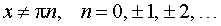 |
| Производная арксинуса |
Функция: y = arcsin x , Формула для производной: 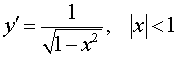 |
| Производная арккосинуса |
Функция: y = arccos x , Формула для производной:  |
| Производная арктангенса |
Функция: y = arctg x Формула для производной: 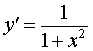 |
| Производная арккотангенса |
Функция: y = arcctg x Формула для производной: 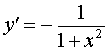 |
Таблица производных сложных функций
В следующей таблице приведены формулы для производных сложных функций.
В отдельных строках (с желтым фоном) приведены формулы для производных сложных функций в случае, когда внутренняя функция является линейной функцией и имеет вид f (x) = kx + b , где k и b – любые числа, 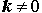 .
.
| Функция | Формула для производной |
y = (kx + b) c , где c – любое число. | y’ = kc (kx + b) c – 1 , |
y = ( f (x)) c , где c – любое число. | 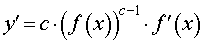 |
| y = ekx + b | y = kekx + b |
| y = e f (x) |  |
y = akx + b где a – любое положительное число, не равное 1 | 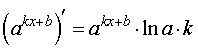 |
y = a f (x) где a – любое положительное число, не равное 1 |  |
| y = ln (kx + b) , kx + b > 0 | 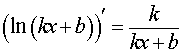 , ,kx + b > 0 |
| y = ln ( f (x)) , f (x) > 0 | 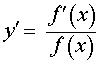 , ,f (x) > 0 |
y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 |  , kx + b > 0 , kx + b > 0 |
y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 | 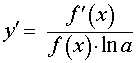 , f (x) > 0 , f (x) > 0 |
| y = sin (kx + b) | y’ = k cos (kx + b) |
| y = sin ( f (x)) | 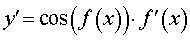 |
| y = cos (kx + b) | y’ = – k sin (kx + b) |
| y = cos ( f (x)) | 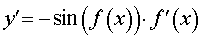 |
y = tg (kx + b), где | 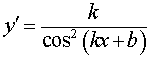 , , 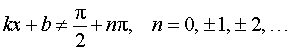 |
y = tg ( f (x)), где | 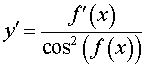 , , 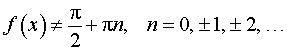 |
y = ctg (kx + b), где | 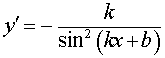 , ,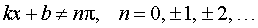 |
y = ctg ( f (x)), где | 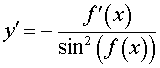 , ,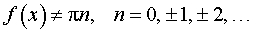 |
y = arcsin (kx + b), 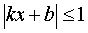 | 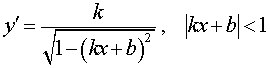 |
y = arcsin ( f (x)), 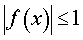 |  |
y = arccos (kx + b), 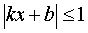 | 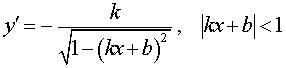 |
y = arccos ( f (x)), 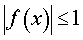 | 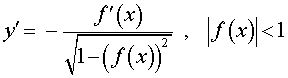 |
| y = arctg (kx + b) | 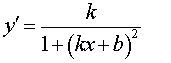 |
| y = arctg ( f (x)) | 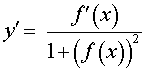 |
| y = arcctg (kx + b) | 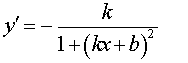 |
| y = arcctg ( f (x)) | 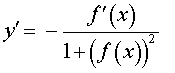 |
Функция: y = (kx + b) c , где c – любое число. Формула для производной: y’ = kc (kx + b) c – 1 , |
Функция: y = ( f (x)) c , где c – любое число. Формула для производной: 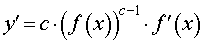 |
Функция: y = ekx + b Формула для производной: y = kekx + b |
Функция: y = e f (x) Формула для производной:  |
Функция: y = akx + b где a – любое положительное число, не равное 1 Формула для производной: 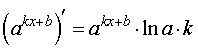 |
Функция: y = a f (x) где a – любое положительное число, не равное 1 Формула для производной:  |
Функция: y = ln (kx + b) , kx + b > 0 Формула для производной:
|
Функция: y = ln ( f (x)) , f (x) > 0 Формула для производной:
|
Функция: y = log a (kx + b) , kx + b > 0 где a – любое положительное число, не равное 1 Формула для производной:  , kx + b > 0 , kx + b > 0 |
Функция: y = log a ( f (x)) , f (x) > 0 где a – любое положительное число, не равное 1 Формула для производной: 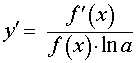 , f (x) > 0 , f (x) > 0 |
Функция: y = sin (kx + b) Формула для производной: y’ = k cos (kx + b) |
Функция: y = sin ( f (x)) Формула для производной: 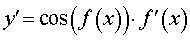 |
Функция: y = cos (kx + b) Формула для производной: y’ = – k sin (kx + b) |
Функция: y = cos ( f (x)) Формула для производной: 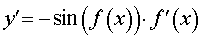 |
Функция: y = tg (kx + b), где Формула для производной: 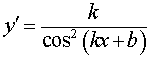 , , 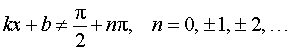 |
Функция: y = tg ( f (x)), где Формула для производной: 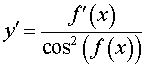 , , 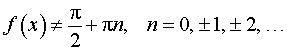 |
Функция: y = ctg (kx + b), где Формула для производной: 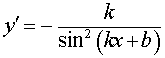 , , 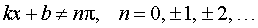 |
Функция: y = ctg ( f (x)), где Формула для производной: 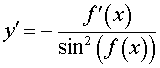 , , 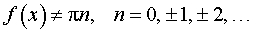 |
Функция: y = arcsin (kx + b), Формула для производной: 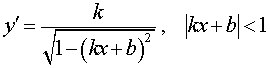 |
Функция: y = arcsin ( f (x)), Формула для производной:  |
Функция: y = arccos (kx + b), Формула для производной: 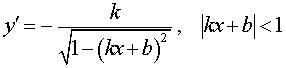 |
Функция: y = arccos ( f (x)), Формула для производной: 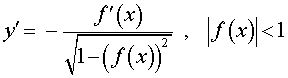 |
Функция: y = arctg (kx + b) Формула для производной: 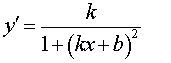 |
Функция: y = arctg ( f (x)) Формула для производной: 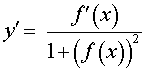 |
Функция: y = arcctg (kx + b) Формула для производной: 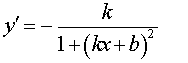 |
Функция: y = arcctg ( f (x)) Формула для производной: 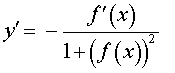 |

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на свет таблицы производных и правил дифференцирования. Начало положено в статье о смысле производной, которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий: Как найти производную? и Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это без пределов функций. Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, что производная
функции 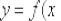 в точке
в точке 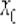 определяется формулой:
определяется формулой:
Напоминаю обозначения и термины: 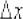 называют приращением аргумента;
называют приращением аргумента;
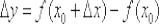 – приращением функции;
– приращением функции;
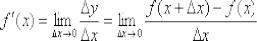
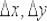 – это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что 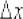 является «динамической» переменной,
является «динамической» переменной, 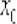 – константой и результат вычисления предела
– константой и результат вычисления предела 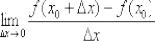 – числом (иногда – «плюс» либо «минус» бесконечностью).
– числом (иногда – «плюс» либо «минус» бесконечностью).
В качестве точки 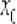
 , принадлежащее области определения функции
, принадлежащее области определения функции 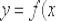 , в котором существует производная.
, в котором существует производная.! Примечание: оговорка «в котором существует производная» – в общем случае существенна! Так, например, точка 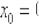 хоть и входит в область определения функции
хоть и входит в область определения функции 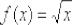 , но производной
, но производной
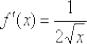 там не существует. Поэтому формула
там не существует. Поэтому формула
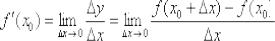 не применима в точке
не применима в точке 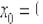
и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены 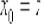 , получаем вторую рабочую формулу:
, получаем вторую рабочую формулу:
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение 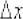 . Результатом вычисления предела
. Результатом вычисления предела
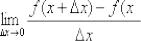 является производная функция
является производная функция 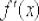
Исходя из вышесказанного, сформулируем условия двух типовых задач:
–Найти производную в точке, используя определение производной.
–Найти производную функцию, используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность), а во втором –
функцию. Кроме того, производной может и вовсе не существовать.
Как найти производную по определению?
Составить отношение 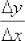 и вычислить предел
и вычислить предел 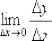 .
.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу

действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожить таблицу производных, оттачивая алгоритм и технические приёмы решения:
Пример 1
Найти производную функции 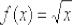 , пользуясь определением производной
, пользуясь определением производной

По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: 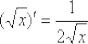 .
.
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую (конкретную) точку 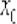 , принадлежащую области определения функции
, принадлежащую области определения функции 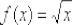 , в которой существует производная. Зададим в данной точке приращение
, в которой существует производная. Зададим в данной точке приращение 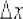 (разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
(разумеется, не выходящее за рамки о/о-я) и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим
числитель и знаменатель на сопряженное выражение 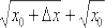 :
:
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций.
Итак, 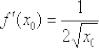 .
.
Поскольку в качестве 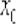 можно выбрать ЛЮБУЮ точку
можно выбрать ЛЮБУЮ точку  интервала
интервала

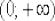 , то, осуществив замену
, то, осуществив замену 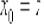 , получаем:
, получаем:
Ответ: по определению производной: 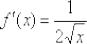
Готово.
В который раз порадуемся логарифмам:
Пример 2
Найти производную функции  , пользуясь определением производной
, пользуясь определением производной
Решение: рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от
подстрочного индекса и вместо буквы 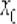 использовать букву
использовать букву  .
.
Рассмотрим произвольную точку 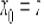 , принадлежащую области определения функции
, принадлежащую области определения функции 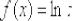 (интервалу
(интервалу 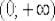
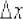 . А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
. А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может
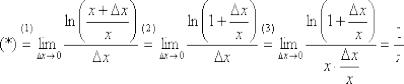
возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому:  – античная статуя, а
– античная статуя, а 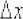 – живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости  закомментирую пошагово:
закомментирую пошагово:
(1)Используем свойство логарифма 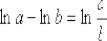 .
.
(2)В скобках почленно делим числитель на знаменатель.
(3)В знаменателе искусственно домножаем и делим на «икс» чтобы
воспользоваться замечательным пределом 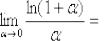 , при этом в качестве бесконечно малой величины выступает
, при этом в качестве бесконечно малой величины выступает 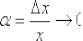 .
.
Ответ: по определению производной: 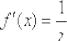
Или сокращённо: 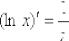
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Пример 3
Найти производную 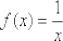 по определению
по определению

тоже вполне конкретное число | и так же подставляем его в | |
функцию | вместо «икса»: | |
|
| . Записываем разность |
| , при этом | необходимо полностью взять в |
скобки. |
|
|
Составленное приращение функции 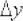 бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
бывает выгодно сразу же упростить. Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы 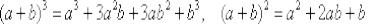 , раскрываем скобки и сокращаем всё, что можно сократить:
, раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
В итоге: 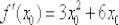
Поскольку в качестве 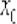 можно выбрать любое действительное число, то проведём замену
можно выбрать любое действительное число, то проведём замену 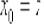 и получим
и получим 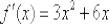 .
.
Ответ: 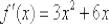 по определению.
по определению.
В целях проверки найдём производную с помощью правил

дифференцирования и таблицы:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Пример 6
Найти производную функции 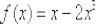 по определению производной
по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Вернёмся к стилю №2: Пример 7
Пользуясь определением, найти производную функции
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции:
Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую 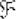 , зададим в ней приращение аргумента
, зададим в ней приращение аргумента 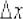 и составим приращение
и составим приращение
функции:
Найдём производную:

(1) Используем тригонометрическую формулу
.
(2)Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3)Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4)В силу нечётности синуса выносим «минус». Под косинусом
указываем, что слагаемое 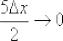 .
.
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел 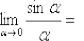 . Таким образом, неопределённость устранена, причёсываем результат.
. Таким образом, неопределённость устранена, причёсываем результат.
Ответ: 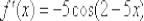 по определению Как видите, основная трудность рассматриваемой задачи упирается в
по определению Как видите, основная трудность рассматриваемой задачи упирается в
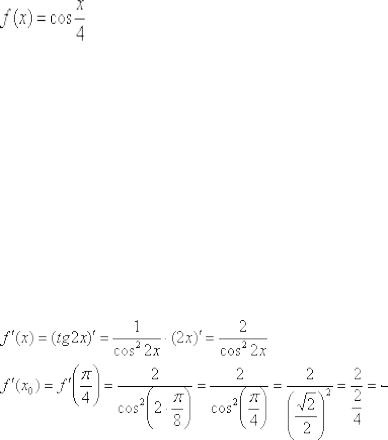
сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пример 8
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Пример 9
Найти производную функции  в точке
в точке 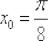 , пользуясь определением производной.
, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число Вычислим ответ стандартным способом:
Решение: с точки зрения наглядности это задание значительно проще, так как в формуле 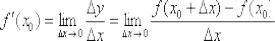 вместо
вместо 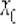
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Пример 11
Будет ли дифференцируема функция 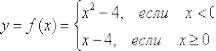 в точке
в точке 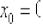 ?
?
Решение: очевидно, что кусочно-заданная функция непрерывна в точке 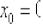 , но будет ли она там дифференцируема?
, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1)Находим левостороннюю производную в данной точке: 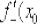 .
.
2)Находим правостороннюю производную в данной точке: 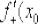 .
.
3)Если односторонние производные конечны и совпадают:
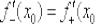 , то функция
, то функция 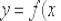 дифференцируема в точке
дифференцируема в точке 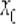 и
и
геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной).
Если получены два разных значения: 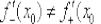 (одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке
(одно из которых может оказаться и бесконечным), то функция не дифференцируема в точке 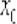 .
.
Если же обе односторонние производные равны бесконечности
(пусть даже разных знаков), то функция 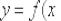 не
не
дифференцируема в точке 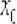 , но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).
, но там существует бесконечная производная и общая вертикальная касательная к графику (см. Пример 5 урока Уравнение нормали).

Ответ: 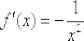 по определению производной
по определению производной

Ответ: 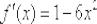 по определению.
по определению.
Пример 8: Решение: рассмотрим произвольную точку  , принадлежащую
, принадлежащую 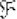 , зададим в ней приращение
, зададим в ней приращение 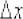 и составим приращение функции:
и составим приращение функции:
Найдём производную:
Используем тригонометрическую формулу
и первый замечательный
предел:
Ответ: 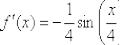 по определению
по определению
Пример 10: Решение: Зададим приращение 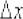 в точке
в точке  . Тогда приращение функции:
. Тогда приращение функции:
Вычислим производную в точке:
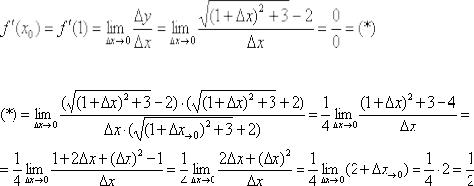
Умножим числитель и знаменатель на сопряженное выражение:
Ответ: 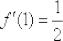 по определению производной в точке
по определению производной в точке
производных правил
Производная сообщает нам наклон функции в любой точке.
Существует правил , которым мы можем следовать, чтобы найти много производных.
Например:
- Наклон значения константы (например, 3) всегда 0
- Уклон линии , такой как 2x, равен 2, или 3x равен 3 и т. Д.
- и тд.
Вот полезные правила, которые помогут вам определить производные многих функций (с примерами ниже).Примечание: маленькая метка ’означает« производная от », а f и g — функции.
Журнал Правило власти Суммарное правило| Общие функции | Функция | Производная |
|---|---|---|
| Константа | с | 0 |
| Линия | х | 1 |
| топор | а | |
| Площадь | x 2 | 2x |
| квадратный корень | √x | (½) x -½ |
| экспоненциальный | е x | е x |
| а x | ln (a) a x | |
| логарифмов | лн (х) | 1 / х |
| a (x) | 1 / (x ln (a)) | |
| Тригонометрия (х в радианах) | грех (х) | cos (x) |
| cos (x) | син (х) | |
| загар (х) | с 2 (х) | |
| Обратная тригонометрия | грех -1 (х) | 1 / √ (1-x 2 ) |
| cos -1 (x) | -1 / √ (1 − x 2 ) | |
| загар -1 (х) | 1 / (1 + x 2 ) | |
| Правила | Функция | Производная |
| Умножение на константу | ср | ср ’ |
| x n | nx n − 1 | |
| ф + г | f ’+ g’ | |
| Разница Правило | ф — г | f ‘- g’ |
| Правило продукта | фг | ф г + ф г г41 |
| частное правило | ф / г | (ф ‘г — г’ ф) / г 2 |
| Взаимное правило | 1 / ф | -f ’/ f 2 |
| Цепное правило (как «Композиция функций») | г ºG | (f ’º g) × g’ |
| Цепное правило (используя ’) | ф (г (х)) | ф (г (х)) г (х) |
| Цепное правило (с помощью д дх ) | ди дх знак равно ди du du дх | |
«Производная» также написано д дх
Так д дх sin (x) и sin (x) ’означают« производная от греха (x) »
Примеры
Пример: что является производной от греха (х)?
Из приведенной выше таблицы он указан как cos (x)
Это может быть записано как:
грех (х) = соз (х)
или:
sin (x) ’= cos (x)
Power Rule
Пример: что такое х 3 ?
Вопрос задается «что является производной от х 3 ?»
Мы можем использовать Правило Власти, где n = 3:
x n = nx n − 1
x 3 = 3x 3−1 = 3x 2
(Другими словами, производная x 3 равна 3x 2 )
Так что это просто так:
«умножьте на мощность
, затем уменьшите мощность на 1″
Может также использоваться в таких случаях:
Пример: что такое (1 / x)?
1 / x также x -1
Мы можем использовать Правило Власти, где n = −1:
x n = nx n − 1
x -1 = -1x -1-1
= −x −2
= -1 x 2
Итак, мы только что сделали это:
, что упрощает до -1 / x 2
Умножение на константу
Пример: что такое 5x 3 ?
производная от cf = cf ’
производная от 5f = 5f ’
Мы знаем (из правила власти):
x 3 = 3x 3−1 = 3x 2
Итак:
5x 3 = 5x 3 = 5 × 3x 2 = 15x 2
Сумма Правило
Пример: Какова производная от х 2 + х 3 ?
Суммарное правило гласит:
производная от f + g = f ’+ g’
Таким образом, мы можем обработать каждую производную отдельно и затем добавить их
Использование правила власти:
- x 2 = 2x
- x 3 = 3x 2
И так:
производная х 2 + х 3 = 2x + 3x 2
Разница Правило
Это не обязательно должно быть x , мы можем различить, например, против :
Пример: Что такое (v 3 −v 4 )?
Правило Различия говорит
производная от f — g = f ’- g’
Таким образом, мы можем обработать каждую производную отдельно, а затем вычесть их.
Использование правила власти:
- В 3 = 3 В 2
- В 4 = 4 В 3
И так:
производная v 3 — v 4 = 3v 2 — 4v 3
правила сумм, разностей, умножения постоянных и степеней
Правило продукта
Пример: что является производной от cos (x) sin (x)?
Правило продукта гласит:
производная от fg = f g ’+ f’ g
В нашем случае:
Мы знаем (из таблицы выше):
- cos (x) = −sin (x)
- грех (х) = соз (х)
Итак:
производная от cos (x) sin (x) = cos (x) cos (x) — sin (x) sin (x)
= cos 2 (x) — sin 2 (x)
частное правило
Чтобы помочь вам вспомнить:
( f г ) ’= гс’ — fg ’ г 2
Производная от «High over Low»:
«Низкий dHigh минус High dLow, над линией и возведи в квадрат низкий»
Пример: какова производная от cos (x) / x?
В нашем случае:
Мы знаем (из таблицы выше):
Итак:
производная cos (x) x = Low dHigh минус High dLow над линией и возведите в квадрат Low
= x (−sin (x)) — cos (x) (1) x 2
= — xsin (x) + cos (x) x 2
Взаимное Правило
Пример: что такое (1 / x)?
Взаимное правило гласит:
производная 1 f = -f ’ f 2
При f (x) = x мы знаем, что f ’(x) = 1
Итак:
производная 1 x = -1 x 2
Это тот же результат, который мы получили выше, используя правило силы.
Цепное правило
Пример: что такое д дх грех (х 2 )?
грех (х 2 ) состоит из грех () и х 2 :
Цепное правило гласит:
производная от f (g (x)) = f ‘(g (x)) g’ (x)
Отдельные производные:
- f ‘(г) = cos (г)
- г ‘(х) = 2х
Итак:
д дх грех (х 2 ) = соз (г (х)) (2х)
= 2x cos (x 2 )
Другой способ написания правила цепочки: ди дх знак равно ди du du дх
Давайте сделаем предыдущий пример снова, используя эту формулу:
Пример: что такое д дх грех (х 2 )?
, Книжное решение «Фьючерсы на опционы и другие производные», Джон К. Халл — Главы 1,2,7,9,11,14,25
главы 1,2,7,9,11,14,25
Комментарии
- Пожалуйста, войдите или зарегистрируйтесь, чтобы оставлять комментарии.
- MSMoses •
2191 — Торговля опционами и стратегии
at uft
Показать еще 5 комментариев.
Предварительный просмотр
ГЛАВА 1 Введение Практические вопросы Задача 1.1 В чем разница между длинной передней и короткой передней позициями? Когда трейдер заключает долгосрочный форвардный контракт, он соглашается купить базовый актив по определенной цене в определенное время в будущем.Когда трейдер заключает короткий форвардный контракт, он соглашается продать базовый актив по определенной цене в определенное время в будущем. Задача 1.2. Тщательно объясните разницу между хеджированием, спекуляцией и арбитражем. Трейдер хеджирует, когда он подвержен влиянию цены актива, и занимает позицию в производной, чтобы компенсировать риск. В спекуляции трейдер не имеет возможности смещения. Она делает ставку на будущие движения цены актива. Арбитраж предполагает принятие позиции на двух или более различных рынках для фиксации прибыли.Задача 1.3. В чем разница между заключением длинного форвардного контракта, когда цена форвардна, и открытием длинной позиции в опционе колл с ценой страйка? В первом случае трейдер обязан купить актив для (трейдер не имеет выбор.) Во втором случае у трейдера есть возможность купить актив за (трейдер не обязан использовать опцион.) Задача 1.4. Тщательно объясните разницу между продажей опциона колл и покупкой опциона пут. Продажа опциона колл предполагает предоставление кому-либо права купить актив у вас.Это дает вам максимальный выигрыш (ST K 0) мин (K ST 0). Покупка опциона пут включает покупку опциона у кого-то другого. Это дает выигрыш max (K ST 0). В обоих случаях потенциальный выигрыш составляет K ST. Когда вы пишете опцион колл, выплата будет отрицательной или нулевой. (Это потому, что контрагент выбирает, выполнять ли.) Когда вы покупаете опцион пут, выплата равна нулю или положительна. (Это потому, что вы выбираете, следует ли заниматься спортом.) Задача 1.5. Инвестор заключает короткий форвардный контракт на продажу британских фунтов за доллары США по курсу доллара США за фунт.Сколько инвестор получает или теряет, если обменный курс в конце контракта составляет (а) 1,3900 и (б) 1,4200? (а) Инвестор обязан продать фунты за, когда они стоят 1,3900. Прибыль (б) Инвестор обязан продать фунты за, когда они стоят 1,4200. Потеря — это проблема 1.6. Трейдер заключает короткий фьючерсный контракт на хлопок, когда цена фьючерса составляет 50 центов за фунт. Контракт заключен на доставку фунтов. Сколько трейдер получает или теряет, если цена хлопка в конце контракта составляет (а) 48.20 центов за (б) 51,30 центов за фунт? (а) Трейдер продает за 50 центов за фунт что-то, что стоит 48,20 центов за фунт. Усиление . (б) Трейдер продает за 50 центов за фунт что-то, что стоит 51,30 центов за фунт. Потеря Задача 1.7. Предположим, вы написали пут-контракт с ценой исполнения и сроком действия через три месяца. Текущая цена акций и контракт на 100 акций. Что вы посвятили себя? Сколько вы можете получить или потерять? Вы продали опцион пут.Вы согласились купить 100 акций за акцию, если сторона на другой стороне контракта решит воспользоваться правом продажи по этой цене. Опцион будет исполнен только в том случае, если цена акций ниже. Предположим, например, что опцион реализуется, если цена указана: Вы должны покупать акции, которые стоят того, что вы потеряли за акцию, или полностью. Если опцион осуществляется при цене, вы теряете за акцию, или в целом. Худшее, что может случиться, это то, что цена акций в течение периода снижается почти до нуля.Это крайне маловероятное событие обойдется вам. В ответ на возможные будущие убытки вы получите цену опциона от покупателя. Задача 1.8. В чем разница между рынком и рынком? Каковы котировки заявок и предложений маркет-мейкера на рынке? Рынок представляет собой сеть финансовых учреждений, управляющих фондами и корпоративных казначеев, где два участника могут заключить любой взаимоприемлемый договор. Рынок — это рынок, организованный биржей, на которой трейдеры либо встречаются физически, либо общаются в электронном виде, а договоры, которыми можно торговать, были определены биржей.Когда маркет-мейкер цитирует заявку и предложение, заявка — это цена, по которой маркет-мейкер готов купить, а предложение — цена, по которой маркет-мейкер готов продать. Владелец опциона выиграет, если цена акции будет выше в марте. (Это игнорирует временную стоимость денег.) Опцион будет исполнен, если цена акции выше в марте. Прибыль как функция цены акций показана на рисунке S1.1. Рисунок S1.1 Прибыль с длинной позиции в задаче 1.13 Задача 1.14. Предположим, что июньский опцион пут на продажу акций по цене и держится до июня. При каких обстоятельствах продавец опциона (т. Е. Сторона с короткой позицией) получит прибыль? При каких обстоятельствах этот вариант будет реализован? Нарисуйте диаграмму, показывающую, как прибыль от короткой позиции в опционе зависит от цены акции в конце срока опциона. Продавец опциона потеряет деньги, если цена акции будет ниже в июне. (Это игнорирует временную стоимость денег.) Опцион будет исполнен, если цена акций ниже в июне. Прибыль как функция цены акций показана на рисунке S1.2. Рисунок S1.2 Прибыль от короткой позиции в Задаче 1.14 Задача 1.15. Это май, и трейдер пишет сентябрьский опцион колл со страйк-ценой «Цена акции», а цена опциона «Опишите денежные потоки», если опцион держится до сентября, а цена акции в это время. Трейдер имеет приток в мае и отток в сентябре. Денежные средства, полученные от продажи опциона.Это результат реализации опциона. Инвестор должен купить акцию в сентябре и продать ее покупателю опциона по Задаче 1.16. Трейдер записывает опцион пут на декабрь со страйк-ценой, равной цене опциона. При каких обстоятельствах трейдер получает прибыль? Трейдер получает прибыль, если цена акции выше во время исполнения. (Это игнорирует временную стоимость денег.) Задача 1.17. Компания знает, что она должна получить определенное количество иностранной валюты в течение четырех месяцев.Какой тип опционного контракта подходит для хеджирования? Длинная позиция в опционе «пут» может обеспечить страховку от падения обменного курса ниже цены исполнения. Это гарантирует, что иностранная валюта может быть продана по крайней мере по цене исполнения. Задача 1.18. Американская компания рассчитывает выплатить 1 миллион канадских долларов в течение шести месяцев. Объясните, как можно хеджировать валютный риск, используя (a) форвард (b) опцион. Компания может заключить долгосрочный форвардный контракт на покупку 1 миллиона канадских долларов за шесть месяцев.Это приведет к блокировке обменного курса, равного текущему. Прибыль равна терминальной стоимости опциона колл за вычетом суммы, уплаченной за опцион пут. (Заключение форвардного контракта ничего не стоит. Рисунок S1.3. Прибыль от портфеля в задаче 1.22. Задача 1.23. В 1980-х годах Bankers Trust разработал индексные валютные опционные облигации (ICON). Это облигации, в которых сумма получила срок погашения зависит от курса обмена валют, например, его торговля с Банком долгосрочного кредита Японии.ICON уточнил, что если курс доллара ST превышает 169 иен за доллар в конце срока погашения (в 1995 году), держатель облигации получает, если он меньше 169 иен за доллар, сумма, полученная держателем облигации. 169 макс. ST Когда обменный курс ниже 84,5, ничего не получено держателю в конце срока. Покажите, что эта иконка представляет собой сочетание обычной облигации и двух вариантов. Предположим, что обменный курс иены (иена за доллар) при погашении ICON равен ST. Выплата от ICON составляет ST 169, если 169, если ST 0, если ST 169. Когда ST 169, выплата может быть записана ST ST. Выплата от ICON — это выплата от: (a) Регулярной облигации (b) Короткой позиции в вызове Опционы на покупку иены с ценой исполнения (c) Длинная позиция в опционе на покупку опциона на покупку иены с ценой исполнения Это продемонстрировано в следующей таблице, в которой показана предельная стоимость различных компонентов позиции ST 169 Bond ST 169 Короткие вызовы ST 0 Длинные вызовы 0 1 ST 1 169 1 ST 1 169 Всего позиций 0 1 ST 0 Проблема 1.24. 1 июля 2011 года компания заключает форвардный контракт на покупку 10 миллионов японских иен 1 января 2012 года. 1 сентября 2011 года она заключает форвардный контракт на продажу 10 миллионов японских иен 1 января 2012 года Опишите отдачу от этой стратегии. Предположим, что форвардная цена контракта, заключенного 1 июля 2011 года, равна F1, а форвардная цена контракта, заключенного 1 сентября 2011 года, равна F2, а F1 и F2 измеряются в долларах за иену. Если на 1 января 2012 года стоимость одной японской иены (в долларах США) равна ST, тогда стоимость первого контракта (в миллионах долларов) в это время составляет 10 (ST F1), тогда как стоимость второго контракта (за проданную иену) в это время: 10 (F2 ST). Таким образом, общая выплата по двум контрактам составляет 10 (ST F1) 10 (F2 ST) 10 (F2 F1). Таким образом, если форвардная цена для доставки 1 января, 2012 год увеличился с 1 июля 2011 года по 1 сентября 2011 года, компания получит прибыль.(Обратите внимание, что обменный курс обычно выражается как количество иен за доллар США, а не как количество долларов за иену). Задача 1.25. Предположим, что спотовые и форвардные обменные курсы следующие: Спот форвард форвард 1.4580 1.4556 1.4518 Какие возможности открыты для арбитражера в следующих ситуациях? (а) Европейский опцион колл на покупку по цене 2 цента. (б) Европейский опцион пут на продажу по цене 2 цента. (a) Арбитраж покупает опцион колл и занимает короткую позицию в форвардном контракте. Если ST — это спотовая ставка терминала, прибыль от опциона колл будет на рисунке S1.4: Прибыль трейдеру A и трейдеру B в задаче 1.26. Задача 1.27. В марте американский инвестор поручает брокеру продать один июльский опцион на покупку пут на акцию. Цена акции и цена исполнения являются ценой опциона. Объясните, на что согласился инвестор. При каких обстоятельствах сделка окажется прибыльной? Каковы риски? Инвестор согласился купить 100 акций в июле (или ранее), если сторона на другой стороне сделки решит продать. Сделка окажется прибыльной, если опцион не будет исполнен или если цена акций будет выше во время исполнения.Риск для инвестора заключается в том, что цена акций падает до низкого уровня. Например, если цена акций падает до июля (маловероятно, но возможно), инвестор проигрывает. Это связано с тем, что опционы пут исполняются и оплачиваются за 100 акций, когда цена за акцию равна. Это приводит к потере, которая составляет лишь немного возмещать премию, полученную за опционы. Задача 1.28. Американская компания знает, что через три месяца ей придется заплатить 3 миллиона евро. Текущий обменный курс составляет 1,40000 долларов за евро. Обсудите, как форвардные и опционные контракты могут быть использованы компанией для хеджирования своего риска.Компания может заключить форвардный контракт, обязывающий ее купить 3 миллиона евро за три месяца по фиксированной цене (форвардная цена). Форвардная цена будет близка к текущей спотовой цене 1.4500, но не будет точно такой же. Альтернативой может быть покупка опциона колл, дающего компании право, но не обязательство купить 3 миллиона евро по определенному курсу (цене исполнения) в течение трех месяцев. Использование форвардного контракта бесплатно фиксирует обменный курс, который будет применяться через три месяца.Использование опциона колл обеспечивает за счет страховки от обменного курса, превышающего цену исполнения. Задача 1.29 (файл Excel). Цена акции — это то, что инвестор покупает один опционный контракт на покупку акций с ценой исполнения и продает опционный контракт на покупку акций с ценой исполнения рыночных цен опционов, соответственно. Опционы имеют одинаковую дату погашения. Опишите положение. Это известно как бычий спред и будет обсуждаться в главе 11. Прибыль показана на рисунке S1.5. Рисунок S1.5. Прибыль в задаче 1.29 Задача 1.30 Цена золота в настоящее время указана за унцию. Форвардная цена за доставку в течение одного года. Арбитражер может занимать деньги в год. Что должен делать арбитражер? Предположим, что стоимость хранения золота равна нулю и что золото не приносит дохода. Арбитражер должен занять деньги, чтобы купить определенное количество унций золота сегодня и заключить короткие форвардные контракты на такое же количество унций золота для доставки в течение одного года. Это означает, что золото покупается за унцию и продается за унцию.Предполагая, что стоимость заемных средств меньше, чем в год, это создает безрисковую прибыль. Задача 1.31. Текущая цена акции и опционы колл со страйк-ценой в настоящее время продаются для Инвестора, который чувствует, что цена акции вырастет, пытается выбрать между покупкой 100 акций и покупкой опционов колл (20 контрактов). Обе стратегии включают в себя инвестиции. Какой совет вы бы дали? Насколько высоко должна расти цена акций, чтобы стратегия опциона была более прибыльной? Вложение в опционы колл влечет за собой более высокие риски, но может привести к более высокой прибыли.Если цена акций остается у инвестора, который покупает опционы колл, теряет, тогда как инвестор, который покупает акции, не получает и не теряет ничего. Если цена акций повышается до инвестора, который покупает опционы колл, получает (120 95) 9400 600 бычий спред по нефти. Это обсуждается в главе 11. Задача 1.34. Предположим, что в ситуации с таблицей 1.1 корпоративный казначей сказал: будет миллион, чтобы продать через шесть месяцев. Если обменный курс составляет менее 1,41, я хочу, чтобы вы дали мне 1,41. Если оно больше 1,47, я приму 1.47. Если обменный курс будет между 1,41 и 1,47, я продам фунт стерлингов за обмен. Как вы можете использовать опционы, чтобы удовлетворить казначея? Вы продаете казначею пут-опцион на GBP со страйк-ценой 1,41 и покупаете у казначея опцион колл на GBP со страйк-ценой 1,47. Оба варианта стоят по миллиону фунтов и имеют срок погашения шесть месяцев. Это называется форвардным контрактом диапазона и обсуждается в главе 16. Задача 1.35. Опишите, как валютные опционы могут использоваться для хеджирования в ситуации, описанной в разделе 1.7, чтобы (а) ImportCo гарантировал, что его обменный курс будет меньше 1,4600, и (б) ExportCo гарантирован, что его обменный курс будет составлять не менее 1,4200. Используйте DerivaGem для расчета стоимости установки хеджирования в каждом случае, предполагая, что волатильность обменного курса — это процентные ставки в Соединенных Штатах, а процентные ставки в Великобритании — предположим. Предположим, что текущий обменный курс представляет собой среднее значение ставки и предложения в таблице. 1.1. ImportCo должен купить опционы на миллион с ценой исполнения 1.4600. ExportCo должен купить пут-опционы на миллион с ценой исполнения 1.4200. В этом случае валютный курс составляет 1,4409 (среднее значение котировок заявок и предложений в таблице 1.1.), (Внутренний) курс — это иностранный курс, волатильность и время исполнения — 0,25. Используя лист Equity_FX_Index_Futures_Options в калькуляторе параметров DerivaGem, выберите «Валюта» в качестве базового, а «Европейский» BlackScholes в качестве типа параметра. Программное обеспечение показывает, что звонок с ценой страйка 1.46 стоит 0,0245, а пут с ударом 1,42 стоит 0,0256. Это означает, что хеджирование будет стоить либо для ImportCo, либо для ExportCo. Задача 1.36. Трейдер покупает европейский опцион колл и продает европейский опцион пут. Опционы имеют одинаковый базовый актив, цену исполнения и срок погашения. Опишите положение. При каких обстоятельствах цена колла равна цене пута? У трейдера есть длинный европейский опцион колл со страйк-ценой K и короткий европейский опцион пут со страйк-ценой K.Предположим, что цена базового актива в конце срока действия опциона — ST. Если ST K, опцион колл исполняется инвестором, а опцион пут истекает бесполезно. Вознаграждение из портфеля тогда будет ST K. Если ST K, опцион колл истекает бесполезно, и опцион пут исполняется против инвестора. Стоимость для инвестора составляет K ST. В качестве альтернативы мы можем сказать, что выплата инвестору в этом случае является ST K (отрицательная сумма). Во всех случаях выплата является ST K, такой же, как выплата по форвардному контракту.Позиция эквивалентна форвардному контракту с ценой поставки K. Предположим, что F — форвардная цена. Если K F, созданный форвардный контракт имеет нулевое значение. Поскольку форвардный контракт эквивалентен длинному и короткому путам, это показывает, что цена колла равна цене пута, когда цена исполнения равна F. Дальнейшие 400 реализуются на основе между 1 января 2013 года и Март 2013 года. Хеджер будет облагаться налогом на всю прибыль в 2013 году. Спекулянт будет облагаться налогом в 2012 и 2013 годах.Задача 2.5. Что означает стоп-ордер на продажу? Когда это может быть использовано? Что означает лимитный ордер на продажу? Когда это может быть использовано? Стоп-ордер на продажу — это ордер на продажу по наилучшей доступной цене после достижения цены или ниже. Это может быть использовано для ограничения убытков от существующей длинной позиции. Лимитный ордер на продажу — это ордер на продажу по цене или более. Его можно использовать для указания брокеру, что следует открывать короткую позицию, при условии, что она может быть сделана по цене, более выгодной, чем Задача 2.6. В чем разница между операциями на маржинальных счетах, управляемых клиринговой палатой, и теми, которые администрируются брокером? Маржинальный счет, находящийся в ведении клирингового центра, отмечается ежедневно на рынке, и член клирингового центра должен ежедневно возвращать счет на установленный уровень. Маржинальный счет, управляемый брокером, также отмечается на рынке ежедневно. Однако счет не должен быть переведен на начальный уровень маржи на ежедневной основе. Его необходимо довести до начального уровня маржи, когда остаток на счете падает ниже уровня маржи обслуживания.Маржа поддержки обычно составляет около начальной маржи. Задача 2.7. Какие существуют различия в том, как котируются цены на валютном фьючерсном рынке, валютном спотовом рынке и валютном форвардном рынке? На фьючерсных рынках цены указаны как количество долларов США за единицу иностранной валюты. Спотовые и форвардные курсы котируются таким образом для британского фунта, евро, австралийского доллара и новозеландского доллара. Для других основных валют спотовые и форвардные курсы указаны как количество единиц иностранной валюты на доллар США.Задача 2.8. У стороны с короткой позицией в фьючерсном контракте иногда есть варианты относительно точного актива, который будет доставлен, где будет осуществляться доставка, когда будет осуществляться доставка и так далее. Эти опционы увеличивают или уменьшают цену фьючерса? Объясните свои рассуждения. Эти варианты делают контракт менее привлекательным для стороны с длинной позицией и более привлекательным для стороны с короткой позицией. Поэтому они имеют тенденцию снижать цену фьючерса. Задача 2.9. Каковы наиболее важные аспекты разработки нового фьючерсного контракта? Наиболее важными аспектами разработки нового фьючерсного контракта являются спецификация базового актива, размер контракта, условия поставки и месяцы поставки.Проблема 2.10. Объясните, как маржа защищает инвесторов от возможности дефолта. Маржа — это сумма денег, депонированная инвестором у его или ее брокера. Это является гарантией того, что инвестор может покрыть любые убытки по фьючерсному контракту. Остаток на счете маржи корректируется ежедневно, чтобы отражать прибыли и убытки по фьючерсному контракту. Если убытки выше определенного уровня, инвестор обязан внести дополнительную маржу. Эта система делает маловероятным, что инвестор будет дефолт.Подобная система наценок делает маловероятным, что брокер не выполнит свои обязательства по договору, который он имеет с участником клиринговой палаты, и маловероятно, что член клиринговой палаты выполнит дефолт с расчетной палатой. Проблема 2.11. Трейдер покупает два июльских фьючерсных контракта на замороженный апельсиновый сок. Каждый контракт на доставку фунтов. Текущая цена фьючерса составляет 160 центов за фунт, начальная маржа — за контракт, а маржа за обслуживание — за контракт. Какое изменение цены приведет к объявлению маржи? При каких обстоятельствах можно снять средства с маржинального счета? Существует маржинальный колл, если по одному контракту потеряно больше чем.Это происходит, если фьючерсная цена замороженного апельсинового сока падает более чем на 10 центов до уровня ниже 150 центов за фунт. может быть снята с маржинального счета, если есть прибыль по одному контракту. Это произойдет, если цена фьючерса вырастет с 6,67 цента до 166,67 цента за фунт. Задача 2.12. Покажите, что, если фьючерсная цена товара больше, чем спотовая цена в течение периода поставки, тогда существует арбитражная возможность. Существует ли возможность арбитража, если цена фьючерса меньше, чем спотовая цена? Поясните свой ответ.Если цена фьючерса больше, чем спотовая цена в течение периода поставки, арбитражер покупает актив, укорачивает фьючерсный контракт и осуществляет поставку с немедленной прибылью. Если цена фьючерса меньше спотовой цены в течение периода поставки, подобной совершенной арбитражной стратегии не существует. Арбитраж может занять длинную фьючерсную позицию, но не может форсировать немедленную доставку актива. Решение о том, когда будет произведена доставка, принимается партией с короткой позицией. Тем не менее, компании, заинтересованные в приобретении актива, могут посчитать привлекательным заключение второго контракта (F2 S) млн. Иен.Таким образом, общая сумма выплаты составляет (S F1) (F2 S) (F2 F1) млн. Иен. Задача 2.17. Форвардная цена на швейцарский франк для доставки через 45 дней указывается как Фьючерсная цена за контракт, который будет доставлен через 45 дней. Объясните эти две цитаты. Что является более выгодным для инвестора, желающего продать швейцарские франки? Форвардная котировка — это количество швейцарских франков на доллар. Котировки фьючерсов — это количество долларов за швейцарский франк. Когда котируется так же, как цена фьючерса, форвардная цена равна 1.Таким образом, швейцарский франк более ценен на срочном рынке, чем на срочном рынке. Таким образом, форвардный рынок более привлекателен для инвестора, желающего продать швейцарские франки. Задача 2.18. Предположим, вы позвонили своему брокеру и дали инструкции продать один июльский контракт на свиней. Опишите, что происходит. Фьючерсы на живых свиней торгуются на Чикагской товарной бирже. Брокер запросит некоторую начальную маржу. Заказ будет передан по телефону в вашу торговую стойку на этаже биржи (или в торговую стойку другого брокера).Затем он будет отправлен курьером комиссионному брокеру, который выполнит сделку в соответствии с вашими инструкциями. Подтверждение сделки в конечном итоге приходит к вам. В случае неблагоприятных изменений цены фьючерса ваш брокер может связаться с вами, чтобы запросить дополнительную маржу. Задача 2.19. на фьючерсных рынках чисто азартные игры. Не в общественных интересах разрешать спекулянтам торговать на фьючерсах. Обсудите эту точку зрения. Спекулянты являются важными участниками рынка, потому что они добавляют ликвидность на рынок.Однако контракты должны быть полезны как для хеджирования, так и для спекуляций. Это связано с тем, что регулирующие органы обычно утверждают контракты только тогда, когда они могут представлять интерес как для хеджеров, так и для спекулянтов. Проблема 2.20. Торговля фьючерсами на крупный рогатый скот осуществляется в июне, августе, октябре, декабре, феврале и апреле. Почему вы думаете, что открытый интерес для июньского контракта меньше, чем для августовского контракта в таблице 2.2? Как правило, чем короче срок погашения контракта, тем выше открытый интерес.Тем не менее, трейдеры, как правило, закрывают свои позиции в этом месяце непосредственно перед месяцем погашения. Это означает, что открытый интерес для ближайшего месяца погашения может быть меньше, чем для следующего ближайшего месяца погашения. Проблема 2.21. Как вы думаете, что произойдет, если биржа начнет торговать контрактом, в котором качество базового актива было указано не полностью? Контракт не будет успешным. Стороны с короткими позициями будут удерживать свои контракты до поставки, а затем доставлять самую дешевую форму актива.Вполне возможно, что партию с длинной позицией можно считать мусором! Как только новости о проблеме качества станут широко известны, никто не будет готов купить контракт. Это показывает, что фьючерсные контракты осуществимы, только если в отрасли существуют строгие стандарты для определения качества актива. Многие фьючерсные контракты на практике провалились из-за проблемы определения качества. Задача 2.22. фьючерсный контракт торгуется на полу биржи, это может быть случай, когда открытый интерес увеличивается, остается неизменным или уменьшается Объясните это утверждение.Если обе стороны сделки заключают новый договор, открытый интерес увеличивается на единицу. Если обе стороны сделки закрывают существующие позиции, открытый интерес уменьшается на единицу. Если одна сторона заключает новый контракт, в то время как другая сторона закрывает существующую позицию, открытый интерес остается тем же. Задача 2.23. Предположим, что 24 октября 2012 года компания продает один фьючерсный контракт на апрель 2013 года. Он закрывает свои позиции 21 января 2013 года. Цена фьючерса (за фунт) составляет 91.20 центов при заключении контракта, 88,30 центов при закрытии своей позиции и 88,80 центов в конце декабря 2012 года. Один контракт на поставку фунтов крупного рогатого скота. Какова общая прибыль? Как облагается налогом, если компания является (а) хеджером и (б) спекулянтом? Предположим, что компания имеет конец декабря 31 года. Общая прибыль: если компания является хеджером, все это облагается налогом в 2013 году. Если это спекулянт, то облагается налогом в 2012 году и облагается налогом в 2013 году.
