10 формул по физике
Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“
Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.
Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.
В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.
Соотношения закона Ома
Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:
| Искомая величина | Формула |
| Напряжение, В | U=I*R |
| Ток, А | I=U/R |
| Сопротивление, Ом | R=U/I |
| Мощность, Вт | P=U*I |
В этой таблице используются следующие общепринятые обозначения физических величин:
U — напряжение (В),
I — ток (А),
Р — мощность (Вт),
R — сопротивление (Ом),
Потренируемся на следующем примере: пусть нужно найти мощность схемы. Известно, что напряжение на ее выводах составляет 100 В, а ток— 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.
А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:
I = U / R
Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.
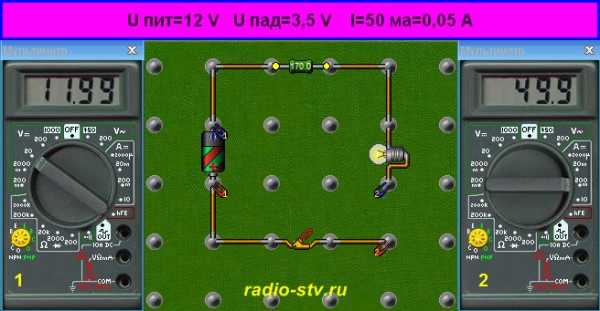
Что же в этой формуле есть что? Рассмотрим переменные подробнее.
> I: ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.
> R: искомое сопротивление токоограничивающего резистора, в омах.
В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:
R = U/I = 8,5 В / 0,050 А= 170 Ом
Расчёты сопротивления
Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.
Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.
> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.
> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.
Расчет сопротивления последовательных резисторов
Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)
В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.
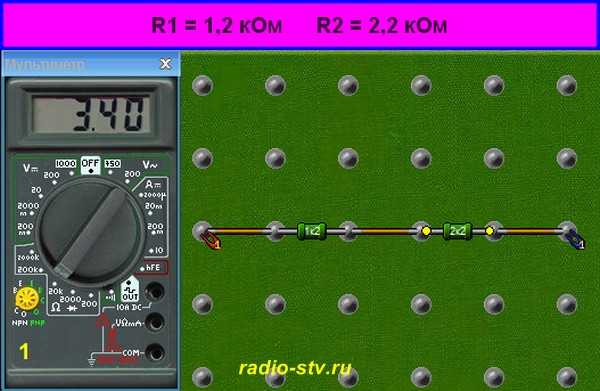
Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.
Расчет сопротивления параллельных резисторов
Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:
R общ = R1 * R2 / (R1 + R2)
где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим
776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:
Здесь снова величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов, a Rобщ — суммарная величина.
Расчёты ёмкости
Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.
Расчет емкости параллельных конденсаторов
Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:
Собщ = CI + С2 + СЗ + …
В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.
Расчет емкости последовательных конденсаторов
Собщ = С1 * С2 /( С1+С2)
где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи
Расчет емкости трех и более последовательно соединенных конденсаторов
В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:
И здесь опять величины C1, С2, СЗ и так далее — емкости отдельных конденсаторов, а Собщ. — суммарная величина.
Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.
Расчёт энергетических уравнений
Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:
ватт-часы = Р х Т
В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.
Расчёт постоянной ёмкости RC-цепочки
В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).
Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.
Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.
T = RC
В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.
Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.
Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:
| Значение емкости конденсатора, мкФ | Емкость конденсатора для расчета |
| 10 | 0,000 01 |
| 1 | 0,000 001 |
| 0,1 | 0,000 000 1 |
| 0,01 | 0,000 000 01 |
Расчёты частоты и длины волны
Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.
Расчет частоты сигнала
Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:
Частота = 300000 / длина волны
Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.
Расчет длины волны сигнала
Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:
Длина волны = 300000 / Частота
Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.
Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:
6000 миллиметров = 300000 / 50 МГц
Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!
radio-stv.ru
Практическое применение математических формул — MicroArticles
Формулы для промоугольника
Формула периметра Р=2(а+b)
Формула площади S=ab, где а и в – стороны прямоугольника
Формула для квадрата
Формула периметра Р=4а
Формула площади S=a 2, где а– сторона квадрата
Формулы для прямоугольного параллелепипеда
Формула объема V=abc
Формула площади поверхности S=2ab+2ac+2bc=2(ab+ac+bc)
Формула длины ребер L=4a+4b+4c=4(a+b+c), где а, в, с – измерения прямоугольного параллелепипеда
Формулы для куба
Формула объема V=a3
Формула площади поверхности S=6a2
Формула длины ребер L=12a, где а – ребро куба
Эмпирическая формула
Из дополнительной литературы по математике я узнала о том, что существуют эмпирические формулы, верность которых подтверждена практикой.
Вот одна из этих формул.
Вычисление живой массы коровы находится по формуле m=PL:50, где m- живая масса коровы, P – обхват туловища за лопатками в см, L – расстояние от середины холки до корня хвоста в см.
Эту формулу я применила в хозяйстве своего дяди.
Измерила: обхват туловища за лопаткамиP =180см; расстояние от середины холки до корня хвоста L =15осм.
И по формуле посчитала живую массу коровы m=180*150:50=540 (кг).
Знать живую массу коровы необходимо, например, при ее лечении, когда лекарство рассчитывается по весу животного или при экономических сделках.
Практическая задача
Но вернемся к формулам из школьного учебника.
На дачном участке наших родственников есть много свободного места, и они мечтают построить детскую площадку. Узнав о том, что я работаю над темой «Формулы», они попросили меня составить проект построения детской площадки. Может быть, они пошутили, но я отнеслась к этому серьезно, и этот проект представляю в виде решения практических задач.
Участок имеет размеры: длина – 12м, ширина – 10м. На данном участке я предлагаю построить:бассейн, стадион, песочницу и веранду.
Остановлюсь подробнее.
Чтобы сделать бассейн, я предлагаювыкопать котлован в форме прямоугольного параллелепипеда длиной 5 м, шириной 3 м и глубиной 1 м. Для этого придется вынуть15 м 3земли.Бассейн нужно выложить плиткой из кафеля. А для этого необходимо знать площади поверхностей 5 граней прямоугольного параллелепипеда. Вычислим их: S = 3*5 + 2*3*1 + 2*5*1=15+6+10= 31 (м2). При решении этой задачи воспользовалась формулами вычисления объема и площади поверхности прямоугольного параллелепипеда.
Чтобы оборудовать песочницуназемле, предлагаю выкопать котлован в форме прямоугольного параллелепипеда длиной 3 м, шириной 2 м и глубиной 0,5 м. Для этого придется вынуть 3 м 3земли и засыпать 6 м 3песка. При решении этой задачи использовала формулу объема прямоугольного параллелепипеда.
Чтобы построить мини-стадион, я предлагаю построить на земле прямоугольник длиной 6 м ишириной 4 м. По периметру установить бордюр, а для этого понадобится 20 (20,5) метров материала (желательно пластиковая трубка).Для подсчета количества длины пластиковой трубки использованаформула периметра прямоугольника.
Веранду я предлагаю сделать по эскизам:
Для этого можноизготовить:
- пол в видепрямоугольникаиз дерева, длиной 3м и шириной 2м;
- деревянные стойки (4штуки)в виде цилиндров диаметром 0,1мпо 3м или прямоугольных параллелепипедов (0,1м*0,08м*3м)
- деревянные рейки (12 штук)в видепрямоугольных параллелепипедов (0,03м*0,01м*3,5м)или цилиндров диаметром 0,03м и длиной 3,5м;
- крышасостоит из круга иконуса: круг –радиусом 2м, а конус радиусом 2м и высотой 0,5м.
Круг можно сделать из пластика, а конус – из водонепроницаемой ткани. Тогда дляустановки сегмента необходим каркас из проволоки.
Если АО=2м, а ОМ=0,5м, то математические расчеты показывают, что МВ≈ 2,1м. Для изготовления каркаса конуса нужна проволока длиной, равной длине окружности радиуса 2м, и длиной высоты ОМ= 0,5м, и длиной 6 МВ по 2,1м. Всю длину проволоки находим сложением 2*3,14*2+0,5+6*2,1=12,56+0,5+12,6=25,66(м) или, округляя, получим 26м. Для вычисления количества, необходимой ткани для покрытия каркаса, воспользуемся формулой нахождения площади круга. Если радиус круга равен 2,1м, то S= 3,14*2,1 2 =3,14*4, 41=13,8474 (м 2) или, округляя, получим14(м 2). При решении этой задачимне понадобились формулы, которые мы будем изучать и на следующий год, и в старших классах. Это формулы и для вычислениясторон прямоугольного треугольника с 2 = в 2 +а 2, и для вычисления длины окружности l=2πrи площади круга S=πr 2, где S – площадь круга, l – длина окружности, π≈3,14, аr – радиус круга (окружности).
www.microarticles.ru
ООО «ФОРМУЛА-Р» — г. РОСТОВ-НА-ДОНУ, ул. ТЕКУЧЕВА, 352А
федеральное казенное учреждение «Центр хозяйственного и сервисного обеспечения Главного управления Министерства внутренних дел Российской Федерации по Ростовской области»
Территориальный фонд обязательного медицинского страхования Ростовской области
РАЗМЕЩЕНИЕ ЗАКАЗА НА ВЫПОЛНЕНИЕ РАБОТ ПО ТЕХНИЧЕСКОМУ ОБСЛУЖИВАНИЮ АВТОМОБИЛЯ VOLKSWAGEN 7 HC CARAVELLE
Территориальный фонд обязательного медицинского страхования Ростовской области
ОКАЗАНИЕ УСЛУГ ПО ТЕХНИЧЕСКОМУ ОБСЛУЖИВАНИЮ И ТЕКУЩЕМУ РЕМОНТУ АВТОМОБИЛЯ ФОРД FUSION ГОС. НОМЕР М 775 КС ДЛЯ НУЖД ФГБОУ ВПО ЮРГПУ(НПИ) ИМЕНИ М.И. ПЛАТОВА.
федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова»
РАЗМЕЩЕНИЕ ЗАКАЗА НА РЕМОНТ ТРАНСПОРТНОГО СРЕДСТВА TOYOTA HIACE
Федеральное казенное учреждение «Главное бюро медико-социальной экспертизы по Ростовской области» Министерства труда и социальной защиты Российской Федерации
УСЛУГИ ПО РЕМОНТУ АВТОМОБИЛЯ УАЗ 3909
государственное казенное учреждение Ростовской области «Ростовская областная поисково-спасательная служба»
НА ПРАВО ЗАКЛЮЧЕНИЯ ГОСУДАРСТВЕННОГО КОНТРАКТА НА ВЫПОЛНЕНИЕ РАБОТ И ОКАЗАНИЕ УСЛУГ ПО ТЕХНИЧЕСКОМУ ОБСЛУЖИВАНИЮ И РЕМОНТУ АВТОТРАНСПОРТА ГУ МВД РОССИИ ПО РОСТОВСКОЙ ОБЛАСТИ (О МВД РОССИИ ПО КАМЕНСКОМУ РАЙОНУ) В РАМКАХ ГОСУДАРСТВЕННОГО ОБОРОННОГО ЗАКАЗА
федеральное казенное учреждение «Центр хозяйственного и сервисного обеспечения Главного управления Министерства внутренних дел Российской Федерации по Ростовской области»
Спасатели более часа пытаются потушить крупный пожар у Западного мостаКрупный пожар в Ростове, вспыхнувший на 1-й Луговой у Западного моста, пытаются погасить вот уже больше часа пожарные расчёты. Возгорание произошло на местности, где очень много сухой растительности. Огнём охвачено уже 30 соток территории с сухостоем.
В Каменске-Шахтинском горит Дом офицеровВ ночь с 9 по 10 октября в Каменске-Шахтинском Ростовской области загорелся Дом офицеров, расположенный в переулке Володарского, 68. Отметим, что уже несколько лет здание считается аварийным, а в декабре прошлого года обрушилась центральная часть здания.
rostov-na-donu7m.ru
Формула Р — адрес, телефон
Особенности
оплата картой
бесплатный wi-fi
марка автомобиля
ПодробнееRenault
виды работ
Подробнеезамена масла, развал-схождение, ремонт двигателя, ремонт АКПП, сигнализация, тонировка стекол, ремонт ходовой части, ремонт автоэлектрики, компьютерная диагностика автомобиля, установка парктроника, промывка инжектора, ремонт глушителей, ремонт рулевых реек
официальный дилер
продажа автомобилей
Подробнееновые
тест-драйв
трейд-ин
выкуп авто
автокредит
лизинг
банкомат
кафе, зона отдыха
оформление страховки
детская комната
Расстояние от центра Ростова-на-Дону до организации 1.6 км.
Расположение на карте
Отзывы
Отзывов о компании Формула Р по указанному адресу пока еще нет.
Добавить отзыв
Еще Автозапчасти в Ростове-на-Дону
- Дельта Моторс
Ростов-на-Дону, ул. Малиновского, 172/3а
ежедневно, 08:00-20:00 - Вектор
Ростов-на-Дону, ул. Малое Зеленое Кольцо, 3, р-к Алмаз, пав. 174-175
ежедневно, 09:00-18:00 - Автозапчасти
Ростов-на-Дону, пл. Толстого, 2/7
ежедневно, 08:00-17:00 - 3139393.ru
Ростов-на-Дону, ул. Шаумяна, 47в, оф. 1
пн-пт 10:00-19:00; сб 10:00-18:00 - БелМАЗдизель
Ростов-на-Дону, ул. Страны Советов, 3
пн-пт 09:00-17:00 - Спецприцеп Запасные части
Ростов-на-Дону, ул. Менжинского, 2
пн-пт 09:00-18:00 - ТД Веста
Ростов-на-Дону, ул. Доватора, 148, оф. 417
пн-пт 09:00-18:00 - Респект авто
Ростов-на-Дону, ул. Каширская, 7, оф. 8
пн-пт 10:00-18:00; сб 10:00-14:00 - Магазин Пикап
Ростов-на-Дону, ул. 14-я Линия, 50а/63а
пн-пт 09:00-18:00; сб 09:00-16:00
rostov-na-donu.spravka-region.ru
К-Р формулы — это… Что такое К-Р формулы?
Формулы сокращённого умножения — многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для кубов … Википедия
Формулы сокращенного умножения — Формулы сокращённого умножения многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для кубов … Википедия
Формулы сокращенного умножения многочленов — Формулы сокращённого умножения многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для кубов … Википедия
Формулы сокращённого умножения многочленов — Формулы сокращённого умножения многочленов часто встречающиеся случаи умножения многочленов. Многие из них являются частным случаем Бинома Ньютона. Изучаются в средней школе в курсе алгебры. Содержание 1 Формулы для квадратов 2 Формулы для… … Википедия
Формулы Виета — Формулы Виета формулы, выражающие коэффициенты многочлена через его корни. Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням. Содержание 1… … Википедия
Формулы Фруллани — относятся к нахождению несобственных интегралов Римана вида: к которым с помощью элементарных преобразовании, дифференцирования и интегрирования по параметру можно свести много других несобственных интегралов. Содержание 1 Формулы Фруллани … Википедия
Формулы Грина-Кубо — Формулы Грина Кубо, соотношения Грина Кубо связывают кинетические коэффициенты (коэффициенты переноса) линейных диссипативных процессов с временными корреляционными функциями соответствующих потоков. Названы по именам предложивших их М. Грина… … Википедия
Формулы Грина — Кубо или соотношения Грина Кубо связывают кинетические коэффициенты (коэффициенты переноса) линейных диссипативных процессов с временными корреляционными функциями соответствующих потоков. Названы по именам предложивших их М. Грина (Melville S.… … Википедия
ФОРМУЛЫ ДЛЯ РАСЧЕТА ПЛОЩАДЕЙ ПРУДОВ ОТДЕЛЬНЫХ КАТЕГОРИЙ ПРУДОВОГО ХОЗЯЙСТВА — соотношение площадей отдельных категорий прудов рыбоводного хозяйства зависит от естественной продуктивности прудов, степени интенсификации хозяйства, от весовых стандартов, норм посадки рыбы в зимовальные пруды и технической структуры хозяйства … Прудовое рыбоводство
ФОРМУЛЫ КРИСТАЛЛОХИМИЧЕСКИЕ — см. Кристаллохимические формулы. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
ФОРМУЛЫ МИНЕРАЛОВ — в настоящее время применяется много способов написания хим. формул м лов. Так, при отражении качественного состава важнейших компонентов и их количественных соотношений используется, напр., для кислородных соединений, написание в виде окислов… … Геологическая энциклопедия
psychology_dictionary.academic.ru
|
Как известно, вероятностью события А называют отношение числа m исходов испытаний, благоприятствующих наступлению события А, к общему числу n всех равновозможных несовместных исходов: Р(А)=m/n. Кроме того, условной вероятностью события А (вероятностью события А при условии, что наступило событие В) называется число РВ(А) = Р(АВ)/Р(В), где А и В – два случайных события одного и того же испытания. Поскольку события представимы в виде суммы и произведения, то и существуют правила сложения вероятностей событий и, соответственно, правила умножения вероятностей. Теперь дадим понятие полной вероятности. Предположим, что событие А может наступить только вместе с одним из попарно несовместных событий Н1, Н2, Н3, …, Нn, называемых гипотезами. Тогда справедлива следующая формула полной вероятности: Р(А) = Р(Н1)*РН1(А)+ Р(Н2)*РН2(А)+…+ Р(Нn)*РНn(А) = ∑Р(Нi) *РНi(А), т.е. вероятность события А равна сумме произведений условных вероятностей этого события по каждой из гипотез на вероятность самих гипотез. Если событие А уже произошло, то вероятности гипотез (априорные вероятности) могут быть переоценены (апостериорные вероятности) по формулам Бейеса: Примеры решения задач по теме «Формула полной вероятности. Формулы Бейеса»Задача 1. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 3% брака, второй – 2% и третий – 4%. Найти вероятность того, что на сборку попадает бракованная деталь, если с первого автомата поступает 100 деталей, со второго – 200 и с третьего – 250 деталей. Решение. 1. Рассматриваем следующие события и гипотезы:
2. Условные вероятности того, что деталь бракованная составляют РН1(А)=3%=0,03, РН2(А)=2%=0,02, РН3(А)=4%=0,04. 3. По формуле полной вероятности находим Задача 2. Имеются две одинаковые урны. Первая содержит 2 черных и 3 белых шара, вторая – 2 черных и 1 белый шар. Сначала произвольно выбирают урну, а затем из нее наугад извлекают один шар. Какова вероятность того, что будет выбран белый шар? Решение. 1. Рассматриваем следующие события и гипотезы:
2. Условная вероятность того, что белый шар принадлежит первой урне РН1(А)=3/(2+3)=3/5, а условная вероятность того, что белый шар принадлежит второй урне РН2(А)=1/(2+1)=1/3; 3. По формуле полной вероятности получим Р(А) = Р(Н1)*РН1(А)+Р(Н2)*РН2(А) = 0,5*3/5 + 0,5*1/3 = 3/10 + 1/6 = 7/15 ≈ 0,47 Задача 3. Литье в болванках поступает из двух заготовительных цехов: из первого цеха – 70%, из второго цеха 30%. Литье первого цеха имеет 10% брака, литье из второго – 20% брака. Взятая наудачу болванка оказалась без дефекта. Какова вероятность ее изготовления первым цехом? Решение. 1. Рассматриваем следующие события и гипотезы:
2. Так как литье первого цеха имеет 10% брака, то 90% болванок, изготовленных первым цехом,
не имеют дефекта, т.е. РН1(А)=0,9. 3. По формулу Бейеса найдем РА(Н1) = 0,7*0,9/(0,7*0,9+0,3*0,8)= 0,63/0,87≈0,724. Другие статьи по данной теме:Список использованных источников
|
www.ekonomika-st.ru
Психологическая энциклопедия — значение слова К-р Формулы
См. формулы Кудера-Ричардсона.
Смотреть значение К-р Формулы в других словарях
Планы-формулы — ИНВЕСТИЦИЙ(FORMULA PLANS). Планы, нацеленные на автоматическое произведение начальных приобретений с последующим изменением инвестиционного портфеля в соответствии с определенными……..
Экономический словарь
Зависимый Пункт Формулы — — пункт формулы, включающий характеристику развития и/или уточнения совокупности признаков изобретения, приведенных в независимом пункте, признаками, характеризующими……..
Юридический словарь
Формулы Привязки (формула Прикрепления) — — см. Коллизионная привязка.
Юридический словарь
Приближенные Формулы — математические — получаются из формул вида f(x) =f*(x) + ?(x), где ?(x) — остаточный член, или погрешность, — малаявеличина, которая после оценки отбрасывается. Напр., приближенная……..
Большой энциклопедический словарь
Френеля Формулы — определяют амплитуды, фазы и поляризации отраженной ипреломленной плоских волн, возникающих при падении плоскоймонохроматической световой волны на неподвижную плоскую……..
Большой энциклопедический словарь
Формулы — (лат. formula — форма, правило, предписание) — группа ист. источников эпохи раннего средневековья в Зап. Европе, отражающих гл. обр. социально-экономич. отношения этого периода………
Советская историческая энциклопедия
Вейнгартена Деривационные Формулы — формулы, дающие разложение производной единичного вектора нормали к поверхности по первым производным радиус-вектора этой поверхности. Если — радиус-вектор поверхности,……..
Математическая энциклопедия
Грина Формулы — — формулы интегрального исчисления функций многих переменных, связывающие значения га-кратного интеграла по области D n -мерного евклидова пространства и -кратного……..
Математическая энциклопедия
Индекса Формулы — — соотношения между аналитич. и топологич. инвариантами операторов нек-рого класса. Именно, И. ф. устанавливают связь между аналитич. индексом линейного оператора(L0,……..
Математическая энциклопедия
Котеса Формулы — — формулы для приближенного вычисления определенных интегралов по значениям подинтегральной функции в конечном числе равноотстоящих точек, т. е. квадратурные формулы……..
Математическая энциклопедия
Плюккера Формулы — — формулы, связывающие внешние, т. е. отвечающие проективным вложениям, и внутренние характеристики алгебраич. многообразий. Наиболее старыми и известными среди численных……..
Математическая энциклопедия
Сохоцкого Формулы — — формулы, найденные впервые Ю. В. Сохоцким [1] и выражающие граничные значения интеграла типа Коши. С более полными доказательствами, но значительно позже С. ф. были получены……..
Математическая энциклопедия
Френе Формулы — формулы, выражающие производные единичных векторов касательной нормали v и бинормали к регулярной кривой по натуральному параметру s через эти же векторы и значения……..
Математическая энциклопедия
Определение Лейкоцитарной Формулы (differential Leucocyte Count), Анализ Крови Дифференциальный (dif — определение соотношения различных видов лейкоцитов, присутствующих во взятом образце крови. Обычно 100 белых клеток крови подсчитываются и определяются под микроскопом……..
Медицинский словарь
Аккерета Формулы — — формулы для расчёта коэффициентов давления ср, подъёмной силы суа и волнового сопротивления схва тонкого профиля в сверхзвуковом потоке (см. Аэродинамические коэффициенты)………
Энциклопедия техники
ЭЙЛЕРА ФОРМУЛЫ — ЭЙЛЕРА ФОРМУЛЫ — формулы, выражающие тригонометрические функции переменного x через показательную функцию:Установлены Леонардом Эйлером.
Большой энциклопедический словарь
Посмотреть еще слова :
slovariki.org
