Три признака подобия треугольников: Три признака подобия треугольников

Содержание

Три признака подобия треугольников

Теорема 1. Два треугольника подобны, если два угла одного треугольника соответственно равны двум углам другого.

Пусть в треугольниках ABC и А’В’С ∠A = ∠А’ ∠В = ∠B’ (в подобных треугольниках вершины соответственно равных углов часто обозначают одинаковыми буквами).

Доказать, что $\Delta$ABС $\sim$ $\Delta$А’В’С (рис. 367).

Прежде всего отметим, что из равенства двух углов данных треугольников следует, что и третьи углы их равны, т. е. ∠C = ∠С’.

Отложим от вершины В, например, на стороне AB треугольника ABC отрезок ВМ, равный отрезку А’В’. Из точки М проведём прямую MN || АС. Мы получили $\Delta$MBN, который подобен $\Delta$ABC. Но $\Delta$MBN = $\Delta$А’В’С’, так как ∠В = ∠В’ по условию теоремы; сторона MB = A’B’ по построению; ∠BMN = ∠A’ (∠BMN и ∠А’ порознь равны одному и тому же ∠А).

Если $\Delta$MBN $\sim$ $\Delta$AВС, то $\Delta$А’В’С’ $\sim$ $\Delta$ABC. Эта теорема выражает 1-й признак подобия треугольников.

Следствия. 1. Равносторонние треугольники подобны.

2. Равнобедренные треугольники подобны, если они имеют по равному углу при вершине или при основании.

3. Два прямоугольных треугольника подобны, если она имеют по равному острому углу.

4. Равнобедренные прямоугольные треугольники подобны.

Теорема 2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, лежащие между ними, равны.

Пусть в треугольниках ABC и А’В’С’ $\frac{AB}{A’B’} = \frac{BC}{B’C’}$ и ∠В = ∠В’

Требуется доказать, что $\Delta$ABC $\sim$ $\Delta$А’В’С’ (рис. 368).

Для доказательства отложим, например, на стороне AB треугольника ABC от вершины В отрезок ВМ, равный отрезку А’В’. Через точку М проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC.

Докажем, что $\Delta$MBN = $\Delta$А’В’С’. В этих треугольниках ∠В = ∠В’ по условию теоремы, MB = А’В’ по построению. Чтобы убедиться в равенстве сторон BN и В’С, составим пропорцию ^AB/_MB = ^BC/_BN (она вытекает из параллельности АС и MN) и сравним её с пропорцией, которая дана в условии теоремы: $\frac{AB}{A’B’} = \frac{BC}{B’C’}$. В этих двух пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены,

т. е. В’С’ = BN. Отсюда следует равенство треугольников MBN и А’В’С’.

Так как $\Delta$MBN $\sim$ $\Delta$А’В’С’, то, следовательно, и $\Delta$А’В’С’ $\sim$ $\Delta$ABС.

Эта теорема выражает 2-й признак подобия треугольников.

Следствие. Прямоугольные треугольники подобны, если катеты одного из них пропорциональны катетам другого.

Теорема 3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трём сторонам другого треугольника.

Пусть в треугольниках ABC и А’В’С’ $\frac{AB}{A’B’} = \frac{BC}{B’C’} = \frac{AC}{A’C’}$ (рис. 369).

Требуется доказать, что $\Delta$ABC $\sim$ $\Delta$А’В’С’

Для доказательства отложим на стороне AB треугольника ABC от вершины В отрезок BM = А’В’. Из точки M проведём прямую MN || АС. Полученный треугольник MBN подобен треугольнику ABC. Следовательно, $\frac{AB}{MB} = \frac{BC}{BN} = \frac{AC}{MN}$.

Докажем, что $\Delta$MBN = $\Delta$А’В’С’. Для доказательства сравним две пропорции

$\frac{AB}{MB} = \frac{BC}{NB}$ и $\frac{AB}{A’B’} = \frac{BC}{B’C’}$.
В этих пропорциях имеется по три равных члена, следовательно, равны и четвёртые их члены, т.е. BN = В’С’.

Сравним ещё две пропорции: $\frac{AB}{MB} = \frac{AC}{MN}$ и $\frac{AB}{A’B’} = \frac{AC}{A’C’}$ . В этих пропорциях также имеется по три равных члена, следовательно, равны и четвёртые члены их, т. е. MN =А’С’.

Оказалось, что три стороны $\Delta$BMN равны трём сторонам $\Delta$А’В’С’, а именно:

MB = А’В’, BN = В’С’ и MN = А’С’.

Следовательно, $\Delta$MBN = $\Delta$А’В’С’, а $\Delta$ABC $\sim$ $\Delta$А’В’С’.

Эта теорема выражает 3-й признак подобия треугольников.

Признаки подобных треугольников | Треугольники

Признаки подобия треугольников позволяют доказать, что треугольники являются подобными, на основании 2-3 равенств (вместо 6 по определению).

В школьном курсе геометрии, как правило, изучают три признака подобия произвольных треугольников.

1-й признак подобия треугольников

( подобие треугольников по двум углам)

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2-й признак подобия треугольников

( подобие треугольников по двум сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.

3-й признак подобия треугольников

( подобие треугольников по трём сторонам)

Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.

Есть еще 4-й признак подобия треугольников —

( подобие треугольников по двум сторонам и наибольшему углу)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а наибольший угол одного равен наибольшему углу другого, то такие треугольники подобны.

Доказав, что треугольники подобны, можно использовать свойства подобных треугольников.

Для доказательства подобия прямоугольных треугольников используют другие признаки. Их мы запишем в следующий раз.

Подобие правильных и подобие равнобедренных треугольников рассмотрим позже.

Признаки подобия треугольников широко используются при решении задач как в курсе планиметрии, так и в курсе стереометрии. Например, на основании подобия прямоугольных треугольников доказывается свойство биссектрисы треугольника.

Признаки подобия треугольников

Напомним для начала определение подобных треугольников.

Определение 1

Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны.

Для определения подобия треугольников существуют три признака подобия треугольников. Рассмотрим и докажем их.

Первый признак подобия треугольников

Теорема 1

Теорема 1: Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle A=\angle A_1,\ \angle B=\angle B_1$. (рис. 1).

Рисунок 1. Иллюстрация теоремы 1

Нам нужно доказать, что $\angle C=\angle C_1,$ и что $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$.

По теореме о сумме углов треугольника, имеем:

Далее будем пользоваться следующей теоремой:

Теорема 2

Теорема 0: Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.

Готовые работы на аналогичную тему

По теореме 0, получим

Из этих равенств, получим

Теорема доказана.

Второй признак подобия треугольников

Теорема 3

Теорема 2: Если две стороны одного треугольника пропорциональны соответствующим сторонам второго треугольника и углы между этими сторонами равны, то данные треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\angle A=\angle A_1$ и$\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$ (рис. 2).

Рисунок 2. Иллюстрация теоремы 2

Используя теорему 1, видим, что для доказательства этой теоремы, достаточно доказать, что $\angle C=\angle C_1$. Построим треугольник $ACB_2$, так, что $\angle CAB_2=\angle A_1$, а $\angle B_2CA=\angle C_1$ (рис. 2).

Рисунок 3. Дополнительное построение

Треугольник $ACB_2$ подобен треугольнику $ABC$ (по теореме 1), следовательно,$\ \frac{AC}{A_1C_1}$ $=\frac{AB_2}{A_1B_1}$. По условию $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}$, следовательно, $AB=AB_2$. Тогда треугольник $ACB_2$ равен треугольнику $ABC$ по двум сторонам и углу между ними. Следовательно, $\angle B_2CA=\angle C$, а так как $\angle B_2CA=\angle C_1,\ то\ \angle C=\angle C_1.$

По первому признаку подобия треугольника получаем доказательство теоремы.

Третий признак подобия треугольников

Теорема 4

Теорема 3: Если три стороны одного треугольника пропорциональны трем соответствующим сторонам второго треугольника, то такие треугольники подобны.

Доказательство.

Рассмотрим треугольники $ABC$ и $A_1B_1C_1$, у которых $\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}=k$.

Используя теорему 2, видим, что для доказательства этой теоремы, достаточно доказать, что $\angle A=\angle A_1$. Построим треугольник $ACB_2$, так, что $\angle CAB_2=\angle A_1$, а $\angle B_2CA=\angle C_1$ (рис. 3).

Рисунок 4. Дополнительное построение

Треугольник $ACB_2$ подобен треугольнику $ABC$ (по теореме 1), следовательно,$\ \frac{AC}{A_1C_1}$ $=\frac{AB_2}{A_1B_1}=\frac{CB_2}{C_1B_1}$. Принимая во внимание равенства$\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$, получим, что $CB_2=CB,\ AB_2=AB$. Тогда треугольник $ACB_2$ равен треугольнику $ABC$ по трем сторонам. Следовательно, $\angle A=\angle A_1$.

Теорема доказана.

Пример задачи на использование признаков подобия

Пример 1

Доказать, что любые два равнобедренных треугольника, у которых углы между равными сторонами равны, являются подобными.

Решение.

Пусть даны равнобедренные треугольники $ABC$ и $A_1B_1C_1$ с $\angle A=\angle A_1.$ Так как треугольник $ABC$ равнобедренный, то

\[\angle B=\angle C=\frac{180-\angle A}{2}\]

Так как треугольник $A_1B_1C_1$ равнобедренный, то

\[\angle B_1=\angle C_1=\frac{180-A_1}{2}=\frac{180-\angle A}{2}=\angle B=\angle C\]

То есть $\angle B=\angle B_1,\ \ \angle C=\angle C_1$. По теореме 1, получаем, что треугольники $ABC$ и $A_1B_1C_1$ подобны.

ч. т. д.

Признаки подобия треугольников [wiki.eduVdom.com]

Теорема 1. Первый признак подобия треугольников. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.

Доказательство. Пусть ABC и $А_1В_1С_1$ — треугольники, у которых $\angle A = \angle A_1 ; \angle B = \angle B_1$ , и, следовательно, $\angle C = \angle C_1$ . Докажем, что $\triangle ABC \sim \triangle A_1B_1C_1$ (рис.1).

Рис.1
Отложим на ВА от точки В отрезок $ВА_2$, равный отрезку $A_1B_1$ , и через точку $А_2$ проведем прямую, параллельную прямой АС. Эта прямая пересечет ВС в некоторой точке $С_2$ . Треугольники $А_1В_1С_1\text{ и }А_2ВС_2$ равны: $А_1В_1 = А_2В$ по построению, $\angle В = \angle В_1$ по условию и $\angle А_1 = \angle А_2$ , так как $\angle А_1 = \angle А$ по условию и $\angle А = \angle А_2$ как соответственные углы. По лемме 1 о подобных треугольниках имеем: $\triangle A_2BC_2 \sim \triangle ABC$ , и значит, $\triangle ABC \sim \triangle A_1B_1C_1$ . Теорема доказана.
По аналогичной схеме устанавливаются теоремы 2 и 3.
Теорема 2. Второй признак подобия треугольников. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то треугольники подобны.
Теорема 3. Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Из теоремы 1 вытекает следующее.
Следствие 1. В подобных треугольниках сходственные стороны пропорциональны сходственным высотам, т. е. тем высотам, которые опущены на сходственные стороны.
Пример 1. Подобны ли два равносторонних треугольника?
Решение. Так как в равностороннем треугольнике каждый внутренний угол равен 60° (следствие 3), то два равносторонних треугольника подобны по первому признаку.
Пример 2. В треугольниках ABC и $А_1В_1С_1$ известно, что $\angle A = \angle A_1 ; \angle B = \angle B_1 ; АВ = 5 м, ВС = 7 м, А_1В_1 = 10 м, А_1С_1 = 8 м.$ Найти неизвестные стороны треугольников.
Решение. Треугольники, определенные условием задачи, подобны по первому признаку подобия. Из подобия треугольников следует: $$ \frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = \frac{AC}{A_1C_1} \,\,\, (1) $$ Подставив в равенство (1) данные из условия задачи, получим: $$ \frac{5}{10} = \frac{7}{B_1C_1} = \frac{AC}{8} \,\,\, (2) $$ Из равенства (2) составим две пропорции $$ \frac{5}{10} = \frac{7}{B_1C_1} \\ \frac{5}{10} = \frac{AC}{8} \\ \text{ откуда }В_1С_1 = 14 (м), АС = 4 (м). $$
Пример 3. Углы В и $В_1$ треугольников ABC и $А_1В_1С_1$ равны. Стороны АВ и ВС треугольника ABC в 2,5 раза больше сторон $A_1B_1$ и $B_1C_1$ треугольника $A_1B_1C_1$. Найти АС и $A_1C_1$ , если их сумма равна 4,2 м.
Решение. Пусть условию задачи отвечает рисунок 2.
Рис.2
Из условия задачи: $$ 1) \angle B = \angle B_1 ; \\ 2) \frac{AB}{A_1B_1} = \frac{BC}{B_1C_1} = 2,5 \\ 3) AC + A_1C_1 = 4,2 м. $$ Следовательно, $\triangle ABC \sim \triangle А_1В_1С_1$. Из подобия этих треугольников следует $$ \frac{AC}{A_1C_1} = 2,5\text{ , или }АС = 2,5\bullet А_1С_1 $$ Так как АС = 2,5 • А₁С₁, то АС + А₁C₁ = 2,5 • А₁С₁ + A₁C₁ = 4,2, откуда A₁C₁ = 1,2 (м), АС = 3 (м).
Пример 4. Подобны ли треугольники ABC и А₁В₁С₁, если АВ = 3 см, ВС = 5 см, АС = 7 см, А₁В₁ = 4,5 см, B₁C₁ = 7,5 см, A₁C₁ = 10,5 см?
Решение. Имеем: $$ \frac{AB}{A_1B_1} = \frac{3}{4,5} = \frac{1}{1,5} \\ \frac{BC}{B_1C_1} = \frac{5}{7,5} = \frac{1}{1,5} \\ \frac{AC}{A_1C_1} = \frac{7}{10,5} = \frac{1}{1,5} $$ Следовательно, треугольники подобны по третьему признаку.
Пример 5. Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Решение. Рассмотрим произвольный треугольник ABC. Обозначим буквой О точку пересечения его медиан $АА_1\text{ и }ВВ_1$ и проведем среднюю линию $A_1B_1$ этого треугольника (рис.3).
Рис.3
Отрезок $A_1B_1$ параллелен стороне АВ, поэтому $\angle 1 = \angle2 \text{ и } \angle 3 = \angle 4 $. Следовательно, треугольники АОВ и $A_1OB_1$ подобны по двум углам, и, значит, их стороны пропорциональны: $$ \frac{AO}{A_1O} = \frac{BO}{B_1O} = \frac{AB}{A_1B_1} $$
Но $AB = 2A_1B_1$ , поэтому $AO = 2A_1O$ и $BO = 2B_1O$ .
Аналогично доказывается, что точка пересечения медиан $BB_1\text{ и }CC_1} делит каждую из них в отношении 2:1, считая от вершины, и, следовательно, совпадает с точкой О.
Итак, все три медианы треугольника ABC пересекаются в точке О и делятся ею в отношении 2:1, считая от вершины.
Замечание. Ранее отмечалось, что биссектрисы треугольника пересекаются в одной точке, серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. На основе последнего утверждения устанавливается, что и высоты треугольника (или их продолжения) пересекаются в одной точке. Эти три точки и точка пересечения медиан называются замечательными точками треугольника.
Пример 6. Проектор полностью освещает экран А высотой 90 см, расположенный на расстоянии 240 см. На каком наименьшем расстоянии в см. от проектора нужно расположить экран Б, высотой 150 см, так, что бы он был полностью освещён, если настройки проектора остаются неизменными.
Видео-решение.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Подобные треугольники
Рассмотрим два треугольника KLM и TRP (рис.1) и введём следующие обозначения.
Рис.1
Обозначим
a₁ , b₁ , c₁
длины сторон треугольника KLM, расположенные в порядке возрастания.
Обозначим
a₂, b₂, c₂
длины сторон треугольника TRP, расположенные в порядке возрастания.
Переобозначим вершины треугольников KLM и TRP так, как показано на рисунке 2.
Рис.2
На рисунке 2 треугольник KLM обозначается как треугольник A₁B₁C₁, а треугольник TRP обозначается как треугольник A₂B₂C₂.
Определение 1. В треугольниках A₁B₁C₁ и A₂B₂C₂, изображённых на рисунке 2,
вершины A₁ и A₂, B₁ и B₂, C₁ и C₂ называют сходственными вершинами,
стороны A₁B₁ и A₂B₂, A₁C₁ и A₂C₂, B₁C₁ и B₂C₂ называют сходственными сторонами,
углы A₁ и A₂, B₁ и B₂, C₁ и C₂ называют сходственными углами
Определение 2. Треугольники A₁B₁C₁ и A₂B₂C₂ называют подобными треугольниками, если их сходственные углы равны, а сходственные стороны пропорциональны.
Другими словами, треугольники A₁B₁C₁ и A₂B₂C₂ подобны, если, во-первых,
а, во-вторых, существует положительное число k, такое, что справедливы равенства:
a₁ = k a₂, b₁ = k b₂ , c₁ = k c₂. (1)
Определение 3. В случае, когда треугольники A₁B₁C₁ и A₂B₂C₂ подобны, число k, заданное формулами (1), называют коэффициентом подобия треугольников A₁B₁C₁ и A₂B₂C₂ .
Признаки подобия треугольников
Название признака Рисунок Формулировка признака
Признак подобия треугольников по двум сторонам и углу между ними
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.
Признак подобия треугольников по двум углам
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Признак подобия треугольников по трём сторонам
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
Признак подобия треугольников по двум сторонам и углу между ними
Формулировка признака подобия:
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны.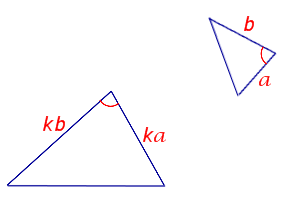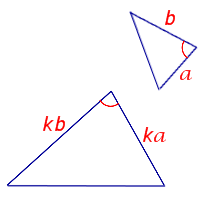
Признак подобия треугольников по двум углам
Формулировка признака подобия:
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Признак подобия треугольников по трём сторонам
Формулировка признака подобия:
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны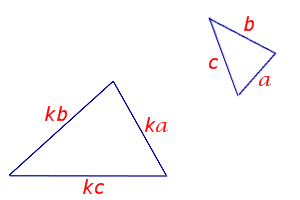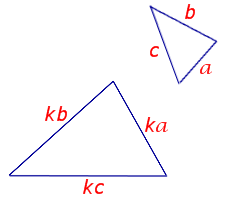
Признаки подобия прямоугольных треугольников
Название признака Рисунок Формулировка признака
Признак подобияпрямоугольных треугольников по двум катетам
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Признак подобия прямоугольных треугольников по острому углу
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Признак подобия прямоугольных треугольников по гипотенузе и катету
Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.
Признак подобия прямоугольных треугольников по двум катетам
Формулировка признака подобия прямоугольных треугольников:
Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.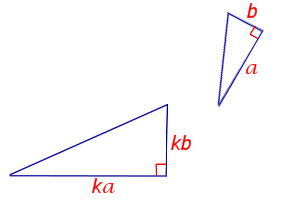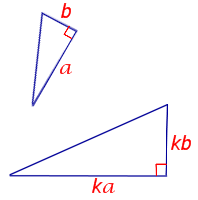
Признак подобия прямоугольных треугольников по острому углу
Формулировка признака подобия прямоугольных треугольников:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.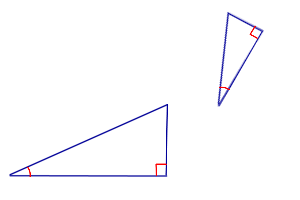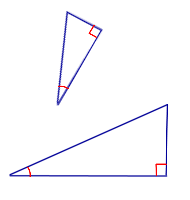
Признак подобия прямоугольных треугольников по гипотенузе и катету
Формулировка признака подобия прямоугольных треугольников:
Если гипотенуза и катет одного прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника, то такие прямоугольные треугольники подобны.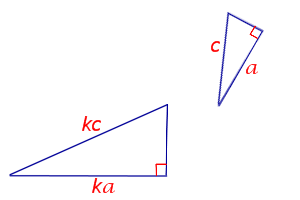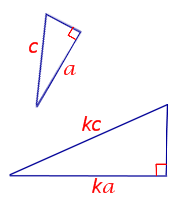
Следствие 1. Прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник (рис. 3).
Рис.3
Следствие 2. Отношение площадей подобных треугольников равно квадрату коэффициента подобия (рис. 4)
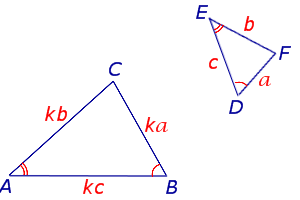
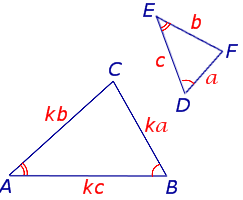
Рис.4

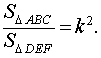
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Признаки подобия треугольников
Прежде чем разобрать задачи, повторим признаки подобия треугольников и свойства подобных треугольников.
Для доказательства подобия произвольных треугольников в школьном курсе используют три признака.
I. Признак подобия треугольников по двум углам.

Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
II. Признак подобия треугольников по двум сторонам и углу между ними.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
III. Признак подобия треугольников по трем сторонам.
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
Признак подобия прямоугольных треугольников
Для подобия прямоугольных треугольников достаточно, чтобы у них было по одному острому углу.
Из подобия треугольников следует равенство соответствующих углов и пропорциональность сторон:
Периметры подобных треугольников пропорциональны:

k — коэффициент подобия.
Все линейные размеры подобных треугольников также пропорциональны, то есть отношение соответствующих биссектрис, высот, медиан также равно k.
Углы между соответствующими линиями подобных треугольников равны.
Площади подобных фигур относятся как квадраты их соответствующих линейных размеров:

Подобные треугольники. Признаки подобия | Геометрия
Подобные треугольники — это треугольники, у которых все три угла равны, а все стороны одного треугольника в одно и то же число раз длиннее (или короче) сторон другого треугольника, то есть треугольники подобны если их углы равны, а сходственные стороны пропорциональны.
Сходственные стороны — это стороны двух треугольников, лежащие против равных углов.
Рассмотрим два треугольника ABC и A₁B₁C₁, у которых ∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁:
Стороны AB и A₁B₁, BC и B₁C₁, CA и C₁A₁, лежащие напротив равных углов, называются сходственными сторонами. Следовательно, отношения сходственных сторон равны:

AB = BC = AC = k,

A₁B₁ B₁C₁ A₁C₁

k — это коэффициент подобия ( число, равное отношению сходственных сторон подобных треугольников). Если k = 1, то треугольники равны, то есть равенство треугольников – это частный случай подобия.
Подобие треугольников обозначается знаком ~: ABC ~ A₁B₁C₁.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия. Если обозначить площади двух подобных треугольников буквами S и S₁, то:
Первый признак подобия треугольников
Если два угла одного треугольника равны двум углам другого, то треугольники подобны.
Если ∠A = ∠A₁, ∠C = ∠C₁,
то ABC ~ A₁B₁C₁.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то треугольники подобны.

Если AB = AC , ∠A = ∠A₁,

A₁B₁ A₁C₁

то ABC ~ A₁B₁C₁.

Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.

Если AB = BC = AC ,

A₁B₁ B₁C₁ A₁C₁

то ABC ~ A₁B₁C₁.

Как найти, если треугольники похожи
Два треугольника похожи, если они имеют:
все их углы равны
соответствующие стороны в том же соотношении
Но нам не нужно знать все три стороны и все три угла … двух или трех из шести обычно достаточно.
Существует три способа определения схожести двух треугольников: AA , SAS и SSS :
AA
AA означает «угол, угол» и означает, что треугольники имеют два равных угла.
Если два треугольника имеют два равных угла, треугольники похожи.
Пример: эти два треугольника похожи:
Если два их угла равны, то третий угол также должен быть равен, потому что углы треугольника всегда складываются, чтобы составить 180 °.
В этом случае угол пропуска составляет 180 ° — (72 ° + 35 °) = 73 °
Таким образом, AA также можно назвать AAA (потому что, когда два угла равны, все три угла должны быть равны).
SAS
SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, где:
соотношение между двумя сторонами такое же, как соотношение между двумя другими сторонами
и мы также знаем, что включенные углы равны.
Если два треугольника имеют две пары сторон в одинаковом соотношении и включенные углы также равны, то треугольники аналогичны.
Пример:
В этом примере мы видим, что:
одна пара сторон находится в соотношении 21: 14 = 3: 2
другая пара сторон находится в соотношении 15: 10 = 3: 2
между ними имеется угол в 75 °
Итак, достаточно информации, чтобы сказать нам, что два треугольника похожи на .
с использованием тригонометрии
Мы также могли бы использовать тригонометрию для вычисления двух других сторон, используя закон косинусов:
Пример продолжения
в треугольнике ABC:
a ² = b ² + c ² — 2 млрд. Долл. США cos A
a ² = 21 ² + 15 ² — 2 × 21 × 15 × Cos75 °
a ² = 441 + 225 — 630 × 0,2588 …
а ² = 666 — 163.055 …
a ² = 502.944 …
So a = √502,94 = 22,426 …
в треугольнике XYZ:
x ² = y ² + z ² — 2yz cos X
x ² = 14 ² + 10 ² — 2 × 14 × 10 × Cos75 °
x ² = 196 + 100 — 280 × 0,2588 …
x ² = 296 — 72,469 …
x ² = 223,530 …
Итак, х = √223.530 … = 14,950 …
Теперь давайте проверим соотношение этих двух сторон:
: х = 22,426 …: 14,950 … = 3: 2
такое же соотношение, как и раньше!
Примечание: мы также можем использовать закон синусов, чтобы показать, что два других угла равны.
SSS
SSS означает «сторона, сторона, сторона» и означает, что у нас есть два треугольника со всеми тремя парами соответствующих сторон в одинаковом соотношении.
Если два треугольника имеют три пары сторон в одинаковом соотношении, то треугольники похожи.
Пример:
В этом примере соотношения сторон:
а: х = 6: 7,5 = 12: 15 = 4: 5
b: y = 8: 10 = 4: 5
c: z = 4: 5
Все эти соотношения равны, поэтому два треугольника похожи.
с использованием тригонометрии
Используя тригонометрию, мы можем показать, что два треугольника имеют равные углы, используя закон косинусов в каждом треугольнике:
в треугольнике ABC:
cos A = (b ² + c ² — a ²) / 2bc
cos A = (8 ² + 4 ² — 6 ²) / (2 × 8 × 4)
cos A = (64 + 16 — 36) / 64
cos A = 44/64
cos A = 0.6875
So Angle A = 46,6 °
в треугольнике XYZ:
cos X = (y ² + z ² — x ²) / 2yz
cos X = (10 ² + 5 ² — 7,5 ²) / (2 × 10 × 5)
cos X = (100 + 25 — 56,25) / 100
cos X = 68,75 / 100
cos X = 0,6875
So Angle X = 46,6 °
Так что углы А и Х равны!
Аналогичным образом мы можем показать, что углы B и Y равны, а углы C и Z равны.
,
Сходство в треугольниках | Shmoop

Вы устали слышать, что подобные треугольники имеют совпадающие углы и пропорциональные стороны? Мы говорим это только потому, что это важно. И правда. И важно.
Если мы знаем, что два треугольника имеют конгруэнтные углы и пропорциональные стороны, то мы знаем, что они похожи. На самом деле, если мы знаем, что два треугольника имеют совпадающие углы и / или пропорциональные стороны, то мы знаем, что они похожи. Нам не нужно знать и то и другое, хотя хорошо, когда у вас есть все базы.
Проверьте эти треугольники.
Они, конечно, похожи, но иногда рисунки могут бросить нам кривая. К счастью, нам даны длины сторон треугольников, что очень удобно, потому что мы не можем просто определить, совпадают ли углы.
Давайте настроим соотношения и сравним. Они равны?
Да, действительно, длины сторон пропорциональны, поэтому мы можем быть уверены, что ∆ OAK ~ ∆ MIL .
Пример задачи
∆ PIT имеет длины сторон 4, 5 и 8, а ∆ KAN имеет длины сторон 12, 15 и 22. Они похожи?
Давайте установим некоторые соотношения и посмотрим.
Нет. Так что они не похожи.
Это целая игра в мяч, когда мы имеем дело с углами. В то время как длина сторон пропорциональна в подобных треугольниках, углы должны быть конгруэнтными. Если мы вырежем любые два одинаковых треугольника (которые мы не рекомендуем делать на вашем экране, но не стесняемся распечатать страницу, а затем приступить к работе) и поместим их друг на друга, мы могли бы выстроить в ряд каждый набор соответствующие углы и видим, что углы точно такого же размера.
Треугольники ∆ TEX и ∆ WAS похожи, потому что их углы совпадают. В частности, Т , Вт , Е , А и X , S .
Пример задачи
∆ NYM имеет углы, которые составляют 50 °, 87 ° и 43 °. ∆ PHI имеет углы, которые составляют 87 °, 50 ° и 43 °. Они похожи?
Да. Запишите это: тройная игра с тремя парами конгруэнтных углов.Это делает треугольники похожими.
Напрашивается интересный вопрос. Должны ли мы знать меры всех углов, чтобы решить, похожи ли два треугольника?
Короче, нет.
Длинный ответ основан на том факте, что три угла внутри каждого треугольника всегда складываются до 180 ° (помните теорему об угле сумме для треугольников?). Это означает, что если мы знаем только меру двух углов, мы можем вычислить меру третьего.Тем не менее, приблизительные цифры не помогут.
Так что насчет этих двух треугольников? Они похожи?
В первом треугольнике мы знаем 20 P = 48 ° и ∠ I = 79 °. Поскольку m∠ P + m∠ I + m∠ T = 180, мы можем рассчитать, что m∠ T = 53 °. Во втором треугольнике m∠ L = 48 ° и m∠ A = 79 °. Опять же, поскольку m∠ L + m∠ A + m∠ D = 180, мы знаем, что ∠ D также должно быть 53 °.Оба треугольника имеют три равных угла, что означает, что они должны быть похожими.
Чтобы написать утверждение сходства, мы должны получить наши письма в правильном порядке. Конгруэнтные углы должны быть в одном и том же месте в названии каждого треугольника: ∠ P , ≅ L , ∠ I , ∠ A и ∠ T , 20 D , поэтому мы пишем ∆ PIT ~ LAD .
Но нам действительно не нужно было вычислять размер этих третьих углов. И вот почему:
Заявления Причины
1.m∠ P + m∠ I + m∠ T = 180 Теорема об углах сумм для треугольников
2. m∠ L + m∠ A + m∠ D = 180 Теорема об углах суммы для треугольников
3. m∠ P = m∠ L , m∠ I = m∠ A Данные (на рисунке)
4. m∠ T = 180 — (m∠ P + m∠ I ) Перегруппировка (1)
5.m∠ D = 180 — (m∠ L + m∠ A ) Перегруппировка (2)
6. m∠ T = 180 — (m∠ L + m∠ A ) Замена (3, 4)
7. m∠ D = m∠ T Замена (5, 6)
8. 9009 D ∠ T Определение конгруэнтных углов (7)

Даже без необходимости точных измерений любого из углов мы знаем, что ∠ T и ∠ D равны по величине, что означает, что они также конгруэнтны.
И мы только что обнаружили нечто, называемое «Угловой постулат-угол» , в котором говорится, что если два треугольника имеют две пары конгруэнтных углов, то треугольники похожи. Видишь, разве это не приятно?
Пример задачи
Два угла в ∆ BOS измеряют 22 ° и 108 °, а два угла в ∆ CLE измеряют 108 ° и 48 °. Треугольники похожи?
Мы знаем из задачи, что у них есть хотя бы один конгруэнтный угол (108 °).Но у них есть другой набор? Чтобы найти отсутствующий угол в ∆ BOS , мы решим 180 ° — (108 ° + 22 °) = x или x = 50 °. Три угла в BOS составляют 22 °, 50 ° и 108 °. Ни один из них не равен 48 °, поэтому мы уже знаем (не вычисляя размер третьего угла ∆ CLE ), что наши два треугольника не имеют по крайней мере два равных угла. Они не совпадают, поэтому два треугольника не похожи. Качели и мисс.
Похожие треугольники
Два треугольника похожи, если единственное отличие — это размер (и, возможно, необходимость повернуть или перевернуть один).
Все эти треугольники похожи:
(Равные углы отмечены одинаковым количеством дуг)
Некоторые из них имеют разные размеры, а некоторые повернуты или перевернуты.
Для похожих треугольников:

Все соответствующие углы равны
и

Все соответствующие стороны имеют одинаковое соотношение
Также обратите внимание, что соответствующие стороны обращены к соответствующим углам.Например, стороны, которые обращены к углам с двумя дугами, соответствуют.
Соответствующие стороны
В похожих треугольниках соответствующие стороны всегда находятся в одинаковом соотношении.
Например:
Треугольники R и S аналогичны. Равные углы обозначены одинаковыми номерами дуг.
Какие длины соответствуют?
Длина 7 и a соответствуют (они обращены к углу, отмеченному одной дугой)
Длина 8 и 6.4 соответствуют (они обращены к углу, обозначенному двумя дугами)
Соответствуют длины 6 и b (они обращены к углу, обозначенному тремя дугами)
Расчет длины соответствующих сторон
Иногда мы можем вычислить длины, которые мы еще не знаем.
Шаг 1: Найти отношение соответствующих сторон
Шаг 2: Используйте это соотношение, чтобы найти неизвестные длины
Пример: Найти длины a и b треугольника S
Шаг 1: Найти соотношение
Мы знаем все стороны в Треугольнике R , и
Мы знаем сторону 6.4 в треугольнике S
Элемент 6.4 обращен к углу, обозначенному двумя дугами, а также стороне длины 8 в треугольнике R .
Таким образом, мы можем сопоставить 6,4 с 8 , и поэтому соотношение сторон в треугольнике S к треугольнику R равно:
от 6,4 до 8
Теперь мы знаем, что длины сторон в треугольнике S равны 6,4 / 8 раз длины сторон в треугольнике R .
Шаг 2: используйте соотношение
a обращен к углу одной дугой, как и сторона длины 7 в треугольнике R .
a = (6,4 / 8) × 7 = 5,6
b обращены к углу с тремя дугами, как и сторона длины 6 в треугольнике R .
b = (6,4 / 8) × 6 = 4,8
Готово!
,
Сходство треугольников — теоремы, свойства, примеры и доказательства
Классы
Класс 1 — 3
Класс 4 — 5
Класс 6 — 10
Класс 11 — 12
КОНКУРСЫ
BBS
000000000 Книги
NCERT Книги для 5 класса
NCERT Книги Класс 6
NCERT Книги для 7 класса
NCERT Книги для 8 класса
NCERT Книги для 9 класса
NCERT Книги для 10 класса
NCERT Книги для 11 класса
NCERT Книги для 12-го класса
NCERT Exemplar
NCERT Exemplar Class 8
NCERT Exemplar Class 9
NCERT Exemplar Class 10
NCERT Exemplar Class 11
NCERT Exemplar Class 12
9000al Aggar Agaris Agard Agard Agard Agard Agard 2000 12000000
Решения RS Aggarwal класса 10
Решения RS Aggarwal класса 11
Решения RS Aggarwal класса 10
90 003 Решения RS Aggarwal класса 9
Решения RS Aggarwal класса 8
Решения RS Aggarwal класса 7
Решения RS Aggarwal класса 6
Решения RD Sharma
Решения класса RD Sharma
Решения класса 9 Шарма 7 Решения RD Sharma Class 8
Решения RD Sharma Class 9
Решения RD Sharma Class 10
Решения RD Sharma Class 11
Решения RD Sharma Class 12
ФИЗИКА
Механика
000000 Электромагнетизм
ХИМИЯ
Органическая химия
Неорганическая химия
Периодическая таблица
МАТС
Теорема Пифагора
Отношения и функции
Последовательности и серии
Таблицы умножения
Детерминанты и матрицы
Прибыль и убыток
Полиномиальные уравнения
Делительные дроби
000 ФОРМУЛЫ
Математические формулы
Алгебровые формулы
Тригонометрические формулы
Геометрические формулы
КАЛЬКУЛЯТОРЫ
Математические калькуляторы
S000
S0003
Pегипс Класс 6
Образцы документов CBSE для класса 7
Образцы документов CBSE для класса 8
Образцы документов CBSE для класса 9
Образцы документов CBSE для класса 10
Образцы документов CBSE для класса 11
Образец образца CBSE pers for Class 12
CBSE Документ с вопросами о предыдущем году
CBSE Документы за предыдущий год Class 10
CBSE Вопросы за предыдущий год Class 12
HC Verma Solutions
HC Verma Solutions Класс 11 Физика
Решения HC Verma Class 12 Physics
Решения Lakhmir Singh
Решения Lakhmir Singh Class 9
Решения Lakhmir Singh Class 10
Решения Lakhmir Singh Class 8
Примечания
CBSE
Notes
CBSE Класс 7 Примечания CBSE
Класс 8 Примечания CBSE
Класс 9 Примечания CBSE
Класс 10 Примечания CBSE
Класс 11 Примечания CBSE
Класс 12 Примечания CBSE
Примечания пересмотра
CBSE Редакция
CBSE
CBSE Class 10 Примечания к пересмотру
CBSE Class 11 Примечания к пересмотру 9000 4
Замечания по пересмотру CBSE класса 12
Дополнительные вопросы CBSE
Дополнительные вопросы CBSE 8 класса
Дополнительные вопросы CBSE 8 по естественным наукам
CBSE 9 класса Дополнительные вопросы
CBSE 9 дополнительных вопросов по науке CBSE
9000 Класс 10 Дополнительные вопросы по математике
CBSE Класс 10 Дополнительные вопросы по науке
Класс CBSE
Класс 3
Класс 4
Класс 5
Класс 6
Класс 7
Класс 8
Класс 9
Класс 10
Класс 11
Класс 12
Решения для учебников
Решения NCERT
Решения NCERT для класса 11
Решения NCERT для физики класса 11
Решения NCERT для класса 11 Химия
Решения для класса 11 Биология
NCERT Решения для класса 11 Математика
9 0003 NCERT Solutions Class 11 Бухгалтерия
NCERT Solutions Class 11 Бизнес исследования
NCERT Solutions Class 11 Экономика
NCERT Solutions Class 11 Статистика
NCERT Solutions Class 11 Коммерция
NCERT Solutions для класса 12
NCERT Solutions для Класс 12 Физика
Решения NCERT для 12 класса Химия
Решения NCERT для 12 класса Биология
Решения NCERT для 12 класса Математика
Решения NCERT Класс 12 Бухгалтерский учет
Решения NCERT Класс 12 Бизнес исследования
Решения NCERT Класс 12 Экономика
NCERT Solutions Class 12 Бухгалтерский учет Часть 1
NCERT Solutions Class 12 Бухгалтерский учет Часть 2
NCERT Solutions Class 12 Микроэкономика
NCERT Solutions Class 12 Коммерция
NCERT Solutions Class 12 Макроэкономика
NCERT Solutions Для Класс 4
Решения NCERT для математики класса 4
Решения NCERT для класса 4 EVS
Решения NCERT для класса 5
Решения NCERT для математики класса 5
Решения NCERT для класса 5 EVS
Решения NCERT для класса 6
Решения NCERT для класса 6 Maths
Решения NCERT для класса 6 Science
Решения NCERT для класса 6 Общественные науки
Решения NCERT для класса 6 Английский
Решения NCERT для класса 7
Решения NCERT для класса 7 Математика
Решения NCERT для 7 класса Science
Решения NCERT для 7 класса Общественные науки
Решения NCERT для 7 класса Английский
Решения NCERT для 8 класса Математические решения
для 8 класса Математика
Решения NCERT для класса 8 Science
Решения NCERT для класса 8 Общественные науки
NCERT Solutio ns для класса 8 Английский
Решения NCERT для класса 9
Решения NCERT для класса 9 Общественные науки
Решения NCERT для класса 9 Математика
Решения NCERT для класса 9 Математика Глава 1
Решения NCERT Для класса 9 Математика 9 класса Глава 2
Решения NCERT для математики 9 класса Глава 3
Решения NCERT для математики 9 класса Глава 4
Решения NCERT для математики 9 класса Глава 5
Решения NCERT для математики 9 класса Глава 6
Решения NCERT для Математика 9 класса Глава 7
Решения NCERT для математики 9 класса Глава 8
Решения NCERT для математики 9 класса Глава 9
Решения NCERT для математики 9 класса Глава 10
Решения NCERT для математики 9 класса Глава 11
Решения NCERT для Математика 9 класса Глава 12
Решения NCERT для математики 9 класса Глава 13
Решения NCERT для математики 9 класса Глава 14
Решения NCERT для математики класса 9 Глава 15
Решения NCERT для науки 9 класса
Решения NCERT для науки 9 класса Глава 1
Решения NCERT для науки 9 класса Глава 2
Решения NCERT для класса 9 Наука Глава 3
Решения NCERT для 9 класса Наука Глава 4
Решения NCERT для 9 класса Наука Глава 5
Решения NCERT для 9 класса Наука Глава 6
Решения NCERT для 9 класса Наука Глава 7
Решения NCERT для 9 класса Научная глава 8
Решения NCERT для 9 класса Научная глава
Научные решения NCERT для 9 класса Научная глава 10
Научные решения NCERT для 9 класса Научная глава 12
Научные решения NCERT для 9 класса Научная глава 11
Решения NCERT для 9 класса Научная глава 13
Решения NCERT для 9 класса Научная глава 14
Решения NCERT для класса 9 Science Глава 15
Решения NCERT для класса 10
Решения NCERT для класса 10 Общественные науки
Решения NCERT для математики класса 10
Решения NCERT для математики класса 10 Глава 1
Решения NCERT для математики класса 10 Глава 2
решения NCERT для математики класса 10 глава 3
решения NCERT для математики класса 10 глава 4
решения NCERT для математики класса 10 глава 5
решения NCERT для математики класса 10 глава 6
решения NCERT для математики класса 10 Глава 7
решения NCERT для математики класса 10 глава 8
решения NCERT для математики класса 10 глава 9
решения NCERT для математики класса 10 глава 10
решения NCERT для математики класса 10 глава 11
решения NCERT для математики класса 10, глава 12
Решения NCERT для математики класса 10, глава 13
соль NCERT Решения для математики класса 10 Глава 14
Решения NCERT для математики класса 10 Глава 15
Решения NCERT для науки 10 класса
Решения NCERT для науки 10 класса Глава 1
Решения NCERT для науки 10 класса Глава 2
Решения NCERT для науки 10 класса, глава 3
Решения NCERT для науки 10 класса, глава 4
Решения NCERT для науки 10 класса, глава 5
Решения NCERT для науки 10 класса, глава 6
Решения NCERT для науки 10 класса, глава 7
Решения NCERT для науки 10 класса, глава 8
Решения NCERT для науки 10 класса, глава 9
Решения NCERT для науки 10 класса, глава 10
Решения NCERT для науки 10 класса, глава 11
Решения NCERT для науки 10 класса, глава 12
Решения NCERT для 10 класса Science Глава 9
Решения NCERT для 10 класса Science Глава 14
Решения NCERT для науки 10 класса Глава 15
Решения NCERT для науки 10 класса Глава 16
Программа NCERT
NCERT
Коммерция
Класс 11 Коммерческая программа Syllabus
Учебный курс по бизнес-классу 11000
Учебная программа по экономическому классу
Учебная программа по коммерческому классу
Учебная программа по 12 классу
Учебная программа по 12 классу
Учебная программа по экономическому классу
000000000000000000
Образцы коммерческих документов класса 11
Образцы коммерческих документов класса 12
Решения TS Grewal
Решения TS Grewal Класс 12 Бухгалтерский учет
Решения TS Grewal Класс 11 Бухгалтерский учет
Отчет о движении денежных средств
eurship
Защита потребителей
Что такое фиксированный актив
Что такое баланс
Формат баланса
Что такое акции
Разница между продажами и маркетингом
P000S Документы ICSE
ML Решения Aggarwal
ML Решения Aggarwal Class 10 Maths
ML Решения Aggarwal Class 9 Математика
ML Решения Aggarwal Class 8 Maths
ML Решения Aggarwal Class 7 Математические решения
ML 6 0004
ML 6
Selina Solutions
Selina Solution для 8 класса
Selina Solutions для 10 класса
Selina Solution для 9 класса 9
Frank Solutions
Frank Solutions для класса 10 Maths
Frank Solutions для класса 9 Maths
ICSE Class 9000 2
ICSE Class 6
ICSE Class 7
ICSE Class 8
ICSE Class 9
ICSE Class 10
ISC Class 11
ISC Class 12
IAS
Сервисный экзамен
UPSC Syllabus
Бесплатно IAS Prep
Текущая информация
Список статей IAS
IAS 2019 Mock Test
IAS 2019 Mock Test 1
IAS 2019 Mock Test 2
KPSC KAS экзамен
UPPSC PCS экзамен
MPSC экзамен
RPSC RAS экзамен
TNPSC группа 1
APPSC группа 1
BPSC экзамен
экзамен
JPS
экзамен
экзамен
WPSS
экзамен
JPS
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
экзамен
Вопросник UPSC 2019
Ключ ответа UPSC 2019
Коучинг IAS
IA S Коучинг Бангалор
IAS Коучинг Дели
IAS Коучинг Ченнаи
IAS Коучинг Хайдарабад
IAS Коучинг Мумбаи
JEE
Бумага
JEE JEE 9000
JEE
JEE-код
JEE
J0003 S0004000
JEE Вопрос
Биноминальная теорема
JEE Статьи
Квадратичное уравнение
NEET
Программа Бьюя NEET
NEET 2020
NEET Подготовка к экзамену NEET
S0003
образца
Поддержка
Жалоба Разрешение
Customer Care
Поддержка центр
Государственные платы
GSEB
GSEB Силабус
GSEB Вопрос бумаги
GSEB образец бумаги
GSEB Книги
90 004
MSBSHSE
MSBSHSE Syllabus
MSBSHSE Учебники
MSBSHSE Образцы документов
MSBSHSE Вопросные записки
AP Board
-й год APSERT
-й год SBSUS
-й год
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS SUBSUS SUBSUS SUBSUS SUBSUS
SUBSUS
SUBSUS
SUBSUS
SUBSUS SUBSUS
SUBSUS
Всеобщая справка
MP Board
MP Board Syllabus
MP Board Образцы документов
MP Board Учебники
Assam Board
Assam Board Syllabus
Assam Board Учебники
Sample Board Paperss Sample3 P0003 BSEB
Бихарская доска Syllabus
Бихарская доска Учебники
Бихарская доска Вопросные бумаги
Бихарская модель Бумажные макеты
БСЭ Одиша
доска
Sislabus
Совет 9408 S0008
Sisplus
S0008
Sample P000S
Sample
S000S PSEB Syllabus
Учебники PSEB
Документы PSEB
RBSE
Учебное пособие Раджастхана Syllabus
Учебники RBSE
Документы RBSE
PCB
HPE HPSBE
JKBOSE
JKBOSE Syllabus
JKBOSE Образцы документов
JKBOSE Образец экзамена
TN Board
TN Board Syllabus
Board 931 JAC
JAC Силабус
JAC учебники
JAC Вопрос Papers
Telangana Совет
Telangana Совет Силабус
Telangana совет учебники
Telangana Совет Вопрос Papers
KSEEB KSEEB Силабус
KSEEB Модель Вопрос Papers
KBPE
KBPE Силабус
KBPE Учебники
KBPE Вопрос Papers
UPMSP
UP Совет Силабус
UP Совет Книги
UP Совет Вопрос Papers
Западная Бенгалия Совет
Западная Бенгалия Совет Силабус
Западная Бенгалия Совет учебниками
West Bengal совет Вопрос документы
UBSE
TBSE
Goa Board
NbSe
CGBSE
MBSE
Meghalaya Совет
Manipur Совет
Харьяны Совет
Государственные экзамены
Банк экзаменов
SBI Exams
PIL, Exams
RBI Exams
PIL, РРБ экзамен
SSC Exams
SSC JE
SSC GD
SSC CPO 900 04
SSC CHSL
SSC CGL
RRB экзаменов
RRB JE
RRB NTPC
RRB ALP
L0003000000 L0003000000000000 UPSC CAPF
Список государственных экзаменов Статьи
Обучающие дети
Класс 1
Класс 2
Класс 3
Академические вопросы
Вопросы физики
Вопросы химии
Химические вопросы
Химические вопросы
Вопросы химии
Биология
Вопросы
Вопросы по науке
Вопросы ГК
Обучение онлайн
Обучение на дому
Полные формы
CAT
Программа CAT BYJU’S
CAT
CAT
CAT
CAT
CAT
CAT
CAT
CAT
FreeBS
40004 CAT 2020 Exam Pattern
Обзор приложения Byju на CAT
КУПИТЬ КУРС
+919243500460
.
No related posts.