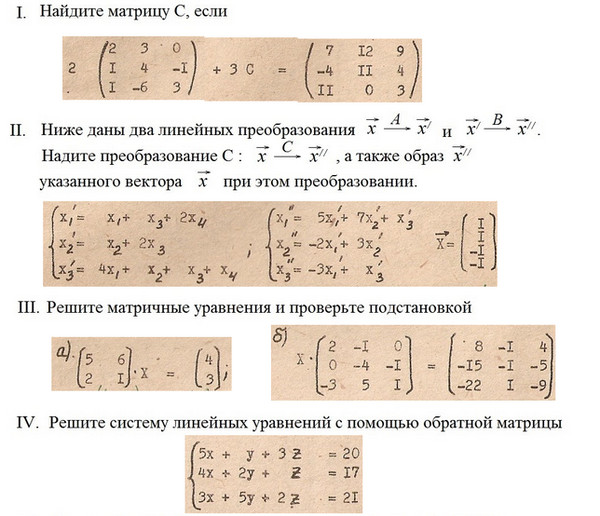
ТЕМА 3. Решение систем линейных уравнений методом Жордана – Гаусса
⇐ ПредыдущаяСтр 3 из 9Следующая ⇒
Общим решением системы m линейных уравнений с n неизвестными называется
!решение, в котором базисные неизвестные линейно выражаются через свободные
Частным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения, если свободным неизвестным придать произвольные значения
При отыскании общего решения системы m линейных уравнений с n неизвестными методом Жордана – Гаусса в качестве разрешающего элемента выбирается
!любой отличный от нуля элемент таблицы, кроме элементов столбца свободных членов и контрольного столбца
любой элемент таблицы
Система m линейных уравнений с n неизвестными не имеет решений, если на некоторой итерации
!все элементы какой – либо строки таблицы Жордана – Гаусса, кроме свободного члена, равны нулю
Базисным решением системы m линейных уравнений с n неизвестными называется
!решение, полученное из общего решения системы, в котором свободные неизвестные равны 0
Если r – число базисных неизвестных, а n – общее число неизвестных в произвольной системе m линейных уравнений, то система имеет бесконечное множество решений при !
Если дано матричное уравнение , то его решение определяется по формуле !
Если в таблице Жордана – Гаусса — разрешающий элемент, то элемент находится по формуле (правило прямоугольника) !
Итерацией в методе Жордана — Гаусса называется !расчет элементов одной таблицы Жордана – Гаусса
Метод Жордана – Гаусса это !последовательное исключение неизвестных
Если в таблице Жордана – Гаусса имеются две одинаковые строки, то !одну из них можно вычеркнуть
Единичным называется столбец таблицы Жордана – Гаусса, который состоит из !одной единицы и остальных 0Переменная называется базисной, если в таблице Жордана – Гаусса столбец коэффициентов !единичным
Если в таблице Жордана – Гаусса имеются две пропорциональные строки, то!одну из них нужно вычеркнуть
Переменная называется свободной, если в таблице Жордана – Гаусса !она не входит в столбец — базис
Система m линейных уравнений с n неизвестными называется однородной, если свободные !равны 0
Матрица коэффициентов при неизвестных системы m линейных уравнений с n неизвестными является !прямоугольной
Число частных решений равно !бесчисленному множеству решений
Переход от одного базисного решения к другому осуществляется путем !проведения еще одной итерации метода Жордана – Гаусса
Элементы вводимой строки в таблице Жордана – Гаусса находятся !делением элементов разрешающей строки предыдущей таблицы на разрешающей элемент
Число базисных решений произвольной системы m линейных уравнений с n неизвестными определяется !формулой
Решение системы m линейных уравнений с n неизвестными, в котором базисные неизвестные линейно выражаются через свободные, называется !общим
Систему можно решить матричным способом, если !число уравнений равно числу неизвестных
Решение, полученное из общего решения, если свободным неизвестным придать произвольные значения, называется !частным
Значение базисных переменных в таблице Жордана – Гаусса находится в вводимой строке !столбце
В контрольный столбец 1-й таблицы Жордана – Гаусса записывается !сумма коэффициентов при неизвестных по каждой строке
Матрица коэффициентов при неизвестных при решении системы n линейных уравнений с n неизвестными матричным способом является !невырожденной
В столбце таблицы Жордана – Гаусса находятся значения неизвестных !базисных
Решение системы линейных уравнений с n неизвестными находится с применением обратной матрицы, если число уравнений равно !n
Решение, матричного уравнения находится по формуле , если оно имеет вид !
Решение, полученное из общего решения, если свободным неизвестным придать нулевые значения называется !базисным
Если в таблице Жордана – Гаусса все элементы какой – либо строки, кроме свободного члена, равны нулю, то система m линейных уравнений с n неизвестными !не имеет решений
Если в системе m линейных уравнений с n неизвестными r — число базисных неизвестных и при этом , то система имеет !бесчисленное множество решений
Если при решении системы m линейных уравнений c n неизвестными в разрешающей строке таблицы Жордана – Гаусса находится нуль, то столбец, содержащий этот нульь!переносится в следующую таблицу без изменения
Если при решении системы m линейных уравнений c n неизвестными в разрешающем столбце таблицы Жордана – Гаусса имеется нуль, то строка, содержащая этот нуль !переносится в следующую таблицу без изменения
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно !30
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно !16
Если в системе m линейных уравнений с n неизвестными , то система называется !неопределенной
Если в системе m линейных уравнений с n неизвестными , то система называется !переопределенной
В системе m линейных уравнений с n неизвестными число базисных решений равно!
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно !6
Если в базисном решении системы линейных уравнений , − базисные переменные, то равно !6
⇐ Предыдущая123456789Следующая ⇒
Поиск по сайту:
⇐ ПредыдущаяСтр 4 из 11Следующая ⇒ Пример 1. Решение:
Записываем полученные данные в таблицу. Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Выбранному разрешающему элементу соответствовала переменная , следовательно, переменную записываем в базис. Переходим к следующему шагу. 2-й шаг. Выбираем разрешающий элемент из второй и третьей строчки, для удобства вычислений берем . Все элементы второй строки делим на этот разрешающий элемент. Все элементы разрешающего столбца , кроме элемента , обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника. Третий столбец в новую таблицу можно переписать без изменений, т.к. в разрешающей стоке в третьем столбце стоит ноль. Записываем полученные данные в таблицу. Осуществляем контроль: Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Переходим к следующему шагу. 3-й шаг. Выбираем разрешающий элемент из третьей строчки, т.к. в этой третьей строке только один элемент отличный от нуля, то в качестве разрешающего элемента выбираем этот элемент . Все элементы третьей строки делим на этот разрешающий элемент. Все элементы разрешающего столбца , кроме элемента , обнуляем. Все остальные элементы таблицы вычисляем по правилу прямоугольника. Первый, третий и контрольный столбцы в новую таблицу можно переписать без изменений, т.к. в разрешающей строке в первом, третьем и контрольном столбцах стоят нули. Записываем полученные данные в таблицу. Осуществляем контроль: Т.к. элементы контрольного столбца, вычисленные по правилу прямоугольника, равны элементам контрольного столбца, вычисленные суммированием элементов по строке, то полученная таблица составлена верно. Т.к. все строки побывали разрешающими и система приведена к единичному базису, то выписываем ответ: Ответ: . Задание 1.117.Решить систему линейных уравнений методом Жордана – Гаусса. 1) 2) 3) 4) 5) ⇐ Предыдущая12345678910Следующая ⇒ ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
Решить систему методом Жордана-Гаусса
Осуществляем контроль:
Система линейных уравнений
Система линейных уравнений Math Task
|
1.Линейные уравнения. 2.Решение системы линейных уравнений методом Жордана-Гаусса. 
|
|||||||||||||||||||||||||||||
| 2 3 4 5 6 7 8 9 10 | |||||||||||||||||||||||||||||
1.Линейные уравнения.Линейное уравнение — это уравнение вида: а1х1 + а2х2 + а3х3 + … + аnxn = b a1,a2,a3,…,an — коэффициенты уравнения.
|
|||||||||||||||||||||||||||||
Совокупность линейных уравнений, связанных переменными х1,х2,х3 . a11,a12,a13,…,an — коэффициенты уравнения. |
|||||||||||||||||||||||||||||
Если система имеет одно решение, то она называется определенной. Если система имеет бесконечное множество решений, то она называется неопределенной. |
|||||||||||||||||||||||||||||
2.Решение системы линейных уравнений методом Жордана-Гаусса. Метод Жордана-Гаусса широко используется при решении системы линейных уравнений, т. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
Пример 1. |
|||||||||||||||||||||||||||||
Пример 2. |
|||||||||||||||||||||||||||||
| 2 3 4 5 6 7 8 9 10 | |||||||||||||||||||||||||||||
.. xn называется системой линейных уравнений.
к. данный метод наименее трудоемок при решении подобных задач. Суть данного метода заключается в том, что после некоторых преобразований одно из уравнений состоит из одной переменной, которое легко решается в обычном порядке. Например:
|
|
||
www. mathtask.ru |
||
линейная алгебра — решение системы уравнений с использованием Гаусса/Гаусса-Жордана (матрица)
$\begingroup$
Система уравнений $$\begin{выравнивание*} х -2у +3г &= 2\\ 2x -3y +8z &= 7\\ 3x -4y +13z &= 8 \end{align*}$$
В расширенной матрице $3\times 4$ $$\left(\begin{массив}{crc|c} 1 &-2 &3 &2\\ 2&-3&8&7\\ 3 &-4 &13& 8\\ \end{array}\right).$$
Выше приведены уравнения/строки. Используя эти операции со строками: постоянное число, умноженное на строку, обмен/переключение уравнений/строки и, наконец, добавление двух уравнений/строк вместе после умножения одного из них на константу — я все еще не могу решить и в конечном итоге должен отменить часть диагонали матрицы при попытке добиться результата, аналогичного или равного единичной матрице.
Под отменой я подразумеваю превращение в 0, что делает его невозможным для восстановления с помощью этих операций. Это проблема при попытке достичь верхней треугольной матрицы (эшелон строк или уменьшенный эшелон строк, но в данном случае в зависимости от того, что именно).
Похоже, что аналогичная ситуация имеет место с двумя неизвестными и теми же тремя числами уравнений
$$\begin{align*} х + у &= 1\\ 9x -y &= 0\\ х -19у &= -17 \end{align*}$$
- линейная алгебра
- матрицы
- матричные уравнения
- джордан-нормальная форма
- исключение Гаусса
$\endgroup$
4
$\begingroup$
Система несовместима: второе уравнение минус удвоенное первое уравнение дает $y+2z=3$, а третье уравнение минус тройное второе уравнение дает $2y+4z=2$. Эти два уравнения несовместимы, поэтому система не имеет решений.
Вы можете видеть это при выполнении исключения Гаусса:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 &-2 &3 &2\\
2&-3&8&7\\
3 &-4 &13& 8\\
\end{массив}\right) &\stackrel{R_2-2R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
3 и -4 и 13 и 8
\end{массив}\right) \stackrel{R_3-3R_1}{\longrightarrow} \left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 2
\конец{массив}\справа)\\
&\stackrel{R_3-2R_2}{\longrightarrow} \left(\begin{array}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и -4
\end{массив}\right) \stackrel{-\frac{1}{4}R_3}{\longrightarrow}
\left(\begin{массив}{rrr|r}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
И коэффициент, и расширенная матрица теперь имеют эшелонированную форму строк: первый ненулевой элемент каждой строки — это $1$, и $1$ в каждой строке появляется справа от $1$ в предыдущей строке, и все строки $0$ находятся внизу.
Поскольку ранг уменьшенной матрицы коэффициентов равен $2$, а ранг расширенной матрицы равен $3$, система несовместна.
Вы можете продолжить отсюда, чтобы получить форму эшелона с уменьшенной строкой, но это не «решит» проблему внезапно:
$$\begin{выравнивание*}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right)&\stackrel{R_1-2R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 1
\end{массив}\right) \stackrel{R_2-3R_3}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 0\\
0 и 1 и 2 и 0 \\
0 и 0 и 0 и 1
\конец{массив}\справа)\\
&\stackrel{R_1+2R_2}{\longrightarrow}
\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 0\\
0 и 1 и 2 и 0\\
0 и 0 и 0 и 1
\конец{массив}\справа).
\end{выравнивание*}$$
Это в сокращенной эшелонированной форме строк (дополнительное условие состоит в том, что начальные $1$ в каждой строке являются единственными ненулевыми элементами в своих столбцах), но опять же вы видите, что это соответствует несогласованной системе.
Теперь предположим, что последнее уравнение было $3x-4y+13z=12$ вместо $8$.
Тогда на третьем шаге приведения выше мы получили бы матрицу
$$\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 2 и 4 и 6
\end{массив}\right)\stackrel{R_3-2R_2}{\longrightarrow}
\left(\begin{массив}{crc|c}
1 и -2 и 3 и 2\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\конец{массив}\справа).$$
Это совершенно прекрасная матрица формы строки-эшелона; просто вы получите одну свободную переменную и бесконечно много решений. Затем вы можете перейти к уменьшенной форме эшелона строк, дважды добавив вторую строку к первой строке, и вы получите
$$\left(\begin{массив}{ccc|c}
1 и 0 и 7 и 8\\
0 и 1 и 2 и 3\\
0 и 0 и 0 и 0
\end{массив}\right)$$
который дает решения
$$\begin{выравнивание*}
х &= 8 — 7t\\
у &= 3 — 2t\\
г &= т
\end{align*},\qquad t\text{произвольный.}$$
$\endgroup$
8
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
🧮 Метод Гаусса-Жордана для решения систем линейных уравнений — документация
Карл Фридрих Гаусс был математиком и физиком, родившимся в Германии в 1777 году. и разработал такое огромное количество работ в стольких различных областях, что любой студент, изучающий естественные науки, найдет его имя много раз в разных предметах, вплоть до точка веры в то, что Гаусс повсюду.
Среди всех вкладов Гаусса в математику мы находим метод решения систем линейных уравнений, которые широко используются сейчас, когда компьютеры могут быть запрограммированным на выполнение всей тяжелой работы. Этот метод имеет то преимущество, что легко программируется, поскольку использует последовательность повторяющихся операций после уравнения сохраняются в памяти компьютера в виде массива термов, подобного матрица, содержащая коэффициенты каждого уравнения в одной строке.
Гаусс решил проблему, используя некоторые свойства систем
Линейные уравнения, чтобы внести изменения в матрицу, изменив коэффициенты на
получение эквивалентных уравнений, которые не изменят Систему.
Эти изменения могут быть:
A) Поменяйте местами два ряда, поставив каждый на место другого
B) Умножить каждое слагаемое в одной из строк (уравнений) на одно и то же число отличное от нуля.
C) Добавьте или вычтите каждое слагаемое в одной из строк (уравнений) из соответствующий термин из другой строки, в результате чего получается новая строка, которая также принадлежит к той же системе уравнений.
Вы можете выполнить любую из этих операций, и система уравнений останется прежней, решения будут одинаковыми. Гаусс придумал способ использовать это для преобразования исходную группу уравнений в одну, которую будет легче решить.
Метод Гаусса
Метод очень оригинальный и очень простой. Давайте покажем, как он это сделал это с одним примером; система из 4 уравнений с 4 неизвестными (w, x, y, z):
В матрице столько столбцов, сколько уравнений (и неизвестных), сколько в системе, плюс
один столбец из-за постоянных членов, поэтому в этом случае матрица имеет 5
столбцы х 4 ряда.
Гаусс считал, что хорошим способом решения этих систем является «избавление» от некоторых члены, сделав их равными нулю, пока он не смог получить уравнение только с нулями за исключением одного неизвестного и постоянного члена, что позволяет очень легко найти тогда неизвестный. Как это сделать?
Мы должны помнить операции (A, B, C), которые мы можем выполнять, не меняя система. Теперь давайте сосредоточимся на втором уравнении:
.ш-4х-2у+2г=-5
Первая неизвестная (w) умножается на коэффициент 1, не пишется. Это почему первый член во второй строке матрицы равен 1,
Как я могу избавиться от этого неизвестного, внеся изменения во второе уравнение? Как могу ли я превратить эту 1 в ноль, чтобы w просто исчезла из уравнения?
Не самая очевидная идея — умножать все уравнение на ноль. Если мы снова прочитаем
операцию B, как объяснялось ранее, мы находим там очень ясно сказано, что
мы не можем умножать на ноль. Другой способ — добавить -1 к первому члену.
Третья операция, о которой мы говорили ранее, C, утверждает, что мы можем сложить два
уравнения, принадлежащие системе, почленно, и полученное уравнение
тоже принадлежит системе. Итак, если бы в системе было еще одно уравнение
системы с -1 в качестве первого коэффициента, мы бы только добавили это уравнение, член на
срок, ко второму и первый член стал бы просто нулем, он пошел бы
прочь. Но, конечно, нет этого желаемого уравнения с -1, умножающим w.
Жизнь никогда не бывает такой легкой.
Какое решение нашел Гаусс? Ну, он думал умножить любой другой уравнение на число, которое превратит его первый коэффициент в -1. Если мы умножьте каждый член линейного уравнения на одно и то же число, в результате уравнение эквивалентно исходному, как указано на Б.
Если мы сделаем это с первым уравнением (3w — 2x + 3y + z = 12), коэффициент
умножая неизвестное w, первое, равно 3, поэтому в этом случае нам понадобится
умножить все первое уравнение член за членом на число, которое
3 в -1.
Это число будет равно -1/3, так что операция будет выглядеть как
это:
Где искомый -1 является первым коэффициентом. Теперь мы можем добавить это уравнение к второе уравнение системы, чтобы превратить его первый коэффициент в нуль.
Мы видим, что первый коэффициент во втором уравнении теперь равен нулю, поэтому теперь на один срок меньше.
Система уравнений и матрица коэффициентов теперь будут выглядеть так:
Теперь мы на шаг ближе к решению системы, так как оно у нас есть уравнение с тремя неизвестными вместо четырех. Можем ли мы продолжать делать то же самое с большим количеством уравнений? Конечно можем, и Гаусс сделал именно это для третьего и четвертое уравнения. Его метод избавляется от всех первых членов, кроме случай первого уравнения; вам всегда понадобится хотя бы одно уравнение с первый член, чтобы можно было вычислить значение w.
Повтор шагов вниз
Итак, проделав аналогичные операции над третьим и четвертым уравнениями, получим:
Теперь в системе, если игнорировать первое уравнение, всего три неизвестных (x, y,
z) и три уравнения (второе, третье и четвертое уравнения).
Как только мы поймем, что мы здесь сделали, мы сможем понять весь метод Гаусса. придумано так умно, потому что если мы забудем о первом уравнении и повторим предыдущий процесс, оставив теперь второе уравнение нетронутым, и мы модифицируем третье и четвертое уравнения так, что их первый член (коэффициент при x) равно нулю, мы получим меньшую систему уравнений только с двумя неизвестными и два уравнения.
Метод Гаусса продолжает уменьшать размер системы уравнений до меньших системы, которые легче решить. Вот так выглядит система уравнений как только это сводится всего к двум уравнениям:
Таким образом, мы можем продолжать уменьшать размер системы, пока не получим только один уравнение и одно неизвестное, которое решается напрямую:
Добиться результатов и переломить ситуацию, чтобы двигаться вверх
Таким образом, из четвертого уравнения мы можем получить непосредственно значение z, наше первое результат:
До этого момента метод работает сверху вниз, получая наш первый результат
из последнего уравнения, но теперь поток меняется на противоположный, и мы начинаем двигаться вверх.
Имея значение z, мы можем использовать его в третьем уравнении (z=4, тогда 3z=12)
получение:
-10 лет + 12 = -18
Откуда мы можем получить непосредственно следующий результат, значение для y:
г = (-18-12) / (-10) = 3
Затем, имея z=4 и y=3, мы можем продолжить движение вверх и использовать эти значения в второе уравнение, чтобы получить следующее неизвестное, x, и, наконец, мы используем эти три результата (x, y, z) в первом уравнении, чтобы получить последний результат, неизвестный ж.
Следуя этой процедуре, мы подсчитали все результаты:
ш=1 х=2 у=3 з=4
И этот метод можно использовать для любой системы линейных уравнений, независимо от ее размера. сколько же у него уравнений, спасибо Карлу Фридриху Гауссу.
Некоторые детали, которые следует учитывать при программировании этого метода
Когда мы работали над преобразованием первого столбца в нули, мы оставили первый столбец
уравнение нетронуто, оно было использовано для изменения других уравнений, сосредоточив внимание на
первый член первого уравнения; этот термин, который мы используем, известен как «стержень».
Один раз
мы изменили все коэффициенты ниже этого первого члена на нули, мы переместились вниз
и использовал второе уравнение, оставив его нетронутым, чтобы изменить третье и четвертое
уравнение. Мы использовали первый ненулевой член, чтобы превратить в нули все
коэффициенты ниже (второй столбец), так что в этом случае этот второй член является
вращаться. Когда мы повторяем процедуру, используя третье уравнение, третий член равен
стержень и так далее.
Матрица, которую мы показывали в правой части системы, представляет собой представление о том, как коэффициенты могут быть сохранены на компьютере, чтобы сделать все эти операции в цифровом виде, используя программируемую версию этого метода, алгоритм. Есть некоторые детали, которые следует учитывать при разработке этого алгоритма.
Элемент, который мы используем в качестве точки опоры, не может быть нулем. Чтобы этого не произошло,
обычная процедура использует уравнение, которое имеет большее число, поскольку оно
первый коэффициент как основное уравнение.
Мы должны помнить, что мы можем поменять местами два
уравнения из системы без изменения системы, поэтому перед использованием первого
уравнение, чтобы изменить другие, мы ищем уравнение с большей первой
коэффициент и поменять местами его на первую строку, далее продолжаем. То же самое происходит, когда
мы будем использовать второе уравнение, мы сравниваем его второй коэффициент (поскольку
первая единица была заменена нулем) с соответствующими коэффициентами на
третье и четвертое уравнения, а затем поменять местами то с наибольшим
коэффициент во вторую строку.
Такую же замену следует выполнять до тех пор, пока весь нижний левый треугольник не будет заполнен нулями, так что последнее уравнение готово к прямому решению. Это способ гарантировать, что каждый стержень не будет нулем.
Улучшение Джордана
Вильгельм Йордан был немецким геодезистом, родившимся в 1842 году, а также писателем.
с интересом к математике и геометрии. Работал по методу, разработанному
Гауссом и улучшил его, пока пытался применить к некоторым геодезическим данным.
Позже он опубликовал свою методику в своей книге «Учебник геодезии».
Чтобы понять работу Джордана, мы должны помнить, что метод Гаусса превращает в нули весь нижний левый треугольник матрицы. У Джордана была идея сохранить используя ту же процедуру для верхнего правого треугольника, повернув все эти коэффициенты тоже в нули, оставив только члены по диагонали, т.е. повороты, так что каждое уравнение будет иметь только одно неизвестное, а затем оперируя эти члены, чтобы они были заменены единицами (1) и каждое уравнение приносят сразу один результат. Мы можем лучше понять все это, взглянув на системы после того, как верхний правый треугольник был заменен нулями, а шарниры по диагонали превратились в единицы.
В системе уравнения мы оставили обнуленными членами, чтобы сделать очевидным соответствие уравнений матрице, а обычный способ записи эти уравнения были бы проще, не записывая нулевые члены и не записывая число 1 при умножении неизвестных, например:
Глядя на упрощенные уравнения, становится ясно, почему Джордан хотел
добавить эти шаги к методу Гаусса.
Каждое уравнение является просто результатом для
каждый неизвестный. Очень элегантный.
Хотя эти методы были разработаны задолго до компьютеров, очевидно, авторы хотели разработать алгоритм с простыми и повторяющимися шагами, который будет работать даже для больших систем уравнений; идеально подходит для компьютеров, итеративный процесс может быть запрограммирован и выполнен в цифровом виде очень точным образом просто вводя матрицу коэффициентов. Собственно говоря, вот как компьютеры решают системы линейных уравнений в настоящее время, иногда запуская Метод Гаусса, а иногда и вариация Гаусса-Жордана.
Мы можем только восхищаться такими умами, которые, посылая свои интеллект и мудрость сквозь века могут помочь нам решить наши проблемы Cегодня.
Об авторе
Хорхе Араика
Графический дизайнер
с техническим образованием, профессионал старой школы с некоторыми знаниями в
области инженерии и программирования, а также сторонник критических и рациональных
мышление как способ распространения научного отношения к знаниям.
Свобода это
его другая страсть, и он будет отстаивать ее при каждом удобном случае.
7.3 — Метод исключения
7.3 — Метод исключения7.3 — Метод исключения
Щелкните здесь, если вам нужны инструкции по использованию тренера по алгебре . провести метод исключения.В этом разделе мы объясняем метод исключения. Этот метод использует тот факт, что решение уравнения не изменится, если мы
- умножьте обе части уравнения на один и тот же коэффициент.
- вычесть равные количества из обеих частей уравнения.
Метод исключения использует этот факт для решения системы линейных уравнений.
Предположим, мы начинаем с системы из 90 210 n 90 211 уравнений с 90 210 n 90 211 неизвестными.
Выберите первое уравнение и вычтите подходящие кратные ему из другого n − 1 уравнения.
В каждом случае выбирается кратность
так что вычитание отменяет или устраняет ту же самую переменную , скажем, x .
В результате уравнения n − 1 содержат только n − 1 неизвестно ( x больше не отображается).
Мы повторяем этот процесс исключения, пока не получим 1 уравнение в 1 неизвестном, которая затем легко решается.
Последним шагом является обратная замена решения, уже полученного для 1 неизвестных в предыдущие уравнения, чтобы найти значения всех остальных неизвестных.
Пример: Решите эту систему уравнений методом исключения: Решение: Возьмем дважды первое уравнение, а именно:
2 х + 2 у = 8и вычесть его из второго уравнения, вот так: В результате получается одно уравнение в одном неизвестном, y . Другое неизвестное, x , было устранено. Решение этого уравнения дает г = 0,4.
Осталось найти х . Если мы подставим обратно y = 0,4 в любое из исходных уравнений получаем х = 3,6. Таким образом, решение:
{ х = 3,6, у = 0,4}.(Обратите внимание, что вместо этого мы могли бы найти x без обратной подстановки, если бы мы вычли 3 раза первое уравнение из второго уравнения, так как это исключает y .)
Расширенная матрица
Мы объяснили суть исключения. Для больших систем нам нужен систематическая процедура, чтобы не запутаться. Двумя такими процедурами являются исключение Гаусса и исключение Гаусса-Жордана.Прежде чем мы опишем их, мы введем некоторые сокращения. Система уравнений типа:
будет представлен прямоугольным массивом чисел, называемым расширенная матрица :Определения:
- Отдельные числа в матрице называются элементами .
- Столбцы идут вниз по матрице. например столбец 4 th содержит элементы 80, 7 и 22.
- Ряды пересекаются. Строка 3 rd содержит 3, −1, 2 и 22. Обратите внимание, что количество столбцов в расширенной матрице всегда на 1 больше. чем количество строк.
- Диагональ — это набор элементов, который начинается сверху слева углу матрицы и проходит по диагонали вниз и вправо. Диагональ вышеуказанной матрицы состоит из чисел 4, 1 и 2.
- Любые числа в позиции D называются по диагонали , любой в позиции a выше диагонали , и любой в позиции б — это ниже диагонали .
- i -я строка расширенной матрицы представляет i -е уравнение.
- j -ая колонка (слева от вертикальной черты) содержит коэффициенты j -й переменной или неизвестной.
- Вертикальная линия представляет знаки равенства.
- Столбец справа от вертикальной линии представляет правую часть уравнений.
Элементарные операции со строками
Мы видели, что решение системы уравнений не изменится, если мы:- разделить обе части уравнения на константу или
- вычесть кратное одному уравнению из другого уравнения.
| Элементарные операции с строками (E.R.O.):
|
Пример: Этот пример показывает, как мы применяем E.R.O.#1 и обозначения мы используем, чтобы указать на это. Разделим первый ряд дополненной матрица слева на 2, чтобы создать новую расширенную матрицу справа:
Примечание: ← ÷ на 2 означает » разделить строку на указание 2 произвести новую матрицу ».Пример: Этот пример показывает, как мы применяем E.R.O.#2 и обозначения мы используем, чтобы указать на это. В расширенной матрице слева мы будем возьмите вторую строку и из нее вычтите 3 раза первую строку, чтобы получить новая расширенная матрица справа: Примечание: ← Р 2 − 3 · R 1 означает « возьмите строку, на которую указывает (строка 2), и вычтите 3 раза строку 1 из для создания новой строки 2.
”Пример: Этот пример показывает, как мы применяем E.R.O.#3 и обозначения мы используем, чтобы указать на это. В расширенной матрице слева мы поменяем местами строки 1 и 2, чтобы получить новая расширенная матрица справа: Примечание: R 1 ↔ R 2 означает « поменять местами строки 1 и 2. »
Исключение Гаусса
Процедура исключения Гаусса представляет собой определенную последовательность операций E.R.O. который преобразует расширенную матрицу в форму Гаусса (также известная как форма эшелона строк ) Эта форма характеризуется единицами по диагонали и нулями под диагональю. и любые числа выше диагонали. Вот пример: Эта расширенная матрица представляет система уравнений: Решается обратной заменой. Подключение z = 3 к второе уравнение дает y = 5.
Тогда подставив оба z = 3 и y = 5 в первом уравнении дает x = 7.| Алгоритм исключения Гаусса Мы преобразуем по одному столбцу за раз в эшелонированную (или гауссовую) форму. Преобразуемый в данный момент столбец называется поворотная колонна . Мы действуем систематически, позволяя сводной колонке быть первым столбцом, затем вторым столбцом и т. д. до последнего столбца перед вертикальной линией расширенной матрицы. Для каждого сводного столбца мы делаем следующие два шага, прежде чем перейти к следующему сводному столбцу:
|
Пример: Используйте Исключение Гаусса для решения системы уравнений:
Решение: Выполните следующую последовательность E.R.O. на расширенной матрице:Установите опорный столбец в столбец 1. Получите 1 в диагональной позиции (красный):
Затем установите 0 ниже опорной точки (выделено красным):
Теперь пусть сводная колонка = вторая колонка.
Сначала получите 1 в диагональной позиции:
Далее получаем 0 в позиции ниже точки разворота:
Теперь пусть сводная колонка = третья колонка.
Получите 1 в диагональной позиции: Эта матрица, которая теперь находится в форме Гаусса, представляет эту систему 3 уравнения:
Решается обратной заменой. Подставив z = 3 во второй Уравнение получаем y = 5. И затыкая z = 3 и y = 5 в первое уравнение мы получаем x = 7. Таким образом, решение:
{ x = 7, y = 5, z = 3}.
Исключение Гаусса-Джордана
Процедура исключения Гаусса-Жордана — это немного другая последовательность ERO, которые преобразуют расширенную матрицу в форму Gauss-Jordan (также известный как уменьшенная форма эшелона ряда ). Эта форма характеризуется единицами по диагонали, 0 над и под диагональю слева от вертикальной линии, и любые числа справа от вертикальной линии. Вот пример: Эта расширенная матрица представляет собой систему уравнений: Эта система уже решена: x = 7, y = 5, z = 3.
Обратная замена не требуется.
Однако для производства
Форма Гаусса-Жордана как форма Гаусса.| Алгоритм исключения Гаусса-Жордана Мы преобразовываем по одному столбцу за раз в сокращенную ступенчатую (или Гаусса-Жордана) форму строк. Преобразуемый в данный момент столбец называется поворотная колонна . Мы действуем систематически, позволяя сводной колонке быть первым столбцом, затем вторым столбцом и т. д. до последнего столбца перед вертикальной линией расширенной матрицы. Для каждого сводного столбца мы делаем следующие два шага, прежде чем перейти к следующему сводному столбцу:
|
Обратите внимание, что единственное отличие от процедуры Гаусса состоит в том, что на втором шаге мы получаем 0s выше диагонали , а также ниже диагонали. Важно получить все эти 0, прежде чем переходить к следующему сводному столбцу.
Пример: Используйте исключение Гаусса-Жордана для решения системы уравнений:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установите опорный столбец на столбец 1. Получите 1 в диагональной позиции. (красным) с помощью E.
R.O. № 1: Затем, используя E.R.O., получите 0 ниже опорной точки (красного цвета). № 2: Теперь пусть сводная колонка = вторая колонка. Во-первых, получить 1 в диагональной позиции
с помощью E.R.O. № 1: Затем получите 0 в позициях выше и ниже точки разворота (обозначены красным), используя E.R.O. № 2: Теперь пусть сводная колонка = третья колонка. Получите 1 в диагональной позиции, используя E.R.O. № 1: Затем, используя E.R.O., получите 0 в позициях над точкой разворота (красный). № 2: Эта матрица, которая теперь находится в форме Гаусса-Жордана или сокращенной ступенчатой форме строки, представляет решение:{ x = 49, y = -18, z = 8}.
Избыточные и несогласованные системы
Если количество уравнений больше числа неизвестных, то системы гарантированно либо избыточны, или непоследовательный.
Но если количество
уравнений равно или меньше числа неизвестных, то вы, как правило,
не распознавать систему как избыточную или противоречивую
до самого конца расчета.
Особенно это актуально, если система большая.Если вы решаете систему уравнений методом подстановки и система избыточна, то вы получите окончательное уравнение, в котором говорится 0 = 0. Или, если система противоречива, то вы получите ту, которая утверждает противоречие вроде 0 = 5. Нечто подобное происходит при использовании исключения Гаусса или Гаусса-Жордана. Если система избыточна, то по окончании процедуры исключения, когда у вас есть расширенная матрица в форме Гаусса или Гаусса-Жордана, последняя строка расширенной матрицы будет:
Эта последняя строка представляет собой уравнение 0 = 0, бесполезную информацию.Если система несовместима, то последняя строка расширенной матрицы будет выглядеть примерно так:
Последняя строка представляет уравнение 0 = 5, противоречие.
Попробуйте выполнить упражнения, которые содержат примеры
избыточные и противоречивые системы уравнений.Пример: Используйте исключение Гаусса, чтобы представить эту систему уравнений в форме эшелона строк и интерпретировать результат:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установите опорный столбец на столбец 1. В опорной позиции уже есть 1, поэтому продолжайте получать 0 в двух позициях ниже опорной:
Теперь установите сводную колонку на вторую колонку. Во-первых, получите 1 в диагональной позиции:
Далее получаем 0 в позиции ниже точки разворота:
Теперь установите сводную колонку в третью колонку.
Первое, что нужно сделать, это получить 1 в диагональной позиции, но сделать это невозможно. На самом деле эта матрица уже имеет форму эшелона строк и представляет собой:
Эта система уравнений не может быть решена обратной подстановкой, потому что у нас нет значения для z . Последнее уравнение просто утверждает, что 0=0. Единственного решения нет, потому что z может принимать любое значение.
Причина этой проблемы в том, что если у нас есть 3 неизвестных, то нам нужно 3 части информацию (уравнения) о них для их решения. Математики говорят, что уравнения должны быть линейно независимыми . В избыточной системе часть информации просто дублирует другую информацию. В этом примере небольшой эксперимент показывает, что третье уравнение — это всего лишь удвоенное второе уравнение минус первое уравнение.
В общем случае расширенная матрица, представленная в виде эшелона строк и содержащая одну или несколько строк с нулями внизу матрицы, указывает на избыточную систему уравнений.
Пример: Используйте метод исключения Гаусса, чтобы представить эту систему уравнений в форме эшелона строк и интерпретировать результат:
Решение: Выполните эту последовательность E.R.O. на расширенной матрице. Установите опорный столбец на столбец 1. В опорной позиции уже есть 1, поэтому продолжайте получать 0 ниже опорной:
Теперь установите сводную колонку на вторую колонку. В опорной позиции уже есть 1, поэтому продолжайте получать 0 ниже опорной точки:
Теперь установите сводную колонку в третью колонку. Первое, что нужно сделать, это получить 1 в диагональной позиции, но сделать это невозможно. На самом деле эта матрица уже имеет форму эшелона строк и представляет собой:
Эта система уравнений несовместна и не имеет решения.
Последнее уравнение утверждает противоречие, а именно 0 = −50.
В общем, расширенная матрица, представленная в виде эшелона строк и содержащая одну или несколько нижних строк, состоящих из нулей слева от вертикальной линии и ненулевого числа справа, указывает на несогласованную систему уравнения без решения.
Уравнений меньше, чем неизвестных
Если количество уравнений в системе меньше числа неизвестных, то вы достигнете точки в Гауссе или Гаусс-Жордан процедура, в которой вы не можете преобразовать сводную столбец, потому что у вас закончились сводные строки. Вот пример: В третьем столбце нет сводной строки и нет сводной строки, поэтому вам нужно остановиться. Эта расширенная матрица представляет эту систему уравнений: Во второй форме мы видим, что если значение задано для z , то x и и могут быть выражены через него.