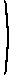Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
- Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $\Delta\neq 0$.
- Для каждой переменной $x_i$($i=\overline{1,n}$) необходимо составить определитель $\Delta_{x_i}$, полученный из определителя $\Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
- Найти значения неизвестных по формуле $x_i=\frac{\Delta_{x_{i}}}{\Delta}$ ($i=\overline{1,n}$).
Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.
Пример №1
Решить СЛАУ $\left\{\begin{aligned} & 3x_1+2x_2=-11;\\ & -x_1+5x_2=15. \end{aligned}\right.$ методом Крамера.
Решение
Матрица системы такова: $ A=\left( \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array} \right) $. Определитель этой матрицы $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|=3\cdot 5-2\cdot(-1)=17$. Как вычисляется определитель второго порядка можете глянуть здесь.
Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $\Delta_{x_1}$ и $\Delta_{x_2}$. Определитель $\Delta_{x_1}$ получаем из определителя $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|$ заменой первого столбца (именно первый столбец содержит коэффициенты при $x_1$) столбцом свободных членов $\left(\begin{array} {c} -11\\ 15\end{array}\right)$:
$$ \Delta_{x_1}=\left|\begin{array}{cc}-11&2\\15&5\end{array}\right|=-55-30=-85. $$Аналогично, заменяя второй столбец в $\Delta=\left|\begin{array}{cc}3&2\\-1&5\end{array}\right|$ столбцом свободных членов, получим:
$$ \Delta_{x_2}=\left|\begin{array} {cc} 3 & -11\\ -1 & 15\end{array}\right|=45-11=34. $$Теперь можно найти значения неизвестных $x_1$ и $x_2$.
$$x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{-85}{17}=-5;\;x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{34}{17}=2.$$В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:
$$\left\{\begin{aligned} & 3x_1+2x_2=3\cdot(-5)+2\cdot{2}=-11;\\ & -x_1+5x_2=-(-5)+5\cdot{2}=15. \end{aligned}\right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.
Ответ: $x_1=-5$, $x_2=2$.
Пример №2
Решить СЛАУ $ \left\{\begin{aligned} & 2x_1+x_2-x_3=3;\\ & 3x_1+2x_2+2x_3=-7;\\ & x_1+x_3=-2. \end{aligned} \right.$, используя метод Крамера.
Решение
Определитель системы: $\Delta=\left| \begin{array} {ccc} 2 & 1 & -1\\ 3 & 2 & 2 \\ 1 & 0 & 1 \end{array}\right|=4+2+2-3=5$. Как вычисляется определитель третьего порядка можете глянуть здесь.
Заменяя первый столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_1}$:
$$ \Delta_{x_1}=\left| \begin{array} {ccc} 3 & 1 & -1\\ -7 & 2 & 2 \\ -2 & 0 & 1 \end{array}\right|=6-4-4+7=5. $$Заменяя второй столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_2}$:
$$ \Delta_{x_2}=\left| \begin{array} {ccc} 2 & 3 & -1\\ 3 & -7 & 2 \\ 1 & -2 & 1 \end{array}\right|=-14+6+6-7-9+8=-10. $$ Заменяя третий столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_3}$: $$ \Delta_{x_3}=\left| \begin{array} {ccc} 2 & 1 & 3\\ 3 & 2 & -7 \\ 1 & 0 & -2 \end{array}\right|=-8-7-6+6=-15. $$Учитывая все вышеизложенное, имеем:
$$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{5}{5}=1;\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-10}{5}=-2; \; x_3=\frac{\Delta_{x_3}}{\Delta}=\frac{-15}{5}=-3. $$Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:
$$\left\{\begin{aligned} & 2x_1+x_2-x_3=2\cdot{1}+(-2)-(-3)=3;\\ & 3x_1+2x_2+2x_3=3\cdot{1}+2\cdot(-2)+2\cdot(-3)=-7;\\ & x_1+x_3=1+(-3)=-2. \end{aligned} \right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно.
Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & 2x_1+3x_2-x_3=15;\\ & -9x_1-2x_2+5x_3=-7. \end{aligned}\right.$ используя метод Крамера.
Решение
Матрица системы $ \left( \begin{array} {ccc} 2 & 3 & -1\\ -9 & -2 & 5 \end{array} \right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:
$$ \left \{ \begin{aligned} & 2x_1+3x_2=x_3+15;\\ & -9x_1-2x_2=-5x_3-7. \end{aligned} \right. $$Теперь матрица системы $ \left( \begin{array} {cc} 2 & 3 \\ -9 & -2 \end{array} \right) $ стала квадратной, и определитель её $\Delta=\left| \begin{array} {cc} 2 & 3\\ -9 & -2 \end{array}\right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:

Ответ можно записать в таком виде: $\left\{\begin{aligned} & x_1=\frac{13x_3-9}{23};\\ & x_2=\frac{-x_3+121}{23};\\ & x_3\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
Примечание
В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ $\left\{\begin{aligned} & 2x_1-5x_2+10x_3=14;\\ & -4x_1+10x_2-7x_3=5. \end{aligned}\right.$. Если перенести в правые части уравнений $x_3$, получим: $ \left\{\begin{aligned} &2x_1-5x_2=-10x_3+14;\\ &-4x_1+10x_2=7x_3+5. \end{aligned}\right.$. Определитель данной системы $\Delta=\left| \begin{array} {cc} 2 & -5\\ -4 & 10 \end{array}\right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $ \left\{\begin{aligned} &2x_1+10x_3=5x_2+14;\\ &-4x_1-7x_3=-10x_2+5. \end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
Пример №4
Решить СЛАУ $\left\{\begin{aligned} &x_1-5x_2-x_3-2x_4+3x_5=0;\\ &2x_1-6x_2+x_3-4x_4-2x_5=0; \\ &-x_1+4x_2+5x_3-3x_4=0. \end{aligned}\right.$ методом Крамера.
Решение
Матрица системы $\left(\begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \\ 2 & -6 & 1 & -4 & -2 \\ -1 & 4 & 5 & -3 & 0 \end{array}\right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:
$$ \left\{\begin{aligned} & x_1-5x_2-x_3=2x_4-3x_5;\\ & 2x_1-6x_2+x_3=4x_4+2x_5; \\ & -x_1+4x_2+5x_3=3x_4. \end{aligned}\right.$$
Ответ таков: $\left\{\begin{aligned} & x_1=\frac{-17x_4+144x_5}{19};\\ & x_2=\frac{-15x_4+41x_5}{19};\\ & x_3=\frac{20x_4-4x_5}{19}; \\ & x_4\in R; \; x_5\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.
Метод Крамера
Метод Крамера или так называемое правило Крамера – это способ поиска неизвестных величин из систем уравнений. Его можно использовать только если число искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть образуемая из системы основная матрица должна быть квадратной и не содержать нулевых строчек, а также если её детерминант не должен являться нулевым.
Теорема 1
Теорема Крамера Если главный определитель $D$ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений совместна, причём решение у неё существует единственное. Решение такой системы вычисляется через так называемые формулы Крамера для решения систем линейных уравнений: $x_i = \frac{D_i}{D}$
В чем заключается метод Крамера
Суть метода Крамера в следующем:
- Чтобы найти решение системы методом Крамера, первым делом вычисляем главный определитель матрицы $D$. Когда вычисленный детерминант основной матрицы при подсчёте методом Крамера оказался равен нулю, то система не имеет ни одного решения или имеет нескончаемое количество решений. В этом случае для нахождения общего или какого-либо базисного ответа для системы рекомендуется применить метод Гаусса.
- Затем нужно заменить крайний столбец главной матрицы на столбец свободных членов и высчитать определитель $D_1$.
- Повторить то же самое для всех столбцов, получив определители от $D_1$ до $D_n$, где $n$ — номер крайнего справа столбца.
- После того как найдены все детерминанты $D_1$…$D_n$, можно высчитать неизвестные переменные по формуле $x_i = \frac{D_i}{D}$.
Готовые работы на аналогичную тему
Приёмы для вычисления определителя матрицы
Для вычисления определителя матрицы с размерностью больше чем 2 на 2, можно использовать несколько способов:
- Правило треугольников, или правило Саррюса, напоминающее это же правило. Суть метода треугольников в том, что при вычислении определителя произведения всех чисел, соединённых на рисунке красной линией справа, записываются со знаком плюс, а все числа, соединённые аналогичным образом на рисунке слева – со знаком минус. B то, и другое правило подходит для матриц размером 3 х 3. В случае же правила Саррюса сначала переписывается сама матрица, а рядом с ней рядом переписываются ещё раз её первый и второй столбец. Через матрицу и эти дополнительные столбцы проводятся диагонали, члены матрицы, лежащие на главной диагонали или на параллельной ей записываются со знаком плюс, а элементы, лежащие на побочной диагонали или параллельно ей — со знаком минус.
Рисунок 1. Правило треугольников для вычисления определителя для метода Крамера
- С помощью метода, известного как метод Гаусса, также иногда этот метод называют понижением порядка определителя. В этом случае матрица преобразуется и приводится к треугольному виду, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя нельзя домножать или делить строчки или столбцы на числа без вынесения их как множителя или делителя. В случае поиска определителя возможно только вычитать и складывать строки и столбы между собой, предварительно помножив вычитаемую строку на ненулевой множитель. Также при каждой перестановке строчек или столбцов матрицы местами следует помнить о необходимости смены конечного знака у матрицы.
- При решении методом Крамера СЛАУ с 4 неизвестными, лучше всего будет применять именно метод Гаусса для поиска и нахождения определителей или опредлять детерминант через поиск миноров.
Решение систем уравнений методом Крамера
Применим метод Крамера для системы из 2 уравнений и двумя искомыми величинами:
$\begin{cases} a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end{cases}$
Отобразим её в расширенной форме для удобства:
$A = \begin{array}{cc|c} a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end{array}$
Найдём определитель основной матрицы, также называемый главным определителем системы:
$D = \begin{array}{|cc|} a_1 & a_2 \\ a_3 & a_4 \\ \end{array} = a_1 \cdot a_4 – a_3 \cdot a_2$
Если главный определитель не равен нулю, то для решения слау методом Крамера необходимо высчитать ещё парочку определителей от двух матриц с заменёнными столбцами основной матрицы на строчку свободных членов:
$D_1 = \begin{array}{|cc|} b_1 & a_2 \\ b_2 & a_4 \\ \end{array} = b_1 \cdot a_4 – b_2 \cdot a_4$
$D_2 = \begin{array}{|cc|} a_1 & b_1 \\ a_3 & b_2 \\ \end{array} = a_1 \cdot b_2 – a_3 \cdot b_1$
Теперь найдём неизвестные $x_1$ и $x_2$:
$x_1 = \frac {D_1}{D}$
$x_2 = \frac {D_2}{D}$
Пример 1
Метод Крамера для решения СЛАУ с основной матрицей 3 порядка (3 x 3) и тремя искомыми.
Решите систему уравнений:
$\begin{cases} 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 — x_3 = 10 \\ \end{cases}$
Сосчитаем главный детерминант матрицы пользуясь вышеизложенным под пунктом номер 1 правилом:
$D = \begin{array}{|ccc|} 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end{array} = 3 \cdot 4 \cdot (-1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 3 = — 12 – 8 -12 -32 – 6 + 6 = — 64$
А теперь три других детерминанта:
$D_1 = \begin{array}{|ccc|} 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end{array} = 21 \cdot 4 \cdot 1 + (-2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) — (-1) \cdot 2 \cdot 21 = — 84 – 40 – 36 – 160 – 18 + 42 = — 296$
$D_2 = \begin{array}{|ccc|} 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end{array} = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = — 27 + 120 + 84 – 72 + 63 – 60 = 108$
$D_3 = \begin{array}{|ccc|} 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end{array} = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 — (-2) \cdot 3 \cdot 10 — (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = — 60$
Найдём искомые величины:
$x_1 = \frac{D_1} {D} = \frac{- 296}{-64} = 4 \frac{5}{8}$
$x_2 = \frac{D_1} {D} = \frac{108} {-64} = — 1 \frac {11} {16}$
$x_3 = \frac{D_1} {D} = \frac{-60} {-64} = \frac {15} {16}$
Метод Крамера решения систем линейных уравнений — Студопедия
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид
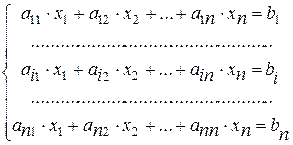 . (1.5)
. (1.5)
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
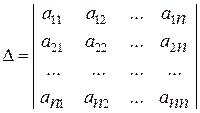 . (1.6)
. (1.6)
Если в главном определителе произвольный (j-ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
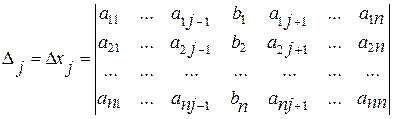 (j = 1, 2, …, n). (1.7)
(j = 1, 2, …, n). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
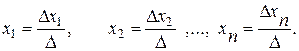 (1.8)
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
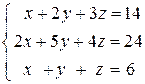 .
.
Вычислим главный определитель системы:
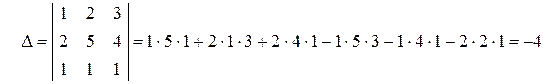 .
.
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
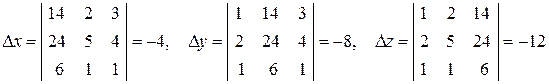 .
.
Таким образом, 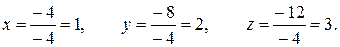
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
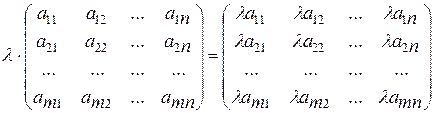 . (1.9)
. (1.9)
Пример 1.6. 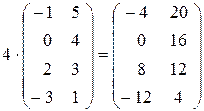 .
.
Сложение матриц.
Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
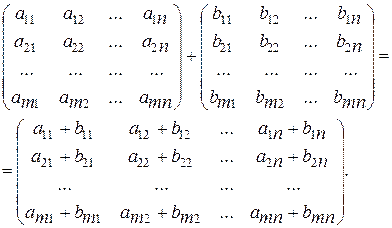 (1.10)
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. 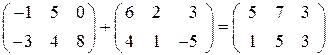 .
.
Умножение матриц.
Если число столбцов матрицы А совпадает с числом строк матрицы В, то для таких матриц вводится операция умножения:
2 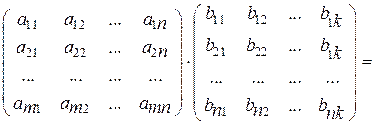
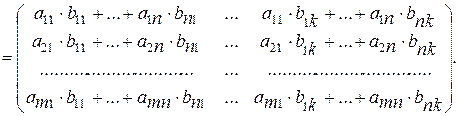
Таким образом, при умножении матрицы А размерности m´n на матрицу В размерности n´k мы получаем матрицу С размерности m´k. При этом элементы матрицы С вычисляются по следующим формулам:
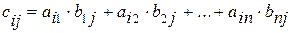 . (1.11)
. (1.11)
Задача 1.8. Найти, если это возможно, произведение матриц AB и BA:
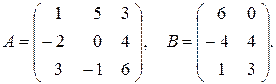
Решение. 1) Для того чтобы найти произведение AB, необходимо строки матрицы A умножить на столбцы матрицы B:
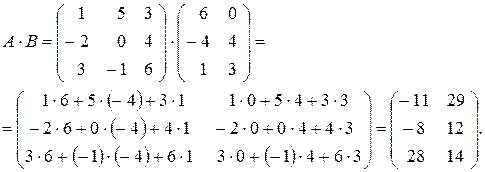
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A.
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A—1 называется обратной к квадратной матрице А, если выполнено равенство:
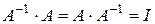 , (1.12)
, (1.12)
где через I обозначается единичная матрица того же порядка, что и матрица А:
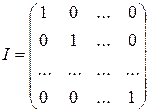 .
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
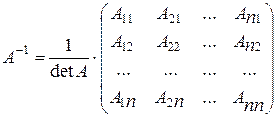 , (1.13)
, (1.13)
где Aij – алгебраические дополнения к элементам aij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A—1 к матрице
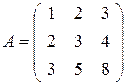 .
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
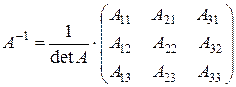 .
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 – 3 × 3 × 3 – 1 × 5 × 4 – 2 × 2 × 8 = 24 + 30 + 24 – 27 – 20 – 32 = – 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения Aij:
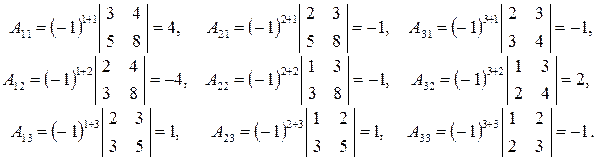
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A. Таким образом, мы получим обратную матрицу:
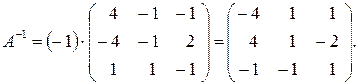
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
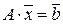 , (1.14)
, (1.14)
где 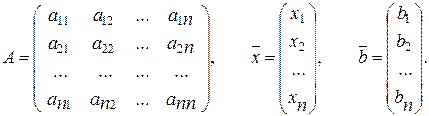
Умножая обе части равенства (1.14) слева на A—1, мы получим решение системы:
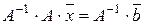 , откуда
, откуда
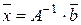 . (1.15)
. (1.15)
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
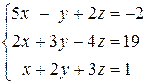
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: 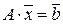 ,
,
где 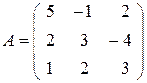 – основная матрица системы,
– основная матрица системы, 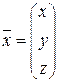 – столбец неизвестных и
– столбец неизвестных и 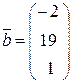 – столбец свободных членов. Так как главный определитель системы
– столбец свободных членов. Так как главный определитель системы 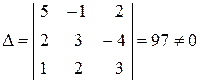 , то основная матрица системы А имеет обратную матрицу А-1. Для нахождения обратной матрицы А-1, вычислим алгебраические дополнения ко всем элементам матрицы А:
, то основная матрица системы А имеет обратную матрицу А-1. Для нахождения обратной матрицы А-1, вычислим алгебраические дополнения ко всем элементам матрицы А:
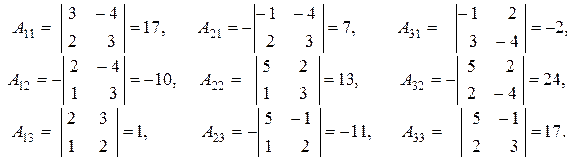
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
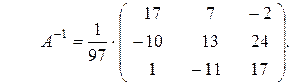
Решение системы находим по формуле (1.15):
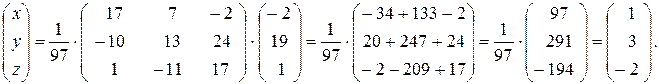
Таким образом, 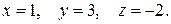
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
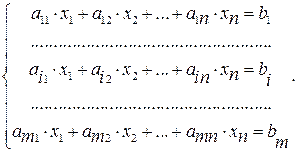 (1.16)
(1.16)
Требуется найти решение системы, т.е. такой набор переменных 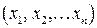 , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
, который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например 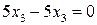 . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например
. Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например 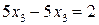 ), то мы делаем вывод, что система не имеет решения.
), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11. Решить систему линейных уравнений методом исключения неизвестных:
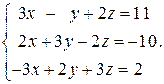
Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:

После запоминания первого уравнения 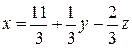 и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
и приведения подобных членов во втором и третьем уравнении мы приходим к системе:

Выразим y из второго уравнения и подставим его в первое уравнение:
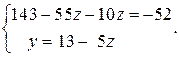
Запомним второе уравнение, а из первого найдем z:
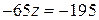 , или
, или 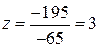
Совершая обратный ход, последовательно найдем y и z. Для этого сначала подставим 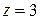 в последнее запомненное уравнение
в последнее запомненное уравнение 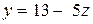 , откуда найдем y:
, откуда найдем y:
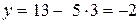 .
.
Затем подставим 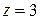 и
и 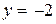 в первое запомненное уравнение
в первое запомненное уравнение 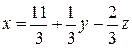 , откуда найдем x:
, откуда найдем x:
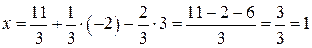
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
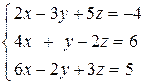 . (1.17)
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
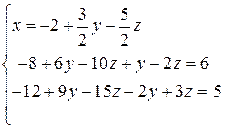 .
.
Запомним первое уравнение  и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
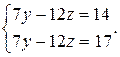
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y из первого уравнения 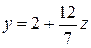 и подставляя его во второе уравнение
и подставляя его во второе уравнение 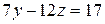 , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x, y, и z. Следовательно, система (1.17) несовместна, т.е. не имеет решения.
, получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x, y, и z. Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
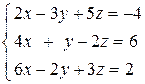 . (1.18)
. (1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
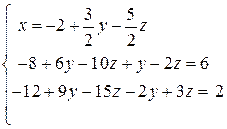 .
.
Запомним первое уравнение  и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
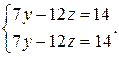
Выражая y из первого уравнения 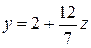 и подставляя его во второе уравнение
и подставляя его во второе уравнение 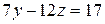 , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
, мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем  . Тогда
. Тогда
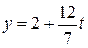 .
.
Подставим y и z в первое запомненное равенство и найдем x:
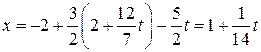 .
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t:
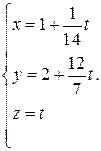 (1.19)
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1.18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
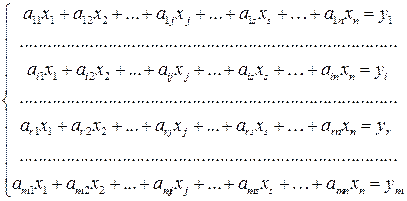 , (1.20)
, (1.20)
где xj – независимые (искомые) переменные, aij – постоянные коэффициенты
(i = 1, 2,…, m; j = 1, 2,…, n). Правые части системы yi (i = 1, 2,…, m) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (xs) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда ars ¹ 0. Коэффициент ars называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
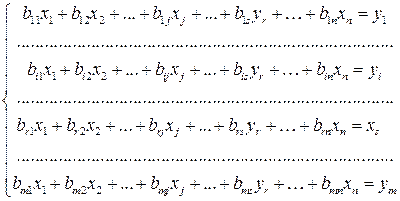 . (1.21)
. (1.21)
Из s-го равенства системы (1.21) мы впоследствии найдем переменную xs (после того, как будут найдены остальные переменные). S-я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r-го уравнения, которое после выражения переменной xs через остальные переменные будет выглядеть следующим образом:
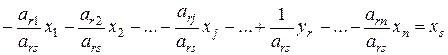 . (1.22)
. (1.22)
Таким образом, новые коэффициенты r-го уравнения вычисляются по следующим формулам:
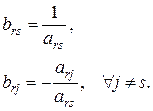 (1.23)
(1.23)
Вычислим теперь новые коэффициенты bij (i ¹ r) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную xs в i-е уравнение системы (1.20):
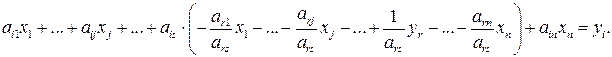
После приведения подобных членов, получим:
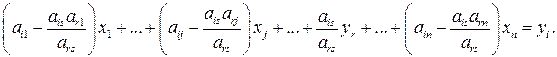 (1.24)
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r-го уравнения):
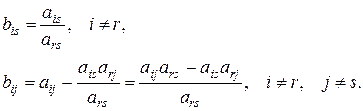 (1.25)
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x1 | x2 | … | xj | … | xs | … | xn | |
| y1= | a11 | a12 | a1j | a1s | a1n | |||
| ………………………………………………………………….. | ||||||||
| yi= | ai1 | ai2 | aij | ais | ain | |||
| ………………………………………………………………….. | ||||||||
| yr= | ar1 | ar2 | arj | ars | arn | |||
| …………………………………………………………………. | ||||||||
| yn= | am1 | am2 | amj | ams | amn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу 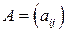 коэффициентов системы (1.20). Если умножить матрицу А на матрицу
коэффициентов системы (1.20). Если умножить матрицу А на матрицу 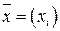 , состоящую из элементов верхней заглавной строки, то получится матрица
, состоящую из элементов верхней заглавной строки, то получится матрица 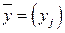 , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений:
, состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: 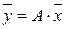 . Системе (1.21) при этом соответствует следующая жорданова таблица:
. Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x1 | x2 | … | xj | … | yr | … | xn | |
| y1= | b11 | b12 | b1j | b1s | b1n | |||
| ………………………………………………………………….. | ||||||||
| yi= | bi1 | bi2 | bij | bis | bin | |||
| ………………………………………………………………….. | ||||||||
| xs= | br1 | br2 | brj | brs | brn | |||
| …………………………………………………………………. | ||||||||
| yn= | bm1 | bm2 | bmj | bms | bmn |
Разрешающий элемент ars мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (xs) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (yr) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом: 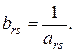
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный: 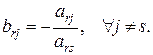
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент: 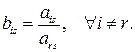
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам: 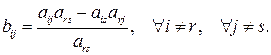
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь 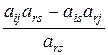 , находятся на пересечении i-ой и r-ой строк и j-го и s-го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы
, находятся на пересечении i-ой и r-ой строк и j-го и s-го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы 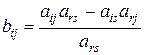 можно использовать следующую диаграмму:
можно использовать следующую диаграмму:
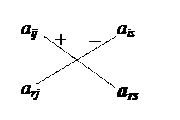

Задача 1.14. Найти общее решение системы линейных уравнений методом обыкновенных жордановых исключений:
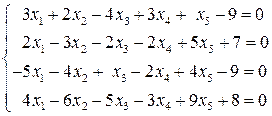 . (1.26)
. (1.26)
Решение. Запишем систему (1.26) в виде жордановой таблицы (табл. 1.3):
Таблица 1.3 Таблица 1.4
| x1 | x2 | x3 | x4 | x5 | x1 | x2 | x4 | x5 | |||||
| 0= | –4 | –9 | 0= | –17 | –14 | –5 | –45 | ||||||
| 0= | –3 | –2 | –2 | 0= | –8 | –11 | –6 | –11 | |||||
| 0= | –5 | –4 | –2 | –9 | x3= | –4 | |||||||
| 0= | –6 | –5 | –3 | 0= | –21 | –26 | –13 | –37 |
Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x1,…, x5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т.к. требуется находить независимые переменные x1,…, x5. Выбираем, например, коэффициент 1 при переменной x3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x3 выражается через остальные переменные.
Строку x3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца bi3 все соответствующие ему слагаемые каждого уравнения 0·bi3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x3). Выбирая в таблице 1.4 в качестве разрешающего элемента b14 = –5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
| x1 | x2 | x5 | x1 | x5 | |||||
| x4= | –3,4 | –2,8 | 3,4 | –9 | x2= | –62/29 | 37/29 | –215/29 | |
| 0= | 12,4 | 5,8 | –7,4 | 0= | 28/29 | –56/29 | 84/29 | ||
| 0= | 23,2 | 10,4 | –15,2 |
Далее, выбирая разрешающие элементы 5,8 и 28/29 в таблицах 1.5 и 1.6, соответственно, мы приходим к таблице 1.7:
Таблица 1.7
Из последней таблицы 1.7 находим: x1 = – 3 + 2x5.
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
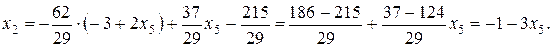
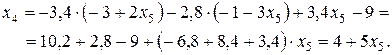
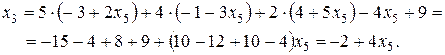
Таким образом, система имеет бесчисленное множество решений. Переменной x5, можно придавать произвольные значения. Данная переменная выступает в роли параметра x5 = t. Мы доказали совместность системы и нашли ее общее решение:
x1 = – 3 + 2t
x2 = – 1 – 3t
x3 = – 2 + 4t . (1.27)
x4 = 4 + 5t
x5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (– 3; – 1; – 2; 4; 0).
Метод Крамера . Применение для систем линейных уравнений
Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится.
Если определитель матрицы не равен нулю
то система линейных алгебраических уравнений имеет единственное решение.
Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.
Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой.
Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.
Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:
— определители, образованные с заменой -го столбца, столбцом из свободных членов.
Если , а хотя бы один из
Решение методом Крамера системы линейных уравнений 3-4-го порядка
Решать системы линейных алгебраических уравнений второго, третьего, изредка четвертого порядка методом Крамера достаточно часто придется студентам младших курсов учебы при изучении основ линейной алгебры. Для большинства студентов стационарной формы учебы такие задания не являются сложными, однако кто выбрал заочную учебу или дистанционную, или пропустил по определенным причинам практические занятия, вычисления выглядят непонятными и тяжелыми. Чтобы исправить такую ситуацию в данной статье будут приведены наиболее распространены примеры данной темы и схема их решения. Если Вы хорошо поймете принцип их решения, то на практике у Вас не будет трудностей с подобными заданиями.
Для начала выберем задание из сборника задач Дубовика В.П., Юрика І.І. «Высшая математика».
————————————
Примеры
Решить систему линейных алгебраических уравнений.
1) (1. 153)
2) (4. 165)
3) (4. 174)
Решение.
1) В случае двух уравнений решение можно получить более простым способом. Выражаемый из второго уравнения
и подставим в первое
Раскрыв скобки, сгруппируем подобные слагаемые
Отсюда получим решение
Переменнуюнайдем подстановкой в любое из уравнений
Таким образом решением системы двух уравнений будут следующие значения
Поскольку цель статьи научить студентов решать по методике Крамера то решим данный пример и етим методом.
Для этого выпишем систему линейных уравнений в виде
Найдем детерминант основной части
Для вычисления вспомогательных определителей ставим столбец свободных членов на место первой строки для и на место второй для . В результате получим
Подставим найденные значения в формулы Крамера
и найдем неизвестные
Из рассмотренного примера видим что вычисление при двух уравнениях с двумя неизвестными достаточно простые.
2) Запишем систему трех алгебраических уравнений в удобном для решения виде
Найдем детерминант системы по правилу треугольников
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим
Вычисляем неизвестные за формулами Крамера
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.
3) Записываем систему уравнений четвертого порядка в виде
Находим главный определитель системы. При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой
и найдем соответствующие детермиінанты третьего порядка
Подставим найденные значения в определитель
По такой же схеме вычисляем вспомогательные определители, напомню ли
Решение системы линейных уравнений (метод Крамера)
Этот онлайн калькулятор позволит вам очень просто решить систему линейных уравнений (СЛУ) методом Крамера.
Для того чтобы решить систему линейных уравнений методом Крамера, выберите количество неизвестных величин: 2 3 4 5
Заполните систему линейных уравнений
Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа. Если в вашем уравнение отсутствует какой-то коэффициент, то на его месте в калькуляторе введите ноль. Вводить можно числа или дроби. Например: 1.5 или 1/7 или -1/4 и т.д.
Решить системуВоспользуйтесь также:
Решение системы линейных уравнений (метод подстановки)
Решение системы линейных уравнений (метод Гаусса)
Решение системы линейных уравнений (матричный метод)
Решение системы линейных уравнений методом Крамера
Метод Крамера
Метод Крамера — это метод решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (то есть в случае, когда система уравнений имеет единственное решение). Основным математическим действием при решении системы уравнения методом Крамера является вычисление определителей матриц размерностью n (где n — количество уравнений в системе).
На нашем сайте вы можете решать системы уравнений методом Крамера в режиме онлайн. При этом решение вы получаете мгновенно, и оно является полным и подробным. При решении системы уравнений нужно находить определители нескольких разных матриц. Для сокращения решения эта операция упрощена (выдаётся лишь результат). Но вы можете при необходимости получить полное решение нахождения детерминанта матрицы. Соответствующий калькулятор имеется на нашем ресурсе.
Практическая работа «Решение систем линейных уравнений третьего порядка методом Крамера»
Практическая работа
«Решение систем линейных уравнений третьего порядка методом Крамера»
Цели работы:
расширить представление о методах решения СЛУ и отработать алгоритм решения СЛУ методом Крамора;
развивать логическое мышление студентов, умение находить рациональное решение задачи;
воспитывать у студентов аккуратность и культуру письменной математической речи при оформлении ими своего решения.
Основной теоретический материал.
Метод Крамера . Применение для систем линейных уравнений.
Задана система N линейных алгебраических уравнений (СЛАУ) с  неизвестными, коэффициентами при которых являются элементы матрицы
неизвестными, коэффициентами при которых являются элементы матрицы  , а свободными членами — числа
, а свободными членами — числа
Первый индекс  возле коэффициентов
возле коэффициентов  указывает в каком уравнении находится коэффициент, а второй
указывает в каком уравнении находится коэффициент, а второй  — при котором из неизвестным он находится.
— при котором из неизвестным он находится.
Если определитель матрицы  не равен нулю
не равен нулю
то система линейных алгебраических уравнений имеет единственное решение. Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность  чисел
чисел  , которая при
, которая при превращает каждое из уравнений системы в правильную равенство. Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
превращает каждое из уравнений системы в правильную равенство. Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной  Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой. Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственное, систему уравнений называют неопределенной. Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой. Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственное, систему уравнений называют неопределенной. Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами, например , по формулам Крамера (метод Крамера)
Теорема Крамера. Если определитель  системы
системы  линейных алгебраических уравнений с
линейных алгебраических уравнений с  неизвестными отличен от нуля
неизвестными отличен от нуля  то эта система имеет единственное решение, которое находится по формулам Крамера:
то эта система имеет единственное решение, которое находится по формулам Крамера: 
 — определители, образованные с
— определители, образованные с  заменой
заменой  -го столбца, столбцом из свободных членов.
-го столбца, столбцом из свободных членов.
Если  , а хотя бы один из
, а хотя бы один из  отличен от нуля, то СЛАУ решений не имеет. Если же
отличен от нуля, то СЛАУ решений не имеет. Если же  , то СЛАУ имеет множество решений.
, то СЛАУ имеет множество решений.
Задача 1.
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера
Решение.
Найдем определитель матрицы коэффициентов при неизвестных


Так как  , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:
, то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:






По формулам Крамера находим неизвестные 
Итак  единственное решение системы.
единственное решение системы.
Задача 2.
Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.

Решение.
Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.


Найдем составляющие определителя:




Подставим найденные значения в определитель 
Детерминант  , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:
, следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:

Разложим каждый из определителей по столбцу в котором есть больше нулей.




По формулам Крамера находим

Решение системы 
Задания для самостоятельного решения:
ВАРИАНТ 1 Решите систему уравнений по формулам Крамера
ВАРИАНТ 2
 1)
1) 
2) 
3) 
Критерии оценивания:
Работа оценивается на «3»,если: самостоятельно полностью и верно решена одна из систем.
Работа оценивается на «4»,если: самостоятельно полностью и верно решены любые две системы.
Работа оценивается на «5»,если: самостоятельно полностью и верно решены три системы.
9.9: Решение систем с помощью правила Крамера
Мы узнали, как решать системы уравнений с двумя переменными и тремя переменными, и с помощью нескольких методов: подстановки, сложения, исключения Гаусса, использования обратной матрицы и построения графиков. Некоторые из этих методов легче применять, чем другие, и они более подходят в определенных ситуациях. В этом разделе мы изучим еще две стратегии решения систем уравнений.
Вычисление определителя матрицы 2 × 2
Определитель — это действительное число, которое может быть очень полезно в математике, потому что у него есть несколько приложений, таких как вычисление площади, объема и других величин.Здесь мы будем использовать определители, чтобы определить, является ли матрица обратимой, используя элементы квадратной матрицы, чтобы определить, существует ли решение системы уравнений. Однако, возможно, одним из наиболее интересных приложений является их использование в криптографии. Защищенные сигналы или сообщения иногда отправляются в виде матрицы. Расшифровать данные можно только с помощью обратимой матрицы и определителя. Для наших целей мы ориентируемся на определитель как на показатель обратимости матрицы.Вычисление определителя матрицы требует следования определенным шаблонам, описанным в этом разделе.
НАЙТИ ОПРЕДЕЛЕНИЕ МАТРИЦЫ 2 × 2
Определитель матрицы 2 × 2, учитывая
\ (A = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \)
определяется как
Обратите внимание на изменение обозначений. Есть несколько способов указать определитель, включая \ (\ det (A) \) и замену скобок в матрице прямыми линиями, \ (| A | \).
Пример \ (\ PageIndex {1} \): поиск определителя матрицы \ (2 × 2 \)
Найдите определитель заданной матрицы.
\ (A = \ begin {bmatrix} 5 & 2 \\ — 6 & 3 \ end {bmatrix} \)
Решение
\ [\ begin {align *} \ det (A) & = \ begin {vmatrix} 5 & 2 \\ — 6 & 3 \ end {vmatrix} \\ & = 5 (3) — (- 6) (2) \\ & = 27 \ end {align *} \]
Использование правила Крамера для решения системы двух уравнений с двумя переменными
Теперь мы представим последний метод решения систем уравнений, использующий определители.Этот метод, известный как правило Крамера , восходит к середине 18 века и назван в честь своего новатора, швейцарского математика Габриэля Крамера (1704-1752), который представил его в 1750 году в Introduction à l’Analyse des lignes Courbes algébriques . Правило Крамера — это жизнеспособный и эффективный метод поиска решений систем с произвольным числом неизвестных при условии, что у нас есть такое же количество уравнений, что и неизвестных.
Правило Крамера даст нам единственное решение системы уравнений, если оно существует.Однако, если система не имеет решения или бесконечное количество решений, это будет обозначено нулевым определителем. Чтобы выяснить, является ли система непоследовательной или зависимой, необходимо использовать другой метод, например исключение.
Чтобы понять правило Крамера, давайте внимательно рассмотрим, как мы решаем системы линейных уравнений с использованием основных операций со строками. Рассмотрим систему двух уравнений с двумя переменными.
\ [\ begin {align} a_1x + b_1y & = c_1 (1) \ label {eq1} \\ a_2x + b_2y & = c_2 (2) \ label {eq2} \\ \ end {align} \]
Мы исключаем одну переменную, используя операции со строками, и решаем для другой.Скажите, что мы хотим найти \ (x \). Если уравнение \ ref {eq2} умножается на коэффициент, противоположный коэффициенту \ (y \) в уравнении \ ref {eq1}, уравнение \ ref {eq1} умножается на коэффициент при \ (y \) в уравнении \ ref {eq2}, и мы добавляем два уравнения, переменная \ (y \) будет удалена.
\ [\ begin {align *} & b_2a_1x + b_2b_1y = b_2c_1 & \ text {Умножение} R_1 \ text {by} b_2 \\ — & \ underline {b_1a_2x − b_1b_2y = −b_1c_2} & \ text {Умножение} R_2 \ text {by} −b_1 \\ & b_2a_1x − b_1a_2x = b_2c_1 − b_1c_2 \ end {align *} \]
Теперь решите относительно \ (x \).
\ [\ begin {align *} b_2a_1x − b_1a_2x & = b_2c_1 − b_1c_2 \\ x (b_2a_1 − b_1a_2) & = b_2c_1 − b_1c_2 \\ x & = \ dfrac {b_2c_1 − b_1c_2} {b_2a_1 − b_1a_2} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align *} \]
Аналогично, чтобы найти \ (y \), мы исключим \ (x \).
\ [\ begin {align *} & a_2a_1x + a_2b_1y = a_2c_1 & \ text {Multiply} R_1 \ text {by} a_2 \\ — & \ underline {a_1a_2x − a_1b_2y = −a_1c_2} & \ text {Multiply} R_2 \ текст {by} −a_1 \\ & a_2b_1y − a_1b_2y = a_2c_1 − a_1c_2 \ end {align *} \]
Решение относительно \ (y \) дает
\ [\ begin {align *} a_2b_1y − a_1b_2y & = a_2c_1 − a_1c_2 \\ y (a_2b_1 − a_1b_2) & = a_2c_1 − a_1c_2 \\ y & = \ dfrac {a_2c_1 − a_1c_2} {a_2b_1 − a_1b_2} = \ dfrac {a_1c_2 − a_2c_1} {a_1b_2 − a_2b_1} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix}} \ end {align * } \]
Обратите внимание, что знаменатель для \ (x \) и \ (y \) является определителем матрицы коэффициентов.
Мы можем использовать эти формулы для решения относительно \ (x \) и \ (y \), но правило Крамера также вводит новые обозначения:
- \ (D \): определитель матрицы коэффициентов
- \ (D_x \): определитель числителя в решении \ (x \)
\ [x = \ dfrac {D_x} {D} \]
- \ (D_y \): определитель числителя в решении \ (y \)
\ [y = \ dfrac {D_y} {D} \]
Ключом к правилу Крамера является замена интересующего нас переменного столбца на постоянный и вычисление детерминант.Тогда мы можем выразить \ (x \) и \ (y \) как частное двух определителей.
ПРАВИЛО КРЕМЕРА ДЛЯ СИСТЕМ \ (2 × 2 \)
Правило Крамера — это метод, использующий детерминанты для решения систем уравнений, которые имеют то же количество уравнений, что и переменные.
Рассмотрим систему двух линейных уравнений с двумя переменными.
\ [\ begin {align *} a_1x + b_1y & = c_1 \\ a_2x + b_2y & = c_2 \ end {align *} \]
Решение с использованием правила Крамера представлено как
\ [\ begin {align} x & = \ dfrac {D_x} {D} = \ dfrac {\ begin {bmatrix} c_1 & b_1 \\ c_2 & b_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end { bmatrix}} \; , D \ neq 0 \\ y & = \ dfrac {D_y} {D} = \ dfrac {\ begin {bmatrix} a_1 & c_1 \\ a_2 & c_2 \ end {bmatrix}} {\ begin {bmatrix} a_1 & b_1 \\ a_2 & b_2 \ end {bmatrix }} \; , D \ neq 0 \ end {align} \]
Если мы решаем для \ (x \), столбец \ (x \) заменяется постоянным столбцом.Если мы решаем для \ (y \), столбец \ (y \) заменяется постоянным столбцом.
Пример \ (\ PageIndex {2} \): Использование правила Крамера для решения системы \ (2 × 2 \)
Решите следующую систему \ (2 × 2 \), используя правило Крамера.
\ [\ begin {align *} 12x + 3y & = 15 \\ 2x-3y & = 13 \ end {align *} \]
Решение
Решите относительно \ (x \).
\ [\ begin {align *} x & = \ dfrac {D_x} {D} \\ & = \ dfrac {\ begin {bmatrix} 15 & 3 \\ 13 & -3 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {-45-39} {- 36-6} \\ & = \ dfrac {-84} {- 42} \\ & = 2 \ end {align *} \]
Решите относительно \ (y \).
\ [\ begin {align *} y & = \ dfrac {D_y} {D} \\ & = \ dfrac {\ begin {bmatrix} 12 & 15 \\ 2 & 13 \ end {bmatrix}} {\ begin {bmatrix} 12 & 3 \\ 2 & -3 \ end {bmatrix}} \\ & = \ dfrac {156-30} {- 36-6} \\ & = — \ dfrac {126} {42} \\ & = -3 \ end {align * } \]
Решение: \ ((2, −3) \).
Упражнение \ (\ PageIndex {1} \)
Воспользуйтесь правилом Крамера для решения системы уравнений \ (2 × 2 \).
\ [\ begin {align *} x + 2y & = -11 \\ -2x + y & = -13 \ end {align *} \]
- Ответ
\ ((3, −7) \)
Вычисление определителя матрицы 3 × 3
Найти определитель матрицы 2 × 2 несложно, но найти определитель матрицы 3 × 3 сложнее.Один из методов состоит в том, чтобы увеличить матрицу 3 × 3 повторением первых двух столбцов, получив матрицу 3 × 5. Затем мы вычисляем сумму произведений записей на по каждой из трех диагоналей (от верхнего левого угла к нижнему правому) и вычитаем произведение записей на по каждой из трех диагоналей (от нижнего левого угла к верхнему правому). Это легче понять с помощью наглядного пособия и примера.
Найдите определитель матрицы 3 × 3.
\ (A = \ begin {bmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {bmatrix} \)
- Дополните \ (A \) первыми двумя столбцами.
\ (\ det (A) = \ left | \ begin {array} {ccc | cc} a_1 & b_1 & c_1 & a_1 & b_1 \\ a_2 & b_2 & c_2 & a_2 & b_2 \\ a_3 & b_3 & c_3 & a_3 & b_3 \ end {array} \ right | \)
- С верхнего левого угла в нижний правый: умножение значений по первой диагонали. Добавьте результат к произведению входов по второй диагонали. Добавьте этот результат к произведению записей по третьей диагонали.
- От левого нижнего угла до правого верхнего: вычтите произведение входов вверх по первой диагонали.Из этого результата вычтите произведение входов до второй диагонали. Из этого результата вычтите произведение входов до третьей диагонали.
Алгебра выглядит следующим образом:
\ (| A | = a_1b_2c_3 + b_1c_2a_3 + c_1a_2b_3 − a_3b_2c_1 − b_3c_2a_1 − c_3a_2b_1 \)
Пример \ (\ PageIndex {3} \): поиск определителя матрицы 3 × 3
Найдите определитель матрицы \ (3 × 3 \) при
\ (A = \ begin {bmatrix} 0 & 2 & 1 \\ 3 & −1 & 1 \\ 4 & 0 & 1 \ end {bmatrix} \)
Решение
Дополните матрицу первыми двумя столбцами, а затем следуйте формуле.Таким образом,
\ [\ begin {align *} | А | & = \ left | \ begin {array} {ccc | cc} 0 & 2 & 1 & 0 & 2 \\ 3 & -1 & 1 & 3 & -1 \\ 4 & 0 & 1 & 4 & 0 \ end {array} \ right | \\ & = 0 (-1) (1) +2 (1) (4) +1 (3) (0) −4 (-1) (1) -0 (1) (0) -1 (3) (2) \\ & = 0 + 8 + 0 + 4−0−6 \\ & = 6 \ end {align *} \]
Упражнение \ (\ PageIndex {2} \)
Найдите определитель матрицы 3 × 3.
\ (\ det (A) = \ begin {vmatrix} 1 & −3 & 7 \\ 1 & 1 & 1 \\ 1 & −2 & 3 \ end {vmatrix} \)
- Ответ
\ (- 10 \)
Q&A: Можем ли мы использовать тот же метод, чтобы найти определитель большей матрицы?
Нет, этот метод работает только для матриц 2 × 2 и 3 × 3.Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Использование правила Крамера для решения системы трех уравнений с тремя переменными
Теперь, когда мы можем найти определитель матрицы \ (3 × 3 \), мы можем применить правило Крамера для решения системы трех уравнений с тремя переменными. Правило Крамера простое и следует шаблону, соответствующему правилу Крамера для матриц \ (2 × 2 \). Однако по мере увеличения порядка матрицы до \ (3 × 3 \) требуется гораздо больше вычислений.
Когда мы вычисляем детерминант, равный нулю, правило Крамера не дает никаких указаний на то, что у системы нет решения или есть бесконечное количество решений. Чтобы выяснить это, мы должны выполнить устранение в системе.
Рассмотрим систему уравнений \ (3 × 3 \).
\ [\ begin {align} a_1x + b_1y + c_1z & = \ color {blue} d_1 \\ a_2x + b_2y + c_2z & = \ color {blue} d_2 \\ a_3x + b_3y + c_3z & = \ color {blue} d_3 \\ \ end {align} \]
\ (x = \ dfrac {D_x} {D} \), \ (y = \ dfrac {D_y} {D} \), \ (z = \ dfrac {D_z} {D} \), \ (D ≠ 0 \)
где
\ [D = \ begin {vmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_x = \ begin {vmatrix} \ color {blue} d_1 & b_1 & c_1 \\ \ color {blue} d_2 & b_2 & c_2 \\ \ color {blue} d_3 & b_3 & c_3 \ end {vmatrix} \; , \; D_y = \ begin {vmatrix} a_1 & \ color {blue} d_1 & c_1 \\ a_2 & \ color {blue} d_2 & c_2 \\ a_3 & \ color {blue} d_3 & c_3 \ end {vmatrix} \; , \; D_z = \ begin {vmatrix} a_1 & b_1 & \ color {blue} d_1 \\ a_2 & b_2 & \ color {blue} d_2 \\ a_3 & b_3 & \ color {blue} d_3 \ end {vmatrix} \]
Если мы записываем определитель \ (D_x \), мы заменяем столбец \ (x \) постоянным столбцом.Если мы пишем определитель \ (D_y \), мы заменяем столбец y на столбец констант. Если мы записываем определитель \ (D_z \), мы заменяем столбец \ (z \) постоянным столбцом. Всегда проверяйте ответ.
Пример \ (\ PageIndex {4} \): решение системы \ (3 × 3 \) с использованием правила Крамера
Найдите решение данной системы \ (3 × 3 \), используя правило Крамера.
\ [\ begin {align *} x + y-z & = 6 \\ 3x-2y + z & = -5 \\ x + 3y-2z & = 14 \ end {align *} \]
Решение
Используйте правило Крамера.
\ (D = \ begin {vmatrix} 1 & 1 & −1 \\ 3 & −2 & 1 \\ 1 & 3 & −2 \ end {vmatrix} \), \ (D_x = \ begin {vmatrix} 6 & 1 & −1 \\ — 5 & −2 & 1 \ \ 14 & 3 & −2 \ end {vmatrix} \), \ (D_y = \ begin {vmatrix} 1 & 6 & −1 \\ 3 & −5 & 1 \\ 1 & 14 & −2 \ end {vmatrix} \), \ (D_z = \ begin {vmatrix } 1 & 1 & 6 \\ 3 & −2 & −5 \\ 1 & 3 & 14 \ end {vmatrix} \)
Затем,
\ [\ begin {align *} x & = \ dfrac {D_x} {D} & = \ dfrac {-3} {- 3} & = 1 \\ y & = \ dfrac {D_y} {D} & = \ dfrac {-9} {- 3} & = 3 \\ z & = \ dfrac {D_z} {D} & = \ dfrac {6} {- 3} & = -2 \\ \ end {align *} \]
Решение: \ ((1,3, −2) \).
Упражнение \ (\ PageIndex {3} \)
Используйте правило Крамера, чтобы решить матрицу \ (3 × 3 \).
\ [\ begin {align *} x-3y + 7z & = 13 \\ x + y + z & = 1 \\ x-2y + 3z & = 4 \ end {align *} \]
- Ответ
\ (\ left (−2, \ dfrac {3} {5}, \ dfrac {12} {5} \ right) \)
Пример \ (\ PageIndex {5A} \): Использование правила Крамера для решения несовместимой системы
Решите систему уравнений, используя правило Крамера.
\ [\ begin {align} 3x-2y & = 4 \ label {eq3} \\ 6x-4y & = 0 \ label {eq4} \ end {align} \]
Решение
Начнем с нахождения определителей \ (D \), \ (D_x \) и \ (D_y \).
\ (D = \ begin {vmatrix} 3 & −2 \\ 6 & −4 \ end {vmatrix} = 3 (−4) −6 (−2) = 0 \)
Мы знаем, что нулевой определитель означает, что либо система не имеет решения, либо имеет бесконечное количество решений. Чтобы узнать, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
- Умножьте уравнение \ ref {eq3} на \ (- 2 \).
- Добавьте результат в уравнение \ ref {eq4}.
\ [\ begin {align *} & −6x + 4y = −8 \\ & \; \; \; \ underline {6x − 4y = 0} \\ & \; \; \; \; \; \; \; \; \; \; 0 = −8 \ end {align *} \]
Получаем уравнение \ (0 = −8 \), которое неверно. Следовательно, у системы нет решения. На графике системы видны две параллельные линии. См. Рисунок \ (\ PageIndex {1} \).
Рисунок \ (\ PageIndex {1} \)Пример \ (\ PageIndex {5B} \): использование правила Крамера для решения зависимой системы
Решите систему с бесконечным количеством решений.
\ [\ begin {align} x-2y + 3z & = 0 \ label {eq5} \\ 3x + y-2z & = 0 \ label {eq6} \\ 2x-4y + 6z & = 0 \ label {eq7} \ end {align} \]
Решение
Давайте сначала найдем определитель. Создайте матрицу, дополненную первыми двумя столбцами.
\ (\ left | \ begin {array} {ccc | cc} 1 & −2 & 3 & 1 & -2 \\ 3 & 1 & −2 & 3 & 1 \\ 2 & −4 & 6 & 2 & -4 \ end {array} \ right | \)
Затем,
\ (1 (1) (6) + (- 2) (- 2) (2) +3 (3) (- 4) −2 (1) (3) — (- 4) (- 2) (1 ) −6 (3) (- 2) = 0 \)
Так как определитель равен нулю, решения либо нет, либо существует бесконечное количество решений.Чтобы выяснить это, нам нужно провести отбор.
1. Умножьте уравнение \ ref {eq5} на \ (- 2 \) и добавьте результат к уравнению \ ref {eq7}:
\ [\ begin {align *} & −2x + 4y − 6x = 0 \\ & \; \; \ underline {2x − 4y + 6z = 0} \\ & \; \; \; \; \; \ ; \; \; \; \; \; \; \; \; \; \; 0 = 0 \ end {align *} \]
2. Получение ответа \ (0 = 0 \), утверждение, которое всегда верно, означает, что система имеет бесконечное количество решений. Изобразив систему, мы видим, что две плоскости одинаковы, и обе они пересекают третью плоскость по прямой.См. Рисунок \ (\ PageIndex {2} \).
Рисунок \ (\ PageIndex {2} \)Понимание свойств детерминантов
Есть много свойств определителей. Здесь перечислены некоторые свойства, которые могут быть полезны при вычислении определителя матрицы.
СВОЙСТВА ДЕТЕРМИНАНТОВ
- Если матрица имеет верхнюю треугольную форму, определитель равен произведению элементов по главной диагонали.
- Когда две строки меняются местами, определитель меняет знак.{−1} \) — величина, обратная определителю матрицы \ (A \).
- Если какая-либо строка или столбец умножается на константу, определитель умножается на тот же коэффициент.
Пример \ (\ PageIndex {6} \): иллюстрация свойств детерминантов
Проиллюстрируйте каждое из свойств определителей.
Решение
Свойство 1 гласит, что если матрица имеет верхнюю треугольную форму, определитель является произведением элементов по главной диагонали.
\ (A = \ begin {bmatrix} 1 & 2 & 3 \\ 0 & 2 & 1 \\ 0 & 0 & −1 \ end {bmatrix} \)
Дополните \ (A \) первыми двумя столбцами.
\ (A = \ left [\ begin {array} {ccc | cc} 1 & 2 & 3 & 1 & 2 \\ 0 & 2 & 1 & 0 & 2 \\ 0 & 0 & −1 & 0 & 0 \ end {array} \ right] \)
Затем
\ [\ begin {align *} \ det (A) & = 1 (2) (- 1) +2 (1) (0) +3 (0) (0) -0 (2) (3) -0 (1) (1) +1 (0) (2) \\ & = -2 \ end {align *} \]
Свойство 2 утверждает, что перестановка строк меняет знак.Учитывая
\ [\ begin {align *} A & = \ begin {bmatrix} -1 & 5 \\ 4 & -3 \ end {bmatrix} \\ \ det (A) & = (-1) (- 3) — (4) ( 5) \\ & = 3-20 \\ & = -17 \ end {align *} \]
\ [\ begin {align *} B & = \ begin {bmatrix} 4 & -3 \\ — 1 & 5 \ end {bmatrix} \\ \ det (B) & = (4) (5) — (- 1) (- 3) \\ & = 20-3 \\ & = 17 \ end {align *} \]
Свойство 3 утверждает, что если две строки или два столбца идентичны, определитель равен нулю.
\ [\ begin {align *} A & = \ left [\ begin {array} {ccc | cc} 1 & 2 & 2 & 1 & 2 \\ 2 & 2 & 2 & 2 & 2 \\ — 1 & 2 & 2 & -1 & 2 \ end {array} \ right] \\ \ det (A) & = 1 (2) (2) +2 (2) (- 1) +2 (2) (2) +1 (2) (2) -2 (2) (1) -2 (2) (2) \ \ & = 4-4 + 8 + 4-4-8 \\ & = 0 \ end {align *} \]
Свойство 4 утверждает, что если строка или столбец равны нулю, определитель равен нулю.{-1}) & = — 2 \ left (- \ dfrac {1} {2} \ right) — \ dfrac {3} {2} (1) \\ & = — \ dfrac {1} {2} \ конец {выравнивание *} \]
Свойство 6 утверждает, что если любая строка или столбец матрицы умножается на константу, определитель умножается на тот же коэффициент. Таким образом,
\ [\ begin {align *} A & = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \\ \ det (A) & = 1 (4) -2 (3) \\ & = — 2 \ конец {выравнивание *} \]
\ [\ begin {align *} B & = \ begin {bmatrix} 2 (1) & 2 (2) \\ 3 & 4 \ end {bmatrix} \\ \ det (B) & = 2 (4) -3 (4) \\ & = — 4 \ end {align *} \]
Пример \ (\ PageIndex {7} \): использование правила Крамера и определяющих свойств для решения системы
Найдите решение данной системы \ (3 × 3 \).
\ [\ begin {align} 2x + 4y + 4z & = 2 \ label {eq8} \\ 3x + 7y + 7z & = — 5 \ label {eq9} \\ x + 2y + 2z & = 4 \ label {eq10} \ конец {align} \]
Решение
Используя правило Крамера, имеем
\ (D = \ begin {bmatrix} 2 & 4 & 4 \\ 3 & 7 & 7 \\ 1 & 2 & 2 \ end {bmatrix} \)
Обратите внимание, что второй и третий столбцы идентичны. Согласно свойству 3 определитель будет равен нулю, так что решения либо нет, либо существует бесконечное число решений.Чтобы выяснить это, нам нужно провести отбор.
1. Умножьте уравнение \ ref {eq10} на \ (- 2 \) и добавьте результат в уравнение \ ref {eq8}.
\ [\ begin {align *} -2x-4y-4x & = — 8 \\ 2x + 4y + 4z & = 2 \\ 0 & = — 6 \ end {align *} \]
Получение противоречивого утверждения означает, что система не имеет решения.
Медиа
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с правилом Крамера.
.Правило Крамера и обращение матрицы
1.3 Решение систем линейных уравнений: правило Крамера и обращение матрицы
Два уравнения с двумя переменными
Рассмотрим систему двух уравнений с двумя переменными x 1 и x 2 :
| a x 1 + b x 2 | = или |
| c x 1 + d x 2 | = против , |
Один из простых способов решить для x 1 и x 2 — выделить одну из переменных в одном из уравнений и подставить результат в другое уравнение. Например, из второго уравнения имеем
x 2 = ( v — c x 1 ) / d .
Подставляя это выражение для x 2 в первое уравнение, получаемa x 1 + b ( v — c x 1 ) / d = u ,
который мы можем написать как( a — b c / d ) x 1 + b v / d = u .
Сначала предположим, что a ≠ b c / d . затем или Чтобы найти x 2 , мы используем тот факт, что x 2 = ( v — c x 1 ) / d , чтобы получитьТеперь предположим, что a = b c / d . Тогда уравнения имеют вид
| a x 1 + b x 2 | = или |
| ( a d / b ) x 1 + d x 2 | = v |
| a d x 1 + b d x 2 | = u d |
| a d x 1 + b d x 2 | = v b . |
Таким образом, решения системы уравнений имеют три возможных вида.
- Если a d ≠ b c , то уравнения имеют уникальное решение,
( x 1 , x 2 ) = 
, 
. - Если a d = b c и u d = v b , то набор решений уравнений представляет собой набор пар
на любой номер x 1 .
x 1 , 
- Если a d = b c и u d ≠ v b , то уравнения не имеют решения.
Этот метод выделения переменной в одном уравнении и подстановки ее в другое уравнение является громоздким, когда система состоит из более чем двух уравнений и двух переменных. Теперь я опишу более элегантный метод.
n уравнений в n переменных
Мы можем записать систему двух уравнений с двумя переменными из предыдущего раздела в матричной форме, как
Общая система уравнений n в переменных n может быть записана какA x = b ,
где A — это матрица n × n , а x и b — векторы-столбцы n × 1.Если A неособое число, то умножение каждой стороны на обратное A −1 от A дает
x = A −1 b ,
единственное решение в этом случае. Таким образом, решение системы уравнений в данном случае сводится к нахождению обратной матрицы A .Если определитель A равен нулю, то будет ли система уравнений иметь много решений или ни одного, зависит от рангов A и расширенной матрицы, определенной следующим образом.
- Определение
- Пусть A — это матрица n × n , а b — вектор-столбец n × 1. Расширенная матрица ( A , b ) — это матрица с n строк и n + 1 столбцами, в которой A составляет первые n строк и столбцов, а b — последний столбец. .
- Источник предложения
- Пусть A будет матрицей n × n и пусть b будет вектором-столбцом n × 1. Если A неособая, то система уравнений
A x = b
имеет уникальное решение, x = A −1 b . Если определитель A равен нулю, то система имеет бесконечно много решений, если ранг расширенной матрицы ( A , b ) равен рангу A , и в противном случае не имеет решения.
- Источник скрыть
- Для доказательства см. Hadley (1961), стр. 168–169.
Если n = 2 или n = 3, обратное значение A относительно легко вычислить, так что решение системы может быть легко найдено, как показывают следующие примеры.
- Пример
- Рассмотрим систему уравнений
Запишите это в матричной форме. Если a d ≠ b c , то существует обратная матрица слева иa x 1 + b x 2 = или c x 1 + d x 2 = против .
так что у нас есть Таким образом и как мы обнаружили раньше.
д — б 
– с а
- Пример
- Рассмотрим систему уравнений
При записи в матричной форме матрица слева имеет вид2 x 1 + x 2 + 2 х 3 = 1 x 1 — x 2 + x 3 = 0 2 x 2 — x 3 = 3.
Определитель этой матрицы равен 3 ≠ 0, поэтому матрица невырожденная. Используя общую формулу для обратной матрицы, обратная матрица равна
2 1 2 
1 -1 1 0 2 -1 .
Умножение b , которое является транспонированием (1, 0, 3), на эту матрицу дает ( x 1 , x 2 , x 3 ) = (8/3, 1/3, −7/3), что, таким образом, является единственным решением системы уравнений. (Подставив этот список значений в исходные уравнения, вы можете убедиться, что это действительно решение.)
-1/3 5/3 1 
1/3 -2/3 0 2/3 −4/3 -1 .
- Пример
- Рассмотрим систему уравнений
При записи в матричной форме матрица слева имеет вид4 x 1 + 2 x 2 + х 3 = 1 2 x 1 — 2 x 2 + 2 x 3 = 0 4 x 2 — 2 x 3 = 3.
Определитель этой матрицы равен 0; ее ранг равен 2. Расширенная матрица
4 2 1 
2 −2 2 0 4 −2 .
Эта матрица имеет ранг 3 (определитель матрицы 3 × 3, состоящей из последних трех строк и столбцов, равен 14 ≠ 0), поэтому, согласно предыдущему результату, система уравнений не имеет решения. (Еще один способ убедиться, что система не имеет решения, — это умножить второе уравнение на 2, а третье уравнение на 1,5 и добавить их вместе. Полученное уравнение несовместимо с первым уравнением.)
4 2 1 1 
2 −2 2 0 0 4 −2 3 .
Правило Крамера
Полезный вывод из того факта, что решение системы A x = b дается как x = A −1 b , если A неособое, следующий результат ( из-за Габриэля Крамера, 1704-1752), который дает явное выражение для значения каждой переменной по отдельности.- Предложение (правило Крамера)
- Пусть A будет матрицей n × n , пусть b будет вектор-столбцом n × 1, и рассмотрим систему уравнений
A x = b
где x — вектор-столбец n × 1. Если A неособое, тогда (уникальное) значение x , которое удовлетворяет системе, определяется какx i = | A * ( b , i ) | / | A | для i = 1,…, n ,
где A * ( b , i ) — это матрица, полученная из A заменой i -го столбца на b .
- Проба
- Имеем x = A −1 b , так что
x i = ∑ n
где v i j — ( i , j ) -й компонент A −1 .
j = 1 v i j b j ,Теперь, согласно предыдущему результату, ( i , j ) -й компонент A −1 равен (−1) i + j | A j i | / | A |. Таким образом
x i = ∑ n
Наконец, вычислите определитель A * ( b , i ) в выражении результата, развернув его по столбцу i . В этом столбце b , поэтому согласно второй части предыдущего результата мы имеем
j = 1 (−1) i + j | A j i | b j / | A |.| A * ( b , i ) | = ∑ n
установление результата.(Обратите внимание, что, поскольку i является индексом столбца , по которому мы расширяемся, роли i и j здесь меняются местами относительно их ролей в формулировке результата, который мы используем.)
j = 1 (−1) i + j b j | A j i |,
- Пример
- Применение правила Крамера к системе
если a d ≠ b c получаемa x 1 + b x 2 = или c x 1 + d x 2 = против ,
иx 1 = 
u б 
в д а г — б в
Вычисляя определители в числителях, имеем иx 2 = 
а u 
с в а г — б в .
- Пример
- Значение x 2 в решении системы уравнений
является, по правилу Крамера, определителем2 x 1 + x 2 + 2 х 3 = 1 x 1 — x 2 + x 3 = 0 2 x 2 — x 3 = 3
Калькулятор правила Крамера — система уравнений 2 и 3
Правило и калькулятор Крамера для анализа линейных цепей | Шаг за шагом с решенными примерами
Обновление: Мы добавили онлайн-калькулятор правил Крамера, в котором вы можете решить систему двух уравнений, а также систему трех уравнений. Проверьте оба калькулятора правил Крамера в обоих разделах сообщения. Спасибо


Калькулятор правила Крамера для 2 × 2 (система двух уравнений)
Калькулятор правила Крамера 2 x 2 (система двух уравнений):
Поиск двух переменных по правилу Крамера:
Пример 1:
(В нашем случае неизвестными значениями являются два тока: i 1 и i 2 ) по правилу Крамера.А теперь приступим.
Как показано ниже, это простая электрическая схема, и мы собираемся решить ее по правилу Крамера.
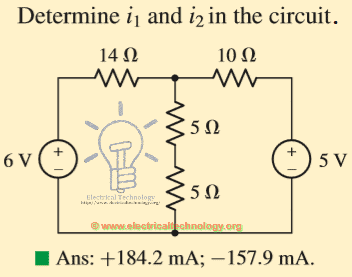
 Правило Крамера для анализа линейных цепей | 2 переменных (2 × 2) Решенный пример.
Правило Крамера для анализа линейных цепей | 2 переменных (2 × 2) Решенный пример.Решение:
Во-первых, переставьте схему с соответствующими метками (поскольку два резистора 5 Ом включены последовательно, поэтому мы заменим их на 10 Ом.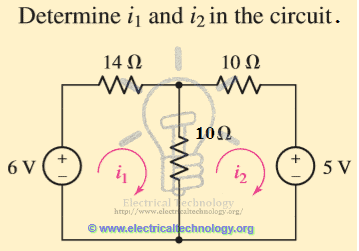
 Примените анализ сетки и упростите его по правилу Крамера, чтобы найти неизвестные значения токов i 1 и i 2 .
Примените анализ сетки и упростите его по правилу Крамера, чтобы найти неизвестные значения токов i 1 и i 2 .Теперь мы напишем уравнения KVL неизвестных значений для данной схемы.
Применим KVL к Mesh (1).
6 = 14 i 1 + 10 ( i 1 — i 2 )
6 = 24 i 1 — 10 i 2 … .. → Уравнение (1)
Также примените KVL к сетке (2).
-5 = 10 i 2 + 10 ( i 2 — i 1 )
-5 = — 10 i 1 + 20 i 2 ….. → Уравнение (2)
Здесь мы получили два уравнения, т.е.
24 i 1 — 10 i 2 = 6
— 10 i 1 + 20 i 2 = -5
Теперь мы решим эти два уравнения по правилу Крамера, чтобы найти неизвестные значения (токов), которые равны i 1 и i 2 .
Решение по правилу Крамера:
Шаг 1:
Прежде всего, запишите приведенные выше уравнения в матричной форме. то есть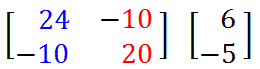
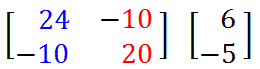
Шаг 2:
Теперь напишите матрицу коэффициентов приведенных выше уравнений и назовите ее ∆. Убедитесь, что он квадратный, то есть количество строк x количество столбцов. В приведенном выше случае у него 2 строки и 2 столбца.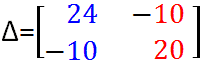
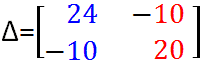
Шаг 3:
Теперь найдите определитель | ∆ | матрицы коэффициентов ∆ следующим методом.(В этом вам поможет приведенный ниже рисунок.)
Щелкните изображение, чтобы увеличить
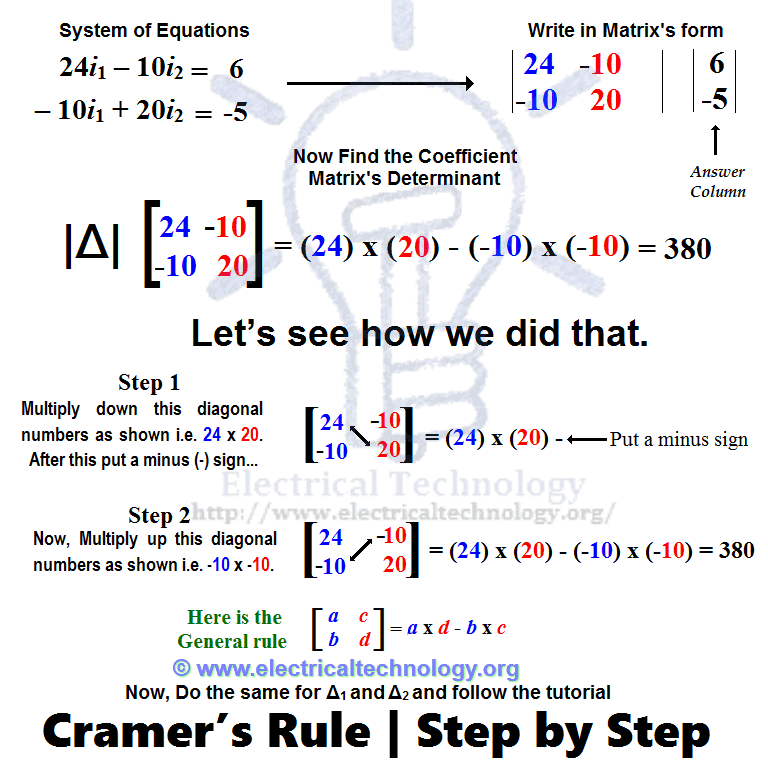
 Нахождение матрицы коэффициентов ∆ для правила Крамера. Простое объяснение. Согласно приведенному выше рис. последний шаг будет таким.
Нахождение матрицы коэффициентов ∆ для правила Крамера. Простое объяснение. Согласно приведенному выше рис. последний шаг будет таким. 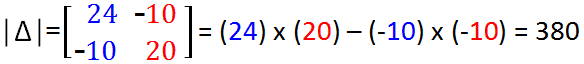
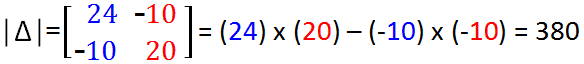
Шаг 4:
Теперь найдите определитель коэффициента Δ 1 тем же способом, как указано выше, но замените первый столбец Δ столбцом «Ответ» (если вы не не уловил суть столбца ответов, см. рис. на шаге 2 выше или проверьте инфографику в конце примера, просто обратитесь к второму примеру ниже, где мы сделали то же самое, чтобы найти Δ 1 ), то есть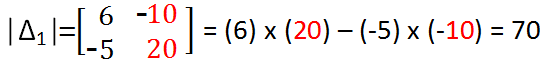
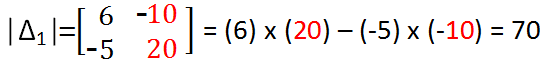
Шаг 5:
Теперь найдите определитель коэффициента Δ 2 , просто замените второй столбец столбцом ответа, который равен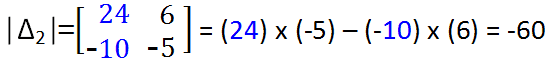
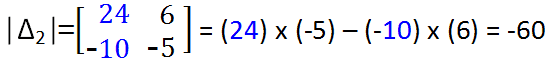
Шаг 6:
Согласно правилу Крамера, i 1 = Δ 1 / Δ и i 9 2 9000 004 Δ 2 / Δ .
Теперь найдите i 1 и i 2 по правилу Крамера.
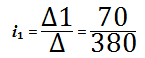
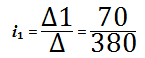
i 1 = 0,184,2 A или 184,2 мА
And,
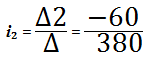
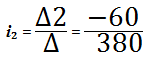
i 2 = 0,184,9 мА
Ниже приводится сводка инфографики правила Крамера для определения двух переменных или неизвестных значений.

 Правило Крамера Инфографическая диаграмма простых шагов
Правило Крамера Инфографическая диаграмма простых шаговХорошо, это было легко… А как насчет трех переменных…. Давайте попробуем решить линейные уравнения с тремя переменными с помощью правила Крамера.
Поиск трех переменных по правилу Крамера:
(В нашем случае эти неизвестные значения представляют собой три тока, которые равны i 1 , i 2 и i 3 ) по правилу Крамера.А теперь приступим.
Калькулятор правила Крамера для 3 × 3 (система трех уравнений)
Калькулятор правила Крамера 3 x 3 (системы трех уравнений):
Пример 2:
Используйте анализ сетки для определения трех сетка токов в схеме ниже. Используйте правило Крамера для упрощения.
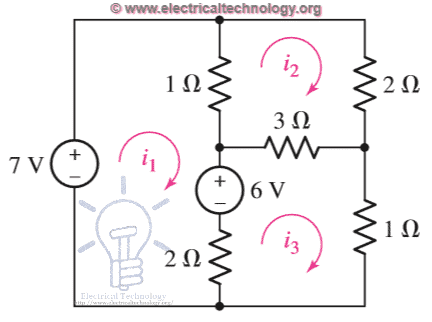
 Найдите три неизвестных значения токов по правилу Крамера.
Найдите три неизвестных значения токов по правилу Крамера.Прежде всего, примените KVL к каждой сетке одну за другой и напишите ее уравнения.
-7 + 1 ( i 1 — i 2 ) + 6 + 2 ( i 1 — i 3 ) = 0
1 ( i 2 — i 1 ) + 2 i 2 + 3 ( i 2 — i 3 ) = 0
2 ( i 3 — i 1 ) — 6 + 3 ( i 3 — i 2 ) + 1 i 3 = 0
Упрощение,
3 i 1 — i 2 — 2 i 3 = 1… уравнение….. (1)
— i 1 + 6 i 2 — 3 i 3 = 0… уравнение… .. (2)
-2 i 1 — 3 i 2 + 6 i 3 = 6… уравнение… .. (3)
Теперь запишите приведенные выше уравнения в матричной форме.
3 i 1 — i 2 — 2 i 3 = 1
— i 1 + 6 i 2 — 3 i 3 = 0
-2 i 1 — 3 i 2 + 6 i 3 = 6
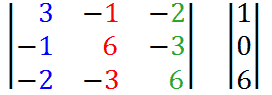
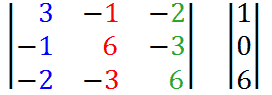
Теперь мы найдем определитель коэффициента ∆.Как мы это сделаем? Для лучшего объяснения просто посмотрите на рис ниже.
Щелкните изображение, чтобы увеличить
 Итак, полный шаг показан ниже.
Итак, полный шаг показан ниже. 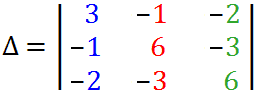
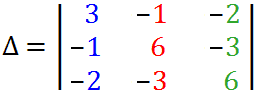
∆ = +3 (6 x 6) — (- 3 x –3) — (-1 (-1 x 6) — (- 2 x –3) + (-2 (-1 x –3) — (-2 x 6)
∆ = 81-12-30 = 39
Теперь найдите ∆ 1 таким же способом, как описано выше. Но просто замените первый столбец матрицы на «Столбец ответов». Подробности см. На рис. Ниже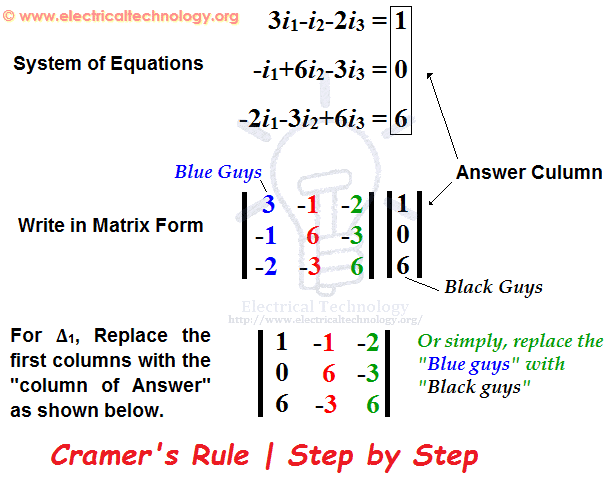 Итак, вот полный шаг, чтобы найти ∆ 1 .Здесь мы заменили «Синие парни» в первой колонке на «Черные парни» :).
Итак, вот полный шаг, чтобы найти ∆ 1 .Здесь мы заменили «Синие парни» в первой колонке на «Черные парни» :). 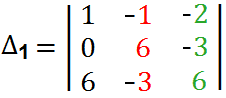
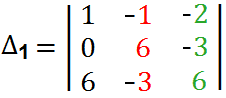
= +1 (36-9) — (–1 [0 + 18]) –2 (0-36)
= 27 + 18 + 72
∆ 1 = 117
Снова найти ∆ 2 тем же методом, что объясняется ранее. Просто замените второй столбец матрицы на «столбец ответов», т.е. замените «красных парней» в центральном столбце на «черных парней», как показано ниже.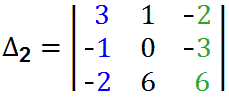
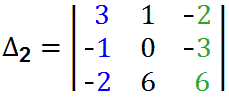
= +3 (0 +18) -1 [(- 6) — (+ 6)] –2 (-6-0)
= 54 + 12 + 12 = 78
∆ 2 = 78
Наконец, найдите последний ∆ 3 .Просто замените третью колонку колонкой ответов, т.е. замените «Зеленых парней в третьей колонке» на «Черные парни», как показано ниже.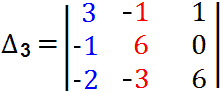
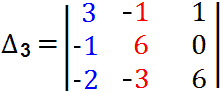
= +3 (6 x 6) — (-3 x 0) — [-1 (-1 x 6) — (-2 x 0)] + [1 (-1) x (-3) — ( -2) x (6)]
= 108 + 6 + 15
∆ 3 = 117
Теперь решите и найдите неизвестные значения тока, т.е. i 1 , i 2 и i 3 .
As, правило Крамера гласит, что переменные i.е. i 1 = ∆1 / ∆ 1 , i 2 = ∆ / ∆ 2 и i 3 = ∆ / ∆ 3 .
Следовательно,
i 1 = ∆1 / ∆ 1
= 117/39
i 1 11 = 3 11 И i 2 , i 2 = = ∆ / ∆ 2 = 78/39 i
И, наконец, i 3 ;
i 3 = ∆ / ∆ 3
= 117/39
i 3 = 3A.
Я надеюсь, что вы очень хорошо поняли правило крамера и получили удовольствие от пошагового руководства. Пожалуйста, не забудьте поделиться с друзьями. Также введите свой адрес электронной почты в поле ниже, чтобы подписаться. Итак, мы пришлем вам больше руководств, подобных приведенному выше. Спасибо.
Вы также можете прочитать:
.Правило Крамера: метод определителей
Содержание | Дом
Урок 35
Одновременные уравнения: Раздел 2
Вернуться в раздел 1
Правило Крамера: метод определителей
Пример 4. Решите эту систему одновременных уравнений:
| 1) | 3 x | + | 4 y | = | 19 |
| 2) | 2 х | – | y | = | 9 |
Решение .Если мы сложим уравнения как есть, ни одно из неизвестных не сократится. Теперь, если бы коэффициент y в уравнении 2) был -4, тогда y были бы сокращены. Поэтому мы расширим нашу стратегию следующим образом:
Сделайте одну пару коэффициентов отрицательными друг друга — на , умножив
обеих частей уравнения на одно и то же число. После добавления уравнений это неизвестное будет удалено.
Чтобы получить коэффициенты при y , равные 4 и −4, мы умножим обе части уравнения 2) на 4:
.| 1) | 3 x | + | 4 y | = | 19 | 3 x | + | 4 y | = | 19 | |
| 2) | 2 х | – | y | = | 9 | 8 x | – | 4 y | = | 36 | |
| 11 х | = | 55 | |||||||||
| х | = | 55 11 | |||||||||
| х | = | 5 | |||||||||
Число 4 над стрелкой в уравнении 2) означает, что обе части этого уравнения умножены на 4.Уравнение 1) не изменилось.
Чтобы найти y , подставьте x = 5 в любое из исходных уравнений. В уравнении 1):
| 3 · 5 + 4 y | = | 19 |
| 4 y | = | 19–15 |
| 4 y | = | 4 |
| y | = | 1 |
Решение (5, 1).
Учащийся должен всегда проверять решение, заменяя x и y на (5, 1) в исходных уравнениях.
Пример 5. Решить одновременно:
| 1) | 3 x | + | 2 y | = | −2 |
| 2) | 2 х | + | 5 y | = | −5 |
Решение .Мы должны сделать одну пару коэффициентов отрицательной по отношению друг к другу. В этом примере мы должны решить, какие из неизвестных нужно исключить: x или y . В любом случае мы сделаем новые коэффициенты наименьшим общим кратным (НОК) исходных коэффициентов, но с противоположными знаками.
Таким образом, если мы исключим x , мы получим новые коэффициенты 6 и −6. (НОК 3 и 2 равно 6.) Если мы исключим y , мы сделаем их новые коэффициенты 10 и −10.(НОК 2 и 5 равно 10.)
Давайте выберем исключение x :
| 1) | 3 x | + | 2 y | = | −2 | 6 x | + | 4 y | = | −4 | |
| 2) | 2 х | + | 5 y | = | −5 | −6 x | – | 15 y | = | 15 | |
| ________________________________________________________________________ | |||||||||||
| – | 11 y | = | 11 | ||||||||
| y | = | -1. | |||||||||
Уравнение 1) было умножено на 2. Уравнение 2) было умножено на −3 — потому что мы хотим сделать эти коэффициенты 6 и −6, так что при сложении y отменяются.
Чтобы найти x , мы подставим y = −1 в исходное уравнение 1):
| 3 х + 2 (-1) | = | −2 |
| 3 x -2 | = | −2 |
| 3 x | = | 0 |
| х | = | 0 |
Решение: (0, −1).
Проблема 3. Решайте одновременно.
| 1) | 2 х | + | 3 y | = | 13 |
| 2) | 5 х | – | y | = | 7 |
Для отмены y умножьте уравнение 2) на 3:
| 1) | 2 х | + | 3 y | = | 13 | 2 х | + | 3 y | = | 13 | |
| 2) | 5 х | – | y | = | 7 | 15 x | – | 3 y | = | 21 | |
| ________________________________________________________________________ | |||||||||||
| 17 x | = | 34 | |||||||||
| х | = | 2 | |||||||||
Чтобы решить для y :
Подставьте x = 2 в одно из исходных уравнений.
В уравнении 1:
| 2 · 2 + 3 y | = | 13 |
| 4 + 3 л | = | 13 |
| 3 y | = | 9 |
| y | = | 3 |
Решение: (2, 3).
Проблема 4. Решайте одновременно.
| 1) | x | + | 2 y | = | -1 |
| 2) | 2 х | – | 3 y | = | 5 |
Для отмены x умножьте уравнение 1) на −2:
| 1) | х | + | 2 y | = | -1 | −2 x | – | 4 y | = | 2 | |
| 2) | 2 х | – | 3 y | = | 5 | 2 х | – | 3 y | = | 5 | |
| ________________________________________________________________________ | |||||||||||
| – | 7 y | = | 7 | ||||||||
| y | = | -1 | |||||||||
Чтобы найти x :
Подставим y = −1 в одно из исходных уравнений.
В уравнении 1:
| х + 2 (-1) | = | -1 |
| x — 2 | = | -1 |
| х | = | −1 + 2 |
| х | = | 1 |
Решение: (1, −1).
Мы могли бы исключить y , умножив уравнение 1) на 3 и уравнение 2) на 2.
Задача 5. Решить одновременно:
| 1) | 3 x | – | 4 y | = | 1 |
| 2) | 2 х | + | 3 y | = | 12 |
Чтобы отменить y :
Умножьте уравнение 1) на 3 и уравнение 2) на 4:
.| 1) | 3 x | – | 4 y | = | 1 | 9 х | – | 12 y | = | 3 | |
| 2) | 2 х | + | 3 y | = | 12 | 8 x | + | 12 y | = | 48 | |
| ________________________________________________________________________ | |||||||||||
| 17 x | = | 51 | |||||||||
| х | = | 51 17 | |||||||||
| х | = | 3 | |||||||||
Чтобы решить для y :
Подставьте x = 3 в одно из исходных уравнений.
В уравнении 2 (поскольку знак y уже положительный):
| 2 · 3 + 3 y | = | 12 |
| 6 + 3 л | = | 12 |
| 3 y | = | 6 |
| y | = | 2 |
Решение: (3, 2).
Задача 6. Решить одновременно:
| 1) | 3 x | + | 2 y | = | −4 |
| 2) | 2 х | + | 5 y | = | 1 |
Чтобы отменить x :
Умножьте уравнение 1) на 2 и уравнение 2) на −3:
.| 1) | 3 x | + | 2 y | = | −4 | 6 x | + | 4 y | = | −8 | |
| 2) | 2 х | + | 5 y | = | 1 | −6 x | – | 15 y | = | −3 | |
| ________________________________________________________________________ | |||||||||||
| – | 11 y | = | −11 | ||||||||
| y | = | 1 | |||||||||
Чтобы найти x :
Подставьте y = 1 в одно из исходных уравнений.
В уравнении 1:
| 3 x + 2 · 1 | = | −4 |
| 3 x + 2 | = | −4 |
| 3 x | = | −4 — 2 |
| 3 x | = | −6 |
| х | = | −2 |
Решение — (−2, 1).
Мы могли бы исключить y , умножив уравнение 1) на 5 и уравнение 2) на −2.
Задача 7. Решить одновременно:
| 1) | 5 х | + | 3 y | = | −11 |
| 2) | 2 х | + | 4 y | = | −10 |
Чтобы отменить x :
Умножьте уравнение 1) на 2 и уравнение 2) на −5:
.| 1) | 5 х | + | 3 y | = | −11 | 10 х | + | 6 y | = | −22 | |
| 2) | 2 х | + | 4 y | = | −10 | −10 x | – | 20 y | = | 50 | |
| ________________________________________________________________________ | |||||||||||
| – | 14 y | = | 28 | ||||||||
| y | = | −2 | |||||||||
Чтобы найти x :
Подставим y = −2 в одно из исходных уравнений.
В уравнении 1:
| 5 х + 3 (−2) | = | −11 |
| 5 x — 6 | = | −11 |
| 5 х | = | −11 + 6 |
| 5 х | = | −5 |
| х | = | -1 |
Решение (−1, −2).
Мы могли бы исключить y , умножив уравнение 1) на 4 и уравнение 2) на −3.
Правило Крамера: метод определителей
Система двух уравнений с двумя неизвестными имеет следующий вид:
и — это коэффициенты x . b являются коэффициентами y . Ниже приводится матрица этих коэффициентов.
Число a 1 b 2 — b 1 a 2 называется определителем этой матрицы.
| дет | = | a 1 b 2 — b 1 a 2 |
Обозначим этот определитель через D.
Теперь рассмотрим эту матрицу, в которой c заменяют коэффициенты x :
Тогда определитель этой матрицы, которую мы назовем D x , равен
c 1 b 2 — b 1 c 2
И рассмотрим эту матрицу, в которой c заменяют коэффициенты y :
Определитель этой матрицы — D y — равен
a 1 c 2 — c 1 a 2
Правило Крамера гласит следующее:
В каждой системе двух уравнений с двумя неизвестными
, в которой определитель D не равен 0,
| х | = | D x D |
| y | = | D y D |
Пример.Используйте правило Крамера для решения этой системы уравнений (Задача 7):
| 5 х | + | 3 y | = | −11 |
| 2 х | + | 4 y | = | −10 |
Решение .
| D | = | дет | = | 5 · 4 — 3 · 2 | |
| = | 20–6 | ||||
| = | 14. | ||||
| D x | = | дет | = | −11 · 4 — 3 · −10 | |
| = | −44 + 30 | ||||
| = | −14. | ||||
| D y | = | дет | = | 5 · −10 — (−11) · 2 | |
| = | −50 + 22 | ||||
| = | −28. | ||||
Следовательно,
| х | = | D x D | = | −14 14 | = | -1. |
| y | = | D y D | = | −28 14 | = | -2. |
Проблема. Используйте правило Крамера для решения этих одновременных уравнений.
| 3 x | – | 5 y | = | −31 |
| 2 х | + | y | = | 1 |
| D | = | дет | = | 3 · 1 — (−5) · 2 | |
| = | 3 + 10 | ||||
| = | 13. | ||||
| D x | = | дет | = | −31 · 1 — (−5) · 1 | |
| = | −31 + 5 | ||||
| = | −26. | ||||
| D y | = | дет | = | 3 · 1 — (−31) · 2 | |
| = | 3 + 62 | ||||
| = | 65. | ||||
Следовательно,
| х | = | D x D | = | −26 13 | = | -2. |
| y | = | D y D | = | 65 13 | = | 5. |
Когда определитель D не равен 0, мы говорим, что уравнения линейно независимы . В любой системе линейно независимых уравнений есть одно и только одно решение.
Когда определитель D равен 0, то либо 1) нет единственного решения, можно назвать много; или 2) решения нет вообще. В случае 1) уравнения линейно зависимы . Один из них просто кратен другому.Например,
x + y = 3
2 x + 2 y = 6.
В случае 2) уравнения несовместимы .
x + y = 3
x + y = 4.
Раздел 3: Три уравнения с тремя неизвестными
Вернуться в раздел 1
Следующий урок: проблемы со словами, которые приводят к одновременным уравнениям
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2020 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
.