Обыкновенные дифференциальные уравнения и система Maple
Книга посвящена основным разделам теории обыкновенных дифференциальных уравнений. Более полно рассмотрены краевые задачи для уравнений второго порядка, особые решения уравнений и систем уравнений, а также применение групп Ли в теории уравнений. Главная ее особенность состоит в широком использовании системы Maple. Анализ многочисленных примеров демонстрирует высокую ее эффективность при исследовании и решении разнообразных задач. Основная цель книги состоит в том, чтобы показать, что использование системы Maple позволяет более глубоко изучить теорию уравнений и научиться пользоваться этой системой в решении различных задач.
Книга предназначена тем читателям, которые изучают теорию обыкновенных дифференциальных уравнений или используют их в своей практической деятельности.
Оглавление
Ведение ……………………………………………… 8
Глава 1. Классификация уравнений.
Определение и анализ решений
1. Дифференциальные уравнения и их решения . . . ………. 13
1.1. Уравнения. ……………………………………….. 13
1.2. Решение и интеграл дифференциального уравнения ………. 13
2. Простейшие уравнения первого порядка ……………… 23
2.1. Уравнения с разделенными переменными ……………….. 23
2.2. Уравнения с разделяющимися переменными …………….. 27
3. Задача Коши. Классификация решений уравнений первого порядка ……29
3.1. Основные определения. Теоремы Пеано и Осгуда. ………… 30
3.2. Теорема Коши и классификация решений ………………. 32
3,3, Зависимость решений от начальных данных. Общие и особые решения …..34
3.4. Зависимость решений от параметров …………………… 39
3.5. Уравнения, не разрешенные относительно производной ……. 41
Глава 2. Методы решения уравнений первого порядка .
45
1. Интегрирование простейших уравнений . . . …………… 45
1.1. Однородные и приводящиеся кним однородные уравнения …. 46
2. Линейные однородные и неоднородные уравнения …….. 47
2.1. Линейные уравнения ……………………………….. 47
2.2. Уравнения, приводящиеся клинейным …………………. 50
3. Уравнение Риккати ………………………………… 54
3.1. Общие свойства решений ……………………………. 56
4. Уравнения в полных дифференциалах ……………….. 57
4.1. Уравнения в полных дифференциалах…57
4.2. Интегрирующий множитель …………………………. 60
5. Уравнения, не разрешенные относительно производной…67
5.1. Уравнения, не содержащие одну из переменных ………….. 67
5.2. Общий метод введения параметра …………………….. 68
5.3. Уравнение Лагранжа ……………………………….. 70
5.4. Уравнение Клеро .
…………………………………. 74
6. Анализ особых решений . ……………………………. 78
6.1. c- дискриминантная кривая и ее свойства ……………….. 78
6.2. Необходимые и достаточные условия существования
особой интегральной кривой …………………………….. 85
6.3. Кривая касаний и некоторые ее свойства ……………….. 89
7. Практические способы построения особых решений . . 91
8. Параметрическая форма представления плоских кривых 95
8.1. Теоремы об огибающих семейства кривых на плоскости …97
8.2. Точки возврата огибающей ………………………….. 99
Заключение …………………………………………. 102
Глава 3. Уравнения n-го порядка
……………………. 1031. Линейные однородные уравнения выше первого порядка103
1.1. Общие свойства линейных однородных уравнений ……….. 103
2. Решение линейных однородных уравнений с постоянными коэффициентами .
..109
2.1. Решение линейных однородных уравнений с постоянными коэффициентами …..109
3. Решение линейных неоднородных уравнений выше первого порядка. …….114
3.1. Структура общего решения ………………………… 114
4. Применение операционного исчисления ……………… 116
4.1. Основные определения и формулы операционного исчисления 116
4.2. Применение операционного исчисления ……………….. 121
5. Различные задачи для уравнений второго порядка . . . . . . 125
5.1. Общее решение уравнение второго порядка ……………. 125
6. Cуществование решений краевых задач…………… 132
6.1. Положительные и положительно определенные операторы . . . 133
6.2. Энергетические пространства ……………………….. 139
6.3. Обобщенные решения краевых задач ………………….. 140
7. Собственные значения и собственные функции краевой задачи .
…148
7.1. Основные свойства собственных функций и собственных значений …. 149
7.2. Оценка собственных значений и собственных функций ……. 151
7.3. Ряды Фурье …………………………………….. 152
8. Аналитические решения уравнений второго порядка . . . . 154
8.2. Интегрирование уравнений с помощью.степенных рядов ….. 156
9. Нелинейные уравнения n-го порядка ……………….. 160
9.1. Существование решений ……………………………. 160
9.2. Промежуточный интеграл ………………………….. 163
9.3. Уравнения, допускающие понижение порядка …………… 163
9.4. Многопараметрические семейства кривых на плоскости
и в пространстве …………………………………….. 168
10. Огибающие семейства поверхностей с двумя параметрами …170
10.2. Огибающие поверхности …………………………… 171
10.1. Неявно заданные двупараметрические семейства поверхностей.
..173
Глава 4. Частные и общие решения систем линейных уравнений ……177
1. Системы линейных уравнений ……………………… 177
1.1. Основные понятия и определения ……………………. 177
1.2. Теорема Коши для линейных систем …………………. 180
1.3. Анализ примеров …………………………………. 180
1.4. Системы линейных однородных уравнений …………….. 184
2. Системы линейных однородных уравнений с постоянными коэффициентами …187
2.1. Случай простых собственных значений ………………… 187
2.1.1. Случай простых вещественных собственных значений …. 188
2.1.2. Собственные значения простые, но не все вещественные . 189
2.2. Собственные значения вещественны и произвольной кратности191
2.3. Решение систем уравнений ………………………….. 194
3. Применение функций от матриц . …………………… 203
3.1. Функция от матрицы, матричная экспонента .
…………. 203
3.2. Практическое построение функции от матрицы ………… 205
3.3. Случай кратных корней характеристического уравнения… 208
3.4. Применение полинома Лагранжа ……………………212
4. Системы линейных неоднородных уравнений ……216
4.1. Структура решений системы. Матрица Коши …………. 216
4.2. Системы неоднородных уравнений с постоянными коэффициентами …..218
5. Приводимые системы……………………………. 220
5.1. Теорема Еругина ………………………………… 220
5.2. Линейные системы с периодическими коэффициентами …… 221
6. Уравнения Риккати и линейные системы . . . …………. 225
6.1. Системы уравнений Риккати ………………………… 227
7. Матричные многочленные уравнения . ………………. 230
7.1. Уравнения AX − XA =Θ ………………………….. 230
7.2. Перестановочные матрицы ……………………
…….. 235
7.3. Решение линейного неоднородного уравнения …………… 238
7.4. Скалярное уравнение ……………………………… 241
7.5. Полиномиальные уравнения ………………………… 244
8. Квадратный корень из матрицы . . ………………….. 245
8.1. Уравнение с жордановой матрицей …………………… 244
8.2. Уравнение с особенной матрицей …………………….. 252
8.3. Матричные уравнения второй степени ………………… 260
9. Линейные дифференциальные уравнения ……………….. 260
9.1. Однородное уравнение …………………………….. 260
9.2. Неоднородное уравнение ……………………………. 265
9.3. Частное решение неоднородного уравнения. Формула Коши . . 268
9.4. Уравнение Бернулли ………………………………. 269
10. Матричное дифференциальное уравнение Риккати . . . . . 270
10.1. Простейшие свойства уравнения ……….
……………. 272
10.2. Уравнения с постоянными матрицами ………………… 274
10.3. Существование решения ………………………….. 279
Глава 5. Системы нелинейных уравнений …………… 282
1. Теорема существования и единственности решения . ….. 282
1.1. Предварительный анализ системы уравнений …………… 282
1.2. Теорема Коши …………………………………… 284
1.3. Основные следствия ………………………………. 285
1.4. Зависимость решений от параметров ………………….. 286
1.5. Частные и общие решения системы уравнений ………….. 289
2. Нелинейные системы уравнений первого порядка . . . …. 290
2.1. Основные свойства системы в нормальной форме ……….. 291
2.2. Интегралы системы уравнений ………………………. 293
3. Автономные системы уравнений . . . …………………. 295
3.1. Симметричная форма системы уравнений .
…………….. 295
4. Особые решения системы уравнений . ……………….. 299
4.1. Параметризованные семейства поверхностей и их огибающие . 300
5. Семейства неявно заданных поверхностей и их огибающие …..307
Глава 6. Уравнения с частными производными первого порядка ….315
1. Основные задачи интегрирования уравнений с частными производными ….315
2. Линейные однородные уравнения первого порядка …. 319
2.1. Общее решение …………………………………… 319
2.2. Задача Коши …………………………………….. 321
3. Квазилинейные уравнения . . . ………………………. 324
3.1. Случай двух независимых переменных ………………… 324
3.2. Задача Коши для уравнения с двумя независимыми переменными ….326
3.3. Квазилинейные уравнения. Общий случай ……………… 328
3.4. Решение задачи Коши ……………………………… 331
Глава 7 Групповой анализ дифференциальных уравнений .
…. 333
1. Группы точечных преобразований………………… 334
1.1. Основные определения и теоремы теории групп Ли…….. 334
1.2. Инфинитезимальный оператор и инварианты группы …….. 336
2. Интегрирование уравнения, допускающего группу . . . . . . 343
2.1. Продолжение группы и инфинитезимального оператора …… 343
2.2. Уравнения, допускающие группу …………………….. 345
2.3. Интегрирование уравнений первого порядка ……………. 347
2.3.1. Первый способ (замена переменных) ………………. 347
2.3.2. Второй способ (построение интегрирующего множителя) . 351
2.4. Интегрирование уравнений второго порядка ……………. 352
3. Дифференциальные уравнения и допускаемые ими группы …..354
3.1. Определяюшее уравнение. Алгебра Ли ………………… 354
4. Фундаментальная система решений . . ……………….. 360
4.1. Заключение ………………………………………
363
Приложения ……………………………………… 365
1. Краткое описание систем Maple ………………………. 365
2. Приложение 1. Работа с числами, наборами и списками ……. 368
3. Приложение 2. Матрицы и векторы ……………………. 370
4. Приложение 3. Функции …………………………….. 373
5. Приложение 4, Операции над функциями ……………….. 374
6. Приложение 5. Обыкновенные дифференциальные уравнения . . 376
7. Приложение 6. Визуализация …………………………. 378
8. Приложение 7. Визуализация в дифференциальных уравнениях…381
Литература ………………………………………….. 382
Предметный указатель ………………………………. 386
| Информация о книге | |
| Автор | Егоров А. И. |
| Формат | 70×100/16 |
| Объем, стр | 392 стр. |
Написать отзыв
Ваше имя:
Ваш отзыв:
Примечание: HTML разметка не поддерживается! Используйте обычный текст.
Оценка: Плохо Хорошо
Имя
Телефон
Вопрос
Отправить
Maplesoft — Maple
Система компьютерной алгебры Maple
Система Maple позволяет пользователям решать математические задачи любой сложности. Она содержит более 5000 встроенных функций, покрывающих почти все разделы математики, включая математический анализ, линейную алгебру, дифференциальные уравнения, статистику, геометрию и многое другое.
В Maple есть символьные, численные и гибридные алгоритмы, алгоритмическое ядро системы содержит методы недоступные другим платформам. Помимо этого, система обладает функционалом для создания 2D- и 3D- визуализации и анимации, и также предлагает пользователям эффективные алгоритмы для высокопроизводительных вычислений. Вне зависимости от того, делаете ли вы простой расчет или разрабатываете сложный алгоритм, иллюстрируете концепцию или создаете интерактивный технический документ, система Maple поможет легко справиться с работой. Она предлагает пользователю интеллектуальное контекстное меню, которое позволяет решать математические задачи исключительно с помощью мышки без знания синтаксиса системы. Maple основана на собственном языке программирования, ориентированном на математику, и предлагает специальные образовательные инструменты для преподавания всех основных математических курсов.
На протяжении многих версий система Maple позволяла пользователям импортировать данные из большого числа форматов, взаимодействовать с различными системами, например, САПР или MATLAB, а также генерировать код на всех современных языках программирования.
На сегодняшний день Maple позволяет не только генерировать код, но и, например, запускать интерпретатор Python внутри системы, таким образом выполняя скрипты и получая результаты не покидая Maple. Новый пакет DeepLearning предлагает API для доступа к нейронным сетям ресурса TensorFlow.
Новые возможности Maple 2022
Новый релиз уникальной системы компьютерной алгебры Maple 2022 предлагает множество полезных функциональных возможностей как для новых пользователей, так и для тех, кто работает с системой уже долгие годы! Обновленное алгоритмическое ядро позволяет решать еще больше математических задач, включая улучшенные инструменты для работы со степенными рядами, обработку сигналов, единицы измерения, а также библиотеки для решения физических задач. Также в версии Maple 2022 улучшены как программные, так и интерактивные инструменты визуализации, появились новые возможности форматирования документов и многое другое!
Maple 2022 представляет большое число новшеств, направленных на усиление математического ядра системы и расширение класса решаемых задач.
Были усовершенствованы алгоритмы решения дифференциальных уравнений в частных производных, инструментарий теории графов, методы решения рекуррентных соотношений и др. Особое внимание было уделено методам интегрирования — были исправлены существующие недостатки и добавлены новые методы, а также полностью переработаны библиотеки для работы с формальными степенными рядами.
Интерактивный Plot Builder теперь поддерживает работу одновременно с несколькими выражениями, что позволяет создавать 2D и 3D графики и анимацию, а также управлять глобальными настройками группы графиков и вносить локальные изменения в отдельные графики. Все функции визуализации в Maple 2022 теперь автоматически распознают разрывы и используют новый адаптивный алгоритм отрисовки при выполнении операций по масштабированию и повороту графиков. Также обновлены цветовые схемы и настройки отдельных специализированных графиков.
В Maple 2022 существенно упростилась подготовка документов для печати или экспорта в PDF — появился специальный режим в котором пользователи могут редактировать содержимое документа таким образом, чтобы оно не выходило за границы страницы, добавляя разрывы или изменяя размер таблиц и графиков.
Также была обновлена навигация по встроенной документации, улучшено масштабирование примеров из документации и многое другое.
В новой версии появилась возможность использовать Maple в качестве вычислительного ядра при работе в Jupyter Notebooks, а также конвертировать документы Maple в Jupyter Notebooks. Была улучшена интеграция с библиотекой Google TensorFlow, благодаря которой внутри Maple можно создавать и использовать различные модели машинного обучения.
Релиз Maple 2022 предоставляет новые интерактивные инструменты для обучения. Добавлены возможности программной генерации документов с интерактивными элементами управления и трехмерными графиками. Появилась возможность создавать документы, в которых студент будет выполнять решения пошагово, получая обратную связь на каждом шаге, а при создании наборов тестов можно добавлять или скрывать кнопку, выводящую правильное решение.
В Maple 2022 улучшена производительность многих базовых команд, что существенно повышает эффективность работы практически в любой области знаний.
Теперь намного быстрее работают расчеты с единицами измерения и обыкновенные дифференциальные уравнения. Ускорены команды теории чисел, команды для работы со списками, регулярными цепями и многое другое.
Maple Learn — онлайн среда, предназначенная для преподавания математики в средней школе и на первых курсах университетов. Maple 2022 предлагает новые инструменты для создания интерактивных учебных материалов, которые могут использоваться как в Maple так и в Maple Learn. Подробнее о Maple Learn.
Приложение Maple Calculator — бесплатное приложение для перевода математических задач из книг или тетрадей напрямую в Maple с использованием камеры смартфона. Это позволяет быстро исследовать задачу благодаря мощному вычислительному ядру Maple. Как самостоятельный инструмент, Calculator помогает студентам в работе над домашними заданиями — с помощью встроенного функционала они могут выполнять базовый анализ и проверять правильность своего решения, строить графики, вычислять интегралы и производные, выполнять матричный операции, решать системы уравнений и многое другое.
Приложение доступно на iOS и Android на русском языке!
Помимо всего вышеперечисленного, в Maple 2022 также представлено множество других модификаций и нововведений, включая обновления библиотеки для обработки сигналов в области генерации и анализа, теплофизические данные, модуль квантовой химии и многое другое!
Если у Вас возникли дополнительные вопросы по данному продукту, мы всегда будем рады на них ответить!
maple — Решение системы уравнений с предположениями
Пытаюсь решить систему уравнений в Maple, и у меня есть некоторые предположения. Однако я получаю предупреждение о том, что «Решение может игнорировать предположения о входных переменных».
Цель состоит в том, чтобы найти кинетические константы скорости ряда связанных ферментативных реакций.
$$ V + S_0 <=> W <=> X <=> Y <=> Z $$
Химический пакет здесь не работает, но каждая стрелка имеет соответствующую константу скорости: первая прямая (от V до W) равна $k_1$, первая обратная (от W к V) равна $k_2$, второй набор стрелок (между W и X) равны $k_3$ и $k_4$ и т.
д.
Эта система имеет связанный набор дифференциальных уравнений: $$\frac{dV}{dt}=-k_1S_0Vk_2W$$ $$\frac{dY}{dt}= k_1S_0V — (k_2 + k_3)W + k_4X$$ $$и т.д…$$ Что может быть выражено в виде матрицы: $$ \begin{bmatrix} -k_1S_0&k_2&0&0&0\\ k_1S_0&-k_2-k_3&k_4&0&0\\ 0&k_3&-k_4-k_5&k_6&0\\ 0&0&k_5&-k_6-k_7&k_8\\ 0&0&0&k_7&-k_8\\ \end{bmatrix} \begin{bmatrix} V\\W\\X\\Y\\Z \end{bmatrix} $$ Матрица коэффициентов имеет соответствующий характеристический полином (для упрощения я сделал $k_1S_0 -> a, k_2 -> b, $ и т. д.) 92-(-aceg-aceh-acfh-adfh-bdfh)x$$
Меня не особо интересуют корни этого уравнения, поэтому я не хочу искать собственные значения. Вместо этого я использую формулы Виетаса, чтобы смотреть только на коэффициенты многочлена.
$$1. k_{obs_1}+k_{obs_2}+k_{obs_3}k_{obs_4} = a+b+c+d+e+f+g+h$$
$$2. k_{obs_1}k_{obs_2}+k_{obs_1}k_{obs_3}+k_{obs_1}k_{obs_4}+k_{obs_2}k_{obs_3} … = (ac+ad+ae+af+ag+ ah+bd+be+bf+bg+bh+ce+cf+cg+ch+df+dg+dh+eg+efh)$$
$$3. k_{obs_1}k_{obs_2}k_{obs_3}+k_{obs_1}k_{obs_2}k_{obs_4}+ .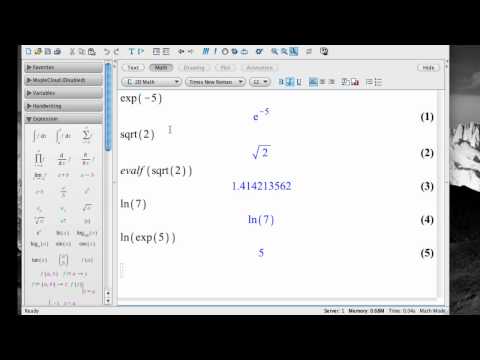
.. = (ace+acf+acg+ach+adf+adg+adh+aeg+aeh+afh +bdf+bdg+bdh+beg+beh+bfh+ceg+ceh+cfh+dfh)$$
$$4. k_{obs_1}k_{obs_2}k_{obs_3}k_{obs_4} = aceg+aceh+acfh+adfh+bdfh$$
Поскольку $a = k_1S_0$, мы замечаем, что каждое из этих уравнений является линейным относительно $S_0$. Разделение этих 4 уравнений на 8 дает нам 8 уравнений и 8 неизвестных, поэтому оно должно быть решаемо.
Отсюда я вычисляю c, d, e, f, g, h через s, u, v, w, x, y, z. У меня уже есть выражения a и b из уравнения 1. Вот что у меня есть на листе Maple, обратите внимание, что для каждого выражения я уже заменил a и b там, где они принадлежат системе.
а := с:
b := t - (ед/с):
u := s*(c+d+e+f+g+h):
v := (t-(u/s))*(d+e+f+g+h)+c*(e+f+g+h) + d*(f+g+h) + e*( г+ч) + е*ч:
w := s*(c*(g+e+f+h)+d*(f+g+h)+e*(g+h)+f*h):
x := (t-u/s)*(d*(f+g+h)+e*(g+h)+f*h)+c*(e*(g+h)+f*h)+d *ф*ч:
y := s*(c*(e*g+e*h+f*h)+d*f*h):
z := (t-u/s)*d*f*h:
92)/e, g=(d(d+e))/e, h=0}
{c=0,d=0,e=0,f=-g,g=h,h=0}
{с=0,d=-e,e=e,g=-h,h=h}
Особенно последние решения вообще бесполезны.
Я устанавливаю свои предположения или решаю неправильно? Еще раз спасибо заранее.
СПРАВОЧНЫЕ ЛИСТЫ MAPLE: НУЛИ
Этот справочный лист демонстрирует, как использовать Maple для решения:
- одно уравнение для одной переменной и
- система уравнений для нескольких переменных.
> plot( f(x), x = -2.0 .. 2.0, толщина = 5, цвет = синий, размер = [500, 300] ) ;
> решить(f(x),x) ; результат: -2, 3И, -3И, 1, 1, 1
> fsolve( f(x), x) ; результат: -2., 1., 1., 1.
> fsolve( f(x), x = 0.0 .. 2.0 ) ; результат: 1., 1., 1.
ПРИМЕЧАНИЕ: Комплексный номер i — это I
> f := x -> cos(x) ;
> g := x -> sqrt(x) ;
> plot([ f(x), g(x)], x = 0.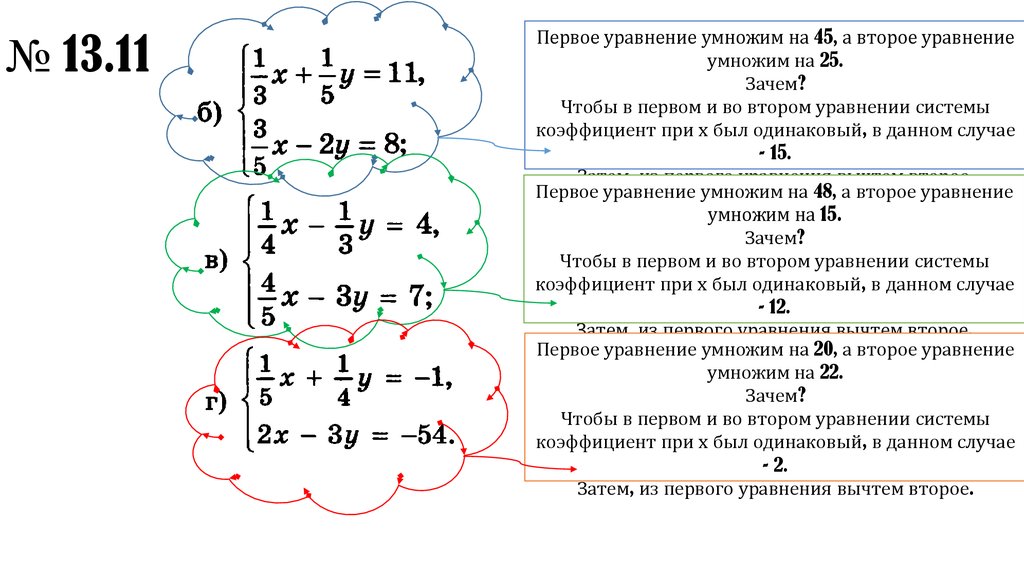
0 .. 1.0, толщина = 5, цвет = [синий, красный], размер = [600, 450]) ;
графики f и g на общем графике
> fsolve( f(x) = g(x), x = 0,0 .. 1,0 ) ; определяет, где функции f и g пересекаются между x = 0 и 92 — 115*х + 78;
> plot( f(x), x = 1.0 .. 3.0 , -2.0 .. 10.0, толщина = 5, цвет = синий, размер = [ 600, 450 ] ) ;
> решить(f(x),x) ; результат: 2, 3/2, 2+3И, 2-3И
> fsolve( f(x), x ) ; результат: 2.000000000, 1.500000000
> f := x -> exp(-x) — cos(x) ;
> решить(f(x),x) ; результат: 0
> fsolve( f(x), x ) ; результат: 0
> fsolve( f(x), x = 1.0 .. 2.0 ) ; результат: 1.292695719
> fsolve( f(x), x = -1.0 .. 1.0 ) ; результат: 0
ПРИМЕЧАНИЕ.
В приведенном выше примере показано, что Maple может не найти все нулей.
функции.
Таким образом, вы должны иметь хорошее представление о том, где нули без
доверяя клен, чтобы найти их правильно.
92 = 9;
> eq2 := х — у = 1 ;
> with(графики, неявный сюжет); загружает команду implicitplot
> implicitplot([eq1, eq2], x = -4.0 .. 4.0, y = -4.0 .. 4.0, толщина = 5, цвет = [синий, красный], масштабирование = ограничено);
строит оба уравнения в плоскости xy на
указанный диапазон
> решить({eq1, eq2}, {x,y}) ;
пытается решить систему символически — может не получиться
> fsolve({eq1, eq2}, {x,y}) ;
пытается решить систему численно, но
может дать только одно решение, так как диапазон не указан
> fsolve({eq1, eq2}, {x,y},
{ х = 0,0 .