Метод минимального элемента
Получаемый методом северо-западного угла, начальный план перевозок не зависит от их стоимости и поэтому в общем случае далек от наилучшего. В методе минимального элемента учитываются затраты на перевозку. Соответствующий начальный план позволяет обеспечить суммарную стоимость перевозок, более близкую к оптимальной.
В этом методе по формуле (11) последовательно заполняются клетки с наименьшей стоимостью перевозок. Если есть несколько клеток с наименьшей стоимостью, то из них выбирается любая.
Пример 4. Найти начальный план перевозок в ТЗ (пример 3) методом минимального элемента.
Запишем матрицу перевозок (табл. 3.3).
Таблица 3.3
Bj Ai | B1 | B2 | В3 | B4 | Запасы ai |
A1 | 10 0 | 0 15 | 20 * | 11 | 15 |
A2 | 12 | 7 0 | 9 15 | 20 10 | 25 |
A3 | 0 5 | 14 * | 16 * | 18 | 5 |
Потребности bj | 5 | 15 | 15 | 10 | 45 45 |
Заполняем клетку с наименьшей стоимостью:
.
Потребности в пункте В2
Среди оставшихся клеток ищем клетку с наименьшей стоимостью:
–случай вырождения, базисный нуль .
Из оставшихся клеток заполняем клетку с наименьшей стоимостью:
.
Потребности в пункте В3 удовлетворены, выбывает третий столбец.
.
Получен начальный план перевозок:
с суммарной стоимостью
,
которая меньше стоимости, полученной методом северо-западного угла. Число базисных клеток m + n – 1 = 3 + 4 – 1 = 6.
Метод потенциалов
Метод потенциалов
— метод, обеспечивающий улучшение
начального плана перевозок.
Циклы матрицы перевозок
Цикл – замкнутая ломаная с вершинами в клетках и звеньями, расположенными вдоль строк и столбцов матрицы перевозок. В каждой вершине встречаются два звена, причем одно из них располагается по строке, а другое – по столбцу. Число вершин цикла чётно. Циклом может быть самопересекающаяся ломаная, но точки ее самопересечения не могут быть вершинами цикла.
а б в
Рис. 3. Простейшие циклы
На рис. 3 звездочкой отмечены клетки матрицы, включенные в состав цикла. На
Означенный цикл – цикл, в котором некоторой вершине
приписан знак +, а затем при обходе цикла
в каком-либо направлении знаки чередуются.
Сдвигом по циклу на величину назовем увеличение объемов перевозок во всех клетках, отмеченных знаком + и уменьшение объемов перевозок наво всех клетках цикла, отмеченных знаком –.
Метод потенциалов, его алгоритм
Теорема | Если план транспортной задачи является оптимальным, то ему соответствует система изm+ n чисел и, удовлетворяющих условиям: для , для ,. Числа ,называются потенциалами соответственно поставщиков и потребителей. |
Данная теорема позволяет построить алгоритм нахождения решения транспортной задачи.
АЛГОРИТМ
Для ТЗ с правильным балансом находим начальный план перевозок методом северо-западного угла или методом минимального элемента.
Для каждой базисной клетки составляем уравнение . Так как число базисных клетокm + n – 1, то система m + n – 1 уравнений с m + n неизвестными имеет бесконечное множество решений. Для определенности положим u1 = 0. Тогда все остальные потенциалы находятся однозначно. Вносим их в матрицу перевозок.
- Для свободных клеток находим суммы соответствующих потенциалов, помещаем их в нижний правый угол свободных клеток матрицы.
Для всех свободных клеток проверяем выполнение условия оптимальности:
если для всех свободных клеток (), то задача решена; выписываем полученный оптимальный план перевозок из последней матрицы, подсчитываем его стоимость;
если для одной или нескольких свободных клеток, то переходим к п.
5.
5.Находим ту свободную клетку, для которой имеетнаибольшее по модулю отрицательное значение. Строим для нее означенный цикл. Свободной клетке приписываем знак +. Все вершины означенного цикла, кроме расположенной в клетке (i,j), должны находиться в базисных клетках.
Выполняем сдвиг по циклу на величину , равную наименьшему из чисел, стоящих в «отрицательных» вершинах цикла. Если наименьшее значениедостигается в нескольких «–» клетках, то при сдвиге следует поставить базисный нуль во всех таких клетках, кроме одной. Тогда число базисных клеток сохранится и будет равноm + n – 1, это необходимо проверять при расчетах.
Клетки матрицы, не входящие в цикл, остаются без изменения.
Строим новую матрицу перевозок.
Переход к шагу 2.
Примечание.
При решении задачи может возникнуть
ситуация, в которой
.
Тогда при сдвиге свободная клетка
становится базисной.
Пример 5. Составить математическую модель ТЗ, решить ТЗ:
Запишем матрицу перевозок (табл. 3.4).
Таблица 3.4
Bj Ai | B1 | B2 | В3 | B4 | Запасы ai |
A1 | 10 | 0 | 20 | 11 | 15 |
A2 | 12 | 7 | 9 | 20 | 25 |
A3 | 0 | 14 | 16 | 18 | 5 |
Потребности bj | 5 | 15 | 15 | 10 | 45 45 |
Пусть – количество единиц груза, которое нужно перевезти из пункта
Ограничения:
а) по запасам
б) по потребностям
Целевая функция: . Требуется составить план перевозок, чтобы их суммарная стоимость была минимальной.
Данная ТЗ с правильным балансом: 15 + 25 + 5 = 5 + 15 + 10; 45 = 45.
Начальный план перевозок найден в п. 3.3.2 методом минимального элемента (табл.3.3) Выпишем найденную матрицу перевозок.
Находим потенциалы базисных клеток:
Матрица перевозок
Bj Ai | B1 | B2 | В3 | B4 | Запасы ai | |
u1=0 | A1 | 10 0 | 0 15 | 20 2 | 11 13 | 15 |
u2=7 | A2 | 12 17 | 7 0 | 9 15 | 20 10 | 25 |
u3= -10 | A3 | 0 5 | 14 -10 | 16 -8 | 18 3 | 5 |
Потребности bj | 5 | 15 | 15 | 10 | 45 45 |
Для свободных клеток находим суммы соответствующих потенциалов, заносим их в матрицу в нижний правый угол свободных клеток.
Для свободных клеток проверяем выполнение условия оптимальности: для. Для клеток (1,4) и (2,1) условие не выполнено.
, Для свободных клеток строим обозначенный цикл.
Производим сдвиг по циклу на Клетка (2,1) становится базисной, а клетка (1,1) – свободной.
Переходим к шагу 2 алгоритма метода потенциалов.
Строим новую матрицу перевозок.
Матрица перевозок.
|
Для свободной
клетки (1,4) условие оптимальности не
выполнено.
Строим для нее обозначенный
цикл, осуществляем сдвиг по циклу на
Клетка (1,4) становится базисной,
клетка (2,4) – свободной. Строим новую
матрицу перевозок.
Матрица перевозок
|
Переходим к шагу 2 метода потенциалов:
Для всех
свободных клеток
.
Полученный план является оптимальным:
.
При данном плане стоимость перевозок:
.
Методы северо-западного угла, минимального элемента, Фогеля и двойного предпочтения
- Метод северо-западного угла
- Метод минимального элемента
- Метод Фогеля
- Метод двойного предпочтения
Метод северо-западного угла
Рассмотрим метод северо-западного угла. Сущность его состоит в
следующем. Будем распределять груз в
таблице, начиная с загрузки левой верхней, условно называемой
«северо-западной», клетки (1,1), двигаясь затем от нее по строке вправо или по
столбцу вниз. В клетку (1,1) занесем меньшее из чисел
,
то есть
.
Если
,
то
и первый потребитель
будет полностью удовлетворен. В дальнейшем 1-й
столбец таблицы в расчет не принимается: в нем переменные
для
.
Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1,2) меньшее из чисел и , то есть . Если , то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика.
Если , то . При этом запас первого поставщика будет исчерпан, а потому для . Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению запасов второго поставщика. В клетку (2,1) заносим наименьшее из чисел .
Заполнив таким образом клетку (1,2) или
(2,1), переходим к загрузке следующей клетки по второй строке либо по второму
столбцу. Процесс распределения по второй, третьей и последующим строкам
(столбцам) производится аналогично распределению по первой строке или по
первому столбцу до тех пор, пока не исчерпаются ресурсы.
Последней
заполняется клетка
.
Задача 1
Однородный продукт, сосредоточенный на трех складах фирмы в количествах единиц, необходимо распределить между четырьмя магазинами, которым необходимо соответственно единиц продукта. Стоимость перевозки единицы продукта из i-го пункта отправления (i = 1, 2, 3) в j-й пункт назначения (j = 1, 2, 3, 4) равна и известна для всех маршрутов.
Вектор запасов продукта на складах
вектор запросов продукта магазинами
и матрица транспортных тарифов
Построить начальный опорный план транспортной задачи методом северо-западного угла.
Решение
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи закрытая.
Построим начальный опорный план по правилу северо-западного угла.
Начинаем заполнение с левого верхнего угла и далее двигаемся по диагонали к правому нижнему углу.
Число занятых клеток должно быть .
В нашем случае число занятых клеток равно 6 — опорный план является невырожденным.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении оптимального плана перевозок, производится методом потенциалов .
Метод минимального элемента
Рассмотрим правило
минимального элемента. Сущность его состоит в следующем. Просматриваются
тарифы таблицы и в первую очередь заполняется клетка с минимальным
значением тарифа. При этом в клетку записывается максимально возможное значение
поставки.
Затем из рассмотрения исключают строку, соответствующую поставщику,
запасы которого полностью израсходованы, или столбец, соответствующий
потребителю, спрос которого полностью удовлетворен. После этого из оставшихся
клеток таблицы снова выбирают клетку с наименьшим тарифом. Процесс
распределения заканчивается, когда все запасы поставщиков исчерпаны, а спрос
потребителей полностью удовлетворен. В результате получаем опорный план,
который должен содержать
загруженных
клеток.
В процессе заполнения таблицы могут быть одновременно исключены строка и столбец. Так бывает, когда полностью исчерпывается запас груза и полностью удовлетворяется спрос (вырожденная задача). В этом случае в свободные клетки надо записать число 0 – «нуль загрузка», условно считая эту клетку занятой. Однако число 0 записывается в те свободные клетки, которые не образуют циклов с ранее занятыми клетками.
Задача 2
На предприятиях
производится однородная продукция в количестве
единиц.
Себестоимость производства одной
единицы продукции на i-м предприятии равна соответственно
ден.ед. Готовая продукция поставляется
потребителям
, потребности которых составляют
единиц. Для полного удовлетворения
потребностей необходимо увеличить выпуск продукции. Для этого освоить выпуск
данной продукции на предприятии
с
себестоимостью производства продукции
ден.ед.
Стоимости перевозки одной единицы продукции от каждого предприятия
каждому потребителю задаются матрицей
.
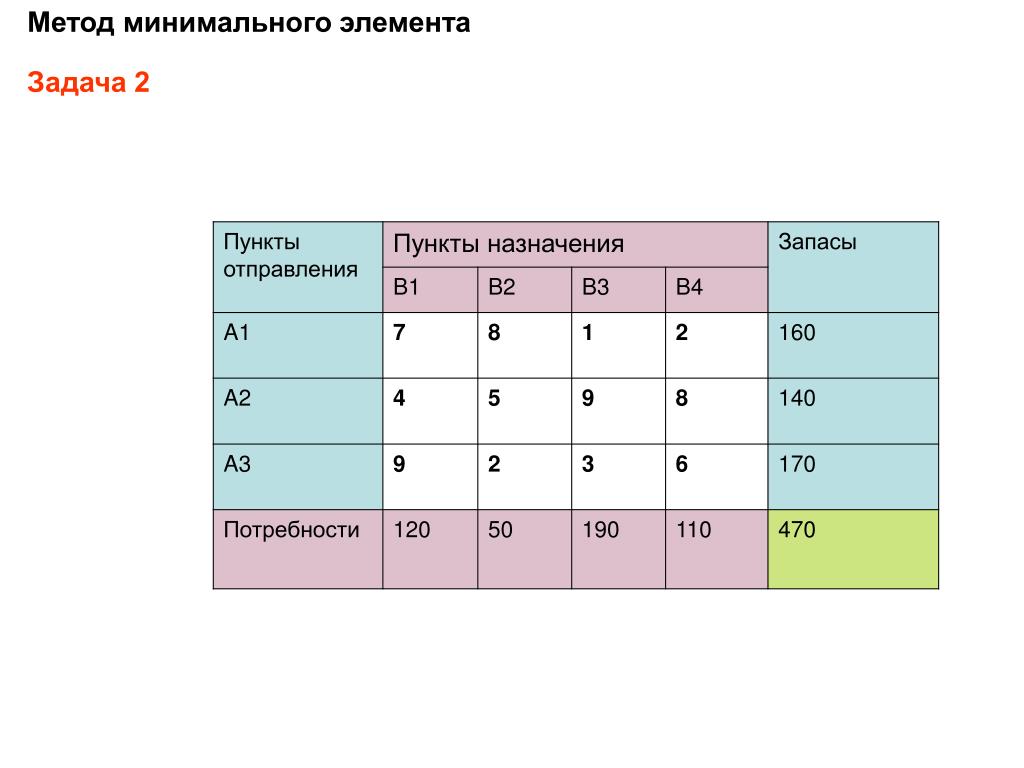
Требуется построить начальный опорный план транспортной задачи методом минимального элемента.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа.
Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Условие баланса:
В нашем случае:
Вводим дополнительного поставщика , у которого имеется 2600-1800=800 единиц груза.
Составим матрицу затрат на производство и транспортировку продукции.
Построим начальный опорный план по правилу минимального элемента.
Просматривая таблицу замечаем, что наименьшие затраты соответствуют маршруту (2,4), поэтому в клетку помещаем . В этом случае 2-я строка в расчет не принимается. Просматриваем оставшиеся таблицы клетки. Наименьший тариф имеет клетка (4,3).
Далее, действуя по аналогичной схеме, получаем:
Число занятых клеток должно быть
.
В нашем случае число занятых клеток равно 7 — опорный план является невырожденным.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении оптимального плана перевозок, производится методом потенциалов .
Метод Фогеля
Сущность его состоит в следующем. В таблице по строкам и столбцам определяется разность между двумя наименьшими тарифами. Отмечается наибольшая разность рамкой. Далее в строке (столбце) с наибольшей разностью заполняется клетка с наименьшим тарифом. Строки (столбцы) с нулевым остатком груза в дальнейшем в расчет не принимаются. На каждом этапе загружается только одна клетка. Распределение груза производится, как и по выше рассмотренным правилам.
Задача 3
Ниже приведены числовые
данные транспортной задачи. Стоимость перевозки единицы продукции записана в клетках
таблицы.
Запасы указаны справа от таблиц, а потребности – снизу.
Требуется построить начальный план методом Фогеля.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи закрытая.
Воспользуемся способом Фогеля для нахождения начального опорного
плана транспортной задачи. В каждом ряду и столбце матрицы
найдем минимальный и ближайший к нему элементы
и их разность по абсолютной величине записываем в конце соответствующего ряда
справа и снизу.
Находим максимальную из этих разностей (число
29 заключено в рамку). В ряду (или столбце), соответствующем максимальной
разности, находим минимальный элемент
.
В клетку (3,5) вписываем число
С оставшейся матрицей поступаем аналогично предыдущему. Все вычисления сведены в таблицу.
Получили начальный опорный план транспортной задачи методом Фогеля.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении оптимального плана перевозок, производится методом потенциалов .
Метод двойного предпочтения
Суть метода двойного
предпочтения отражена в его названии. В таблице найдем наименьшие элементы в
каждой строке и в каждом столбце. Поставим в соответствующую клетку знак *.
Если встречаются такие клетки, отмеченные двумя знаками, то их заполняем в
первую очередь.
Распределение груза производится, как и по выше рассмотренным
правилам.
Задача 4
Составить план перевозки зерна из районов на пять элеваторов (запасы районов и мощности элеваторов приведены) с минимальными издержками за перевозку. Затраты на перевозку 1 ц заданы.
Начальный план перевозок составить по правилу двойного предпочтения.
Решение
Стандартная транспортная задача разрешима только в том случае, когда выполняется условие баланса:
В нашем случае:
Модель транспортной задачи закрытая.
Заполняем таблицу по правилу двойного предпочтения.
Сначала в каждой строке находим клетку с минимальным тарифом. Если таких клеток несколько (одинаковые значения) то выбираем их все. В выбранных ячейках ставим отметку *.
Затем выполняем те же самые действия, только на тот раз по столбцам. То
есть в каждом столбце тоже находим клетку (клетки) с минимальным тарифом и
ставим в ней отметку – *.
Начинаем заполнять транспортную таблицу. В первую очередь заполняем ячейки с двумя звездочками (если их несколько, выбираем ту в которой меньший тариф). Далее заполняем клетки с одной звездочкой. Если остались нераспределенные запасы и неудовлетворенные потребности – заполняем оставшиеся клетки без звездочек.
Найдем стоимость перевозок опорного плана:
Дальнейшее решение транспортной задачи, заключающееся в нахождении оптимального плана перевозок, производится методом потенциалов .
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка.
Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Для помощи во время экзамена/зачета в онлайн режиме необходимо договариваться заранее.
Метод наименьшей стоимости | метод решения транспортной задачи | Транспортная модель
Метод наименьших затрат является одним из методов получения допустимого решения транспортной задачи. Мы уже понимаем метод северо-западного угла | метод решения транспортной задачи | Транспортная модель для транспортной задачи, чтобы получить возможное решение.
Чтобы понять метод наименьших затрат, мы пройдемся по цифрам, представленным ниже (тот же номер, который мы использовали в Метод северо-западного угла | метод решения транспортной задачи | Транспортная модель) :
ЧисловойКомпания по производству мобильных телефонов имеет три филиала, расположенных в трех разных регионах, скажем, в Джайпуре, Удайпуре и Мумбаи. Компания должна доставить мобильные телефоны в три пункта назначения, например, в Канпур, Пуну и Дели.
Доступность из Джайпура, Удайпура и Мумбаи составляет 40, 60 и 70 единиц соответственно. Спрос в Канпуре, Пуне и Дели составляет 70, 40 и 60 соответственно. Стоимость перевозки указана в матрице ниже (в рублях). Используйте метод наименьших затрат, чтобы найти базовое допустимое решение (BFS).Обратите внимание, что все пояснения даны в «ГОЛУБОМ» цвете. Вы должны написать на экзамене единственное, что дано этим обычным цветом под каждым шагом (если есть), иначе вы можете напрямую решить матрицу задачи, как описано здесь.
Решение:
Шаг 1: Сбалансируйте проблему
Сбалансируйте проблему, что означает, что мы должны проверить, что если;
Σ Предложение=Σ Спрос\цвет{#32c5d4} \Sigma \text { Предложение} = \Sigma \text { Спрос} Σ Предложение=Σ Спрос
Если это так, то будем рассматривать данную задачу как сбалансированную.
Что, если он не сбалансирован?
т. е. Σ Предложение≠Σ Спрос\цвет{#32c5d4} \text {т.е. } \Sigma \text { Предложение} \not = \Sigma \text { Спрос}т.е. Σ Предложение=Σ Спрос
Если такое условие возникает, то мы должны добавить фиктивный источник или рынок; в зависимости от того, что делает проблему сбалансированной.
Вы можете посмотреть видео об этом типе числовых задач, известном как несбалансированные транспортные задачи.
→\to→ Данная транспортная задача сбалансирована.
Шаг 2: Выберите наименьшую стоимость из всей матрицы и распределите минимум спроса или предложения.
Здесь мы используем метод наименьших затрат, поэтому мы будем определять наименьшее значение ячейки во всей этой матрице.
Здесь в этой матрице у нас есть 1 (для ячейки: Джайпур-Дели) как наименьшее значение.
Итак, перемещаемся с этой ячейкой и распределяем минимум спроса или предложения, т.е. размещаем здесь 40 (поскольку значение предложения равно 40, тогда как спрос равен 60).
Проверяем первую строку, а не последнюю колонку, потому что мы выделяем 40 в ячейке для снабжения, так как это минимум.
Вычитание выделенного значения (например, 40) из соответствующего спроса и предложения.
Шаг 3: Удалите строку или столбец, предложение или спрос которых удовлетворены, и подготовьте новую матрицу
Когда мы удовлетворим спрос или предложение для этой строки или столбца соответственно, удалите эту строку или столбец и подготовьте новую матрицу, как показано ниже:
Шаг 4: Повторяйте процедуру до тех пор, пока все распределения не превысят
Повторите ту же процедуру распределения наименьшего значения в новой сгенерированной матрице и проверьте спрос или предложение на основе наименьшего значения (спроса или предложения), как показано ниже, пока не закончатся все распределения.
Вы можете найти галстук в выборе ячейки здесь в приведенной выше матрице, поскольку у нас есть минимальное значение ячейки 3 для двух ячеек в приведенной выше матрице.
Итак, всякий раз, когда вы сталкиваетесь с такой ситуацией при оценке матрицы методом наименьших затрат, у вас будет несколько решений проблемы, называемых альтернативными решениями.
Альтернативное решение этой проблемы приведено в конце этой заметки-блога. В нем мы будем выбирать пересекающуюся ячейку Удайпур — Канпур.
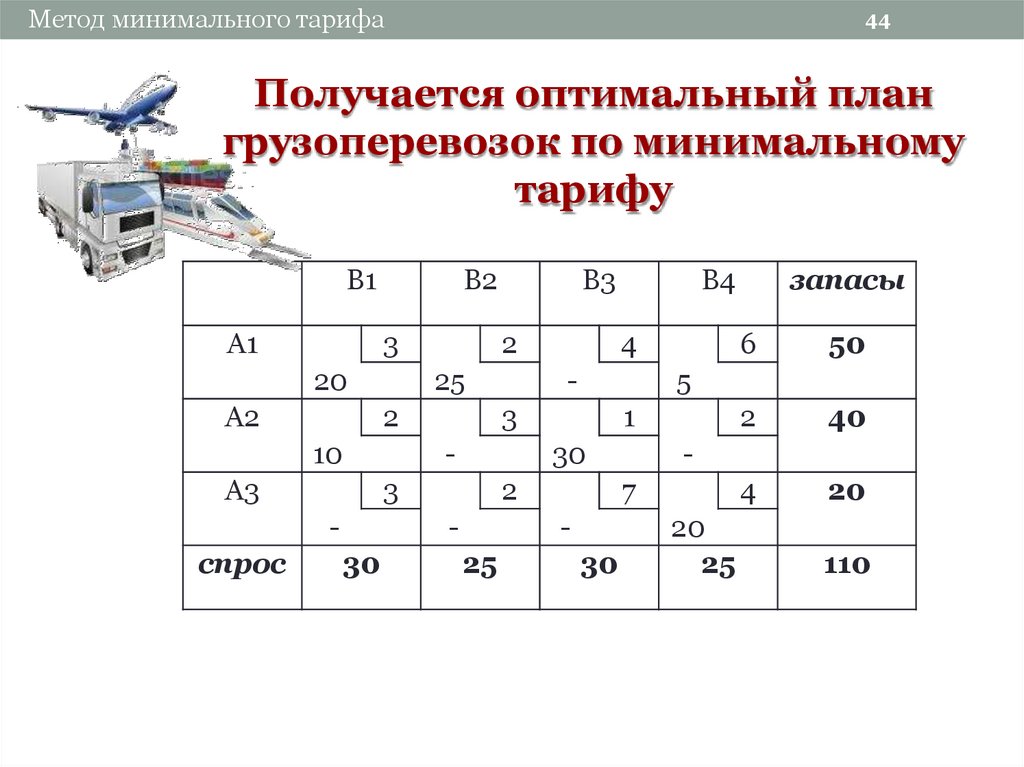
Шаг 5: После завершения всех распределений запишите распределения и рассчитайте транспортные расходы
После завершения всех распределений подготовьте таблицу со всеми отмеченными распределениями и рассчитайте транспортные расходы следующим образом:
→ Транспортные расходы = (1 × 40) + (3 × 40) + (3 × 20) + (6 × 30) + (2 × 40) = 480 рупий \ begin {align} \to \\text {Транспортные расходы} &= (1 \times 40) + (3 \times 40) + (3 \times 20) + (6 \times 30) + (2 \times 40) \\ &= \text {рупий} 480 \end{align}→ Транспортные расходы=(1×40)+(3×40)+(3×20)+(6×30)+(2×40)=480 рупий
Альтернативное решение
As у нас есть связь в выборе минимального значения на этом шаге.
Мы можем выбрать любую из этих ячеек, как упоминалось ранее.
Мы уже видели выше решение, выбрав минимальное значение в ячейке пересечения Удайпур-Дели, теперь мы выберем другое и продолжим распределение с использованием метода наименьших затрат следующим образом:
Итак, у нас будет альтернативное решение, как указано выше, и альтернативная стоимость транспортировки следующим образом:
→ Транспортные стоимости=(1×40)+(3×60)+(6×10)+(2×40) +(8×20)=520 рупий\begin{выровнено} \to \\text {Транспортные расходы} &= (1 \times 40) + (3 \times 60) + (6 \times 10) + (2 \times 40) + (8 \times 20) \\ &= \text {рупий} 520 \end{align}→ Транспортные стоимости=(1×40)+(3×60)+(6×10)+(2×40)+(8×20)=520 рупий
→\to→ Таким образом, мы имеем оптимальную стоимость перевозки в размере рупий. 480.
Найти решение того же числа с помощью :
Метод приближения Фогеля (VAM)
Метод северо-западного угла | метод решения транспортной задачи | Транспортная модель
[Решено] .
1. Найдите решение с минимальной стоимостью для следующего…Вопрос задан BrigadierComputerSnake96 на сайте coursehero.com
Текст транскрипции изображения
1. Найдите решение с минимальной стоимостью для следующей транспортной задачи, которая имеет стоимость структура как: В / из п Вопрос р Доступность А 16 19 12 14 Б 22 13 19 16 С 14 28 18 12 Требование 10 15 17 2. Кратко опишите симплекс-метод, целевое программирование и целочисленное программирование….
BusinessBusiness — Другое
Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam
sec
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestisectetur adipiscing e Разблокировать доступ к этому и более
10 000 пошаговых объяснений
Есть учетная запись? Войти
sectetur adipiscing elit.
Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, c
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing eli
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna.
Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet, consectetur adipiscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet.
sectetur adipiscing elit. Nam lacinia pulvinar tortor nec
| sectetu | sec | sec | sec | sectetur adi |
| сек | сек | сек | сек< /p> | сек |
| сек | сек | сек | сек | сек |
| сек | сек | сек | сек< /p> | секта |
| секта adip | секта < /td> | раздел | se |
|
sectetur adipiscing elit.