Уравнения. 5 класс — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Уравнения
Выполнила: АрзамасАнастасия
2. 5 класс
Задачи на уравнение – 1 часУметь: анализировать условие задачи; иллюстрировать
схематически рисунками условие задачи; решать задачи на
уравнивание различными способами.
3. 6 класс. Выражения, формулы, уравнения
Решение уравнений – 1 часЗнать понятие: уравнение, решение уравнения, корень
уравнения.
Уметь решать уравнения.Решение задач уравнением – 1 час
Знать понятие: уравнение, решение уравнения, корень
уравнения. Уметь решать задачи уравнением.
4. 7 класс. Уравнения
Алгебраический способ решения задач. Составлениеуравнений – 1 час
Знать понятие: уравнение. Уметь составлять уравнения.
Корни уравнения. Определение корня уравнения – 1 час
Знать понятие: корня уравнения. Уметь определять корни
уравнения.
Корни уравнения. Проверка корней – 1 час
Знать понятие: корня уравнения. Уметь определять корни
уравнения, делать проверку корней.
Решение уравнения. Правила преобразования уравнений –
1 час
Знать: простейшие правила преобразования уравнений.
Уметь решать простейшие уравнения.
Решение уравнений. Перенос слагаемых – 1 час
Знать: правило переноса слагаемых в уравнении. Уметь
решать уравнения.
Решение уравнений. Умножение на число – 1 час
Знать: правило умножения на число в уравнении. Уметь
решать уравнения.
Решение уравнений с дробной чертой – 1 час
Уметь: решать уравнения, содержащих дробную черту.
Решение уравнений. Отработка навыков – 1 час
Уметь: решать различные уравнения.
Решение задач с помощью уравнений. Анализ текста
задачи – 1 час
Уметь: анализировать текст задачи, решать простейшие
задачи с помощью уравнений.
Решение задач с помощью уравнений. Практические
правила составления уравнений к задаче – 1 час
Знать: практические правила составления уравнений к
задаче.Уметь решать задачи с помощью уравнений
Решение задач с помощью уравнений. Задачи на части,
соотношения – 1 час
Уметь: решать задачи на части и на соотношения с
помощью уравнений
Решение задач с помощью уравнений. Задачи на движение
– 1 час
Уметь: решать задачи на движение с помощью уравнени
Решение задач с помощью уравнений. Различные типы
задач – 1 час
Уметь: решать различные типы задач с помощью
уравнений
Какие уравнения называют квадратными – 2 часа
Формула корней квадратного уравнения – 4 часа
Знать: определение квадратного уравнения; что первый
коэффициент не может быть равен нулю.
Уметь: записать квадратное уравнение в общем виде;
неприведенное квадратное уравнение преобразовать в
приведенное; свободно владеть терминологией
Вторая формула корней квадратного уравнения – 2 часа
Знать: формулу корней квадратного уравнения.
Уметь: решать квадратные уравнения по формуле; решать
уравнения высших степеней заменой переменной
Решение задач – 3 часа
Уметь: составить уравнение по условию задачи; соотнести
найденные корни с условием задачи
Неполные квадратные уравнения – 3 часа
Знать: термин «неполное квадратное уравнение»; приемы
решения неполных квадратных уравнений.
Уметь: распознавать и решать неполные квадратные
уравнения
Теорема Виета – 2 часа
Знать: формулы Виета. Уметь применять теорему Виета
для решения упражнений
Разложение квадратного трехчлена на множители – 3 часа
Знать: что если квадратный трехчлен имеет корни, то его
можно разложить на множители; что если квадратный
трехчлен не имеет корней, то разложить его на множители
нельзя
12.
8 класс. Системы уравненийЛинейное уравнение с двумя переменными и его график – 3 часаУметь: выражать из линейного уравнения одну переменную через
другую; находить пары чисел, являющиеся решением уравнения;
строить график заданного линейного уравнения
Уравнение прямой вида у = кх +l – 3 часа
Системы уравнений. Решение систем способом сложения – 3 часа
Знать/понимать: уравнение прямой; алгоритм построения прямой.
Уметь: перейти от уравнения вида ах + by = с к уравнению вида y =
kx + l, указать коэффициенты к,1; схематически показать
положение прямой, заданной уравнением указанного вида; решать
системы способом сложения
Решение систем способом подстановки – 3 часа
Знать/понимать: если графики имеют общие точки, то
система имеет решения; если у графиков нет общих точек,
то система решений не имеет; алгоритм решения систем
уравнений.
Уметь: решать системы способом подстановки
Решение задач с помощью систем уравнений – 4 часа
Знать/понимать: значимость и полезность математического
аппарата.
Уметь: ввести переменные; перевести условие на
математический язык; решить систему или уравнение;
соотнести полученный результат с условием задачи
Задачи на координатной плоскости – 2 часа
Знать: геометрический смысл коэффициентов; условие
параллельности прямых.
Уметь: свободно решать системы линейных уравнений
15. 9 класс. Уравнения и системы уравнений
Рациональные выражения – 4 часаЦелые уравнения – 2 часа
Знать/понимать: смысл понятия «целые выражения» и
«целые уравнения»
Уметь: решать целые уравнения; применять полученные
знания при выполнении действий с целыми выражениями
и уравнениями
Дробные уравнения – 4 часа
Знать/понимать: смысл понятия «дробные уравнения»,
способы преобразования и решения дробных уравнений,
Уметь: выделять из ряда уравнений дробные,
преобразовывать их; решать дробные уравнения;
применять полученные знания при выполнении действий с
дробными выражениями и уравнениями
Знать/понимать: как составлять математическую модель
текстовой задачи и решать её
Уметь: составлять и решать текстовые задачи
Решение задач – 4 часа
Системы уравнений с двумя переменными – 4 часа
Знать/понимать: смысл понятия «системы уравнений с
двумя переменными», способы решения этих систем
Уметь: решать системы уравнений с двумя переменными
разными способами
Решение задач – 2 часа
Графическое исследование уравнений – 4 часа
Знать: способы исследования уравнения с помощью
графиков
Уметь: находить точки пересечения графиков различных
функций и исследовать уравнения с помощью графиков
Знать: основные способы решения задач и систем
уравнений
Уметь: применять полученные знания при решении задач и
систем уравнений
English Русский Правила
Конспект урока по математике по теме «Уравнение» 6 класс | План-конспект урока по алгебре по теме:
Урок в 6 классе по теме: «Решение уравнений и задач с помощью составления уравнений»
Тип: урок-рефлексия.
Цели урока: Обобщить и систематизировать изученный материал и знания учащихся по теме: «Уравнения».
Обучающие цели:
Учащиеся умеют решать простейшие уравнения на основе зависимости между компонентами арифметических действий (кроме двух), используют свойства (перенос слагаемых из одной части уравнения в другую, знают и применяют распределительное свойство умножения, деление обеих частей уравнения на число отличное от нуля, свойство модуля и т.д.)
Продолжить работу по формированию умений учащихся составлять аналитическую модель уравнения по условию задачи (схеме), организовать деятельность учащихся по отработке и закреплению умений решать уравнения и задачи.
Продолжить работу по совершенствованию вычислительных навыков учащихся.
Развивающие цели: продолжить работу по развитию логического мышления учащихся (в процессе решения задач), умений моделировать жизненные ситуации, выделять в условии задачи данные, строить логическую цепочку рассуждений, сопоставлять полученные результаты с условием.
Воспитательные цели: продолжить работу по формированию навыков культуры математической записи и речи, формированию положительной мотивации, воспитанию чувства товарищества, взаимопомощи, умений слышать других, участвовать в диалоге, воспитывать качества личности, отвечающие требованиям информационного общества.
Оборудование: Компьютер, презентация, плакаты с высказываниями известных людей, флажки, листы настроения.
Ход урока.
- Организационный момент:
«Посмотрите всё ль в порядке
Ручка, книжка и тетрадка
Прозвенел уже звонок, начинается урок»
Выбираем лист настроения с физиономией, соответствующей вашему настроению на начало урока, а потом в конце урока то же самое действие и
на доске прикрепим, чтобы увидеть изменения. ( Мотив) Итак ребята тема урока: (дети сами называют тему: «Решение уравнений и задач на составление уравнений»
Напутствие детям: У всех есть свои проблемы и каждый пытается их решать.
Я желаю вам успеха, надеюсь на вас, всё у нас получится и, в дальнейшем изучении математики, вам легче будет справляться с любыми заданиями. Флажками будете сигналы подавать о выполнении заданий и в конце урока расставите их на координатном луче в соответствии с цветом и количеством полученных знаний.
Записываем число (дата). Тема урока вам знакома ещё из начальной школы.
Мы сейчас её определим вместе с вами
2)Актуализация опорных знаний учащихся: Блиц-опрос (слайд 2)
На экране равенства: 1) Х-2/12 =3/12; 2) 3Х = 18,6 3) Х : 4 = 2,5
4) У+ 4,7 = 17,7 5) 15/16 – У =3/16 6) 125:/ Х/ = 5. Как называют эти равенства?
Что значит решить уравнение?
Что необходимо знать, чтобы найти корни уравнения?
Стихотворение:
«Когда уравненье решаешь дружок,
Ты должен найти его корень милок.
Значение буквы проверить несложно,
Поставь в уравнение его осторожно.
Коль верное равенство выйдет у вас,
То корнем значенье зовите тотчас».
Найдите корни данных уравнений.
Шарада: «Мой первый слог-предлог
А во втором живём мы летом.
А целое от вас и нас давно уж ждёт ответа»
2) Итак ребята тема урока: (дети сами называют тему: «Решение уравнений и задач на составление уравнений»
Вы недавно готовили презентации по разным темам и у одного учащегося была об Аль- Хорезми, учёном, из Египта (аль джебр, алгебра взяла своё название), а греки от египтян унаследовали знания и ещё в третьем веке до н.э. Диофант добился больших результатов в математике и не только. О нём даже писали: «Он уйму всяких разрешил проблем. И запахи предсказывал и ливни. Поистине его познанья дивны»
Презентация.
- Задача на концентрацию внимания! « Секретная сказка» (слайд 5), зашифрованная в числах.
- Графический диктант, слайд7 ( 5 мин.) : Верно ли равенство Х-3,2=5,2, при Х=10 ?
Можно ли делить левую и правую части уравнения на число?
Верно ли раскрыты скобки в уравнении 2 (Х-1,6)=2Х-3,2?
Имеет ли уравнение /Х/+ 8,9=5,9 корни?
Взаимопроверка.
Ключ для проверки:
- Коллективная работа (слайд8):)
Задача на составление аналитической модели к задаче по условию: Атлетика Х
Гимнастика Х+8
Борьба Х-3
Всего: 41
6) Задание: Составить задачу по схеме (слайд9): Костя — п
Игорь – ( п-8)
Ната – ( п+15), если Коля и Игорь вместе столько же как Ната. Какое из чисел 10 или 23 является корнем уравнения?
7)Физкультминутка (слайд10), упражнения для глаз, пальчиков рук, проводит ученик.
8)Задача про «Ледокол» (слайд 11) самостоятельно разбираем условие и даём 8 минут, в это время 3 учащихся решают у доски:
9) 9 1/4 –Х = 2 7/10 -Х=6 2/3 + (-6 1/5) /Х-5/- 3= 12
10)Далее проверка у доски.
11)Оценки (комментированные).
12) Рефлексия:
Ребята, что вам понравилось сегодня на уроке больше всего?
Как вы думаете, можно на шаг вперёд продвинуть себя в этой теме или нет?
Какие затруднения вы испытали?
Всё ли вы решаете самостоятельно?
Можете ли вы помочь другу, объяснить ему эту тему?
Поставьте флажки на единичном отрезке координатного луча так, чтобы можно это было наглядно представить. Спасибо! Д/задание (индивидуально).
Решение одношаговых уравнений с дробями Выражения Уравнения 6 класс – Otosection
Поделиться на Facebook Поделиться на Twitter
и для некоторых из них 0-6-битные являются нормальными, некоторые из которых 1-2 получают то, что говорят, становятся более волосатыми, поэтому Let39s let39s they39re в равных 1-2 имеют уравнения, собирающиеся до маленьких десятичных знаков c Решение уравнений в один шаг с Дроби Выражения Уравнения 6 9 класс0009
А вот и список изображений Решение одношаговых уравнений с дробями Выражения Уравнения 6 класс самое лучшее После простого размещения символов мы можем создать одну статью в столько полностью удобных для читателей версий, сколько вам нравится, чтобы люди рассказывали в дополнение к показу Создание историй это очень весело для вашего аккаунта.
Решение одношаговых уравнений с десятичными дробями
Давайте немного попрактикуемся в решении некоторых уравнений, и мы собираемся составить некоторые уравнения, которые немного сложнее, чем обычно, в них будут десятичные дроби и дроби. Итак, скажем, у меня было уравнение, умноженное на 1,2, с равно 0,6. так что мне нужно умножить на 1,2, чтобы получить 0,6?. Уравнения умножения в один шаг: моделирование дробных коэффициентов с помощью уравнений в один шаг Практика уравнений умножения и деления в один шаг: дроби и десятичные дроби получают 5 из 7 вопросов для повышения уровня! практика дополнительная практика: уравнения учатся находить ошибки в один шаг уравнения находить ошибки в один шаг уравнения викторина 1.
6-й класс Уравнения с дробями в один шаг Рабочий лист
Рабочие листы с одношаговыми уравнениями содержат эксклюзивные страницы для решения уравнений, включающих дроби, целые числа и десятичные дроби.
выполнять основные арифметические операции сложения, вычитания, умножения и деления для решения уравнений. упражнения по применению уравнений в реальной жизни доступны здесь для передачи практических знаний. ©s p2k0p1 e2r vkourtpab hsio7f7tow3atrbe4 il7lzct.a a ta 7l sl o cr7i7gwhrt csz qrjeesgegrkvce td z.e r gm qazd ceq 0wgi6t1h 7 iixnvf ditnmi2tbe g 8pgrre1 vakkl software by grvaskul Раздел 2. Большая идея 1 – читать и писать целые числа и десятичные дроби. 2 1: десятичные дроби равными делениями. 2 2: тысячи до тысячных. 2 3: приравнять и сравнить тысячные. большая идея 2 – сложение и вычитание. 2 4: сложение и вычитание десятичных знаков. 2 5: добавить целые числа и десятичные дроби. 2 6: вычитание целых чисел и десятичных дробей.
Линейные уравнения с дробями Math Tutorvista Дроби
А вот и список изображений Решение одношаговых уравнений с дробями Выражения Уравнения 6 класс самое лучшее После простого размещения символов мы можем создать одну статью в любом количестве полностью удобных для читателя версий, которые люди рассказывают в дополнение к показу Создание историй много удовольствия на ваш счет.
Мы получаем удивительно много Ниццы около Решение одношаговых уравнений с дробями Выражения Уравнения 6 класс интересное фото, но многие из нас представляют только то, что люди считают лучшим.
Решение одношаговых уравнений с дробями | Выражения и уравнения | 6 класс
mathissimple #grade6 #выражения #уравнения любят изучать больше математических задач от средней школы до алгебры по математике mathissimple #grade6 #выражения #уравнения решают одношаговые уравнения с десятичными знаками и дробями | Курсы выражений в академии хана всегда на 100% бесплатны. начните практиковаться — и сохраняйте свой прогресс — прямо сейчас: научитесь решать одношаговые линейные уравнения. под одним шагом мы подразумеваем уравнения, для решения которых требуется один шаг.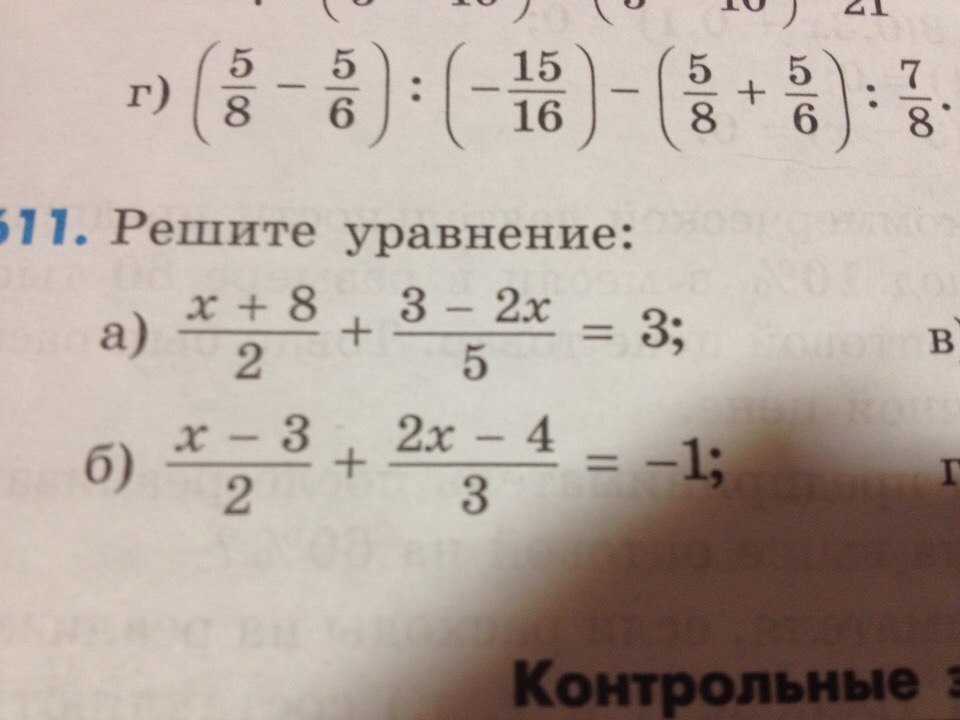
один шаг — это mathissimple #grade7 #expressions #equations решение одношаговых уравнений с дробями и десятичными знаками | выражения Это видео показывает зрителям, как решать одношаговые уравнения с дробными коэффициентами. подпишись на математику отряда мошенников продолжай в том же духе! ознакомьтесь со следующим уроком и попрактикуйтесь в том, что вы изучаете: mathissimple #grade6 #expressions #equations решение одношаговых уравнений | выражения и уравнения | 6-й класс хотел бы узнать, как решать одношаговые уравнения с мистером. Дж! нужна помощь с одношаговыми уравнениями? ты в правильном месте! научиться ли решать линейные уравнения за один шаг. под одним шагом мы подразумеваем уравнения, для решения которых требуется один шаг. один шаг — это mathissimple #grade6 #equations #алгебра одношаговые уравнения с дробными коэффициентами (часть 2) | выражения и уравнения mathissimple #grade6 #expressions #equations решение одношаговых уравнений | выражения и уравнения | 6 класс нравится учиться
Связанное изображение с решением одношаговых уравнений с уравнениями в виде дробей 6 класс
Связанное изображение с решением одношаговых уравнений с уравнениями с дробями 6 класс
Математика, 6 класс, уравнения и неравенства
CCSS.
Math.Content.6. ЕЕ.В.5
6 класс, Выражения и уравнения
Кластер: Обоснование и решение уравнений и неравенств с одной переменной
Стандарт: Понимание решения уравнения или неравенства как процесса ответа на вопрос: какие значения из заданного набора, если таковые имеются, составляют равенство или неравенство верно? Используйте подстановку, чтобы определить, делает ли данное число в указанном наборе уравнение или неравенство верным.
CCSS.Math.Content.6.EE.B.6 6 класс, Выражения и уравнения
Кластер: Обоснование и решение уравнений и неравенств с одной переменной
Стандарт: Использование переменных для представления чисел и записи выражений при решении реальных или математических задач; понимать, что переменная может представлять неизвестное число или, в зависимости от поставленной цели, любое число в указанном наборе.
CCSS.Math.Content.6.EE.B.7 6 класс, Выражения и уравнения
Кластер: Обоснование и решение уравнений и неравенств с одной переменной
Стандарт: Решение реальных и математических задач путем написания и решения уравнений формы x + p = q и px = q для случаев в котором p, q и x все неотрицательные рациональные числа.
CCSS.Math.Content.6.RP.A.3 6 класс, Соотношения и пропорциональные отношения
Кластер: понимание концепций соотношений и использование рассуждений об отношениях для решения задач
Стандарт: используйте рассуждения о соотношениях и скоростях для решения реальных и математических задач, например, рассуждая о таблицах эквивалентных соотношений, ленточных диаграммах, линейных диаграммах с двойными числами или уравнениях.
CCSS.Math.Practice.MP.1 Математические практики
Кластер: Математические практики
Стандарт: Разбираться в проблемах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении.
CCSS.Math.Practice.MP.2 Математические практики
Кластер: Математические практики
Стандарт: Рассуждать абстрактно и количественно.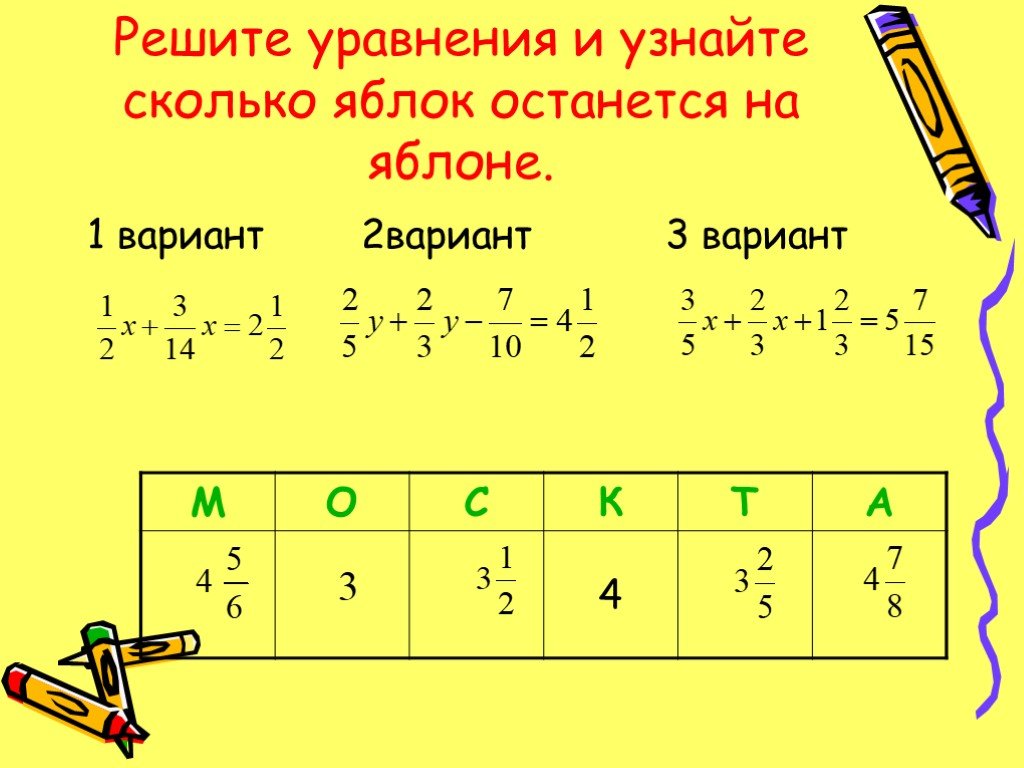
Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP.3 Математические практики
Кластер: Математические практики
Стандарт: Придумывать жизнеспособные аргументы и критиковать рассуждения других.
Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов.
Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP.4 Математические практики
Кластер: Математические практики
Стандарт: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой.
Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
CCSS.Math.Practice.MP.5 Математические практики
Кластер: Математические практики
Стандарт: Стратегическое использование соответствующих инструментов. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии.
Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP.6 Математические практики
Кластер: Математические практики
Стандарт: Следите за точностью. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
CCSS.Math.Practice.MP.7 Математические практики
Кластер: Математические практики
Стандарт: Ищите и используйте структуру.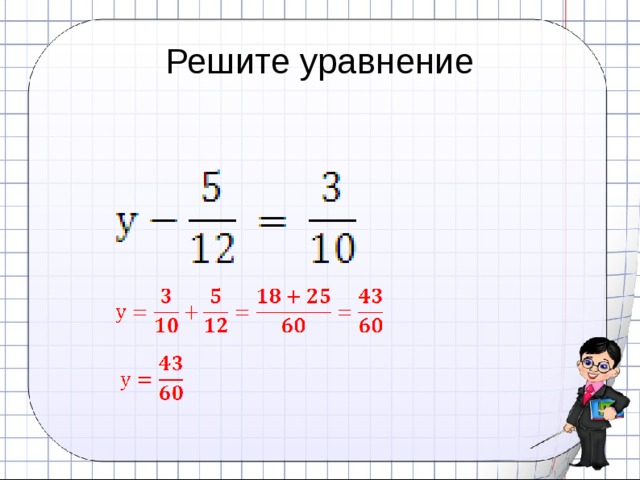
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
MCCRS.Math.Content.6.RP.A.3 6 класс
Область обучения: Отношения и отношения пропорциональности
Стандарт: Понимание концепций отношений и использование рассуждений об отношениях для решения задач
Индикатор: Использование рассуждений об отношениях и пропорциях для решения реальных и математических задач, например, путем рассуждений о таблицах эквивалентные отношения, ленточные диаграммы, линейные диаграммы с двойным числом или уравнения.
MCCRS.Math.Content.6.EE.B.5 6 класс
Область обучения: выражения и уравнения
Стандарт: рассуждать и решать уравнения и неравенства с одной переменной
Индикатор: понимать решение уравнения или неравенства как процесс ответа на вопрос: какие значения из заданного набора, если любой, сделать уравнение или неравенство верным? Используйте подстановку, чтобы определить, делает ли данное число в указанном наборе уравнение или неравенство верным.
MCCRS.Math.Content.6.EE.B.6 6 класс
Область обучения: Выражения и уравнения
Стандарт: Обоснование и решение уравнений и неравенств с одной переменной
Индикатор: Использование переменных для представления чисел и записи выражений при решении реальных или математических задач; понимать, что переменная может представлять неизвестное число или, в зависимости от поставленной цели, любое число в указанном наборе.
MCCRS.Math.Content.6.EE.B.7 6 класс
Область обучения: Выражения и уравнения
Стандарт: Обоснование и решение уравнений и неравенств с одной переменной
Индикатор: Решение реальных и математических задач путем написания и решения уравнений вида x + p = q и px = q для случаев, когда p, q и x все неотрицательные рациональные числа.
MCCRS.Math.Practice.MP.1 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Разберитесь в проблемах и настойчиво решайте их.
Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему.
Математически подкованные учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
MCCRS.Math.Practice.MP.2 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов.
Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
MCCRS.Math.Practice.MP.3 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Придумывать обоснованные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других.
Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
MCCRS.Math.Practice.MP.4 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Модель с математикой.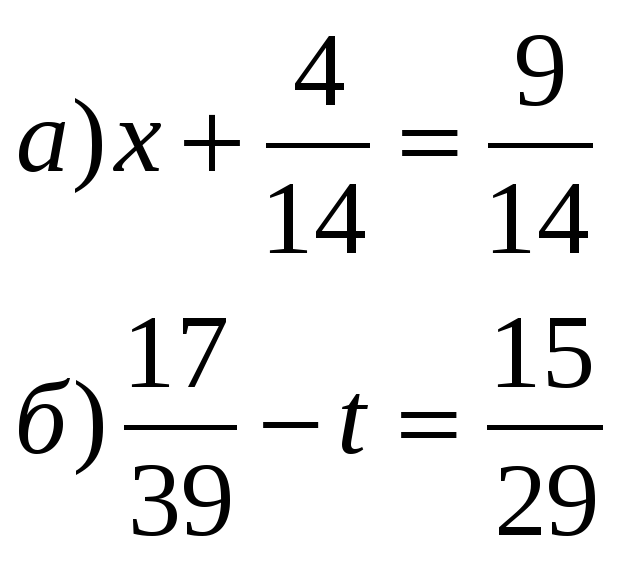
Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы.
Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
MCCRS.Math.Practice.MP.5 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Стратегически используйте соответствующие инструменты. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения.
Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
MCCRS.Math.Practice.MP.6 Классы K-12
Область обучения: математические практики
Стандарт: математические практики
Показатель: внимание к точности. Математически подкованные ученики стараются точно общаться с другими.
Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. В начальных классах учащиеся дают тщательно сформулированные объяснения друг другу. К тому времени, когда они переходят в старшие классы, они уже научились анализировать утверждения и явно использовать определения.
MCCRS.Math.Practice.MP.7 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Ищите и используйте структуру. Математически подкованные учащиеся внимательно смотрят, чтобы различить закономерность или структуру. Например, учащиеся младшего возраста могут заметить, что три и еще семь — это то же самое, что семь и еще три, или они могут отсортировать набор фигур по количеству сторон у фигур.
2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
MCCRS.Math.Practice.MP.8 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Ищите и выражайте регулярность в повторяющихся рассуждениях. Подкованные в математике учащиеся замечают, повторяются ли вычисления, и ищут как общие методы, так и упрощения. Учащиеся старших классов могут заметить, что при делении 25 на 11 они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь. Уделяя внимание вычислению наклона, постоянно проверяя, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, учащиеся средней школы могут абстрагироваться от уравнения (y — 2)/(x -1) = 3. Заметив регулярность в том, как члены сокращаются при расширении (x — 1) (x + 1), (x — 1) (x ^ 2 + x + 1) и (x — 1) (x ^ 3 + x ^ 2 + x + 1) может привести их к общей формуле суммы геометрического ряда.