Решение уравнений графически: Графическое решение уравнений — урок. Алгебра, 7 класс.

Вся элементарная математика — Средняя математическая интернет-школа

Графическое решение уравнений

Приближённое решение уравнений.

Графическое решение уравнений с одним неизвестным.

Графическое решение систем уравнений с двумя неизвестными.

Графическое представление функций позволяет приближённо решить любое уравнение с одним неизвестным и систему двух уравнений с двумя неизвестными. Чтобы решить систему двух уравнений с двумя неизвестными x и y , мы рассматриваем каждое из уравнений как функциональную зависимость между переменными x и y и строим графики этих двух функций.

Координаты точек пересечения этих графиков дают нам искомые значения неизвестных x и y ( т. e . решение этой системы уравнений ).

В соответствии с графиками координаты точки пересечения

K приближённо равны: x = 1.25, y = 2.5.  Точное решение

этой системы уравнений:

После построения графиков находим абсциссы точек

пересечения A и B : x ₁ » 2.25 , x ₂ » -1.1 .

Точные значения

корней этого уравнения:

Относительная погрешность графического решения в этом

примере  ~3.5 %.

Чтобы решить графически уравнение с одним неизвестным, необходимо перенести все его члены в одну часть, т. e . привести к виду:

f ( x ) = 0 ,

и построить график функции y = f ( x ) . Абсциссы точек пересечения графика с осью Х будут корнями этого уравнения ( нулями этой функции ).

По этому графику находим нули функции: x

₁ » 2.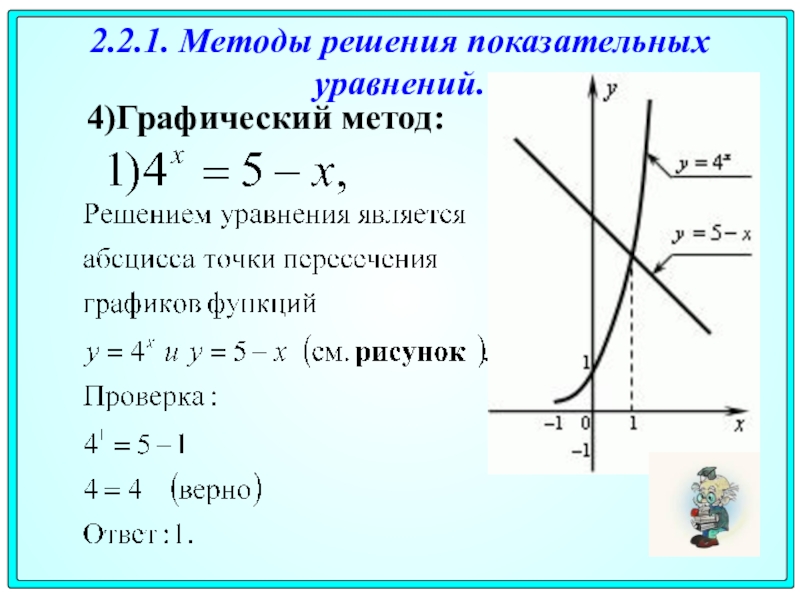 25 , x ₂ » -1.1 .

Назад

Графический метод решения уравнений, содержащих переменную под знаком абсолютной величины — Студопедия

Поделись с друзьями: 

Одним из путей решения уравнений, содержащих модуль, является графический метод.

Суть метода состоит в следующем. Решить уравнение – следовательно, найти все значения x, для которых значения функций равны, то есть найти абсциссы всех точек пересечения графиков этих функций. Если же графики не имеют общих точек, то уравнение не имеет корней.

Данный метод, реже других применяют для решения уравнений, содержащих модуль, так как он занимает достаточно много времени, не всегда рационален, результаты, полученные при построении графиков, не всегда являются точными. Кроме того, графическим методом можно решать уравнения с модулем любого вида, однако практическая реализация метода иногда бывает довольно сложной.

Следует также отметить, что точное построение графиков функций практически невозможно, поэтому решение, найденное графическим способом, требует проверки.

Проиллюстрируем применение графического метода для решения уравнений, содержащих переменную под знаком абсолютной величины.

Пример. Решим уравнение:

Решение. Построим графики двух функций

Для построения графика функции , построим график вспомогательной функции – это прямая, пересекающая ось в точке (2; 0), а ось в точке , затем часть прямой, лежащую ниже оси зеркально отразить в оси .

Графиком функции является прямая, параллельная оси и проходящая через точку (0; 3) на оси .

Графики функций представлены на рисунке 25.

Рис.25

Из рисунка 25 видно, что графики имеют две общие точки. Координаты одной точки: Координаты другой:

Следовательно, исходное уравнение имеет два решения: Как отмечалось выше, при таком методе значения корней уравнения определяются приблизительно, и только проверка позволит доказать, что найденные значения действительно являются корнями исходного уравнения.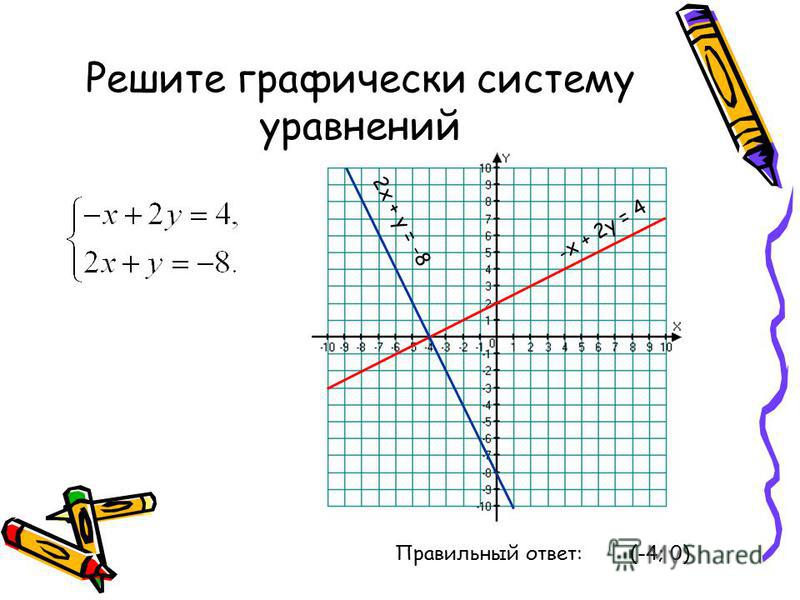 При подстановке в уравнение получаем, соответственно, два верных числовых равенства.

Ответ. .

Пример. Решим уравнение:

Решение. Построим графики функций и

Для построения графика функции построим график вспомогательной функции График функции пересекает ось в точках с абсциссами ось в точке Для построения графика функции часть графика вспомогательной функции , которая расположена ниже оси симметрично отразим относительно данной оси вверх (Рис. 26)

Построим график функции с помощью преобразований графика элементарной функции

Построим график вспомогательной функции затем симметричным отражением части графика вспомогательной функции которая расположена ниже оси , относительно данной оси вверх.

Строим график функции симметричным отражением графика вспомогательной функции относительно оси .

Строим график функции сдвигом графика вспомогательной функции , как жесткого тела на четыре единичных отрезка вправо.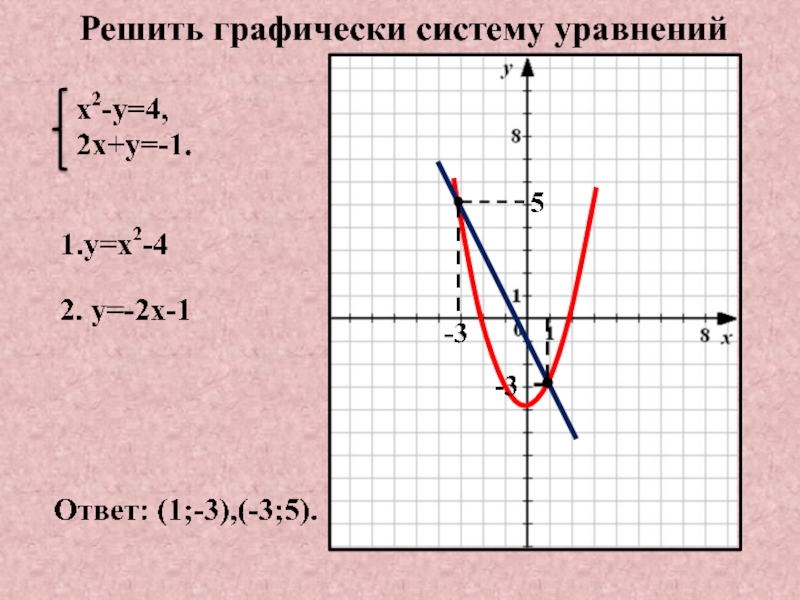

Строим график функции сдвигом графика вспомогательной функции , как жесткого тела на один единичный отрезок вверх. График функции представлен на рисунке 26.

Графики функций и пересекаются в одной точке Проверка показывает, что – корень исходного уравнения.

Рис.26

Ответ.

Заметим, что при графическом методе решения не всегда удается найти точное значение корня, то применение данного метода бывает особенно эффективно, если требуется найти не сами корни, а определить их количество.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Графическое решение системы линейных уравнений

Линейное уравнение представляет собой прямую линию на графике. Если два линейных уравнения, прямые прямые пересекаются друг с другом в точке, они называются системой линейных уравнений . Точка пересечения – общая решение этих линейных уравнений и, следовательно, является решением системы линейных уравнений.

**********************

10 математических задач  официально объявляет о выпуске  Quick Math Solver , приложение Android APP в Google Play Store  для учащихся со всего мира.

**********************

Посмотрите на пример двух линейных уравнений x + y = 7 и x – y = 3, пересекающихся в точке (5, 2), так что они представляют собой систему линейных уравнений, и решение (5, 2).

В то время как грабительски решая систему линейных уравнений , мы находим несколько пар решений для каждого из двух заданных линейных уравнений в двух отдельных таблицах. Пара решений (точек) каждого уравнения нанесена на график и соединены прямой линией. координаты точки пересечения этих двух прямых являются решением заданных одновременных уравнений.

Шаги для графического решения системы линейных уравнений:

Шаг 1 : Возьмите первое уравнение и приравнять его для одной переменной x или y через другую переменную и найти некоторое точек (значение x и y) в таблице.

Шаг 2 : Возьмите второе уравнение и приравнять его для одной переменной x или y через другую переменную и найти некоторое точек (значение x и y) в таблице.

Шаг 3 : Нанесите точки обоих уравнения на графике и соедините линии.

Шаг 4 : Найдите точку пересечения двух прямых (значения x и y), которая является решением системы линейных уравнений.

Этот процесс из графического решения системы линейных уравнений  будет понятна на следующих отработанных примерах. Пример 1 Решите x + y = 7 и x – y = 3 графическим методом.

Решение: Здесь,

x + y = 7 ……………… (I)

x — y = 3 ………… (II)

Из уравнения (i)

        x + у = 7

или,    х = 7 – у

х	3	2
г	4	5

∴ О. О. 3

или,    x = 3 + y

х	2	4
г	-1	1

 

 

∴ Points are: (3, 4) and (2, 5)

Now, plotting the точек на графике,

Из приведенного выше графика точка пересечения (5, 2),

∴ Решение: x = 5 и y = 2

Пример 2: Решите 3x + y = 6 и x – 2y = 2 графическим методом.

Решение: Здесь,

3x + y = 6 ……………… (I)

x — 2y = 2 …………… (II)

9002 444 Из уравнения (i)

        3x + у = 6

или,    у = 6 – 3x

х	1	2
г	3	0

       

∴ О.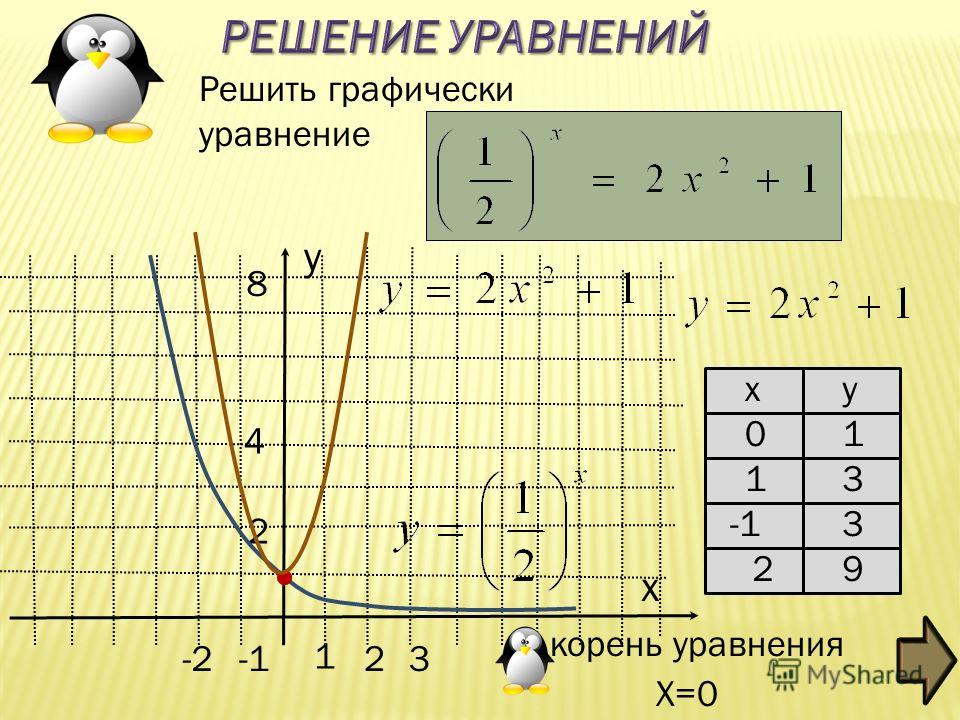 = 2 + 2 года

х	4	6
г	1	2

∴ Точки: (4, 1) и (6, 2)

Теперь построим график точек на графике,

Из графика, точка пересечения (2, 0),

∴ Решение: x = 2 и y = 0

Пример 3: Решите 3x + 2y = 4 и 5x – y = 11 графическим методом.

Решение: Здесь,

3x + 2y = 4 ……………… (I)

5x — Y = 11 …………… (II)

9002 444444444444444444444444444444444444444444444444444444444444444444444444444 Из уравнения (i)

3x + 2y = 4

или    3x = 4 – 2 года

или,    х = (4 – 2 года)/3

х	0	2
г	2	-1

∴ Точки: (0, 2) и (2, -1)

от Equation (II),

4.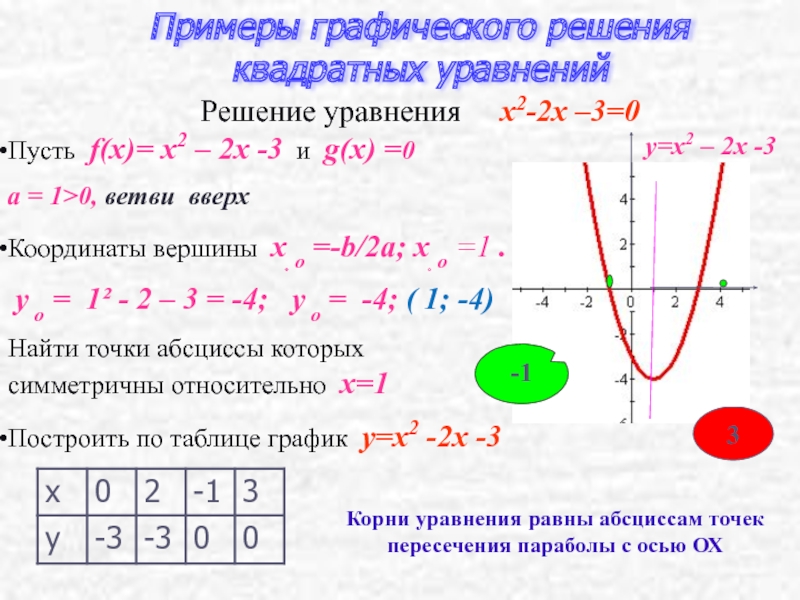 = 11

или,    5x – 11 = y

или,    y = 5x – 11

х	2	3
г	-1	4

 

       

∴ Точки: (2, -1) и (3, 4)

Теперь построим график точек на графике,

Из графика, точка пересечения (2, -1),

∴ Решение: x = 2 и y = -1

 

17 У вас есть вопросы по графическому решению системы линейных уравнений?

Вы можете задать свои вопросы или проблемы в раздел комментариев ниже.

Была ли эта статья полезна? СТАВЬТЕ НРАВИТСЯ и ПОДЕЛИТЕСЬ с друзьями…

Решение систем уравнений графическим способом | Алгебра II | Академия Хана — SchoolTube

Решение систем уравнений графическим способом | Алгебра II | Академия Хана

Из сообщества

Просмотры

• Детали

Этот плейлист состоит из 22 видеороликов о системах линейных уравнений. Учителя могут использовать эти видео для поддержки своих планов уроков и вовлечения учащихся. Каждое из этих видео охватывает определенные темы и концепции, изучаемые на уроках алгебры I. Плейлист является отличным ресурсом для студентов, чтобы просмотреть или подготовиться к тесту или выпускному экзамену. Для согласования Common Core см. ниже. К концу этого плейлиста учащиеся смогут понимать и решать задачи, связанные с линейными уравнениями.

Соответствие общим стандартам штата

CCSS.MATH.CONTENT.HSA.REI.C.6

Точное и приближенное решение систем линейных уравнений (например, с помощью графиков), уделяя особое внимание парам линейных уравнений с двумя переменными.

CCSS.MATH.CONTENT.HSA.REI.C.7

Решить простую систему, состоящую из линейного уравнения и квадратного уравнения с двумя переменными, алгебраическим и графическим способом. Например, найдите точки пересечения прямой y = -3x и окружности x2 + y2 = 3.

CCSS.MATH.CONTENT.HSA.REI.C.8

(+) Представление системы линейных уравнений в виде одного матричного уравнения с векторной переменной.

CCSS.MATH.CONTENT.HSA.REI.C.9

(+) Найти обратную матрицу, если она существует, и использовать ее для решения систем линейных уравнений (используя технологию для матриц размерности 3 × 3 или больше ).

  
  

 Попрактикуйтесь в графическом решении систем

Попрактикуйтесь в этом уроке на KhanAcademy. org прямо сейчас:
https://www.khanacademy.org/math/алгебра2/systems_eq_ineq/systems_tutorial_precalc/e/graphing_system…

Смотрите следующий урок: https://www.khanacademy.org/math/алгебра2/systems_eq_ineq/systems_tutorial_precalc/ v/king-s-cupcakes…

Пропустили предыдущий урок?
https://www.khanacademy.org/math/алгебра2/systems_eq_ineq/systems_tutorial_precalc/v/solving-the-tro…

Алгебра II в Академии Хана: Ваши исследования по алгебре 1 заложили прочный фундамент, на котором вы может исследовать линейные уравнения, неравенства и функции. В алгебре 2 мы опираемся на этот фундамент и не только расширяем наши знания по алгебре 1, но и постепенно становимся способными решать БОЛЬШИЕ вопросы вселенной. Мы снова коснемся систем уравнений, неравенств и функций… но мы также обратимся к экспоненциальным и логарифмическим функциям, логарифмам, мнимым и комплексным числам, коническим сечениям и матрицам. Не позволяйте этим громким словам запугать вас. Мы в этом путешествии с вами!

Об Академии Хана: Академия Хана предлагает практические упражнения, обучающие видео и персонализированную панель обучения, которая позволяет учащимся учиться в своем собственном темпе в классе и за его пределами.