Скорее, правильнее будет сказать извлечёт квадратный корень
Вариант № 1 извлечь квадратный корень онлайн
Как посчитать квадратный корень онлайн!?
В поле ввода вставляем то число из которого нужно вывести квадратный корень! И нажимаем извлечь!Справа от квадратного корня есть равно и после него будет показан результат извлечения квадратного корня из числа онлайн!
Вариант № 2 извлечь квадратный корень онлайн
Второй вариант извлечения корня квадратного онлайн вам потребуется наш калькулятор онлайн.Вводите число, и нажимаете корень квадратный. Вот так быстро и просто… можно извлечь квадратный корень из числа онлайн.

Написать что-нибудь…
квадратный корень онлайн , корень квадратный онлайн калькулятор , найти квадратный корень онлайн , решение квадратных корней онлайн , вычислить корень квадратный онлайн , число из квадратного корня онлайн , извлечь квадратный корень онлайн , извлечь квадратный корень онлайн калькулятор , вычислить квадратный корень онлайн калькулятор , решить корень квадратный онлайн , нахождение квадратного корня онлайн , квадратные корни класс тест онлайн , вычисление квадратного корня онлайн , найти квадратный корень из числа онлайн , корень квадратный онлайн калькулятор с решением , корень квадратный из числа онлайн калькулятор , арифметический квадратный корень онлайн , найти квадратный корень онлайн калькулятор , извлечение квадратного корня онлайн , решение уравнений с квадратным корнем онлайн , степень квадратного корня онлайн , квадратный корень онлайн калькулятор дробей , формула корень квадратный онлайн , найти корень квадратный из числа онлайн калькулятор , посчитать квадратный корень онлайн , вычислить квадратный корень из числа онлайн , извлечь квадратный корень из числа онлайн ,Решение квадратных уравнений онлайн калькулятор.
 Основные понятия и определения.
Основные понятия и определения.Квадратным уравнением называется уравнение следующего вида: ax2+bx+c=0, где a, b, с — любые действительные числа, но a не равно 0, x — неизвестная искомая переменная.
Коэффициенты a, b, c имеют соответственно названия: a— старший коэффициент (коэффициент при ), — второй коэффициент (коэффициент при ), — свободный член.
Если старший коэффициент , то квадратное уравнение является
Квадратное уравнение называется полным, если оно содержит все три слагаемых (то есть коэффициенты и не равны нулю).
Квадратное уравнение называется неполным, если оно содержит не все три слагаемых ( то есть коэффициент или , или и ).
Корнем квадратного уравнения называется такое значение переменной , при подстановке которого квадратный трехчлен обращается в ноль.
Решить квадратное уравнение – это значит найти все его корни или установить, что корней нет.
Теория для школьников.
При решении квадратного уравнения школьникам необходимо придерживаться следующей схемы:
1) Найти так называемый дискриминант по формуле:
2) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:
— Если , то квадратное уравнение корней не имеет;
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Решение квадратного уравнения также можно получить, используя следующие формулы :
1) Найти значение :
2) Найти дискриминант по формуле:
3) Найти корни квадратного уравнения или установить их отсутствие, опираясь на следующие рассуждения:
— Если , то квадратное уравнение корней не имеет;
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Теория для студентов.
При обучении в высшем учебном заведении нередко приходится сталкиваться с таким понятием, как комплексные корни уравнения.
Решение квадратных уравнений студентами – именно такой случай.
Напомним, что комплексное число имеет вид:
Где и — действительные числа, — так называемая мнимая единица. При этом носит название действительной части, а — мнимой части комплексного числа.
Мнимая единица обладает свойством:
Именно свойство мнимой единицы и будет использовано при решении квадратных уравнений.
При решении квадратного уравнения студентам необходимо придерживаться следующей схемы:
1) Найти так называемый дискриминант по формуле:
2) Найти корни квадратного уравнения, опираясь на следующие рассуждения:
— Если , то квадратное уравнение имеет два комплексных корня:
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Решение квадратного уравнения также можно получить, используя следующие формулы :
1) Найти значение :
2) Найти дискриминант по формуле:
3) Найти корни квадратного уравнения, опираясь на следующие рассуждения:
— Если , то квадратное уравнение имеет два комплексных корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет два корня, которые находятся по формулам:
— Если , то квадратное уравнение имеет один корень, который находится по формуле:
Примеры решения квадратных уравнений для школьников.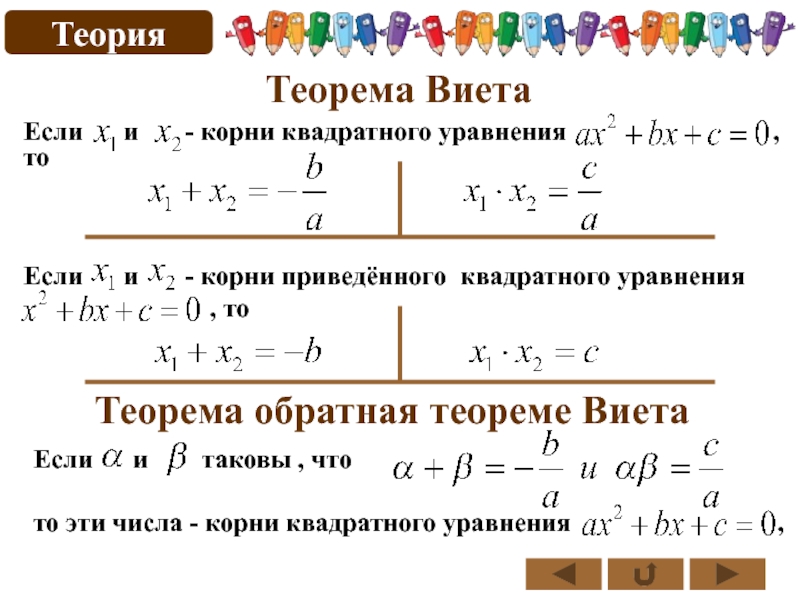
Пример 1: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 2: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение не имеет корней.
Ответ: Корней нет.
Пример 3: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 4: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Решим заданное уравнение вторым способом, предложенным в теории:
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 5: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным.
Для удобства расчетов умножим обе части уравнения на 9 и получим:
Будем решать полученное уравнение. Оно имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 6: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Во всех примерах, рассмотренных выше, были заданы полные квадратные уравнения.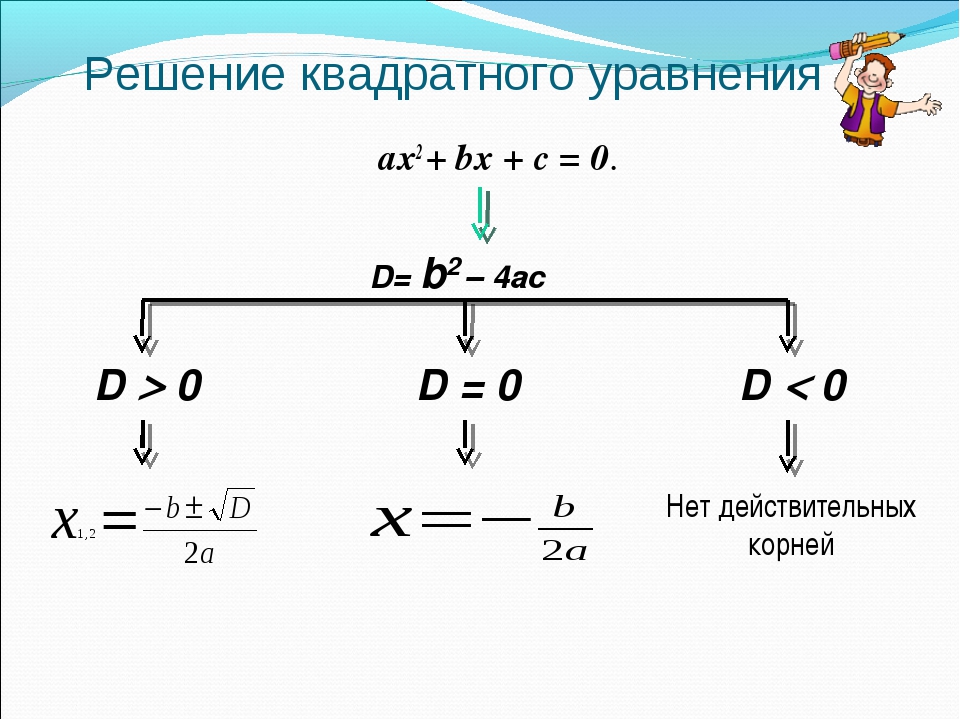 Как же решать неполные уравнения? Рассмотрим решения на примерах.
Как же решать неполные уравнения? Рассмотрим решения на примерах.
Пример 7: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Поэтому либо , либо
Ответ:
Пример 8: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня. Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Ответ:
Пример 9: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение корней не имеет.
Ответ: Корней нет.
Пример 10: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение имеет один корень .
Ответ: .
Примеры решения квадратных уравнений для студентов.
Пример 1: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 2: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два комплексных корня:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 3: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 4: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Воспользуемся вторым способом решения квадратных уравнений студентами, описанный в теории:
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Пример 5: Решить квадратное уравнение .
Данное квадратное уравнение является полным неприведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет один корень.
Найдем его:
Таким образом, решением квадратного уравнения будет корень
Ответ:
Пример 6: Решить квадратное уравнение .
Данное квадратное уравнение является полным приведенным и имеет следующие коэффициенты: .
Тогда .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два комплексных корня:
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Ответ:
Во всех примерах, рассмотренных выше, были заданы полные квадратные уравнения. Как же решать неполные уравнения? Рассмотрим решения на примерах.
Пример 7: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Можно решать данное квадратное уравнение по представленным выше схемам. Воспользуемся первой из них.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня.
Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Поэтому либо , либо
Ответ:
Пример 8: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным.
Квадратное уравнение имеет следующие коэффициенты: .
Найдем дискриминант: .
Так как , то квадратное уравнение имеет два корня. Найдем их:
Таким образом, решением квадратного уравнения будут корни
Но возможно решить квадратное уравнение следующим, более простым, образом:
Ответ:
Пример 9: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Ответ:
Пример 10: Решить квадратное уравнение .
Данное квадратное уравнение является неполным неприведенным и имеет следующие коэффициенты: .
Будем решать его следующим образом:
Данное квадратное уравнение имеет один корень .
Ответ: .
Калькулятор квадратных уравнений — решение квадратных уравнений онлайн
Этот калькулятор квадратных формул работает как решить квадратное уравнение решатель квадратных уравнений, который помогает решить квадратное уравнение заданное квадратное уравнение с помощью формулы квадратного уравнения.
Что ж, прежде чем узнать об этом калькулятор квадратных уравнений квадратных уравнений, давайте начнем с некоторых основ!
Что такое квадратичная формула?Квадратичная формула считается одним из самых эффективных инструментов математики. Эта формула является решение квадратного уравнения полиномиального уравнения второй степени. Стандартная форма квадратного уравнения упоминается ниже:
ax1 bx c = 0
Куда;
- ‘A’ – квадратичный коэффициент
- «X» – неизвестное
- ‘B’ – линейный коэффициент
- “C” – постоянная
Решение этого уравнения называется корнем уравнения. 2 – 4ac}} {2a} \]
2 – 4ac}} {2a} \]
Наш калькулятор квадратных формул также использует ту же формулу для [решения квадратного уравнения].
Есть три возможности получить корни (квадратного уравнения), но помните, что эти возможности зависят от значения Дискриминанта.
- Если b2 – 4ac = 0, то будет только один корень
- Если b2 – 4ac> 0, то будет только два действительных корня
- Если b2 – 4ac <0, то будет два комплексных корня
Коэффициенты квадратного уравнения:
Также важно отметить, что числа, то есть a, b и c, считаются коэффициентами уравнения и не могут быть «0». Все они действительные числа, не зависящие от x. Если A = 0, то уравнение называется не квадратичным, а линейным.
Если B² <4AC, то определитель Δ будет отрицательным, как решать квадратные уравнения уравнение это уравнение не имеет действительных корней.
Наш квадратичный калькулятор также может вам помочь, если вы можете записать уравнение в такой форме:
ax2 bx c = 0
Калькулятор квадратной формулы:Этот калькулятор квадратных уравнений квадратной формулы представляет собой инструмент, который помогает решить квадратное уравнение квадратное уравнение, используя квадратную формулу или завершив метод квадратов. Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Вам просто нужно сформировать уравнение, метод вычисления и ввести параметры уравнения; этот решатель квадратной формулы лучше всего подойдет вам!
Не волнуйтесь; этот решатель решение квадратного уравнения квадратных уравнений онлайн довольно прост в использовании и имеет продуманный и удобный интерфейс!
Входы:Форма уравнения:
Вы должны выбрать форму уравнения; это форма, в соответствии с которой вы должны ввести значения в обозначенные поля нашего калькулятора квадратичных функций.
В этом калькулятор квадратных уравнений используется следующая форма:
- Ax2 Bx C = 0 (стандартная форма)
- A (x – H) 2 K = 0 (форма вершины)
- A (x-x₁) (x-x₂) = 0 (Факторная форма)
Наш калькулятор квадратных уравнений квадратного уравнения позволяет вам решить квадратное уравнение квадратное уравнение, используя формулу корней квадратного уравнения и завершив метод квадратов.
Если вы выбрали форму Ax2 Bx C = 0, вам необходимо ввести значения A, B и C
Если вы выбрали форму A (x – H) 2 K = 0, то вам необходимо ввести значения A, H и K
Если вы выбрали форму A (x-x₁) (x-x₂) = 0, вам необходимо ввести значения A, x1 и x2
Вывод:После того, как решить квадратное уравнение указанные выше значения, наш решатель (квадратного уравнения) покажет следующее:
Показать корни:Этот калькулятор квадратного корня показывает корень или корни вашего данного уравнения.
Покажите упрощение:Калькулятор шаг за шагом упростит данное уравнение.
Показать дискриминант:Если вы решите решение квадратных уравнений онлайн с помощью формулы квадратичного, то наш калькулятор квадратичного дискриминанта покажет дискриминант
Покажите квадратичный график:Этот калькулятор квадратичных графиков показывает вам полный квадратичный график для данного уравнения!
Как решать квадратные уравнения?Когда дело доходит до решения квадратных уравнений, квадратная формула используется для выполнения вычислений. 2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
2x. Говорят, что «b» является коэффициентом, который появляется при умножении линейного члена x, а коэффициент «c» считается постоянным.
как решать квадратные уравнения следующего выражения x2 3x 1?
В этом случае a = 1 (это коэффициент умножения на квадратный член x2), b = 3b = 3 (коэффициент, умноженный на линейный член x) и c = 1 (константа).
Пример №2:Какие сейчас коэффициенты, если у вас есть следующее выражение: 5/4 3/4 x 1/2 x2
В этом случае a = 1/2 (это коэффициент умножения на квадратичный член x2), b = 3/4 (коэффициент, умноженный на линейный член x) и c = 5/4 (константа).
Пример №3:Какие коэффициенты, если у вас есть следующее выражение: -3 1/2
В этом случае a = 0, поскольку данное выражение не содержит квадратичного члена x2. Итак, это не считается квадратичным выражением.
Подставьте коэффициенты, которые вы нашли в формуле (шаг 2):
Формула:\ [x = \ dfrac {-b \ pm \ sqrt {b ^ 2 – 4ac}} {2a} \]
Теперь вам нужно заменить значения коэффициентов a, b и c. 2 – 4 (-3) (1)}} {2 (-3)} \]
2 – 4 (-3) (1)}} {2 (-3)} \]
После того, как вы подставили значения a, b и c, вы должны упростить значения в уравнении. Из предыдущего примера у вас есть:
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
Загляните внутрь квадратного корня (шаг 4):Если значение положительное, то уравнение имеет два действительных корня. Если значение равно 0, то существует только один действительный корень, а если значение внутри квадратного корня отрицательное, то будет два комплексных корня. В предыдущем примере у вас есть -8 внутри квадратного корня, что означает, что у вас есть два сложных решения (как показано ниже):
\ [x = \ dfrac {-2 \ pm \ sqrt {4 – 12}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {-8}} {(- 6)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8} \, i} {(- 6)} \]
К счастью, вы узнали, как решать квадратные уравнения (вручную). 2 – 4ac}} {2a} \]
2 – 4ac}} {2a} \]
Имейте в виду, поскольку b2 – 4ac <0, квадратный корень из определителя будет мнимым значением. Отсюда:
Re (x) = -B / 2A
Im (x) = ± (√Δ) / 2A
Решение квадратного уравнения методом построения графиков:Итак, из графика параболы узнайте вершину, ось симметрии, точку пересечения по оси y, точку пересечения с x.
Задача имеет два решения, и они демонстрируют точки пересечения уравнения, которые являются точкой пересечения с осью x (это точка, в которой ось x пересекается кривой. При этом составляется график данного уравнения x2 3x – 4 = 0, можно рассматривать как решить квадратное уравнение:
Вершина:Это демонстрация пика. Итак, вершина (квадратного уравнения) указывает точку пика параболы. Если парабола открывается вверх, то говорят, что вершина – это самая высокая точка, а если парабола открывается вниз, то вершина называется самой низкой точкой.
Ось симметрии:Ось симметрии делит параболу на две равные половины; он всегда проходит через вершину параболы.
Корни также называют пересечением по оси x. Он расположен ниже оси x или выше оси x на графике. Поэтому для определения корня квадратичной функции положим y = 0
Y-перехват:Каждая парабола имеет точку пересечения с осью y, и говорят, что это точка, в которой функция пересекает ось y. Это вычисляется путем установки переменной x в уравнении на 0.
Итак, давайте начнем решать графически,
Сначала возьмем уравнение f (x) = 2×2 – 4x-1 или Y = 2×2 – 4x-1.
Здесь a = 2, b = -4 и c = -1.
Если «a» имеет положительное значение, то помните, что парабола открывается вверх на графике. Сначала вам нужно найти вершину x:
х = (- Ь) / 2а
х = (- (- 4)) / 2 (2)
х = 1
Теперь вам нужно найти вершину Y:
Вы должны подставить значение x в уравнение 2×2 – 4x-1
у = 2 (1) 2-4 (1) -1
у = 2 – 4 – 1
у = 3
Итак, у вас есть ось симметрии: x = 1
Теперь вам нужно найти точку пересечения по оси x, используя формулу корней квадратного уравнения:
\ [x = \ dfrac {- (- 4) \ pm \ sqrt {(- 4) ^ 2 – 4 (2) (- 1)}} {2 (2)} \]
\ [x = \ dfrac {4 \ pm \ sqrt {16 8}} {4} \]
\ [x = \ dfrac {4 \ pm \ sqrt {24}} {4} \]
\ [x = \ dfrac {4 \ pm 4. 2 – 4 (-1) (1)}} {2 (-1)} \]
2 – 4 (-1) (1)}} {2 (-1)} \]
\ [x = \ dfrac {-2 \ pm \ sqrt {8}} {-2} \]
х1 = – 0,414214
х2 = 2,414214
Теперь найдите y-точку пересечения:
х2 2х 1 = 0
(0) 2 2 (0) 1 = 0
y-intercept = 1, теперь вам нужно нанести значения на график!
Для чего используется квадратичная формула?Квадратичная формула – это хорошо известная формула, которая встречается повсюду в математике. Он часто учитывается при решении всевозможных геометрических задач, таких как:
- Увеличение площади
- Учитывая фиксированный периметр
- Многочисленные проблемы с Word
Есть много людей, которые задаются вопросом, есть ли какая-либо связь между этой формулой (квадратным уравнением) и методом завершения квадрата. Проще говоря, вы получите квадратную формулу, просто решив решение квадратных уравнений онлайн, заполнив квадрат. Это в точности та же идея, которая вытекает из известной всем нам формулы квадратичных уравнений!
Важность квадратного уравнения в реальной жизни:Будучи студентом, вас могут принимать во внимание по различным вопросам математики. Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
Кроме того, студенты обычно используют это уравнение в таких предметах, как решать квадратные уравнения инженерия и физика. Есть и другие профессии, которые используют (квадратные уравнения):
- Военные и правоохранительные органы – (для определения траектории ракет, выпущенных артиллерией)
- Инженеры – (относится к гражданскому строительству)
- Уравнение движения (как на игровой площадке, так и в игровых ситуациях, оно описывает траекторию полета мяча и определяет высоту брошенного мяча)
- Наука (Астрономы – описывают орбиту планет, солнечных систем и галактик)
- Сферы сельского хозяйства (оптимальное расположение границ для производства самого большого поля)
- Проще говоря, вам просто нужно заполнить квадрат ax2 bx c = 0, чтобы получить формулу корней
- квадратного уравнения
- Вам следует разделить обе части уравнения на «а», чтобы коэффициент при x2 был равен 1.
 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.Как узнать, имеет ли квадратное уравнение одно решить квадратное уравнение онлайн, два или нет?
Это помогает определить, сколько существует решений (квадратного уравнения). Если дискриминант положительный, говорят, что есть 2 корня. Если он равен нулю, значит есть только 1 корень. Если дискриминант отрицательный, то говорят, что корней 0.
Other Languages: Quadratic Formula Calculator, Løs Andengradsligning, Quadratische Gleichungen Lösen, Kinci Dereceden Denklem Çözücü, Rozwiązywanie Równań Kwadratowych, Kalkulator Persamaan Kuadrat, Risolvere Equazioni Di Secondo Grado, Résoudre Une Équation Du Second Degré, Equazioni Di Secondo Grado, Resolver Ecuaciones De Segundo Grado, Toisen Asteen Yhtälön Ratkaisu, Řešení Kvadratické Rovnice, 二次方程式の解, حل المعادلات التربيعية, 이차방정식 계산기
Калькулятор корней онлайн — особенности извлечения корней с подробным объяснением
Калькулятор
Заполните поля для вычисления корня из числа
Онлайн-калькулятор – удобный ресурс, помогающий решать задачи, примеры, в котроых встречаются квадратные или степенные корни.
 Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).Таблица корней от 0 до 99
Извлечение корней
Представить работу калькулятора можно с помощью таблицы квадратов двузначных чисел. По горизонтали в каждом из столбцов указаны единицы от одного до девяти, по вертикали – десятки. Достаточно выяснить, в какой из ячеек находится подкоренное число. Несложно догадаться, что по горизонтали в левой крайней колонке указаны десятки, в верхней строчке таблицы – единицы.
Допустим, под корнем стоит 7056. Находим значение в таблице. Это 8 десятков и 4 единицы, число 84. То есть, 84 это квадратный корень онлайн из 7056. Онлайн-калькулятор находит значения любого подкоренного выражения по подобным таблицам.

При перемножении отрицательных величин получается величина, больше нуля. Извлечение арифметического квадратного корня возможно только из положительного числа (матрицы).
Свойства арифметического квадратного корня
Пользоваться онлайн-калькулятором будет проще, если сначала упростить выражение, привести в удобный для вычисления вид. Чтобы преобразовать подкоренное значение, стоит воспользоваться правилами умножения, деления корней, возведение их в степень. Свойства корней стоит вызубрить, их всего три. Каждое рассмотрено ниже отдельно. Решение корней онлайн упрощается после математических преобразований подкоренного значения или выражения. Для этого достаточно знаний арифметики и азов алгебры.
Умножение корней
Если произведение подкоренного выражения можно представить в виде двух множителей, достаточно перемножить корни, извлеченные из этих множителей: допустим, под корнем стоит число 576. Преобразуем его в два множителя: 64 и 9.
 Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.Формулой свойство изображается так:
Раскладывая подкоренное значение на множители, можно значительно упростить процесс вычисления квадратных корней.
Деление корней
Следующее свойство удобно для извлечения корней из дробных чисел. Когда подкоренное выражение представлено в виде дроби, следует воспользоваться правилом деления. Проще запомнить это свойство по формуле:
Обратная формула трактуется следующим образом: корень из частного равен частному корней.
Допустим, нужно извлечь квадратный корень из дроби 25/144. Для этого необходимо извлечь корень из 25, это 5. Затем подобную манипуляцию произвести с делителем дроби: корень 144 равен двенадцати. После извлечения корня из 25/144 получаем дробь 5/8.
 Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.Возведение в степень
Последнее свойство корней – это возведение его в степень. Тут все просто: достаточно перенести степень под корень, подставить к подкоренному выражению.
При возведении подкоренного числа в квадрат с последующим извлечением квадратного корня получаем первоначальное подкоренное выражение. На слух выражение воспринимается сложно. Проще усвоить формулу:
Из формулы видно, что этим свойством удобно пользоваться при возведении квадратного корня в четную степень, ее можно сразу делить на два и убирать знак корня. Как всегда, пример: чтобы возвести в шестую степень квадратный корень числа 3, необходимо возвести число 3 в куб, степенной показатель 6 поделить пополам.

Внесение под знак корня
При решении задач и примеров возникает необходимость вносить под корень множитель. Например, чтобы вычислить 4 корня из 4, можно представить выражение в виде двух корней: первым подкоренным выражением будет 42, второе останется неизменным. Финальное выражение нетрудно произвести, воспользовавшись формулами:
Формулу запомнить легко, она может пригодиться на экзамене.
Сравнение корней
Для графического решения уравнений нередко приходится сравнивать корни. Как это сделать быстро при сравнении квадратных корней? Воспользоваться еще одним правилом: чем больше подкоренное выражение, тем больше значение корня. Допустим, нужно сравнить
2√3 и 3√2. Вносим числа в подкоренные выражения. Получаем под знаками корней два выражения: 22х3 и 32х2. Осталось сравнить числа 12 и 18. Второе больше.
Свойства квадратных корней распространяются на другие коренные значения: четные или нечетные.
 Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.На этом экскурс по свойствам, сравнению корней можно считать исчерпывающим. Зная эти правила обращения с корнями, можно упростить сложное выражение. Пользоваться нашим онлайн-калькулятором с подсказками очень просто.
Решение (корни) квадратного уравнения
Квадратным уравнением называется уравнение вида ax² + bx + c = 0, где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.
Например, квадратным является уравнение
2x² — 3x + 1 = 0,
в котором a = 2, b = — 3, c = 1.

В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.
Уравнения вида ax² + bx = 0,
где c =0,
ax² + c = 0,
где b =0, и
ax² = 0,
где a =0 и b =0,
называются неполными квадратными уравнениями.
Найти корни квадратного уравнения значит решить квадратное уравнение.
Для вычисления корней квадратного уравния служит выражение b² — 4ac, которое называется дискриминантом квадратного уравнения и обозначается буквой D.
Корни квадратного уравнения имеют следующие сферы применения:
— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.
 д.) в частности,
при нахождении пределов, производных и интегралов;
д.) в частности,
при нахождении пределов, производных и интегралов;— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).
График квадратичного трёхлена ax² + bx + c — левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна оси 0y. Число точек пересечения параболы с осью 0x определяет число корней квадратного уравнения. Если точек пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает ось 0x, то квадратное уравнение не имеет действительных корней. На рисунке ниже изображены три упомянутых случая.
Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x.

1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.
Они вычисляются по формулам:
и
.
Часто пишется так: .
2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .
3. Если дискриминант меньше нуля (), то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней в этой статье рассматривать не будем. В общем случае правильным решением является констатация того, что квадратное уравнение не имеет действительных корней.
Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение.
 Найдём дискриминант:
Найдём дискриминант:.
Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.
Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.
Пример 3.
 Определить, сколько действительных корней имеет квадратное уравнение:
Определить, сколько действительных корней имеет квадратное уравнение:.
Решение. Найдём дискриминант:
.
Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.
Пример 4. Найти корни квадратного уравнения:
.
В примере 1 нашли дискриминант этого уравнения:
,
Решение квадратного уравнения найдём по формуле для корней:
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.

Корни приведённого квадратного уравнения
Формула корней приведённого уравнения имеет вид:
.
Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.
Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a, а произведение равно с/a:
Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то
Пояснение формул: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.
Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:
.
Этот приём часто используется для упрощения выражений, особенно сокращения дробей.
Пример 9. Упростить выражение:
.
Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:
.
Корни квадратного уравнения будут следующими:
.
Разложим квадратный многочлен на множители:
.

Упростили выражение, проще не бывает:
.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 10. Упростить выражение:
.
Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:
.
Корни первого квадратного уравнения будут следующими:
.
Находим дискриминант второго квадратного уравнения:
.
Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:
.
Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:
.

Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.
Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).

Площадь большого квадрата равна (x + 5)². Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:
Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?
Решение. Примем количество ткани в отрезке за x и получим уравнение:
Приведём обе части уравнения к общему знаменателю:
Произведём дальнейшие преобразования:
Получили квадратное уравнение, которое и решим:
Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.

Ответ: в отрезке 20 м ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?
Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:
Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:
Найдём дискриминант:
Найдём корни квадратного уравнения:
Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.

Ответ: в одном ящике взвешивают 12,5 кг ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Другие темы в блоке «Школьная математика»
Как решать квадратные уравнения? Формулы и Примеры
Понятие квадратного уравнения
Уравнения — это математическое равенство, в котором неизвестна одна или несколько величин. Значения неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать выражение 3 + x = 7, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение.

Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Чтобы запомнить месторасположение коэффициентов, давайте потренируемся определять их.
Есть три вида квадратных уравнений:
- не имеют корней;
- имеют один корень;
- имеют два различных корня.
Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac. А вот свойства дискриминанта:
- если D < 0, корней нет;
- если D = 0, есть один корень;
- если D > 0, есть два различных корня.
С этим разобрались. А сейчас посмотрим подробнее на различные виды квадратных уравнений.
Приведенные и неприведенные квадратные уравнения
Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.

Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
Давайте-ка на примерах — вот у нас есть два уравнения:
- x2 — 2x + 6 = 0
- x2 — x — 1/4 = 0
В каждом из них старший коэффициент равен единице (которую мы мысленно представляем при x2 ), а значит уравнение называется приведенным.
- 2x2 − 4x — 12 = 0 — первый коэффициент отличен от единицы (2), значит это неприведенное квадратное уравнение.
Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.
Запоминаем!
У преобразованного уравнения те же корни, что и у первоначального. Ну или вообще нет корней.
Пример 1.
 Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.Для этого разделим обе части исходного уравнения на старший коэффициент 8:
Ответ: равносильное данному приведенное уравнение x2 + 2,5x — 1,125 = 0.
Полные и неполные квадратные уравнения
В определении квадратного уравнения есть условие: a ≠ 0. Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.
Неполное квадратное уравнение —— это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.
Для самых любопытных объясняем откуда появились такие названия: - Если b = 0, то квадратное уравнение принимает вид ax2 + 0x+c=0 и оно равносильно ax2 + c = 0.

- Если c = 0, то квадратное уравнение выглядит так ax2 + bx + 0 = 0, иначе его можно написать как ax2 + bx = 0.
- Если b = 0 и c = 0, то квадратное уравнение выглядит так ax2 = 0.
Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.
Решение неполных квадратных уравнений
Как мы уже знаем, есть три вида неполных квадратных уравнений:
- ax2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
- ax2 + c = 0, при b = 0;
- ax2 + bx = 0, при c = 0.
Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.
Как решить уравнение ax
2 = 0Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.

Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.
Пример 1. Решить −6x2 = 0.
Как решаем:
- Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.
- По шагам решение выглядит так:
−6x2 = 0
x2 = 0
x = √0
x = 0
Ответ: 0.
Как решить уравнение ax
2 + с = 0Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.
Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax2 + c = 0:
- перенесем c в правую часть: ax2 = — c,
- разделим обе части на a: x2 = — c/а.
Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.
Если — c/а < 0, то уравнение x2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р2 = — c/а не является верным.
Если — c/а > 0, то корни уравнения x2 = — c/а будут другими.
 Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.В двух словах Неполное квадратное уравнение ax2 + c = 0 равносильно уравнению ax2 + c = 0, которое:
- не имеет корней при — c/а < 0;
- имеет два корня х = √- c/а и х = -√- c/а при — c/а > 0.
Пример 1. Найти решение уравнения 8x2 + 5 = 0.
Как решать:
- Перенесем свободный член в правую часть:
8x2 = — 5
- Разделим обе части на 8:
x2 = — 5/8
- В правой части осталось число со знаком минус, значит у данного уравнения нет корней.
Ответ: уравнение 8x2 + 5 = 0 не имеет корней.

Как решить уравнение ax
2 + bx = 0Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.
Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.
Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:
Пример 1. Решить уравнение 0,5x2 + 0,125x = 0
Как решать:
- Вынести х за скобки
х(0,5x + 0,125) = 0
- Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.
- Решить линейное уравнение:
0,5x = 0,125,
х = 0,125/0,5 - Разделить:
х = 0,25
- Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.
Формула Виета
Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:
Теорема Виета
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:
Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.
Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:
Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:
Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
Результат проделанных вычислений в том, что мы убедились в справедливости выражения:
Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней.
 Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:Обратная теорема Виета
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x2 + bx + c = 0.
Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x1 и x2 равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.
Пример 1. Решить при помощи теоремы Пифагора: x2 − 6x + 8 = 0.
Как решаем:
- Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.
- Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.
Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x1 + x2 = 6. А значения 4 и 2 подходят обоим равенствам:
- Значит числа 4 и 2 — корни уравнения x2 − 6x + 8 = 0. p>
Дискриминант: формула корней квадратного уравнения
Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:
где D = b2 − 4ac — дискриминант квадратного уравнения.
Эта запись означает:
Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.
Выводим формулу корней квадратного уравнения
Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:
Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.
Отсюда выводы про корни уравнения :
И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части. При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D.
По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.
Повторим:
Алгоритм решения квадратных уравнений по формулам корней
Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения.
 Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
- вычислить его значение дискриминанта по формуле D = b2−4ac;
- если дискриминант отрицательный, зафиксировать, что действительных корней нет;
- если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
- если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней
Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!
Примеры решения квадратных уравнений
Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.
Пример 1. Решить уравнение −4x2 + 28x — 49 = 0.

Как решаем:
- Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
- Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
- Найдем корень
х = — 28/2(-4)
х = 3,5
Ответ: единственный корень 3,5.
Пример 2. Решить уравнение 54 — 6x2 = 0.
Как решаем:
- Произведем равносильные преобразования. Умножим обе части на −1
54 — 6x2 = 0 | *(-1)
6x2 — 54 = 0
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
6x2 = 54
х2 = 9
х = ±√9
х1 = 3, х2 = — 3
Ответ: два корня 3 и — 3.
Пример 3. Решить уравнение x2— х = 0.
Как решаем:
- Преобразуем уравнение так, чтобы появились множители
х(х — 1) = 0
х₁ = 0, х₂ = 1
Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.
Как решаем:
- Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую
x2— 10 = 39
x2= 39 + 10
x2= 49
х = ±√49
х₁ = 7, х₂ = −7
Ответ: два корня 7 и −7.
Пример 5. Решить уравнение 3x2— 4x+94 = 0.
Как решаем:
- Найдем дискриминант по формуле
D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112
- Дискриминант отрицательный, поэтому корней нет.
Ответ: корней нет.
В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.
Формула корней для четных вторых коэффициентов
Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x.
 Рассмотрим, как появилась эта формула.
Рассмотрим, как появилась эта формула.Например, нам нужно решить квадратное уравнение ax2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n)2— 4ac = 4n2 — 4ac = 4(n2— ac) и подставим в формулу корней:
Для удобства вычислений обозначим выражение n2 -ac как D1. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:
где D1 = n2— ac.
Самые внимательные уже заметили, что D = 4D1, или D1= D/4. Проще говоря, D1 — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.
Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:
- вычислить D1= n2— ac;
- если D1< 0, значит действительных корней нет;
- если D1= 0, значит можно вычислить единственный корень уравнения по формуле;
- если же D1> 0, значит можно найти два действительных корня по формуле
Упрощаем вид квадратных уравнений
Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x2 — 4 x — 6 = 0, чем 1100x2 — 400x — 600 = 0.
Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x2 — 400x — 600 = 0, просто разделив обе части на 100.
Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.
Покажем, как это работает на примере 12x2— 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x2 — 7x + 8 = 0. Вот так просто.
А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов.
 Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравненияумножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x2 + 4x — 18 = 0.
Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x2— 3x + 7 = 0 перейти к решению 2x2 + 3x — 7 = 0.
Связь между корнями и коэффициентами
Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:
Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.
Например, можно применить формулы из теоремы Виета:
- x₁ + x₂ = — b/a,
- x₁* x₂ = c/a.
Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену.
 Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:
А еще найти корни квадратного уравнения можно с помощью онлайн-калькулятора. Пользуйтесь им, если уже разобрались с темой и щелкаете задачки легко и без помощников:
Арифметический квадратный корень. Мини-курс. Уроки 1-5. — Math
Арифметический квадратный корень. Мини-курс. Уроки 1-5.
Урок 1. Арифметический квадратный корень. Определение арифметического квадратного корня. Основные понятия. Базовые свойства. Как извлечь арифметический квадратный корень. Свойства корня. Математика. Алгебра 8 класс. Образование. Примеры с решением.

- Пример 1: Найдите значение арифметического квадратного корня.
- Пример 2: Имеет ли смысл выражение.
- Пример 3-4: Найдите значение выражения.
- Пример 5: Найдите значение корня.
Урок 2. Уравнения, содержащие знак корня. Простейшие иррациональные уравнения.
Уравнения со знаком корня. Иррациональные уравнения. Методы и способы решения уравнений, содержащие знак корня. Алгебра 8 класс. Математика. Образование. Примеры с решением. Задания с объяснением. Пример 1: Решить уравнение. Математика. Задания с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Урок 3. Неполные квадратные уравнения.
 х2=а. Алгебра 8 класс. Математика. Образование.
х2=а. Алгебра 8 класс. Математика. Образование.Простейшее неполное квадратное уравнение. Уравнение х2 = а и способы его решения. Алгебра 8 класс. Математика. Образование. Примеры с решением. Задания с объяснением. Пример 1: Решить неполное квадратное уравнение. Математика. Задания с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
Уроки 6 — 10
Урок 4. Свойства арифметического квадратного корня. Корень из а в квадрате. Алгебра 8 класс.
Арифметический квадратный корень. Свойства квадратного корня. Преобразование выражений с квадратным корнем. Свойство «Корень из а в квадрате». Алгебра 8 класс. Математика. Образование. Как правильно извлечь квадратный корень и открыть модуль. Разница между свойством «корень из а в квадрате» и Корень из а и все это в квадрате».
 Что обязательно надо учесть при извлечении квадратного корня. Сокращение корня и степени. Как извлечь корень из выражения в степени. Примеры с решением. Задания с объяснением. Пример 1: Найдите значение выражения. Пример 2: Упростить выражение.
Что обязательно надо учесть при извлечении квадратного корня. Сокращение корня и степени. Как извлечь корень из выражения в степени. Примеры с решением. Задания с объяснением. Пример 1: Найдите значение выражения. Пример 2: Упростить выражение.
Урок 5. Решение уравнений и построение графиков с квадратным корнем. Алгебра 8 класс.Преобразования арифметического квадратного корня. Свойство «Корень из а в квадрате». Решение уравнений. Построение графиков. Алгебра 8 класс. Математика. Образование. Как правильно извлечь квадратный корень и открыть модуль. Разница между свойством «корень из а в квадрате» и Корень из а и все это в квадрате». Что обязательно надо учесть при извлечении квадратного корня. Сокращение корня и степени. Примеры с решением. Задания с объяснением.
- Пример 1: Решить уравнение. Найдите корни уравнения, выполнив преобразование квадратного корня.

- Пример 2: Построить график функции.
Арифметический квадратный корень. Ответы к заданиям из видео уроков.
Арифметический квадратный корень. Мини-курс. Уроки 6 — 10.
Арифметический квадратный корень. Мини-курс. Уроки 11 — 16.
2-1Пример задачи Ничья Количество решаемых уравнений: 23456789 Пример задачи Решить
калькулятор уравнения квадратного корняВведите неравенство в график, например.  грамм. y
грамм. yПример задачи Ничья Количество решаемых неравенств: 23456789 Пример задачи Решить
Связанные темы:
преобразование дробей в десятичные | решение одношаговых уравнений весело рабочий лист | перевозки с «линейным программированием» | gcse двойные неравенства в уравнении | практиковать бесплатную алгебру в 9 классе онлайн | тест по алгебре в конце курса | математическая алгебра Холта | калькулятор факторизации алгебры 2 | геометрические решения подходящие | формула квадратного корняАвтор Сообщение Vament Зарегистрирован: 06.
 08.2002
08.2002
Из: ГерманияРазмещено: 28 декабря, четверг, 07:07 Привет, волшебники математики, мне срочно нужна помощь.У меня есть набор математических задач, на которые мне нужно ответить, и я безнадежно заблудился. Я не знаю, с чего начать и как поступить, и эта статья должна быть опубликована на следующей неделе. Пожалуйста, дайте мне знать, хорошо ли вы умеете строить графики или есть хороший сайт, который может мне помочь. Наверх ameich Зарегистрировано: 21.
 03.20202005 г.
03.20202005 г.
Вылет: Прага, Чешская РеспубликаРазмещено: 28 декабря, четверг, 16:45 Ха-ха! пропуски являются довольно неприятным явлением, особенно если вы пропустили такую важную тему, как калькулятор квадратного корня, который на самом деле довольно сложен.Вы пробовали раньше использовать Алгебратор? На данный момент я могу вам посоветовать следующее: попробуйте это программное обеспечение, и у вас не будет проблем с пониманием калькулятора квадратного корня. Его очень полезно использовать, потому что он не только решает математические задачи, но и объясняет, давая подробное решение.  Вы не поверите, но благодаря этому программному обеспечению мои оценки за тесты значительно улучшились. Я просто хочу поделиться этим, потому что я в восторге от великолепия программы.
Вы не поверите, но благодаря этому программному обеспечению мои оценки за тесты значительно улучшились. Я просто хочу поделиться этим, потому что я в восторге от великолепия программы.Наверх caxee Зарегистрировано: 05.12.2002
Откуда: Бостон, Массачусетс, СШАРазмещено: 29 декабря, пятница, 11:31 Полностью согласен, Алгебратор великолепен! Сейчас я очень хорошо разбираюсь в алгебре, и у меня лучшие оценки в классе! Он помогал мне даже с самыми запутанными математическими задачами, такими как умножение матриц или квадратных уравнений.  Я определенно думаю, что тебе стоит попробовать.
Я определенно думаю, что тебе стоит попробовать.Наверх Sdefom Koopmansshab Зарегистрировано: 28.10.2001
Откуда: Вуденберг, НидерландыРазмещено: суббота, 30 декабря, 11:09 Я помню, что у меня были трудности с разными знаменателями, добавлением дробей и построением парабол.  Алгебратор — действительно отличная программа для алгебры. Я использовал его на нескольких уроках алгебры — лечебной алгебре, студенческой алгебре и предалгебре. Я просто набираю проблему из книги и, нажимая «Решить», появляется пошаговое решение. Программа очень рекомендуется.
Алгебратор — действительно отличная программа для алгебры. Я использовал его на нескольких уроках алгебры — лечебной алгебре, студенческой алгебре и предалгебре. Я просто набираю проблему из книги и, нажимая «Решить», появляется пошаговое решение. Программа очень рекомендуется.Наверх xkevinx Зарегистрировано: 05.11.2002
Вылет: КалифорнияРазмещено: 31 декабря, воскресенье, 10:29 Спасибо, парни.  Нет ничего плохого в том, чтобы попробовать это один раз. Дайте пожалуйста ссылку на программу.
Нет ничего плохого в том, чтобы попробовать это один раз. Дайте пожалуйста ссылку на программу.Наверх LifiIcPoin Зарегистрировано: 01.10.2002
Откуда: Дорога позадиНаверх Решение радикальных уравнений
Как решать уравнения с квадратными корнями, кубическими корнями и т. Д.
Радикальные уравнения
Решение радикальных уравнений
Мы можем избавиться от квадратного корня возведением в квадрат. (Или кубические корни кубиками и т.
 Д.)
Д.)Но предупреждение: иногда это может создавать «решения», которые на самом деле не работают, когда мы помещаем их в исходное уравнение. Так что нам нужно проверить!
Выполните следующие действия:
- изолируйте квадратный корень с одной стороны уравнения
- возвести в квадрат обе части уравнения
Тогда продолжайте наше решение!
Пример: решить √ (2x + 9) — 5 = 0
вычлените квадратный корень: √ (2x + 9) = 5
квадрат с обеих сторон: 2x + 9 = 25
Теперь решать должно быть проще!
Переместите 9 вправо: 2x = 25 — 9 = 16
Разделить на 2: x = 16/2 = 8
Ответ: x = 8
Проверка: √ (2 · 8 + 9) — 5 = √ (25) — 5 = 5 — 5 = 0
Тот работал отлично.
Более одного квадратного корня
Что делать, если есть два или более квадратных корня? Легкий! Просто повторите процесс для каждого.
Это займет больше времени (намного больше шагов) .
 .. но ничего особенного.
.. но ничего особенного.Пример: решить √ (2x − 5) — √ (x − 1) = 1
выделить один из квадратных корней: √ (2x − 5) = 1 + √ (x − 1)
квадрат с обеих сторон: 2x − 5 = (1 + √ (x − 1)) 2
Мы удалили один квадратный корень.
развернуть правую часть: 2x − 5 = 1 + 2√ (x − 1) + (x − 1)
упростить: 2x − 5 = 2√ (x − 1) + x
вычтем x из обеих частей: x − 5 = 2√ (x − 1)
Теперь снова вычислим квадратный корень:
выделите квадратный корень: √ (x − 1) = (x − 5) / 2
квадрат с обеих сторон: x − 1 = ((x − 5) / 2) 2
Мы успешно удалили оба квадратных корня.
Давайте продолжим решение.
Разверните правую часть: x − 1 = (x 2 — 10x + 25) / 4
Это квадратное уравнение! Так что давайте представим это в стандартной форме.
Умножьте на 4, чтобы удалить деление: 4x − 4 = x 2 — 10x + 25
Переместите все налево: 4x — 4 — x 2 + 10x — 25 = 0
Объедините похожие термины: −x 2 + 14x — 29 = 0
Поменять местами все знаки: x 2 — 14x + 29 = 0
Использование квадратичной формулы (a = 1, b = −14, c = 29) дает решения:
2.
 53 и 11,47 (с точностью до 2 знаков после запятой)
53 и 11,47 (с точностью до 2 знаков после запятой)Проверим решения:
2,53: √ (2 × 2,53−5) — √ (2,53−1) ≈ −1 Ой! Должно быть плюс 1.
11,47: √ (2 × 11,47−5) — √ (11,47−1) ≈ 1 Да, это работает.
Есть реально только одно решение :
Ответ: 11,47 (с точностью до 2 знаков после запятой)
Видите? Этот метод может иногда давать решения, которые на самом деле не работают!
Корень, который казался работоспособным, но был неправильным, когда мы его проверили, называется «Посторонний корень»
Итак: Проверка важна.
Калькулятор квадратного корня
Автор Сообщение Enberon Memg Зарегистрировано: 16.
 01.2003
01.2003
Откуда: МонгоРазмещено: 28 декабря, четверг, 14:02 Привет, девчонки и ребята, я был бы очень благодарен за некоторую поддержку с калькулятором квадратного корня, на котором я действительно застрял.Мне нужно выполнить домашнее задание, и я не знаю, как решать тригонометрические функции, смешанные числа и экспоненциальные уравнения. Я был бы уверен, что буду ценить вашу помощь, а не нанимать дорогого репетитора по математике. Наверх IlbendF Зарегистрировано: 11.
 03.2004
03.2004
Откуда: НидерландыРазмещено: Пятница, 29 декабря, 10:00 Что ж, я не могу решить твою домашнюю работу за тебя, это означало бы обман.Однако я могу дать вам предложение. Попробуйте использовать Алгебратор. Вы можете найти подробные и хорошо объясненные ответы на все свои проблемы в калькуляторе квадратного корня. Наверх TihBoasten Зарегистрировано: 14.
 10.2002
10.2002
Из:Размещено: суббота, 30 декабря, 10:30 Пользуюсь этой программой уже год, и она меня ни разу не подводила.Он не просто решит проблему за вас, но также предоставит подробную информацию о каждом шаге, который был предпринят, чтобы прийти к конкретному ответу. И это, на мой взгляд, лучшая особенность. У меня было много проблем с ответами на вопросы, основанные на калькуляторе квадратного корня, но с тех пор, как я купил это программное обеспечение, математика стала для меня просто куском пирога. 
Наверх Pagnee Зарегистрировано: 27.09.2002
Из: исламабадРазмещено: 31 декабря, воскресенье, 11:13 Хорошо, теперь я слышал довольно много хороших отзывов об алгебраторе, думаю, его определенно стоит попробовать.Как мне это достать? Наверх DVH Зарегистрировано: 20.
 12.2001
12.2001
Из:Размещено: 31 декабря, воскресенье, 16:17 Что ж, вы можете заказать это онлайн через этот веб-сайт — https: // polymathlove.ru / factoring-by-grouping.html. Они даже предлагают гарантию возврата денег «без мелкого шрифта», которой, я уверен, никому бы и не пришлось воспользоваться! Это действительно здорово . Наверх Momepi Зарегистрировано: 22.
 07.2004
07.2004
Откуда: ИрландияРазмещено: 2 января, вторник, 08:37 Я помню, что часто сталкивался с трудностями со смешанными числами, построением линий и решением неравенств.Поистине замечательная программа по алгебре — это программа Algebrator. Если просто ввести проблему из книги, появится пошаговое решение, щелкнув «Решить». Я использовал ее во многих математических классах — Алгебре 2, Алгебре 2 и Алгебре 1. Я очень рекомендую эту программу. Наверх Math 1010 on-line — Корни и радикалы
Math 1010 on-line — Корни и радикалыКафедра математики — Колледж наук — Университет Юты
Корни и радикалы
Корни и радикалы заслуживают отдельной главы и домашнего задания, потому что они часто встречаются в приложениях.

Пусть будет натуральное число, и пусть будет настоящий номер . -й корень из это число, которое удовлетворяет Номер обозначается
Например, с тех пор, и поскольку .
Символ называется радикальным символом , и выражение, включающее его, называется радикалом (выражение) .
Если тогда это квадратный корень из, и это число обычно опускается. Например,
Если, то это кубический корень из.Например, кубический корень из есть и кубический корень из есть.
Если четное и положительное, то есть два -го числа. корни, каждый из которых является отрицательным для другого. Например, поскольку есть два квадратных корня из. В в этом случае условно символ означает положительный -й корень, и он называется главный (-й) корень из .
Если отрицательное и нечетное, то есть только корень 1/4, и он также отрицательный. Например,
На этом этапе нам неизвестен корень -й степени, если он даже и отрицательный.
 Это приводит к теме
комплексные числа, которые мы рассмотрим позже в этом курсе.
Это приводит к теме
комплексные числа, которые мы рассмотрим позже в этом курсе.Радикалы — это просто частные случаи полномочий , и вы Помните об этом факте, что может упростить ваше мышление:
Непосредственно из этого наблюдения и свойств силы, которые
Решение радикальных уравнений
Уравнение, включающее радикалы, называется радикальным уравнением (естественно). Чтобы решить эту проблему, вы просто применяете нашу общую принцип:
Чтобы решить уравнение, выясните, что вас беспокоит, и сделайте то же самое. вещь по обе стороны уравнения, чтобы избавиться от него.
Чтобы избавиться от радикала, вы приводите его к власти, которая изменит рациональный показатель до натурального числа. Это будет работать, если радикал находится на одной стороне уравнения сам по себе.
Давайте посмотрим на несколько простых примеров :
Предполагать
Действуем следующим образом:Вот немного более сложная проблема:
Мы получаемНаш последний пример показывает, как избавиться от более чем одного радикала:
Чтобы избавиться от квадратных корней, мы изолируем их и возведем в квадрат время:
В каждом случае мы проверяем наш ответ, подставляя его в исходный.
 уравнение.Например, в последнем уравнении получаем:
уравнение.Например, в последнем уравнении получаем:Позже в курсе мы рассмотрим более сложные случаи радикальные уравнения.
Числовые значения
Все радикалы в приведенных выше примерах были натуральными числами. Это связано только с разумным подбором примеров. Часто корни в приложениях встречаются иррациональные числа с десятичными разложениями, которые никогда не повторяются и не заканчиваются. В следующей таблице приведены приблизительные значения несколько специфических радикалов.
Некоторые радикалы (приблизительно)
Решение квадратных уравнений
Решение квадратных уравнений
Квадратичное уравнение — это уравнение, которое можно записать как
топор 2 + bx + c = 0
, когда a 0.
Существует три основных метода решения квадратных уравнений: разложение на множители, использование формулы квадратов и завершение квадрата.
Факторинг
Чтобы решить квадратное уравнение на множители,
Поместите все члены с одной стороны от знака равенства, оставив ноль с другой стороны.
- Коэффициент
.
Установите каждый коэффициент равным нулю.
Решите каждое из этих уравнений.
Проверьте, подставив свой ответ в исходное уравнение.
Пример 1
Решить x 2 -6 x = 16.
Следуя инструкциям,
x 2 — 6 x = 16 становится x 2 — 6 x — 16 = 0
Коэффициент.
( x -8) ( x + 2) = 0
Установка каждого коэффициента на ноль,
Затем проверить,
Оба значения, 8 и –2, являются решениями исходного уравнения.
Пример 2
Решить y 2 = — 6 y — 5.
Устанавливая все члены равными нулю,
y 2 + 6 y + 5 = 0
Коэффициент.
( y + 5) ( y + 1) = 0
Установка каждого коэффициента на 0,
Для проверки, y 2 = –6 y — 5
Квадратичный с отсутствующим членом называется неполным квадратичным (если не пропущен член ax 2 ).
Пример 3
Решить x 2 — 16 = 0.
Коэффициент.
Для проверки, x 2 — 16 = 0
Пример 4
Решить x 2 + 6 x = 0.
Коэффициент.
Для проверки, x 2 + 6 x = 0
Пример 5
Решить 2 x 2 + 2 x — 1 = x 2 + 6 x — 5.
Во-первых, упростите, поместив все термины в одну сторону и комбинируя одинаковые термины.
Теперь фактор.
Для проверки, 2 x 2 + 2 x — 1 = x 2 + 6 x — 5
Квадратичная формула
Многие квадратные уравнения не могут быть решены факторизацией. Обычно это верно, когда корни или ответы не являются рациональными числами. Второй метод решения квадратных уравнений включает использование следующей формулы:
a, b, и c взяты из квадратного уравнения, записанного в его общей форме
топор 2 + bx + c = 0
, где a — это число перед x 2 , b — это число перед x , а c — это число без переменной рядом с ним (a .k.a., «постоянная»).
При использовании формулы квадратного уравнения вы должны знать о трех возможностях. Эти три возможности различаются частью формулы, называемой дискриминантом. Дискриминант — это значение под знаком корня, b 2 — 4 ac . Квадратное уравнение с действительными числами в качестве коэффициентов может иметь следующее:
Два разных действительных корня, если дискриминант b 2 -4 ac является положительным числом.
Один действительный корень, если дискриминант b 2 — 4 ac равен 0.
Нет действительного корня, если дискриминант b 2 -4 ac является отрицательным числом.
Пример 6
Решить относительно x : x 2 — 5 x = –6.
Установка всех членов равными 0,
x 2 -5 x + 6 = 0
Затем замените 1 (который, как предполагается, стоит перед x 2 ), –5 и 6 вместо a , b и c, соответственно в формуле корней квадратного уравнения и упростите.
Поскольку дискриминант b 2 -4 ac положительный, вы получаете два разных действительных корня.
Пример производит рациональные корни. В примере , квадратная формула используется для решения уравнения, корни которого нерациональны.
Пример 7
Решить относительно y : y 2 = –2y + 2.
Установка всех членов равными 0,
y 2 + 2 y — 2 = 0
Затем замените 1, 2 и –2 на a , b и c, соответственно в формуле корней квадратного уравнения и упростите.
Обратите внимание, что два корня иррациональны.
Пример 8
Решить относительно x : x 2 + 2 x + 1 = 0.
Подставляя в формулу корней квадратного уравнения,
Поскольку дискриминант b 2 -4 ac равен 0, уравнение имеет один корень.
Квадратичная формула также может использоваться для решения квадратных уравнений, корни которых являются мнимыми числами, то есть они не имеют решения в действительной системе счисления.
Пример 9
Решите относительно x : x ( x + 2) + 2 = 0 или x 2 + 2 x + 2 = 0.
Подставляя в формулу корней квадратного уравнения,
Поскольку дискриминант b 2 -4 ac отрицателен, это уравнение не имеет решения в системе действительных чисел.
Но если бы вы выразили решение с помощью мнимых чисел, решения были бы такими.
Завершение квадрата
Третий метод решения квадратных уравнений, который работает как с действительными, так и с мнимыми корнями, называется завершением квадрата.
Запишите уравнение в виде ax 2 + bx = — c .
Убедитесь, что a = 1 (если a ≠ 1, умножьте уравнение на, прежде чем продолжить).
Используя значение b из этого нового уравнения, сложите обе части уравнения, чтобы получить полный квадрат в левой части уравнения.
Найдите квадратный корень из обеих частей уравнения.
Решите полученное уравнение.
Пример 10
Решить относительно x : x 2 — 6 x + 5 = 0.
Оформить в виде
Поскольку a = 1, прибавьте или 9 к обеим сторонам, чтобы завершить квадрат.
Извлеките квадратный корень из обеих частей.
x — 3 = ± 2
Решить.
Пример 11
Решить относительно y : y 2 + 2 y — 4 = 0.
Оформить в виде
Поскольку a = 1, прибавьте или 1 к обеим сторонам, чтобы завершить квадрат.
Извлеките квадратный корень из обеих частей.
Решить.
Пример 12
Решить относительно x : 2 x 2 + 3 x + 2 = 0.
Оформить в виде
Поскольку a ≠ 1, умножаем уравнение на.
Добавьте или с обеих сторон.
Извлеките квадратный корень из обеих частей.
В действительной системе счисления нет решения. Вам может быть интересно узнать, что завершение квадратного процесса для решения квадратных уравнений использовалось в уравнении ax 2 + bx + c = 0 для вывода формулы квадратов.
Вычислить квадратный корень без калькулятора
Вы здесь: Главная → Статьи → Алгоритм извлечения квадратного корняБольшинство людей в современном мире считают, что, поскольку калькуляторы могут находить квадратные корни, детям не нужно учиться находить квадратные корни, используя какой-либо метод карандаша и бумаги. Однако изучение, по крайней мере, метода «угадай и проверь» для нахождения квадратного корня на самом деле поможет студентам ПОНИМАТЬ и запомнить саму концепцию квадратного корня!
Таким образом, даже если в вашем учебнике по математике тема нахождения квадратного корня без калькулятора может полностью отсутствовать, подумайте о том, чтобы позволить студентам изучить и практиковать хотя бы метод «угадывай и проверяй».Поскольку на самом деле он имеет дело с КОНЦЕПЦИЕЙ квадратного корня, я бы посчитал его необходимым для обучения студентов.
В зависимости от ситуации и учащихся, метод «угадай и проверь» можно выполнить либо с помощью простого калькулятора, не имеющего кнопки квадратного корня, либо с помощью вычислений с использованием бумаги и карандаша.
Нахождение квадратных корней методом угадывания и проверки
Чтобы найти десятичное приближение, скажем, к √2, сначала сделайте первоначальное предположение, затем возведите его в квадрат и, в зависимости от того, насколько близко вы подошли, улучшите свое предположение.Поскольку этот метод включает возведение в квадрат предположения (умножение самого числа на само число), он использует фактическое определение квадратного корня , и поэтому может быть очень полезным при обучении концепции квадратного корня.
Пример: что такое квадратный корень из 20?
Вы можете начать с того, что заметите, что, поскольку √16 = 4 и √25 = 5, то √20 должно быть между 4 и 5.
Тогда угадайте √20; скажем, например, что это 4.5. Возведите это в квадрат, посмотрите, будет ли результат больше или меньше 20, и улучшите свое предположение на основе этого.Повторяйте этот процесс, пока не получите желаемую точность (количество десятичных знаков). Это так просто, и это может стать отличным экспериментом для студентов!
Пример: найти √6 с точностью до 4 знаков после запятой
Поскольку 2 2 = 4 и 3 2 = 9, мы знаем, что √6 находится между 2 и 3. Давайте предположим (или оценим), что это 2,5. Возводя в квадрат, получаем 2,5 2 = 6,25. Это слишком много, поэтому мы немного уменьшаем нашу оценку. Давайте попробуем 2.4 дальше. Чтобы найти квадратный корень из 6 до четырех знаков после запятой, нам нужно повторять этот процесс, пока у нас не будет пяти десятичных знаков, а затем мы округлим результат.
Оценка Площадь оценки Высокая / низкая 2,4 5,76 Слишком низкая 2,45 6,0025 Слишком высокая 16 944 944 Слишком высокая цена закрытия 5,997601 Слишком мало 2,4495 6,00005025 Слишком много, поэтому квадратный корень из 6 должен быть между 2.449 и 2.4495. 2.4493 5.99 9
Слишком низко 2.4494 5.99956036 Слишком мало, поэтому квадратный корень из 6 должен находиться в диапазоне от 2,4494 до 2,4495 2.44945 2.44945 900oo поэтому квадратный корень из 6 должен находиться в диапазоне от 2,44945 до 2,4495. Этого достаточно итераций, поскольку теперь мы знаем, что √6 будет округлено до 2,4495 (а не до 2,4494).
Нахождение квадратных корней с помощью алгоритма
Существует также алгоритм вычисления квадратного корня, напоминающий алгоритм деления в столбик, и его изучали в школах за несколько дней до появления калькуляторов. См. Пример ниже, чтобы узнать это. Хотя изучение этого алгоритма может быть необязательным в современном мире с калькуляторами, разработка некоторых примеров может использоваться в качестве упражнения в основных операциях для учащихся средней школы, а изучение логики, лежащей в основе этого, может быть хорошим упражнением для мышления для учащихся средней школы.
Пример: Найдите √645 с точностью до одного десятичного знака.
Сначала сгруппируйте числа под корнем попарно справа налево, оставляя одна или две цифры слева (в данном случае 6). Для каждой пары чисел вы получите одну цифру квадратного корня.
Для начала найдите номер чей квадрат меньше или равен первой паре или первому числу, и напишите это над линией квадратного корня (2):Затем продолжайте так:
2 √ 6 .45 — 4 (4 _) 2 45 2 √ 6 .45 — 4 (45) 3 45Квадрат 2, получая 4, напишите, что под 6 и вычтите.Сбейте следующую пару цифр. Затем удвойте число над квадратным корнем символьная строка (выделена) и запишите его в скобках, поставив рядом с ним пустую строку, как показано. Дальше подумайте, какое однозначное число что-то могло перейдите в пустую строку так, чтобы сорок что-то умножить на что-то быть меньше или равно 245.
45 х 5 = 225
46 x 6 = 276, поэтому 5 работает.2 5
√ 6 ,45 . 00 -4 (45) 2 45 — 2 25 20 00 2 5
√ 6 .45 . 00 -4 (45) 2 45 — 2 25 (50_) 20 00 2 5
. 3 √ 6 ,45 . 00 -4 (45) 2 45 — 2 25 (503) 20 00 Напишите 5 в начале строки.Вычислите 5 x 45, напишите, что ниже 245, вычтите, введите следующую пару цифр (в данном случае десятичные цифры 00). Затем удвойте число над линией (25) и напишите удвоенное число (50) в скобках с пустой строкой рядом с ним как указано: Подумайте, что однозначное число что-то может пойти на пустом линия так что пятьсот- что-то раз что-то будет меньше или равно 2000.503 х 3 = 1509
504 x 4 = 2016, поэтому 3 работает.2 5
. 3 √ 6 ,45 . 00 ,00 -4 (45) 2 45 — 2 25 (503) 20 00 — 15 09 4
91 00 2 5
. 3 √ 6 ,45 . 00 ,00 -4 (45) 2 45 — 2 25 (503) 20 00 — 15 09 (506_) 4
91 00 2 5
. 3 9 √ 6 ,45 . 00 ,00 -4 (45) 2 45 — 2 25 (503) 20 00 — 15 09 (506_) 4 91 00 Вычислите 3 x 503, напишите, что ниже 2000, вычесть, сбейте следующие цифры. Затем удвойте «число» 253, которое находится над линией (без учета десятичной точки), и в скобках напишите удвоенное число 506 с пустой строкой рядом как указано: 5068 х 8 = 40544
5069 x 9 = 45621, что меньше 49100, поэтому 9 работает.Таким образом, до одного десятичного знака, √ 645 = 25.4
Комментарии посетителей
Я смутно помню, как изучал алгоритм извлечения квадратного корня в K-12, но, честно говоря, я не вижу в этом алгоритме никакой ценности, кроме любопытства. И я не из «реформаторской» толпы. Я полностью верю, что студентам не дадут калькулятор для использования до продвинутой алгебры или предварительного исчисления, а затем только научный калькулятор (не построение графиков). Вы действительно верите, что ученик уровня K-7 поймет, как / почему работает этот алгоритм?Я был рад узнать, что вы рекомендовали метод «оценки и проверки».Это то, что я также порекомендовал своей дочери, которая сейчас изучает квадратные корни в программе своей домашней школы. Метод «оценки и проверки» — хорошее упражнение в вычислении, умножении, а также запоминании полных квадратов.
Другой метод, более подходящий для студентов класса алгебры, — это упрощение радикала с помощью принятого метода. Затем найдите оставшийся квадратный корень с помощью метода оценки. Например, чтобы найти SQRT (1400), упростите его до SQRT (100) * SQRT (14), что равно 10 * SQRT (14).Затем найдите SQRT (14) методом оценки. Для квадратных корней из полных квадратов даже оценка не требуется.
Можно даже превратить задачу поиска квадратного корня в упражнение по компьютерному программированию, попросив студентов написать программу на javascript или другом языке, чтобы использовать систематический числовой метод оценки этого квадратного корня с помощью метода проверки и предположения. Или, на уровне исчисления, студент может написать программу, которая использует полином Тейлора для вычисления квадратного корня.
Майкл Саковски
Инструктор математики
Привет,Заметил несколько комментариев, связанных с использованием алгоритма для поиска квадратный корень из числа. В некоторых комментариях говорилось, что находить результат с помощью бумаги и ручки против калькулятора — это архаично. Что Может быть и так. Однако, когда я был на первом курсе в старшей школе (начало 70-х) Герр Куиннелл упомянул — когда класс подходил к концу — некоторые из того, что можно делать с математикой, в том числе находить квадратные корни.Итак, я спросил его, как это было сделано. Он показал мне метод алгоритма на борту.
Я не могу говорить о ценности знания того, как это используется в других профессии. В электронике нахождение квадратного корня является неотъемлемой частью часть дизайна. У нас есть детали, называемые резисторами. Они помогают в ограничении тока в схемах. Эти детали имеют номинальную мощность. Номинал резистора измеряется в «омах». В математическом смысле это можно найти, разделив вольт по амперам.10 вольт разделить на 0,001 ампера — это сопротивление 10 000 Ом. В качестве примера квадратного корня, если я знаю, что резистор на 10000 Ом имеет сопротивление мощность 0,25 Вт Я могу рассчитать максимальное напряжение наихудшего случая, которое может появиться на нем, прежде, чем может произойти повреждение. Это можно найти, взяв сопротивление значение — умножение номинальная мощность — и нахождение квадратного корня. Корень квадратный из 2500 равен 50. Эта часть выдерживала 50 вольт.
Моя точка зрения — я мог рассчитать результат «искусственными средствами».Так как кто-то нашел время, чтобы показать мне, как вычислить квадратный корень на доске, Мне не нужно было искать калькулятор. К тому времени я бы нашел калькулятор я уже придумал ответ. Найдите время, чтобы показать студентам то, как делаются такие вещи, как квадратный корень, имеет значение. На самом деле они не могут поставить это можно использовать позже в жизни — но некоторые просто могут.
Гарт Цена, CET
Я просто писал еще один комментарий, и каким-то образом компьютер отправил его до того, как я закончил.Я, должно быть, нажал не ту клавишу. Итак, позвольте мне закончить, сказав, что дети впервые в мире и исследуют его. Вычисление квадратного корня от руки было бы для них увлекательным занятием и отличным способом узнать о других темах математики. Да, кстати, у меня вообще не было никаких уроков по квадратным корням до старшей школы, а потом мы не научились их вычислять. Нас учили множить число под радикалом и извлекать точные квадраты, оставляя не- идеальные квадраты под корень.ПОТОМУ ЧТО ДАЖЕ УЧИТЕЛЬ НЕ ЗНАЛ, КАК СДЕЛАТЬ ПРАВИЛЬНО. До свидания с БогомРоберт Монро
это один из лучших сайтов, которые я посетил для правильного решения проблемы. Вы можете называть меня аркаиком, но когда я ходил в школу, они учили деление в столбик, чтобы находить квадратный корень из числа.
В БОЛЬШИНСТВЕ ЭТО УЧИТ ДУМАТЬ. Использование калькулятора — это чистая лень. Я чувствую, что наши дети думают, что получение основ в школе (РАННЕЕ) — это архаично.Вот почему, когда вы заходите в магазин и выставляете счет 16,75, и вы передаете кассиру двадцатидолларовую купюру, однодолларовую купюру и 75 центов, они понятия не имеют, какой должна быть сдача, если кассовый аппарат не сообщает им, сколько чтобы дать тебе. Это приводит к ленивому мышлению ИЛИ НЕМЫШЛЕНИЮ ВООБЩЕ.
Спасибо за ваше время.Раш Керлин
Я искал в Интернете давно забытую процедуру нахождения квадратного корня вручную и наткнулся на вашу веб-страницу. и хотел сказать, что многие (или вся) критика стандартного алгоритма называет его «архаичным», «тупиковым» методом и т. д.в пользу вавилонского метода не может быть оправдано. Дело в том, что использование бумаги и карандаша для деления длинных чисел или нахождения квадратных корней является архаичным и представляет собой тупиковый процесс в 21-м веке, независимо от того, какую рутину мы используем, поскольку мы больше не делаем этого из практических соображений. расчеты. Итак, вопрос в том, чему мы должны научить, чтобы познакомить студентов с фундаментальными техниками? Вавилонский метод — это численный метод, в отличие от другого метода, и имеет смысл обучить стандартной программе, которая работает сначала для любых чисел, а затем для других приближенных численных методов, вместо того, чтобы использовать численные методы типа предиктора-корректора, утверждающие, что они имеют применение где-то еще.Если мы пойдем с методами типа предиктор-корректор, необходимо также провести анализ ошибок, что не требуется для стандартного метода, поскольку в стандартной подпрограмме правильные цифры добавляются одну за другой на каждом шаге (в отличие от вавилонского метода, где содержание цифр может изменяться при каждом усреднении).С наилучшими пожеланиями,
Карл I. Яков
Профессор, Школа инженерии полимеров, текстиля и волокон
Профессор, Школа машиностроения им. Г. В. Вудрафа,
Технологический институт Джорджии
Вы ответили на вопрос «Поиск квадратного корня с помощью алгоритма».Я заметил, что ответ был оспорен несколькими людьми по нескольким причинам. Я хотел бы отметить, что предложенное решение является старейшим методом вычисления квадратного корня в западном мире. Меня описал Леонардо Пикано, иначе известный как Фибоначчи, в его книге Liber Abaci, глава 14. Первое издание было «написано» в 1202 году, а второе издание было «написано» в 1228 году. Я говорю «написано», потому что это было буквально написано от руки, как и все копии. Работа Иоганна Гутенберга над печатным станком началась только в 1436 году.
Леонардо научился этому методу во время своих арабских путешествий по Средиземному морю, а арабы научились этому у индуистской нации вокруг современной Индии. Метод в примере, который вы показываете, включает в себя некоторую современную интерпретацию, облегчающую чтение. Леонардо также показал геометрическую взаимосвязь, которая связана с тем, что мы сегодня понимаем под «аккордами». Это очень простое решение вопроса без использования калькулятора.Дэвид Т. Кэрротт, доктор философии
Я прочитал ваше предложение по вычислению квадратного корня без калькулятора.Я преподаю математику для учителей начальной школы и развивающие математические курсы (алгебра) для взрослых. Я считаю, что следует сосредоточиться на понимании числа, а не на упражнении по заученному алгоритму. Я предлагаю вам попросить ученика определить пару полных квадратов, между которыми находится число. Например, при нахождении sqrt 645 он попадает между sqrt 625, который равен 25, и sqrt 676, который равен 26. Таким образом, sqrt 645 должен быть между 25 и 26. Где он находится между? Всего 50 номеров от 676 до 625.645 — это 20 чисел больше 625, поэтому 20/50 = 0,4. Таким образом, sqrt 645 очень близко к 25,4
Этот метод предоставляет учащимся процесс, который улучшает их понимание чисел, не ожидая, что они запомнят алгоритм, и дает ответ с точностью до десятых.Андреа С. Леви, ред.
В настоящее время я учусь в MCC. Я изучаю курс для учителей начальной математики. Мы должны составить план урока, чтобы научить младших школьников пользоваться теоремой Пифагора.Мне нужно научиться разбирать теорию Пифагора для элементарного ребенка. Я застрял в квадратной корневой части.
Прочтите мой ответ на этот вопрос.
Метод, который вы показываете в статье, архаичен. Есть НАМНОГО более эффективный алгоритм. (Это алгоритм, который фактически используется негласно внутри калькулятора, когда вы нажимаете кнопку извлечения квадратного корня.)1. Оцените квадратный корень как минимум с 1 цифрой.
2. Разделите эту оценку на число, квадратный корень которого вы хотите найти.
3. Найдите среднее значение частного и делителя. Результатом становится новая оценка.Прелесть этого метода в том, что точность оценки растет очень быстро. Каждый цикл по существу удваивает количество правильных цифр. От 1-значной начальной точки вы можете получить 4-значный результат за два цикла. Если вы уже знаете квадратный корень из нескольких цифр, например sqrt (2) = 1,414, один цикл деления и среднего даст вам удвоение цифр (в данном случае восемь).
Этот метод не только позволяет вручную находить квадратные корни, но и может использоваться, если у вас есть только дешевый четырехфункциональный калькулятор. Если ученики могут получить квадратный корень вручную, они не найдут квадратного корня таким загадочным. Также этот метод является хорошим первым примером последовательного решения проблемы.
Дэвид Чендлер
Другой способ называется Вавилонский метод угадать и разделить, и он действительно быстрее. Это также то же самое, что и при применении метода Ньютона.См., Например, поиск квадратного корня из 20 с использованием 10 в качестве начального предположения:
Предположение Разделить Найти среднее 10 20/10 = 2 среднее 10 и 2, чтобы дать новое предположение 6 6 20/6 = 3,333 среднее значение 3,333 и 6 дает 4,6666 4,666 20 / 4,666 = 4,1414 среднее 4.666,4,1414 = 4,4048 4,4048 20 / 4,4048 = 4,5454 в среднем = 4,4700 4,4700 20 / 4,4700 = 4,4742 в среднем = 4,4721 2021 4,47217 среднее = 4,47214 Это уже с 4 десятичными знаками 4,47214 20 / 4,47214 = 4,472132 среднее = 4,472135 4.472135 20 / 4,472135 = 4,472137 среднее = 4,472136
Плакат утверждает, что метод статьи «архаичен» и что «вавилонский метод» более эффективен. На первый взгляд может показаться, что это так, потому что в примере с плакатом вычисляется квадратный корень из двузначного целого числа 20 вместо 645 в примере статьи.Однако я фактически разработал пример статьи (квадратный корень из 645), используя оба метода, и обнаружил, что вавилонский метод требует 9 «циклов деления и среднего», чтобы прийти к ответу.Кроме того, вавилонский метод требует от ученика выполнения пятизначного деления в столбик — немалый подвиг для ученика начальной или средней школы. С другой стороны, метод, описанный в статье, требует от студента выполнить только одну задачу из четырех шагов и длинного деления, решив самое большее полдюжины или около того задач умножения из четырех цифр на 1 цифру.
Следовательно, разумно сделать вывод, что вавилонский метод больше подходит для решения с помощью калькулятора или решения с помощью компьютера, в то время как метод статьи больше подходит для решения с помощью карандаша и бумаги.
Поскольку предметом статьи было то, как научить ученика начальной или средней школы легко находить квадратные корни карандашным методом, «архаичный» метод статьи кажется наиболее подходящим.
Алексей
В ответ на сообщение Алекса: как вам понадобилось 9 циклов, чтобы произвести 25,4 цикла с использованием вавилонского метода на 645? Это займет 1,5 шага, если вы используете свое предположение как 25
1) 645/25 = 25,8
(25 + 25,8) / 2 = 25,42) 645/25.4 ≈ 25,39
Вавилонский метод очень эффективен, если уже известно много полных квадратов для приближения к исходному значению. Я считаю, что студенты не могут понять причины, лежащие в основе алгоритма в этом посте, в то время как метод деления и среднего кажется более интуитивным, если они раньше работали со средними.
Даниил
Я сомневаюсь в том, чтобы обучать методу деления в столбик для извлечения квадратных корней. Вавилонский метод легче запомнить и понять, и он дает столько же практики в базовой арифметике.Что еще более важно, он имеет четкую связь с такими темами, как метод Ньютона и рекурсивные последовательности, которые будут встречаться в исчислении и за его пределами. Метод длинного деления несколько быстрее для ручного расчета, но он не приводит к другим важным темам — это тупик.Давид
Я учился на старых компьютерных схемах и двоичных аппаратных алгоритмах. Метод, используемый для вычисления корня из 645, является методом, используемым в высокопроизводительных двоичных вычислениях, поскольку он требует только сдвига, вычитания и сравнения, которые являются командами одного цикла / этапа или перенаправлены на сопроцессор.Преобразуйте число в двоичное, разделите его на 2 битовые группы и используйте описанную выше процедуру. Умножение и деление требует от 10 до сотен циклов / стадий и уничтожает преформ и конвейеры. Квадратный корень вычисляется быстрее, чем деление, поскольку деление выполняется через 1 бит за цикл / этап, а квадратный корень проходит через 2 бита за цикл.Брэд
что такое квадратный корень из -1?Тамара Ярдли
-1 не может иметь квадратный корень (по крайней мере, не действительный), потому что любые два числа с одинаковым «знаком» (+/- положительный или отрицательный) при умножении будут равны положительному числу.Попробуйте: +2 × +2 = 4 и -2 × -2 = 4.
Так как квадратный корень из числа должен равняться этому числу при умножении на себя. Когда вы умножаете это число на себя и задаете его как полное уравнение (n * n = x), два множителя (n и n) либо положительны, либо отрицательны, поскольку это одно и то же число. Следовательно, их продукт будет положительным. Никакое действительное число, умноженное само на себя, не будет равно отрицательному числу, поэтому -1 не может иметь действительный квадратный корень.
Блейк
Квадратный корень из -1 не является действительным числом.Обозначается буквой i и называется мнимой единицей. Из i и его кратных мы получаем чисто мнимые числа, такие как 2i, 5.6i, -12i и так далее. Это приводит к совершенно новой системе счисления комплексных чисел, в которой числа имеют действительную и мнимую части (например, 5 + 3i или -20 — 40i). И с помощью этой системы счисления можно сделать много увлекательной математики!
Я пытался найти в сети старый способ вычисления квадратного корня путем деления в столбик. ДА, я нашел это.Прочтите ответы и не соглашусь со многими плакатами.Найти квадрат 645 легко, если вы знаете 252 и 262, но я никогда не запоминал квадраты чисел от 1 до 30 или около того, я запоминал только до 12X12 (старая имперская система)
Угадать, что в квадрате 645 будет около 25, — это здорово, но если вы угадаете, что это 2, то перед вами стоит более серьезная проблема.
Я вижу, что «другие» плакаты находят более легкие и быстрые способы … вот в чем проблема сегодня. Будем искать легкий путь без понимания.С вашим методом это может сделать любой, у кого есть навыки деления в столбик и простое умножение. Самое простое решение — купить калькулятор и избегать всех умственных способностей. ржу не могу
корень квадратный из 645 мммм 20
645/20 = 32,25, среднее 52,25 = 26,25
645 / 26,25 = 24,57, среднее значение 50,82 = 25,41Метод усреднения, кажется, работает, но он не учит большому делению … вроде как выше / ниже в The Price is Right.
Я предполагаю, что квадрат 645 равен 25.41 …. ничего себе, это работает с первого раза, чему я научился, ничего.
Используя метод усреднения, каков квадратный корень из 9331671 …. моя первая предполагаемая оценка — 10, получайте удовольствие!
9331671/10 = 933167,1 + 10 = 9331681,1 / 2 = 466588,55
9331671 / 466588,55 = 19,999785 + 466588,55 = 466607,57 / 2 = 233303,285
9331671 / 233303,285 = 39,99802 + 233303,285 = 233343,27 / 2 = 116671,235
…
…
…
…
…
Ах да, это дети из 3 или 4 класса, которые занимаются длинной математикой с 8-значными числами… так много для усреднения. И какова степень значимости, поскольку мы работаем с одним десятичным знаком или 3 … не нужно «усреднять» слишком рано, иначе мы можем потерять значащие цифры. Если мы работаем с миллиардами, то слишком быстрое снижение цифр может иметь ОГРОМНУЮ разницу.Адриан
Я непрофессионал, который зашел на сайт через поиск в Google на тему «как вычислить квадратный корень». Я прочитал презентацию, затем посмотрел ответы. Я должен сказать, что был встревожен комментарием Андреа С.Леви, редактор Д., где она предположила, что запоминание алгоритма менее желательно, чем понимание числа.В настоящее время я работаю техническим писателем в фирме, которая занимается разработкой программного обеспечения для кредитных союзов. Понимание всех алгоритмов, используемых в финансовом мире, крайне важно для нас, чтобы делать то, что мы делаем. Фактически, один из расчетов, который мы используем для определения амортизации потребительского кредита с комиссией за определенный период времени, поразительно похож на представление квадратного корня. Расчет должен быть написан инженером-программистом для машины, чтобы в конечном итоге он оставался в сознании человека.Если инженер не знает алгоритма, последствия будут нести тысячи потребителей. Я полагаю, что запоминание — это просто еще один инструмент в коробке. Используйте его, когда это уместно.
С уважением,
Майкл Келли
Ньюбери-Парк, Калифорния.
Последний комментатор на странице (Адриан) сказал, что она никогда не учила квадраты от 1 до 30. Это напоминает трюк, который я недавно изучил для нахождения квадратов, близких к 50. Начните с квадрата 50, 2500, добавьте 100 раз расстояние между 50 и числом, а затем сложите квадрат расстояния 50 и числа.Например, 43 2 = 2500 — 700 + 49 = 1849. Это происходит от простого тождества FOIL (50 + x) 2 = 2500 — 100x + x 2 . В этом тождестве x — это расстояние между 50 и числом. Если число 43 (как в моем примере), x равно -7. Если число 54, то x равно 4. Таким образом, если вы запомните свои квадраты от 1 до 25, вы получите квадраты от 26 до 75 «бесплатно».Если идея запоминания квадратов от 1 до 25 кажется сложной, это не так. Несколько недель назад, не зная этого трюка, я знал сразу около 13 человек, а еще несколько разбросались тут и там.Я составил в Excel таблицу, в которой перечислены числа от 1 до 25 рядом с их квадратами, распечатал ее и повесил на стену своего кабинета. Квадраты, которые я не запомнил в этих первых 25, теперь я могу получить за несколько секунд (например, для квадрата 23 я все еще считаю от 20 квадратов: 400, 441, 484, * 529 *). Даже не зная их всех, я могу найти квадраты от 1 до 75 менее чем за 10 секунд (мыслительный процесс для нахождения 73 в квадрате навскидку: «73 больше 23, чем 50. Что снова возведено в квадрат 23?» 400, 441, 484, 529! 2500 + 2300 + 529 = 5329.Сделанный!»)
Дэвид Леви
См. Также
Другой пример использования алгоритма извлечения квадратного корня
Объяснение того, почему работает этот алгоритм извлечения квадратного корня.
Бесплатные рабочие листы для вычисления квадратного корня, включая генератор рабочих листов
Геометрический вид алгоритма извлечения квадратного корня
Квадратный корень методом деления и среднего
Объяснение и пример старинного алгоритма приближения квадратных корней.Алгоритмы извлечения квадратного корня
Формулы для рекуррентного отношения и итерации Ньютона, которые можно использовать для аппроксимации квадратных корней. Для математически мыслящих.Кромка
Новый способ получения квадратного корня из специальной группы чисел более простым способом.Решение квадратных уравнений путем извлечения квадратного корня
Purplemath
Давайте еще раз посмотрим на последнюю проблему на предыдущей странице:
На предыдущей странице я решил это квадратное уравнение, разложив на множители разность квадратов в левой части уравнения, а затем установив каждый коэффициент равным нулю и т. Д., И т. Д.Решение было « x = ± 2». Однако —
Я также могу попытаться выделить член в квадрате переменной в левой части уравнения (то есть я могу попытаться получить член x 2 сам по себе на одной стороне знака «равно»), переместив числовую часть (то есть 4) в правую часть, например:
MathHelp.com
Когда я решаю уравнение, я знаю, что могу делать все, что захочу, с этим уравнением , если я проделываю одно и то же с обеими сторонами этого уравнения . В левой части этого конкретного уравнения у меня есть x 2 , и мне нужен старый добрый x .Чтобы превратить x 2 в x , я могу извлечь квадратный корень из каждой части уравнения, например:
x = ± 2
Тогда решение будет x = ± 2, точно так же, как это было, когда я решил путем факторизации разности квадратов.
Зачем мне понадобился знак «±» (то есть «плюс-минус») на 2, когда я извлек квадратный корень из 4? Потому что я пытаюсь найти всех значений переменной, которые делают исходное утверждение истинным, и это могло быть либо положительное 2, либо отрицательное 2, возведенное в квадрат, чтобы получить 4 в исходном уравнении.
Эта двойственность похожа на то, как у меня было два фактора, один «плюс» и один «минус», когда я использовал формулу разности квадратов для решения того же уравнения на предыдущей странице.
«Нахождение решения уравнения» — это процесс, сильно отличающийся от «вычисления квадратного корня из числа». При нахождении «квадратного корня» числа мы имеем дело исключительно с положительным значением. Почему? Потому что именно так определяется квадратный корень из числа.Значение квадратного корня из числа может быть только положительным, потому что так определяется «квадратный корень из числа».
С другой стороны, решение уравнения, то есть нахождение всех возможных значений переменной, которые мог бы использовать в уравнении, отличается от простой оценки выражения, которое уже определило как имеющее только одно значение.
Держите этих двоих прямо! Число с квадратным корнем имеет только одно значение, а уравнение с квадратным корнем имеет два из-за переменной.
В математике мы должны иметь возможность получить один и тот же ответ, независимо от того, какой действительный метод мы использовали, чтобы прийти к этому ответу. Итак, сравнение ответа, полученного мной выше, с ответом, полученным мною на предыдущей странице, подтверждает, что мы должны использовать «±» при извлечении квадратного корня для решения.
(Вы можете сомневаться в моей работе выше на этапе, когда я извлекал квадратный корень из любой стороны, потому что я поставил знак «±» только на одной стороне уравнения.Разве я не должен добавить этот символ к обеим сторонам уравнения ? Вроде да. Но если бы я поместил это в обе стороны уравнения, изменилось бы что-нибудь на самом деле? Нет. Попробуйте все варианты, если вы не уверены.)
Преимущество этого процесса извлечения квадратного корня состоит в том, что он позволяет нам решать некоторые квадратичные уравнения, которые мы не могли решить раньше, используя только факторинг. Например:
Эта квадратичная часть имеет квадратную и числовую части.Я начну с добавления числового члена к другой стороне уравнения (чтобы квадрат был сам по себе), а затем извлеку квадратный корень из обеих сторон. Мне нужно не забыть упростить квадратный корень:
x 2 -50 = 0
x 2 = 50
Тогда мое решение:
В то время как мы могли бы получить предыдущее целочисленное решение путем факторизации, мы никогда не смогли бы получить это радикальное решение путем факторизации.Факторинг явно полезен для решения некоторых квадратных уравнений, но дополнительные виды техники позволяют нам находить решения дополнительных видов уравнений.
Решить (
x — 5) 2 — 100 = 0.
Эта квадратичная часть имеет квадратную и числовую части. Я начну с добавления строго числового члена в правую часть уравнения, чтобы квадрат биномиального выражения, содержащего переменную, находился в левой части.Затем я извлечу квадратный корень из обеих частей, запомнив «±» в числовой части, и затем упросту:
( x — 5) 2 — 100 = 0
( x — 5) 2 = 100
x — 5 = ± 10
х = 5 ± 10
x = 5-10 или x = 5 + 10
x = –5 или x = 15
Это уравнение после извлечения квадратного корня из любой стороны не содержит радиальных чисел.Благодаря этому я смог упростить свои результаты вплоть до простых значений. Мой ответ:
Предыдущее уравнение является примером уравнения, в котором неосторожный ученик опускает знак «±» при решении и не понимает, как книга получила ответ « x = –5, 15».
У этих учеников есть дурная привычка не утруждать себя записью знака «±», пока они не проверит свои ответы на обратной стороне книги и внезапно «не вспомнят», что они «имели в виду» поставить «±» там, когда они ‘ d извлекает квадратный корень из любой стороны уравнения.
Но эта «магия» работает только тогда, когда у вас есть ответ (чтобы напомнить вам) и когда раствор содержит радикалы (что не всегда случается). В остальных случаях «напоминания» не будет. Ошибка в пропуске «±» может быть смертельной, особенно при тестировании. Не будь этим учеником. Всегда не забывайте вставлять «±».
Между прочим, поскольку решение предыдущего уравнения состояло из целых чисел, эту квадратичную можно также решить путем умножения квадрата, разложения на множители и т. Д .:
( x — 5) 2 — 100 = 0
x 2 -10 x + 25-100 = 0
x 2 -10 x -75 = 0
( x -15) ( x + 5) = 0
x — 15 = 0, x + 5 = 0
x = 15, –5
Решить (
x — 2) 2 — 12 = 0
Эта квадратичная часть имеет квадратную и числовую части.Я добавлю числовую часть с другой стороны, так что квадратная часть с переменной будет сама по себе. Затем я извлекаю квадратный корень из обеих сторон, не забывая добавлять «±» к числовой стороне, а затем упрощаю:
( x — 2) 2 — 12 = 0
( x -2) 2 = 12
Я не могу больше это упрощать. В моем ответе будут радикалы.Мое решение:
Это квадратное уравнение, в отличие от предыдущего, также не могло быть решено с помощью факторизации. Но как бы я решил это, если бы у них было , а не , давая мне квадратичную, уже переведенную в форму «(часть в квадрате) минус (часть числа)»? Эта проблема приводит к следующей теме: решение путем завершения квадрата.
URL: https: // www.purplemath.com/modules/solvquad2.htm
.

 2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.
2 c = 0. В таком случае вы можете решить это уравнение, используя свойство простого квадратного корня.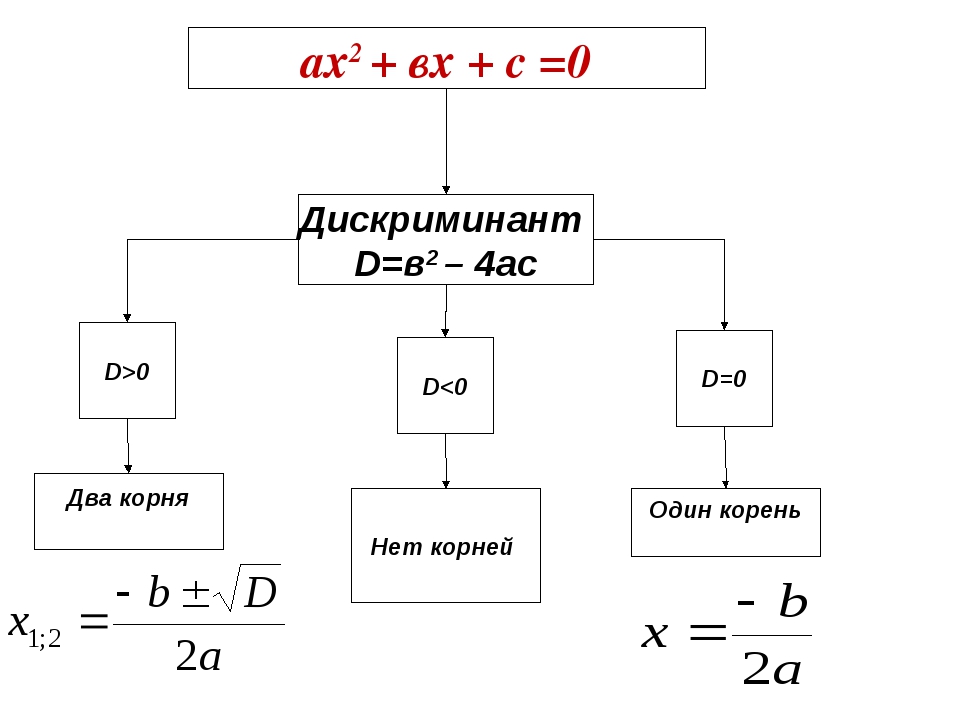 Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
Чтобы правильно извлекать корни уравнения онлайн, важно хорошо знать терминологию, основные математические понятия. Что такое квадратный корень – это процесс, обратный возведению натурального числа в квадрат (перемножению числа или понимаемого под ним математического объекта на самое себя).
 Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24.
Затем извлекаем корень из 64, он равен 8, подобную процедуру проводим со вторым из множителей. Квадратный корень из девяти равен 3. Осталось найти результат: 8х3=24. Корень 576 равен 24. Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
Если корень необходимо вычислить из десятичной дроби, нужно представить ее в виде натуральной. Например, 0,64 это 64/100. В результате получаем 8/10 или 0,8. Все довольно просто. Если из делимого или делителя корень не извлекается, при решении примеров или задач его оставляют под знаком корня.
 Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
Важно помнить, что в подкоренном выражении с четным показателем не может быть отрицательных чисел. С нечетными числами такое возможно. Результат в этом случае тоже будет отрицательным.
 д.) в частности,
при нахождении пределов, производных и интегралов;
д.) в частности,
при нахождении пределов, производных и интегралов;
 Найдём дискриминант:
Найдём дискриминант: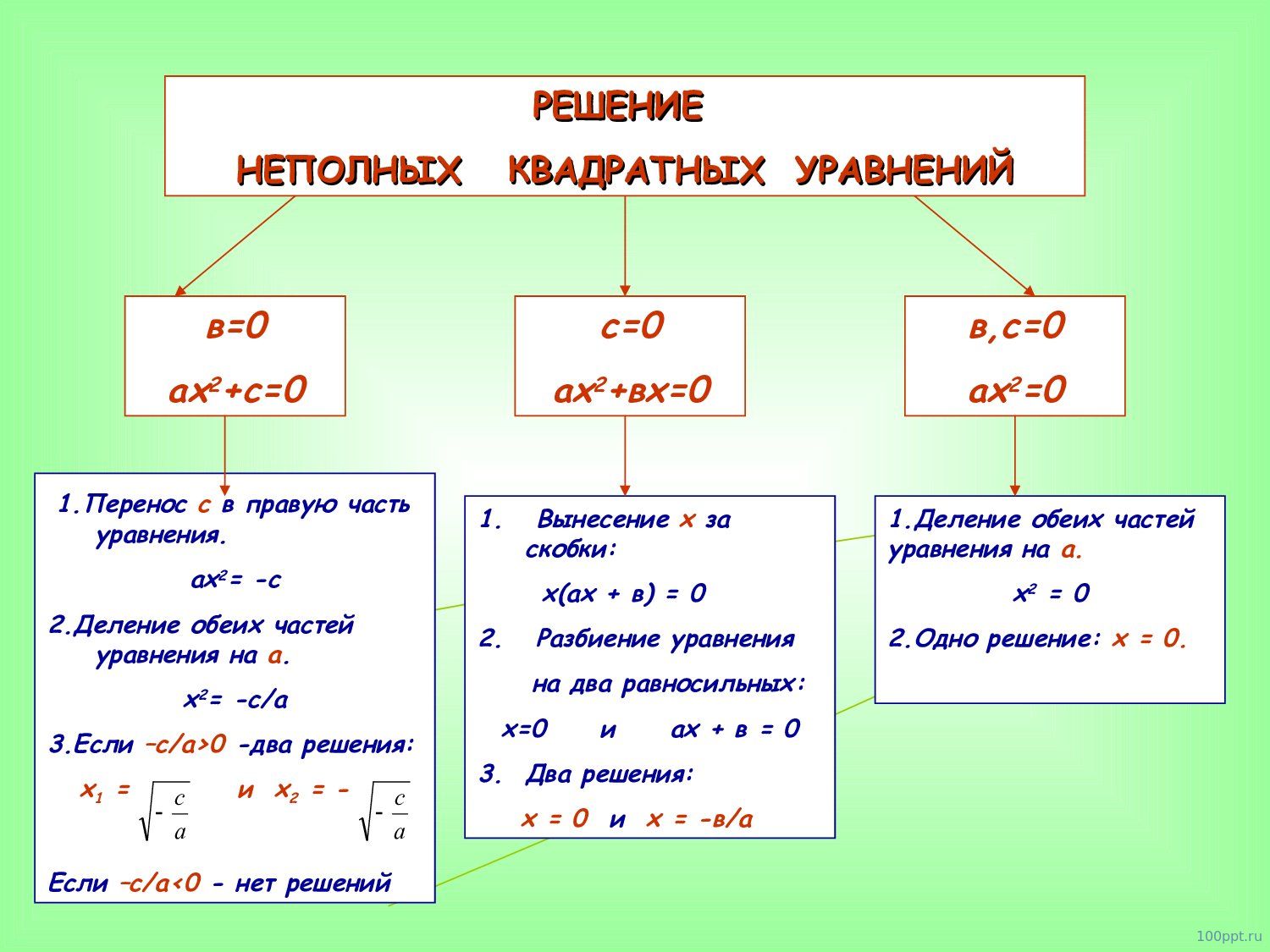 Определить, сколько действительных корней имеет квадратное уравнение:
Определить, сколько действительных корней имеет квадратное уравнение:








 Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.
Превратим неприведенное уравнение: 8x2 + 20x — 9 = 0 — в приведенное.


 Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.
Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = — c/а. Ура, больше у этого уравнения нет корней.


 Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:
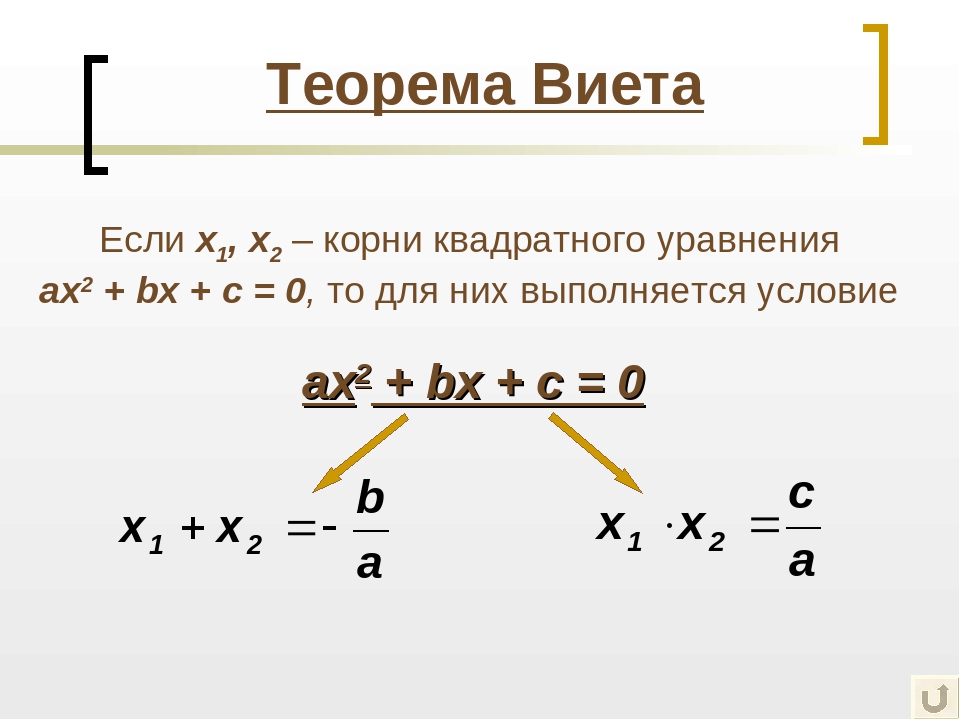
 Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.
Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

 Рассмотрим, как появилась эта формула.
Рассмотрим, как появилась эта формула.
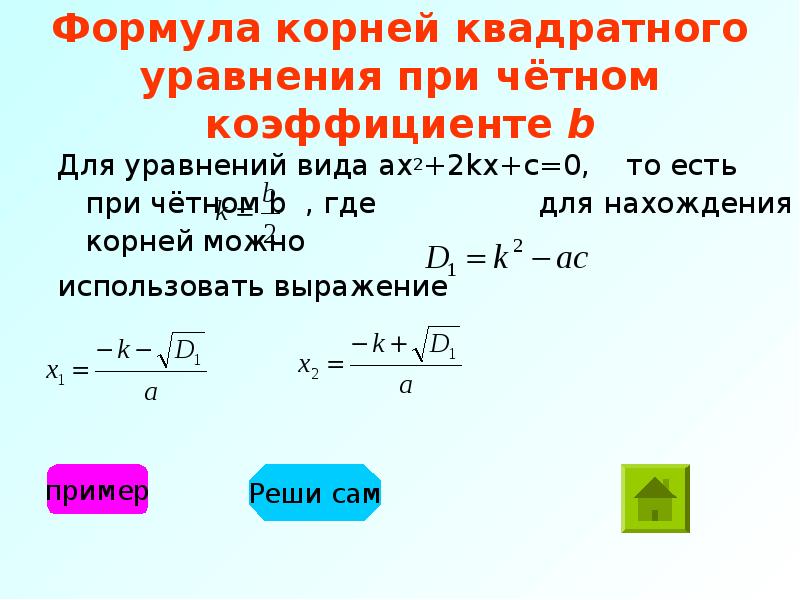 Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения
Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
Например, по виду уравнения 3x2— 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.
 х2=а. Алгебра 8 класс. Математика. Образование.
х2=а. Алгебра 8 класс. Математика. Образование. Что обязательно надо учесть при извлечении квадратного корня. Сокращение корня и степени. Как извлечь корень из выражения в степени. Примеры с решением. Задания с объяснением. Пример 1: Найдите значение выражения. Пример 2: Упростить выражение.
Что обязательно надо учесть при извлечении квадратного корня. Сокращение корня и степени. Как извлечь корень из выражения в степени. Примеры с решением. Задания с объяснением. Пример 1: Найдите значение выражения. Пример 2: Упростить выражение.
 грамм. y
грамм. y 08.2002
08.2002  03.20202005 г.
03.20202005 г.  Вы не поверите, но благодаря этому программному обеспечению мои оценки за тесты значительно улучшились. Я просто хочу поделиться этим, потому что я в восторге от великолепия программы.
Вы не поверите, но благодаря этому программному обеспечению мои оценки за тесты значительно улучшились. Я просто хочу поделиться этим, потому что я в восторге от великолепия программы. Я определенно думаю, что тебе стоит попробовать.
Я определенно думаю, что тебе стоит попробовать. Алгебратор — действительно отличная программа для алгебры. Я использовал его на нескольких уроках алгебры — лечебной алгебре, студенческой алгебре и предалгебре. Я просто набираю проблему из книги и, нажимая «Решить», появляется пошаговое решение. Программа очень рекомендуется.
Алгебратор — действительно отличная программа для алгебры. Я использовал его на нескольких уроках алгебры — лечебной алгебре, студенческой алгебре и предалгебре. Я просто набираю проблему из книги и, нажимая «Решить», появляется пошаговое решение. Программа очень рекомендуется. Нет ничего плохого в том, чтобы попробовать это один раз. Дайте пожалуйста ссылку на программу.
Нет ничего плохого в том, чтобы попробовать это один раз. Дайте пожалуйста ссылку на программу. Д.)
Д.) .. но ничего особенного.
.. но ничего особенного. 53 и 11,47 (с точностью до 2 знаков после запятой)
53 и 11,47 (с точностью до 2 знаков после запятой) 01.2003
01.2003  03.2004
03.2004 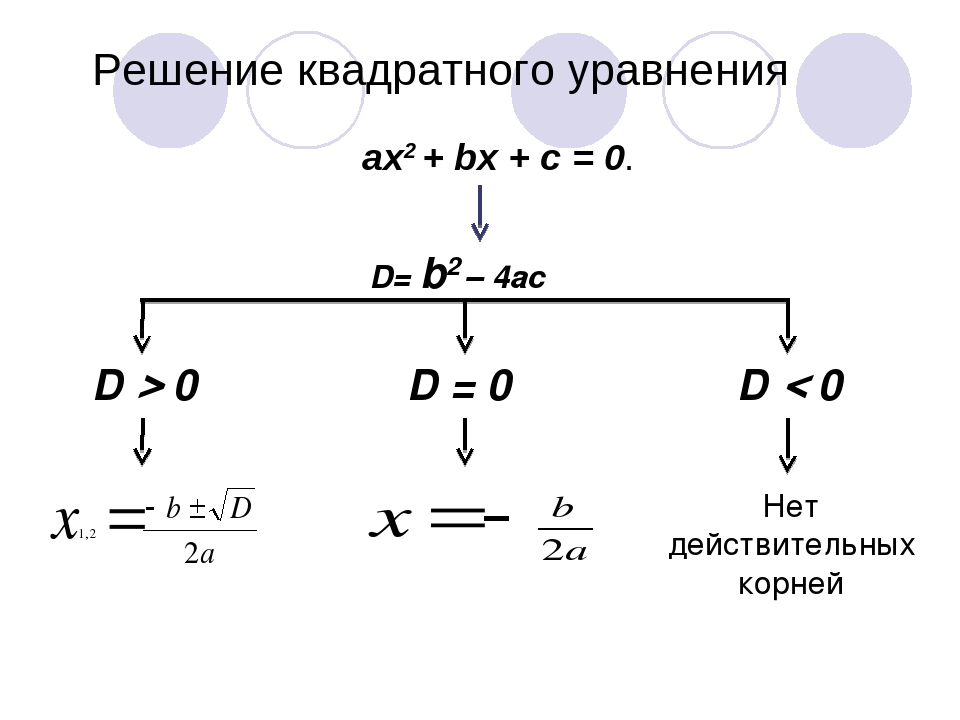 10.2002
10.2002 
 12.2001
12.2001  07.2004
07.2004 
 Это приводит к теме
комплексные числа, которые мы рассмотрим позже в этом курсе.
Это приводит к теме
комплексные числа, которые мы рассмотрим позже в этом курсе. уравнение.Например, в последнем уравнении получаем:
уравнение.Например, в последнем уравнении получаем: