Основные понятия, решение систем линейных неравенств. Калькулятор онлайн
Рассмотрим на примерах, как решить систему линейных неравенств.
4x + 29 \end{array} \right.\]» title=»Rendered by QuickLaTeX.com»>
Чтобы решить систему, нужно каждое из составляющих её неравенств. Только решение принято записывать не по отдельности, а вместе, объединяя их фигурной скобкой.
В каждом из неравенств системы неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
После упрощения обе части неравенства надо разделить на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не изменяется. Второе неравенство делим на отрицательное число, поэтому знак неравенства надо изменить на противоположный:
Title=»Rendered by QuickLaTeX.com»>
Решение неравенств отмечаем на числовых прямых:
В ответ записываем пересечение решений, то есть ту часть, где штриховка есть на обеих прямых.
Ответ: x∈[-2;1).
В первом неравенстве избавимся от дроби. Для этого обе части умножим почленно на наименьший общий знаменатель 2. При умножении на положительное число знак неравенства не изменяется.
Во втором неравенстве раскрываем скобки. Произведение суммы и разности двух выражений равно разности квадратов этих выражений. В правой части — квадрат разности двух выражений.
Title=»Rendered by QuickLaTeX.com»>
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком и упрощаем:
Обе части неравенства делим на число, стоящее перед иксом. В первом неравенстве делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Во втором — делим на положительное число, знак неравенства не изменяется:
Title=»Rendered by QuickLaTeX.com»>
Оба неравенства со знаком «меньше» (не существенно, что один знак — строго «меньше», другой — нестрогий, «меньше либо равно»). Можем не отмечать оба решения, а воспользоваться правилом « «.
Отмечаем его решение на числовой прямой:
Ответ: x∈(-∞;1].
Раскрываем скобки. В первом неравенстве — . Оно равно сумме кубов этих выражений.
Во втором — произведение суммы и разности двух выражений, что равно разности квадратов. Поскольку здесь перед скобками стоит знак «минус», лучше их раскрытие провести в два этапа: сначала воспользоваться формулой, а уже потом раскрывать скобки, меняя знак каждого слагаемого на противоположный.
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком:
Title=»Rendered by QuickLaTeX.com»>
Оба знака «больше». Используя правило «больше большего», сводим систему неравенств к одному неравенству. Большее из двух чисел 5, следоветельно,
Title=»Rendered by QuickLaTeX.com»>
Решение неравенства отмечаем на числовой прямой и записываем ответ:
Ответ: x∈(5;∞).
Поскольку в алгебре системы линейных неравенств встречается не только в качестве самостоятельных заданий, но и в ходе решения разного рода уравнений, неравенств и т.
д., важно вовремя усвоить эту тему.
В следующий раз мы рассмотрим примеры решения систем линейных неравенств в частных случаях, когда одно из неравенств не имеет решений либо его решением является любое число.
Рубрика: |
Не все знают, как решать неравенства, которые по своей структуре имеют сходные и отличительные черты с уравнениями. Уравнение – упражнение, состоящее их двух частей, между которыми стоит знак равенства, а между частями неравенства может стоять знак «больше» или «меньше». Таким образом, прежде чем найти решение конкретного неравенства, мы должны понимать, что стоит учитывать знак числа (положительное или отрицательное), если возникает необходимость умножения обеих частей на какое-либо выражение. Этот же факт следует учитывать, если требуется для решения неравенства возводить в квадрат, поскольку возведение в квадрат проводится путем умножения.
Как решать систему неравенств
Намного сложнее решать системы неравенств, чем обычные неравенства.
Как решать неравенства 9 класс, рассмотрим на конкретных примерах. Следует понимать, что перед тем, как решать квадратные неравенства (системы) или любые иные системы неравенств, необходимо решить каждое неравенство по отдельности, после чего сопоставить их. Решением системы неравенства будет либо положительный, либо отрицательный ответ (имеет система решение или не имеет решения).
Задача — решить совокупность неравенств:
Решим каждое неравенство по отдельности
Строим числовую прямую, на которой изображаем множество решений
Так как совокупность — это объединение множеств решений, то это множество на числовой прямой должно быть подчеркнуто минимум одной линией.
Решение неравенств с модулем
Данный пример покажет, как решать неравенства с модулем. Итак, у нас имеется определение:
Нам необходимо решить неравенство:
Прежде чем решить такое неравенство, необходимо избавиться от модуля (знака)
Запишем, основываясь данными определения:
Теперь следует решать каждую из систем по отдельности.
Построим одну числовую прямую, на которой изобразим множества решений.
В результате у нас получилась совокупность, объединяющая множество решений.
Решение квадратичных неравенств
Используя числовую прямую рассмотрим на примере решение квадратичных неравенств. У нас есть неравенство:
Нам известно, что графиком квадратного трехчлена является парабола. Так же нам известно, что ветви параболы направленные вверх, если а>0.
x 2 -3x-4
Пользуясь теоремой Виета находим корни х 1 = — 1; х 2 = 4
Изобразим параболу, вернее, ее эскиз.
Таким образом, мы выяснили, что значения квадратного трехчлена будут меньше 0 на отрезке от – 1 до 4.
У многих возникают вопросы при решении двойных неравенств типа g(x)
На самом деле, методов решения неравенств несколько, поэтому вы можете использовать для решения сложных неравенств графический способ.
Решение дробных неравенств
Более тщательного подхода требуют к себе дробные неравенства.
Это обусловлено тем, что в процессе решения некоторых дробных неравенств может измениться знак. Перед тем, как решать дробные неравенства, необходимо знать, что для их решения используется метод интервалов. Дробное неравенство необходимо представить таким образом, чтобы одна сторона от знака выглядела, как дробно-рациональное выражение, а вторая – «- 0». Преобразуя неравенство таким образом, мы получим в результате f(x)/g(x) > (.
Решение неравенств методом интервалов
Методика интервалов основана на методе полной индукции, то есть, необходимо для нахождения решения неравенства перебрать все возможные варианты. Данный метод решения, возможно, и не потребуется ученикам 8-х классов, поскольку они должны знать, как решать неравенства 8 класс, которые представляют собой простейшие упражнения. А вот для более старших классов этот метод незаменим, так как помогает решить дробные неравенства. Решение неравенств с помощью данной методики основано и на таком свойстве непрерывной функции, как сохранение знака между значениями, в которых она обращается в 0.
Построим график многочлена. Это непрерывная функция, приобретающая значение 0 3 раза, то есть, f(x) будет равен 0 в точках x 1 , x 2 и x 3 , корнях многочлена. В промежутках между этими точками, знак функции сохраняется.
Так как для решения неравенства f(x)>0 нам необходим знак функции, переходим к координатной прямой, оставив график.
f(x)>0 при x(x 1 ; x 2) и при x(x 3 😉
f(x)x(- ; x 1) и при х (x 2 ; x 3)
На графике наглядно показаны решения неравенств f(x)f(x)>0 (синим цветом решение для первого неравенства, а красным – для второго). Чтобы определить Для определения знак функции на интервале, достаточно того, чтобы вам был известен знак функции в одной из точек. Данная методика позволяет быстро решать неравенства, в которых левая часть разложена на множители, потому что в таких неравенствах достаточно просто найти корни.
На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств.
Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.
Тема : Рацион альные неравенства и их системы
Урок: Основн ые понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства , и квадратные и рациональные. Теперь перейдем к решению систем неравенств — сначала линейных систем . Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратних корня, т.е.
Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.
Изобразим на оси ox множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение.
Такой метод изображения решения системы неравенств иногда называют методом крыш.
Решением системы является пересечение двух множеств.
Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.
Решить систему неравенств:
Ответ: (7; 10].
4. Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
Ответ: система противоречива.
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп.
— М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Портал Естественных Наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Центр образования «Технология обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.
: ил. №№ 53; 54; 56; 57.
Одна из тем, которая требует от учеников максимума внимания и усидчивости, это решение неравенств. Такие похожие на уравнения и при этом сильно от них отличающиеся. Потому что к их решению нужен особый подход.
Свойства, которые потребуются для нахождения ответа
Все они применяются для того, чтобы заменить имеющуюся запись равносильной. Большая их часть похожа на то, что было в уравнениях. Но есть и отличия.
- Функцию, которая определена в ОДЗ, или любое число можно прибавить к обеим частям исходного неравенства.
- Аналогичным образом возможно умножение, но только на положительную функцию или число.
- Если это действие выполняется с отрицательными функцией или числом, то знак неравенства нужно заменить на противоположный.
- Функции, которые являются неотрицательными, можно возводить в положительную степень.
Иногда решение неравенств сопровождается действиями, которые дают посторонние ответы. Их нужно исключить, сравнив область ОДЗ и множество решений.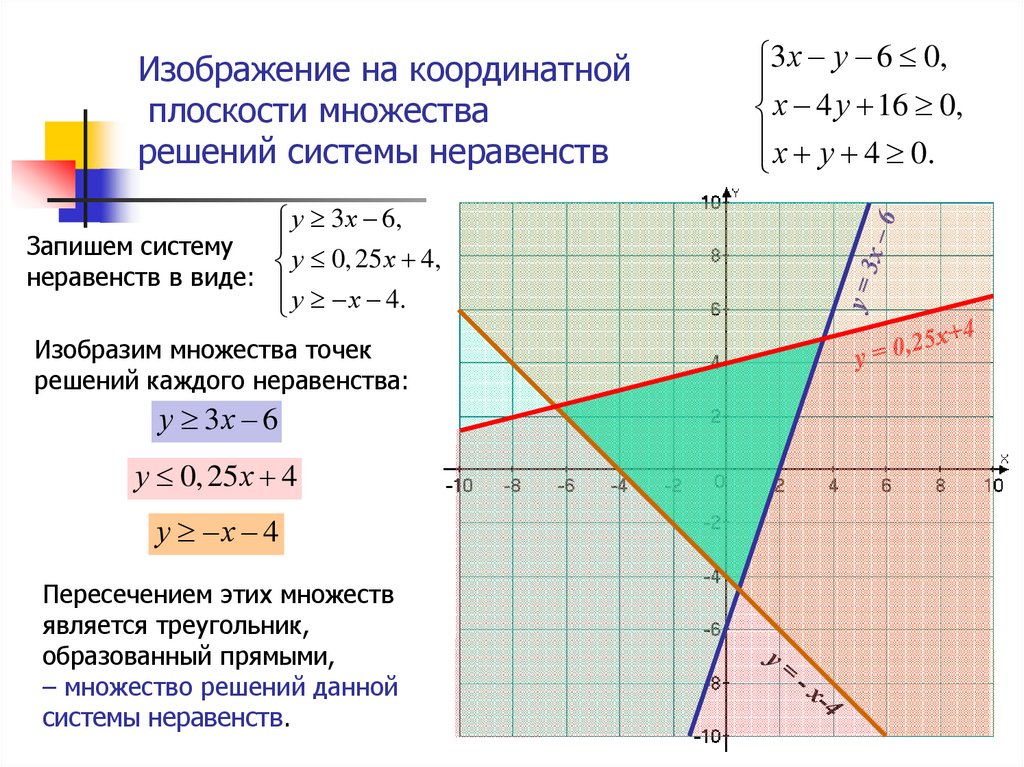
Использование метода интервалов
Его суть состоит в том, чтобы свести неравенство к уравнению, в котором в правой части стоит ноль.
- Определить область, где лежат допустимые значения переменных, то есть ОДЗ.
- Преобразовать неравенство с помощью математических операций так, чтобы в его правой части стоял ноль.
- Знак неравенства заменить на «=» и решить соответствующее уравнение.
- На числовой оси отметить все ответы, которые получились во время решения, а также интервалы ОДЗ. При строгом неравенстве точки нужно нарисовать выколотыми. Если присутствует знак равенства, то их полагается закрасить.
- Определить знак исходной функции на каждом интервале, получившемся из точек ОДЗ и делящих его ответов. Если при переходе через точку знак функции не изменяется, то она входит в ответ. В противном случае — исключается.
- Граничные для ОДЗ точки нужно дополнительно проверить и только потом включать или нет в ответ.
- Ответ, который получается, нужно записать в виде объединенных множеств.
Немного о двойных неравенствах
Они используют в записи сразу два знака неравенства. То есть некоторая функция ограничена условиями сразу дважды. Такие неравенства решаются, как система из двух, когда исходное разбито на части. И в методе интервалов указываются ответы от решения обоих уравнений.
Для их решения также допустимо использовать свойства, указанные выше. С их помощью удобно приводить неравенство к равенству нулю.
Как обстоят дела с неравенствами, в которых имеется модуль?
В этом случае решение неравенств использует следующие свойства, причем они справедливы для положительного значения «а».
Если «х» принимает алгебраическое выражение, то справедливы такие замены:
- |х|
- |х| > a на х a.
Если неравенства нестрогие, то формулы тоже верны, только в них, кроме знака больше или меньше, появляется «=».
Как осуществляется решение системы неравенств?
Это знание потребуется в тех случаях, когда дано такое задание или имеется запись двойного неравенства или в записи появился модуль.
В такой ситуации решением будут такие значения переменных, которые удовлетворяли бы всем имеющимся в записи неравенствам. Если таких чисел нет, то система решений не имеет.
План, по которому выполняется решение системы неравенств:
- решить каждое из них отдельно;
- изобразить на числовой оси все интервалы и определить их пересечения;
- записать ответ системы, который и будет объединением того, что получилось во втором пункте.
Как быть с дробными неравенствами?
Поскольку во время их решения может потребоваться изменение знака неравенства, то нужно очень тщательно и внимательно выполнять все пункты плана. Иначе может получиться противоположный ответ.
Решение дробных неравенств тоже использует метод интервалов. И план действий будет таким:
- Используя описанные свойства, придать дроби такой вид, чтобы справа от знака остался только ноль.
- Заменить неравенство на «=» и определить точки, в которых функция будет равна нулю.
- Отметить их на координатной оси. При этом числа, получившиеся в результате расчетов в знаменателе, всегда будут выколоты. Все другие — исходя из условия неравенства.
- Определить интервалы знакопостоянства.
- В ответ записать объединение тех промежутков, знак которых соответствует тому, который был в исходном неравенстве.
Ситуации, когда в неравенстве появляется иррациональность
Другими словами, в записи присутствует математический корень. Поскольку в школьном курсе алгебры большая часть заданий идет для квадратного корня, то именно он и будет рассмотрен.
Решение иррациональных неравенств сводится к тому, чтобы получить систему из двух или трех, которые будут равносильны исходному.
| Исходное неравенство | условие | равносильная система |
| √ n(х) | m(х) меньше или равно 0 | решений нет |
| m(х) больше 0 | n(х) больше или равно 0 n(х) | |
| √ n(х) > m(х) | m(х) больше или равно 0 n(х) > (m(х)) 2 | |
n(х) больше или равно 0 m(х) меньше 0 | ||
| √n(х) ≤ m(х) | m(х) меньше 0 | решений нет |
| m(х) больше или равно 0 | n(х) больше или равно 0 n(х) ≤ (m(х)) 2 | |
| √n(х) ≥ m(х) | m(х) больше или равно 0 n(х) ≥ (m(х)) 2 | |
n(х) больше или равно 0 m(х) меньше 0 | ||
| √ n(х) | n(х) больше или равно 0 n(х) меньше m(х) | |
| √n(х) * m(х) | n(х) больше 0 m(х) меньше 0 | |
| √n(х) * m(х) > 0 | n(х) больше 0 m(х) больше 0 | |
| √n(х) * m(х) ≤ 0 | n(х) больше 0 | |
n(х) равно 0 m(х) -любое | ||
| √n(х) * m(х) ≥ 0 | n(х) больше 0 | |
n(х) равно 0 m(х) -любое |
Примеры решения разных видов неравенств
Для того чтобы добавить наглядности в теорию про решение неравенств, ниже приведены примеры.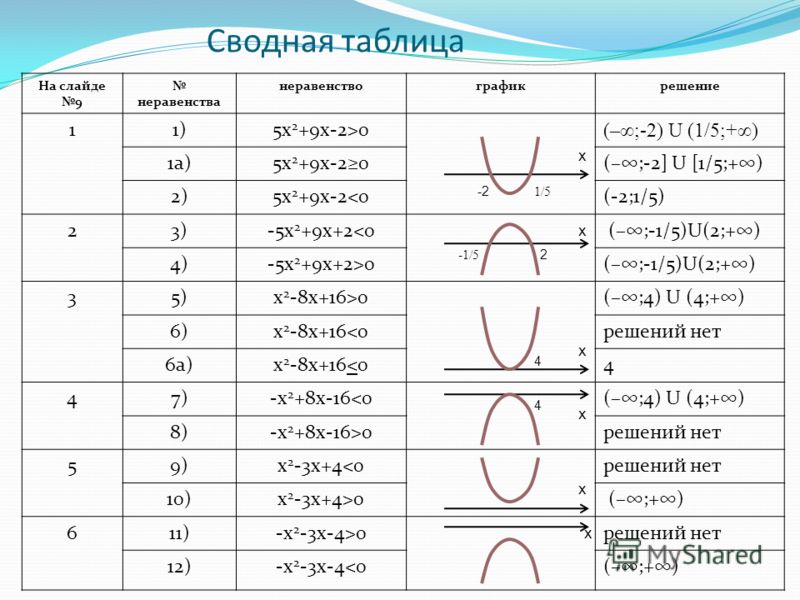
Первый пример. 2х — 4 > 1 + х
Решение: для того чтобы определить ОДЗ, достаточно просто внимательно посмотреть на неравенство. Оно образовано из линейных функций, поэтому определено при всех значениях переменной.
Теперь из обеих частей неравенства нужно вычесть (1 + х). Получается: 2х — 4 — (1 + х) > 0. После того как будут раскрыты скобки и приведены подобные слагаемые неравенство примет такой вид: х — 5 > 0.
Приравняв его к нулю, легко найти его решение: х = 5.
Теперь эту точку с цифрой 5, нужно отметить на координатном луче. Потом проверить знаки исходной функции. На первом интервале от минус бесконечности до 5 можно взять число 0 и подставить его в неравенство, получившееся после преобразований. После расчетов получается -7 >0. под дугой интервала нужно подписать знак минуса.
На следующем интервале от 5 до бесконечности можно выбрать число 6. Тогда получается, что 1 > 0. Под дугой подписан знак «+». Этот второй интервал и будет ответом неравенства.
Ответ: х лежит в интервале (5; ∞).
Второй пример. Требуется решить систему двух уравнений: 3х + 3 ≤ 2х + 1 и 3х — 2 ≤ 4х + 2.
Решение. ОДЗ этих неравенств тоже лежит в области любых чисел, поскольку даны линейные функции.
Второе неравенство примет вид такого уравнения: 3х — 2 — 4х — 2 = 0. После преобразования: -х — 4 =0. Из него получается значение для переменной, равное -4.
Эти два числа нужно отметить на оси, изобразив интервалы. Поскольку неравенство нестрогое, то все точки нужно закрасить. Первый интервал от минус бесконечности до -4. Пусть будет выбрано число -5. Первое неравенство даст значение -3, а второе 1. Значит, этот промежуток не входит в ответ.
Второй интервал от -4 до -2. Можно выбрать число -3 и подставить его в оба неравенства. В первом и во втором получается значение -1. Значит, под дугой «-».
На последнем интервале от -2 до бесконечности самым лучшим числом является ноль. Его и нужно подставить и найти значения неравенств.
В первом из них получается положительное число, а втором ноль. Этот промежуток тоже нужно исключить из ответа.
Из трех интервалов решением неравенства является только один.
Ответ: х принадлежит [-4; -2].
Третий пример. |1 — х| > 2 |х — 1|.
Решение. Первым делом нужно определить точки, в которых функции обращаются в ноль. Для левого этим числом будет 2, для правого — 1. их нужно отметить на луче и определить промежутки знакопостоянства.
На первом интервале, от минус бесконечности до 1, функция из левой части неравенства принимает положительные значения, а из правой — отрицательные. Под дугой нужно записать рядом два знака «+» и «-».
Следующий промежуток от 1 до 2. На нем обе функции принимают положительные значения. Значит, под дугой два плюса.
Третий интервал от 2 до бесконечности даст такой результат: левая функция — отрицательная, правая — положительная.
С учетом получившихся знаков нужно вычислить значения неравенства для всех промежутков.
На первом получается такое неравенство: 2 — х > — 2 (х — 1). Минус перед двойкой во втором неравенстве получился из-за того, что эта функция отрицательная.
После преобразования неравенство выглядит так: х > 0. Оно сразу дает значения переменной. То есть из этого интервала в ответ пойдет только промежуток от 0 до 1.
На втором: 2 — х > 2 (х — 1). Преобразования дадут такое неравенство: -3х + 4 больше ноля. Его нулем будет значение х = 4/3. С учетом знака неравенства получается, что х должен быть меньше этого числа. Значит, этот интервал уменьшается до промежутка от 1 до 4/3.
Последний дает такую запись неравенства: — (2 — х) > 2 (х — 1). Его преобразование приводит к такому: -х > 0. То есть уравнение верно при х меньшем ноля. Это значит, что на искомом промежутке неравенство не дает решений.
На первых двух промежутках граничным оказалось число 1. Его нужно проверить отдельно. То есть подставить в исходное неравенство. Получается: |2 — 1| > 2 |1 — 1|.
Подсчет дает что 1 больше 0. Это верное утверждение, поэтому единица входит в ответ.
Ответ: х лежит в промежутке (0; 4/3).
Неравенства и системы неравенств — это одна из тем, которая проходится в средней школе по алгебре. По уровню сложности она является не самой трудной, т. к. имеет незамысловатые правила (о них немного позже). Как правило, решение систем неравенств школьники усваивают достаточно легко. Это связано ещё и с тем, что учителя попросту «натаскивают» своих учеников по данной теме. И они не могут этого не делать, ведь она изучается и в дальнейшем с применением иных математических величин, а также проверяется на ОГЭ и ЕГЭ. В школьных учебниках тема, посвящённая неравенствам и системам неравенств, раскрыта очень подробно, поэтому если вы собираетесь её изучить, то лучше всего прибегнуть именно к ним. Данная статья лишь пересказывает большие материалы, и в ней могут быть некоторые опущения.
Понятие системы неравенств
Если обратиться к научному языку, то можно дать определение понятию «система неравенств».
Это такая математическая модель, которая представляет собой несколько неравенств. От данной модели, конечно же, требуется решение, и в его качестве будет выступать общий ответ для всех неравенств системы, предложенной в задании (обычно в нём так и пишут, например: «Решите систему неравенств 4 x + 1 > 2 и 30 — x > 6… «). Однако перед тем как перейти к видам и методам решений, нужно ещё кое в чём разобраться.
Системы неравенств и системы уравнений
В процессе изучения новой темы очень часто возникают недопонимания. С одной стороны, всё ясно и скорее хочется приступить к решению заданий, а с другой — какие-то моменты остаются в «тени», не совсем хорошо осмысливаются. Также некоторые элементы уже полученных знаний могут переплетаться с новыми. В результате такого «наложения» зачастую случаются ошибки.
Поэтому перед тем как приступить к разбору нашей темы, следует вспомнить про отличия уравнений и неравенств, их систем. Для этого нужно ещё раз пояснить, что представляют собой данные математические понятия.
Уравнение — это всегда равенство, и оно всегда чему-нибудь равно (в математике это слово обозначается знаком «=»). Неравенство же представляет собой такую модель, в которой одна величина или больше, или меньше другой, или содержит в себе утверждение, что они неодинаковы. Таким образом, в первом случае уместно говорить о равенстве, а во втором, как бы это очевидно ни звучало из самого названия, о неравенстве исходных данных. Системы уравнений и неравенств друг от друга практически не отличаются и методы их решения одинаковы. Единственное различие заключается в том, что в первом случае используются равенства, а во втором применяются неравенства.
Виды неравенств
Выделяют два вида неравенств: числовые и с неизвестной переменной. Первый тип представляет собой предоставленные величины (цифры), неравные друг другу, например, 8 > 10. Второй — это неравенства, содержащие в себе неизвестную переменную (обозначается какой-либо буквой латинского алфавита, чаще всего X). Данная переменная требует своего нахождения.
В зависимости от того, сколько их, в математической модели различают неравенства с одной (составляют систему неравенств с одной переменной) или несколькими переменными (составляют систему неравенств с несколькими переменными).
Два последних вида по степени своего построения и уровню сложности решения делятся на простые и сложные. Простые называют ещё линейными неравенствами. Они, в свою очередь, подразделяются на строгие и нестрогие. Строгие конкретно «говорят», что одна величина обязательно должна быть либо меньше, либо больше, поэтому это в чистом виде неравенство. Можно привести несколько примеров: 8 x + 9 > 2, 100 — 3 x > 5 и т. д. Нестрогие включают в себя ещё и равенство. То есть одна величина может быть больше или равна другой величине (знак «≥») либо меньше или равна другой величине (знак «≤»). Ещё в линейных неравенствах переменная не стоит в корне, квадрате, не делится на что-либо, из-за чего они называются «простыми». Сложные включают в себя неизвестные переменные, нахождение которых требует выполнения большего количества математических операций.
Они часто находятся в квадрате, кубе или под корнем, могут быть модульными, логарифмическими, дробными и пр. Но поскольку нашей задачей становится необходимость разобраться в решении систем неравенств, то мы поговорим о системе линейных неравенств. Однако перед этим следует сказать пару слов об их свойствах.
Свойства неравенств
К свойствам неравенств относятся следующие положения:
- Знак неравенства меняется на обратный, если применяется операция по перемене следования сторон (например, если t 1 ≤ t 2 , то t 2 ≥ t 1).
- Обе части неравенства позволяют прибавить к себе одно и то же число (например, если t 1 ≤ t 2 , то t 1 + число ≤ t 2 + число).
- Два и более неравенств, имеющие знак одного направления, позволяют складывать их левые и правые части (например, если t 1 ≥ t 2 , t 3 ≥ t 4 , то t 1 + t 3 ≥ t 2 + t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же положительное число (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Два и более неравенств, имеющие положительные члены и знак одного направления, позволяют умножать себя друг на друга (например, если t 1 ≤ t 2 , t 3 ≤ t 4 , t 1 , t 2 , t 3 , t 4 ≥ 0 то t 1 · t 3 ≤ t 2 · t 4).
- Обе части неравенства позволяют себя умножать или делить на одно и то же отрицательное число, но при этом знак неравенства меняется (например, если t 1 ≤ t 2 и число ≤ 0, то число · t 1 ≥ число · t 2).
- Все неравенства обладают свойством транзитивности (например, если t 1 ≤ t 2 и t 2 ≤ t 3 , то t 1 ≤ t 3).
Теперь после изучения основных положений теории, относящейся к неравенствам, можно приступить непосредственно к рассмотрению правил решения их систем.
Решение систем неравенств. Общие сведения. Способы решения
Как уже говорилось выше, решением выступают значения переменной, подходящие ко всем неравенствам данной системы. Решение систем неравенств — это осуществление математических действий, которые в итоге приводят к решению всей системы или доказывают, что у неё решений не имеется.
В таком случае говорят, что переменная относится к пустому числовому множеству (записывается так: буква, обозначающая переменную ∈ (знак «принадлежит») ø (знак «пустое множество»), например, x ∈ ø (читается так: «Переменная «икс» принадлежит пустому множеству»). Выделяют несколько способов решения систем неравенств: графический, алгебраический, способ подстановки. Стоит заметить, что они относятся к тем математическим моделям, которые имеют несколько неизвестных переменных. В случае, когда имеется только одна, подойдёт способ интервалов.
Графический способ
Позволяет решить систему неравенств с несколькими неизвестными величинами (от двух и выше). Благодаря данному методу система линейных неравенств решается достаточно легко и быстро, поэтому он является самым распространённым способом. Это объясняется тем, что построение графика сокращает объём написания математических операций. Особенно становится приятным немного отвлечься от ручки, взять в руки карандаш с линейкой и приступить к дальнейшим действиям с их помощью, когда выполнено много работы и хочется небольшого разнообразия.
Однако данный метод некоторые недолюбливают из-за того, что приходится отрываться от задания и переключать свою умственную деятельность на рисование. Тем не менее, это очень действенный способ.
Чтобы выполнить решение системы неравенств с помощью графического способа, необходимо все члены каждого неравенства перенести в их левую часть. Знаки поменяются на противоположные, справа следует записать ноль, затем нужно записать каждое неравенство отдельно. В итоге из неравенств получатся функции. После этого можно доставать карандаш и линейку: теперь потребуется нарисовать график каждой полученной функции. Всё множество чисел, которое окажется в интервале их пересечения, будет являться решением системы неравенств.
Алгебраический способ
Позволяет решить систему неравенств с двумя неизвестными переменными. Также неравенства должны обладать одинаковым знаком неравенства (т. е. обязаны содержать либо только знак «больше», либо только знак «меньше» и пр.) Несмотря на свою ограниченность, этот способ к тому же и более сложный.
Он применяется в двух этапах.
Первый включает себя действия по избавлению от одной из неизвестных переменных. Сначала нужно её выбрать, затем проверить на наличие чисел перед этой переменной. Если их нет (тогда переменная будет выглядеть, как одиночная буква), то ничего не изменяем, если есть (вид переменной будет, например, таким — 5y или 12y), то тогда необходимо сделать так, чтобы в каждом неравенстве число перед выбранной переменной было одинаковым. Для этого нужно умножить каждый член неравенств на общий множитель, например, если в первом неравенстве записано 3y, а во втором 5y, то необходимо все члены первого неравенства умножить на 5, а второго — на 3. Получится 15y и 15y соответственно.
Второй этап решения. Нужно левую часть каждого неравенства перенести в их правые части с изменением знака каждого члена на противоположный, справа записать нуль. Затем наступает самое интересное: избавление от выбранной переменной (по-другому это называется «сокращение») во время складывания неравенств.
Получится неравенство с одной переменной, которое необходимо решить. После этого следует проделать то же самое, только с другой неизвестной переменной. Полученные результаты и будут решением системы.
Способ подстановки
Позволяет решить систему неравенств при наличии возможности ввести новую переменную. Обычно этот способ применяется, когда неизвестная переменная в одном члене неравенства возведена в четвёртую степень, а в другом члене имеет квадрат. Таким образом, данный метод направлен на понижение степени неравенств в системе. Неравенство образца х 4 — х 2 — 1 ≤ 0 данным способом решается так. Вводится новая переменная, например, t. Пишут: «Пусть t = х 2 «, далее модель переписывают в новом виде. В нашем случае получится t 2 — t — 1 ≤0. Это неравенство нужно решить методом интервалов (о нём немного позже), потом обратно вернуться к переменной X, затем проделать то же самое с другим неравенством. Полученные ответы будут решением системы.
Метод интервалов
Это самый простой способ решения систем неравенств, и в то же время он является универсальным и распространённым.
Он используется и в средней школе, и даже в высшей. Его суть заключается в том, что ученик ищет промежутки неравенства на числовой прямой, которая рисуется в тетради (это не график, а просто обычная прямая с числами). Там, где промежутки неравенств пересекаются, находится решение системы. Чтобы использовать метод интервалов, необходимо выполнить следующие шаги:
- Все члены каждого неравенства переносятся в левую часть с изменением знака на противоположный (справа пишется ноль).
- Неравенства выписываются отдельно, определяется решение каждого из них.
- Находятся пересечения неравенств на числовой прямой. Все числа, находящиеся на этих пересечениях, будут являться решением.
Какой способ использовать?
Очевидно тот, который кажется наиболее лёгким и удобным, но бывают такие случаи, когда задания требуют определённого метода. Чаще всего в них написано, что нужно решать либо с помощью графика, либо методом интервалов. Алгебраический способ и подстановка используются крайне редко или не используются вообще, поскольку они достаточно сложные и запутанные, да и к тому же больше применяемы для решения систем уравнений, а не неравенств, поэтому следует прибегать к рисованию графиков и интервалов.
Они привносят наглядность, которая не может не способствовать эффективному и быстрому проведению математических операций.
Если что-то не получается
Во время изучения той или иной темы по алгебре, естественно, могут возникнуть проблемы с её пониманием. И это нормально, ведь наш мозг устроен так, что он не способен уяснить сложный материал за один раз. Часто требуется перечитать параграф, воспользоваться помощью учителя или заняться практикой по решению типовых заданий. В нашем случае они выглядят, например, так: «Решите систему неравенств 3 x + 1 ≥ 0 и 2 x — 1 > 3». Таким образом, личное стремление, помощь сторонних людей и практика помогают в понимании любой сложной темы.
Решебник?
А ещё очень хорошо подойдёт решебник, только не для списывания домашних заданий, а для самопомощи. В них можно найти системы неравенств с решением, посмотреть на них (как на шаблоны), попытаться понять, как именно автор решения справился с поставленной задачей, а затем попытаться выполнить подобное в самостоятельном порядке.
Выводы
Алгебра — это один из самых сложных предметов в школе. Ну что же тут поделать? Математика всегда была такой: кому-то она даётся легко, а кому-то с затруднением. Но в любом случае следует помнить, что общеобразовательная программа построена так, что с ней может справиться любой ученик. К тому же, надо иметь в виду огромное количество помощников. Некоторые из них были упомянуты выше.
Найти целые решения системы неравенств
Системы в алгебре
В алгебре часто требуется не просто решить систему неравенств, но выбрать из полученного множества решений решения, удовлетворяющие некоторым дополнительным условиям.
Найти целые решения системы неравенств — одно из заданий такого рода.
1) Найти целые решения системы неравенств:
7x — 5\\ 5 — x
Неизвестные переносим в одну сторону, известные — в другую с противоположным знаком:
— 5 — 3\\ — x + 6x
После упрощения разделим обе части каждого неравенства на — 8\_\_\_\left| {:2 > 0} \right.
\\ 5x 0} \right. \end{array} \right.\]» width=»163″ height=»43″ />
— 4\\ x
Отмечаем решения неравенств на числовых прямых. Решением системы является пересечение решений (то есть та часть, где штриховка есть на обеих прямых).
Оба неравенства строгие, поэтому -4 и 2 изображаются выколотыми точками и в решение не входят:
Из промежутка (-4;2) выбираем целые решения.
Ответ: -3; -2; -1; 0; 1.
2) Какие целые решения имеет система неравенств?
17 — 4x \end{array} \right.\]» width=»160″ height=»43″ />
Переносим неизвестные в одну сторону, известные — в другую с противоположным знаком
17 — 37 \end{array} \right.\]» width=»174″ height=»43″ />
Упрощаем и делим обе части на число, стоящее перед иксом. Первое неравенство делим на положительное число, поэтому знак неравенства не меняется, второе — на отрицательное число, поэтому знак неравенства изменяется на противоположный:
0} \right.\\ — 4x > — 20\_\_\_\left| {:( — 4)
Отмечаем решения неравенств на числовых прямых.
Первое неравенство нестрогое, поэтому -2 изображаем закрашенной точкой. Второе неравенство нестрогое, соответственно, 5 изображается выколотой точкой:
Целые решения на промежутке [-2;5) — это -2; -1; 0; 1; 2; 3; 4.
Ответ: -2; -1; 0; 1; 2; 3; 4.
В некоторых примерах не требуется перечислять целые решения, нужно лишь указать их количество.
3) Сколько целых решений имеет система неравенств?
Переносим неизвестные в одну сторону, известные — в другую:
0} \right. \end{array} \right.\]» width=»190″ height=»43″ />
Обе части первого неравенства делим на отрицательное число, поэтому знак неравенства изменяется на противоположный. Обе части второго неравенства делим на положительное число, знак неравенства при этом не меняется:
Решение неравенств отмечаем на числовых прямых. Оба неравенства нестрогие, поэтому -3,5 и 1,7 изображаем закрашенными точками:
Решением системы является промежуток [-3,5; 1,7]. Целые числа, которые входят в данный промежуток — это -3; -2; -1; 0; 1.
Всего их 5.
4) Сколько целых чисел являются решениями системы неравенств?
Неизвестные — в одну сторону, известные — в другую с противоположным знаком:
0} \right. \end{array} \right.\]» width=»214″ height=»43″ />
При делении обеих частей неравенства на положительное число знак неравенства не изменяется, при делении на отрицательное число — меняется на противоположный:
Решение неравенств отмечаем на числовых прямых.
Множество решений системы состоит из единственного элемента — . 2 — целое число, следовательно, решением данной системы является одно целое число.
7x — 5\\ 5 — x
0} \right. \end{array} \right.\]» width=»214″ height=»43″ />
Решением системы является промежуток -3,5; 1,7.
Www. algebraclass. ru
27.03.2020 3:17:07
2020-03-27 03:17:07
Источники:
Https://www. algebraclass. ru/najti-celye-cesheniya-sistemy-neravenstv/
Введение в алгебру Часть 1 Основы алгебры. | | ВКонтакте » /> » /> .
keyword { color: red; }
Системы в алгебре
Введение в алгебру [Часть 1] Основы алгебры [2000] Кострикин
Рассмотрены системы линейных уравнений, элементарная теория матриц, теория определителей, простейшие свойства групп, колец и полей, комплексные числа и корни многочленов. Помещено большое число упражнений различной степени трудности. Специальный раздел посвящен обсуждению некоторых нерешенных задач о многочленах.
Для студентов младших курсов университетов и ВУЗов с повышенными требованиями по математике.
С чего начинается алгебра? С некоторым приближением можно сказать, что истоки алгебры кроются в искусстве складывать, умножать и возводить в степень целые числа. Формальная, но далеко не очевидная и не однозначная замена чисел буквами позволяет действовать по аналогичным правилам в пределах гораздо более общих алгебраических систем. Стало быть, попытка ответить исчерпывающим образом на поставленный вопрос увела бы нас не только в глубь веков, в тайны зарождения математической мысли.
Более трудная часть ответа была бы связана с описанием основных структур алгебры наших дней: групп, колец, полей, модулей и т. п. Но этому как раз и посвящена значительная часть книги, так что цель главы 1 кажется пока недостижимой.
К счастью, под абстрактной оболочкой большинства аксиоматических теорий алгебры скрываются вполне конкретные задачи теоретического или практического характера, решение которых служило в свое время счастливым, а иногда и неизбежным поводом к далеко идущим обобщениям. В свою очередь развитая теория давала импульс и средства к решению новых задач. Сложное взаимодействие теоретических и прикладных аспектов теории, присущее всей математике, в алгебре проступает весьма отчётливо и делает в какой-то мере оправданным принятый нами концентрический стиль изложения.
Введение в алгебру [Часть 2] Линейная алгебра [2000] Кострикин
Наиболее важные разделы линейной алгебры изложены в максимально доступной форме. На первый план выдвигаются простые геометрические понятия, на базе которых идет всестороннее развитие алгебраического аппарата, введенного в части I.
Указаны приложения к разным вопросам анализа, теории линейных групп, алгебр Ли, математической экономики, дифференциальных уравнений, геометрии Лобачевского. Каждый параграф заканчивается упражнениями. Ответы и наброски решений собраны в отдельном разделе. Сформулированы некоторые нерешенные задачи.
Вряд ли стоит объяснять, чем дикий лес отличается от ухоженного парка или от упорядоченного леса, посаженного человеком. При всём различии, однако, в них столько общего, что инопланетянину, не познавшему вкуса грибов и не оценившему прелести подстриженных газонов, леса будут казаться сплошными зелёными массивами, насечёнными различной высоты и формы предметами, которые мы именуем деревьями. Нечто подобное произойдёт, если сравнить содержание настоящей главы и главы 2 из [ВА I], посвящённой координатным векторным пространствам.
Абстрактное линейное пространство, элементы которого именуются векторами и которое по этой причине мы будем чаше называть векторным пространством, вводится аксиоматически.
Соответствующая система аксиом, по существу разработанная еще Дж. Пеано (1888 г.), хорошо приспособлена к теории линейных отображений (в частности, линейных операторов), занимающей центральное место в линейной алгебре. Понятие матрицы при этом как бы отходит на второй план. Первостепенное значение приобретают инвариантные, не зависящие от выбора базиса свойства изучаемых объектов.
Однако прежде чем углубляться в абстрактный лес, рекомендуется ещё раз пройтись по ухоженному парку — конкретному пространству векторов строк длины п. Мы сознательно пошли на частичное повторение известного материала, чтобы сгладить абстрактные шероховатости.
Введение в алгебру [Часть 3] Основные структуры [2004] Кострикин
Алгебраические структуры, известные из первых двух частей учебника (группы, кольца, модули), изучаются на несколько более высоком уровне. Идеи и результаты теории представлений, подкрепленные многочисленными примерами, придают всему изложению общематематическое звучание. Особое место занимают конечно порожденные абелевы группы, теоремы Силова, представления и характеры конечных групп, алгебры над классическими полями.
Имеются теоретико-числовые приложения. В заключительной главе изложены основы теории Галуа. Для студентов младших курсов университетов и ВУЗов с повышенными требованиями по математике.
Более трудная часть ответа была бы связана с описанием основных структур алгебры наших дней групп, колец, полей, модулей и т.
M. vk. com
22.06.2018 23:45:47
2018-06-22 23:45:47
Источники:
Https://m. vk. com/wall-51126445_63576
Перевод систем счисления онлайн, калькулятор онлайн, конвертер » /> » /> .keyword { color: red; }
Системы в алгебре
Калькулятор Перевод систем счисления онлайн позволяет произвести перевод чисел из двоичной, десятичной, восьмиричной, шестнадцатиричной и других систем счисления.
Калькуляторы по алгебре
Математические калькуляторы
Округление чисел, онлайн калькулятор
Перевод римские, индийские, арабские цифры (числа)
Двоичный калькулятор онлайн
Математика 4,5,6,7,8,9,10,11 класс, ЕГЭ, ГИА
Код для вставки без рекламы с прямой ссылкой на сайт
Код для вставки с рекламой без прямой ссылки на сайт
Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.
Калькулятор Перевод систем счисления онлайн позволяет произвести перевод чисел из двоичной, десятичной, восьмиричной, шестнадцатиричной и других систем счисления.
Код для вставки без рекламы с прямой ссылкой на сайт
Код для вставки с рекламой без прямой ссылки на сайт
Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор.
Код для вставки с рекламой без прямой ссылки на сайт.
Www. calc. ru
29.08.2020 20:14:27
2020-08-29 20:14:27
Источники:
Https://www. calc. ru/perevod-sistem-schisleniya. html
Калькулятор неравенств с системой уравнений. Неравенство. Система линейных неравенств
Системой неравенств принято называть любую совокупность двух или более неравенств, содержащих неизвестную величину.
Наглядно данную формулировку иллюстрируют, к примеру, такие системы неравенств :
Решить систему неравенств — означает найти все значения неизвестной переменной, при которых реализуется каждое неравенство системы, либо обосновать, что таких не бывает.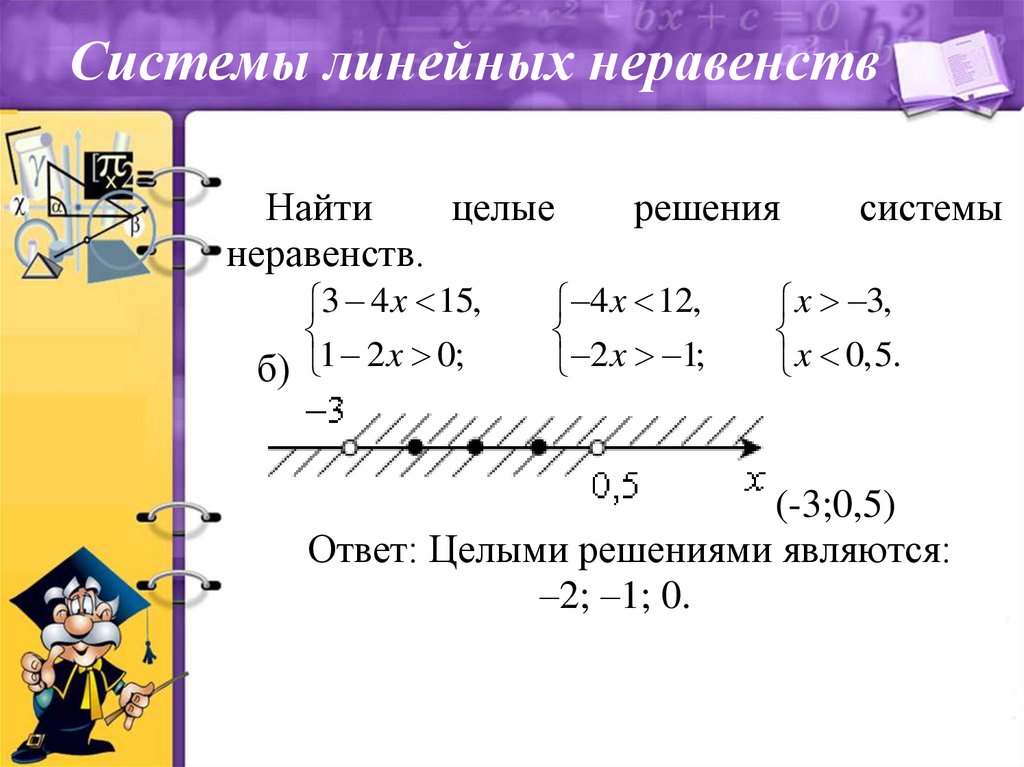
Значит, для каждого отдельного неравенства системы вычисляем неизвестную переменную. Далее из получившихся значений выбирает только те, которые верны и для первого и для второго неравенства. Следовательно, при подстановке выбранного значения оба неравенства системы становятся правильными.
Разберем решение нескольких неравенств:
Разместим одну под другой пару числовых прямых; на верхнею нанесем величину x , при которых первое неравенств о (x > 1) становиться верным, а на нижней—величину х , которые являются решением второго неравенства (х > 4).
Сопоставив данные на числовых прямых , отметим, что решением для обоих неравенств будет х > 4. Ответ, х > 4.
Пример 2.
Вычисляя первое неравенство получаем -3х x
> 2, второе —х > -8, или х х
, при которых реализуется первое неравенство системы , а на нижнюю числовую прямую, все те значения х , при которых реализуется второе неравенство системы.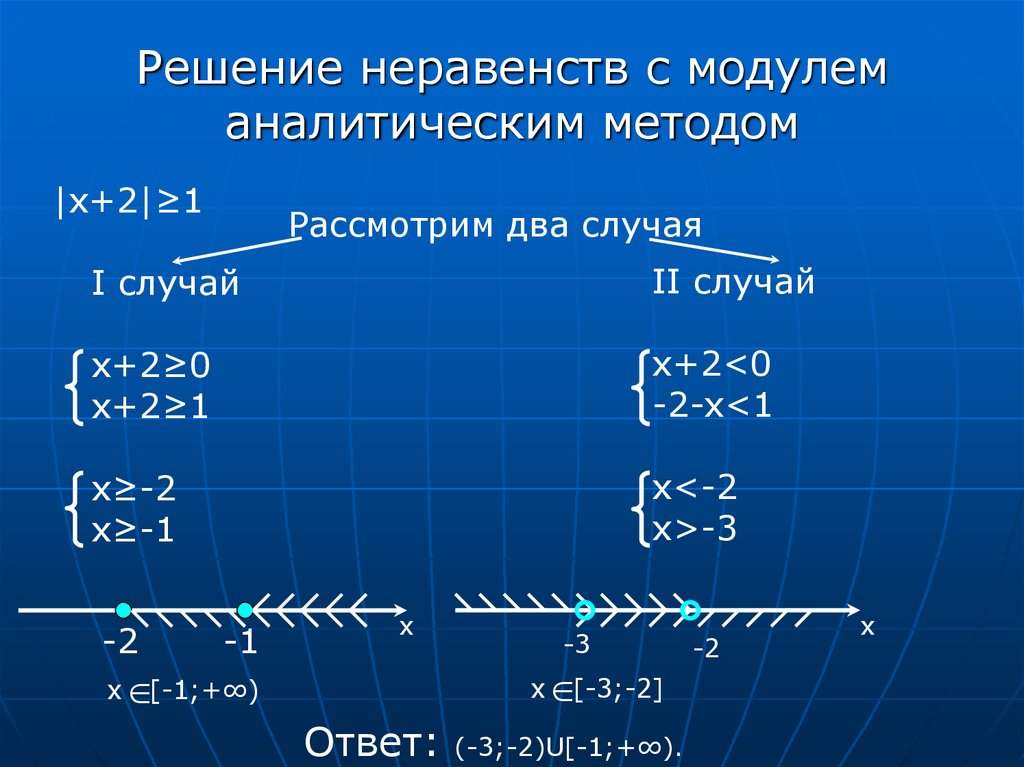
Сопоставив данные, получаем, что оба неравенства будут реализовываться при всех значениях х , размещенных от 2 до 8. Множеств значений х обозначаем двойным неравенством 2 х
Пример 3. Найдем
называется любая совокупность двух или более линейных неравенств, содержащих одну и туже неизвестную величину
Вот образцы подобных систем:
Промежуток пересечения двух лучей и есть наше решение. Следовательно решением данного неравенства выступают все х расположенные между двойкой и восьмеркой.
Ответ: х
Применение такого типа отображения решения системы неравенств иногда именуют методом крыш .
Определение: Пересечением двух множеств А и В называется такое третье множество, которое включает все элементы, входящих и в А и в В . Это смысл пересечения множеств произвольной природы. Нами сейчас детально рассматриваются числовые множества, поэтому при нахождении линейных неравенств такими множествами являются лучи — сонаправленные, противонаправленные и так далее.
Выясним на реальных примерах нахождение линейных систем неравенств, как определить пересечения множеств решений отдельных неравенств, входящих в систему.
Вычислим систему неравенств :
Поместим одну под другой две силовые прямые. На верхней нанесем те значения х, которые выполняют первое неравенство x >7 , а на нижней — которые выступают решением второго неравенства x >10 Соотнесем результаты числовых прямых, выясним, что оба неравенства будут удовлетворятся при x >10.
Ответ: (10;+∞).
Делаем по аналогии с первым образцом. На заданной числовой оси наносим все те значения х при которых существует первое неравенство системы , а на второй числовой оси, размещенной под первой, — все те значения х , при которых выполняется второе неравенство системы. Соотнесем эти два результата и определим, что оба неравенства одновременно будут выполнятся при всех значениях х расположенных между 7 и 10 с учетом знаков получаем 7х≤10
Ответ: (7; 10].
Подобным образом решаются и нижеследующие системы неравенств.
На этом уроке мы начнем изучение систем неравенств. Вначале будем рассматривать системы линейных неравенств. В начале урока рассмотрим, откуда и зачем возникают системы неравенств. Далее изучим, что значит решить систему, и вспомним объединение и пересечение множеств. В конце будем решать конкретные примеры на системы линейных неравенств.
Тема : Рацион альные неравенства и их системы
Урок: Основн ые понятия, решение систем линейных неравенств
До сих пор мы решали отдельные неравенства и применяли к ним метод интервалов, это могли быть и линейные неравенства , и квадратные и рациональные. Теперь перейдем к решению систем неравенств — сначала линейных систем . Посмотрим на примере, откуда берется необходимость рассматривать системы неравенств.
Найти область определения функции
Найти область определения функции
Функция существует, когда существуют оба квадратних корня, т.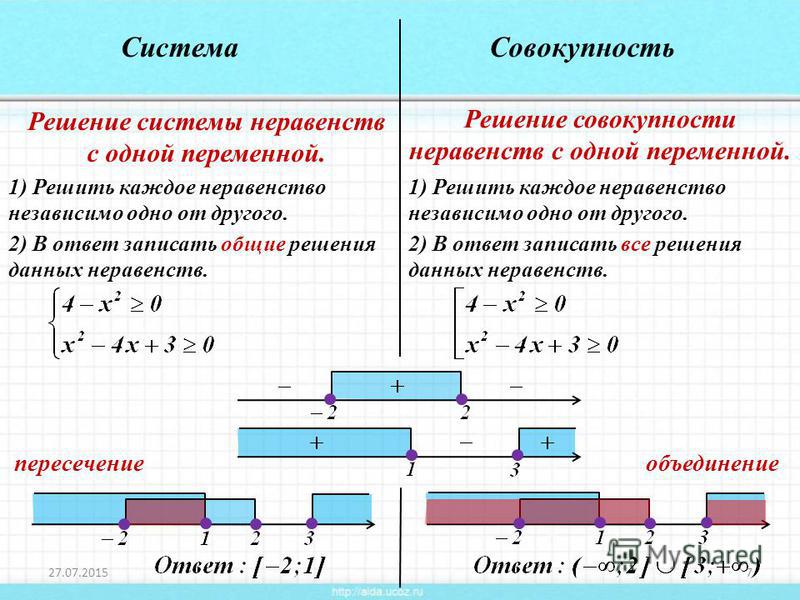
е.
Как решать такую систему? Необходимо найти все x, удовлетворяющие и первому и второму неравенству.
Изобразим на оси ox множество решений первого и второго неравенства.
Промежуток пересечения двух лучей и есть наше решение.
Такой метод изображения решения системы неравенств иногда называют методом крыш.
Решением системы является пересечение двух множеств.
Изобразим это графически. Имеем множество А произвольной природы и множество В произвольной природы, которые пересекаются.
Определение: Пересечением двух множеств А и В называется такое третье множество, которое состоит из всех элементов, входящих и в А и в В.
Рассмотрим на конкретных примерах решения линейных систем неравенств, как находить пересечения множеств решений отдельных неравенств, входящих в систему.
Решить систему неравенств:
Ответ: (7; 10].
4. Решить систему
Откуда может взяться второе неравенство системы? Например, из неравенства
Графически обозначим решения каждого неравенства и найдем промежуток их пересечения.
Таким образом, если мы имеем систему, в которой одно из неравенств удовлетворяет любому значению x, то его можно исключить.
Ответ: система противоречива.
Мы рассмотрели типовые опорные задачи, к которым сводится решение любой линейной системы неравенств.
Рассмотрим следующую систему.
7.
Иногда линейная система задается двойным неравенством, рассмотрим такой случай.
8.
Мы рассмотрели системы линейных неравенств, поняли, откуда они появляются, рассмотрели типовые системы, к которым сводятся все линейные системы, и решили некоторые из них.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю.
Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Портал Естественных Наук ().
2. Электронный учебно-методический комплекс для подготовки 10-11 классов к вступительным экзаменам по информатике, математике, русскому языку ().
4. Центр образования «Технология обучения» ().
5. Раздел College.ru по математике ().
1. Мордкович А.
Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. №№ 53; 54; 56; 57.
В этой статье собрана начальная информация о системах неравенств. Здесь дано определение системы неравенств и определение решения системы неравенств. А также перечислены основные виды систем, с которыми наиболее часто приходится работать на уроках алгебры в школе, и приведены примеры.
Навигация по странице.
Что такое система неравенств?
Системы неравенств удобно определить аналогично тому, как мы вводили определение системы уравнений , то есть, по виду записи и смыслу, вложенному в нее.
Определение.
Система неравенств – это запись, представляющая собой некоторое число записанных друг под другом неравенств, объединенных слева фигурной скобкой, и обозначающая множество всех решений, являющихся одновременно решениями каждого неравенства системы.
Приведем пример системы неравенств.
Возьмем два произвольных , например, 2·x−3>0
и 5−x≥4·x−11
, запишем их одно под другим
2·x−3>0
,
5−x≥4·x−11
и объединим знаком системы – фигурной скобкой, в результате получим систему неравенств такого вида:
Аналогично дается представление о системах неравенств в школьных учебниках. Стоит отметить, что в них определения даются более узко: для неравенств с одной переменной или с двумя переменными .
Основные виды систем неравенств
Понятно, что можно составить бесконечно много различных систем неравенств. Чтобы не заблудиться в этом многообразии, их целесообразно рассматривать по группам, имеющим свои отличительные признаки. Все системы неравенств можно разбить на группы по следующим критериям:
- по числу неравенств в системе;
- по числу переменных, участвующих в записи;
- по виду самих неравенств.
По числу неравенств, входящих в запись, различают системы двух, трех, четырех и т.д. неравенств. В предыдущем пункте мы привели пример системы , которая является системой двух неравенств.
Покажем еще пример системы четырех неравенств .
Отдельно скажем, что нет смысла говорить о системе одного неравенства, в этом случае по сути речь идет о самом неравенстве, а не о системе.
Если смотреть на число переменных, то имеют место системы неравенств с одной, двумя, тремя и т.д. переменными (или, как еще говорят, неизвестными). Посмотрите на последнюю систему неравенств, записанную двумя абзацами выше. Это система с тремя переменными x , y и z . Обратите внимание, что ее два первых неравенства содержат не все три переменные, а лишь по одной из них. В контексте этой системы их стоит понимать как неравенства с тремя переменными вида x+0·y+0·z≥−2 и 0·x+y+0·z≤5 соответственно. Заметим, что в школе основное внимание уделяется неравенствам с одной переменной.
Осталось обговорить, какие виды неравенств участвуют в записи систем. В школе в основном рассматривают системы двух неравенств (реже – трех, еще реже — четырех и более) с одной или двумя переменными, причем сами неравенства обычно являются целыми неравенствами первой или второй степени (реже – более высоких степеней или дробно рациональными).
Но не удивляйтесь, если в материалах по подготовке к ОГЭ столкнетесь с системами неравенств, содержащими иррациональные, логарифмические, показательные и другие неравенства. В качестве примера приведем систему неравенств , она взята из
.
Что называется решением системы неравенств?
Введем еще одно определение, связанное с системами неравенств, — определение решения системы неравенств :
Определение.
Решением системы неравенств с одной переменной называется такое значение переменной, обращающее каждое из неравенств системы в верное , другими словами, являющееся решением каждого неравенства системы.
Поясним на примере. Возьмем систему двух неравенств с одной переменной . Возьмем значение переменной x
, равное 8
, оно является решением нашей системы неравенств по определению, так как его подстановка в неравенства системы дает два верных числовых неравенства 8>7
и 2−3·8≤0
. Напротив, единица не является решением системы, так как при ее подстановке вместо переменной x
первое неравенство обратится в неверное числовое неравенство 1>7
.
Аналогично можно ввести определение решения системы неравенств с двумя, тремя и большим числом переменных:
Определение.
Решением системы неравенств с двумя, тремя и т.д. переменными называется пара, тройка и т.д. значений этих переменных, которая одновременно является решением каждого неравенства системы, то есть, обращает каждое неравенство системы в верное числовое неравенство.
К примеру, пара значений x=1 , y=2 или в другой записи (1, 2) является решением системы неравенств с двумя переменными , так как 1+2
Системы неравенств могут не иметь решений, могут иметь конечное число решений, а могут иметь и бесконечно много решений. Часто говорят о множестве решений системы неравенств. Когда система не имеет решений, то имеет место пустое множество ее решений. Когда решений конечное число, то множество решений содержит конечное число элементов, а когда решений бесконечно много, то и множество решений состоит из бесконечного числа элементов.
В некоторых источниках вводятся определения частного и общего решения системы неравенств, как, например, в учебниках Мордковича . Под частным решением системы неравенств понимают ее одно отдельно взятое решение. В свою очередь общее решение системы неравенств — это все ее частные решения. Однако в этих терминах есть смысл лишь тогда, когда требуется особо подчеркнуть, о каком решении идет речь, но обычно это и так понятно из контекста, поэтому намного чаще говорят просто «решение системы неравенств».
Из введенных в этой статье определений системы неравенств и ее решений следует, что решение системы неравенств представляет собой пересечение множеств решений всех неравенств этой системы.
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Алгебра: 9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.
- Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 13-е изд., стер. — М.: Мнемозина, 2011. — 222 с.: ил. ISBN 978-5-346-01752-3.
- Мордкович А. Г. Алгебра и начала математического анализа. 11 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 2-е изд., стер. — М.: Мнемозина, 2008. — 287 с.: ил. ISBN 978-5-346-01027-2.
- ЕГЭ -2013. Математика: типовые экзаменационные варианты: 30 вариантов / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство «Национальное образование», 2012. – 192 с. – (ЕГЭ-2013. ФИПИ – школе).
для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2009. — 271 с. : ил. — ISBN 978-5-09-021134-5.Graphing linear inequalities calculator
- Expression
- Equation
- Inequality
- Contact us
- Simplify
- Factor
- Expand
- GCF
- LCM
- Solve
- Graph
- System
- Решение
- График
- Система
- Математический решатель на вашем сайте
Наших пользователей:
Возможность увидеть, как решить проблему шаг за шагом, перепроверить свою работу и получить правильный ответ, делает Algebrator лучшим программным обеспечением, которое я покупал за весь год.
Мэтт Канин, ИА
Окончив среднюю школу, я был одним из лучших учеников по математике в классе. Поступление в колледж было унизительным, потому что внезапно я стал едва ли средним. Итак, мои родители помогли мне выбрать Алгебратор, и через несколько недель я снова вернулся. Ваша программа не только отлично подходит для начинающих, как мои младшие братья в старшей школе, но и помогла мне, как новому студенту колледжа!
Колин Берс, Нью-Йорк
Я никогда не жалею о том дне, когда купил Algebrator и был поражен. Пошаговый метод решения задач отличается от любой другой программы алгебры, которую я видел.
Майкл Лили, Миссури
Эта версия вашей программы по алгебре просто великолепна! Большое спасибо! Это очень помогло мне. ПРОДОЛЖАЙТЕ ХОРОШУЮ РАБОТУ!
Алан Кокс, Техас
Ваша программа до сих пор была отличной. Я купил это программное обеспечение для моих 13 лет. старая дочь, у которой проблемы с математикой.
У нас есть репетитор, который приходит на дом, и благодаря вашему программному обеспечению и ему она получила свою первую пятерку в очень сложном тесте по главе. Как вы, возможно, знаете, иногда, когда вы видите другой подход к проблеме, или иногда просто кто-то другой показывает вам разные способы понимания проблемы, этого достаточно. Ваше программное обеспечение, кажется, дает этот подход к решению проблем таким образом, чтобы его было легко понять. Еще раз спасибо всей семье Терли.
Джонсон, Нью-Йорк
Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?
Поисковые фразы, использованные 09.03.2011:
- Рабочий лист для разминки по алгебре
- Метод частных сумм Решение задач 5-го класса
- бесплатных математических листа сложения и вычитания десятичных дробей 5 класс
- Рабочий лист правил делимости по математике
- шпаргалка по алгебре в колледже
- сложный вопрос по алгебре Рабочий лист квадратного корня
- (школы)
- как найти наклон на калькуляторе TI
- проверка сложения и вычитания десятичных знаков
- викторина по заполнению квадрата
- решение системы уравнений на ти-83
- как извлекать кубический корень на калькуляторе
- рабочих листа с неравенствами Алгебра 2
- статистика-комбинированное правило
- бесплатный синтетический решатель деления
- саксонская алгебра 2 ответы
- задачи по алгебре в колледже
- апплет плиток правды
- вычитание отрицательного рабочего листа
- учить алгебре
- математические листы для 6-го класса для печати
- Matlab для построения квадратичных линий
- Перестановки и комбинации Ti-86
- лист деления дробей Десятичное число
- в смешанное число
- рабочие листы для решения уравнений
- Решатель квадратичных дробей
- список положительных и отрицательных слов из реальной жизни
- бесплатно +решатель алгебраических слов
- Математические викторины и викторины
- фактор уравнения с TI-83
- алгебра колледжа второе издание глава 2 ответы
- пример совокупного свойства по математике в 3 классе
- Домашнее задание по высокой геометрии в Арлингтоне ответы
- флорида издание Макдугал Литтел наука класс 7
- удаление знаков препинания из строки на java
- кумон ответы
- алгебра для начинающих
- алекс читер
- факторинг онлайн
- упражнения по факториальному программированию в Java
- Таблица простых чисел для 2-х классов Калькулятор стандартной формы
- наименьший общий знаменатель показателей
- вопрос упрощения показателей и радикала
- mathematica для чайников, решающих уравнение
- баллы по математике для 8-го класса
- Помощь с алгеброй Холта II
- Мастера математики UCSMP
- примеров математических мелочей
- решить систему Лапласа третьего порядка
- настрой на сознание, класс 2007, бумажный вопросник по математике, класс 11
- Наклон 2:1 вычислить как
- ODE Matlab несколько переменных
- словарь четвертого издания glencoe по бухгалтерскому учету
- Предварительно-алгебраические свойства холла
- Примеры факторинговой алгебры для десятого класса
- как разложить полиномы третьего порядка на множители
- вычислить сумму всех целых чисел, делящихся на 9
- ти-89 решить
- общий знаменатель чисел 38 и 46
- учебник по концептуальной физике ответ
- математические задачи с подшипниками
- онлайн калькулятор трехчленного факторинга
- преобразовать решение квадратного уравнения в уравнение
- умножение и деление рациональных выражений одночлена
- основных вопросов по алгебре
- Рабочий лист факторизации кубов
- Рабочие листы по математике для 9 класса
- бесплатных печатных рабочих листа по алгебре, упрощающих выражения
- введите вершину корней параболы
- полином упрощения третьего порядка
- игра умножение и деление отрицательных чисел
- решение многочлена с помощью программного обеспечения R
- учить алгебру 2
- осенние рабочие листы для первого класса
- Образец бумаги Pipal Research для теста на пригодность
- «рабочие листы широты»
- извлечение квадратного корня
- упрощение сложных ридикалов
- калькулятор с основанием 10 в восьмеричный
- решение для y-перехвата
- решить мое уравнение помочь сайты
- смешанные числа до десятичных дробей
- Рабочие листы по математике для 8-го класса
- бесплатных распечатываемых листа вероятностей
- Рабочие листы для печати по квадратным корням и показателям степени
- смешанные задачи в дифференциальных уравнениях
- «текстовое видео интерактивное»
- сложение и вычитание биномов
- бесплатных рабочих листа по математике добавляют целые числа
- вычислить коэффициент разности
- решить нелинейные связанные дифференциальные уравнения Matlab
- скачать ти-84
- Калькулятор подкоренных выражений
- упрощение экспоненциальных выражений с радикалами
- журнал решения на texas ti-89
| Предыдущая | Далее |
Калькулятор решения неравенств
Наших пользователей: Я никогда не понимал алгебру, из-за чего мне было трудно, а в итоге я возненавидел математику. Спасибо и поздравления за вашу впечатляющую программу по алгебре, которая действительно очень помогла мне с моей математикой. Я хотел бы поблагодарить создателя за подготовку такого потрясающего программного обеспечения. Это сделало алгебру простой, предоставляя экспертную помощь с дробями и уравнениями. Недавно я наткнулась в интернете и заказала программу по алгебре для своего ребенка. Я рад сообщить, что визуальный и практический подход — это как раз то, что нужно моему ребенку для понимания фундаментальных понятий алгебры. Эта версия справки по алгебре потрясающая! Улучшенный интерфейс, лучшие подсказки и удобство работы. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою?Поисковые фразы, использованные 19.11.2012:
|
Теперь, когда у меня есть Algebrator, математика больше не кажется мне иностранным языком. Теперь я с удовольствием посещаю занятия по математике! 
На самом деле, я улучшил свою алгебру от провала с тех пор, как начал ее использовать. 
pdf
Наших пользователей: Я пробовал все. Я заказал программное обеспечение однажды поздно вечером, когда у моей дочери были проблемы на уроке алгебры с отличием. Прошло много лет с тех пор, как у меня была алгебра, и некоторые ее части имели смысл, но я не мог понять, как ей помочь. После того, как мы заказали ваше программное обеспечение, она смогла шаг за шагом увидеть, как решать проблемы. Ваше программное обеспечение определенно спасло положение. Алгебратор — мой доктор по алгебре. Уравнения и неравенства были двумя темами, над которыми я боролся, но использование программного обеспечения стерло мои проблемы с предметом. Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение спасает им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 29 августа 2011 г.:
|
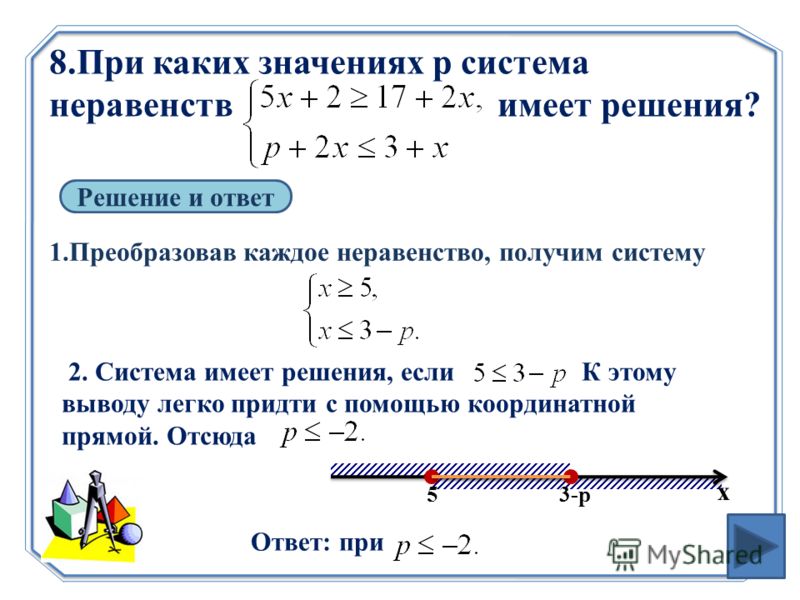Мы используем его каждый день для ее учебы. Отличная программа! 
покажите мне концепцию начальной алгебры