| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Решение тригонометрических неравенств: sin x > a, sin x< a, sin x ≥ a, sin x ≤ a; cos x > a, cos x< a, cos x ≥ a, cos x ≤ a; tg x > a, tg x< a, tg x ≥ a, tg x≤a; ctg x > a, ctg x< a, ctg x ≥ a, ctg x≤a Поделиться:
| ||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | |||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.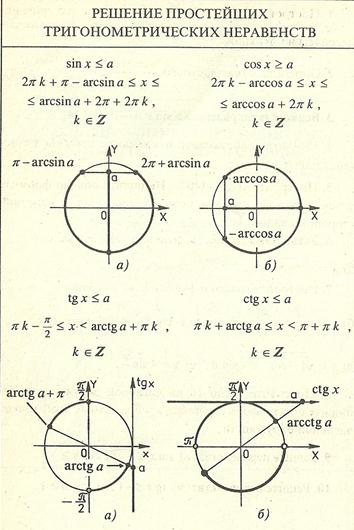 Free xml sitemap generator Free xml sitemap generator | ||||||
Тригонометрические неравенства⚠️: формулы и особенности решения
Что такое тригонометрические неравенства
Тригонометрические неравенства — неравенства, в которых переменные находятся только под знаком тригонометрической функции.
Тригонометрические функции обозначаются как:
- sin α;
- cos α;
- tg α;
- ctg α.
При доказательстве тригонометрических неравенств применяют общие приемы доказательства алгебраических неравенств.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При этом в тригонометрии спектр применяемых математических методов богаче.
- метод от обратного;
- аналитико-синтетический метод;
- методы математического анализа;
- метод математической индукции;
- элементы геометрии;
- векторная алгебра;
- графический метод.
 2\left(x\right)\geq0.\)
2\left(x\right)\geq0.\)
В неоднородных — степени слагаемых будут отличаться друг от друга.
Простейшие
Простейшие тригонометрические неравенства имеют вид:
sin х < m, sin x > m, cos x < m, cos x > m, tg x < т, tg x > m, ctg >m; ctg < m,
где m — заданное число.
Сложные
В сложных тригонометрических неравенствах аргумент функции неравенства имеет вид целого выражения с неизвестной, а не просто переменной.
Они бывают:
- дробные;
- двойные;
- тройные;
\(\sin\left(\frac x2+\frac\pi3\right)<\frac{\sqrt2}2\ \)
\(sin 3x — sin x > 0; \)
\(cos x — 5x + 2 > 0.\)
Методы решения тригонометрических неравенств
Общие сведения по решению тригонометрических неравенств
При решении тригонометрических неравенств используют свойство монотонности тригонометрических функций и промежутки их знакопостоянства.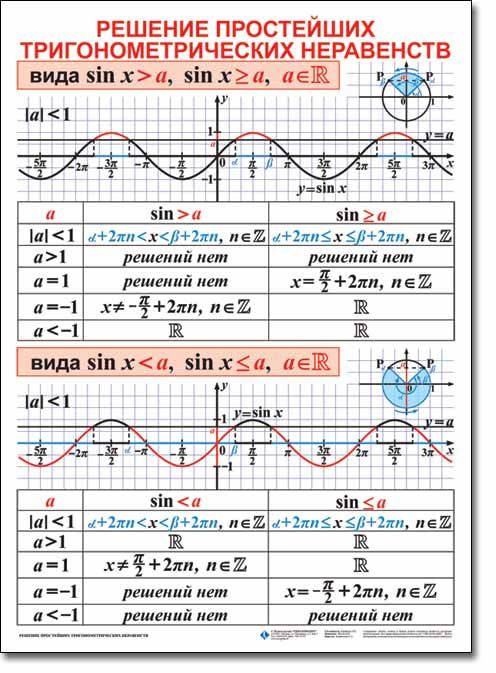
Монотонность характерна как для убывающих, так и для возрастающих функций. Она означает, что в определенном промежутке большему по значению аргумента будет соответствовать большее или меньшее значение функции в зависимости от возрастания или убывания функции, соответственно.
О промежутках знакопостоянства говорят, когда множеству значений аргумента соответствуют только положительные или только отрицательные значения функции.
Чтобы решить простейшее тригонометрическое неравенство, необходимо найти множество всех значений аргумента, которые обращают данное неравенство в верное числовое неравенство.
Важные моменты в решении простейших тригонометрических неравенств:
sin x = 0, если \(\mathrm x=\mathrm{πR}, \ R\in Z;\)
sin x = -1, если \(x=-\frac\pi R+2\pi R\,, \ R\in Z;\)
sin x = 1, если \(x=\frac\pi2+2\pi R, \ R\in Z;\)
sin x > 0, если \(2\pi R<x<\pi+2\pi R, \ R\in Z;\)
sin x < 0, если \(-\pi+2\pi R<x<2\pi R, \ R\in Z. \)
\)
для cos x:
cos x = 0, если \(x=\frac\pi2+\pi R,\ R\in Z;\)
cos x = -1, если \\(x=\pi+2\pi R, \ R\in Z;\)
cos x = 1, если \(x=2\pi R, \ R\in Z;\)
cos x > 0, если \(2\pi R-\frac\pi2<x<\frac\pi2+2\pi R, \ R\in Z;\)
cos x < 0, если \(2\pi R+\frac\pi2<x<\frac32\pi+2\pi R, \ R\in Z.\)
tg x > 0, если \(\pi R<x<\frac\pi2+\pi R, \ R\in Z;\)
tg x < 0, если \(\pi R-\frac\pi2<x<\pi R, \ R\in Z;\)
тангенс не существует, если \(x=\frac\pi2+\pi R, \ R\in Z.\)
Нестандартные способы решения тригонометрических неравенств включают в себя несколько методик:
- Графический метод.
- Метод постановки.
- Метод интервалов.
- Метод секторов.
- Метод концентрических окружностей для систем тригонометрических неравенств.
Для решения простейших тригонометрических неравенств применяют графический способ решения и решение с помощью числовой окружности._10-1200x800.jpg)
Решение тригонометрических неравенств с помощью единичной окружности
Задача № 1Решите неравенство: sin x > ½.
Решение:
Построим единичную окружность. Построим на ней дуги AC и \(AC_1\). Их синус должен быть равен ½.
Источник: scask.ruИз окружности видно, что все дуги, начинающиеся в точке А и заканчивающиеся в любой внутренней точке дуги \(CBC_1\), удовлетворяют данному неравенству.
Соответственно:
\(\frac\pi6<x<\frac{5\pi}6.\)
Чтобы получить все решения данного неравенства, прибавим к концам этого промежутка 2πR.
Ответ: \(\frac\pi6+2\pi R<x<\frac{5\pi}6+2\pi R, \ R\in Z.\)
Задача № 2Решите неравенство: cos 3x > ½.
Решение:
Обозначим 3х через α.
Неравенство примет вид:
\(\cos\left(\alpha\right)\geq-\frac12.\)
Построим окружность.
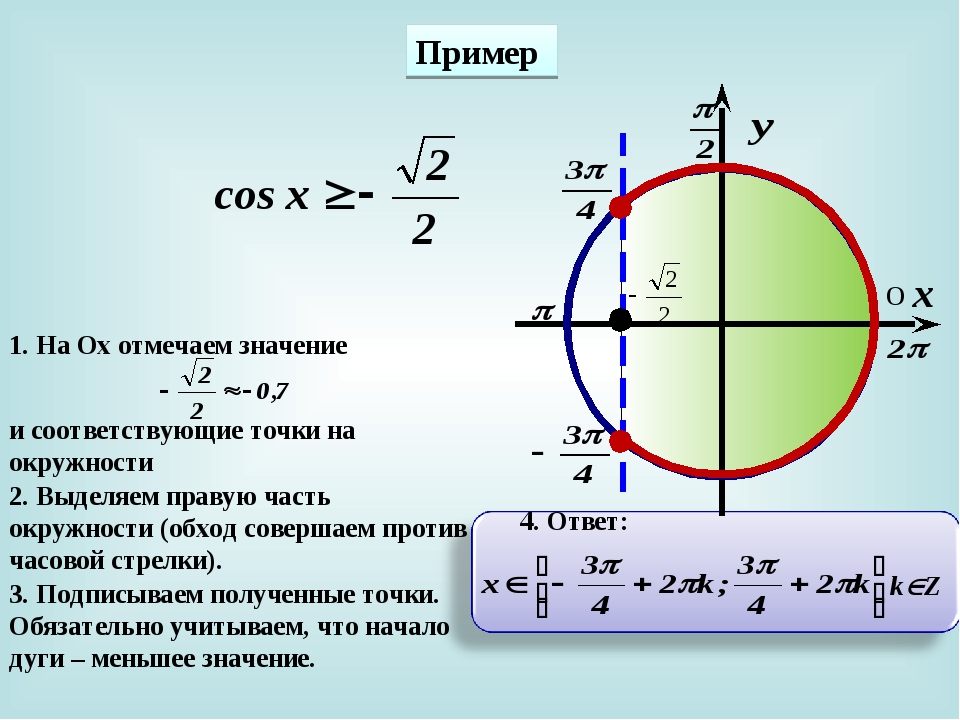
Источник: scask.ruЭтому неравенству удовлетворяют все точки \[P_\alpha\] единичной окружности, абсциссы которых больше или равны -1/2.
На окружности видно, что эти точки дуги лежат на прямой \(х=-1/2\) или правее ее.
Выделенная на рисунке дуга представляет собой множество всех точек, удовлетворяющих данному неравенству. Концы этой дуги входят в искомое множество. Их абсциссы равны -1/2, значит, удовлетворяют неравенству.
Соответственно:
\(-\frac{2\pi}3\leq\alpha\leq\frac{2\pi}3.\)
Учитывая периодичность косинуса, запишем решения для неравенства
\(\cos\left(\alpha\right)\geq-\frac12:\)
\(-\frac{2\pi}3+2\pi R\leq\alpha\leq\frac{2\pi}3+2\pi R, \ R\in Z.\)
Вернемся снова к переменной х, получим искомый ответ:
\(-\frac{2\pi}3+2\pi R\leq3x\leq\frac{2\pi}3+2\pi R,\;R\in Z;\)
\(-\frac{2\pi}9+\frac{2\pi R}3\leq x\leq\frac{2\pi}9+\frac{2\pi R}3,\;R\in Z.\)
Решите неравенство: tg 2x > 1.
Решение:
Обозначим 2х через α.
Неравенство примет вид:
\(tg α > 1.\)
Построим окружность и проведем касательную к окружности в точке (1; 0). Эта линия является тангенсом.
Эта линия является тангенсом.
Так как α является решением неравенства tg α ≥ 1, то ордината точки \(T_\alpha\) линии тангенсов tg α должна быть равна или больше 1. Луч АТ имеет все эти точки.
Точки \(P_\alpha\) окружности, соответствующие точкам \( P_\alpha\), образуют дугу.
Для ее точек выполняется неравенство \(\frac\pi4\leq\alpha<\frac\pi2.\)
Прибавим к этому промежутку период тангенса и получим решение неравенства \(T_\alpha\geq1:\)
\(\pi R+\frac\pi4\leq\alpha<\frac\pi2+\pi , \ R\in Z.\)
Так как \(α=2х\), получим ответ:
\(\frac{\pi R}2+\frac\pi8\leq x<\frac\pi4+\frac{\pi R}2, \ R\in Z.\)
Графическое решение тригонометрических неравенств
Для решения простейших тригонометрических неравенств с помощью графического метода решения строят график тригонометрической функции (sin x, cos x и т. д.) и прямую у=а. Затем выделяют промежутки с помощью построенных графиков.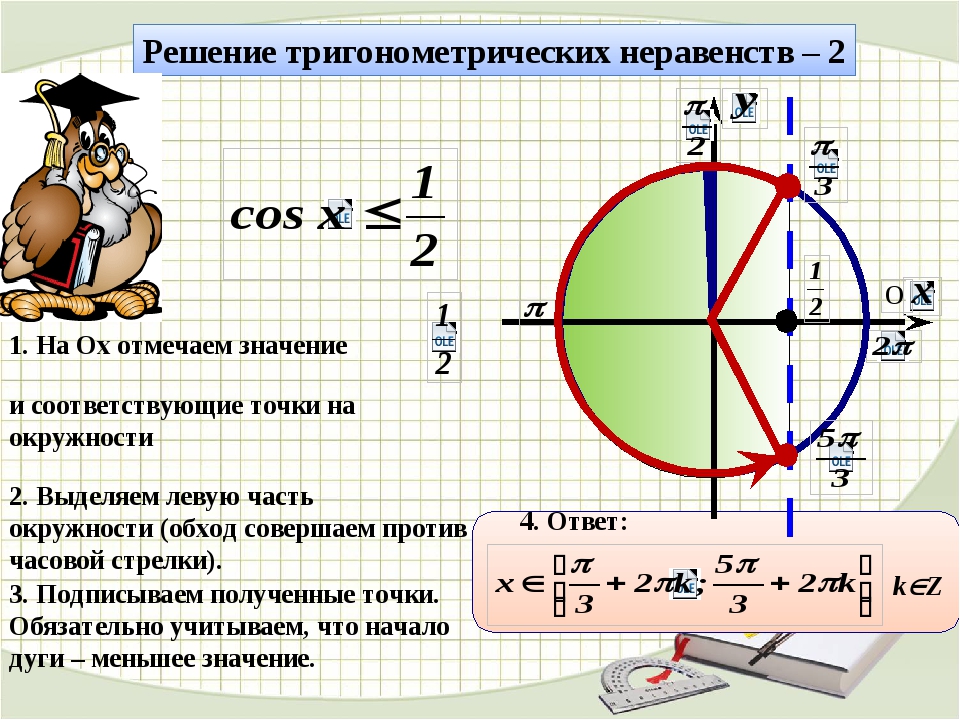 Эти промежутки являются решением неравенства.
Эти промежутки являются решением неравенства.
Решите неравенство: sin x > ½.
Решение:
Построим графики функций \(y=sin\) \(x\) и \(y=1/2.\)
Источник: scask.ruИз графика видно, что прямая у=1/2 пресекает синусоиду в бесконечном числе точек.
На нем выделены несколько значений аргументов, которые удовлетворяют данному неравенству: \(\frac\pi6, \frac{5\pi}6.\)
Учитывая периодичность синуса, запишем окончательный ответ:
\(\frac\pi6+2\pi R<x<\frac{5\pi}6+2\pi R,\) \(R\in Z.\)
Решите неравенство: tg x ≥ -1.
Решение:
Построим графики функций \(y = tg\) \(x \) и \(y = -1.\)
Источник: window.edu.ruИз графика видно, что одним из промежутков, который удовлетворяет неравенств, является:
\(\left[-\frac\pi4;\;\frac\pi2\right].\)
Учтем периодичность тангенса и получим:
\(x\in\left[-\frac\pi4+k\pi;\;\frac\pi2+k\pi\right],\;k\in Z.\)
Получим ответ:
\(\left[-\frac\pi4+k\pi;\;\frac\pi2+k\pi\right],\;k\in Z.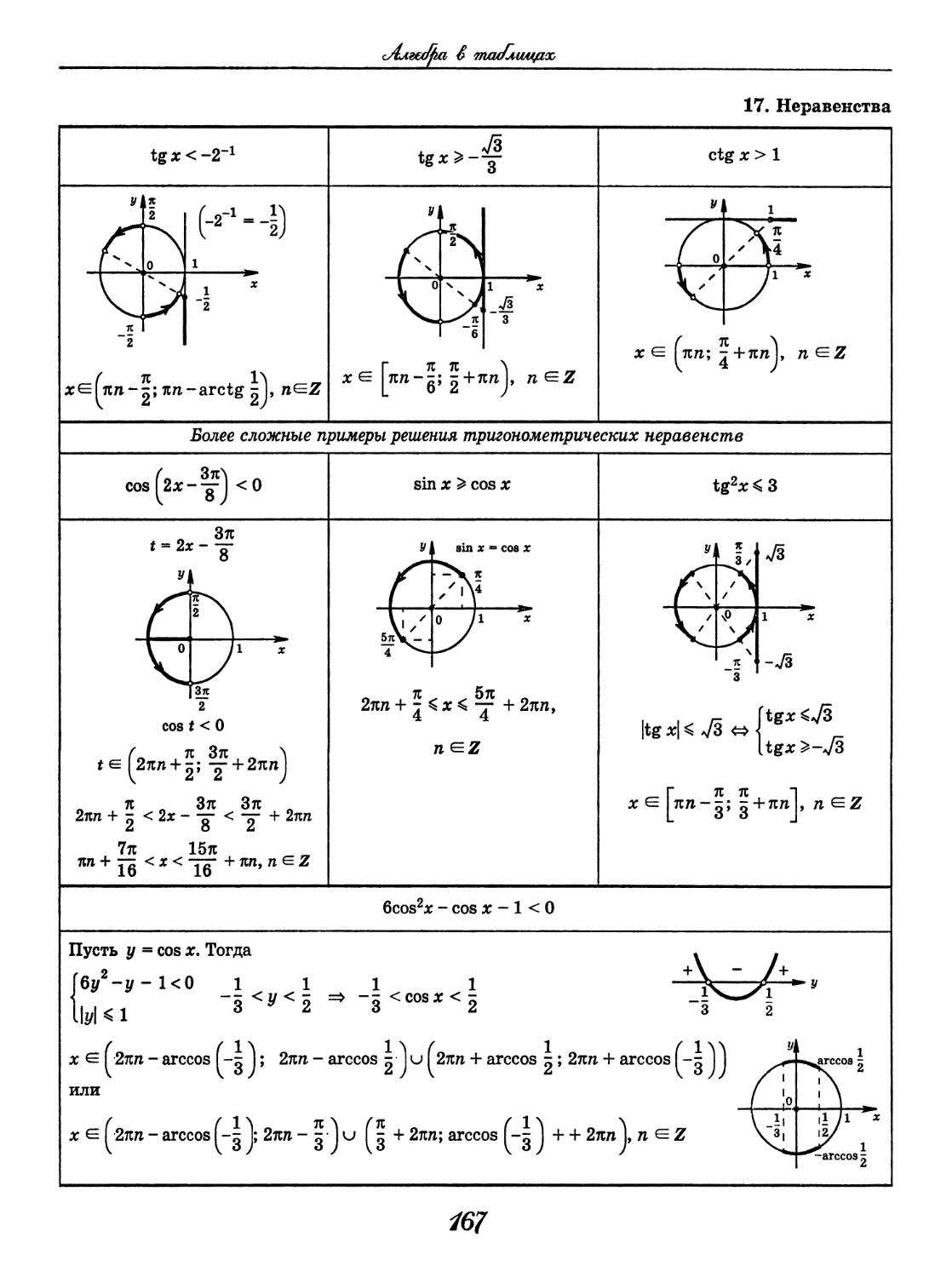 2+5y+1=6(y-\frac13)(y-\frac12)\geq0.\) (1)
2+5y+1=6(y-\frac13)(y-\frac12)\geq0.\) (1)
Используем метод интервалов для его решения.
Объединим промежутки \(y\geq\frac12\) и \(y\leq\frac13.\)
Тогда получим, что
\(\sin\left(x\right)\leq\frac13\) и \(\sin\left(x\right)\geqslant\frac12.\) (2)
Теперь для решения полученных неравенств применим алгоритм решения по методу единичной окружности.
Источник: scask.ruРешая неравенство (1), на построенной слева окружности видим, что ему удовлетворяют такие значения х:
\(-\pi-arc\sin\frac13\leq x\leq arc\sin\frac13\). (3)
Для получения всех решений неравенства к полученному промежутку добавим \(2\pi R.\)
Окончательно имеем:
\(-\pi-arc\sin\;\frac13+2\pi R\leq x\leq arc\sin\;\frac13+2\pi R,\;R\in Z\). (4)
Для решения неравенства (2) так же построим окружность и увидим, что ему удовлетворяют значения х:
\(\frac\pi6+2\pi R\leq x\leq\frac{5\pi}6+2\pi R,\;R\in Z.\) (5)
Значения х, удовлетворяющие неравенствам (4) и (5) являются решением данного неравенства.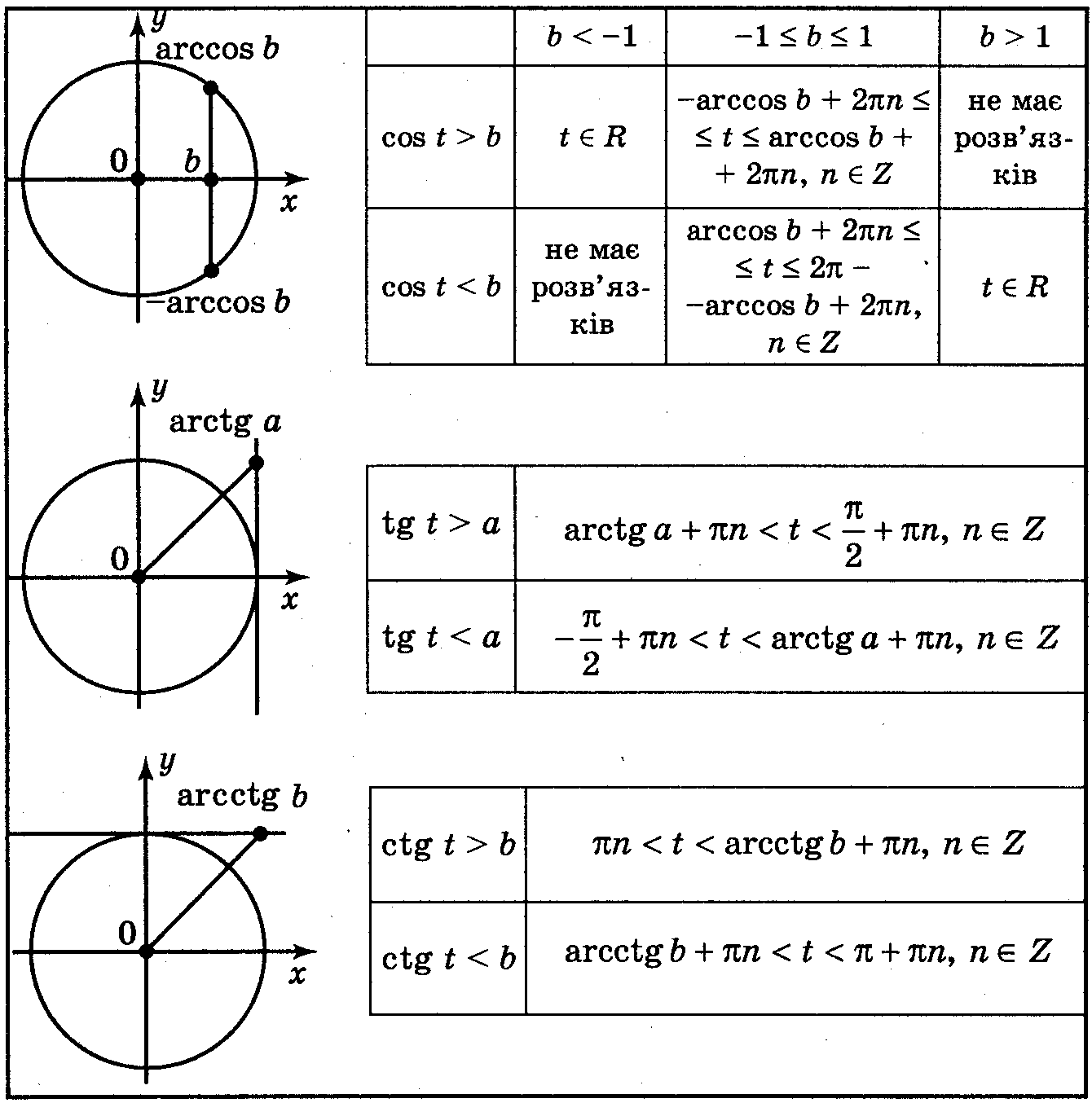
Задача 2
Задача № 2Решите неравенство: \(\frac{15}{\cos\;x\;+1}<11\;-\;2\;\cos\;x.\)
Решение:
Введем новую переменную: \(у = cos x.\)
Неравенство примет вид:
\(\frac{15}{y\;+1}<11\;-\;2y.\)
После преобразований получим:
\(\frac{2(y-4)\left(y-{\displaystyle\frac12}\right)}{y+1}<0.\)
Используем метод интервалов.
Источник: scask.ruРешение неравенства:
\(y<-1;\;\frac12<y<4.\)
Неравенство \(\cos\;x<-1\) решения не имеет.
Так как \(-1\leqslant\cos\;x\leqslant\), то неравенство \(\frac12<\cos\;x<4\) надо заменить другим неравенством:
\(\frac12<\cos\;x\leq1.\)
Его решением будет:
\(2\pi R-\frac\pi3<x<\frac\pi3+2\pi R,\;R\in Z\ \)
Вывод формул для решения тригонометрических неравенств. 10-й класс
Тип урока: комбинированный урок.
Цели урока:
- образовательные — научить учащихся решать тригонометрические неравенства с помощью графиков тригонометрических функций, вывести формулы для решения этих неравенств
- развивающие — развивать речь учащихся через обогащение и усложнение её словарного запаса, развивать мышление учащихся через умение анализировать, обобщать и систематизировать материал
- воспитательные — формирование гуманного отношения у учащихся к участникам образовательного процесса
Оборудование урока:
- интерактивная доска
- плакаты с графиками тригонометрических функций
Структура урока
| № | Основные фрагменты урока | Время |
| 1 | Организационный момент, вводная часть | 2 мин |
| 2 | Повторение | 5 мин |
| 3 | Изучение нового материала | 19 мин |
| 4 | Закрепление нового материала | 10 мин |
| 5 | Самостоятельная работа с последующей взаимопроверкой | 6 мин |
| 6 | Подведение итогов урока. Разбор домашнего
задания Разбор домашнего
задания |
3 мин |
Организационный момент, вводная часть.
Учитель объявляет тему урока, цели урока и основные моменты урока. Проверяет готовность класса к работе.
Повторение.
На доске вывешены плакаты с графиками тригонометрических функций y = sin x, y = cos x, y = tg x, y = ctg x. Рядом написаны вопросы для повторения.
Вопросы:
- Назовите область определения функции.
- Назовите область значений функции.
- Определите чётность функции (вид симметричности графика функции)
- Определите периодичность функции .
- Найдите наибольшее и наименьшее значение функции. В каких точках они достигаются?
- Найдите асимптоты для графика функции.
Изучение нового материала.
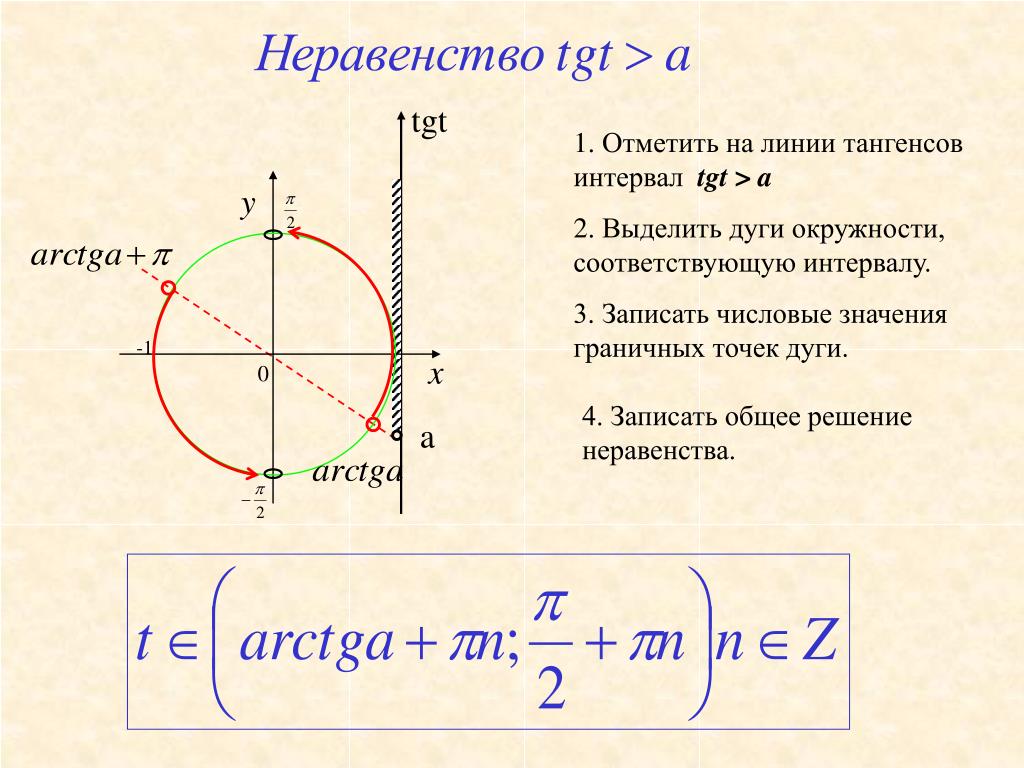
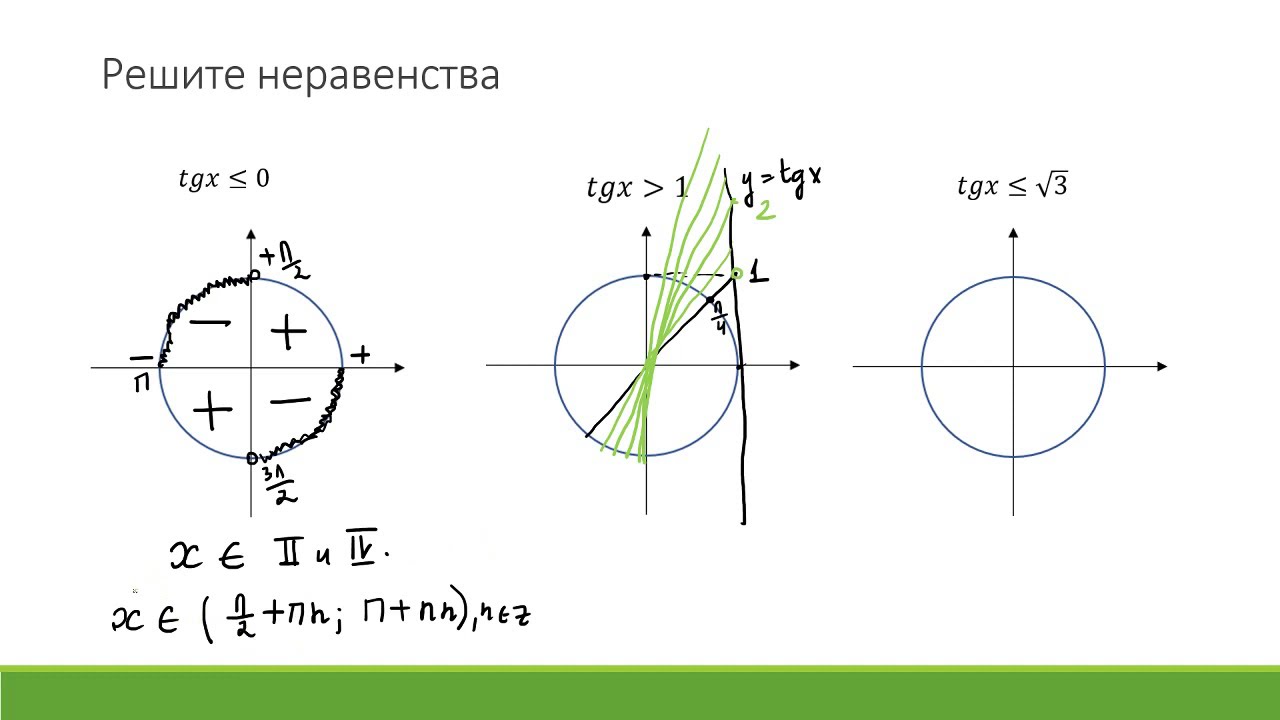
На интерактивную доску выводится <Рисунок1>. Разбирается вывод формулы для решения
неравенства cos ta. Следует обратить внимание учащихся
на запись ответа, если знак неравенства будет
строгий, т.е. cos t >a.
Разбирается вывод формулы для решения
неравенства cos ta. Следует обратить внимание учащихся
на запись ответа, если знак неравенства будет
строгий, т.е. cos t >a.
На интерактивную доску выводится <Рисунок2>. Разбирается вывод формулы для решения неравенства cos ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. cos t <a.
На интерактивную доску выводится <Рисунок3>. Разбирается вывод формулы для решения неравенства sin ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. sin t >a.
На интерактивную доску выводится <Рисунок4>.
Разбирается вывод формулы для решения
неравенства sin ta.
Следует обратить внимание учащихся на запись
ответа, если знак неравенства будет строгий, т.е.
sin t <a.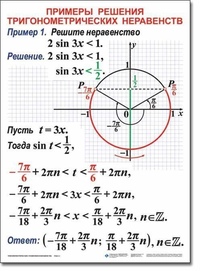
На интерактивную доску выводится <Рисунок5>. Разбирается вывод формулы для решения неравенства tg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. tg t >a.
На интерактивную доску выводится <Рисунок6>. Разбирается вывод формулы для решения неравенства tg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. tg t <a.
На интерактивную доску выводится <Рисунок7>. Разбирается вывод формулы для решения неравенства ctg ta. Следует обратить внимание учащихся на запись ответа, если знак неравенства будет строгий, т.е. ctg t >a.
На интерактивную доску выводится <Рисунок8>.
Разбирается вывод формулы для решения
неравенства сtg ta.
Следует обратить внимание учащихся на запись
ответа, если знак неравенства будет строгий,
т. е.сtg t <a.
е.сtg t <a.
IV. Закрепление нового материала.
Решите неравенства.
Решение неравенств.
V. Самостоятельная работа.
Решите неравенство.
1 вариант:
2 вариант:
Решение самостоятельной работы показывается на интерактивной доске.
VI. Подведение итогов урока.
Во время подведения итогов урока ещё раз следует обратить внимание учащихся на строгие и нестрогие тригонометрические неравенства. Особо следует отметить неравенства с тангенсом и котангенсом.
10.2.5. Решение тригонометрических неравенств. Часть 5.
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 282 Опубликовано
На предыдущих занятиях мы решали графическим способом тригонометрические неравенства вида:
На этом занятии мы решим три неравенства вида: tgt<a.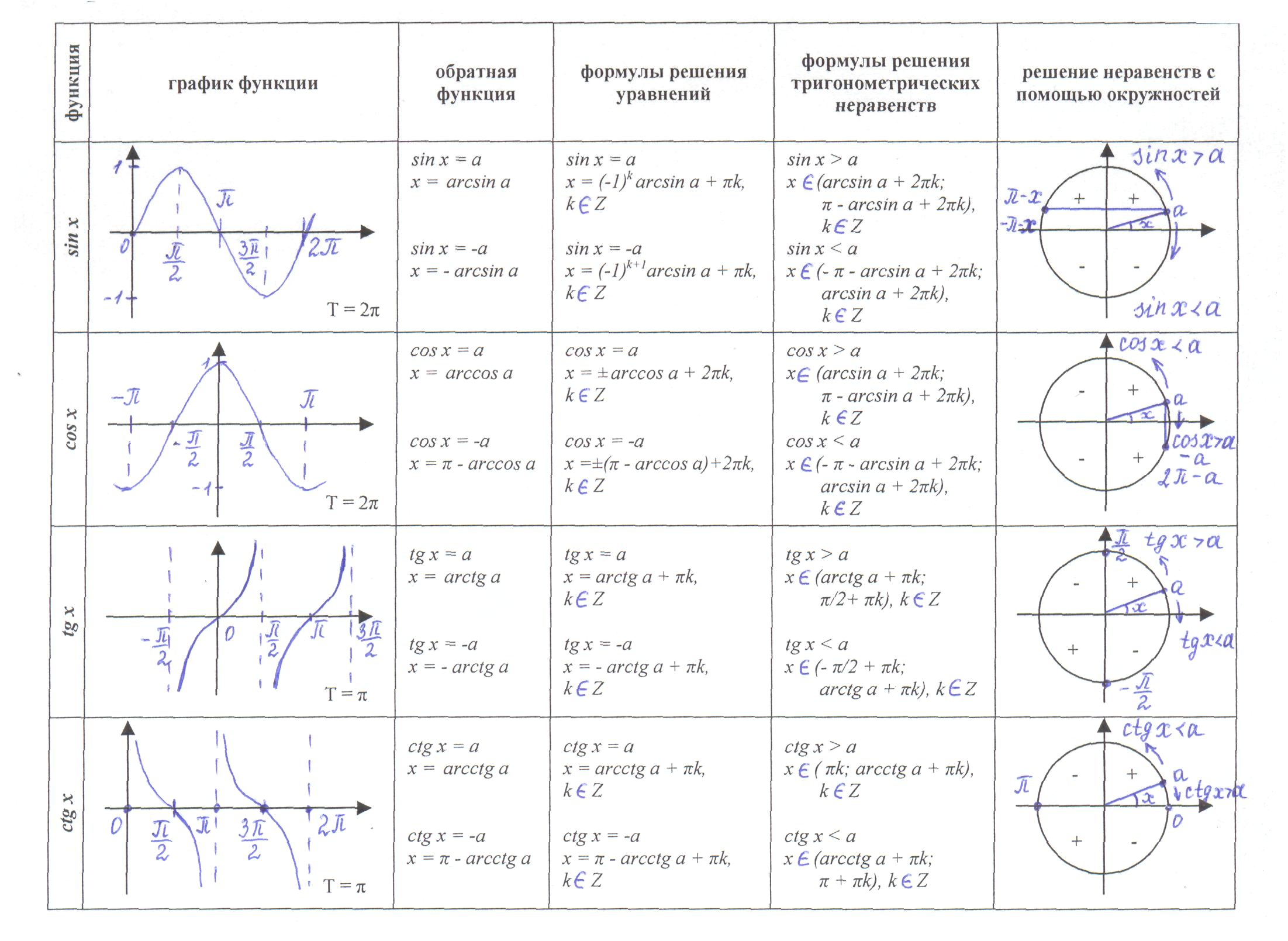
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций y=tgt и y=a.
3. Находим промежуток значений t, при которых тангенсоида располагается ниже прямой у=а. Левая граница этого промежутка всегда (-π/2), а правая arctg a
4. Записываем двойное неравенство для аргумента t, учитывая период тангенса Т=π (t будет между абсциссами(-π/2) и arctg a).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.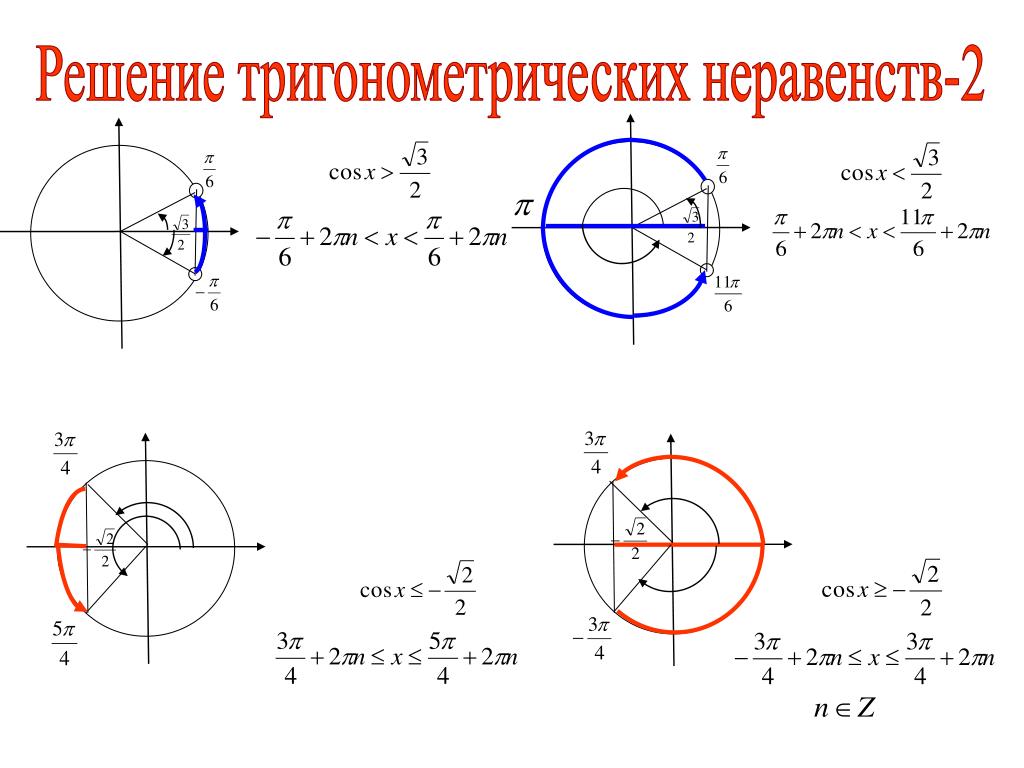
Решение тригонометрических неравенств графическим способом надежно страхует нас от ошибок только в том случае, если мы грамотно построим графики.
Первое неравенство.
Построим графики функций y=tgx и у=1. Подробно рассмотрим построение тангенсоиды. Приготовим координатную плоскость хОу следующим образом:
единичный отрезок равен двум клеткам; так как значение π≈3,14, то π на горизонтальной оси Ох будет изображаться шестью клетками; половина π (это π/2) — тремя клетками. Одна клетка — это π/6; полторы клетки — это π/4; две клетки будут соответствовать аргументу π/3.
Мы знаем, что тангенс 90° не существует, а так как функция тангенса периодическая с наименьшим периодом, равным π, то не существует тангенс (90°+πn). Учтем это при построении графика и проведем две асимптоты: х= — π/2 и х=π/2.
Учтем это при построении графика и проведем две асимптоты: х= — π/2 и х=π/2.
Итак, в промежутке от — π/2 до π/2 тангенс будет «пробегать» все свои значения. Пользуясь значениями тангенса некоторых углов и свойством нечетности функции тангенса (график будет симметричен относительно начала координат), строим точки в приготовленной координатной плоскости, через которые и проведем тангенсоиду.
Построим прямую у=1.
Проведем ее параллельно оси Ох, выше на один единичный отрезок (выше на 2 клетки).
Прямая у=1 пересекает тангенсоиду в точке с координатами (π/4; 1).
Определяем промежуток значений х, при которых неравенство будет верным, т.е. внутри которого тангенсоида располагается ниже прямой у=1. Учтем, что неравенство нестрогое, значит, правый конец промежутка (π/4) входит во множество решений неравенства. Записываем решение в виде двойного неравенства. Ответ запишем в виде промежутка.
Записываем решение в виде двойного неравенства. Ответ запишем в виде промежутка.
Второе неравенство.
Отметим промежуток значений t, при которых точки тангенсоиды находятся ниже точек прямой у=1. Запишем этот промежуток в виде двойного неравенства. Затем перезапишем его для первоначального аргумента и выразим х. Ответ запишем в виде промежутка.
Третье неравенство.
Отмечаем промежуток значений t, при которых неравенство верно. У нас нестрогое неравенство, значит, правый конец промежутка значений t также является решением неравенства. Возвращаемся к первоначальному аргументу и выражаем х. Ответ записываем в виде промежутка значений переменной х.
Смотреть видео: «10.2.5. Решение тригонометрических неравенств. Часть 5.»
Неравенства вида tgt<a можно решать и без графиков, по соответствующей формуле.
Если tgt<a, то — (π/2) + πn < t < arctg a + πn, где nєZ.
Решение простейших тригонометрических неравенств | matematicus.ru
Скачать шпаргалку решения простейших тригонометрических уравнений
Приведена таблица решения простейших тригонометрических неравенств
| Вид тригонометрического неравенства | Решение тригонометрического неравенства |
| Тригонометрические неравенства в сравнении с нулем | |
| sin(x)>0 | 2πk<x<π+2πk, k∈Z |
| sin(x)<0 | -π+2πk<x<π+2πk, k∈Z |
| cos(x)>0 | -π/2+2πk<x<π/2+2πk, k∈Z |
| cos(x)<0 | π/2+2πk<x<3π/2+2πk, k∈Z |
| tg(x)>0 или сtg(x)>0 | πk<x<π/2+πk, k∈Z |
| tg(x)<0 или сtg(x)<0 | -π/2+πk<x<πk, k∈Z |
| Тригонометрические неравенства относящиеся к общему случаю | |
| sin(x)>a, -1<a<1 | arcsin(a)+2πk<x<π-arcsin(a)+2πk, k∈Z |
| sin(x)<a, -1<a<1 | -π—arcsin(a)+2πk<x<arcsin(a)+2πk, k∈Z |
| cos(x)>a, -1<a<1 | -arccos(a)+2πk<x<arccos(a)+2πk, k∈Z |
| cos(x)<a, -1<a<1 | arccos(a)+2πk<x<2π-arccos(a)+2πk, k∈Z |
| tg(x)>a | arctg(a)+πk<x<π/2+πk, k∈Z |
| tg(x)<a | -π/2+πk<x<arctg(a)+πk, k∈Z |
| ctg(x)>a | πk<x<arcctg(a)+πk, k∈Z |
| ctg(x)<a | arcctg(a)+πk<x<π+πk, k∈Z |
Методы решения тригонометрических неравенств
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ
Актуальность. Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Можно сказать, что тригонометрия является одним из важнейших разделов школьного курса и всей математической науки в целом.
Исторически сложилось, что тригонометрическим уравнениям и неравенствам уделялось особое место в школьном курсе. Можно сказать, что тригонометрия является одним из важнейших разделов школьного курса и всей математической науки в целом.
Тригонометрические уравнения и неравенства занимают одно из центральных мест в курсе математики средней школы, как по содержанию учебного материала, так и по способам учебно-познавательной деятельности, которые могут и должны быть сформированы при их изучении и применены к решению большого числа задач теоретического и прикладного характера.
Решение тригонометрических уравнений и неравенств создаёт предпосылки для систематизации знаний учащихся, связанных со всем учебным материалом по тригонометрии (например, свойства тригонометрических функций, приёмы преобразования тригонометрических выражений и т.д.) и даёт возможность установить действенные связи с изученным материалом по алгебре (уравнения, равносильность уравнений, неравенства, тождественные преобразования алгебраических выражений и т.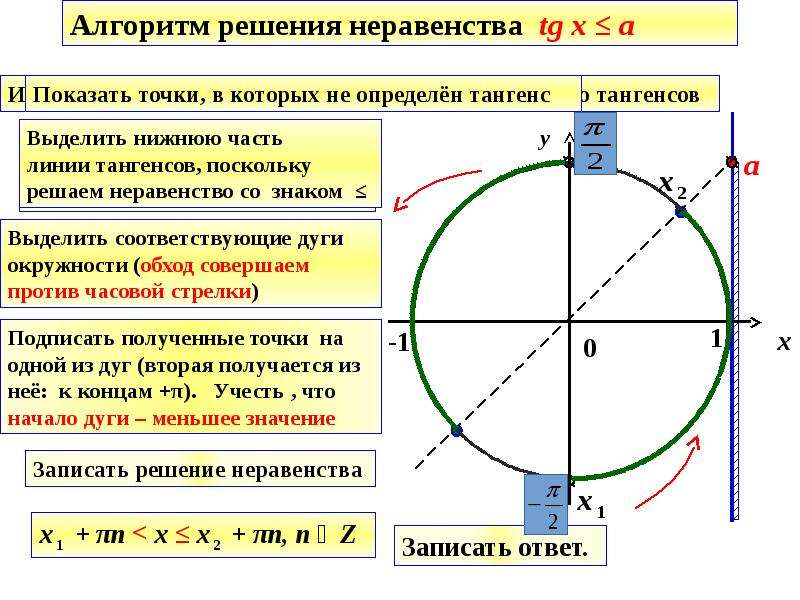 д.).
д.).
Иначе говоря, рассмотрение приёмов решения тригонометрических уравнений и неравенств предполагает своего рода перенос этих умений на новое содержание.
Значимость теории и ее многочисленные применения являются доказательством актуальности выбранной темы. Это в свою очередь позволяет определить цели, задачи и предмет исследования курсовой работы.
Цель исследования: обобщить имеющиеся типы тригонометрических неравенств, основные и специальные методы их решения, подобрать комплекс задач для решения тригонометрических неравенств школьниками.
Задачи исследования:
1. На основе анализа имеющейся литературы по теме исследования систематизировать материал.
2. Привести комплекс заданий, необходимый для закрепления темы «Тригонометрические неравенства».
Объектом исследования являются тригонометрические неравенства в школьном курсе математики.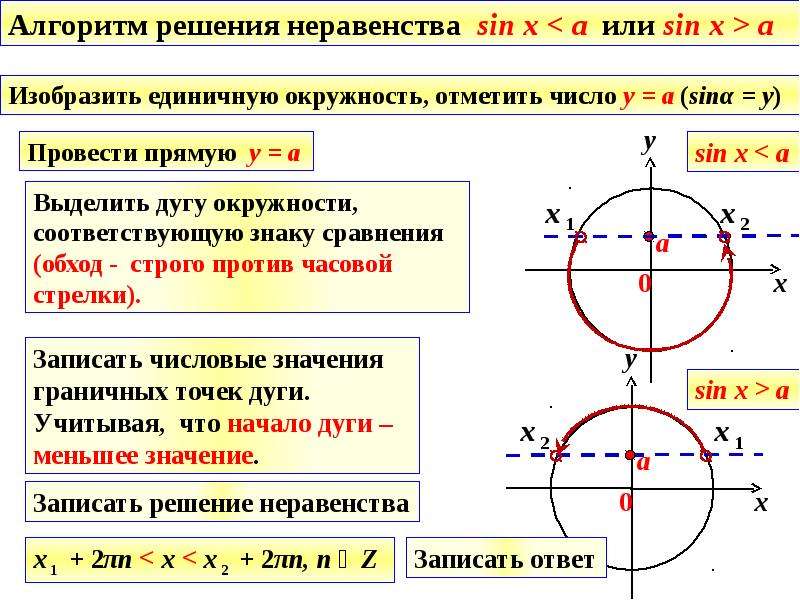
Предмет исследования: типы тригонометрических неравенств и методы их решения.
Теоретическая значимость заключается в систематизации материала.
Практическая значимость: применение теоретических знаний в решении задач; разбор основных часто встречающихся методов решений тригонометрических неравенств.
Методы исследования: анализ научной литературы, синтез и обобщение полученных знаний, анализ решения заданий, поиск оптимального методов решения неравенств.
§1. Типы тригонометрических неравенств и основные методы их решения
1.1. Простейшие тригонометрические неравенства
Два тригонометрических выражения, соединённые между собой знаком или >, называются тригонометрическими неравенствами.
Решить тригонометрическое неравенство – это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.
Основная часть тригонометрических неравенств решается сведением их к решению простейших:
(, , ),
(, , ),
(, , ),
(, , ).
Это может быть метод разложения на множители, замены переменного (, и т.д.), где сначала решается обычное неравенство, а затем неравенство вида и т.д., или другие способы.
Простейшие неравенства решаются двумя способами: с помощью единичной окружности или графически.
Пусть f(х – одна из основных тригонометрических функций. Для решения неравенства достаточно найти его решение на одном периоде, т.е. на любом отрезке, длина которого равна периоду функции fx. Тогда решением исходного неравенства будут все найденные x, а также те значения, которые отличаются от найденных на любое целое число периодов функции. При этом удобно использовать графический метод.
При этом удобно использовать графический метод.
Приведем пример алгоритма решения неравенств () и .
Алгоритм решения неравенства ().
1. Сформулируйте определение синуса числа x на единичной окружности.
2. Нарисуйте единичную окружность.
3. На оси ординат отметьте точку с координатой a.
4. Через данную точку проведите прямую, параллельную оси OX, и отметьте точки пересечения ее с окружностью.
5. Выделите дугу окружности, все точки которой имеют ординату, меньшую a.
6. Укажите направление обхода (против часовой стрелки) и запишите ответ, добавив к концам промежутка период функции 2πn, .
Алгоритм решения неравенства .
1. Сформулируйте определение тангенса числа x на единичной окружности.
2. Нарисуйте единичную окружность.
Нарисуйте единичную окружность.
3. Проведите линию тангенсов и на ней отметьте точку с ординатой a.
4. Соедините данную точку с началом координат и отметьте точку пересечения полученного отрезка с единичной окружностью.
5. Выделите дугу окружности, все точки которой имеют на линии тангенсов ординату, меньшую a.
6. Укажите направление обхода и запишите ответ с учетом области определения функции, добавив период πn, (число, стоящее в записи слева, всегда меньше числа, стоящего справа).
Графическая интерпретация решений простейших уравнений и формулы решения неравенств в общем виде указаны в приложении (Приложения 1 и 2).
Пример 1. Решите неравенство .
На единичной окружности проводим прямую , которая пересекает окружность в точках A и B.
Все значения y на промежутке NM больше , все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших , но меньших , будет принимать значения больше (но не больше единицы).
При всех углах поворота, больших , но меньших , будет принимать значения больше (но не больше единицы).
Рис.1
Таким образом, решением неравенства будут все значения на интервале , т.е. . Для того, чтобы получить все решения данного неравенства, достаточно к концам этого промежутка прибавить , где , т.е. , . Заметим, что значения и являются корнями уравнения ,
т.е. ; .
Ответ: , .
1.2. Графический метод
На практике довольно часто оказывается полезным графический метод решения тригонометрических неравенств. Рассмотрим сущность метода на примере неравенства :
1. Если аргумент – сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости tOy графики функций и .
3. Находим такие две соседние точки пересечения графиков, между которыми синусоида располагается выше прямой . Находим абсциссы этих точек.
Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период косинуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Пример 2. Решить неравенство: .
При решении неравенств графическим методом необходимо как можно более точно построить графики функций. Преобразуем неравенство к виду:
Построим в одной системе координат графики функций и (рис. 2).
Рис.2
Графики функций пересекаются в точке А с координатами ; . На промежутке точки графика ниже точек графика . А при значения функции совпадают. Поэтому при .
Ответ: .
1. 3. Алгебраический метод
3. Алгебраический метод
Довольно часто исходное тригонометрическое неравенство путем удачно выбранной подстановки удается свести к алгебраическому (рациональному или иррациональному) неравенству. Данный метод подразумевает преобразование неравенства, введение подстановки или замену переменной.
Рассмотрим на конкретных примерах применение этого метода.
Пример 3. Приведение к простейшему виду .
(рис. 3)
Рис.3
, .
Ответ: ,
Пример 4. Решить неравенство:
ОДЗ: , .
Используя формулы: ,
запишем неравенство в виде: .
Или, полагая после несложных преобразований получим
,
,
.
Решая последнее неравенство методом интервалов, получаем:
Рис. 4
4
, соответственно . Тогда из рис. 4 следует , где .
Рис.5
Ответ: , .
1.4. Метод интервалов
Общая схема решения тригонометрических неравенств методом интервалов:
С помощью тригонометрических формул разложить на множители.
Найти точки разрыва и нули функции, поставить их на окружность.
Взять любую точку К (но не найденную ранее) и выяснить знак произведения. Если произведение положительно, то поставить точку за единичной окружностью на луче, соответствующему углу. Иначе точку поставить внутри окружности.
Если точка встречается четное число раз, назовем ее точкой четной кратности, если нечетное число раз – точкой нечетной кратности. Провести дуги следующим образом: начать с точки К, если следующая точка нечетной кратности, то дуга пересекает окружность в этой точке, если же точка четной кратности, то не пересекает.

Дуги за окружностью – положительные промежутки; внутри окружности – отрицательные промежутки.
Пример 5. Решить неравенство
, .
Точки первой серии: .
Точки второй серии: .
Каждая точка встречается нечетное число раз, то есть все точки нечетной кратности.
Выясним знак произведения при : . Отметим все точки на единичной окружности (рис.6):
Рис. 6
Ответ: , ; , ; , .
Пример 6. Решите неравенство .
Решение:
Найдём нули выражения .
Получaeм :
, ;
, ;
, ;
, ;
На единичной окружности значения серии х1 представлены точками . Серия х2 дает точки . Из серии х3 получаем две точки . Наконец, серию х4 будут представлять точки . Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
Серия х2 дает точки . Из серии х3 получаем две точки . Наконец, серию х4 будут представлять точки . Нанесем все эти точки на единичную окружность, указав в скобках рядом с каждой из них ее кратность.
Пусть теперь число будет равным . Делаем прикидку по знаку:
Значит, точку A следует выбрать на луче, образующем угол с лучом Ох, вне единичной окружности. (Заметим, что вспомогательный луч ОA совсем не обязательно изображать на рисунке. Точка A выбирается приблизительно.)
Теперь от точки A ведем волнообразную непрерывную линию последовательно ко всем отмеченным точкам. Причем в точках наша линия переходит из одной области в другую: если она находилась вне единичной окружности, то переходит внутрь нее. Подойдя к точке , линия возвращается во внутреннюю область, так как кратность этой точки четная.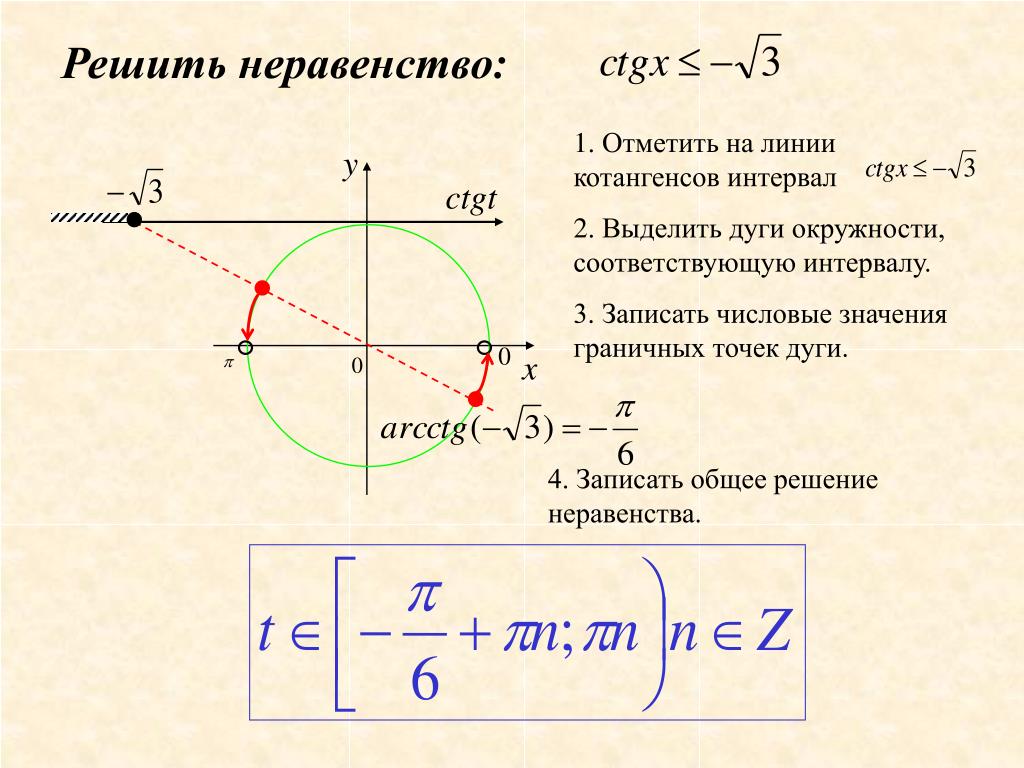 Аналогично в точке (с четной кратностью) линию приходится повернуть во внешнюю область. Итак, начертили некую картинку, изображенную на рис. 7. Она помогает выделить на единичной окружности искомые области. Они обозначены знаком « + ».
Аналогично в точке (с четной кратностью) линию приходится повернуть во внешнюю область. Итак, начертили некую картинку, изображенную на рис. 7. Она помогает выделить на единичной окружности искомые области. Они обозначены знаком « + ».
Рис.7
Окончательный ответ:
Примечание. Если волнообразную линию после обхода ею всех отмеченных на единичной окружности точек не удается вернуть в точку A, не пересекая окружность в «незаконном» месте, то это означает, что в решении допущена ошибка, а именно пропущено нечетное количество корней.
Ответ:.
§2. Комплекс задач по решению тригонометрических неравенств
В процессе формирования у школьников умений решать тригонометрические неравенства, также можно выделить 3 этапа.
1. подготовительный,
2. формирование умений решать простейшие тригонометрические неравенства;
формирование умений решать простейшие тригонометрические неравенства;
3. введение тригонометрических неравенств других видов.
Цель подготовительного этапа состоит в том, что необходимо сформировать у школьников умение использовать тригонометрический круг или график для решения неравенств, а именно:
— умения решать простейшие неравенства вида , , , , с помощью свойств функций синус и косинус;
— умения составлять двойные неравенства для дуг числовой окружности или для дуг графиков функций;
— умения выполнять различные преобразования тригонометрических выражений.
Реализовать этот этап рекомендуется в процессе систематизации знаний школьников о свойствах тригонометрических функций. Основным средством могут служить задания, предлагаемые учащимся и выполняемые либо под руководством учителя, либо самостоятельно, а так же навыки наработанные при решении тригонометрических уравнений.
Приведем примеры таких заданий:
1. Отметьте на единичной окружности точку , если
.
2. В какой четверти координатной плоскости расположена точка , если равно:
3. Отметьте на тригонометрической окружности точки , если:
4. Приведите выражение к тригонометрическим функциям I четверти.
а) , б) , в)
5. Дана дуга МР. М – середина I-ой четверти, Р – середина II-ой четверти. Ограничить значение переменной t для: (составить двойное неравенство) а) дуги МР; б) дуги РМ.
6. Записать двойное неравенство для выделенных участков графика:
Рис. 1
7. Решите неравенства , , , .
8. Преобразовать выражение.
На втором этапе обучения решению тригонометрических неравенств можно предложить следующие рекомендации, связанные с методикой организации деятельности учащихся. При этом нужно ориентироваться на уже имеющиеся у учащихся умения работать с тригонометрической окружностью или графиком, сформированные во время решения простейших тригонометрических уравнений.
Во-первых, мотивировать целесообразность получения общего приема решения простейших тригонометрических неравенств можно, обратившись, например, к неравенству вида . Используя знания и умения, приобретенные на подготовительном этапе, учащиеся приведут предложенное неравенство к виду , но могут затрудниться в нахождении множества решений полученного неравенства, т.к. только лишь используя свойства функции синус решить его невозможно. Этого затруднения можно избежать, если обратиться к соответствующей иллюстрации (решение уравнения графически или с помощью единичной окружности).
Во-вторых, учитель должен обратить внимание учащихся на различные способы выполнения задания, дать соответствующий образец решения неравенства и графическим способом и с помощью тригонометрического круга.
Рассмотрим такие варианты решения неравенства .
1. Решение неравенства с помощью единичной окружности.
На первом занятии по решению тригонометрических неравенств предложим учащимся подробный алгоритм решения, который в пошаговом представлении отражает все основные умения, необходимые для решения неравенства.
Шаг 1. Начертим единичную окружность, отметим на оси ординат точку и проведем через нее прямую, параллельную оси абсцисс. Эта прямая пересечет единичную окружность в двух точках. Каждая из этих точек изображает числа, синус которых равен .
Шаг 2. Эта прямая разделила окружность на две дуги. Выделим ту из них, на которой изображаются числа, имеющие синус больший, чем . Естественно, эта дуга расположена выше проведенной прямой.
Рис. 2
Шаг 3. Выберем один из концов отмеченной дуги. Запишем одно из чисел, которое изображается этой точкой единичной окружности .
Шаг 4. Для того чтобы выбрать число, соответствующее второму концу выделенной дуги, «пройдем» по этой дуге из названного конца к другому. При этом напомним, что при движении против часовой стрелки числа, которые мы будем проходить, увеличиваются (при движении в противоположном направлении числа уменьшались бы). Запишем число, которое изображается на единичной окружности вторым концом отмеченной дуги .
Таким образом, мы видим, что неравенству удовлетворяют числа, для которых справедливо неравенство . Мы решили неравенство для чисел, расположенных на одном периоде функции синус. Поэтому все решения неравенства могут быть записаны в виде
Учащимся нужно предложить внимательно рассмотреть рисунок и разобраться, почему все решения неравенства могут быть записаны в виде , .
Рис. 3
Необходимо обратить внимание учащихся на то, что при решении неравенств для функции косинус, прямую проводим параллельно оси ординат.
Графический способ решения неравенства.
Строим графики и , учитывая, что .
Рис. 4
Затем записываем уравнение и его решение , , , найденное с помощью формул , , .
(Придавая n значения 0, 1, 2, находим три корня составленного уравнения). Значения являются тремя последовательными абсциссами точек пересечения графиков и . Очевидно, что всегда на интервале выполняется неравенство , а на интервале – неравенство . Нас интересует первый случай, и тогда добавив к концам этого промежутка число, кратное периоду синуса, получим решение неравенства в виде: , .
Рис. 5
Подведём итог. Чтобы решить неравенство , надо составить соответствующее уравнение и решить его. Из полученной формулы найти корни и , и записать ответ неравенства в виде: , .
В-третьих, факт о множестве корней соответствующего тригонометрического неравенства очень наглядно подтверждается при решении его графическим способом.
Рис. 6
Необходимо продемонстрировать учащимся, что виток, который является решением неравенства, повторяется через один и тот же промежуток, равный периоду тригонометрической функции. Так же можно рассмотреть аналогичную иллюстрацию для графика функции синус.
В-четвертых, целесообразно провести работу по актуализации у учащихся приемов преобразования суммы (разности) тригонометрических функций в произведение, обратить внимание школьников на роль этих приемов при решении тригонометрических неравенств.
Организовать такую работу можно через самостоятельное выполнение учащимися предложенных учителем заданий, среди которых выделим следующие:
В-пятых, от учащихся необходимо требовать обязательной иллюстрации решения каждого простейшего тригонометрического неравенства с помощью графика или тригонометрического круга.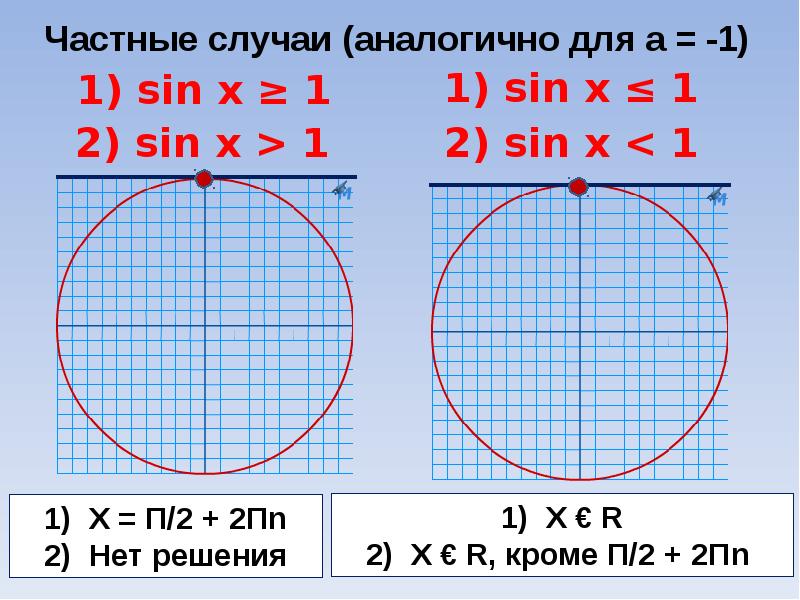 Обязательно следует обратить внимание на ее целесообразность, в особенности на применение круга, так как при решении тригонометрических неравенств соответствующая иллюстрация служит очень удобным средством фиксации множества решений данного неравенства
Обязательно следует обратить внимание на ее целесообразность, в особенности на применение круга, так как при решении тригонометрических неравенств соответствующая иллюстрация служит очень удобным средством фиксации множества решений данного неравенства
Знакомство учащихся с приемами решения тригонометрических неравенств, не являющихся простейшими, целесообразно осуществлять по следующей схеме: обращение к конкретному тригонометрическому неравенству обращение к соответствующему тригонометрическому уравнению совместный поиск (учитель – учащиеся) приема решения самостоятельный перенос найденного приема на другие неравенства этого же вида.
Чтобы систематизировать знания учащихся о тригонометрии, рекомендуем специально подобрать такие неравенства, решение которых требует различных преобразований, которые могут быть реализованы в процессе его решения, акцентировать внимание учащихся на их особенностях.
В качестве таких продуктивных неравенств можно предложить, например, следующие:
В заключение приведем пример комплекса задач по решению тригонометрических неравенств.
1. Решите неравенства:
2. Решите неравенства: 3. Найдите все решения неравенств: 4. Найдите все решения неравенств:а) , удовлетворяющие условию ;
б) , удовлетворяющие условию .
5. Найдите все решения неравенств:
а) ;
б) ;
в) ;
г) ;
д) .
6. Решите неравенства:
а) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) .
7. Решите неравенства:
а) ;
б) ;
в) ;
г) .
8. Решите неравенства:
а) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) .
Задания 6 и 7 целесообразно предложить ученикам, изучающим математику на повышенном уровне, задание 8 – учащимся классов с углубленным изучением математики.
§3. Специальные методы решения тригонометрических неравенств
Специальные методы решения тригонометрических уравнений – то есть те методы, которые можно использовать только для решения тригонометрических уравнений. Эти методы основаны на использовании свойств тригонометрических функций, а также на использовании различных тригонометрических формул и тождеств.
Эти методы основаны на использовании свойств тригонометрических функций, а также на использовании различных тригонометрических формул и тождеств.
3.1. Метод секторов
Рассмотрим метод секторов для решения тригонометрических неравенств. Решение неравенств вида , где P(x) и Q(x) – рациональные тригонометрические функции (синусы, косинусы, тангенсы и котангенсы входят в них рационально), аналогично решению рациональных неравенств. Рациональные неравенства удобно решать методом интервалов на числовой оси. Его аналогом при решении рациональных тригонометрических неравенств является метод секторов в тригонометрическом круге, для sinx и cosx () или тригонометрическом полукруге для tgx и ctgx ().
Неравенства вида
В методе интервалов каждому линейному множителю числителя и знаменателя вида на числовой оси соответствует точка , и при переходе через эту точку меняет знак. В методе секторов каждому множителю вида , где — одна из функций sinx или cosx и , в тригонометрическом круге соответствуют два угла и , которые делят круг на два сектора. При переходе через и функция меняет знак.
В методе секторов каждому множителю вида , где — одна из функций sinx или cosx и , в тригонометрическом круге соответствуют два угла и , которые делят круг на два сектора. При переходе через и функция меняет знак.
Необходимо помнить следующее:
а) Множители вида и , где , сохраняют знак для всех значений . Такие множители числителя и знаменателя отбрасывают, изменяя (если ) при каждом таком отбрасывании знак неравенства на противоположный.
б) Множители вида и также отбрасываются. При этом, если это множители знаменателя, то в эквивалентную систему неравенств добавляются неравенства вида и . Если это множители числителя, то в эквивалентной системе ограничений им соответствуют неравенства и в случае строгого исходного неравенства, и равенства и в случае нестрогого исходного неравенства. При отбрасывании множителя или знак неравенства изменяется на противоположный.
Пример 1. Решить неравенства: а) , б) .
Решить неравенства: а) , б) .
В тригонометрическом круге уравнению соответствуют два угла и . Они делят круг на два сектора, в каждом из которых функция сохраняет знак (рисунок 1).
Рис.1
В секторе имеем . В секторе , очевидно, . Период функции .
Ответ: а) , , б) , .
Неравенства вида
Каждому множителю вида , где одна из функций tgx или ctgx, в тригонометрическом полукруге (или ) соответствует один угол такой, что . При переходе через функция меняет знак. Кроме того, tgx не определен при , и слева, и справа от этих точек имеет разные знаки. Аналогично, ctgx не определен при и , и слева, и справа от этих точек имеет разные знаки.
Пример 2. Решить неравенства а) , б) .
В тригонометрическом полукруге уравнению соответствует один угол . При функция не определена. Указанные три угла делят полукруг на два сектора, в каждом из которых функция сохраняет знак (рисунок 2).
При функция не определена. Указанные три угла делят полукруг на два сектора, в каждом из которых функция сохраняет знак (рисунок 2).
Рис.2
В секторе имеем .
В секторе , очевидно, .
Функция имеет период .
Ответ: а) , , б) , .
Неравенства, содержащие sinx, cosx и tgx, ctgx одновременно, или содержащие тригонометрические функции различных аргументов.
Здесь необходимо найти общий период функций, входящих в неравенство, и, используя различные тождественные преобразования, разложить неравенство на простейшие множители.
Пример 3. Решить неравенство .
Имеем:
,
,
.
Положим . Тогда
Рис.3
, .
Ответ: , .
Пример 4. Решить неравенство .
Решить неравенство .
Воспользуемся формулами , .
Имеем, , , .
Положим , получим .
, .
Рис. 4
Ответ: , .
3.2. Метод концентрических окружностей
Данный метод является аналогом метода параллельных числовых осей при решении систем рациональных неравенств.
Рассмотрим пример системы неравенств.
Пример 5. Решить систему простейших тригонометрических неравенств
Сначала решим каждое неравенство отдельно (рисунок 5). В правом верхнем углу рисунка будем указывать для какого аргумента рассматривается тригонометрическая окружность.
Рис.5
Далее строим систему концентрических окружностей для аргумента х. Рисуем окружность и заштриховываем ее согласно решению первого неравенства, затем рисуем окружность большего радиуса и заштриховываем ее согласно решению второго, далее строим окружность для третьего неравенства и базовую окружность. Из центра системы через концы дуг проводим лучи так, чтобы они пересекали все окружности. На базовой окружности формируем решение (рисунок 6).
Из центра системы через концы дуг проводим лучи так, чтобы они пересекали все окружности. На базовой окружности формируем решение (рисунок 6).
Рис.6
Ответ: , .
Заключение
Все задачи курсового исследования были выполнены. Систематизирован теоретический материал: приведены основные типы тригонометрических неравенств и основные методы их решения (графический, алгебраический, метод интервалов, секторов и метод концентрических окружностей). К каждому методы был приведен пример решения неравенства. За теоретической частью следовала практическая. В ней составлен комплекс заданий по решению тригонометрических неравенств.
Данная курсовая может быть использована учащимися для самостоятельной работы. Школьники могут проконтролировать уровень усвоения данной темы, потренироваться в выполнении заданий различной сложности.
Проработав соответствующую литературу по данному вопросу, очевидно, можно сделать вывод о том, что умение и навыки решать тригонометрические неравенства в школьном курсе алгебры и начал анализа являются очень важными, развитие которых требует значительных усилий со стороны учителя математики.
Поэтому данная работа будет полезна учителям математики, так как дает возможность эффективно организовать подготовку учащихся по теме «Тригонометрические неравенства».
Исследование можно продолжить, расширив его до выпускной квалификационной работы.
Список использованной литературы
Богомолов, Н.В. Сборник задач по математике [Текст] / Н.В. Богомолов. – М.: Дрофа, 2009. – 206 с.
Выгодский, М.Я. Справочник по элементарной математике [Текст] / М.Я. Выгодский. – М.: Дрофа, 2006. – 509 с.
Журбенко, Л.Н. Математика в примерах и задачах [Текст] / Л.Н. Журбенко. – М.: Инфра-М, 2009. – 373 с.
Иванов, О.А. Элементарная математика для школьников, студентов и преподавателей [Текст] / О.А. Иванов. – М.: МЦНМО, 2009. – 384 с.
Карп, А.П. Задания по алгебре и началам анализа для организации итогового повторения и проведения аттестации в 11 классе [Текст] / А.
 П. Карп. – М.: Просвещение, 2005. – 79 с.
П. Карп. – М.: Просвещение, 2005. – 79 с.Куланин, Е.Д. 3000 конкурсных задач по математике [Текст] / Е.Д. Куланин. – М.: Айрис-пресс, 2007. – 624 с.
Лейбсон, К.Л. Сборник практических заданий по математике [Текст] / К.Л. Лейбсон. – М.: Дрофа, 2010. – 182 с.
Локоть, В.В. Задачи с параметрами и их решение. Тригонометрия: уравнения, неравенства, системы. 10 класс [Текст] / В.В. Локоть. – М.: АРКТИ, 2008. – 64 с.
Манова, А.Н. Математика. Экспресс-репетитор для подготовки к ЕГЭ: уч. пособие [Текст] / А.Н. Манова. – Ростов-на-Дону: Феникс, 2012. – 541 с.
Мордкович, А.Г. Алгебра и начала математического анализа. 10-11 классы. Учебник для учащихся общеобразовательных учреждений [Текст] / А.Г. Мордкович. – М.: Айрис-пресс, 2009. – 201 с.
Новиков, А.И. Тригонометрические функции, уравнения и неравенства [Текст] / А.
 И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с.
И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с.Оганесян, В.А. Методика преподавания математики в средней школе: Общая методика. Учеб. пособие для студентов физ. — мат. фак. пед. ин-тов. [Текст] / В.А. Оганесян. – М.: Просвещение, 2006. – 368 с.
Олехник, С.Н. Уравнения и неравенства. Нестандартные методы решения [Текст] / С.Н. Олехник. – М.: Изд-во Факториал, 1997. – 219 с.
Севрюков, П.Ф. Тригонометрические, показательные и логарифмические уравнения и неравенства [Текст] / П.Ф. Севрюков. – М.: Народное образование, 2008. – 352 с.
Сергеев, И.Н. ЕГЭ: 1000 задач с ответами и решениями по математике. Все задания группы С [Текст] / И.Н. Сергеев. – М.: Экзамен, 2012. – 301 с.
Соболев, А.Б. Элементарная математика [Текст] / А.Б. Соболев. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. – 81 с.
Фенько, Л.
 М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с.
М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с.Фридман, Л.М. Теоретические основы методики обучения математике [Текст] / Л.М. Фридман. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 248 с.
Приложение 1
Графическая интерпретация решений простейших неравенств
Рис. 1
Рис. 2
Рис.3
Рис.4
Рис.5
Рис.6
Рис.7
Рис.8
Приложение 2
Решения простейших неравенств
Урок 50.
 тригонометрические неравенства — Алгебра и начала математического анализа — 10 класс
тригонометрические неравенства — Алгебра и начала математического анализа — 10 классАлгебра и начала математического анализа, 10 класс
Урок №50. Тригонометрические неравенства.
Перечень вопросов, рассматриваемых в теме
- решение простейших тригонометрических неравенств с помощью тригонометрической окружности;
- решение тригонометрических неравенств, сводимых к квадратным;
- решение тригонометрических неравенств методом интервалов.
Глоссарий по теме
- Синусом угла называется ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Косинусом угла называется абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол . Обозначается
- Тангенсом угла называется отношение к
Угол может выражаться и в градусах и в радианах.
- Арккосинусом числа называется такое число α, что: .
 Арккосинус числа m обозначают: .
Арккосинус числа m обозначают: . - Арксинусом числаназывается такое число α, что: и . Арксинус числа m обозначают:.
- Арктангенсом числа m называется такое число α, что: и . Арктангенс числа m обозначают: .
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни под ред. А.Б. Жижченко. – 2-е изд. – М.: Просвещение, 2010. – 336 с.: ил. – ISBN 978-5-09-022250-1, сс. 334-337.
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс. 353-367.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru
Теоретический материал для самостоятельного изучения
1. Рассмотрим простейшие тригонометрические неравенства.
Начнем рассматривать с неравенства .
Из рисунка 1 видно, что если a>1, то решений данное неравенство не имеет.
Рисунок 1 – Точки пересечения прямой y=a (a>1) с тригонометрической окружностью
Если a=1, то решений такое неравенство также не имеет (рис.2). Однако, если мы изменим знак на (получим неравенство , то решением его будет множество точек, в которых . Это числа .
Рисунок 2 – Общие точки прямой y=1 с тригонометрической окружностью
Рассмотрим теперь значение (рис.3).
Рисунок 3 – Решение неравенства
Видим, что множество решений данного неравенства представляет собой дугу, начало которой в точке (1) , конец в точке (2) N(π – arcsina) . В зависимости от знака неравенство (строгое оно или нестрогое) промежуток представляет собой интервал или отрезок. Далее множество промежутков получается прибавлением :
(для строгого неравенства) – множество интервалов;
(для нестрогого неравенства) – множество отрезков.
Если значение a= – 1,то получим следующую картинку (рис. 4):
4):
Рисунок 4 – Общие точки прямой y= – 1 с тригонометрической окружностью
Видно. что если неравенство нестрогое, то решением неравенства является любое действительное число. Если неравенство строгое, то решением неравенства является любое действительное число, кроме чисел вида .
Наконец, если , то решением неравенства является любое действительное число.
Решение неравенства рассмотрим более коротко.
Очевидно, что если , то решением неравенства является любое действительное число.
Если , то решением неравенства является любое действительное число, а решением неравенства является любое действительное число, за исключением чисел вида .
Если , то решением неравенства являются числа вида , а неравенство решений не имеет. То же самое можно сказать о решении неравенств и в случае .
Случай рассмотрим более подробно (рис. 5).
Рисунок 5 – Решение неравенства
Решение неравенства для :
(для строгого неравенства) — множество интервалов;
(для нестрогого неравенства) — множество отрезков.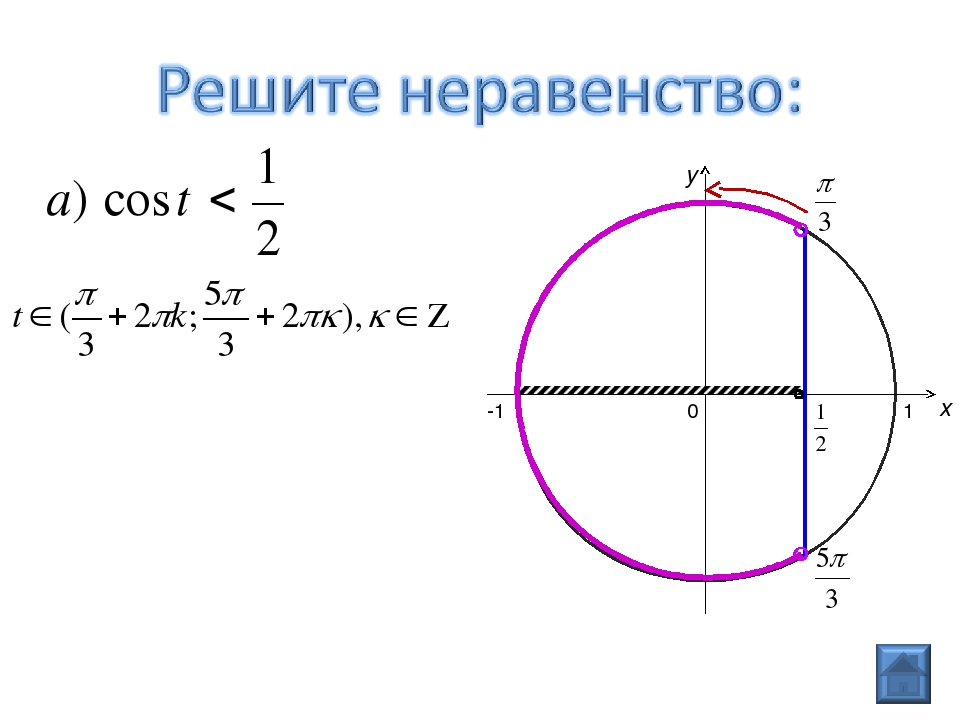
2. Теперь рассмотрим решение неравенств и .
Рассуждая по аналогии с неравенствами относительно синуса, можем сделать вывод, что для неравенство решений не имеет, а решением неравенства является любое действительное число.
Для неравенство решений не имеет, а решением неравенства является любое действительное число.
Рассмотрим случай более подробно.
Рассмотрим решение неравенства (рис. 6).
Рисунок 6 – Решение неравенства
Множество решений этого неравенства:
.
Теперь рассмотрим неравенство (рис. 7).
Рисунок 7 – Решение неравенства
Множество решений этого неравенства:
.
3. Теперь рассмотрим решение простейших неравенств и .
Сначала рассмотрим неравенство (рис. 8).
Рисунок 8 – Решение неравенства
Множество решений этого неравенства:
.
Соответственно, множество решений неравенства :
.
Примеры и разбор решения заданий тренировочного модуля
Пример 1.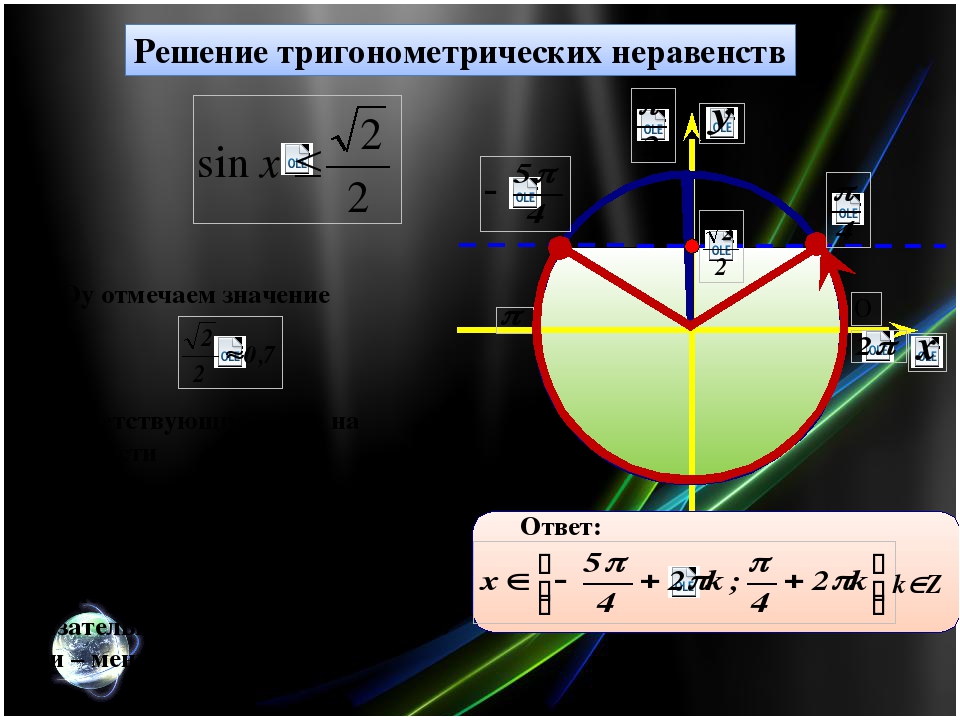
Решите неравенство. Заполните пропуски
Решение:
Ведем новую переменную: .
Вспомогательное неравенство имеет вид:
, .
Вернемся к исходной переменной: .
Второе неравенство решений не имеет. Решением первого неравенства является:
.
Ответ: .
Пример 2.
Решите неравенство. Найдите коэффициенты
Решение:
Выразим
Рисунок 9 – решение неравенства
Ответ:
Основные тригонометрические неравенства
Неизвестная переменная (угол): \ (x \)
Набор целых чисел: \ (\ mathbb {Z} \)
Целое число: \ (n \)
Набор действительных чисел: \ (\ mathbb {R} \)
Действительное число номер: \ (a \)
Тригонометрические функции: \ (\ sin x, \) \ (\ cos x, \) \ (\ tan x, \) \ (\ cot x \)
Обратные тригонометрические функции: \ (\ arcsin a, \) \ (\ arccos a, \) \ (\ arctan a, \) \ (\ text {arccot} a \)
- Неравенство, включающее тригонометрические функции от неизвестного угла, называется тригонометрическим неравенством.

- Следующие \ (16 \) неравенства относятся к основным тригонометрическим неравенствам:
\ (\ sin x \ gt a \), \ (\ sin x \ ge a \), \ (\ sin x \ lt a \), \ (\ sin x \ le a \),
\ (\ cos x \ gt a \), \ (\ cos x \ ge a \), \ (\ cos x \ lt a \), \ (\ cos x \ ле а \),
\ (\ тан х \ gt а \), \ (\ тан х \ ге а \), \ (\ тан х \ lt а \), \ (\ тан х \ ле а \),
\ (\ cot x \ gt a \), \ (\ cot x \ ge a \), \ (\ cot x \ lt a \), \ (\ cot x \ le a \).
Здесь \ (x \) — неизвестная переменная, \ (a \) может быть любым действительным числом. - Если \ (\ left | a \ right | \ ge 1 \), неравенство \ (\ sin x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ lt -1 \), решением неравенства \ (\ sin x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ sin x \ gt a \) выражается в виде
\ (\ arcsin a + 2 \ pi n \ lt x \ ) \ (\ lt \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (1 \)).
- Если \ (a \ gt 1 \), неравенство \ (\ sin x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ le -1 \), решением неравенства \ (\ sin x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Случай \ (a = 1 \)
\ (x = \ pi / 2 +2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ ge a \) включает граничные углы и имеет вид
\ (\ arcsin a + 2 \ pi n \ le x \) \ (\ le \ pi — \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (1 \)). - Если \ (a \ gt 1 \), решением неравенства \ (\ sin x \ lt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a \ le -1 \), неравенство \ (\ sin x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
- Для \ (- 1 \ lt a \ le 1 \) решение неравенства \ (\ sin x \ lt a \) лежит в интервале
\ (- \ pi — \ arcsin a + 2 \ pi n \ lt x \) \ (\ lt \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)).
- Если \ (a \ ge 1 \), решением неравенства \ (\ sin x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a <-1 \), неравенство \ (\ sin x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
- Случай \ (a = -1 \)
\ (x = — \ pi / 2 + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ sin x \ le a \) находится в интервале
\ (- \ pi — \ arcsin a + 2 \ pi n \ le x \) \ (\ le \ arcsin a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (2 \)). - Если \ (a \ ge 1 \), неравенство \ (\ cos x \ gt a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ lt -1 \), решением неравенства \ (\ cos x \ gt a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Для \ (- 1 \ le a \ lt 1 \) решение неравенства \ (\ cos x \ gt a \) имеет вид
\ (- \ arccos a + 2 \ pi n \ lt x \) \ (\ lt \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)).
- Если \ (a \ gt 1 \), неравенство \ (\ cos x \ ge a \) не имеет решений: \ (x \ in \ emptyset \)
- Если \ (a \ le -1 \), решением неравенства \ (\ cos x \ ge a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Случай \ (a = 1 \)
\ (x = 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ ge a \) выражается формулой
\ (- \ arccos a + 2 \ pi n \ le x \) \ (\ le \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (3 \)). - Если \ (a \ gt 1 \), неравенство \ (\ cos x \ lt a \) верно для любого действительного значения \ (x \): \ (x \ in \ mathbb {R} \)
- Если \ (a \ le -1 \), неравенство \ (\ cos x \ lt a \) не имеет решений: \ (x \ in \ emptyset \)
- Для \ (- 1
- Если \ (a \ ge 1 \), решением неравенства \ (\ cos x \ le a \) является любое действительное число: \ (x \ in \ mathbb {R} \)
- Если \ (a \ lt -1 \), неравенство \ (\ cos x \ le a \) не имеет решений: \ (x \ in \ emptyset \)
- Случай \ (a = -1 \)
\ (x = \ pi + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) - Для \ (- 1 \ lt a \ lt 1 \) решение нестрогого неравенства \ (\ cos x \ le a \) записывается как
\ (\ arccos a + 2 \ pi n \ le x \) \ (\ le 2 \ pi — \ arccos a + 2 \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (4 \)). - Для любого действительного значения \ (a \) решение строгого неравенства \ (\ tan x \ gt a \) имеет вид
\ (\ arctan a + \ pi n \ lt x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)).
- Для любого действительного значения \ (a \) решение неравенства \ (\ tan x \ ge a \) выражается в форме
\ (\ arctan a + \ pi n \ le x \) \ (\ lt \ pi / 2 + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (5 \)). - Для любого значения \ (a \) решение неравенства \ (\ tan x \ lt a \) записывается в виде
\ (- \ pi / 2 + \ pi n \ lt x \) \ ( \ lt \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)). - Для любого значения \ (a \) неравенство \ (\ tan x \ le a \) имеет следующее решение:
\ (- \ pi / 2 + \ pi n \ lt x \) \ (\ le \ arctan a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (рисунок \ (6 \)). - Для любого значения \ (a \) решение неравенства \ (\ cot x \ gt a \) имеет вид
\ (\ pi n \ lt x \ lt \ text {arccot} a + \ pi n , \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)).
- Нестрогое неравенство \ (\ cot x \ ge a \) имеет аналогичное решение:
\ (\ pi n \ lt x \ le \ text {arccot} a + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (7 \)). - Для любого значения \ (a \) решение неравенства \ (\ cot x \ lt a \) лежит на открытом интервале
\ (\ text {arccot} a + \ pi n \ lt x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)). - Для любого значения \ (a \) решение нестрогого неравенства \ (\ cot x \ le a \) находится в полуоткрытом интервале
\ (\ text {arccot} a + \ pi n \ le x \) \ (\ lt \ pi + \ pi n, \) \ (n \ in \ mathbb {Z} \) (Рисунок \ (8 \)).
Неравенства вида \ (\ sin x \ gt a, \) \ (\ sin x \ ge a, \) \ (\ sin x \ lt a, \) \ (\ sin x \ le a \)
Фигура 1.
Фигура 2.
Неравенство \ (\ sin x \ gt a \)
Неравенство \ (\ sin x \ ge a \)
Неравенство \ (\ sin x \ lt a \)
Неравенство \ (\ sin x \ le a \)
Неравенства вида \ (\ cos x \ gt a, \) \ (\ cos x \ ge a, \) \ (\ cos x \ lt a, \) \ (\ cos x \ le a \)
Рисунок 3.
Рисунок 4.
Неравенство \ (\ cos x \ gt a \)
Неравенство \ (\ cos x \ ge a \)
Неравенство \ (\ cos x \ lt a \)
Неравенство \ (\ cos x \ le a \)
Неравенства вида \ (\ tan x \ gt a, \) \ (\ tan x \ ge a, \) \ (\ tan x \ lt a, \) \ (\ tan x \ le a \)
Рисунок 5.
Рисунок 6.
Неравенство \ (\ tan x \ gt a \)
Неравенство \ (\ tan x \ ge a \)
Неравенство \ (\ tan x \ lt a \)
Неравенство \ (\ tan x \ le a \)
Неравенства вида \ (\ cot x \ gt a, \) \ (\ cot x \ ge a, \) \ (\ cot x \ lt a, \) \ (\ cot x \ le a \)
Рисунок 7.
Рисунок 8.
Неравенство \ (\ cot x \ gt a \)
Неравенство \ (\ cot x \ ge a \)
Неравенство \ (\ cot x \ lt a \)
Неравенство \ (\ cot x \ le a \)
10.7: Тригонометрические уравнения и неравенства
В разделах \ ref {TheUnitCircle}, \ ref {CircularFunctions} и совсем недавно \ ref {ArcTrig} мы решили несколько основных уравнений, включающих тригонометрические функции. Ниже мы резюмируем методы, которые мы использовали до сих пор. Обратите внимание, что мы используем нейтральную букву `$ u $ ‘в качестве аргумента \ footnote {См. Комментарии в начале раздела \ ref {TrigGraphs} для обзора этой концепции.} Каждой круговой функции для общности.
Ниже мы резюмируем методы, которые мы использовали до сих пор. Обратите внимание, что мы используем нейтральную букву `$ u $ ‘в качестве аргумента \ footnote {См. Комментарии в начале раздела \ ref {TrigGraphs} для обзора этой концепции.} Каждой круговой функции для общности.
Стратегии решения основных уравнений с тригонометрическими функциями
- Чтобы решить \ (\ cos (u) = c \) или \ (\ sin (u) = c \) для \ (- 1 \ leq c \ leq 1 \), сначала решите для \ (u \) в интервал \ ([0,2 \ pi) \) и складываем целые числа, кратные периоду \ (2 \ pi \).Если \ (c <-1 \) или \ (c> 1 \), реальных решений нет.
- Чтобы решить \ (\ sec (u) = c \) или \ (\ csc (u) = c \) для \ (c \ leq -1 \) или \ (c \ geq 1 \), преобразовать в косинус или sine, соответственно, и решите, как указано выше. Если \ (- 1
- Чтобы решить \ (\ tan (u) = c \) для любого действительного числа \ (c \), сначала решите для \ (u \) в интервале \ (\ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right) \) и складываем целые числа, кратные периоду \ (\ pi \).

- Чтобы решить \ (\ cot (u) = c \) для \ (c \ neq 0 \), преобразовать в касательную и решить, как указано выше.Если \ (c = 0 \), решением \ (\ cot (u) = 0 \) будет \ (u = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \) .
- Чтобы решить \ (\ tan (u) = c \) для любого действительного числа \ (c \), сначала решите для \ (u \) в интервале \ (\ left (- \ frac {\ pi} {2} , \ frac {\ pi} {2} \ right) \) и складываем целые числа, кратные периоду \ (\ pi \).
Используя приведенные выше рекомендации, мы можем легко решить \ (\ sin (x) = \ frac {1} {2} \) и найти решение \ (x = \ frac {\ pi} {6} + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Как мы решаем что-то вроде \ (\ sin (3x) = \ frac {1} {2} \)? Поскольку это уравнение имеет вид \ (\ sin (u) = \ frac {1} {2} \), мы знаем, что решения принимают вид \ (u = \ frac {\ pi} {6} + 2 \ pi k \) или \ (u = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \).Поскольку аргумент синуса здесь \ (3x \), мы имеем \ (3x = \ frac {\ pi} {6} + 2 \ pi k \) или \ (3x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Чтобы решить для \ (x \), мы разделим обе части \ footnote {Не забудьте также разделить \ (2 \ pi k \) на \ (3 \)!} Этих уравнений на \ (3 \) и получаем \ (x = \ frac {\ pi} {18} + \ frac {2 \ pi} {3} k \) или \ (x = \ frac {5 \ pi} {18} + \ frac {2 \ pi} {3} k \) для целых чисел \ (k \). Это метод, использованный в примере ниже.
Это метод, использованный в примере ниже.
Пример \ (\ PageIndex {1} \):
Решите следующие уравнения и проверьте свои ответы аналитически.{2} (х) = 4 \)
Решение
- Решение \ (\ cos (u) = — \ frac {\ sqrt {3}} {2} \): \ (u = \ frac {5 \ pi} {6} + 2 \ pi k \) или \ (u = \ frac {7 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Поскольку аргумент косинуса здесь \ (2x \), это означает \ (2x = \ frac {5 \ pi} {6} + 2 \ pi k \) или \ (2x = \ frac {7 \ pi} {6 } + 2 \ pi k \) для целых чисел \ (k \). Решение для \ (x \) дает \ (x = \ frac {5 \ pi} {12} + \ pi k \) или \ (x = \ frac {7 \ pi} {12} + \ pi k \) для целые числа \ (k \).Чтобы проверить эти ответы аналитически, мы подставляем их в исходное уравнение. Для любого целого числа \ (k \) имеем
\ [\ begin {array} {rclr}
\ cos \ left (2 \ left [\ frac {5 \ pi} {12} + \ pi k \ right] \ right) & = & \ cos \ left (\ frac {5 \ pi} {6} + 2 \ pi k \ right) & \\ [3pt]
& = & \ cos \ left (\ frac {5 \ pi} {6} \ right) & \ text {(период косинуса равен \ (2 \ pi $)} \\ [3pt]
& = & — \ frac {\ sqrt {3}} {2} & \\
\ end {array} \]
Аналогичным образом находим \ (\ cos \ left (2 \ left [\ frac {7 \ pi} {12} + \ pi k \ right] \ right) = \ cos \ left (\ frac {7 \ pi} { 6} + 2 \ pi k \ right) = \ cos \ left (\ frac {7 \ pi} {6} \ right) = — \ frac {\ sqrt {3}} {2} \). Чтобы определить, какое из наших решений лежит в \ ([0,2 \ pi) \), мы подставляем целые числа в \ (k \). Сохраняемые нами решения основаны на значениях \ (k = 0 \) и \ (k = 1 \) и равны \ (x = \ frac {5 \ pi} {12} \), \ (\ frac {7 \ pi} {12} \), \ (\ frac {17 \ pi} {12} \) и \ (\ frac {19 \ pi} {12} \). Используя калькулятор, построим графики \ (y = \ cos (2x) \) и \ (y = — \ frac {\ sqrt {3}} {2} \) над \ ([0,2 \ pi) \) и исследуйте, где пересекаются эти два графика. Мы видим, что \ (x \) — координаты точек пересечения соответствуют десятичным представлениям наших точных ответов.
Чтобы определить, какое из наших решений лежит в \ ([0,2 \ pi) \), мы подставляем целые числа в \ (k \). Сохраняемые нами решения основаны на значениях \ (k = 0 \) и \ (k = 1 \) и равны \ (x = \ frac {5 \ pi} {12} \), \ (\ frac {7 \ pi} {12} \), \ (\ frac {17 \ pi} {12} \) и \ (\ frac {19 \ pi} {12} \). Используя калькулятор, построим графики \ (y = \ cos (2x) \) и \ (y = — \ frac {\ sqrt {3}} {2} \) над \ ([0,2 \ pi) \) и исследуйте, где пересекаются эти два графика. Мы видим, что \ (x \) — координаты точек пересечения соответствуют десятичным представлениям наших точных ответов.
- \ item Поскольку это уравнение имеет вид \ (\ csc (u) = \ sqrt {2} \), мы перепишем его как \ (\ sin (u) = \ frac {\ sqrt {2}} {2} \) и найдите \ (u = \ frac {\ pi} {4} + 2 \ pi k \) или \ (u = \ frac {3 \ pi} {4} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку здесь аргумент косеканса равен \ (\ left (\ frac {1} {3} x- \ pi \ right) \),
\ [\ frac {1} {3} x- \ pi = \ frac {\ pi} {4} + 2 \ pi k \ quad \ text {или} \ quad \ frac {1} {3} x- \ pi = \ frac {3 \ pi} {4} + 2 \ pi k \]
Чтобы решить \ (\ frac {1} {3} x- \ pi = \ frac {\ pi} {4} + 2 \ pi k \), мы сначала добавляем \ (\ pi \) к обеим сторонам
\ [\ frac {1} {3} x = \ frac {\ pi} {4} + 2 \ pi k + \ pi \]
Распространенная ошибка — рассматривать термины `$ 2 \ pi k $ ‘и` $ \ pi $’ как « похожие » термины и пытаться объединить их, когда это не так.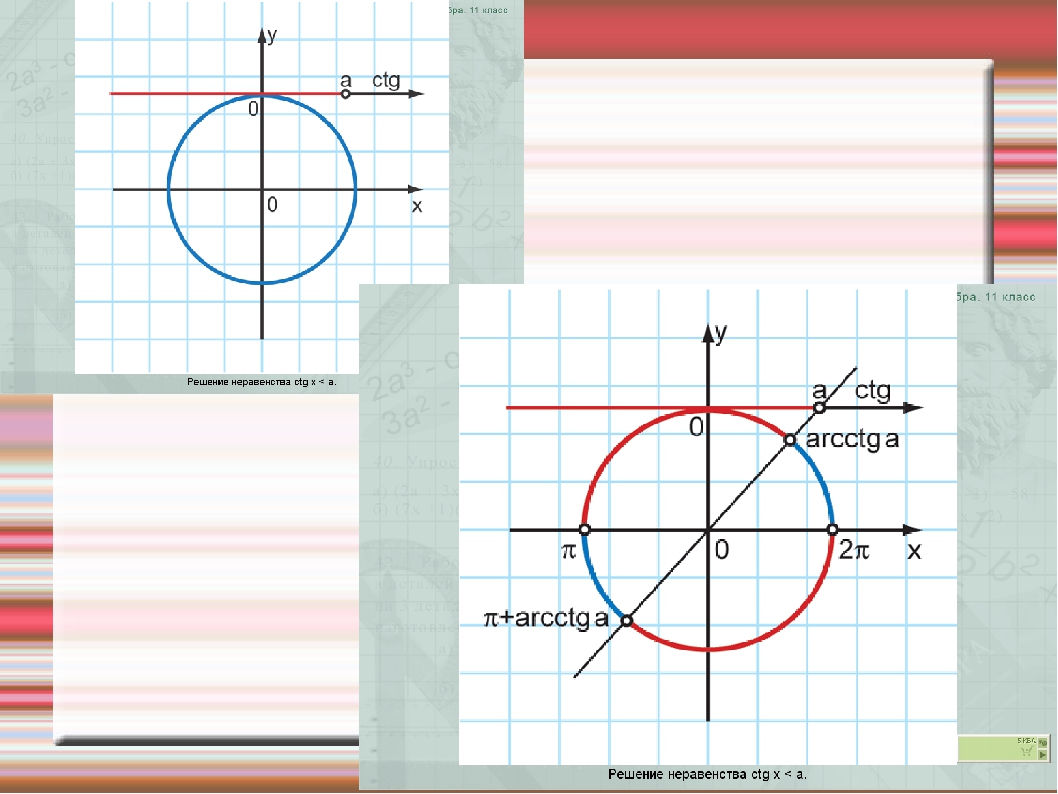 \ footnote {Вы понимаете, почему?} Однако мы можем объединить члены `$ \ pi $ ‘и` $ \ frac {\ pi} {4} $’, чтобы получить
\ footnote {Вы понимаете, почему?} Однако мы можем объединить члены `$ \ pi $ ‘и` $ \ frac {\ pi} {4} $’, чтобы получить
\ [\ frac {1} {3} x = \ frac {5 \ pi} {4} + 2 \ pi k \]
Теперь мы закончим, умножив обе части на \ (3 \), чтобы получить
.\ [x = 3 \ left (\ frac {5 \ pi} {4} + 2 \ pi k \ right) = \ frac {15 \ pi} {4} + 6 \ pi k \]
Решение другого уравнения \ (\ frac {1} {3} x- \ pi = \ frac {3 \ pi} {4} + 2 \ pi k \) дает \ (x = \ frac {21 \ pi} {4} + 6 \ pi k \) для целых чисел \ (k \). Чтобы проверить первую группу ответов, мы заменяем, объединяем строковые термины и упрощаем.
\ [\ begin {array} {rclr}
\ csc \ left (\ frac {1} {3} \ left [\ frac {15 \ pi} {4} + 6 \ pi k \ right] — \ pi \ right) & = & \ csc \ left (\ гидроразрыв {5 \ pi} {4} + 2 \ pi k — \ pi \ right) & \\ [3pt]
& = & \ csc \ left (\ frac {\ pi} {4} + 2 \ pi k \ right) & \\ [3pt]
& = & \ csc \ left (\ frac {\ pi} {4} \ right) & \ text {(период косеканса равен \ (2 \ pi $)} \\
& = & \ sqrt {2} & \\
\ end {array} \]
Семейство \ (x = \ frac {21 \ pi} {4} + 6 \ pi k \) проверяет аналогично. Несмотря на бесконечное множество решений, мы обнаруживаем, что \ textit {none} из них лежат в \ ([0,2 \ pi) \). Чтобы проверить это графически, мы используем взаимное тождество, чтобы переписать косеканс как синус, и находим, что \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right )} \) и \ (y = \ sqrt {2} \) вообще не пересекаются на интервале \ ([0,2 \ pi) \).
Несмотря на бесконечное множество решений, мы обнаруживаем, что \ textit {none} из них лежат в \ ([0,2 \ pi) \). Чтобы проверить это графически, мы используем взаимное тождество, чтобы переписать косеканс как синус, и находим, что \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right )} \) и \ (y = \ sqrt {2} \) вообще не пересекаются на интервале \ ([0,2 \ pi) \).
\ begin {center}
\ begin {tabular} {cc}
\ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq01.jpg} &
\ hspace {0.75 дюймов} \ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq02.jpg} \\
$ y = \ cos (2x) \) и \ boldmath \ (y = — \ frac {\ sqrt {3}} {2} \) &
\ hspace {0,75 дюйма} \ (y = \ frac {1} {\ sin \ left (\ frac {1} {3} x- \ pi \ right)} \) и \ boldmath \ (y = \ sqrt { 2} \) \\
\ end {tabular}
\ end {center}
\ item Поскольку \ (\ cot (3x) = 0 \) имеет форму \ (\ cot (u) = 0 \), мы знаем \ (u = \ frac {\ pi} {2} + \ pi k \ ), поэтому в этом случае \ (3x = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \). Решение относительно \ (x \) дает \ (x = \ frac {\ pi} {6} + \ frac {\ pi} {3} k \). Проверяя наши ответы, получаем
Решение относительно \ (x \) дает \ (x = \ frac {\ pi} {6} + \ frac {\ pi} {3} k \). Проверяя наши ответы, получаем
\ [\ begin {array} {rclr}
\ cot \ left (3 \ left [\ frac {\ pi} {6} + \ frac {\ pi} {3} k \ right] \ right) & = & \ cot \ left (\ frac {\ pi} {2} + \ pi k \ right) & \\ [3pt]
& = & \ cot \ left (\ frac {\ pi} {2} \ right) & \ text {(период котангенса равен \ (\ pi $)} \\ [3pt]
& = & 0 & \\
\ end {array} \]
Когда \ (k \) пробегает целые числа, мы получаем шесть ответов, соответствующих от \ (k = 0 \) до \ (k = 5 \), которые лежат в \ ([0, 2 \ pi) \): \ (x = \ frac {\ pi} {6} \), \ (\ frac {\ pi} {2} \), \ (\ frac {5 \ pi} {6} \), \ (\ frac { 7 \ pi} {6} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {11 \ pi} {6} \).Чтобы подтвердить это графически, мы должны быть осторожны. На многих калькуляторах нет функциональной кнопки для котангенса. Мы выбираем \ footnote {Читателю предлагается увидеть, что произойдет, если вместо этого мы выбрали взаимную идентичность \ (\ cot (3x) = \ frac {1} {\ tan (3x)} \). График на калькуляторе \ textit {выглядит} идентичным, но что происходит, когда вы пытаетесь найти точки пересечения?}, Чтобы использовать тождество частного \ (\ cot (3x) = \ frac {\ cos (3x)} {\ sin (3x)} \). Изобразив \ (y = \ frac {\ cos (3x)} {\ sin (3x)} \) и \ (y = 0 \) (ось \ (x \)), мы видим, что \ (x \ ) -координаты точек пересечения примерно совпадают с нашими решениями.{2} (x) = 4 \) происходит не из аргумента секанса, который есть просто \ (x \), а скорее из того факта, что секанс возводится в квадрат. Чтобы это уравнение выглядело как одна из форм, перечисленных на странице \ pageref {trigeqnstrategy1}, мы извлекаем квадратные корни, чтобы получить \ (\ sec (x) = \ pm 2 \). Преобразуя в косинусы, мы получаем \ (\ cos (x) = \ pm \ frac {1} {2} \). Для \ (\ cos (x) = \ frac {1} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Для \ (\ cos (x) = — \ frac {1} {2} \) мы получаем \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) или \ (x = \ frac {4 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).
График на калькуляторе \ textit {выглядит} идентичным, но что происходит, когда вы пытаетесь найти точки пересечения?}, Чтобы использовать тождество частного \ (\ cot (3x) = \ frac {\ cos (3x)} {\ sin (3x)} \). Изобразив \ (y = \ frac {\ cos (3x)} {\ sin (3x)} \) и \ (y = 0 \) (ось \ (x \)), мы видим, что \ (x \ ) -координаты точек пересечения примерно совпадают с нашими решениями.{2} (x) = 4 \) происходит не из аргумента секанса, который есть просто \ (x \), а скорее из того факта, что секанс возводится в квадрат. Чтобы это уравнение выглядело как одна из форм, перечисленных на странице \ pageref {trigeqnstrategy1}, мы извлекаем квадратные корни, чтобы получить \ (\ sec (x) = \ pm 2 \). Преобразуя в косинусы, мы получаем \ (\ cos (x) = \ pm \ frac {1} {2} \). Для \ (\ cos (x) = \ frac {1} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Для \ (\ cos (x) = — \ frac {1} {2} \) мы получаем \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) или \ (x = \ frac {4 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).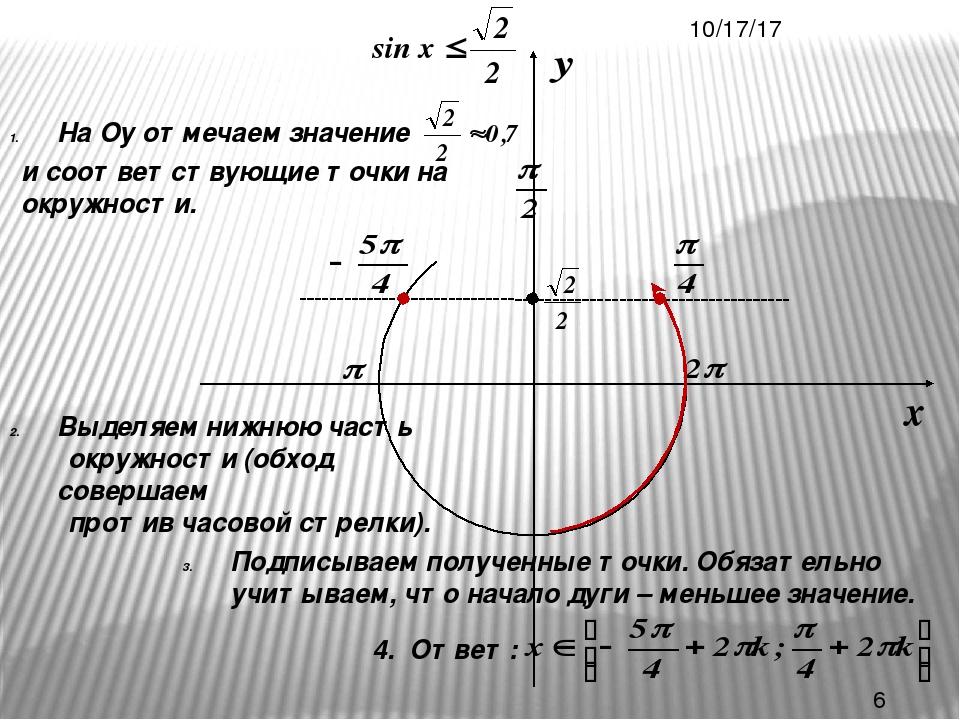 Если мы сделаем шаг назад и подумаем об этих семействах решений геометрически, то увидим, что находим меры всех углов с опорным углом \ (\ frac {\ pi} {3} \). В результате эти решения могут быть объединены, и мы можем записать наши решения как \ (x = \ frac {\ pi} {3} + \ pi k \) и \ (x = \ frac {2 \ pi} {3} + \ pi k \) для целых чисел \ (k \). Чтобы проверить первое семейство решений, отметим, что, в зависимости от целого числа \ (k \), \ (\ sec \ left (\ frac {\ pi} {3} + \ pi k \ right) \) не всегда равно \ (\ sec \ left (\ frac {\ pi} {3} \ right) \).2 & \\ [3pt]
Если мы сделаем шаг назад и подумаем об этих семействах решений геометрически, то увидим, что находим меры всех углов с опорным углом \ (\ frac {\ pi} {3} \). В результате эти решения могут быть объединены, и мы можем записать наши решения как \ (x = \ frac {\ pi} {3} + \ pi k \) и \ (x = \ frac {2 \ pi} {3} + \ pi k \) для целых чисел \ (k \). Чтобы проверить первое семейство решений, отметим, что, в зависимости от целого числа \ (k \), \ (\ sec \ left (\ frac {\ pi} {3} + \ pi k \ right) \) не всегда равно \ (\ sec \ left (\ frac {\ pi} {3} \ right) \).2 & \\ [3pt]
& = & 4 & \\
\ end {array} \]
То же самое верно и для семейства \ (x = \ frac {2 \ pi} {3} + \ pi k \). Решения, лежащие в \ ([0,2 \ pi) \), берутся из значений \ (k = 0 \) и \ (k = 1 \), а именно \ (x = \ frac {\ pi} {3} \), \ (\ frac {2 \ pi} {3} \), \ (\ frac {4 \ pi} {3} \) и \ (\ frac {5 \ pi} {3} \). Чтобы подтвердить графически, мы используем обратную идентичность, чтобы переписать секанс как косинус.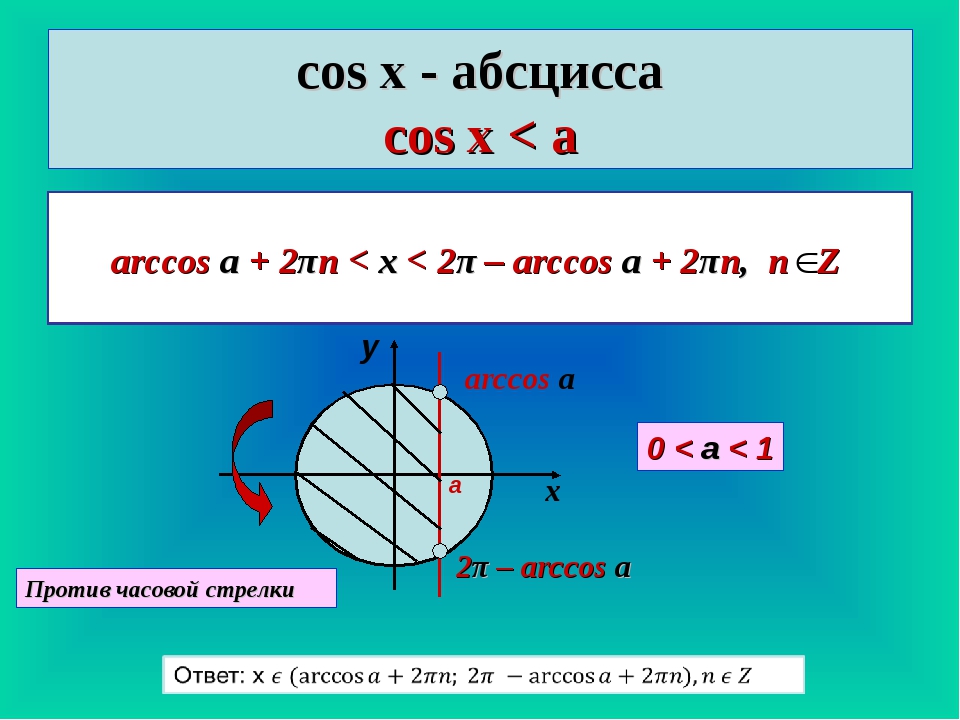 2} \) и \ (y = 4 \) подтверждают наши ответы.{2} (x)} \) и \ boldmath \ (y = 4 \) \\
2} \) и \ (y = 4 \) подтверждают наши ответы.{2} (x)} \) и \ boldmath \ (y = 4 \) \\
\ end {tabular}
\ end {center}
\ item Уравнение \ (\ tan \ left (\ frac {x} {2} \ right) = -3 \) имеет вид \ (\ tan (u) = -3 \), решением которого является \ (u = \ arctan (-3) + \ пи к \). Следовательно, \ (\ frac {x} {2} = \ arctan (-3) + \ pi k \), поэтому \ (x = 2 \ arctan (-3) + 2 \ pi k \) для целых чисел \ (k \). Для проверки отметим
\ [\ begin {array} {rclr}
\ tan \ left (\ frac {2 \ arctan (-3) + 2 \ pi k} {2} \ right) & = & \ tan \ left (\ arctan (-3) + \ pi k \ right) & \\ [3pt]
& = & \ tan \ left (\ arctan (-3) \ right) & \ text {(период касательной равен \ (\ pi $)} \\ [3pt]
& = & -3 & (\ text {См. Теорему} \ ref {arctangentcotangentfunctionprops}) \\
\ end {array} \]
Чтобы определить, какой из наших ответов лежит в интервале \ ([0,2 \ pi) \), нам сначала нужно получить представление о значении \ (2 \ arctan (-3) \). Хотя мы могли бы легко найти приближение с помощью калькулятора, \ footnote {Ваш инструктор сообщит вам, если вы должны отказаться от аналитического маршрута на этом этапе и использовать ваш калькулятор. А если серьезно, что это было бы забавно?} Мы продолжаем аналитически. Поскольку \ (- 3 <0 \), отсюда следует, что \ (- \ frac {\ pi} {2} <\ arctan (-3) <0 \). Умножение на \ (2 \) дает \ (- \ pi <2 \ arctan (-3) <0 \). Теперь мы можем спорить, какое из решений \ (x = 2 \ arctan (-3) + 2 \ pi k \) лежит в \ ([0,2 \ pi) \).Для \ (k = 0 \) мы получаем \ (x = 2 \ arctan (-3) <0 \), поэтому мы отбрасываем этот ответ и все ответы \ (x = 2 \ arctan (-3) + 2 \ pi k \) где \ (k <0 \). Затем обратим внимание на \ (k = 1 \) и получим \ (x = 2 \ arctan (-3) + 2 \ pi \). Начиная с неравенства \ (- \ pi <2 \ arctan (-3) <0 \), складываем \ (2 \ pi \) и получаем \ (\ pi <2 \ arctan (-3) +2 \ pi < 2 \ пи \). Это означает, что \ (x = 2 \ arctan (-3) + 2 \ pi \) лежит в \ ([0,2 \ pi) \). Продвижение \ (k \) к \ (2 \) дает \ (x = 2 \ arctan (-3) + 4 \ pi \).
Хотя мы могли бы легко найти приближение с помощью калькулятора, \ footnote {Ваш инструктор сообщит вам, если вы должны отказаться от аналитического маршрута на этом этапе и использовать ваш калькулятор. А если серьезно, что это было бы забавно?} Мы продолжаем аналитически. Поскольку \ (- 3 <0 \), отсюда следует, что \ (- \ frac {\ pi} {2} <\ arctan (-3) <0 \). Умножение на \ (2 \) дает \ (- \ pi <2 \ arctan (-3) <0 \). Теперь мы можем спорить, какое из решений \ (x = 2 \ arctan (-3) + 2 \ pi k \) лежит в \ ([0,2 \ pi) \).Для \ (k = 0 \) мы получаем \ (x = 2 \ arctan (-3) <0 \), поэтому мы отбрасываем этот ответ и все ответы \ (x = 2 \ arctan (-3) + 2 \ pi k \) где \ (k <0 \). Затем обратим внимание на \ (k = 1 \) и получим \ (x = 2 \ arctan (-3) + 2 \ pi \). Начиная с неравенства \ (- \ pi <2 \ arctan (-3) <0 \), складываем \ (2 \ pi \) и получаем \ (\ pi <2 \ arctan (-3) +2 \ pi < 2 \ пи \). Это означает, что \ (x = 2 \ arctan (-3) + 2 \ pi \) лежит в \ ([0,2 \ pi) \). Продвижение \ (k \) к \ (2 \) дает \ (x = 2 \ arctan (-3) + 4 \ pi \).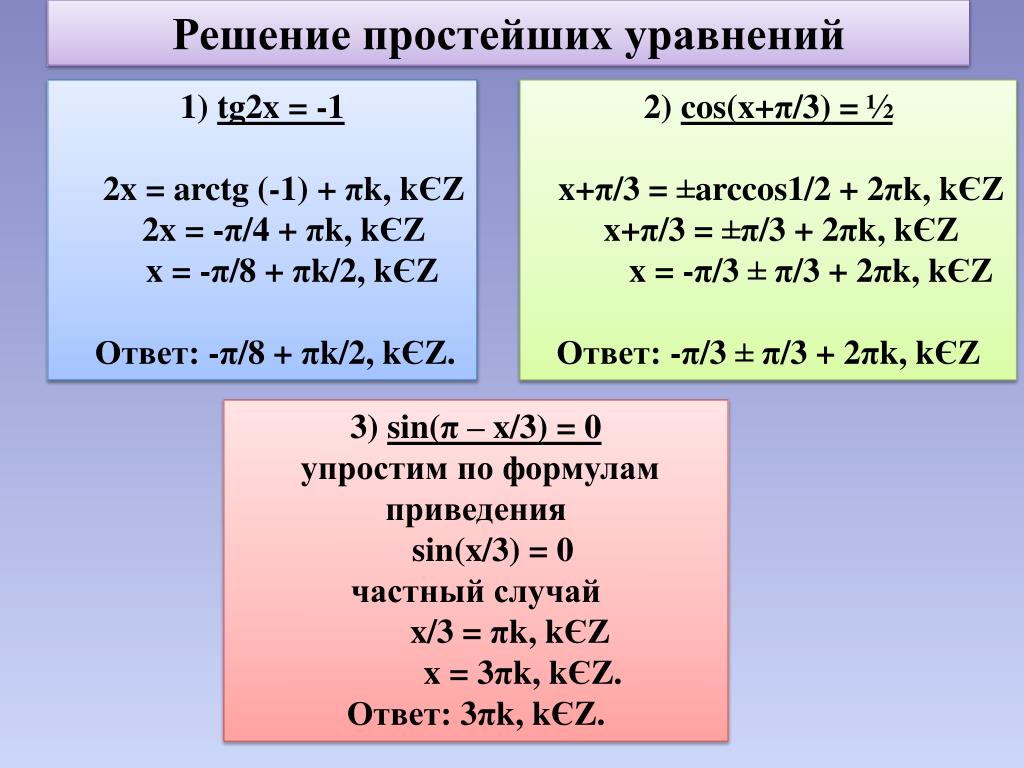 Еще раз, из \ (- \ pi <2 \ arctan (-3) <0 \) получаем \ (3 \ pi <2 \ arctan (-3) + 4 \ pi <4 \ pi \).Поскольку это находится вне интервала \ ([0,2 \ pi) \), мы отбрасываем \ (x = 2 \ arctan (-3) + 4 \ pi \) и все решения вида \ (x = 2 \ arctan (-3) + 2 \ pi k \) для \ (k> 2 \). Графически мы видим, что \ (y = \ tan \ left (\ frac {x} {2} \ right) \) и \ (y = -3 \) пересекаются только один раз на \ ([0,2 \ pi) \) при \ (x = 2 \ arctan (-3) + 2 \ pi \ приблизительно 3,7851 \).
Еще раз, из \ (- \ pi <2 \ arctan (-3) <0 \) получаем \ (3 \ pi <2 \ arctan (-3) + 4 \ pi <4 \ pi \).Поскольку это находится вне интервала \ ([0,2 \ pi) \), мы отбрасываем \ (x = 2 \ arctan (-3) + 4 \ pi \) и все решения вида \ (x = 2 \ arctan (-3) + 2 \ pi k \) для \ (k> 2 \). Графически мы видим, что \ (y = \ tan \ left (\ frac {x} {2} \ right) \) и \ (y = -3 \) пересекаются только один раз на \ ([0,2 \ pi) \) при \ (x = 2 \ arctan (-3) + 2 \ pi \ приблизительно 3,7851 \).
- \ item Чтобы решить \ (\ sin (2x) = 0.87 \), сначала отметим, что оно имеет форму \ (\ sin (u) = 0.87 \), которая имеет семейство решений \ (u = \ arcsin (0.87) + 2 \ pi k \) или \ (u = \ pi — \ arcsin (0.87) + 2 \ pi k \) для целых чисел \ (k \). Поскольку аргумент синуса здесь \ (2x \), мы получаем \ (2x = \ arcsin (0.87) + 2 \ pi k \) или \ (2x = \ pi — \ arcsin (0.87) + 2 \ pi k \ ), что дает \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi k \) или \ (x = \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.
 87) + \ pi k \) для целых чисел \ (k \). Проверить,
87) + \ pi k \) для целых чисел \ (k \). Проверить,
\ [\ begin {array} {rclr}
\ sin \ left (2 \ left [\ frac {1} {2} \ arcsin (0.87) + \ pi k \ right] \ right) & = & \ sin \ left (\ arcsin (0.87) + 2 \ pi k \ right) & \\ [3pt]
& = & \ sin \ left (\ arcsin (0.87) \ right) & \ text {(период синуса равен \ (2 \ pi $)} \\ [3pt]
& = & 0.87 & (\ text {См. Теорему} \ ref {arccosinesinefunctionprops}) \\
\ end {array} \]
Для семейства \ (x = \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) + \ pi k \) получаем
\ [\ begin {array} {rclr}
\ sin \ left (2 \ left [\ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) + \ pi k \ right] \ right) & = & \ sin \ left (\ pi — \ arcsin (0.87) + 2 \ pi k \ right) & \\ [3pt]
& = & \ sin \ left (\ pi — \ arcsin (0.87) \ right) & \ text {(период синуса равен \ (2 \ pi $)} \\ [3pt]
& = & \ sin \ left (\ arcsin (0.87) \ right) & \ text {($ \ sin (\ pi — t) = \ sin (t) $)} \\ [3pt]
& = & 0. 87 & (\ text {См. Теорему} \ ref {arccosinesinefunctionprops}) \\
87 & (\ text {См. Теорему} \ ref {arccosinesinefunctionprops}) \\
\ end {array} \]
Чтобы определить, какое из этих решений лежит в \ ([0,2 \ pi) \), нам сначала нужно получить представление о значении \ (x = \ frac {1} {2} \ arcsin (0.87) \ ). Еще раз, мы могли бы использовать калькулятор, но здесь мы применяем аналитический подход.По определению \ (0 <\ arcsin (0.87) <\ frac {\ pi} {2} \), так что умножение на \ (\ frac {1} {2} \) дает нам \ (0 <\ frac { 1} {2} \ arcsin (0.87) <\ frac {\ pi} {4} \). Начиная с семейства решений \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi k \), мы используем те же аргументы, что и в нашем решении для числа \ ref {arctanin02pi} выше, и найти только решения, соответствующие \ (k = 0 \) и \ (k = 1 \), лежащие в \ ([0,2 \ pi) \): \ (x = \ frac {1} {2} \ arcsin ( 0.87) \) и \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi \).Затем мы переходим к семейству \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) + \ pi k \) для целых чисел \ (k \). Здесь нам нужно получить лучшую оценку \ (\ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) \). Из неравенства \ (0 <\ frac {1} {2} \ arcsin (0.87) <\ frac {\ pi} {4} \) сначала умножаем на \ (- 1 \), а затем складываем \ (\ frac {\ pi} {2} \), чтобы получить \ (\ frac {\ pi} {2}> \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87)> \ frac {\ pi} {4} \) или \ (\ frac {\ pi} {4} <\ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) <\ frac { \ pi} {2} \).Продолжая обычные рассуждения, мы находим единственные решения, лежащие в \ ([0,2 \ pi) \), соответствующие \ (k = 0 \) и \ (k = 1 \), а именно \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \) и \ (x = \ frac {3 \ pi} {2} - \ frac {1} {2} \ arcsin ( 0,87) \). В общем, мы нашли четыре решения \ (\ sin (2x) = 0.87 \) в \ ([0,2 \ pi) \): \ (x = \ frac {1} {2} \ arcsin (0.87) \), \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi \), \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \) и \ (x = \ frac {3 \ pi} {2} - \ frac {1} {2} \ arcsin (0.
Здесь нам нужно получить лучшую оценку \ (\ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87) \). Из неравенства \ (0 <\ frac {1} {2} \ arcsin (0.87) <\ frac {\ pi} {4} \) сначала умножаем на \ (- 1 \), а затем складываем \ (\ frac {\ pi} {2} \), чтобы получить \ (\ frac {\ pi} {2}> \ frac {\ pi} {2} — \ frac {1} {2} \ arcsin (0.87)> \ frac {\ pi} {4} \) или \ (\ frac {\ pi} {4} <\ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) <\ frac { \ pi} {2} \).Продолжая обычные рассуждения, мы находим единственные решения, лежащие в \ ([0,2 \ pi) \), соответствующие \ (k = 0 \) и \ (k = 1 \), а именно \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \) и \ (x = \ frac {3 \ pi} {2} - \ frac {1} {2} \ arcsin ( 0,87) \). В общем, мы нашли четыре решения \ (\ sin (2x) = 0.87 \) в \ ([0,2 \ pi) \): \ (x = \ frac {1} {2} \ arcsin (0.87) \), \ (x = \ frac {1} {2} \ arcsin (0.87) + \ pi \), \ (x = \ frac {\ pi} {2} - \ frac {1} {2} \ arcsin (0.87) \) и \ (x = \ frac {3 \ pi} {2} - \ frac {1} {2} \ arcsin (0.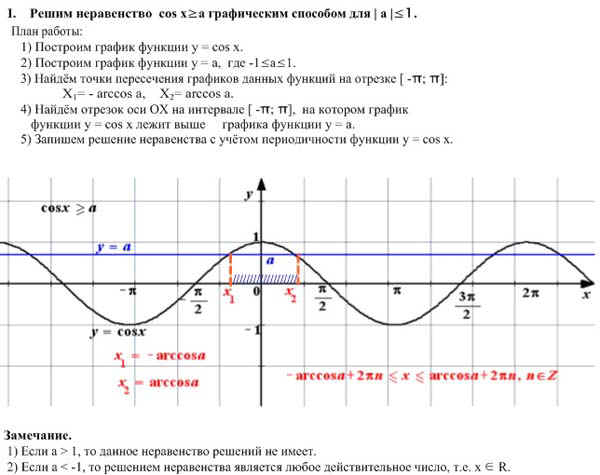 87) \). Построив графики \ (y = \ sin (2x) \) и \ (y = 0.87 \), подтверждаем наши результаты.
87) \). Построив графики \ (y = \ sin (2x) \) и \ (y = 0.87 \), подтверждаем наши результаты.
\ hspace {0,75 дюйма} \ includegraphics [width = 2in] {./ IntroTrigGraphics / TrigEquIneq06.jpg} \\
$ y = \ tan \ left (\ frac {x} {2} \ right) \) и \ boldmath \ (y = -3 \) &
Каждая из задач в примере \ ref {TrigEqnEx1} содержала одну тригонометрическую функцию. Если уравнение включает две разные тригонометрические функции или если уравнение содержит одну и ту же тригонометрическую функцию, но с разными аргументами, нам нужно будет использовать тождества и алгебру, чтобы привести уравнение к той же форме, что и приведенные на странице \ pageref {trigeqnstrategy1}.
Мы повторяем здесь совет, данный при решении систем нелинейных уравнений в разделе \ ref {NonLinear} — когда дело доходит до решения уравнений, включающих тригонометрические функции, полезно просто попробовать что-нибудь.
Далее мы сосредоточимся на решении неравенств, связанных с тригонометрическими функциями. Поскольку эти функции непрерывны в своих доменах, мы можем использовать технику знаковых диаграмм, которую мы использовали в прошлом, для решения неравенств. \ Footnote {См. Страницу \ pageref {firstsigndiagram}, Пример \ ref {polygraphex}, page \ pageref { rationalsigndiagram}, page \ pageref {algebraicsigndiagram}, Пример \ ref {expineq} и Пример \ ref {logineq} для обсуждения этого метода.}
Поскольку эти функции непрерывны в своих доменах, мы можем использовать технику знаковых диаграмм, которую мы использовали в прошлом, для решения неравенств. \ Footnote {См. Страницу \ pageref {firstsigndiagram}, Пример \ ref {polygraphex}, page \ pageref { rationalsigndiagram}, page \ pageref {algebraicsigndiagram}, Пример \ ref {expineq} и Пример \ ref {logineq} для обсуждения этого метода.}
Пример \ (\ PageIndex {2} \):
Решите следующие неравенства на \ ([0,2 \ pi) \). Выразите свои ответы, используя интервальную нотацию, и проверьте свои ответы графически.
- \ (2 \ sin (x) \ leq 1 \)
- \ (\ sin (2x)> \ cos (x) \)
- \ (\ тан (х) \ geq 3 \)
Решение
- Мы начинаем решение \ (2 \ sin (x) \ leq 1 \), собирая все члены с одной стороны уравнения и ноль с другой, чтобы получить \ (2 \ sin (x) — 1 \ leq 0 \).Затем мы положим \ (f (x) = 2 \ sin (x) — 1 \) и отметим, что наше исходное неравенство эквивалентно решению \ (f (x) \ leq 0 \).
 Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \).
Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \). Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \).
Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \). - Сначала перепишем \ (\ sin (2x)> \ cos (x) \) как \ (\ sin (2x) — \ cos (x)> 0 \) и пусть \ (f (x) = \ sin (2x ) — \ соз (х) \). Таким образом, наше исходное неравенство эквивалентно \ (f (x)> 0 \). Область определения \ (f \) — все действительные числа, поэтому мы можем перейти к поиску нулей \ (f \). Установка \ (f (x) = 0 \) дает \ (\ sin (2x) — \ cos (x) = 0 \), который, посредством тождества двойного угла для синуса, становится \ (2 \ sin (x ) \ cos (x) — \ cos (x) = 0 \) или \ (\ cos (x) (2 \ sin (x) — 1) = 0 \).Из \ (\ cos (x) = 0 \) мы получаем \ (x = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \), из которых только \ (x = \ frac {\ pi} {2} \) и \ (x = \ frac {3 \ pi} {2} \) лежат в \ ([0,2 \ pi) \). Для \ (2 \ sin (x) — 1 = 0 \) мы получаем \ (\ sin (x) = \ frac {1} {2} \), что дает \ (x = \ frac {\ pi} {6 } + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ (k \).
 Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах.
Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах.
- Действуя так же, как в последних двух задачах, перепишем \ (\ tan (x) \ geq 3 \) как \ (\ tan (x) — 3 \ geq 0 \) и пусть \ (f (x) = \ tan ( х) — 3 \). Отметим, что на \ ([0,2 \ pi) \), \ (f \) не определено в \ (x = \ frac {\ pi} {2} \) и \ (\ frac {3 \ pi} { 2} \), поэтому для этих значений потребуется обычный отказ от ответственности на диаграмме знаков.\ footnote {См. страницу \ pageref {rationalsigndiagram} для обсуждения нестандартного символа, известного как interrobang.} Переходя к нулям, решение \ (f (x) = \ tan (x) — 3 = 0 \) требует функция арктангенса. Мы находим \ (x = \ arctan (3) + \ pi k \) для целых чисел \ (k \), и из них только \ (x = \ arctan (3) \) и \ (x = \ arctan (3) + \ pi \) лежат в \ ([0,2 \ pi) \). Поскольку \ (3> 0 \), мы знаем \ (0 <\ arctan (3) <\ frac {\ pi} {2} \), который позволяет нам правильно расположить эти нули на диаграмме знаков. Чтобы выбрать тестовые значения, мы начинаем с \ (x = 0 \) и находим \ (f (0) = -3 \).Найти удобное тестовое значение в интервале \ (\ left (\ arctan (3), \ frac {\ pi} {2} \ right) \) немного сложнее.
 Имейте в виду, что функция арктангенса возрастает и ограничена сверху значением \ (\ frac {\ pi} {2} \). Это означает, что число \ (x = \ arctan (117) \) гарантировано \ footnote {Мы могли бы выбрать любое значение \ (\ arctan (t) \), где \ (t> 3 \).}, Чтобы оно находилось между \ (\ arctan (3) \) и \ (\ frac {\ pi} {2} \). Мы видим, что \ (f (\ arctan (117)) = \ tan (\ arctan (117)) — 3 = 114 \). В качестве следующего тестового значения мы берем \ (x = \ pi \) и находим \ (f (\ pi) = -3 \).Чтобы найти следующее тестовое значение, отметим, что, поскольку \ (\ arctan (3) <\ arctan (117) <\ frac {\ pi} {2} \), оно следует за \ footnote {\ ldots, добавляя \ (\ pi \) в силу неравенства \ ldots}, что \ (\ arctan (3) + \ pi <\ arctan (117) + \ pi <\ frac {3 \ pi} {2} \). Оценка \ (f \) в \ (x = \ arctan (117) + \ pi \) дает \ (f (\ arctan (117) + \ pi) = \ tan (\ arctan (117) + \ pi) -3 = \ загар (\ arctan (117)) - 3 = 114 \). Мы выбираем последнее тестовое значение \ (x = \ frac {7 \ pi} {4} \) и находим \ (f \ left (\ frac {7 \ pi} {4} \ right) = -4 \) .
Имейте в виду, что функция арктангенса возрастает и ограничена сверху значением \ (\ frac {\ pi} {2} \). Это означает, что число \ (x = \ arctan (117) \) гарантировано \ footnote {Мы могли бы выбрать любое значение \ (\ arctan (t) \), где \ (t> 3 \).}, Чтобы оно находилось между \ (\ arctan (3) \) и \ (\ frac {\ pi} {2} \). Мы видим, что \ (f (\ arctan (117)) = \ tan (\ arctan (117)) — 3 = 114 \). В качестве следующего тестового значения мы берем \ (x = \ pi \) и находим \ (f (\ pi) = -3 \).Чтобы найти следующее тестовое значение, отметим, что, поскольку \ (\ arctan (3) <\ arctan (117) <\ frac {\ pi} {2} \), оно следует за \ footnote {\ ldots, добавляя \ (\ pi \) в силу неравенства \ ldots}, что \ (\ arctan (3) + \ pi <\ arctan (117) + \ pi <\ frac {3 \ pi} {2} \). Оценка \ (f \) в \ (x = \ arctan (117) + \ pi \) дает \ (f (\ arctan (117) + \ pi) = \ tan (\ arctan (117) + \ pi) -3 = \ загар (\ arctan (117)) - 3 = 114 \). Мы выбираем последнее тестовое значение \ (x = \ frac {7 \ pi} {4} \) и находим \ (f \ left (\ frac {7 \ pi} {4} \ right) = -4 \) . {2} (x) = \ tan (x) + 3 \)
{2} (x) = \ tan (x) + 3 \) - \ (\ соз (2х) = 3 \ соз (х) — 2 \)
- \ (\ соз (3х) = 2- \ соз (х) \)
- \ (\ соз (3x) = \ соз (5x) \)
- \ (\ sin (2x) = \ sqrt {3} \ cos (x) \)
- \ (\ sin (x) \ cos \ left (\ frac {x} {2} \ right) + \ cos (x) \ sin \ left (\ frac {x} {2} \ right) = 1 \)
- \ (\ cos (x) — \ sqrt {3} \ sin (x) = 2 \)
Решение.{2} (x) = 0 \) или \ (3 \ sin (x) — 1 = 0 \). Решая для \ (\ sin (x) \), мы находим \ (\ sin (x) = 0 \) или \ (\ sin (x) = \ frac {1} {3} \). Решением первого уравнения является \ (x = \ pi k \), где \ (x = 0 \) и \ (x = \ pi \) — два решения, которые лежат в \ ([0,2 \ pi) \). Чтобы решить \ (\ sin (x) = \ frac {1} {3} \), мы используем функцию арксинуса, чтобы получить \ (x = \ arcsin \ left (\ frac {1} {3} \ right) + 2 \ pi k \) или \ (x = \ pi — \ arcsin \ left (\ frac {1} {3} \ right) + 2 \ pi k \) для целых чисел \ (k \). Мы находим здесь два решения, лежащих в \ ([0,2 \ pi) \), как \ (x = \ arcsin \ left (\ frac {1} {3} \ right) \) \ »и \ (x = \ пи — \ arcsin \ left (\ frac {1} {3} \ right) \).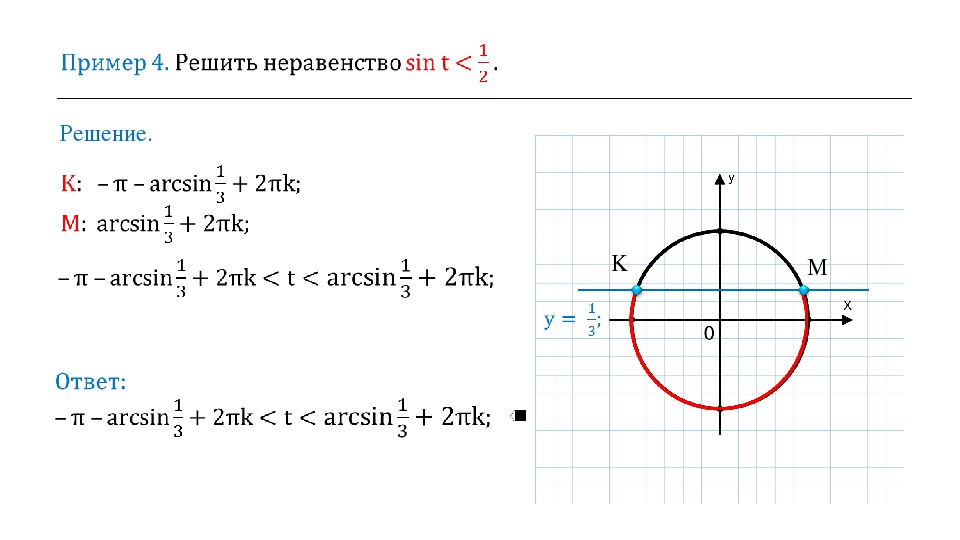 2 \) и найдите \ (x \) — координаты точек пересечения этих двух кривых. Некоторое дополнительное масштабирование требуется около \ (x = 0 \) и \ (x = \ pi \), чтобы убедиться, что эти две кривые действительно пересекаются четыре раза. \ Footnote {Обратите внимание, что мы \ textit {не} считаем точку \ ((2 \ pi, 0) \) в нашем наборе решений, поскольку \ (x = 2 \ pi \) не находится в интервале \ ([0,2 \ pi) \). В следующих решениях помните, что, хотя \ (x = 2 \ pi \) может быть решением уравнения, оно не учитывается среди решений в \ ([0,2 \ pi) \).2 — u — 2 & = & 0 & \ text {Пусть \ (u = \ tan (x) \).} \\
2 \) и найдите \ (x \) — координаты точек пересечения этих двух кривых. Некоторое дополнительное масштабирование требуется около \ (x = 0 \) и \ (x = \ pi \), чтобы убедиться, что эти две кривые действительно пересекаются четыре раза. \ Footnote {Обратите внимание, что мы \ textit {не} считаем точку \ ((2 \ pi, 0) \) в нашем наборе решений, поскольку \ (x = 2 \ pi \) не находится в интервале \ ([0,2 \ pi) \). В следующих решениях помните, что, хотя \ (x = 2 \ pi \) может быть решением уравнения, оно не учитывается среди решений в \ ([0,2 \ pi) \).2 — u — 2 & = & 0 & \ text {Пусть \ (u = \ tan (x) \).} \\
(u + 1) (u — 2) & = & 0 & \\ \ end {array} \]
Это дает \ (u = -1 \) или \ (u = 2 \). Поскольку \ (u = \ tan (x) \), мы имеем \ (\ tan (x) = -1 \) или \ (\ tan (x) = 2 \). Из \ (\ tan (x) = -1 \) мы получаем \ (x = — \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \). Чтобы решить \ (\ tan (x) = 2 \), мы используем функцию арктангенса и получаем \ (x = \ arctan (2) + \ pi k \) для целых чисел \ (k \). Из первого набора решений мы получаем \ (x = \ frac {3 \ pi} {4} \) и \ (x = \ frac {5 \ pi} {4} \) как наши ответы, которые лежат в \ ( [0,2 \ пи) \).2–3 u + 1 & = & 0 & \ text {Пусть \ (u = \ cos (x) \).} \\
Из первого набора решений мы получаем \ (x = \ frac {3 \ pi} {4} \) и \ (x = \ frac {5 \ pi} {4} \) как наши ответы, которые лежат в \ ( [0,2 \ пи) \).2–3 u + 1 & = & 0 & \ text {Пусть \ (u = \ cos (x) \).} \\
(2u — 1) (u — 1) & = & 0 & \\ \ end {array} \]
Это дает \ (u = \ frac {1} {2} \) или \ (u = 1 \). Поскольку \ (u = \ cos (x) \), мы получаем \ (\ cos (x) = \ frac {1} {2} \) или \ (\ cos (x) = 1 \). Решая \ (\ cos (x) = \ frac {1} {2} \), мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac { 5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Из \ (\ cos (x) = 1 \) мы получаем \ (x = 2 \ pi k \) для целых чисел \ (k \). Ответы, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {3} \) и \ (\ frac {5 \ pi} { 3} \).3-2u-2 = 0 \) равно \ (u = 1 \). Поскольку \ (u = \ cos (x) \), мы получаем \ (\ cos (x) = 1 \), поэтому \ (x = 2 \ pi k \) для целых чисел \ (k \). Единственное решение, которое лежит в \ ([0,2 \ pi) \), — это \ (x = 0 \). Построение графиков \ (y = \ cos (3x) \) и \ (y = 2- \ cos (x) \) на одном и том же наборе осей над \ ([0,2 \ pi) \) показывает, что графики пересекаются в что выглядит как \ ((0,1) \), как требуется.
Построение графиков \ (y = \ cos (3x) \) и \ (y = 2- \ cos (x) \) на одном и том же наборе осей над \ ([0,2 \ pi) \) показывает, что графики пересекаются в что выглядит как \ ((0,1) \), как требуется.
- \ item Хотя мы могли бы подойти к \ (\ cos (3x) = \ cos (5x) \) так же, как и к предыдущим двум задачам, вместо этого мы решили продемонстрировать полезность Sum to Product Identities.Из \ (\ cos (3x) = \ cos (5x) \) мы получаем \ (\ cos (5x) — \ cos (3x) = 0 \), и это наличие \ (0 \) на правая сторона, указывающая на то, что переход на продукт будет хорошим ходом. \ footnote {Как всегда, опыт — величайший учитель здесь!} Используя теорему \ ref {sumtoproduct}, мы имеем, что \ (\ cos (5x) — \ cos (3x) = — 2 \ sin \ left (\ frac {5x + 3x} {2} \ right) \ sin \ left (\ frac {5x — 3x} {2} \ right) = -2 \ sin (4x ) \ грех (х) \). Следовательно, уравнение \ (\ cos (5x) = \ cos (3x) \) эквивалентно \ (- 2 \ sin (4x) \ sin (x) = 0 \).Отсюда получаем \ (\ sin (4x) = 0 \) или \ (\ sin (x) \) = 0.
 Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это.
Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это. - \ item Изучая уравнение \ (\ sin (2x) = \ sqrt {3} \ cos (x) \), мы не только задействуем разные круговые функции, а именно синус и косинус, но и имеем разные аргументы. с, а именно \ (2x \) и \ (x \).
 Использование тождества \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \) делает все аргументы одинаковыми, и мы действуем так же, как и при решении любого нелинейного уравнения — собираем все ненулевые члены на одна сторона уравнения и фактор.
Использование тождества \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \) делает все аргументы одинаковыми, и мы действуем так же, как и при решении любого нелинейного уравнения — собираем все ненулевые члены на одна сторона уравнения и фактор.
\ [\ begin {array} {rclr}
\ sin (2x) & = & \ sqrt {3} \ cos (x) & \\
2 \ sin (x) \ cos (x) & = & \ sqrt {3} \ cos (x) & \ text {(Поскольку \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \).)} \\
2 \ sin (x) \ cos (x) — \ sqrt {3} \ cos (x) & = & 0 & \\
\ cos (x) (2 \ sin (x) — \ sqrt {3}) & = & 0 & \\ \ end {array} \]
, откуда получаем \ (\ cos (x) = 0 \) или \ (\ sin (x) = \ frac {\ sqrt {3}} {2} \). Из \ (\ cos (x) = 0 \) получаем \ (x = \ frac {\ pi} {2} + \ pi k \) для целых чисел \ (k \).Из \ (\ sin (x) = \ frac {\ sqrt {3}} {2} \) мы получаем \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac {2 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \). Ответы, которые лежат в \ ([0,2 \ pi) \): \ (x = \ frac {\ pi} {2} \), \ (\ frac {3 \ pi} {2} \), \ ( \ frac {\ pi} {3} \) и \ (\ frac {2 \ pi} {3} \). Мы строим графики \ (y = \ sin (2x) \) и \ (y = \ sqrt {3} \ cos (x) \) и, после некоторого осторожного увеличения, проверяем наши ответы.
Мы строим графики \ (y = \ sin (2x) \) и \ (y = \ sqrt {3} \ cos (x) \) и, после некоторого осторожного увеличения, проверяем наши ответы.
- \ item В отличие от предыдущей проблемы, похоже, нет быстрого способа сопоставить циклические функции или их аргументы в уравнении \ (\ sin (x) \ cos \ left (\ frac {x} {2} \ справа) + \ cos (x) \ sin \ left (\ frac {x} {2} \ right) = 1 \).Однако, если мы посмотрим на него достаточно долго, мы поймем, что левая часть — это развернутая форма формулы суммы для \ (\ sin \ left (x + \ frac {x} {2} \ right) \). Следовательно, наше исходное уравнение эквивалентно \ (\ sin \ left (\ frac {3} {2} x \ right) = 1 \). Решая, находим \ (x = \ frac {\ pi} {3} + \ frac {4 \ pi} {3} k \) для целых чисел \ (k \). Два из этих решений лежат в \ ([0,2 \ pi) \): \ (x = \ frac {\ pi} {3} \) и \ (x = \ frac {5 \ pi} {3} \). . Построение графика \ (y = \ sin (x) \ cos \ left (\ frac {x} {2} \ right) + \ cos (x) \ sin \ left (\ frac {x} {2} \ right) \) и \ (y = 1 \) проверяет наши решения.

- \ item Из-за отсутствия двойных углов или квадратов мы, кажется, мало что можем сделать. Однако, поскольку аргументы косинуса и синуса одинаковы, мы можем переписать левую часть этого уравнения как синусоиду. \ Footnote {По сути, мы «отменяем» формулу суммы / разности для косинуса или синуса, в зависимости от того, какой форма, которую мы используем, поэтому эта проблема на самом деле тесно связана с предыдущей!} Чтобы подогнать \ (f (x) = \ cos (x) — \ sqrt {3} \ sin (x) \) к форме \ (A \ sin (\ omega t + \ phi) + B \), мы используем то, что узнали в примере \ ref {extendedsinusoidex1}, и находим \ (A = 2 \), \ (B = 0 \), \ (\ omega = 1 \) и \ (\ phi = \ frac {5 \ pi} {6} \).Следовательно, мы можем переписать уравнение \ (\ cos (x) — \ sqrt {3} \ sin (x) = 2 \) как \ (2 \ sin \ left (x + \ frac {5 \ pi} {6}) \ right) = 2 \) или \ (\ sin \ left (x + \ frac {5 \ pi} {6} \ right) = 1 \). Решая последнее, мы получаем \ (x = — \ frac {\ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).
 Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.
Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.
Пример \ (\ PageIndex {4} \):
Выразите домен следующих функций, используя нотацию с расширенным интервалом.\ footnote {Подробную информацию об этой нотации см. на странице \ pageref {extendedinterval}.}
- \ (f (x) = \ csc \ left (2x + \ frac {\ pi} {3} \ right) \)
- \ (f (x) = \ dfrac {\ sin (x)} {2 \ cos (x) — 1} \)
- \ (f (x) = \ sqrt {1 — \ cot (x)} \)
Решение
\ item Чтобы найти область значений \ (f (x) = \ csc \ left (2x + \ frac {\ pi} {3} \ right) \), мы перепишем \ (f \) в терминах синуса как \ (f (x) = \ frac {1} {\ sin \ left (2x + \ frac {\ pi} {3} \ right)} \). Поскольку функция синуса определена везде, наша единственная проблема — нули в знаменателе. Решая \ (\ sin \ left (2x + \ frac {\ pi} {3} \ right) = 0 \), получаем \ (x = — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \) для целых чисел \ (k \). В нотации конструктора множеств наш домен \ (\ left \ {x: x \ neq — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \, \ text {для целых чисел \ ( k $} \ right \} \). Чтобы помочь визуализировать область, мы следуем старой мантре «Если сомневаешься, записывай!» Мы получаем \ (\ left \ {x: x \ neq — \ frac {\ pi } {6}, \ frac {2 \ pi} {6}, — \ frac {4 \ pi} {6}, \ frac {5 \ pi} {6}, — \ frac {7 \ pi} {6} , \ frac {8 \ pi} {6}, \ ldots \ right \} \), где мы сохранили знаменатели \ (6 \) повсюду, чтобы помочь увидеть закономерность.Изобразив ситуацию на числовой прямой, имеем
Решая \ (\ sin \ left (2x + \ frac {\ pi} {3} \ right) = 0 \), получаем \ (x = — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \) для целых чисел \ (k \). В нотации конструктора множеств наш домен \ (\ left \ {x: x \ neq — \ frac {\ pi} {6} + \ frac {\ pi} {2} k \, \ text {для целых чисел \ ( k $} \ right \} \). Чтобы помочь визуализировать область, мы следуем старой мантре «Если сомневаешься, записывай!» Мы получаем \ (\ left \ {x: x \ neq — \ frac {\ pi } {6}, \ frac {2 \ pi} {6}, — \ frac {4 \ pi} {6}, \ frac {5 \ pi} {6}, — \ frac {7 \ pi} {6} , \ frac {8 \ pi} {6}, \ ldots \ right \} \), где мы сохранили знаменатели \ (6 \) повсюду, чтобы помочь увидеть закономерность.Изобразив ситуацию на числовой прямой, имеем
Действуя так же, как на странице \ pageref {extendedinterval} в разделе \ ref {roundfunctionsbeyond}, мы позволяем \ (x _ {\ mbox {\ tiny \ (k $}}} \) обозначать \ (k $ th число, исключенное из домен, и у нас есть \ (x _ {\ mbox {\ tiny \ (k $}} = — \ frac {\ pi} {6} + \ frac {\ pi} {2} k = \ frac {(3k-1) \ pi} {6} \) для целых чисел \ (k \). Интервалы, составляющие домен, имеют вид \ (\ left (x _ {\ mbox {\ tiny \ (k $}}), x _ {\ mbox { \ tiny \ (k + 1 $}} \ right) = \ left (\ frac {(3k-1) \ pi} {6}, \ frac {(3k + 2) \ pi} {6} \ right) \ ) как \ (k \) пробегает целые числа.{\ infty} \ left (\ dfrac {(3k-1) \ pi} {6}, \ dfrac {(3k + 2) \ pi} {6} \ right) \]
Интервалы, составляющие домен, имеют вид \ (\ left (x _ {\ mbox {\ tiny \ (k $}}), x _ {\ mbox { \ tiny \ (k + 1 $}} \ right) = \ left (\ frac {(3k-1) \ pi} {6}, \ frac {(3k + 2) \ pi} {6} \ right) \ ) как \ (k \) пробегает целые числа.{\ infty} \ left (\ dfrac {(3k-1) \ pi} {6}, \ dfrac {(3k + 2) \ pi} {6} \ right) \]
Мы можем проверить наш ответ, подставив значения \ (k \), чтобы убедиться, что он соответствует нашей диаграмме.
\ item Поскольку области \ (\ sin (x) \) и \ (\ cos (x) \) — все действительные числа, единственное беспокойство при поиске области \ (f (x) = \ frac {\ sin (x)} {2 \ cos (x) — 1} \) является делением на ноль, поэтому мы устанавливаем знаменатель равным нулю и решаем. Из \ (2 \ cos (x) — 1 = 0 \) получаем \ (\ cos (x) = \ frac {1} {2} \), так что \ (x = \ frac {\ pi} {3} + 2 \ pi k \) или \ (x = \ frac {5 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \).Используя обозначение конструктора множеств, доменом является \ (\ left \ {x: x \ neq \ frac {\ pi} {3} + 2 \ pi k \, \ text {and} \, x \ neq \ frac {5 \ pi} {3} + 2 \ pi k \, \ text {для целых чисел \ (k $} \ right \} \) или \ (\ left \ {x: x \ neq \ pm \ frac {\ pi} {3}, \ pm \ frac {5 \ pi} {3}, \ pm \ frac {7 \ pi} {3}, \ pm \ frac {11 \ pi} {3}, \ ldots \ right \} \ ), так что у нас
В отличие от предыдущего примера, у нас есть \ textit {два} разных семейства точек для рассмотрения, и мы представляем два способа справиться с подобными ситуациями.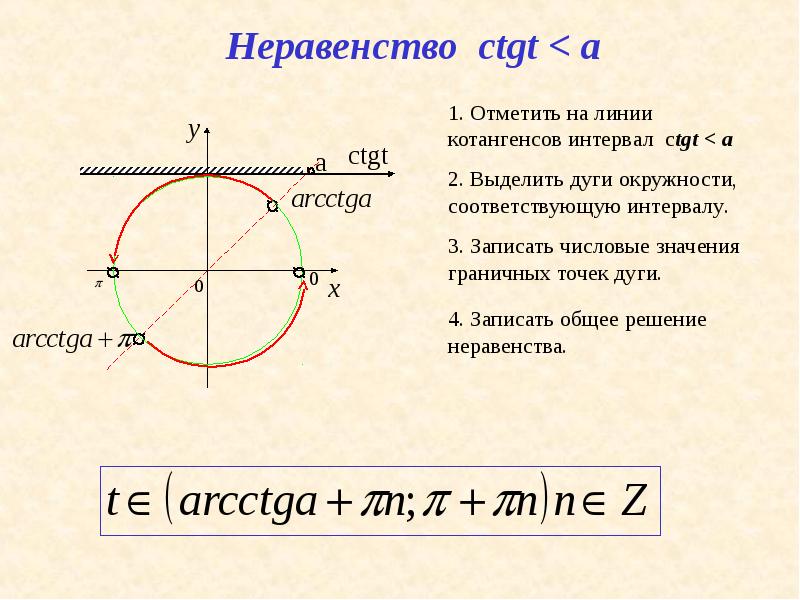 Один из способов — обобщить то, что мы сделали в предыдущем примере, и использовать формулы, которые мы нашли в нашей работе с предметной областью, для описания интервалов.Для этого положим \ (a _ {\ mbox {\ tiny \ (k $}} = \ frac {\ pi} {3} + 2 \ pi k = \ frac {(6k + 1) \ pi} {3 } \) и \ (b _ {\ mbox {\ tiny \ (k $}} = \ frac {5 \ pi} {3} + 2 \ pi k = \ frac {(6k + 5) \ pi} {3}) \) для целых чисел \ (k \). Теперь цель состоит в том, чтобы записать область в терминах \ (a $ ‘s an \ (b $’ s. Мы находим \ (a _ {\ mbox {\ tiny \ (0 $}} = \ frac {\ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (1 $}} = \ frac {7 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {5 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (2 $}} = \ frac {13 \ pi} { 3} \), \ (a _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (0 $}) } = \ frac {5 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (1 $}} = \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {\ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (2 $}} = \ frac {17 \ pi} {3}) \) и \ (b _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {7 \ pi} {3} \).
Один из способов — обобщить то, что мы сделали в предыдущем примере, и использовать формулы, которые мы нашли в нашей работе с предметной областью, для описания интервалов.Для этого положим \ (a _ {\ mbox {\ tiny \ (k $}} = \ frac {\ pi} {3} + 2 \ pi k = \ frac {(6k + 1) \ pi} {3 } \) и \ (b _ {\ mbox {\ tiny \ (k $}} = \ frac {5 \ pi} {3} + 2 \ pi k = \ frac {(6k + 5) \ pi} {3}) \) для целых чисел \ (k \). Теперь цель состоит в том, чтобы записать область в терминах \ (a $ ‘s an \ (b $’ s. Мы находим \ (a _ {\ mbox {\ tiny \ (0 $}} = \ frac {\ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (1 $}} = \ frac {7 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {5 \ pi} {3} \), \ (a _ {\ mbox {\ tiny \ (2 $}} = \ frac {13 \ pi} { 3} \), \ (a _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (0 $}) } = \ frac {5 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (1 $}} = \ frac {11 \ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (- 1 $}} = — \ frac {\ pi} {3} \), \ (b _ {\ mbox {\ tiny \ (2 $}} = \ frac {17 \ pi} {3}) \) и \ (b _ {\ mbox {\ tiny \ (- 2 $}} = — \ frac {7 \ pi} {3} \). Следовательно, с точки зрения \ (a $ и \ (b $), наш домен равен
Следовательно, с точки зрения \ (a $ и \ (b $), наш домен равен
\ [\ ldots \ left (a _ {\ mbox {\ tiny \ (- 2 $}}}, b _ {\ mbox {\ tiny \ (- 2 $}}} \ right) \ cup \ left (b _ {\ mbox { \ tiny \ (- 2 $}}, a _ {\ mbox {\ tiny \ (- 1 $}} \ right) \ cup \ left (a _ {\ mbox {\ tiny \ (- 1 $}}, b _ {\ mbox {\ tiny \ (- 1 $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (- 1 $}}, a _ {\ mbox {\ tiny \ (0 $}} \ right) \ cup \ left (a _ {\ mbox {\ tiny \ (0 $}}, b _ {\ mbox {\ tiny \ (0 $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (0 $}}, a _ {\ mbox {\ tiny \ (1 $}} \ right) \ cup \ left (a _ {\ mbox {\ tiny \ (1 $}}, b _ {\ mbox {\ tiny \ (1 $ }} \ right) \ чашка \ точки \]
Если мы сгруппируем эти интервалы попарно, \ (\ left (a _ {\ mbox {\ tiny \ (- 2 $}}), b _ {\ mbox {\ tiny \ (- 2 $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (- 2 $}}, a _ {\ mbox {\ tiny \ (- 1 $}} \ right) \), \ (\ left (a _ {\ mbox {\ tiny \ ( -1 $}}, b _ {\ mbox {\ tiny \ (- 1 $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (- 1 $}}), a _ {\ mbox {\ tiny \ (0 $}} \ right) \), \ (\ left (a _ {\ mbox {\ tiny \ (0 $}}), b _ {\ mbox {\ tiny \ (0 $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (0 $}}, a _ {\ mbox {\ tiny \ (1 $}} \ right) \) и так далее, мы видим, как появляется шаблон формы \ (\ left (a _ {\ mbox {\ tiny \ (k $}}, b _ {\ mbox {\ tiny \ (k $}} \ right) \ cup \ left (b _ {\ mbox {\ tiny \ (k $}}), a _ {\ mbox {\ tiny \ (k + 1 $}} \ right) \) для целых чисел \ (k \), чтобы наш домен можно было записать как
\ [\ bigcup_ {k = — \ infty} ^ {\ infty} \ left (a _ {\ mbox {\ tiny \ (k $}}, b _ {\ mbox {\ tiny \ (k $}} \ right)) \ cup \ left (b _ {\ mbox {\ tiny \ (k $}}, a _ {\ mbox {\ tiny \ (k + 1 $}} \ right) = \ bigcup_ {k = — \ infty} ^ {\ infty} \ left (\ frac {(6k + 1) \ pi} {3}, \ frac {(6k + 5) \ pi} {3} \ right) \ cup \ left (\ frac {(6k + 5) \ pi} {3}, \ frac {(6k + 7) \ pi} {3} \ right) \]
Второй подход к проблеме использует периодический характер \ (f \). Поскольку \ (\ cos (x) \) и \ (\ sin (x) \) имеют период \ (2 \ pi \), нетрудно показать, что функция \ (f \) повторяется каждые \ (2 \ pi \) единиц. \ footnote {Это не обязательно означает, что период \ (f \) равен \ (2 \ pi \). Касательная функция состоит из \ (\ cos (x) \) и \ (\ sin (x) \), но ее период составляет половину их периода. Читателю предлагается изучить период \ (f \).} Это означает, что если мы можем найти формулу для области на интервале длины \ (2 \ pi \), мы можем выразить всю область, переведя наш ответ слева и справа по оси \ (x \) — путем сложения целых чисел, кратных \ (2 \ pi \).Один из таких интервалов, который возникает в результате нашей работы в области, — это \ (\ left [\ frac {\ pi} {3}, \ frac {7 \ pi} {3} \ right] \). Часть домена здесь \ (\ left (\ frac {\ pi} {3}, \ frac {5 \ pi} {3} \ right) \ cup \ left (\ frac {5 \ pi} {3} , \ frac {7 \ pi} {3} \ right) \). Складывая целые числа, кратные \ (2 \ pi \), мы получаем семейство интервалов \ (\ left (\ frac {\ pi} {3} + 2 \ pi k, \ frac {5 \ pi} {3} + 2 \ pi k \ right) \ cup \ left (\ frac {5 \ pi} {3} + 2 \ pi k, \ frac {7 \ pi} {3} + 2 \ pi k \ right) \) для целых чисел \ (к \).
Поскольку \ (\ cos (x) \) и \ (\ sin (x) \) имеют период \ (2 \ pi \), нетрудно показать, что функция \ (f \) повторяется каждые \ (2 \ pi \) единиц. \ footnote {Это не обязательно означает, что период \ (f \) равен \ (2 \ pi \). Касательная функция состоит из \ (\ cos (x) \) и \ (\ sin (x) \), но ее период составляет половину их периода. Читателю предлагается изучить период \ (f \).} Это означает, что если мы можем найти формулу для области на интервале длины \ (2 \ pi \), мы можем выразить всю область, переведя наш ответ слева и справа по оси \ (x \) — путем сложения целых чисел, кратных \ (2 \ pi \).Один из таких интервалов, который возникает в результате нашей работы в области, — это \ (\ left [\ frac {\ pi} {3}, \ frac {7 \ pi} {3} \ right] \). Часть домена здесь \ (\ left (\ frac {\ pi} {3}, \ frac {5 \ pi} {3} \ right) \ cup \ left (\ frac {5 \ pi} {3} , \ frac {7 \ pi} {3} \ right) \). Складывая целые числа, кратные \ (2 \ pi \), мы получаем семейство интервалов \ (\ left (\ frac {\ pi} {3} + 2 \ pi k, \ frac {5 \ pi} {3} + 2 \ pi k \ right) \ cup \ left (\ frac {5 \ pi} {3} + 2 \ pi k, \ frac {7 \ pi} {3} + 2 \ pi k \ right) \) для целых чисел \ (к \).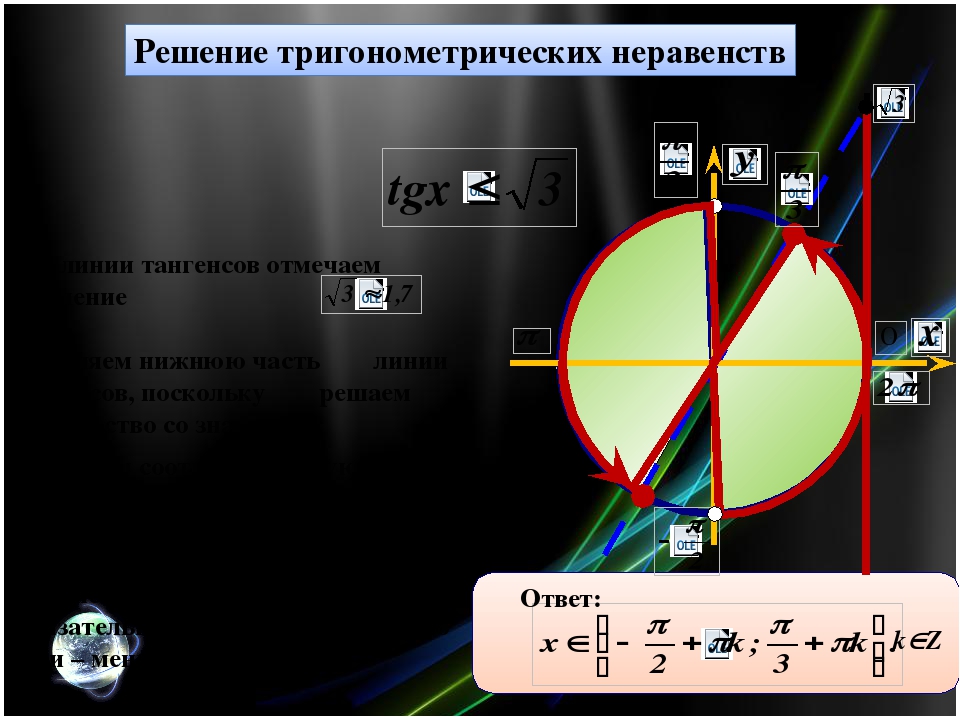 Мы предоставляем читателю показать, что получение общих знаменателей приводит к нашему предыдущему ответу.
Мы предоставляем читателю показать, что получение общих знаменателей приводит к нашему предыдущему ответу.
\ item Чтобы найти область значений \ (f (x) = \ sqrt {1- \ cot (x)} \), сначала отметим, что из-за наличия члена \ (\ cot (x) \) , \ (x \ neq \ pi k \) для целых чисел \ (k \). Далее напомним, что для определения квадратного корня нам потребуется \ (1 — \ cot (x) \ geq 0 \). В отличие от неравенств, которые мы решили в примере \ ref {TrigIneqEx1}, здесь мы не ограничены заданным интервалом. Наша стратегия состоит в том, чтобы решить это неравенство над \ ((0, \ pi) \) (тот же интервал, который порождает фундаментальный цикл котангенса), а затем добавить целые числа, кратные периоду, в данном случае \ (\ pi \).Положим \ (g (x) = 1 — \ cot (x) \) и приступим к построению знаковой диаграммы для \ (g \) на интервале \ ((0, \ pi) \), чтобы найти, где \ (g (х) \ geq 0 \). Отметим, что \ (g \) не определено для \ (x = \ pi k \) для целых чисел \ (k \), в частности, на концах нашего интервала \ (x = 0 \) и \ (x = \ Пи\). Далее ищем нули \ (g \). Решая \ (g (x) = 0 \), мы получаем \ (\ cot (x) = 1 \) или \ (x = \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \) и только один из них, \ (x = \ frac {\ pi} {4} \), лежит в \ ((0, \ pi) \). Выбирая тестовые значения \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {\ pi} {2} \), получаем \ (g \ left (\ frac {\ pi} {6} \ right) = 1 — \ sqrt {3} \) и \ (g \ left (\ frac {\ pi} {2} \ right) = 1 \).{\ infty} \ left [\ dfrac {(4k + 1) \ pi} {4}, (k + 1) \ pi \ right) \]
Далее ищем нули \ (g \). Решая \ (g (x) = 0 \), мы получаем \ (\ cot (x) = 1 \) или \ (x = \ frac {\ pi} {4} + \ pi k \) для целых чисел \ (k \) и только один из них, \ (x = \ frac {\ pi} {4} \), лежит в \ ((0, \ pi) \). Выбирая тестовые значения \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {\ pi} {2} \), получаем \ (g \ left (\ frac {\ pi} {6} \ right) = 1 — \ sqrt {3} \) и \ (g \ left (\ frac {\ pi} {2} \ right) = 1 \).{\ infty} \ left [\ dfrac {(4k + 1) \ pi} {4}, (k + 1) \ pi \ right) \]
Авторы и авторство
- Карл Ститц, доктор философии (Lakeland Community College) и Джефф Зигер, доктор философии. (Общественный колледж округа Лорейн)
Решение тригонометрических уравнений и неравенств
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.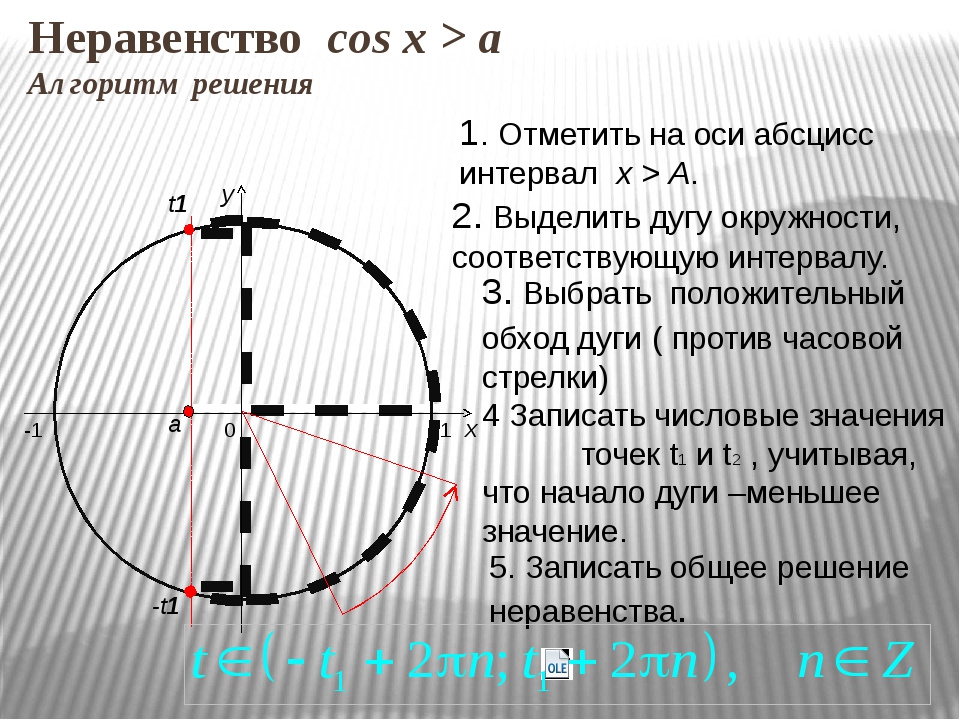 Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.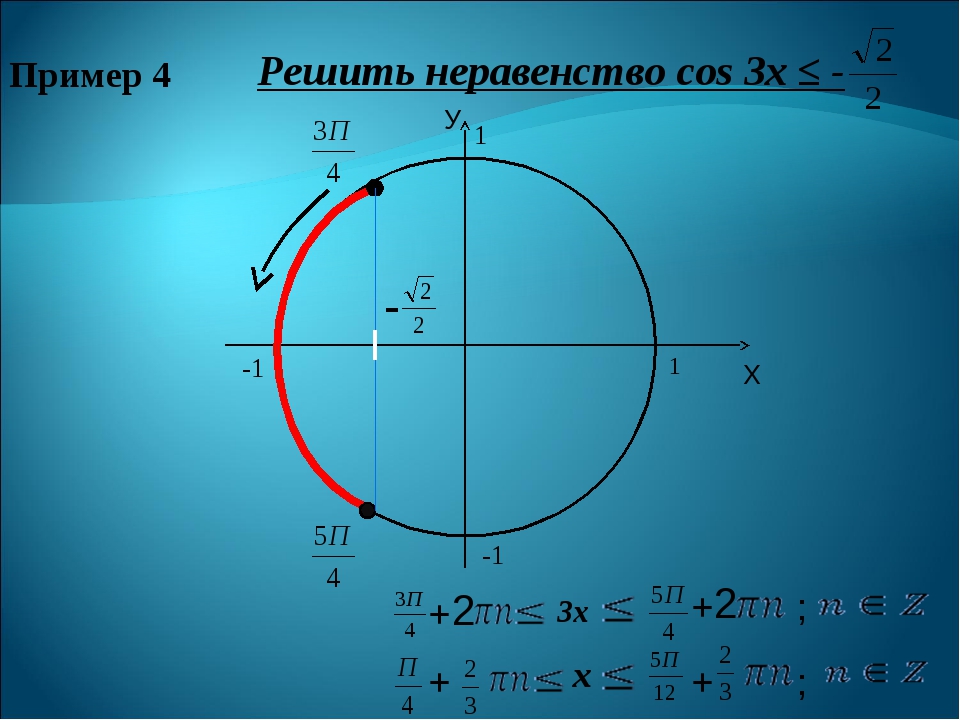 д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ / resolve-trigonometric-inequalities.pdf / PDF4PRO
1 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКОЕ НЕРАВЕНСТВА (КОНЦЕПЦИЯ, МЕТОДЫ И ШАГИ)Нгуен ОПРЕДЕЛЕНИЕ.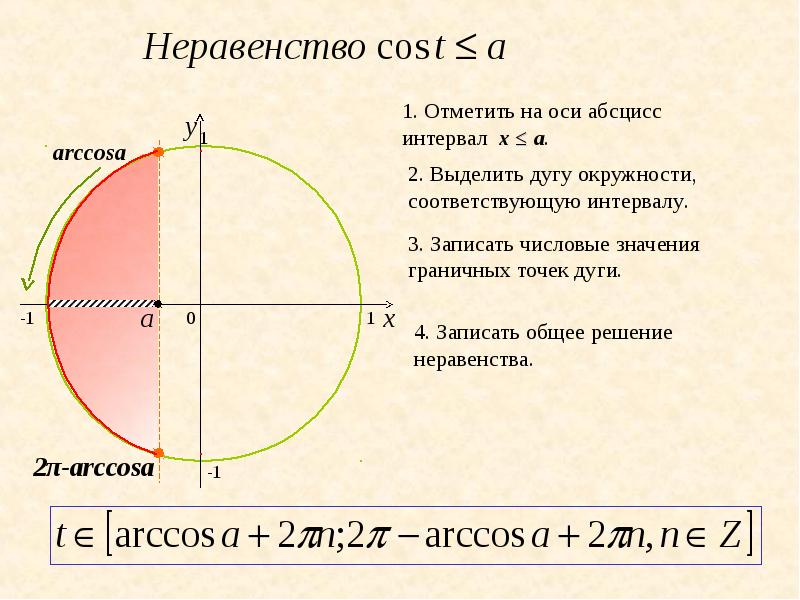 Тригонометрическое неравенство — это неравенство в стандартной форме: R (x)> 0 (или <0), которое содержит одну или несколько триггерных функций переменной arc x. РЕШЕНИЕ неравенство R (x) означает нахождение всех значений переменной arc x, триггерные функции которой делают неравенство R (x) истинным. Все эти значения x составляют множество решений тригонометрического неравенства R (x). Наборы решений триггера НЕРАВЕНСТВА выражаются в интервалах. Примеры trig НЕРАВЕНСТВА : sin (x + 30 градусов)
Тригонометрическое неравенство — это неравенство в стандартной форме: R (x)> 0 (или <0), которое содержит одну или несколько триггерных функций переменной arc x. РЕШЕНИЕ неравенство R (x) означает нахождение всех значений переменной arc x, триггерные функции которой делают неравенство R (x) истинным. Все эти значения x составляют множество решений тригонометрического неравенства R (x). Наборы решений триггера НЕРАВЕНСТВА выражаются в интервалах. Примеры trig НЕРАВЕНСТВА : sin (x + 30 градусов)
2; (30 градусов, 120 градусов) ОБЪЕДИНЕННАЯ КРУГЛОСТЬ Это круг с радиусом R = 1 единица с началом O. Переменная дуга AM, которая вращается против часовой стрелки на единичной окружности триггера, определяет 4 общие триггерные функции дуги x. . Когда дуга AM изменяется на единичной окружности триггера: Горизонтальная ось OAx определяет триггерную функцию f (x) = cos x. Вертикальная ось OBy определяет триггерную функцию f (x) = sin x. Вертикальная ось At определяет триггерную функцию f (x) = tan x. Горизонтальная ось Bu определяет триггерную функцию f (x) = cot x.Круг триггерного блока будет использоваться в качестве доказательства в РЕШЕНИЕ базовых триггерных уравнений и базовых триггеров НЕРАВЕНСТВА . ОБЩИЙ ПЕРИОД ТРИГОВОГО НЕРАВЕНСТВА Общий период тригонометрического неравенства является наименьшим кратным из всех периодов триггерных функций, представленных в неравенстве.
. Когда дуга AM изменяется на единичной окружности триггера: Горизонтальная ось OAx определяет триггерную функцию f (x) = cos x. Вертикальная ось OBy определяет триггерную функцию f (x) = sin x. Вертикальная ось At определяет триггерную функцию f (x) = tan x. Горизонтальная ось Bu определяет триггерную функцию f (x) = cot x.Круг триггерного блока будет использоваться в качестве доказательства в РЕШЕНИЕ базовых триггерных уравнений и базовых триггеров НЕРАВЕНСТВА . ОБЩИЙ ПЕРИОД ТРИГОВОГО НЕРАВЕНСТВА Общий период тригонометрического неравенства является наименьшим кратным из всех периодов триггерных функций, представленных в неравенстве.
3 Примеры: Тригонометрическое неравенство: sin x + sin 2x + cos x / 2 <1 имеет общий период 4Pi. Тригонометрическое неравенство: tan 2x + sin x cos 2x> 2 имеет общий период 2Pi. Тригонометрическое неравенство: tan x + cos x / 2 <3 имеет общий период 4Pi.Если не указано иное, тригонометрическое неравенство должно быть решено, по крайней мере, в течение одного общего периода. Страница 1 из 8 BASIC TRIG НЕРАВЕНСТВА . Существует 4 основных общих типа базовых триггеров НЕРАВЕНСТВА : sin x a) cos x a) a — заданное число tan x a) cot x a) РЕШЕНИЕ базовый триггер НЕРАВЕНСТВА выполняется с использованием таблиц преобразования триггеров (или калькуляторов), а затем путем рассмотрения различных положений переменной дуги x, которая вращается на триггерной окружности.Пример 1. Решите неравенство: sin x> Решение.
Страница 1 из 8 BASIC TRIG НЕРАВЕНСТВА . Существует 4 основных общих типа базовых триггеров НЕРАВЕНСТВА : sin x a) cos x a) a — заданное число tan x a) cot x a) РЕШЕНИЕ базовый триггер НЕРАВЕНСТВА выполняется с использованием таблиц преобразования триггеров (или калькуляторов), а затем путем рассмотрения различных положений переменной дуги x, которая вращается на триггерной окружности.Пример 1. Решите неравенство: sin x> Решение.
4 Набор решений задается как таблицей триггеров, так и кругом триггерных единиц. На триггерной единичной окружности sin x>, когда дуга x изменяется от Pi / 4 до 3Pi / 4: Pi / 4 5 Решить: cot (2x Pi / 6) <(в пределах периода Pi) Решение. Набор решений, заданный тригонометрическим кругом и калькулятором: 2Pi / 3 6 Существует около 31 триггерной идентичности, среди которых последние 14 идентичностей (от №19 до №31) называются идентичностями преобразования, поскольку они являются необходимыми инструментами для преобразования триггерных НЕРАВЕНСТВА (или триггерных уравнений ) в базовые .2 x) -sin x (2sin x + 1) <0 Важное примечание. 7 Процесс преобразования неравенства R (x)> 0 (или <0) точно такой же, как процесс преобразования уравнения R (x) = 0. РЕШЕНИЕ тригонометрическое неравенство R (x) требует сначала чтобы решить уравнение R (x) = 0, чтобы получить все его действительные корни. ШАГИ В РЕШЕНИЕ TRIG НЕРАВЕНСТВА Есть 4 шага в SOLVING trig НЕРАВЕНСТВА . 8 Полный набор решений должен охватывать как минимум один общий период. Пример.Тригонометрическое неравенство R (x) = cos 2x 3sin x — 2 <0 имеет 2Pi в качестве общего периода. Пример. Тригонометрическое неравенство R (x) = sin x cos x / 2 -> 0 имеет общий период 4Pi. Пример. Тригонометрическое неравенство R (x) = tan x + 2 cos x + sin 2x <2 имеет общий период 2Pi. Шаг 3. Решите тригонометрическое уравнение R (x) = 0 Если R (x) содержит только одну тригонометрическую функцию, решите его как основное тригонометрическое уравнение. 9 Шаг 1. Стандартная форма: R (x) = cos x + cos 2x + cos 3x> 0 Шаг 2. Общий период: 2Pi Шаг 3. Решите R (x) = 0. Преобразуйте его в произведение, используя Sum to Идентификатор продукта: R (x) = cos x + cos 2x + cos 3x = cos 2x (1 + 2cos x) = 0. Затем решите 2 основных триггерных уравнения f (x) = cos 2x = 0 и g ( x) = (1 + 2cos x) = 0, чтобы получить все значения x за период 2Pi.Эти значения x будут использоваться на шаге 4. Пример 9. Решить sin x + sin 2x <-sin 3x (0 10 Страница 4 из 8 b. МЕТОД 2. Этот метод преобразует тригонометрическое неравенство с двумя или более триггерами в триггерное неравенство, в котором в качестве переменной используется только одна триггерная функция (называемая t).2 x = детская кроватка x + 2 (0 11,5 Теперь мы собираемся завершить наше исследование неравенств, рассмотрев неравенства, которые включают тригонометрические термины. 21,2 Следует сказать, что они сложнее экспоненциальных или логарифмических неравенств в целом. Фактически, я бы сказал, что они в значительной степени находятся на переднем крае того, что могут сделать люди, прошедшие курс подготовки к расчету. 72,3 Эти, возможно, расплывчатые замечания станут более ясными, если мы рассмотрим определенное количество примеров. Начнем с простого неравенства типа косинус x больше или равен альфа или, возможно, меньше или равен альфа. Первое замечание: если абсолютное значение альфа больше 1, то набор решений будет очевиден. Это будет либо реальная линия, либо пустой набор. Почему? Ну, потому что, например, косинус x больше минус 2 всегда верен для любого x. 115,5 В этом случае существует определенный угол a, косинус которого равен альфе. Это угол, который мы назвали арккозинусом альфа, и, как вы помните, он лежит в интервале 0 пи. Таким образом, два неравенства, которые мы рассматриваем, будут иметь косинус x, больший или равный cos a, или меньший или равный. Начнем с первого.Как решить это неравенство? Один из способов сделать это — посмотреть на график функции косинуса, который мы действительно должны очень хорошо знать. А теперь угол a. Он находится между 0 и пи и генерирует определенное значение косинуса. 153,8 И мы ищем те точки, для которых косинус x будет хотя бы равен тому же значению. Что ж, если вы посмотрите вокруг точки a, вы увидите, что эти точки будут слева от точки a, пока вы не достигнете определенного другого угла.Что это за другой угол? Что ж, вы можете видеть по симметрии, что это угол минус a, тот, который имеет тот же косинус, что и a. 177,6 Также вы можете видеть, что в интервале от минус пи до пи, который представляет собой интервал длиной 2 пи, который является периодом рассматриваемой функции, единственными решениями, для которых cos x будет больше или равно cos a, являются те в интервале от минус до а. И это говорит вам, где x должен лежать, чтобы быть решением нашего неравенства относительно интервала минус пи до пи.Конечно, учитывая, что косинус периодичен с периодом 2 пи, будет много других x, удовлетворяющих тому же неравенству. 212,2 Они будут в каком-то другом интервале, и мы сможем уловить их все, просто добавив к уже идентифицированным целое кратное 2 пи, где целое число k либо положительное, либо отрицательное. Условное обозначение здесь: когда я беру интервал минус -a, a и добавляю число вроде 2 k pi, это означает, что я взял интервал, состоящий из всех чисел в исходном интервале, к которому я это добавил.Другими словами, это интервал от минус плюс 2 к пи до плюс 2 к пи. Условные обозначения. Теперь давайте посмотрим на другой случай, косинус x меньше или равен cos a. 253,8 Ее можно решить аналогичным образом, посмотрев на график функции косинуса. Вот угол а. Он генерирует определенный косинус. Теперь мы ищем те x, значение косинуса которых меньше косинуса a. И мы видим, что справа, под определенным углом, который мы видим по симметрии, это 2 пи минус a, эти косинусы будут меньше или равны тому, что они были в a.Кроме того, мы видим, что относительно интервала 0, 2 пи, это единственные x, те, которые находятся в этом интервале, от a до 2 pi минус a, для которых косинус будет меньше, чем он был в a. 296 Это сразу дает нам первую оценку нашего набора решений, интервал от a до 2 pi минус a. Но, конечно, будет много других решений и в других интервалах длиной 2 пи. И мы захватываем их, добавляя к этому интервалу 2 k pi, где k — любое положительное или отрицательное целое число.Итак, мы нашли решения в обоих случаях нашего простого неравенства. Давайте воспользуемся примером того, как мы можем применить это к неравенствам, например, cos x меньше минус 1/2. Что нам нужно сделать в первую очередь? Что ж, нам нужно найти угол, косинус которого равен минус 1/2. Достаточно легко сделать. Это 2 пи больше 3. 339,8 Итак, мы решаем cos x меньше косинуса 2 пи над 3. Мы могли бы сделать это графически, как я только что проиллюстрировал. Но есть еще одна техника, которую я хотел бы показать вам.Он использует круговое определение синуса и косинуса, единичного круга. Если вы посмотрите на угол 2 пи на 3 и посмотрите на соответствующую ему точку на единичной окружности, а косинус минус 1/2 — это координата x этой точки. Какие точки на единичной окружности будут иметь координату x меньше минус 1/2? Что ж, вы можете довольно легко их идентифицировать. Они будут слева от вертикального сегмента. 381,3 И синяя точка, обозначающая нижнюю точку, соответствует углу минус 2 пи больше 3.Помните, что косинус четный, и косинус минус 2 пи больше 3 будет таким же, как косинус 2 пи больше 3. Какие точки вы пытаетесь захватить? Те точки, которые лежат слева от этого вертикального сегмента. Как вы выразите этот вертикальный сегмент? Какие в нем углы? Ну, это будут углы между этим. Я выразил свой угол минус 2 пи больше 3 в эквивалентной форме как 4 пи больше 3. Это будут углы до этого места, но начиная с 2 пи больше 3. 420.3 Другими словами, это будут все углы между 2 пи больше 3 и 4 пи больше 3. И это наш набор решений. За исключением того, что периодичность даст нам другие решения. Поэтому, конечно, мне нужно добавить к этому любое целое кратное 2 пи, положительное или отрицательное. Мы могли бы решить эту проблему, взглянув на график косинуса, а также альтернативным методом. Некоторым это легче. Некоторые люди предпочитают единичный круг. Как бы это работало графически? Что ж, смотрим на наш угол 2 пи больше 3.Он генерирует определенное значение косинуса. Мы ищем крестики, которые дадут вам что-то меньшее. Они явно не правы. Они идут до 4 пи больше 3. 466,1 И когда мы посмотрим на интервал 0, 2 пи, мы увидим, что это единственные x, которые будут генерировать косинус меньше минус 1/2. И это дает нам тот же ответ. Теперь те же рассуждения, которые мы применили к косинусу, применим к синусу. И мы можем решить неравенства, такие как синус x меньше или равен синусу, почти таким же образом.Теперь a будет между минусом пи больше 2 и пи больше 2, потому что именно здесь функция арксинуса принимает свои значения. Простой пример. Найдите x, для которых синус x меньше или равен корню 3 над 2. Итак, мы начнем с нахождения угла, синус которого равен корню 3 над 2. 511,6 Это, конечно, число пи больше 3. Это одно из наших известных значений, которое мы знаем наизусть. И как мы будем действовать? Что ж, графически мы смотрим на число пи больше 3, и оно генерирует определенный синус.И мы ищем x, для которых синус не больше. Настолько ясно, что мы переместились влево до определенного угла, который имеет тот же синус, что и пи больше 3. Что это за угол? Это дополнительный угол. В данном случае минус 4 пи больше 3. Теперь, в интервале от минус пи до пи, не совсем ясно, что у нас есть единственные решения. 550,7 Так что лучше сдвинуть интервал влево, чтобы мы, очевидно, захватили все возможные решения неравенства в интервале длиной 2 пи.Этот интервал, конечно, представляет собой интервал минус 3 пи больше 2 до пи больше 2. Теперь мы можем быть вполне уверены, что в этом интервале единственными решениями являются те, которые находятся в обозначенном интервале. Итак, мы берем этот интервал, но, конечно, затем продолжаем добавлять 2 k pi, чтобы захватить по периодичности все остальные решения. 586,4 Мы могли бы решить эту проблему с помощью подхода единичного круга. Укажем, как это будет работать. Это изображение, которое вы могли бы использовать для решения этого неравенства.Чему соответствует эта картина? Итак, во-первых, мы определили угол пи больше 3 и поместили точку на единичной окружности, которой он соответствует. Затем мы нашли угол, для которого синус был одинаковым, а именно дополнительный угол 2 пи больше 3. А теперь мы смотрим на точки, которые мы хотим идентифицировать как решение нашего неравенства на единичной окружности. Это означает, что y-координата, синус x, не должна быть больше, чем для этих двух точек. 629,1 Это означает, что мы не в секторе выше.Мы скорее находимся в составе этого сектора. Как мы выразим дополнение этого сектора? Итак, мы видим, что он состоит из всех углов между минус 4 пи более 3 и пи более 3, что дает нам этот интервал в качестве нашего начального набора решений. А затем применяем периодичность. Мы добавляем к этому 2 k pi, чтобы найти набор всех решений. И, конечно же, получаем тот же ответ, что и графическим методом. Теперь вы замечаете, что даже при решении этих простых неравенств вам приходилось действительно учитывать применяемый метод. 669,2 И вам нужно было немного подумать, будь то графически или с единичными кругами. Я бы сказал, что если вы сможете правильно решить эти виды неравенства, вы попадете в элиту неравенства. 1 РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКОЕ НЕРАВЕНСТВА (КОНЦЕПЦИЯ, МЕТОДЫ И ШАГИ)Нгуен ОПРЕДЕЛЕНИЕ. Тригонометрическое неравенство — это неравенство в стандартной форме: R (x)> 0 (или <0), которое содержит одну или несколько триггерных функций переменной arc x. РЕШЕНИЕ неравенство R (x) означает нахождение всех значений переменной arc x, триггерные функции которой делают неравенство R (x) истинным. Все эти значения x составляют множество решений тригонометрического неравенства R (x). Наборы решений триггера НЕРАВЕНСТВА выражаются в интервалах. Примеры trig НЕРАВЕНСТВА : sin (x + 30 градусов) 2 Переменная дуга AM, которая вращается против часовой стрелки на единичной окружности триггера, определяет 4 общие триггерные функции: дуга x. Когда дуга AM изменяется на единичной окружности триггера: Горизонтальная ось OAx определяет триггерную функцию f (x) = cos x. Вертикальная ось OBy определяет триггерную функцию f (x) = sin x. Вертикальная ось At определяет триггерную функцию f (x) = tan x. Горизонтальная ось Bu определяет триггерную функцию f (x) = cot x.Круг триггерного блока будет использоваться в качестве доказательства в базовых триггерных уравнениях , РЕШЕНИЕ и базовых триггерных неравенствах . ОБЩИЙ ПЕРИОД ТРИГОВОГО НЕРАВЕНСТВА Общий период тригонометрического неравенства является наименьшим кратным из всех периодов триггерных функций, представленных в неравенстве. Примеры: Тригонометрическое неравенство: sin x + sin 2x + cos x / 2 <1 имеет общий период 4Pi. Тригонометрическое неравенство: tan 2x + sin x cos 2x> 2 имеет общий период 2Pi. Тригонометрическое неравенство: tan x + cos x / 2 <3 имеет общий период 4Pi.Если не указано иное, тригонометрическое неравенство должно быть решено, по крайней мере, в течение одного общего периода. 3 Стр. 1 из 8 BASIC TRIG НЕРАВЕНСТВА . Существует 4 основных общих типа базовых триггеров НЕРАВЕНСТВА : sin x a) cos x a) a — заданное число tan x a) cot x a) РЕШЕНИЕ базовый триггер НЕРАВЕНСТВА выполняется с использованием таблиц преобразования триггеров (или калькуляторов), а затем путем рассмотрения различных положений переменной дуги x, которая вращается на триггерной окружности.Пример 1. Решите неравенство: sin x> Решение. Набор решений представлен как таблицей триггеров, так и кругом триггерных единиц. На триггерной единичной окружности sin x>, когда дуга x изменяется от Pi / 4 до 3Pi / 4: Pi / 4 4 -Pi / 2 5 Существует около 31 триггерной идентичности, среди них последние 14 идентичностей (от №19 до №31) называются идентичностями преобразования, поскольку они являются необходимыми инструментами для преобразования триггерных НЕРАВЕНСТВА (или триггерных уравнений) в базовые.2 x) -sin x (2sin x + 1) <0 Важное примечание. Процесс преобразования неравенства R (x)> 0 (или <0) точно такой же, как процесс преобразования уравнения R (x) = 0. 6 РЕШЕНИЕ тригонометрическое неравенство R (x) требует сначала чтобы решить уравнение R (x) = 0, чтобы получить все его действительные корни. ШАГИ В РЕШЕНИЕ TRIG НЕРАВЕНСТВА Есть 4 шага в SOLVING trig НЕРАВЕНСТВА . Шаг 1. Преобразуйте данное тригонометрическое неравенство к стандартному виду R (x)> 0 (или <0).Пример. Неравенство (cos 2x <2 + 3sin x) будет преобразовано в стандартную форму: R (x) = cos 2x 3sin x - 2 <0 Страница 3 из 8 Пример. Неравенство (sin x + sin 2x> — sin 3x) преобразуется в стандартную форму R (x) = sin x + sin 2x + sin 3x> 0. Шаг 2. Найдите общий период. Общий период должен быть наименьшим кратным периодам всех триггерных функций, представленных в неравенстве. Полный набор решений должен охватывать как минимум один общий период. Пример. Тригонометрическое неравенство R (x) = cos 2x 3sin x — 2 <0 имеет 2Pi в качестве общего периода. Пример.Тригонометрическое неравенство R (x) = sin x cos x / 2 -> 0 имеет общий период 4Pi. Пример. Тригонометрическое неравенство R (x) = tan x + 2 cos x + sin 2x <2 имеет общий период 2Pi. 7 Шаг 3. Решите триггерное уравнение R (x) = 0 Если R (x) содержит только одну тригонометрическую функцию, решите его как основное тригонометрическое уравнение. Если R (x) содержит 2 или более триггерных функций, есть 2 метода, описанных ниже, для ее решения. а. МЕТОД 1. Преобразуйте R (x) в произведение многих основных тригонометрических уравнений. Затем решите эти базовые триггерные уравнения отдельно, чтобы получить все значения x, которые будут использоваться на шаге 4.Пример 8. Решите: cos x + cos 2x> — cos 3x (0 8 Шаг 1: sin x + sin 2x + sin 3x <0 Шаг 2: Общий период 2Pi. Шаг 3. Решите R (x) = 0. Преобразуйте его в произведение, используя тождество триггера: R (x) = sin x + sin 2x + sin 3x = sin 2x (2cos x + 1) = 0 Затем решите 2 основных триггерные уравнения f (x) = sin 2x = 0 и g (x) = 2cos x + 1 = 0. Найденные значения x будут использоваться на шаге 4. Страница 4 из 8 b. МЕТОД 2. Этот метод преобразует тригонометрическое неравенство с двумя или более триггерами в триггерное неравенство, в котором в качестве переменной используется только одна триггерная функция (называемая t).2 1) = 0 Выносим за скобки (2t + 1) Затем решаем 3 основных тригонометрических уравнения: (2tan x +1) = 0; тангенс х = -1; tan x = 1. Шаг 4. Решите тригонометрическое неравенство R (x) <0 (или> 0). Затем выразите множество решений в виде интервалов. Основываясь на найденных значениях x из шага 3, решите алгебраически тригонометрическое неравенство R (x) <0 (или> 0) по отдельности РЕШЕНИЕ каждого базового тригонометрического неравенства f (x), g (x) .., а затем установив знак соболя (знаковая карта). Пример 12. Решение: sin x + sin 3x <- sin 2x Решение.Шаг 1. Стандартная форма: R (x) = sin x + sin 2x + sin 3x <0 Шаг 2. Общий период 2Pi Шаг 3. Решите R (x) = 0. Преобразуйте R (x) в произведение, используя Trig Identity # 28; R (x) = 2sin 2x (2cos x + 1) = 0 (0 10 Дуги решения x равны: 0 , Пи / 2, Пи, 3Пи / 2, 2Пи. Используя круг триггерного блока в качестве доказательства, определите изменение f (x) от 0 до 2Pi со значениями (+) и (-): Страница 5 из 8 x 0 Pi / 2 Pi 3Pi / 2 2Pi —— ———————————- —————- ———————— ———— f (x) 0 + 0 — 0 + 0 — 0 Решить g (х) = 2cos х + 1 = 0.Дуги решения: 2Pi / 3, 4Pi / 3. Определите изменение g (x) от 0 до 2Pi с помощью (+) и (-) значений: x 0 2Pi / 3 4Pi / 3 2Pi ——————- ——————— —————————— ———— ———— g (x) + 0 — 0 + Шаг 4. Решить неравенство R (x) <0 алгебраическим методом. Сначала создайте таблицу знаков, в верхней строке которой указаны все значения x, полученные на шаге 3 и постепенно меняющиеся от 0 до 2Pi. Эти значения x создают различные интервалы между ними. Затем определите вариации f (x) и g (x) во второй и третьей строке таблицы, поставив + или знак внутри каждого соответствующего интервала. Simply Science — это бесплатная персонализированная платформа для обучения детей в возрасте от 6 до 12 классов на основе STEM. Мы — веб-сайт открытого обучения, который побуждает детей понимать концепции и логику в удобном для них темпе, предлагая помощь с помощью интерактивной навигации. Развивайте навыки решения проблем, творческий подход к дизайну, логику и наблюдательность, не выходя из дома, бесплатно! Наш контент создан специально для привлечения маленьких умов и их любопытства.Разделенные на темы, вы можете выбрать интересующую вас тему и просто узнать все, что вы хотели знать о ней. Упрощенный, умный и интерактивный с помощью примеров, аналогий и симуляций, Simply Science гарантирует, что вы приложите максимум усилий для мышления! Оцените свою способность обрабатывать информацию. Применяйте рассуждения и науку с помощью быстрого бесплатного теста IQ и SQ. Определите свои сильные и слабые стороны и сосредоточьтесь на своих интересах, чтобы построить свой научный коэффициент, который пробуждает ваше любопытство и облегчает изучение STEM.Наши IQ и SQ указывают на формирующую оценку по естествознанию и математике, которая может продвинуть вас вперед и раскрыть новый потенциал. Раскройте науку, математику и их загадки с помощью наших уникальных технологий, основанных на исследованиях на основе тем. Отправьтесь в новый мир с нашими темами полного погружения, наполненными забавными, увлекательными видео, викторинами и персонализированной лентой контента. В то время как формальное школьное и институциональное обучение сосредоточено на языках, когнитивном развитии и многих других вещах, Simply Science является вспомогательной идеей учебной программы, обучая учащихся в 6 и 12 классах в области естественных наук, технологий, инженерии. и математика.Благодаря междисциплинарному подходу, мероприятиям и ресурсам, ориентированным на воздействие, это идеальное занятие для молодых умов после школы. Узнавайте что-то новое каждый день, развивайте интересы и отвечайте на вопросы, которые всегда заставляли вас задуматься! Педагогика Simply Science поощряет вас исследовать, вводить новшества и применять полученные концепции в повседневной жизни, от базовых концепций до подробных бесед. Наша тематическая модель гарантирует, что тема охватывает все темы в дисциплинах, которые она затрагивает — математику, науку и технологии, биологию и химию и все, что между ними. Межотраслевое обучение с сокровищницей ресурсов — мы считаем, что каждый молодой ум должен иметь доступ к связанным и равным возможностям обучения. Наука формирует мир, она всепроникающая и преобразующая. -Pi / 2
-Pi / 2  Чтобы преобразовать тригонометрическое неравенство в базовое, учащиеся могут использовать общие алгебраические преобразования (общий множитель, полином), определения и свойства триггерных функций и триггерные тождества, наиболее необходимые.
Чтобы преобразовать тригонометрическое неравенство в базовое, учащиеся могут использовать общие алгебраические преобразования (общий множитель, полином), определения и свойства триггерных функций и триггерные тождества, наиболее необходимые.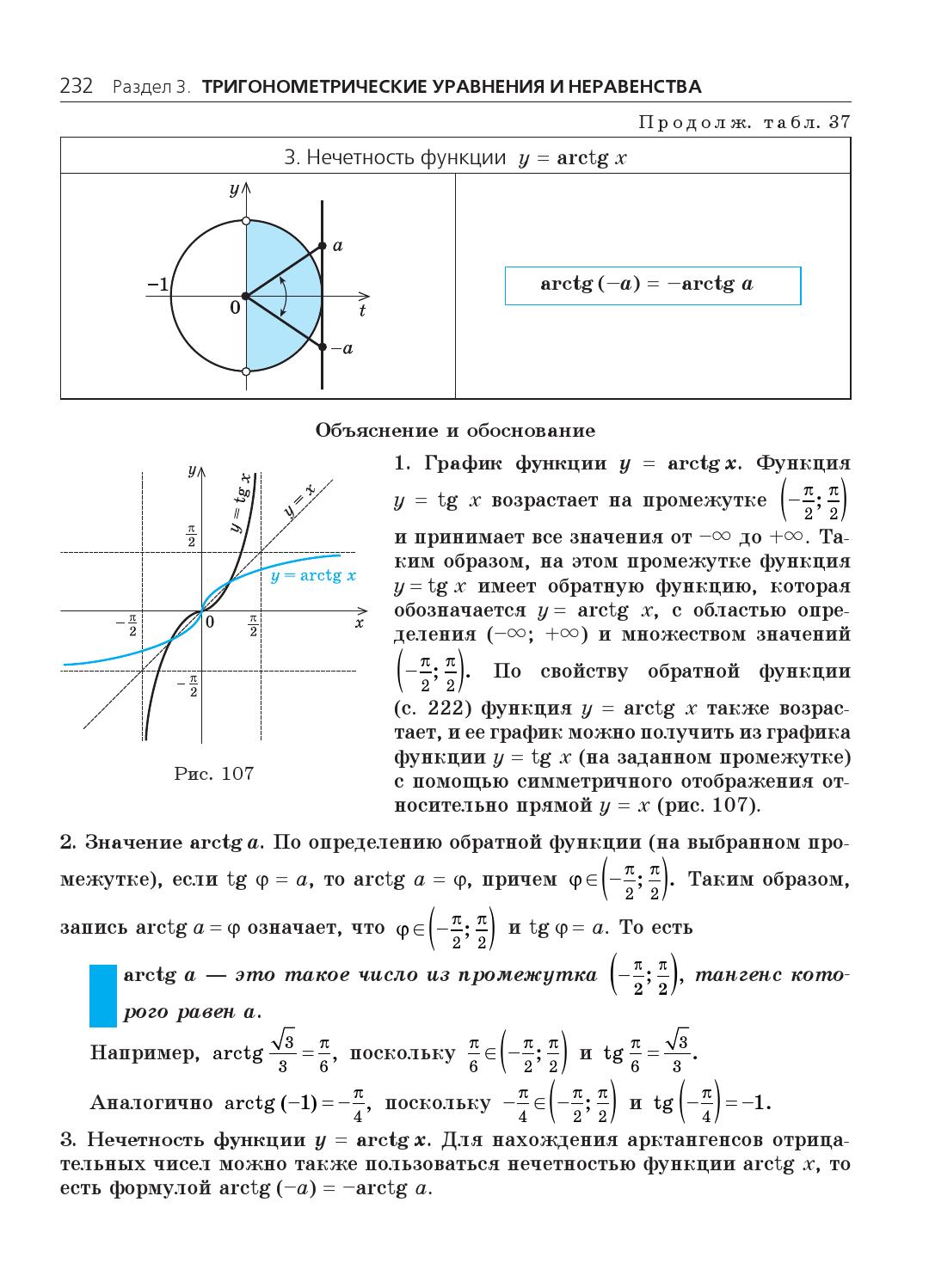 Шаг 1. Преобразуйте данное тригонометрическое неравенство к стандартному виду R (x)> 0 (или <0).Пример. Неравенство (cos 2x <2 + 3sin x) будет преобразовано в стандартную форму: R (x) = cos 2x 3sin x - 2 <0 Страница 3 из 8 Пример. Неравенство (sin x + sin 2x> — sin 3x) преобразуется в стандартную форму R (x) = sin x + sin 2x + sin 3x> 0. Шаг 2. Найдите общий период. Общий период должен быть наименьшим кратным периодам всех триггерных функций, представленных в неравенстве.
Шаг 1. Преобразуйте данное тригонометрическое неравенство к стандартному виду R (x)> 0 (или <0).Пример. Неравенство (cos 2x <2 + 3sin x) будет преобразовано в стандартную форму: R (x) = cos 2x 3sin x - 2 <0 Страница 3 из 8 Пример. Неравенство (sin x + sin 2x> — sin 3x) преобразуется в стандартную форму R (x) = sin x + sin 2x + sin 3x> 0. Шаг 2. Найдите общий период. Общий период должен быть наименьшим кратным периодам всех триггерных функций, представленных в неравенстве. Если R (x) содержит 2 или более триггерных функций, есть 2 метода, описанных ниже, для ее решения. а. МЕТОД 1. Преобразуйте R (x) в произведение многих основных тригонометрических уравнений .Затем решите эти базовые триггерные уравнения отдельно, чтобы получить все значения x, которые будут использоваться на шаге 4. Пример 8. Решите: cos x + cos 2x> — cos 3x (0
Если R (x) содержит 2 или более триггерных функций, есть 2 метода, описанных ниже, для ее решения. а. МЕТОД 1. Преобразуйте R (x) в произведение многих основных тригонометрических уравнений .Затем решите эти базовые триггерные уравнения отдельно, чтобы получить все значения x, которые будут использоваться на шаге 4. Пример 8. Решите: cos x + cos 2x> — cos 3x (0 Тригонометрические неравенства
 Одна из причин, по которой они сложнее, заключается в том, что монотонность, как у экспоненциальных функций, гораздо менее полезна, чем была. И это заменяется периодичностью. И, конечно же, как обычно в тригонометрии, вам нужно хорошо понимать все те тождества и свойства, которые, как мы знаем, имеют место для тригонометрических функций. В качестве общего принципа можно сначала рассмотреть неравенство на подходящем интервале, охватывающем период задействованных функций, а затем найти другие решения неравенства, используя периодичность.
Одна из причин, по которой они сложнее, заключается в том, что монотонность, как у экспоненциальных функций, гораздо менее полезна, чем была. И это заменяется периодичностью. И, конечно же, как обычно в тригонометрии, вам нужно хорошо понимать все те тождества и свойства, которые, как мы знаем, имеют место для тригонометрических функций. В качестве общего принципа можно сначала рассмотреть неравенство на подходящем интервале, охватывающем период задействованных функций, а затем найти другие решения неравенства, используя периодичность. Или косинус x больше 3, например, невозможен. Итак, действительно интересный случай, когда абсолютное значение альфа меньше или равно 1.
Или косинус x больше 3, например, невозможен. Итак, действительно интересный случай, когда абсолютное значение альфа меньше или равно 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ / resolve-trigonometric-inequalities.pdf / PDF4PRO
Персонализированная обучающая платформа для студентов K6-K12
Бесплатная Персонализированная обучающая платформа для студентов
Обучение на основе тем
Знайте свой IQ и SQ
Технологии позволяют обучаться
Лучшая платформа для внеклассных занятий STEM для учащихся
Комплексные темы обучения для детей от 9 до 18 лет
Интерактивный и увлекательный контент и виртуальная помощь

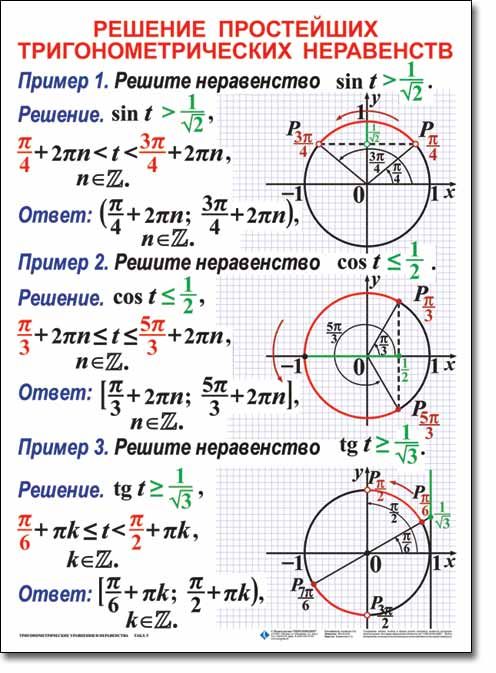 2\left(x\right)\geq0.\)
2\left(x\right)\geq0.\)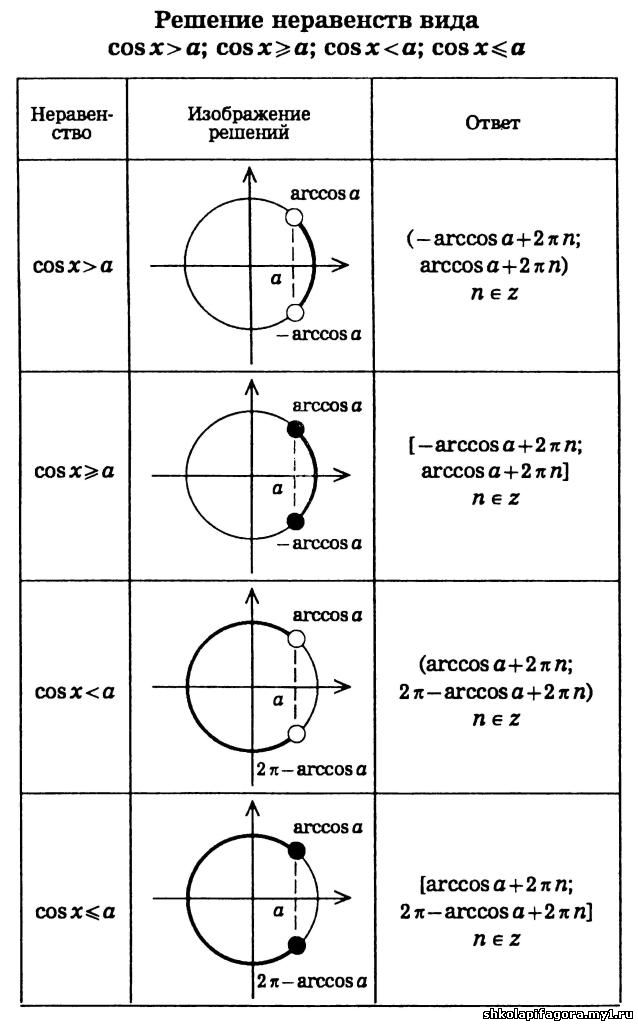
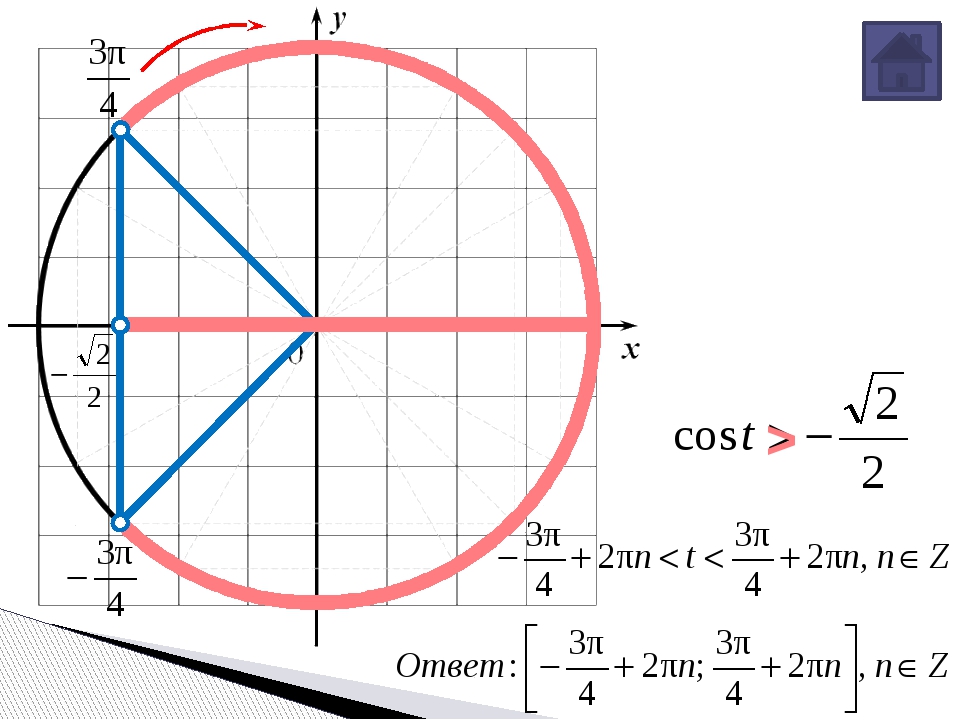 П. Карп. – М.: Просвещение, 2005. – 79 с.
П. Карп. – М.: Просвещение, 2005. – 79 с. И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с.
И. Новиков. – М.: ФИЗМАТЛИТ, 2010. – 260 с. М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с.
М. Метод интервалов в решении неравенств и исследовании функций [Текст] / Л.М. Фенько. – М.: Дрофа, 2005. – 124 с. Арккосинус числа m обозначают: .
Арккосинус числа m обозначают: .
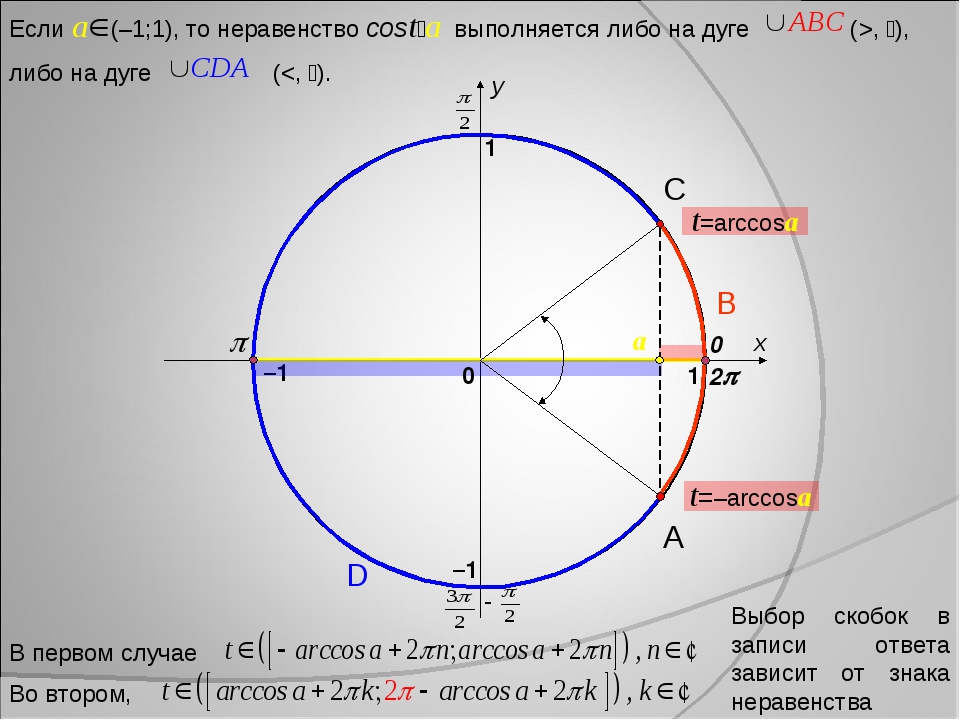

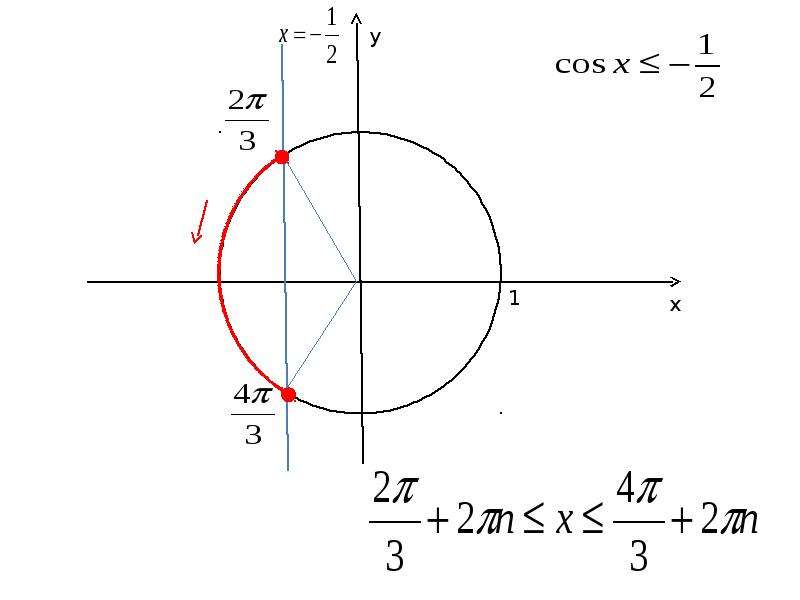
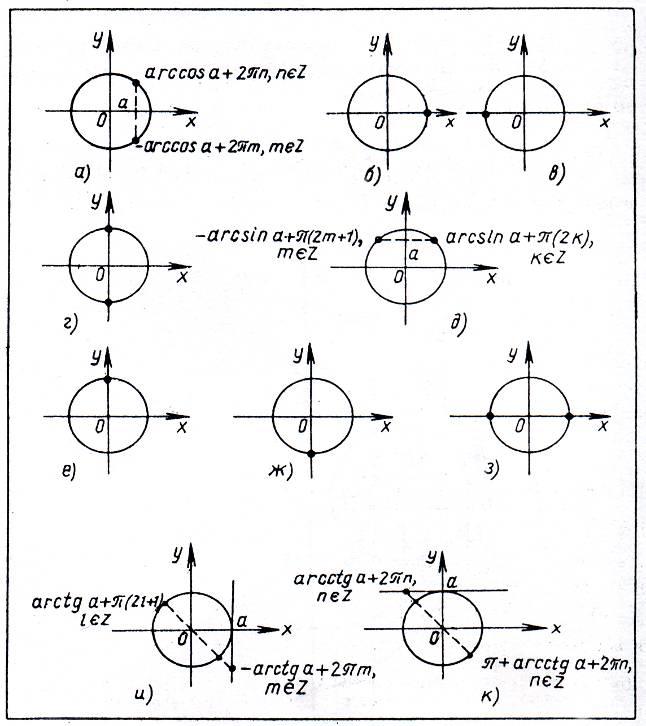

 87) + \ pi k \) для целых чисел \ (k \). Проверить,
87) + \ pi k \) для целых чисел \ (k \). Проверить, Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \).
Теперь посмотрим, где, если вообще, \ (f \) не определено, а где \ (f (x) = 0 \). Поскольку область определения \ (f \) — все действительные числа, мы можем немедленно приступить к поиску нулей \ (f \). Решая \ (f (x) = 0 \), мы имеем \ (2 \ sin (x) — 1 = 0 \) или \ (\ sin (x) = \ frac {1} {2} \). Здесь решениями являются \ (x = \ frac {\ pi} {6} + 2 \ pi k \) и \ (x = \ frac {5 \ pi} {6} + 2 \ pi k \) для целых чисел \ ( к \). Поскольку мы ограничиваем наше внимание \ ([0,2 \ pi) \), только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) нас беспокоят.Затем мы выбираем тестовые значения в \ ([0,2 \ pi) \), отличные от нулей, и определяем, является ли \ (f \) там положительным или отрицательным. Для \ (x = 0 \) имеем \ (f (0) = -1 \), для \ (x = \ frac {\ pi} {2} \) получаем \ (f \ left (\ frac {\ pi} {2} \ right) = 1 \) и для \ (x = \ pi \) получаем \ (f (\ pi) = -1 \). Поскольку наше исходное неравенство эквивалентно \ (f (x) \ leq 0 \), мы ищем, где функция отрицательна \ ((-) \) или \ (0 \), и получаем интервалы \ (\ left [0, \ frac {\ pi} {6} \ right] \ cup \ left [\ frac {5 \ pi} {6}, 2 \ pi \ right) \). Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \).
Мы можем подтвердить наш ответ графически, увидев, где график \ (y = 2 \ sin (x) \) пересекает или находится ниже графика \ (y = 1 \).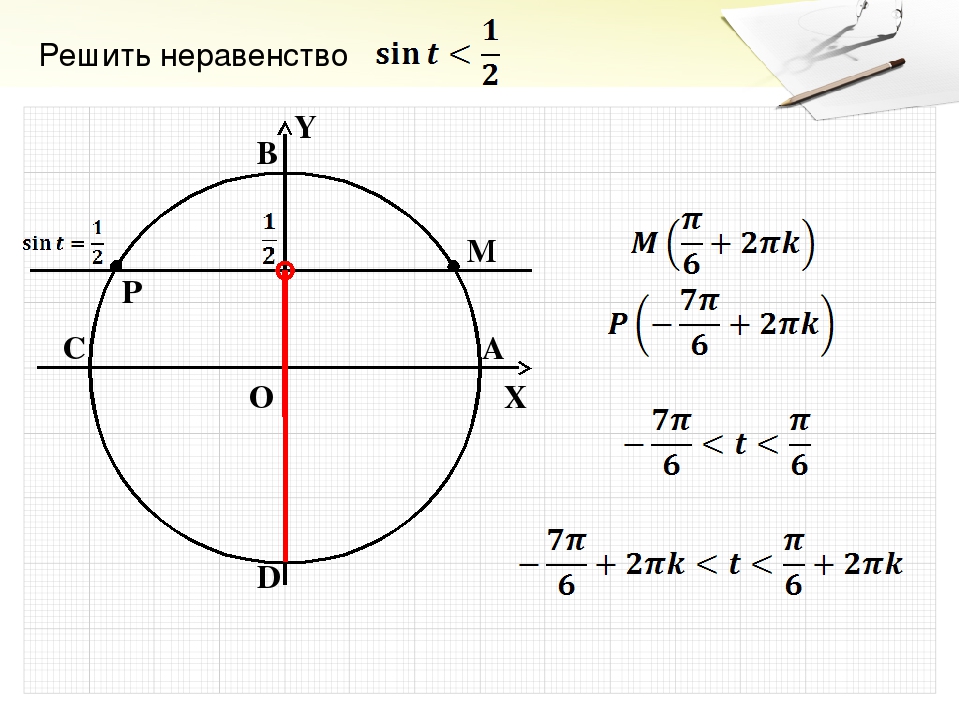 Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах.
Из них только \ (x = \ frac {\ pi} {6} \) и \ (x = \ frac {5 \ pi} {6} \) лежат в \ ([0,2 \ pi) \). Далее мы выбираем наши тестовые значения. Для \ (x = 0 \) находим \ (f (0) = -1 $; когда \ (x = \ frac {\ pi} {4} \) получаем \ (f \ left (\ frac {\ pi } {4} \ right) = 1 — \ frac {\ sqrt {2}} {2} = \ frac {2 — \ sqrt {2}} {2} $; для \ (x = \ frac {3 \ pi } {4} \) получаем \ (f \ left (\ frac {3 \ pi} {4} \ right) = -1 + \ frac {\ sqrt {2}} {2} = \ frac {\ sqrt { 2} — 2} {2} $; когда \ (x = \ pi \) имеем \ (f (\ pi) = 1 \), и, наконец, для \ (x = \ frac {7 \ pi} {4 } \) получаем \ (f \ left (\ frac {7 \ pi} {4} \ right) = -1 — \ frac {\ sqrt {2}} {2} = \ frac {-2 — \ sqrt { 2}} {2} \).Мы видим \ (f (x)> 0 \) на \ (\ left (\ frac {\ pi} {6}, \ frac {\ pi} {2} \ right) \ cup \ left (\ frac {5 \ pi} {6}, \ frac {3 \ pi} {2} \ right) \), так что это наш ответ. Мы можем использовать калькулятор, чтобы проверить, что график \ (y = \ sin (2x) \) действительно находится над графиком \ (y = \ cos (x) \) на этих интервалах.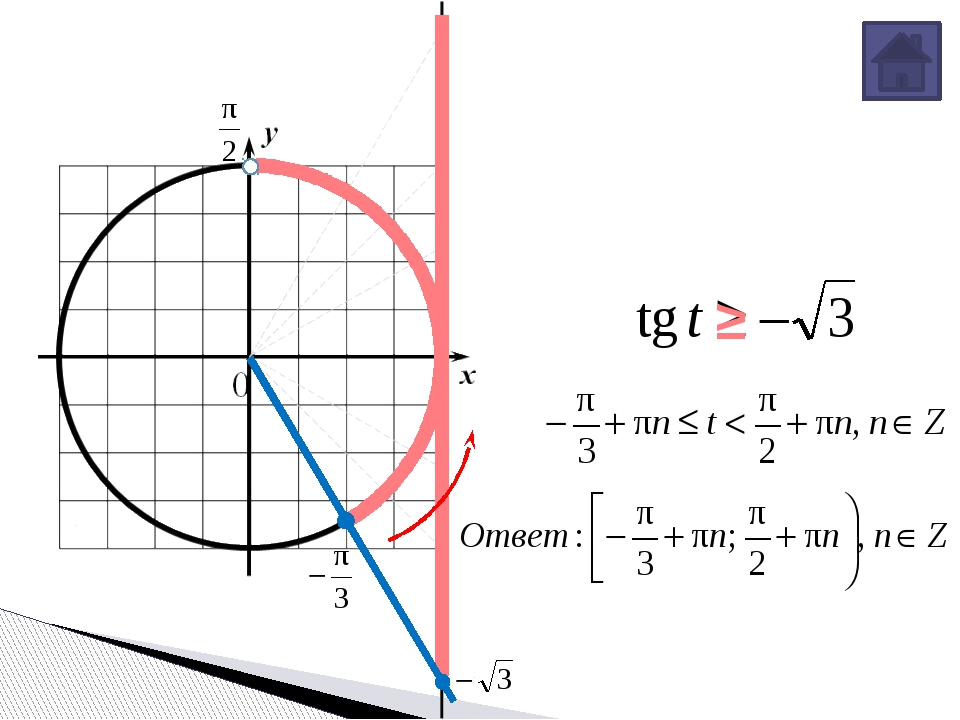
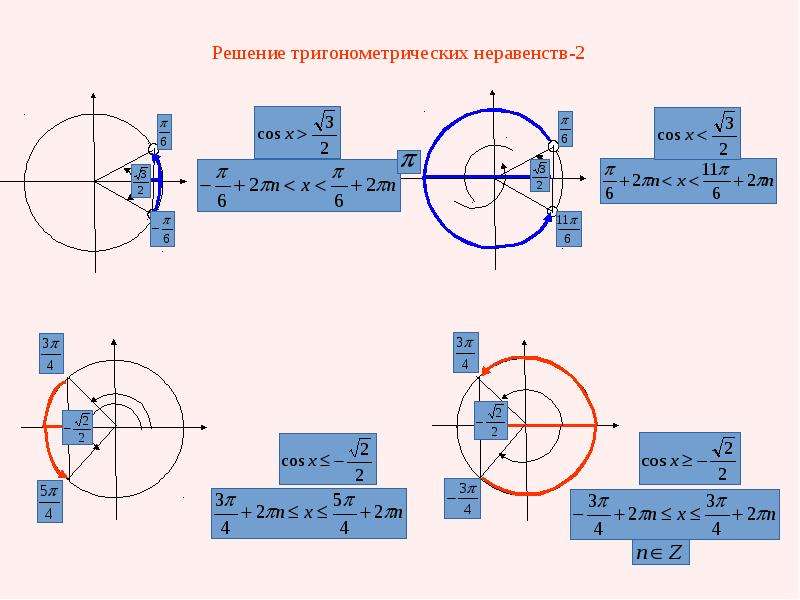 Имейте в виду, что функция арктангенса возрастает и ограничена сверху значением \ (\ frac {\ pi} {2} \). Это означает, что число \ (x = \ arctan (117) \) гарантировано \ footnote {Мы могли бы выбрать любое значение \ (\ arctan (t) \), где \ (t> 3 \).}, Чтобы оно находилось между \ (\ arctan (3) \) и \ (\ frac {\ pi} {2} \). Мы видим, что \ (f (\ arctan (117)) = \ tan (\ arctan (117)) — 3 = 114 \). В качестве следующего тестового значения мы берем \ (x = \ pi \) и находим \ (f (\ pi) = -3 \).Чтобы найти следующее тестовое значение, отметим, что, поскольку \ (\ arctan (3) <\ arctan (117) <\ frac {\ pi} {2} \), оно следует за \ footnote {\ ldots, добавляя \ (\ pi \) в силу неравенства \ ldots}, что \ (\ arctan (3) + \ pi <\ arctan (117) + \ pi <\ frac {3 \ pi} {2} \). Оценка \ (f \) в \ (x = \ arctan (117) + \ pi \) дает \ (f (\ arctan (117) + \ pi) = \ tan (\ arctan (117) + \ pi) -3 = \ загар (\ arctan (117)) - 3 = 114 \). Мы выбираем последнее тестовое значение \ (x = \ frac {7 \ pi} {4} \) и находим \ (f \ left (\ frac {7 \ pi} {4} \ right) = -4 \) .
Имейте в виду, что функция арктангенса возрастает и ограничена сверху значением \ (\ frac {\ pi} {2} \). Это означает, что число \ (x = \ arctan (117) \) гарантировано \ footnote {Мы могли бы выбрать любое значение \ (\ arctan (t) \), где \ (t> 3 \).}, Чтобы оно находилось между \ (\ arctan (3) \) и \ (\ frac {\ pi} {2} \). Мы видим, что \ (f (\ arctan (117)) = \ tan (\ arctan (117)) — 3 = 114 \). В качестве следующего тестового значения мы берем \ (x = \ pi \) и находим \ (f (\ pi) = -3 \).Чтобы найти следующее тестовое значение, отметим, что, поскольку \ (\ arctan (3) <\ arctan (117) <\ frac {\ pi} {2} \), оно следует за \ footnote {\ ldots, добавляя \ (\ pi \) в силу неравенства \ ldots}, что \ (\ arctan (3) + \ pi <\ arctan (117) + \ pi <\ frac {3 \ pi} {2} \). Оценка \ (f \) в \ (x = \ arctan (117) + \ pi \) дает \ (f (\ arctan (117) + \ pi) = \ tan (\ arctan (117) + \ pi) -3 = \ загар (\ arctan (117)) - 3 = 114 \). Мы выбираем последнее тестовое значение \ (x = \ frac {7 \ pi} {4} \) и находим \ (f \ left (\ frac {7 \ pi} {4} \ right) = -4 \) .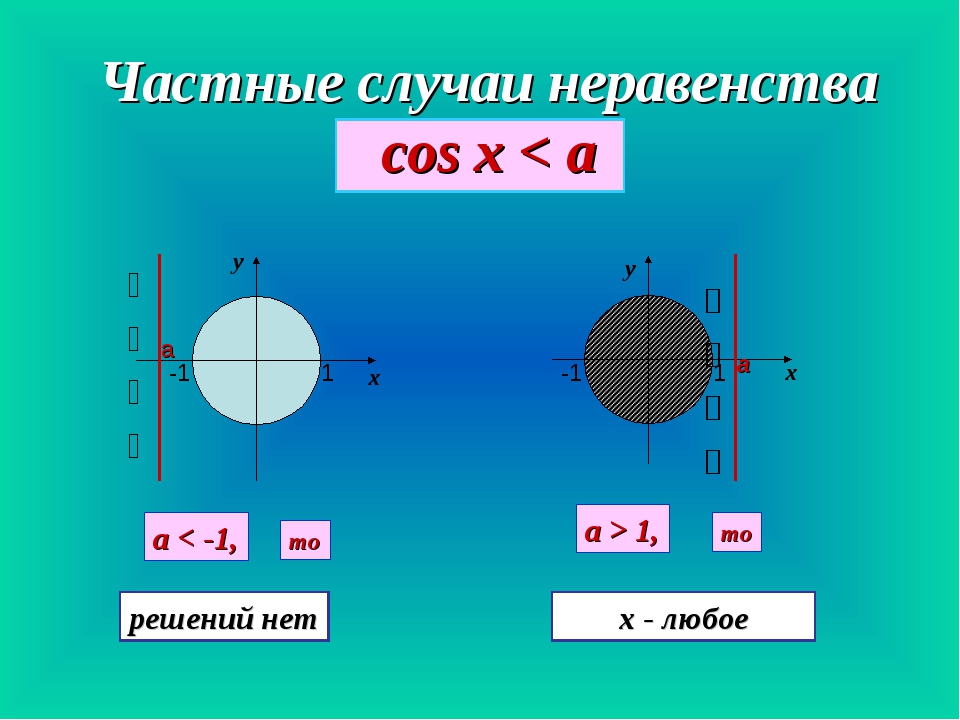 {2} (x) = \ tan (x) + 3 \)
{2} (x) = \ tan (x) + 3 \)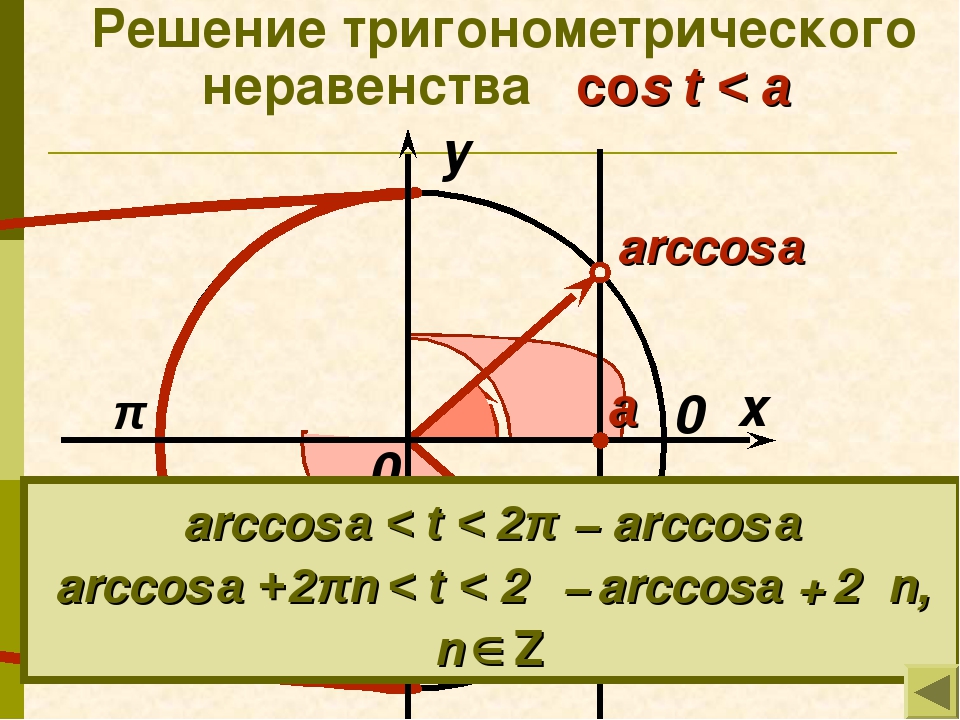 Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это.
Решение \ (\ sin (4x) = 0 \) дает \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \), а решение \ (\ sin (x) = 0 \) — \ (x = \ pi k \) для целых чисел \ (k \). Второй набор решений содержится в первом наборе решений, \ footnote {Как всегда, если есть сомнения, запишите его!}, Поэтому наше окончательное решение для \ (\ cos (5x) = \ cos (3x) \) будет \ (x = \ frac {\ pi} {4} k \) для целых чисел \ (k \). Есть восемь из этих ответов, которые лежат в \ ([0,2 \ pi) \): \ (x = 0 \), \ (\ frac {\ pi} {4} \), \ (\ frac {\ pi } {2} \), \ (\ frac {3 \ pi} {4} \), \ (\ pi \), \ (\ frac {5 \ pi} {4} \), \ (\ frac {3 \ pi} {2} \) и \ (\ frac {7 \ pi} {4} \).Наш график графиков \ (y = \ cos (3x) \) и \ (y = \ cos (5x) \) ниже (после некоторого осторожного увеличения) подтверждает это. Использование тождества \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \) делает все аргументы одинаковыми, и мы действуем так же, как и при решении любого нелинейного уравнения — собираем все ненулевые члены на одна сторона уравнения и фактор.
Использование тождества \ (\ sin (2x) = 2 \ sin (x) \ cos (x) \) делает все аргументы одинаковыми, и мы действуем так же, как и при решении любого нелинейного уравнения — собираем все ненулевые члены на одна сторона уравнения и фактор.
 Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.
Только одно из этих решений, \ (x = \ frac {5 \ pi} {3} \), которое соответствует \ (k = 1 \), лежит в \ ([0,2 \ pi) \). Геометрически мы видим, что \ (y = \ cos (x) — \ sqrt {3} \ sin (x) \) и \ (y = 2 \) пересекаются только один раз, что подтверждает наш ответ.