Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
⇐ ПредыдущаяСтр 2 из 8Следующая ⇒
Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, в которой в каждый конъюнктивный одночлен каждая переменная из набора входит ровно один раз, причем входит либо сама либо ее отрицание .
Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, можно определить так:
Совершенной дизъюнктивной нормальной формой (СДНФ) формулы алгебры высказываний называется ее ДНФ, обладающая следующими свойствами:
1. ДНФ не содержит двух одинаковых конъюнкций.
2. Ни одна конъюнкция не содержит одновременно двух одинаковых переменных.
3. Ни одна конъюнкция не содержит одновременно некоторую переменную и ее отрицание.
4. Каждая конъюнкция содержит либо переменную , либо ее отрицание для всех переменных, входящих в формулу.
Конструктивно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить так:
Совершенной конъюнктивной нормальной формой (СКНФ) данной формулы алгебры высказываний называется такая ее КНФ, которая удовлетворяет следующим свойствам:
1. КНФ не содержит двух одинаковых дизъюнкций.
2. Ни одна из дизъюнкций не содержит одновременно двух одинаковых переменных.
3. Ни одна из дизъюнкций не содержит одновременно некоторую переменную и ее отрицание.
4. Каждая дизъюнкция СКНФ содержит либо переменную ,либо ее отрицание xiдля всех переменных, входящих в формулу.
Сформулируем следующие теоремы:
Теорема 1.Произвольную булеву функцию можно задать формулой , где дизъюнкция берётся по всем , где и
Теорема 2.Произвольную булеву функцию можно задать формулой , где конъюнкция берётся по всем , где и
Эти формулы называются соответственно совершенной дизъюнктивной нормальной формой или совершенной конъюнктивной нормальной формой булевой функции . Исходя из таблицы истинности булевой функции, можно построить СДНФ функции: для каждого набора , такого, что , составляется конъюнкция , а затем все эти конъюнкции соединяем знаком дизъюнкции.
Для построения СКНФ функции выписываем наборы такие, что . Для такого набора составляется дизъюнкция
,
а затем все такие дизъюнкции соединяют знаком конъюнкции.
Приведенные формулы позволяют сформулировать следующие утверждения:
1. Каждая булева функция от п переменных, отличная от константы 0, имеет единственную СДНФ.
2. Каждая булева функция от п переменных, отличная от константы 1, имеет единственную СКНФ.
Многочлены Жегалкина
Согласно сформулированным утверждениям, можно говорить, что система булевых функций полна. Тогда любую булеву функцию можно представить в виде многочлена от своих переменных и такой многочлен называется многочленом Жегалкина.
Многочленом Жегалкинаназывается многочлен, являющийся суммой константы и различных одночленов, в которые каждая из переменных входит не выше, чем в первой степени.
Многочлен Жегалкина константы равен самой же константе; многочлен Жегалкина булевой функции одной переменной ;многочлен Жегалкина булевой функции двух переменных
многочлен Жегалкина булевой функции трех переменных
и т. д. Коэффициенты и свободный член принимают значения 0 или 1, а число слагаемых в формуле равно 2п, где п — число переменных. Знак ⊕ — сумма Жегалкина или сумма по модулю два.
Теорема 3 (Жегалкина).Каждая булева функция может быть представлена в виде многочлена Жегалкина и притом единственным образом, с точностью до порядка слагаемых.
Сформулируем алгоритм построения многочлена Жегалкина.
Выше было указано, что любую функцию, отличную от константы 0, можно представить в виде СДНФ. Если сравним таблицы истинности дизъюнкции и суммы по модулю два, видим, что они отличаются только последней строкой, т. е. на наборе 11. Так как в СДНФ на каждом наборе только одна конъюнкция равна 1, то все дизъюнкции можно заменить суммами по модулю два. Кроме того, известно, что . На этом и основан первый алгоритм построения многочлена Жегалкина:
1. Находим множество тех двоичных наборов, на которых функция принимает значение 1.
2. Составляем СДНФ.
3. В СДНФ каждый знак дизъюнкции меняем на знак суммы Жегалкина.
4. Упрощаем, если можно, полученное выражение, используя тождество .
5. В полученной формуле каждое отрицание заменяем на .
6. Раскрываем скобки в полученной формуле, содержащей только функции ∧ и ⊕ и константу 1.
7. Приводим подобные члены, используя тождество .
Используя метод неопределенных коэффициентов, получаем второй алгоритм определения многочлена Жегалкина: составляем систему линейных уравнений относительно 2пнеизвестных коэффициентов, содержащую 2пуравнений, решением которой являются коэффициенты многочлена Жегалкина.
Многочлен Жегалкина называется нелинейным,если он содержит конъюнкции переменных, а если он не содержит конъюнкции переменных, то он называется линейным.
Функция называется линейной, если ее многочлен Жегалкина имеет вид , и нелинейной в противном случае.
Из определения многочлена Жегалкина следует, что для любой булевой функции коэффициенты при переменных и свободный член вычисляются по формулам:
На этом основан алгоритм определения линейности (или нелинейности) булевой функции.
1. По таблицам истинности булевой функции и выше указанным формулам находим коэффициенты:
2. Выписываем многочлен и проверяем, задаёт ли он эту функцию. Для этого строим таблицу истинности многочлена и сравниваем её с таблицей истинности функции .
Если таблицы истинности совпадают, то функция линейная и – её многочлен Жегалкина. В противном случае функция нелинейна.
МНОЖЕСТВА И ОТОБРАЖЕНИЯ
Понятие множества
Любое понятие дискретной математики можно определить с помощью понятия множества. Под множеством понимают объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью. Таково интуитивное определение понятия множества, данное основателем теории множеств Георгом Кантором. Это понятие в математике является первичным и, следовательно, не имеет строгого определения. Объекты, составляющие множество, будем называть его элементами. Множества будем обозначать прописными буквами латинского алфавита: А, В, С,…, а элементы множеств — строчными буквами а, b, с,…. Основное отношение между элементом а и содержащим его множеством
2.2. Способы задания множеств
Имеется два существенно различных способа задания множеств. Можно либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект, либо дать полный перечень элементов этого множества.
Первый способ мы назовем описанием множества, а второй способ — перечислением множества. Например, обозначение читается: «элементы множества U, обладающие свойством α» — это описание множества. Элементы перечисляемого множества принято заключать в скобки: {1, 2, 3,… } — множество натуральных чисел; {2, 4, 6,… } — множество четных чисел. Под многоточием в первом случае подразумеваются все последующие натуральные числа, а во втором — четные.
Нас часто будут интересовать множества логических возможностей, потому что анализ таких множеств часто играет основную роль при решении той или иной проблемы.
Подмножества
Множество, состоящее из некоторых элементов другого множества, называется подмножеством этого последнего множества. С целью изучения всех подмножеств данного множества введем следующую терминологию. Исходное множество будем называть универсальным множеством; подмножества, содержащие один элемент, будем называть единичными множествами;
В качестве примера возьмем универсальное множество U, состоящее из трех элементов {а,b,с}. Собственные подмножества U — это множества, которые содержат некоторые, но не все элементы U. Этими подмножествами являются три множества из двух элементов {а, b}, {а, с}, {b, с} и три единичных множества {а}, {b}, {с}.
Будем считать подмножеством множества U и пустое множество 0, не содержащее элементов U.
Другими словами, множество А называется подмножеством множества В (обозначаем А ⊂ В), если все элементы множества А принадлежат В. Это означает справедливость следующего утверждения: для любого элемента а, если а ∊ А, то а ∊ В при условии А ⊂ В. Будем говорить также, что множество А содержится в Bили имеется включение множества А в B. Множества А и В называются равными или совпадающими (обозначается А = В), если они состоят из одних и тех же элементов, т. е. если А ⊂ В и
В ⊂ А. Таким образом, чтобы доказать равенство множеств, требуется установить два включения.
Операции над множествами
В первой главе были рассмотрены способы, которыми из данных высказываний могут быть образованы новые высказывания. Теперь мы будем рассматривать аналогичный процесс — образование новых множеств из данных множеств. Мы будем предполагать, что каждое из множеств, которое мы используем в этом процессе, является подмножеством некоторого универсального множества, и будем требовать, чтобы вновь образованное множество было подмножеством того же самого универсального множества. Как и всегда, мы можем задавать вновь образованное множество или путем описания, или путем перечисления.
Следует провести аналогию между логическими операциями и операциями над множествами.
| Отрицание | Дополнение |
| Конъюнкция | Пересечение |
| Дизъюнкция | Объединение |
| Импликация | Разность |
Чтобы нагляднее представить эти операции, изобразим их на диаграмме, называемой диаграммой Эйлера-Венна. Пусть прямоугольник обозначает универсальное множество, а круги внутри прямоугольника — подмножества.
Чтобы нагляднее представить эти операции, изобразим их на диаграмме, называемой диаграммой Эйлера-Венна. Пусть прямоугольник обозначает универсальное множество, а круги внутри прямоугольника — подмножества.
Дополнениемк множеству А называется множество элементов, которые не содержатся в А. Обозначают его и читают «дополнение множества А к U».
Пересечениеммножеств A и В называется множество элементов, принадлежащих и А и В. Обозначают A∩Bи читают «пересечение А и B».
Если А и В — непустые множества, пересечение которых пусто, т. е. A∩B=Ø, то их называют непересекающимися множествами.
Объединениеммножестве и В называется множество элементов, принадлежащих либо А, либо В (либо обоим). Обозначают A ∪ В и читают «объединение А и В».
Разностьюмножестве и В называется множество элементов, принадлежащих А и не принадлежащих В. Обозначают A\B ичитают «разность Aи B».
Рекомендуемые страницы:
lektsia.com
4.2. Конъюнктивная нормальная форма. Совершенная конъюнктивная нормальная форма.
Определение 5. Дизъюнкция
(4.2)
называется элементарной дизъюнкцией или дизъюнктом.
Как и в случае конъюнктов, существует 2n различных элементарных дизюъюнкций от n переменных. При этом значение элементарной дизюъюнкции вида (4.2) равно 0 тогда и только тогда, когда xi=1i для всех i=1, 2, …, n.
Конъюнкция вида (4.1) называется также конституентой нуля.
Определение 6. Конъюнктивной нормальной формой формулы А (КНФА) называется равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций.
Пример 4.2. Для
формулы А= (
( у)
имеем, например, КНФА~ху.
у)
имеем, например, КНФА~ху.
Как и в случае ДНФ, КНФ формулы неединствен. Их можно составить сколько угодно. К КНФ формулы можно прийти по следующему алгоритму:
I шаг: Приведение операций |, , , , к операциям &, или их отрицаниям:
1. Если в формуле участвуют операции |, , и , то от них с помощью операции отрицания переходим к отрицанию соответственно конъюнкций, дизъюнкций или эквиваленций.
2. Если в формуле участвует операция , то от неё с помощью закона т) упражнения 3.2 переходим к операции .
3. Если в формуле участвует операция , то от неё с помощью закона п) упражнения 3.2 преходим к операции .
II шаг. Отнесение отрицаний к пропозициональным переменным.
4. Если в формуле участвуют отрицания конъюнкций или дизъюнкций, то с помощью законов де Моргана отрицания приводим к пропозициональным переменным.
5. Если в формуле участвует двойное отрицание, то с помощью закона снятия двойного отрицания они убираются.
III шаг. Получение КНФ.
С помощью свойства дистрибутивности относительно & все подформулы вида A(B1&B2&…&Bk) приводим к подформулам вида (AB1)&(AB2)&…&(ABk) до тех пор, пока не получим конъюнкцию элементарных дизъюнкций.
Таким образом, мы доказали, что любая формула эквивалентна некоторой КНФ.
Очевидно, А&А&…&А~А, и поэтому в КНФ элементарная дизъюнкция может повторяться сколько угодно раз. В результате мы приходим к тому, КНФ формулы можно построить сколько угодно.
Потребуем, чтобы КНФ удовлетворяла следующим четырём свойствам совершенства:
1. Каждый дизъюнкт КНФ формулы содержит все переменные или их отрицания, входящие в формулу.
2. Все дизъюнкты, входящие в КНФ, различны.
3. Ни один дизъюнкт, из которых состоит КНФ, не содержит одновременно переменную и её отрицание.
4. Ни один дизъюнкт не содержит одну же литеру два и более раз.
Определение 7. КНФ формулы, удовлетворяющей всем условиям совершенства, называется совершенной конъюнктивной нормальной формой данной формулы (СКНФ).
Для того, чтобы получить СКНФ формулы А, достаточно сначала формулу привести к КНФА, а затем применить к полученной КНФ эквивалентные преобразования следующих видов, позволяющие последовательно получать эквивалентную КНФА, удовлетворяющие всем условиям совершенства:
1. Если в КНФА какой-либо дизъюнкт В не содержит переменную хi или её отрицание, то используя
равносильности B~В(хi&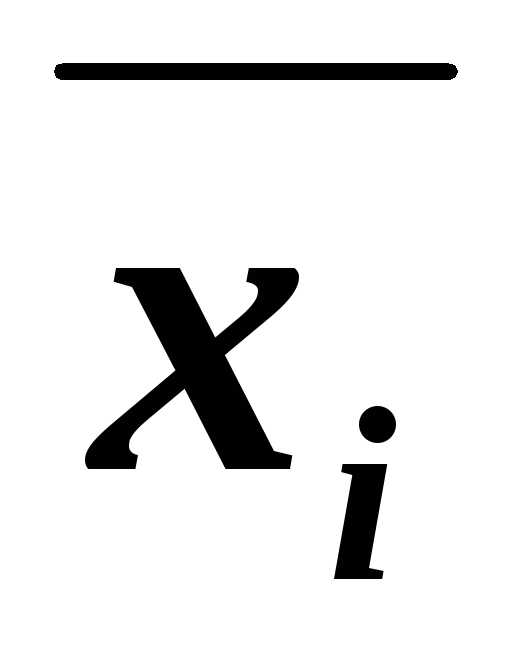 )~
~(Вхi)&(B
)~
~(Вхi)&(B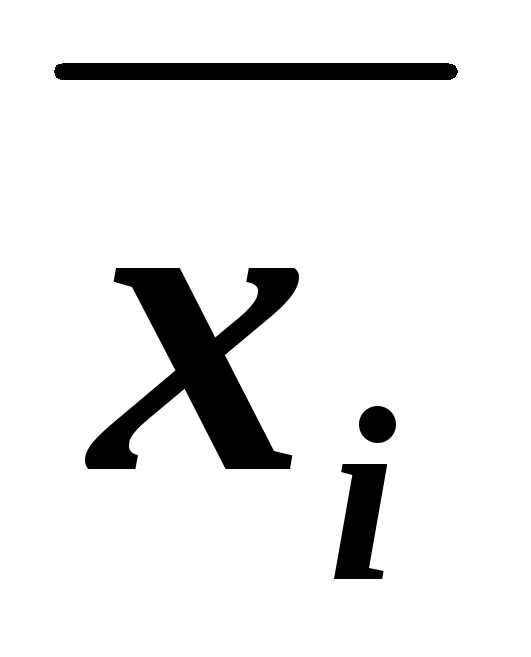 ),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B
),
дизъюнктВ заменяем на два дизъюнкта (Вхi)
и (B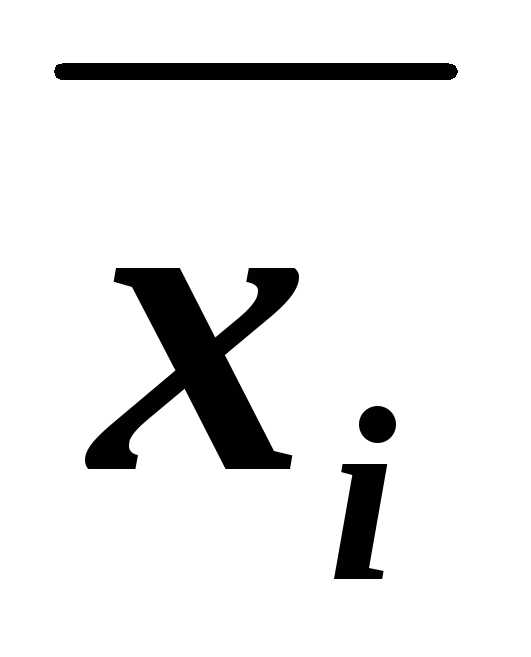 ),
каждая из которых содержитхi или её отрицание
),
каждая из которых содержитхi или её отрицание 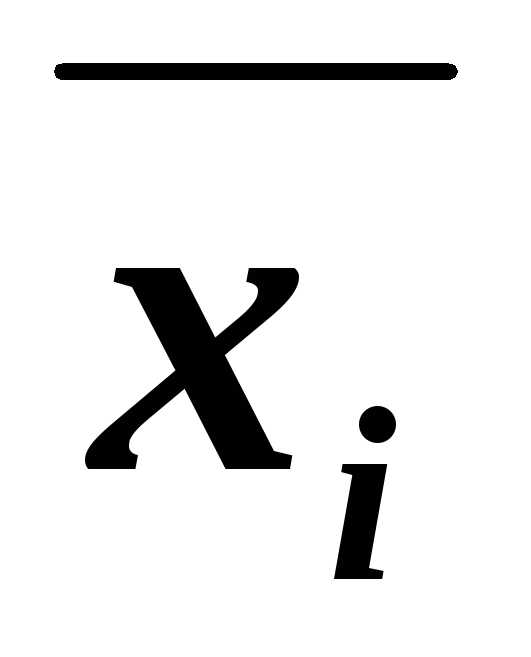 .
.
2. Если в КНФА входят два или более одинаковых дизъюнкта B, то лишние отбрасываем, пользуясь равносильностью B&B&…&B~B.
3. Если некоторый
дизъюнкт В,
входящий в КНФА,
содержит переменную хi и её отрицание 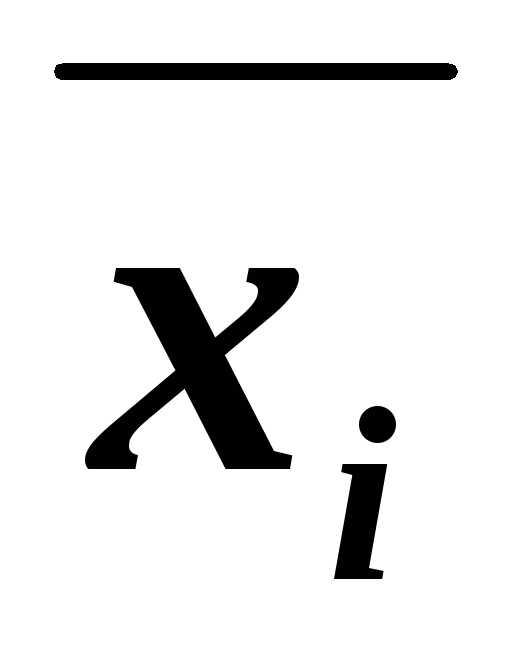 ,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
,
тоВ~1,
и в силу эквивалентности C&1~C, В исключаем из КНФА.
4. Если некоторый
дизъюнкт, входящий в КНФА,
содержит одну и ту же литеру 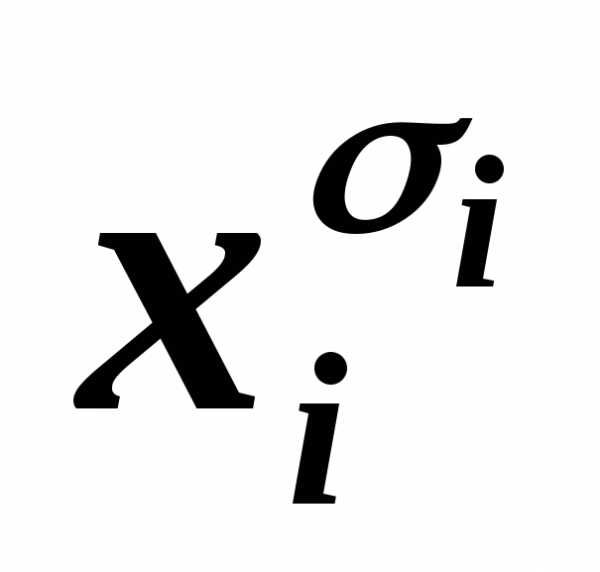 дважды или более, то, пользуясь
равносильностью
дважды или более, то, пользуясь
равносильностью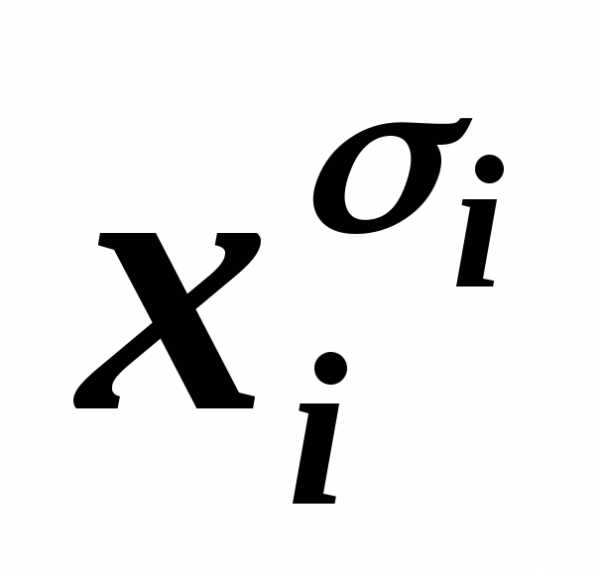
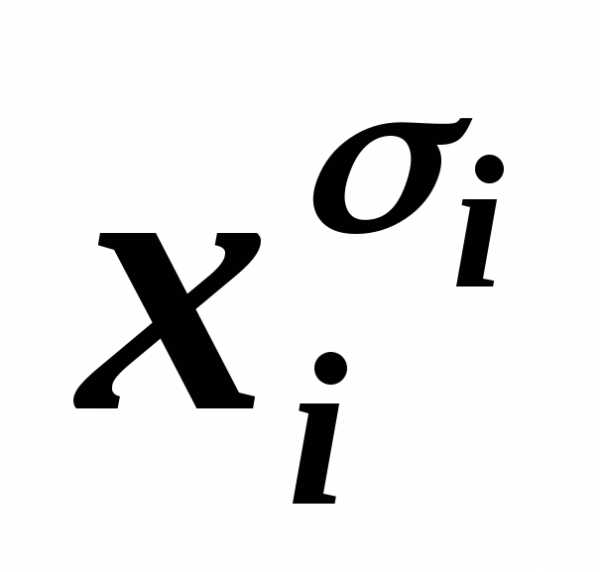 …
…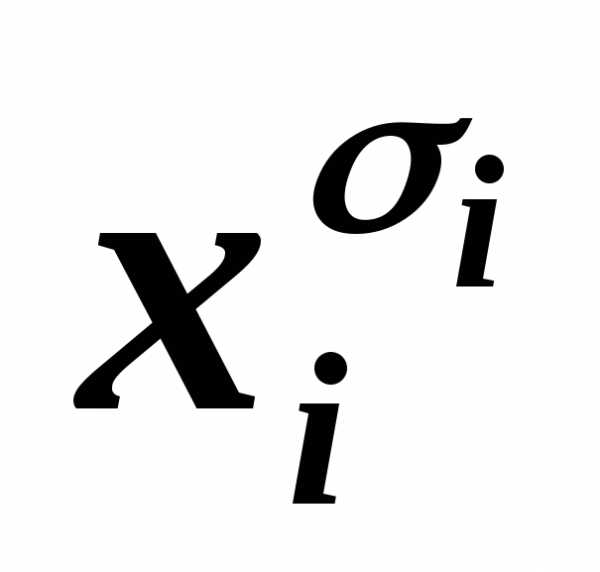 ~
~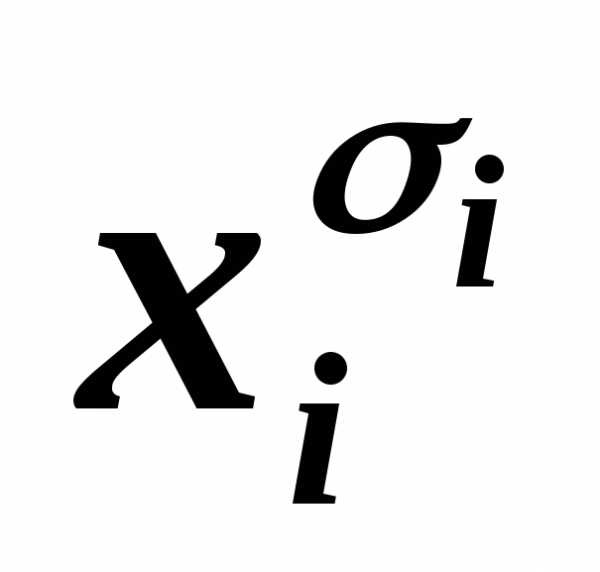 ,
лишние отбрасываем.
,
лишние отбрасываем.
Упражнение 4.3.С помощью эквивалентных преобразований привести формулы упражнения 3.4 к СКНФ.
Решение. з) Приведём формулу к КНФ:
(x| )(z
)(z )
) (
( )(z
)(z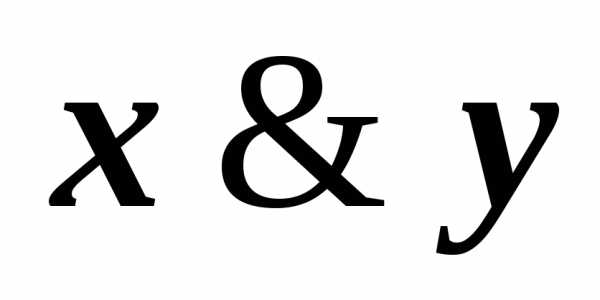 )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)
 (x&
(x& )
) (x&
(x& )
)
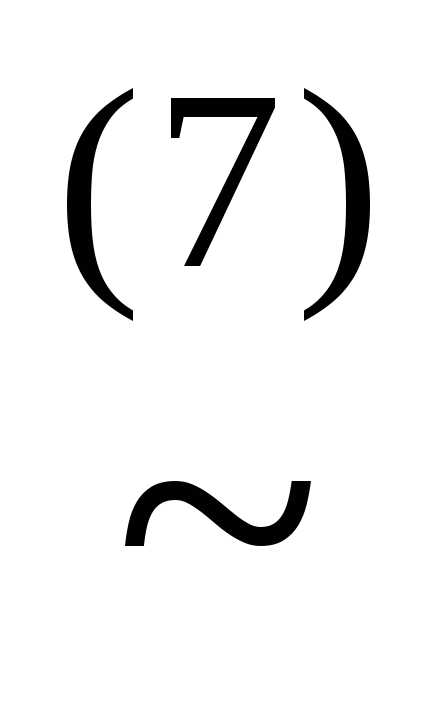 (x&
(x& )(
)( (x&
(x& ))
))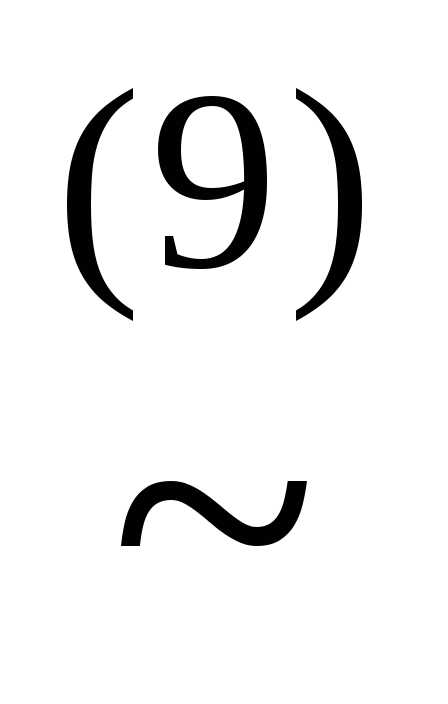
 (x&(
(x&(
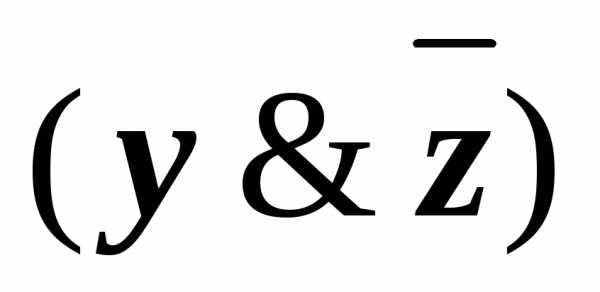 )))
)))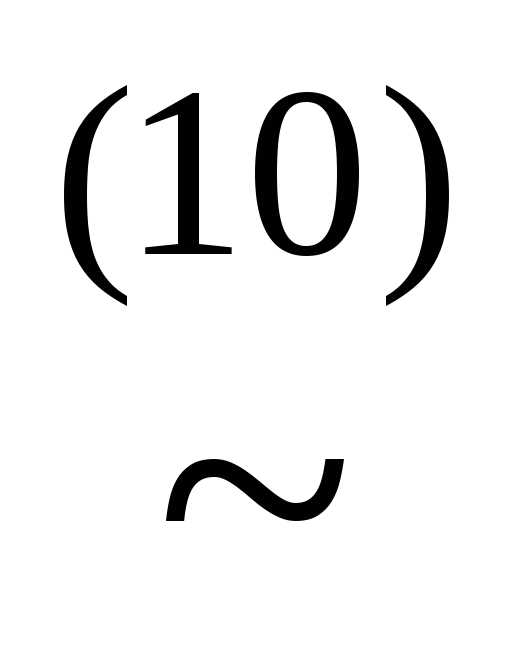 (x&((
(x&(( у)&
у)&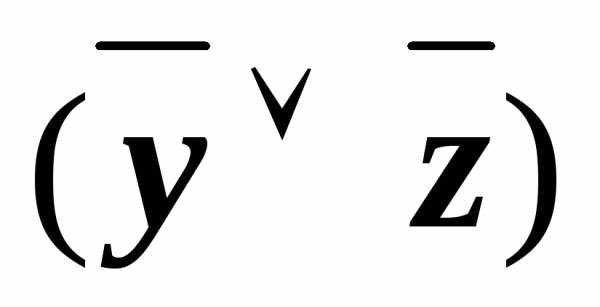 )))
)))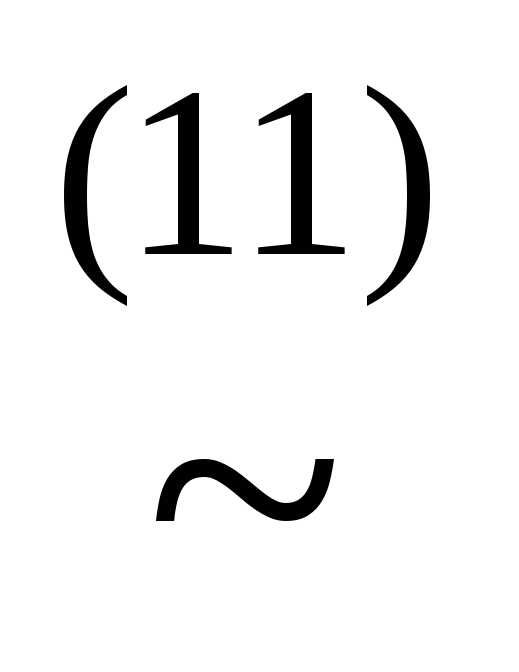
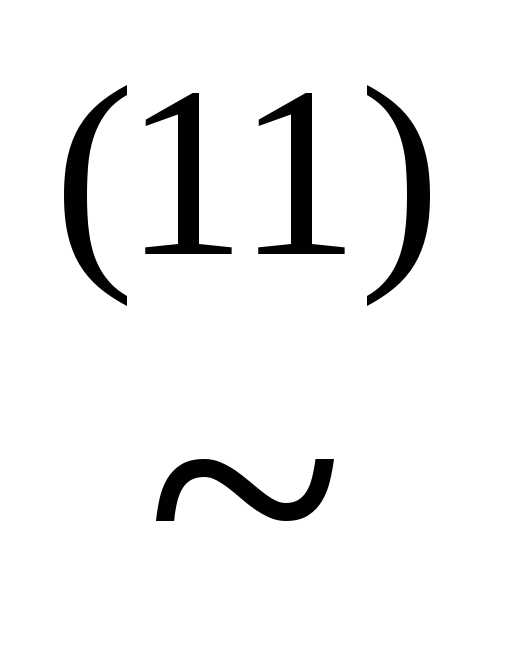 (x&
(x&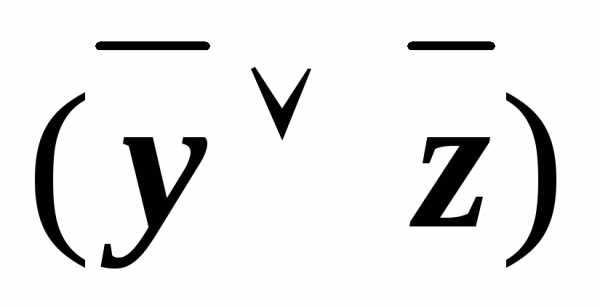 ))
)) (xz)&
(xz)& &&
&&
 (xz)&
(xz)&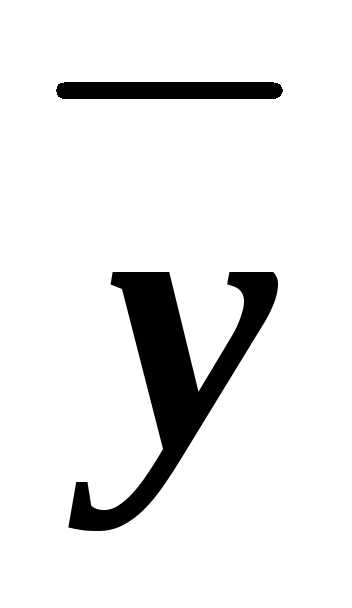 &
&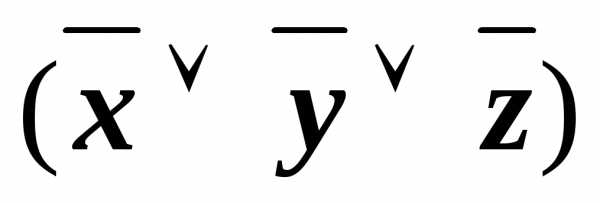

Получили КНФ формулы. Теперь преобразуем КНФ по алгоритму получения всех условий совершенства:
 (xyz)&(x
(xyz)&(x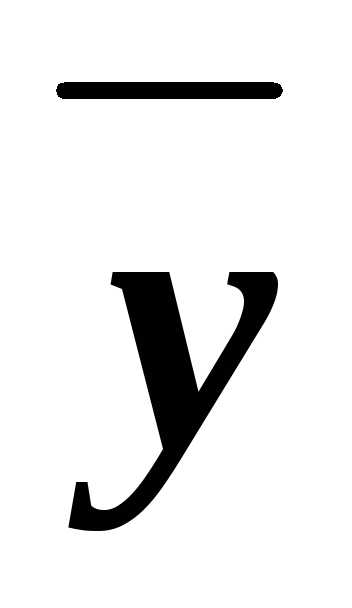 z)&(x
z)&(x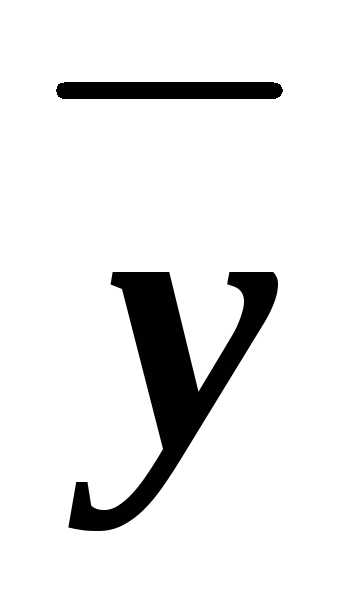 )&
)&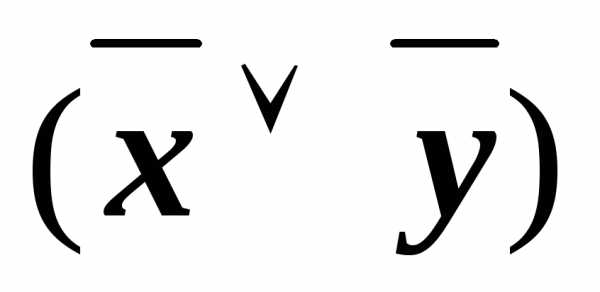 &
&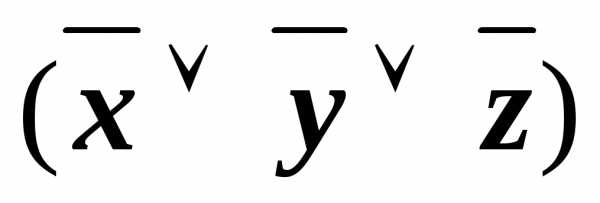

 (xyz)&(x
(xyz)&(x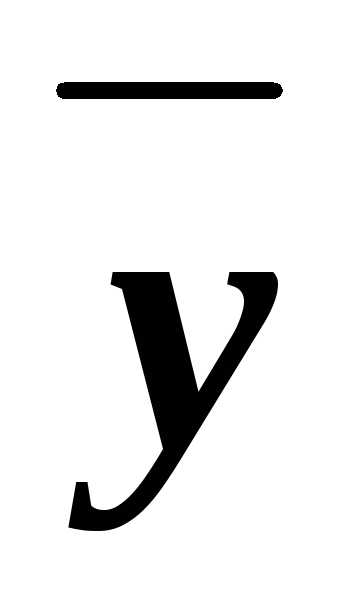 z)&(x
z)&(x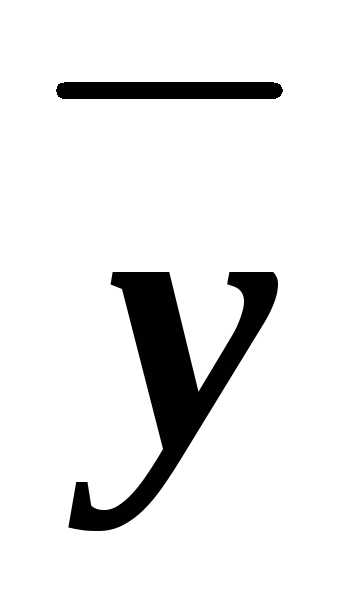 z)&(x
z)&(x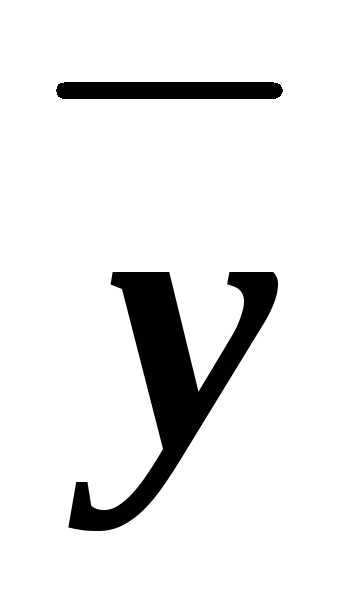
 )&
)&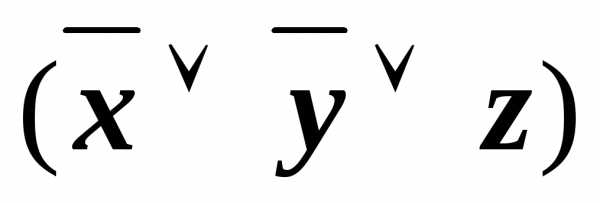 &
&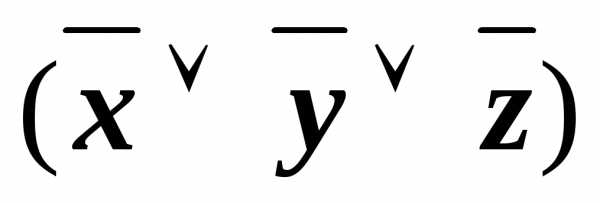 &
&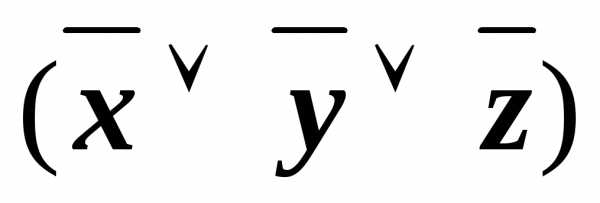
 (xyz)&(x
(xyz)&(x z)&(x
z)&(x
 )&
)&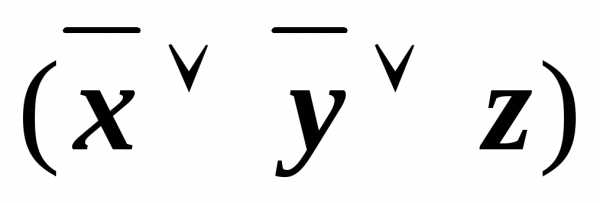 &
&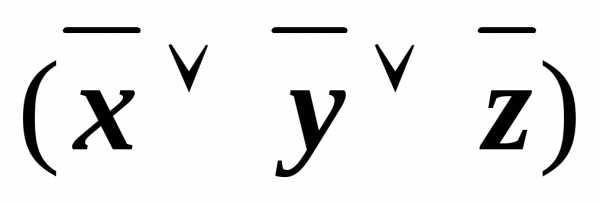
(1) Одновременно заменили | на отрицание операции &,и на отрицание.
(2) Одновременно применили закон двойного отрицания и заменили наи его отрицание.
(3) Операцию заменили на.
(4) Применили закон де Моргана.
(5) Заменили на.
(6), (7) Одновременно применили законы де Моргана и снятия двойного отрицания.
(8) Воспользовались ассоциативностью и коммутативностью .
(9) 1-й и 2-й конъюнкты объединили в один с помощью дистрибутивности & относительно .
(10) К подформуле 
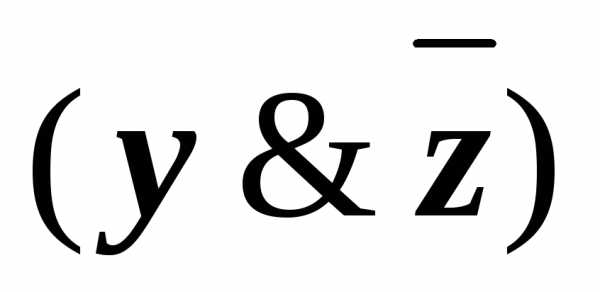 применили закон дистрибутивности.
применили закон дистрибутивности.
(11) Воспользовались тем, что  у~1.
у~1.
(12) Применили сложную дизъюнкцию относительно .
(13) Применили законы исключённого третьего и идемпотентности.
(14) В 1-й и 2-й дизъюнкты добавили недостающие литеры и разбили их по два дизъюнкта каждую (1-я операция приведения к СКНФ).
(15) Операцию, аналогичную (14) проделали с 3-м и 4-м дизъюнктами.
(16) Опустили лишние дизъюнкты.
СДНФ формулы существует и единственна.
Существование СКНФ для любой формулы вытекает из алгоритма её построения.
Другой способ построения СКНФА основывается на следующей эквиваленции:
A(х1, х2,
…, хn)~ .
.
Другими словами,
формула A(х1, х2,
…, хn)
в своей СДНФ содержит те и только те
конъюнкты вида (4.2), значения которых
равны 0 при xi=1i для всех i=1,
2, …, n.
Например, для формулы А= (
( у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х
у),
состоящей из двух переменных, можно
составить всевозможные конъюнкты ху, х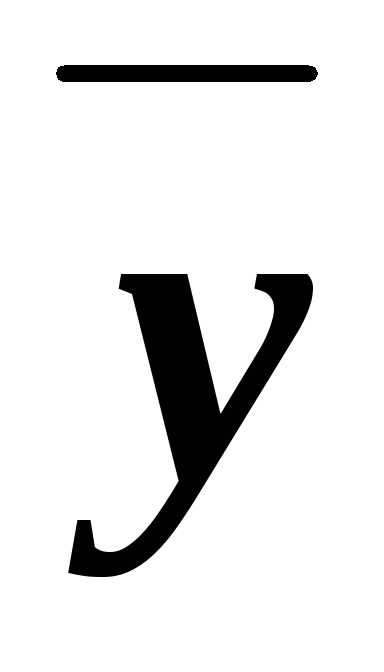 ,
,  у и
у и 
 .
Из них значение 0 принимают только
.
Из них значение 0 принимают только 
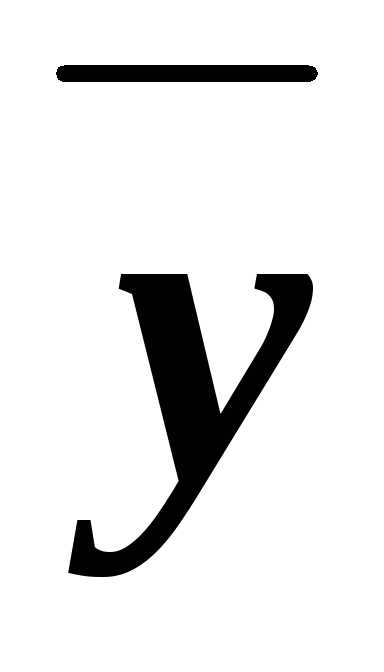 при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
при наборе
(х, у)=(0, 0),
(что можно проверить, непосредственно
составив таблицу истинности). Поэтому,
СКНФА~ху.
Таким образом,
СКНФA(х1, х2,
…, хn)=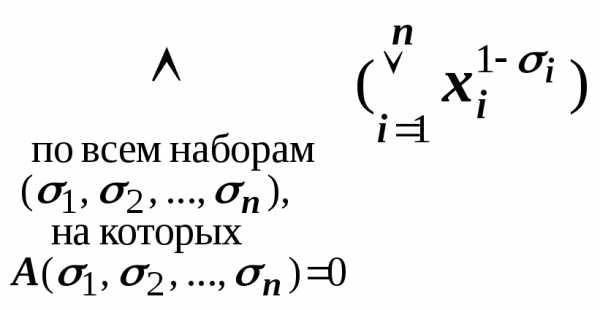 .
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
.
Поэтому для
нахождения СКНФ формулы достаточно:
1) построить
её таблицу истинности;
2) выбрать те
наборы значений переменных (которые входят в формулу), при
которых формула принимает значение 0;
3) составить
соответствующие им дизъюнкты и 4) составить
из них КНФ.
Упражнение 4.3.С помощью таблиц истинности привести формулы упражнения 3.4 к СКНФ.
Решение. д). 1. Составим таблицу истинности формулы (она у нас уже составлена, см. решение задачи д) упражнения 4.2):
2. Выберем те наборы значений переменных, при которых формула принимает значение 0: (0, 0, 1), (0, 1, 1).
3. Составим соответствующие им дизъюнкты: xy ,x
,x
 .
.
4. Составим из них КНФ: (xy )&(x
)&(x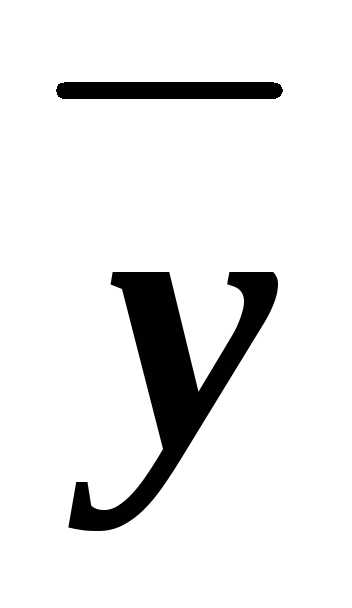
 ).
).
Ответ: д)
СКНФA=(xy )&(x
)&(x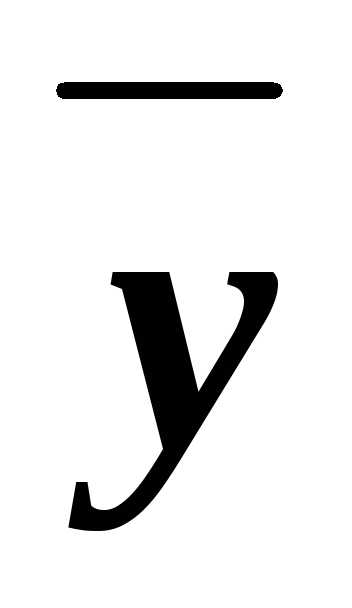
 ).
).
4.3. Принцип двойственности. Операция & называется двойственной к , двойственной к &. Пусть формула А содержит только операции конъюнкции, дизъюнкции и отрицания.
Определение 8. Формула A* называется двойственной к А, если A* получается из A заменой в ней каждой операции на двойственную.
Очевидно, если A* двойственна к A, то A двойственна к A*. Поэтому говорят о взаимно двойственных формулах.
Очевидно также, что если формулы А и В равносильны, то равносильны и двойственные им А* и В*. Кроме того, если A*(х1, х2, …, хп) двойственна к A(х1, х2, …, хп), то ~A*(х1, х2, …, хп). Отсюда следует, что таблица истинности формулы A*, двойственной к А, получается из таблицы истинности А заменой всех 0 на 1 и всех 1 на 0.
Определение 9. Формула А называется самодвойственной, если A*~A.
Из определения следует, что формула A самодвойственна, если при замене 0 на 1, и 1 на 0 её таблица истинности не меняется (естественно, меняются между собой только строки). Очевидно, формула самодвойственна тогда и только тогда, когда на всех противоположных значениях переменных формула принимает противоположные значения.
studfiles.net
Совершенная конъюнктивная нормальная форма — Википедия
Материал из Википедии — свободной энциклопедии
Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
- в ней нет одинаковых элементарных дизъюнкций
- в каждой дизъюнкции нет одинаковых пропозициональных переменных
- каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Любая булева формула, не являющаяся тождественно истинной, может быть приведена к СКНФ.[1].
Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи минимизация логических функций методом Квайна:
В ячейках строки́ f(x1,x2,x3,x4){\displaystyle f(x_{1},x_{2},x_{3},x_{4})} отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
- x1=0{\displaystyle x_{1}=0}
- x2=0{\displaystyle x_{2}=0}
- x3=1{\displaystyle x_{3}=1}
- x4=1{\displaystyle x_{4}=1}
В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: x1∨x2∨x3¯∨x4¯{\displaystyle x_{1}\vee x_{2}\vee {\overline {x_{3}}}\vee {\overline {x_{4}}}}
Остальные члены СКНФ составляются по аналогии:[2]
- (x1∨x2∨x3¯∨x4¯)∧(x1∨x2¯∨x3∨x4)∧(x1∨x2¯∨x3∨x4¯)∧(x1∨x2¯∨x3¯∨x4¯)∧{\displaystyle ({x_{1}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {x_{4}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {\overline {x_{4}}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land }
- (x1¯∨x2∨x3∨x4)∧(x1¯∨x2∨x3∨x4¯)∧(x1¯∨x2∨x3¯∨x4)∧(x1¯∨x2∨x3¯∨x4¯)∧{\displaystyle ({\overline {x_{1}}}\lor {x_{2}}\lor {x_{3}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {x_{3}}\lor {\overline {x_{4}}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land }
- (x1¯∨x2¯∨x3∨x4)∧(x1¯∨x2¯∨x3∨x4¯){\displaystyle ({\overline {x_{1}}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {\overline {x_{4}}})}
См. также
Примечания
wikipedia.green
Совершенная конъюнктивная нормальная форма — Википедия. Что такое Совершенная конъюнктивная нормальная форма
Материал из Википедии — свободной энциклопедииСоверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
- в ней нет одинаковых элементарных дизъюнкций
- в каждой дизъюнкции нет одинаковых пропозициональных переменных
- каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Любая булева формула, не являющаяся тождественно истинной, может быть приведена к СКНФ.[1].
Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи минимизация логических функций методом Квайна:
В ячейках строки́ f(x1,x2,x3,x4){\displaystyle f(x_{1},x_{2},x_{3},x_{4})} отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
- x1=0{\displaystyle x_{1}=0}
- x2=0{\displaystyle x_{2}=0}
- x3=1{\displaystyle x_{3}=1}
- x4=1{\displaystyle x_{4}=1}
В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: x1∨x2∨x3¯∨x4¯{\displaystyle x_{1}\vee x_{2}\vee {\overline {x_{3}}}\vee {\overline {x_{4}}}}
Остальные члены СКНФ составляются по аналогии:[2]
- (x1∨x2∨x3¯∨x4¯)∧(x1∨x2¯∨x3∨x4)∧(x1∨x2¯∨x3∨x4¯)∧(x1∨x2¯∨x3¯∨x4¯)∧{\displaystyle ({x_{1}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {x_{4}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {\overline {x_{4}}})\land ({x_{1}}\lor {\overline {x_{2}}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land }
- (x1¯∨x2∨x3∨x4)∧(x1¯∨x2∨x3∨x4¯)∧(x1¯∨x2∨x3¯∨x4)∧(x1¯∨x2∨x3¯∨x4¯)∧{\displaystyle ({\overline {x_{1}}}\lor {x_{2}}\lor {x_{3}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {x_{3}}\lor {\overline {x_{4}}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {x_{2}}\lor {\overline {x_{3}}}\lor {\overline {x_{4}}})\land }
- (x1¯∨x2¯∨x3∨x4)∧(x1¯∨x2¯∨x3∨x4¯){\displaystyle ({\overline {x_{1}}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {x_{4}})\land ({\overline {x_{1}}}\lor {\overline {x_{2}}}\lor {x_{3}}\lor {\overline {x_{4}}})}
См. также
Примечания
wiki.sc
Совершенные конъюнктивная и дизъюнктивная нормальные формы
Конъюнкт – конъюнкция некоторых переменных или их отрицаний.
Дизъюнкт – дизъюнкция некоторых переменных или их отрицаний.
Если конъюнкт (дизъюнкт) состоит из всех переменных функции или их отрицаний, где каждая переменная участвует лишь единожды, то такой конъюнкт (дизъюнкт) называется совершенным.
Минтерм (конституента единицы) – это логическая функция, принимающая значение истина только на одном наборе значений своих аргументов. Формальная записьминтерма – это конъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от переменных есть минтермов. Минтерм – это совершенный конъюнкт.
Макстерм (конституента нуля) – это логическая функция, принимающая значение ложь только на одном наборе значений своих аргументов. Формальная запись макстерама – это дизъюнкция всех аргументов функции, взятых с отрицанием или без него. Среди множества функций от переменных есть макстермов. Макстерм – это совершенный дизъюнкт.
Дизъюнктивная нормальная форма (ДНФ) – дизъюнкция конечного числа конъюнктов. Совершенная ДНФ(СДНФ)– дизъюнкция совершенных конъюнктов (т.е. минтермов). Любая логическая функция, не являющаяся логическим нулем, имеет только одну СДНФ.
Конъюнктивная нормальная форма (КНФ) – конъюнкция конечного числа дизъюнктов. Совершенная КНФ (СКНФ)– конъюнкция совершенных дизъюнктов (т.е. макстермов). Любая логическая функция, не являющаяся логической единицей, имеет только одну СКНФ.
Выполнимая логическая функция — логическая функция, не являющаяся константой нуля или константой единицы. Представления выполнимой логической функции в виде СКНФ или СДНФ равнозначны, но иногда требуют разного количества операций.
Похожие статьи:
poznayka.org
Совершенная конъюнктивная нормальная форма — Википедия (с комментариями)
Материал из Википедии — свободной энциклопедии
К:Википедия:Статьи без источников (тип: не указан)Соверше́нная конъюнкти́вная норма́льная фо́рма (СКНФ) — это такая КНФ, которая удовлетворяет трём условиям:
- в ней нет одинаковых элементарных дизъюнкций
- в каждой дизъюнкции нет одинаковых пропозициональных переменных
- каждая элементарная дизъюнкция содержит каждую пропозициональную букву из входящих в данную КНФ пропозициональных букв.
Любая булева формула, не являющаяся тождественно истинной, может быть приведена к СКНФ.[1].
Пример нахождения СКНФ
Для того, чтобы получить СКНФ функции, требуется составить её таблицу истинности. К примеру, возьмём одну из таблиц истинности статьи минимизация логических функций методом Квайна:
| <math>x_1</math> | <math>x_2</math> | <math>x_3</math> | <math>x_4</math> | <math>f(x_1, x_2, x_3, x_4)</math> |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
В ячейках строки́ <math>f(x_1, x_2, x_3, x_4)</math> отмечаются лишь те комбинации, которые приводят логическое выражение в состояние нуля.
Четвёртая строка содержит 0 в указанном поле. Отмечаются значения всех четырёх переменных, это:
- <math>x_1 = 0</math>
- <math>x_2 = 0</math>
- <math>x_3 = 1</math>
- <math>x_4 = 1</math>
В дизъюнкцию записывается переменная без инверсии, если она в наборе равна 0, и с инверсией, если она равна 1. Первый член СКНФ рассматриваемой функции выглядит так: <math>x_1 \vee x_2 \vee \overline{x_3} \vee \overline{x_4}</math>
Остальные члены СКНФ составляются по аналогии.
См. также
Напишите отзыв о статье «Совершенная конъюнктивная нормальная форма»
Примечания
- ↑ [window.edu.ru/resource/659/47659/files/pstu021.pdf Математическая логика. Методические указания по курсу «Основы дискретной математики для студентов специальности 220220»].
Отрывок, характеризующий Совершенная конъюнктивная нормальная форма
«Что отвечать ему? – думал князь Андрей, глядя на лоснеющуюся на солнце плешивую голову старика и в выражении лица его читая сознание того, что он сам понимает несвоевременность этих вопросов, но спрашивает только так, чтобы заглушить и свое горе.– Да, отпускай, – сказал он.
– Ежели изволили заметить беспорядки в саду, – говорил Алпатыч, – то невозмежио было предотвратить: три полка проходили и ночевали, в особенности драгуны. Я выписал чин и звание командира для подачи прошения.
– Ну, что ж ты будешь делать? Останешься, ежели неприятель займет? – спросил его князь Андрей.
Алпатыч, повернув свое лицо к князю Андрею, посмотрел на него; и вдруг торжественным жестом поднял руку кверху.
– Он мой покровитель, да будет воля его! – проговорил он.
Толпа мужиков и дворовых шла по лугу, с открытыми головами, приближаясь к князю Андрею.
– Ну прощай! – сказал князь Андрей, нагибаясь к Алпатычу. – Уезжай сам, увози, что можешь, и народу вели уходить в Рязанскую или в Подмосковную. – Алпатыч прижался к его ноге и зарыдал. Князь Андрей осторожно отодвинул его и, тронув лошадь, галопом поехал вниз по аллее.
На выставке все так же безучастно, как муха на лице дорогого мертвеца, сидел старик и стукал по колодке лаптя, и две девочки со сливами в подолах, которые они нарвали с оранжерейных деревьев, бежали оттуда и наткнулись на князя Андрея. Увидав молодого барина, старшая девочка, с выразившимся на лице испугом, схватила за руку свою меньшую товарку и с ней вместе спряталась за березу, не успев подобрать рассыпавшиеся зеленые сливы.
Князь Андрей испуганно поспешно отвернулся от них, боясь дать заметить им, что он их видел. Ему жалко стало эту хорошенькую испуганную девочку. Он боялся взглянуть на нее, по вместе с тем ему этого непреодолимо хотелось. Новое, отрадное и успокоительное чувство охватило его, когда он, глядя на этих девочек, понял существование других, совершенно чуждых ему и столь же законных человеческих интересов, как и те, которые занимали его. Эти девочки, очевидно, страстно желали одного – унести и доесть эти зеленые сливы и не быть пойманными, и князь Андрей желал с ними вместе успеха их предприятию. Он не мог удержаться, чтобы не взглянуть на них еще раз. Полагая себя уже в безопасности, они выскочили из засады и, что то пища тоненькими голосками, придерживая подолы, весело и быстро бежали по траве луга своими загорелыми босыми ножонками.
wiki-org.ru
Конъюнктивная нормальная форма Википедия
Конъюнкти́вная норма́льная фо́рма (КНФ) в булевой логике — нормальная форма, в которой булева формула имеет вид конъюнкции дизъюнкций литералов. Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая булева формула может быть приведена к КНФ.[1] Для этого можно использовать: закон двойного отрицания, закон де Моргана, дистрибутивность.
Примеры и контрпримеры[ | ]
Формулы в КНФ:
- ¬A∧(B∨C),{\displaystyle \neg A\wedge (B\vee C),}
- (A∨B)∧(¬B∨C∨¬D)∧(D∨¬E),{\displaystyle (A\vee B)\wedge (\neg B\vee C\vee \neg D)\wedge (D\vee \neg E),}
- A∧B.{\displaystyle A\wedge B.}
Формулы не в КНФ:
- ¬(B∨C),{\displaystyle \neg (B\vee C),}
- (A∧B)∨C,{\displaystyle (A\wedge B)\vee C,}
- A∧(B∨(D∧E)).{\displaystyle A\wedge (B\vee (D\wedge E)).}
Но эти 3 формулы не в КНФ эквивалентны следующим формулам в КНФ:
- ¬B∧¬C,{\displaystyle \neg B\wedge \neg C,}
- (A∨C)∧(B∨C),
ru-wiki.ru
