Построение и решение графиков Функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Не обязательно делать чертеж на целый тетрадный лист, можно выбрать удобный для вас масштаб, который отразит суть задания.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Как решаем:
Упростим формулу функции:
Задача 2. Построим график функции
Как решаем:
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Как решаем:
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины
Ветви вверх, следовательно, a > 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a < 0.
Точка пересечения с осью Oy — c > 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b < 0.
Задача 4. Построить графики функций:
а) y = 3x — 1
б) y = -x + 2
в) y = 2x
г) y = -1
Как решаем:
Воспользуемся методом построения линейных функций «по точкам».
а) y = 3x — 1
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.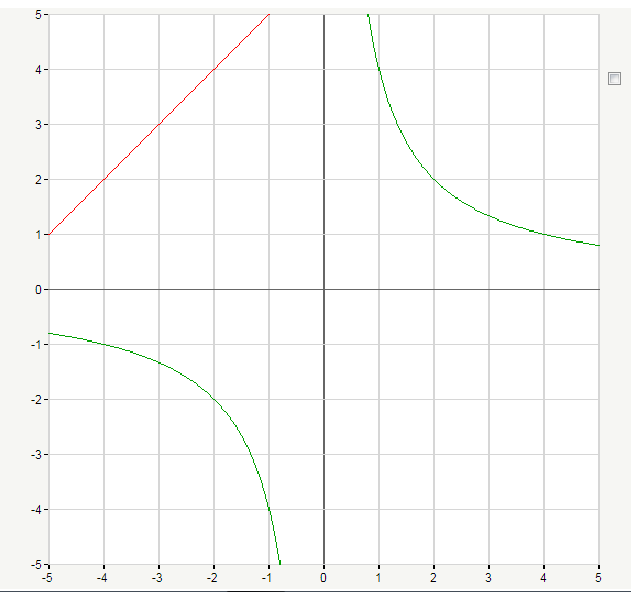
б) y = -x + 2
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
в) y = 2x
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
г) y = -1
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Как решаем:
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
а) y = x² + 1
б)
в) y = (x — 1)² + 2
г)
д)
Как решаем:
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
y = x²
Сдвигаем график вверх на 1:
y = x² + 1
б)
Преобразование в одно действие типа f(x — a).
y = √x
Сдвигаем график вправо на 1:
y = √x — 1
в) y = (x — 1)² + 2
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.
y = x²
Сдвигаем график вправо на 1:
y = (x — 1)²
Сдвигаем график вверх на 2:
y = (x — 1)² + 2
г)
Преобразование в одно действие типаy = cos(x)
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
Построение графика зависимости y = x2
y = x2. (1)
В такой зависимости находятся длина (x) стороны квадрата и его площадь (y).
Для построения графика мы будем поступать так же, как поступали раньше при построении графиков линейной зависимости (см. § 74 и 75) и обратной пропорциональности (§ 76).
Составим, например, такую таблицу значений x и соответствующих значений y:
Построим по таблице точки (черт. 50) на координатной плоскости. Если будем давать x значения, промежуточные между уже взятыми, то точки расположатся на плоскости плотнее. При всевозможных значениях x все точки расположатся на некоторой линии (кривой) называемой параболой (черт. 51).
Из чертежа 51 видно, что весь график расположится в верхней полуплоскости (т.
е. выше оси абсцисс) и лишь одна его точка O (0, 0) лежит на оси абсцисс.
Это и понятно: y есть квадрат числа x, поэтому y не может иметь отрицательных значений; запишем это так: (читают: y – неотрицательное число).
Мы видим далее, что все точки графика расположены попарно симметрично относительно оси ординат. Это и понятно. Так как (–3)2 = 32; (–5)2 = 52 и вообще (–a)2 = a2, то точки, имеющие абсциссы, одинаковые по абсолютной величине, но противоположные по знаку, имеют одинаковые ординаты. Значит, каждой точке A (x; y) графика соответствует точка B (–x; y) того же графика, расположенная по другую сторону оси ординат на том же расстоянии от этой оси. Таким образом, ось ординат является осью симметрии графика зависимости y = x2.
Аккуратно построенный график (например, на миллиметровой бумаге) можно использовать для приближенного возведения чисел в квадрат, если не требуется большая точность вычислений.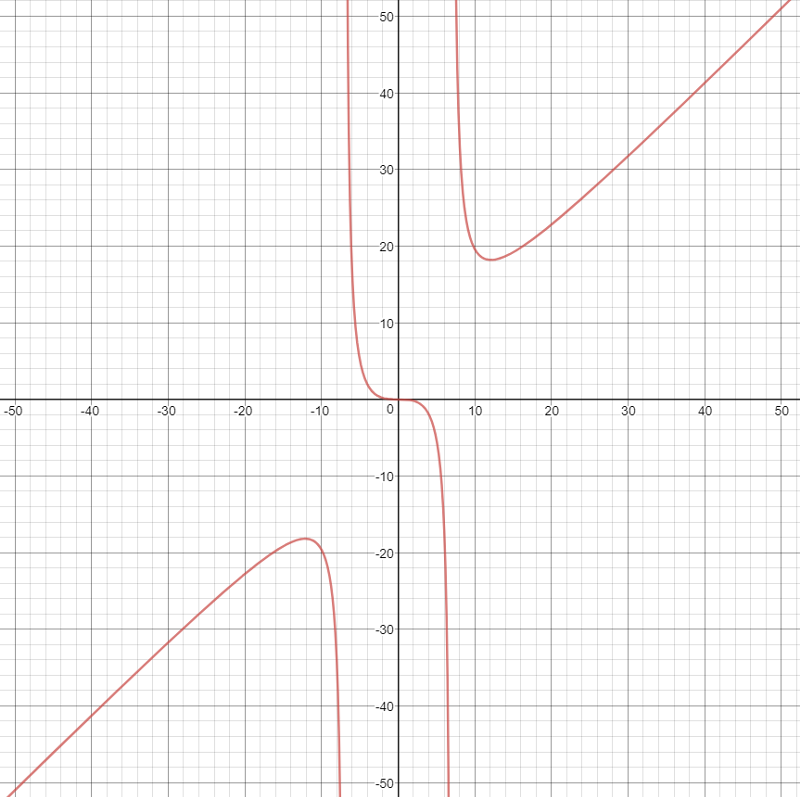
Пусть, например, требуется найти квадрат числа 3,2. На оси абсцисс находим точку 3,2 (точка A) и из нее проводим перпендикуляр к оси абсцисс до пересечения с графиком в точке M. Ордината этой точки, приблизительно равная 10,2, и даст приближенное значение квадрата числа 3,2 (точное значение 10,24). Ординату можно найти или измерив длину перпендикуляра AM, или опустив из точки M перпендикуляр на ось ординат. Полученная точка на оси ординат покажет величину квадрата данного числа.
Примечание. Ввиду симметрии графика для практических вычислений достаточно начертить только ту его часть, которая расположена в первой четверти координатной плоскости. В самом деле, квадрат положительного числа находится непосредственно по графику; если же нужно найти квадрат отрицательного числа, например –3,6, то ищем по графику квадрат числа 3,6, противоположного данному.
Функция y x3 (х в кубе), график функции, урок и презентация
Дата публикации: .
3+ 1$.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
Внеклассный урок — Функции y = ax2 + n, y = a(x – m)2, y = a(x – m)2 + n. Функция y = ax2 + n. Функция y = a(x – m)2. График функций y = ax2 + n и y = a(x – m)2. Ф
Функции y = ax2 + n, y = a(x – m)2, y = a(x – m)2 + n
График функции y = ax2 + n.
Графиком функции y = ax2 + n является парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси y на n единиц вверх, если n > 0, или на –n единиц вниз, если n < 0. |
Пояснение.
Например, надо построить график функции y = 2x2 + 4.
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на четыре единицы вверх по оси y. Разумеется, при этом все значения y закономерно увеличиваются на 4.
Вот таблица значений функции y = 2x2:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 32 | 18 | 8 | 2 | 0 | 2 | 8 | 18 | 32 |
А вот таблица значений y = 2x2 + 4:
x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
y | 36 | 22 | 12 | 6 | 4 | 6 | 12 | 22 | 36 |
Мы видим по таблице, что вершина параболы второй функции на 4 единицы выше вершины параболы первой (ее координаты 0;4).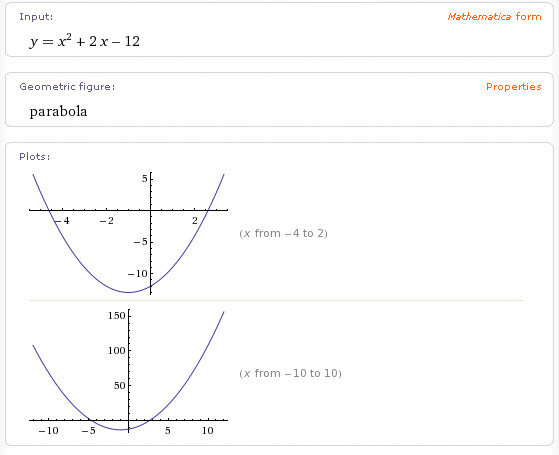
А значения y второй функции на 4 больше значений y первой функции.
График функции y = a(x – m)2.
Графиком функции y = a(x – m)2 является парабола, которую можно получить из графика функции y = ax2 с помощью параллельного переноса вдоль оси x на m единиц вправо, если m>0, или на –m, если m<0. |
Пояснение.
Например, надо построить график функции y = 2(x – 6)2.
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на шесть единиц вправо вдоль оси x (на графике – красная парабола).
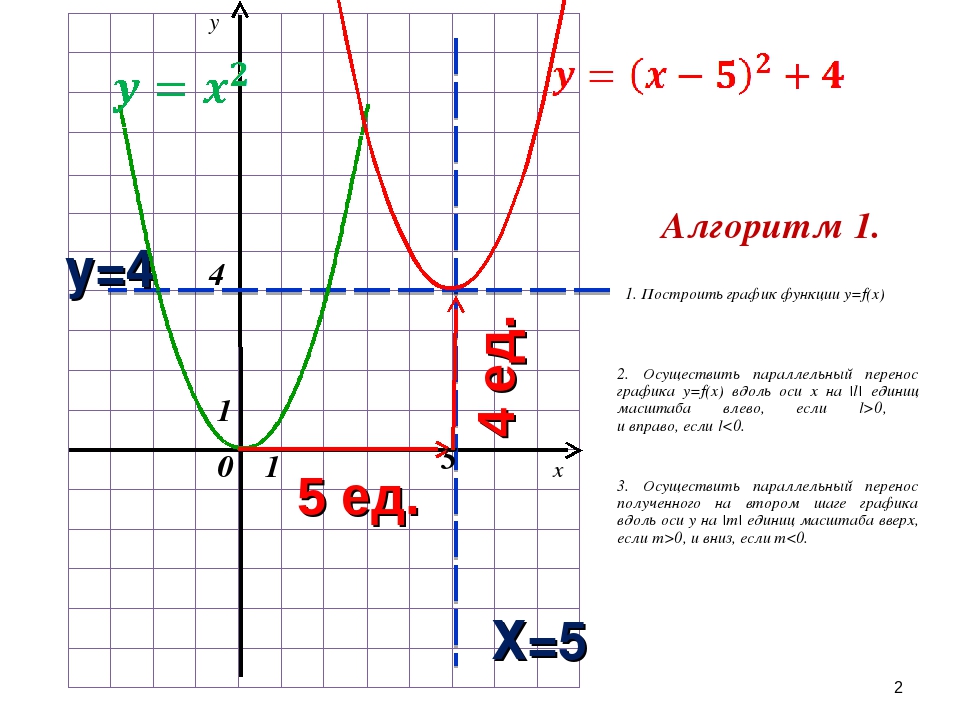
График функции y = a(x – m)2 + n.
Две функции приводят нас к третьей функции: y = a(x – m)2 + n.
Графиком функции y = a(x – m)2 + n является парабола, которую можно получить из графика функции y = ax2 с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо или влево и сдвига вдоль оси y на n единиц вверх или вниз. |
Пояснение:
Например, надо построить график функции y = 2(x – 6)2 + 2.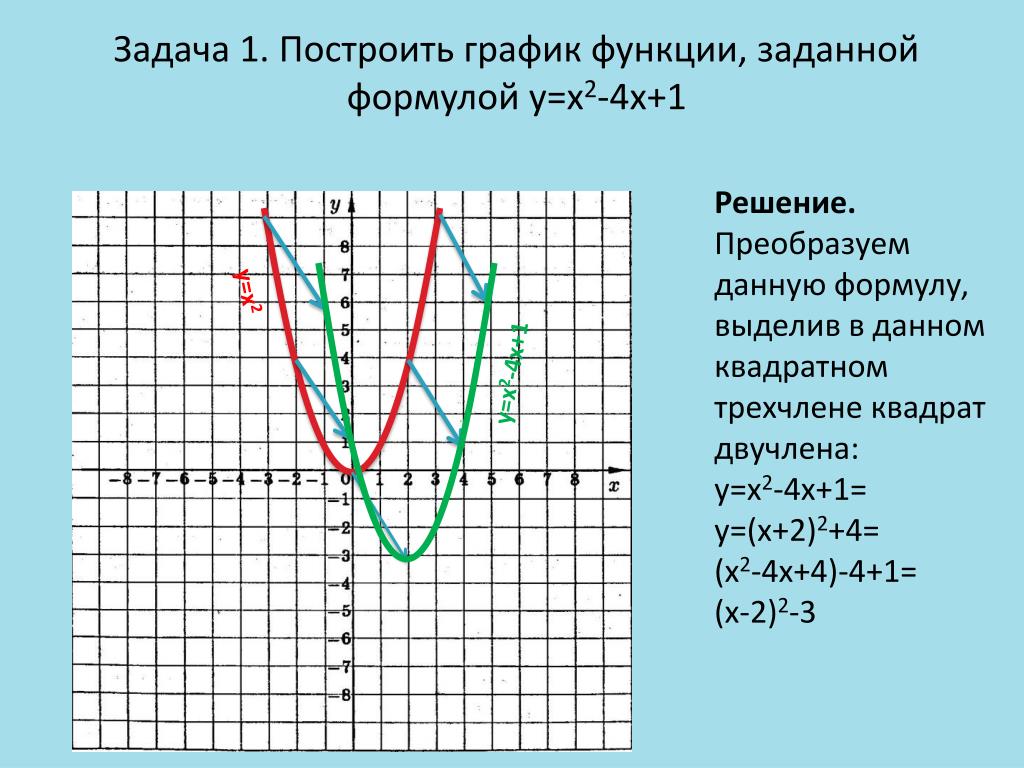
Это значит, что парабола, которая является графиком функции y = 2x2, перемещается на 6 единиц вправо (значение m) и на 2 единицы вверх (значение n). Красная парабола на графике – результат этих перемещений.
Функция y = корень квадратный из x, ее свойства и график
Основные цели:
1) сформировать представление о целесообразности обобщённого исследования зависимостей реальных величин на примере величин, связанных отношением у=
2) формировать способность к построению графика у= и его свойства;
3) повторить и закрепить приёмы устных и письменных вычислений, возведение в квадрат, извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный материал.
1. Алгоритм:
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной работы:
4.
Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной работе.
4) Я допустил ошибки в самостоятельной работе (перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока: продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали множество действительных чисел, действия с ними, построили алгоритм для описания свойств функции, повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством действительных чисел, функцией.
2.
Актуализация знаний и фиксация затруднений в
деятельности
Цель этапа:
1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: функция, независимая переменная, зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x2, y = — x2 ,
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать зависимости между величинами? (С помощью текста, формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).
Как называется х? (Независимая переменная - аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c, y =x2, y = — x2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x2, y = ?
3. Выявление причин затруднений и постановка цели деятельности
Цель этапа:
1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y =
, ее
свойствами и графиком.
Функцией в таблице
определять вид зависимости, строить формулу и
график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам, предложив группам построить график y = , затем проанализировать получившиеся результаты. Также группам можно предложить по алгоритму описать свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное
учебное содержание во внешней речи.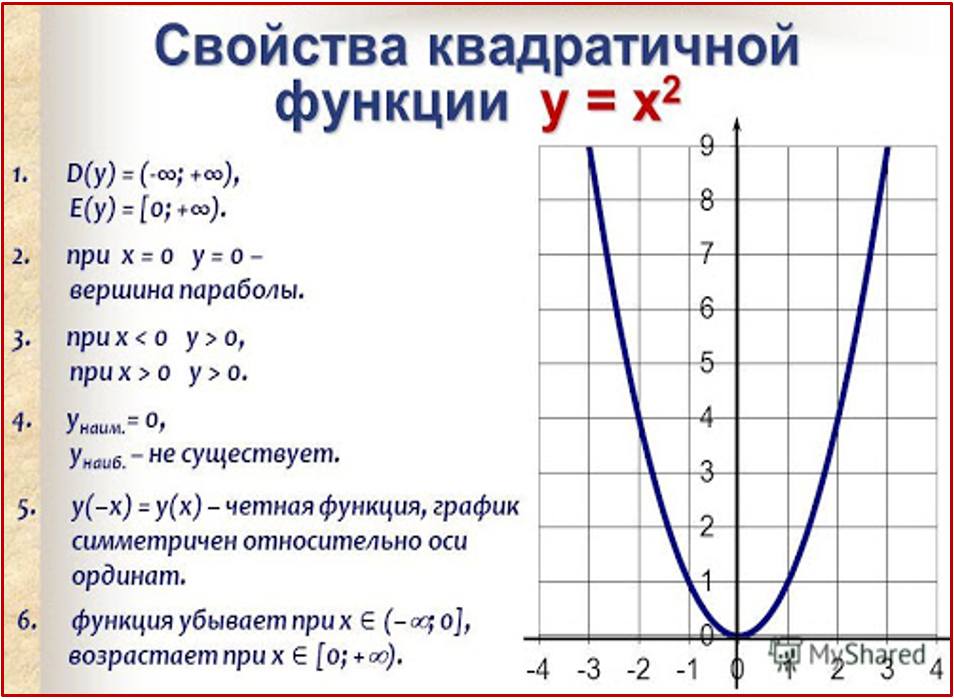
Организация учебного процесса на этапе 5:
Постройте график у= — и опишите его свойства.
Свойства у= — .
1.Область определения функции.
D(y) =
2.Область значений функции.
E(y) =
3. y = 0, y> 0, y<0.
y =0, если x = 0.
y<0, если х(0;+)
4.Возрастания, убывания функции.
Функция убывает при х [0;+ )
5. Ограниченность функции.
Функция ограничена сверху, и не ограничена снизу.
6.Наибольшее, наименьшее значения функции.
у наиб. = нет у наим. = 0.
7.Непрерывность функции.
Функция непрерывна на все области определения.
№13.2(в)
Используя график функции у=, найдите наименьшее и наибольшее значения функции на отрезке [1; 9].
Построим график у=.
Выделим его часть на отрезке [1;9]. Заметим, что у наим.
= 1 при х = 1, а у наиб.
=3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по эталону
Цель этапа: проверить своё умение применять новое учебное содержание в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
№ 13.1(в)
Учащиеся выполняют задание самостоятельно, проводят самопроверку по эталону, анализируют, исправляют ошибки.
Построим график у=.
С помощью графика найдите наименьшее и наибольшее значения функции на отрезке [0; 4].
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.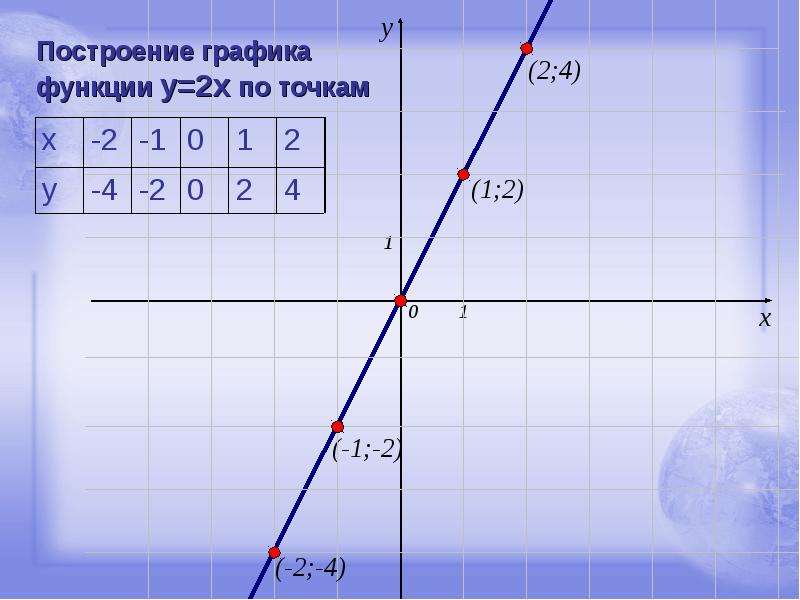
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.
Ответ: 9.
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами? (Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели? (Умение искать закономерности, умение читать графики.)
– Проанализируйте свою деятельность на уроке.
(Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение:
Постройте график функции и опишите его свойства:
| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. |
|
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. | |
| Квадратичная функция | y = ax2 + bx + c | Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа | |
| Степенная функция | y = x3 | Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
|
| Степенная — корень квадратный | y = x1/2 | График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Степенная — обратная пропорциональность | y = k/x | Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. | |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590. .. |
|
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). | |
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. |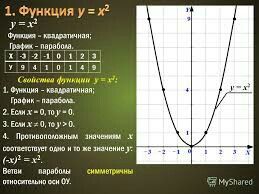
|
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Ограниченные и неограниченные функции
Обозначим буквой X некоторое множество чисел, входящих в область определения D ( f ) функции y = f (x).
Определение 1. Функцию y = f (x) называют ограниченной сверху на множестве X , если существует такое число a , что для любого x из множества X выполнено неравенство
Определение 2. Функцию y = f (x) называют ограниченной снизу на множестве X , если существует такое число b , что для любого x из множества X выполнено неравенство
Определение 3. Функцию y = f (x) называют ограниченной на множестве X , если существуют такие числа a и b , что для любого x из множества X выполнено неравенство
Определение 4. Функцию y = f (x) называют неограниченной сверху на множестве X , если для любого числа a существует такой x из множества X , для которого выполнено неравенство
Определение 5. Функцию y = f (x) называют неограниченной снизу на множестве X , если для любого числа b существует такой x из множества X , для которого выполнено неравенство
Определение 6. Функцию y = f (x) называют неограниченной на множестве X , если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.
Проиллюстрируем эти определения следующими примерами.
Пример 1. Функция y = x2 (рис. 1) является ограниченной снизу и неограниченной сверху на множестве
Рис.1
Пример 2. Функция y = – x2 (рис. 2) является ограниченной сверху и неограниченной снизу на множестве
Рис.2
Пример 3. Функция y = x (рис. 3) неограничена сверху и неограничена снизу на множестве
Рис.3
Пример 4. Функция y = arctg x (рис. 4) ограничена на множестве
Рис.4
Монотонные и строго монотонные функции
Определение 7. Функцию y = f (x) называют возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
Замечание 1. Возрастающие функции также называют неубывающими функциями.
Определение 8. Функцию y = f (x) называют убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
Замечание 2. Убывающие функции также называют невозрастающими функциями.
Определение 9. Функцию y = f (x) называют строго возрастающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
f (x1) < f (x2)
Определение 10. Функцию y = f (x) называют строго убывающей на множестве X , если для любых чисел и , удовлетворяющих неравенству x1 < x2 , выполнено неравенство
f (x1) > f (x2)
Определение 11. Возрастающие и убывающие функции называют монотонными, строго возрастающие и строго убывающие функции называют строго монотонными.
Пример 5. Функция y = x2 (рис. 1) является строго убывающей функцией на множестве и строго возрастающей на множестве
Пример 6. Функция y = – x2 (рис. 2) является строго возрастающей функцией на множестве и строго убывающей на множестве
Пример 7. Функция y = x (рис. 3) является строго возрастающей функцией на множестве
Пример 8. Функция y = arctg x (рис. 4) является строго возрастающей на множестве
Четные и нечетные функции
Определение 12. Функцию y = f (x) , определенную на множестве X , называют четной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство
f (– x) = f (x)
Определение 13. Функцию y = f (x) , определенную на множестве X , называют нечетной функцией, если для любого числа x из множества X число – x также принадлежит множеству X и выполняется равенство
f (– x) = – f (x)
Пример 9. Функции y = x2 и y = – x2 являются четными функциями (рис. 1 и рис. 2), а функции y = x и y = arctg x являются нечетными функциями (рис. 3 и рис. 4).
Пример 10. Примерами функций, которые не являются ни четными, ни нечетными функциями, являются показательные и логарифмические функции.
Утверждение. Любую функцию y = f (x) , определенную на симметричном относительно точки x = 0 множестве X , можно представить в виде суммы четной и нечетной функций.
Доказательство. Рассмотрим две функции:
сумма которых равна f (x) , и заметим, что функция g1 (x) является четной функцией, а функция g2 (x) является нечетной функцией. Действительно,
что и завершает доказательство утверждения.
Замечание 3. Раскладывая функцию y = e x в сумму четной и нечетной функций, получаем:
Функцию g1 (x) называют гиперболическим косинусом и обозначают ch x :
Функцию g2 (x) называют гиперболическим синусом и обозначают sh x :
Таким образом, справедливо равенство
e x= sh x + ch x
Периодические и непериодические функции. Период функции
Определение 14. Число называют периодом функции y = f (x) , если для любого числа числа x + T и x – T также принадлежат области определения D ( f ) и справедливы равенства
f ( x + T ) = f (x) ,
f ( x – T ) = f (x)
Определение 15. Если функция имеет период, то ее называют периодической. Если же у функции периода нет, то ее называют непериодической.
Замечание 4. Если число T является периодом некоторой функции, то и число kT , где k – любое целое число, отличное от нуля, также является периодом этой функции.
Пример 11. Функции y = sin x и y = cos x являются периодическими функциями с периодом 2π , функции y = tg x и y = ctg x являются периодическими функциями с периодом π .
Подробнее об этом можно прочитать в разделе «Свойства тригонометрических функций» → «Периодичность тригонометрических функций. Полупериодичность синуса и косинуса» нашего справочника.
Пример 12. Показательные, логарифмические и степенные функции являются непериодическими функциями.
График функции. Свойства графиков четных, нечетных, периодических функций
Рассмотрим плоскость с заданной прямоугольной системой координат Oxy .
Определение 16. Графиком функции y = f (x) называют множество всех точек, координаты которых имеют вид (x; f (x)) , где .
Замечание 5. График четной функции симметричен относительно оси ординат Oy (см., например, рис. 1 и рис. 2), график нечетной функции симметричен относительно начала координат (см., например, рис. 3 и рис. 4).
Замечание 6. График периодической функции не изменяется при сдвиге вдоль оси абсцисс Ox на период вправо или влево (см., например, раздел «Графики тригонометрических функций» нашего справочника). Поэтому для того, чтобы построить график периодической функции с периодом T, достаточно построить график этой функции на любом отрезке оси абсцисс Ox длины T, а затем сдвигать его влево и вправо на расстояния nT , где n – любое натуральное число.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Графики Экспоненциальные функции: примеры (стр. 4 из 4) Разделы: Вводные концепции, пошаговые инструкции по построению графиков, Работал примеров Это может показаться немного сложнее построить график, потому что почти все мои значения и будут десятичные приближения.Но если я округлюсь до разумного числа десятичных знаков (один или два, как правило, подходят для построение графиков), то этот график будет довольно простым. Мне просто нужно сделать уверен, что я нарисовал красивый аккуратный график с последовательным масштабом на моем топоры. Если степень в экспоненте не линейный (например, « x «), но вместо этого является квадратичным (например, «2 x 2 «) или что-то еще, тогда график может выглядеть иначе.Также, если есть если в функции больше одного экспоненциального члена, график может выглядеть иначе. Ниже приведены несколько примеров, чтобы показать вам, как они работают.
Это на самом деле полезный функция (называемая «функцией гиперболического синуса»), но вы вероятно, не увижу его снова до исчисления.В любом случае я подсчитываю очки и участок, как обычно: Иногда вы увидите более сложные экспоненциальные функции, подобные этим. На этом этапе в ваша математическая карьера, скорее всего, вы будете в основном иметь дело со стандартной экспоненциальной формой. Так что убедитесь, что вам удобно с его общей формой и поведением. На рассмотрение: ниже приведены некоторые различные вариации одной и той же базовой экспоненциальной функции с соответствующий график под каждым уравнением. Обратите внимание, что даже если график перемещен влево или вправо, вверх или вниз, или перевернут вверх ногами, он все еще отображает ту же кривую. Убедитесь, что вы знакомы с этой формой!
|
Графики и решения систем линейных уравнений
Результаты обучения
- Графические системы уравнений
- Постройте систему двух линейных уравнений
- Постройте систему двух линейных неравенств
- Оцените заказанные пары как решения для систем
- Определить, является ли упорядоченная пара решением системы линейных уравнений
- Определить, является ли упорядоченная пара решением системы линейных неравенств
- Классифицируйте решения по системам
- Определите, какой тип решения будет иметь система, на основе ее графика
Путь течения реки зависит от многих переменных, включая размер реки, количество воды в ней, какие предметы плавают в реке, идет ли дождь или нет, и так далее.Если вы хотите лучше всего описать его поток, вы должны принять во внимание эти другие переменные. В этом может помочь система линейных уравнений.
Система линейных уравнений состоит из двух или более линейных уравнений, составленных из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Вы найдете системы уравнений во всех приложениях математики. Они являются полезным инструментом для обнаружения и описания взаимосвязи поведения или процессов.Например, редко можно найти схему транспортного потока, на которую влияет только погода. Несчастные случаи, время суток и крупные спортивные события — это лишь некоторые из других переменных, которые могут повлиять на движение транспорта в городе. В этом разделе мы исследуем некоторые основные принципы построения графиков и описания пересечения двух линий, составляющих систему уравнений.
Построение системы линейных уравнений
В этом разделе мы рассмотрим системы линейных уравнений и неравенств с двумя переменными.Сначала мы попрактикуемся в построении графиков двух уравнений на одном и том же наборе осей, а затем изучим различные соображения, которые необходимо учитывать при построении графиков двух линейных неравенств на одном и том же наборе осей. Для построения графика системы линейных уравнений используются те же методы, что и для построения графиков отдельных линейных уравнений. Мы можем использовать таблицы значений, уклона и пересечения y или x и y -пересечения, чтобы построить обе линии на одном и том же наборе осей.
Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Давайте изобразим их на графике с использованием формы пересечения наклона на одном и том же наборе осей. Помните, что форма пересечения наклона выглядит как [latex] y = mx + b [/ latex], поэтому мы захотим решить оба уравнения для [latex] y [/ latex].
Сначала найдите y в [latex] 2x + y = -8 [/ latex]
[латекс] \ begin {array} {c} 2x + y = -8 \\ y = -2x — 8 \ end {array} [/ latex]
Во-вторых, решите относительно y в [latex] x-y = -1 [/ latex]
[латекс] \ begin {array} {r} x-y = -1 \, \, \, \, \, \\ y = x + 1 \ end {array} [/ latex]
Теперь система записывается как
[латекс] \ begin {массив} {c} y = -2x — 8 \\ y = x + 1 \ end {array} [/ latex]
Теперь вы можете построить оба уравнения, используя их наклоны и точки пересечения на одном и том же наборе осей, как показано на рисунке ниже.Обратите внимание на то, что графики имеют одну общую точку. Это их точка пересечения, точка, которая лежит на обеих линиях. В следующем разделе мы проверим, что эта точка является решением системы.
В следующем примере вам будет предоставлена система для построения графика, состоящая из двух параллельных линий.
Пример
Постройте график системы [latex] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex], используя наклоны и пересечения линий по оси Y.
Показать решениеСначала построим график [латекс] y = 2x + 1 [/ latex], используя наклон m = 2 и точку пересечения по оси y (0,1).
Затем добавьте [латекс] y = 2x-3 [/ latex], используя наклон m = 2 и точку пересечения оси y (0, -3).
Обратите внимание на то, что это параллельные линии, и они не пересекаются.В следующем разделе мы обсудим, как не существует решений системы уравнений, представляющих собой параллельные прямые.
В следующем примере вам будет предоставлена система, уравнения которой выглядят по-разному, но после построения графика оказываются той же линией.
Пример
Изобразите систему [латекс] \ begin {array} {c} y = \ frac {1} {2} x + 2 \\ 2y-x = 4 \ end {array} [/ latex], используя x — и y -перехватывает.
Показать решениеСначала найдите точки пересечения по осям x и y [latex] y = \ frac {1} {2} x + 2 [/ latex]
Пересечение x будет иметь значение 0 для y, поэтому подставьте y = 0 в уравнение и выделите переменную x.
[латекс] \ begin {array} {c} 0 = \ frac {1} {2} x + 2 \\\ подчеркивание {\, \, \, \, \, \, \, \, — 2 \, \, \, \, \, \, — 2} \\ — 2 = \ frac {1} {2} x \\\ left (2 \ right) \ left (-2 \ right) = \ left (2 \ справа) \ frac {1} {2} x \\ — 4 = x \ end {array} [/ latex]
Х-точка пересечения [latex] y = \ frac {1} {2} x + 2 [/ latex] равна [latex] \ left (-4,0 \ right) [/ latex].
Пересечение оси Y легче найти, поскольку это уравнение имеет форму точки пересечения с угловым коэффициентом. Y-точка пересечения равна (2,0).
Теперь мы можем построить [latex] y = \ frac {1} {2} x + 2 [/ latex], используя точки пересечения
Теперь найдите перехваты [latex] 2y-x = 4 [/ latex]
Подставьте y = 0 в уравнение, чтобы найти точку пересечения с x.
[латекс] \ begin {array} {c} 2y-x = 4 \\ 2 \ left (0 \ right) -x = 4 \\ x = -4 \ end {array} [/ latex]
Перехватчик x [latex] 2y-x = 4 [/ latex] равен [latex] \ left (-4,0 \ right) [/ latex].
Теперь подставьте x = 0 в уравнение, чтобы найти точку пересечения оси y.
[латекс] \ begin {array} {c} 2y-x = 4 \\ 2y-0 = 4 \\ 2y = 4 \\ y = 2 \ end {array} [/ latex]
Y-пересечение [latex] 2y-x = 4 [/ latex] равно [latex] \ left (0,2 \ right) [/ latex].
ПОДОЖДИТЕ, это те же перехваты, что и [latex] y = \ frac {1} {2} x + 2 [/ latex]! Фактически, [latex] y = \ frac {1} {2} x + 2 [/ latex] и [latex] 2y-x = 4 [/ latex] на самом деле являются одним и тем же уравнением, выраженным по-разному.Если бы вы записали их оба в форме пересечения наклона, вы бы увидели, что это одно и то же уравнение.
На графике они представляют собой одну и ту же линию. В следующем разделе мы увидим, что системы с двумя одинаковыми уравнениями в них имеют бесконечное число решений.
Построение графика системы линейных уравнений состоит из выбора метода построения графиков, который вы хотите использовать, и построения графиков обоих уравнений на одном и том же наборе осей. Когда вы строите график системы линейных неравенств на одном и том же наборе осей, вам необходимо учесть еще несколько вещей.
Изобразите систему двух неравенств
Помните из модуля по построению графиков, что график одного линейного неравенства разбивает координатную плоскость на две области. По одну сторону лежат все решения неравенства. С другой стороны, решений нет. Рассмотрим график неравенства [латекс] y <2x + 5 [/ latex].
Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным.Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство — вы увидите, что они работают. Итак, заштрихованной областью показаны все решения этого неравенства.
Граничная линия делит координатную плоскость пополам. В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной.
Изобразим еще одно неравенство: [latex] y> −x [/ latex].Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения. Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности.
Чтобы создать систему неравенств, вам необходимо построить график двух или более неравенств вместе. Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них.
Фиолетовая область показывает, где перекрываются решения двух неравенств.Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex].
В следующем примере вам дана система двух неравенств, граничные линии которых параллельны друг другу.
Примеры
Изобразите систему [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex]
Показать решениеГраницы для этой системы такие же, как и для системы уравнений из предыдущего примера:
[латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex]
Построение граничных линий будет аналогичным, за исключением того, что неравенство [латекс] y \ lt2x-3 [/ latex] требует, чтобы мы нарисовали пунктирную линию, а неравенство [латекс] y \ ge2x + 1 [/ латекс] потребует сплошная линия.Графики будут выглядеть так:
Теперь нам нужно добавить регионы, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область закрасить. Давайте проверим [латекс] \ left (0,0 \ right) [/ latex], чтобы упростить задачу.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex]
[латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex].График теперь будет выглядеть так:
Теперь закрасим область, которая показывает решения неравенства [latex] y \ lt2x-3 [/ latex]. Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру.
Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex]
[латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ]
Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ lt2x-3 [/ latex].График теперь будет выглядеть так:
У этой системы неравенства нет общих черт.
Как бы выглядел график, если бы система выглядела так?
[латекс] \ begin {массив} {c} y \ ge2x + 1 \\ y \ gt2x-3 \ end {array} [/ latex].
Проверка точки [latex] \ left (0,0 \ right) [/ latex] вернет положительный результат для неравенства [latex] y \ gt2x-3 [/ latex], и тогда график будет выглядеть следующим образом:
Фиолетовая область — это область перекрытия обоих неравенств.
В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства.
Определить, является ли упорядоченная пара решением системы линейных уравнений
Линии на графике выше определены как
[латекс] \ begin {массив} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex].
Они пересекаются в том, что выглядит как [латекс] \ left (-3, -2 \ right) [/ latex].
Используя алгебру, мы можем проверить, что эта общая точка на самом деле [latex] \ left (-3, -2 \ right) [/ latex], а не [latex] \ left (-2.999, -1.999 \ right) [/ latex ]. Подставляя значения x и y упорядоченной пары в уравнение каждой линии, вы можете проверить, находится ли точка на обеих линиях. Если подстановка приводит к истинному утверждению, значит, вы нашли решение системы уравнений!
Поскольку решение системы должно быть решением всех уравнений в системе, вам нужно будет проверить точку в каждом уравнении.В следующем примере мы заменим -3 на x и -2 на y в каждом уравнении, чтобы проверить, действительно ли это решение.
Пример
[латекс] \ left (-3, -2 \ right) [/ latex] решение системы
[латекс] \ begin {array} {r} 2x + y = -8 \\ x-y = -1 \ end {array} [/ latex]
Показать решение Сначала проверьте [латекс] 2x + y = -8 [/ latex]:[латекс] \ begin {массив} {r} 2 (-3) + (- 2) = -8 \\ — 8 = -8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Теперь проверьте [латекс] x-y = -1 [/ latex].
[латекс] \ begin {array} {r} (- 3) — (- 2) = -1 \\ — 1 = -1 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ left (-3, -2 \ right) [/ latex] — это решение [latex] x-y = -1 [/ latex]
Поскольку [latex] \ left (-3, -2 \ right) [/ latex] является решением каждого из уравнений в системе, [latex] \ left (-3, -2 \ right) [/ latex] это решение системы.
Ответ
[латекс] \ left (-3, -2 \ right) [/ latex] — это решение системы.
Пример
— это (3, 9) решение системы
[латекс] \ begin {array} {r} y = 3x \\ 2x – y = 6 \ end {array} [/ latex]
Показать решение Поскольку решение системы должно быть решением всех уравнений в системе, отметьте точку в каждом уравнении.Замените 3 на x и 9 на y в каждом уравнении.
[латекс] \ begin {массив} {l} y = 3x \\ 9 = 3 \ left (3 \ right) \\\ text {TRUE} \ end {array} [/ latex]
(3, 9) представляет собой раствор [латекс] y = 3x [/ латекс].
[латекс] \ begin {array} {r} 2x – y = 6 \\ 2 \ left (3 \ right) –9 = 6 \\ 6–9 = 6 \\ — 3 = 6 \ text {FALSE } \ end {array} [/ latex]
(3, 9) — это , а не раствор [латекса] 2x – y = 6 [/ латекс].
Поскольку (3, 9) не является решением одного из уравнений системы, оно не может быть решением системы.
Ответ
(3, 9) не является решением системы.
Подумай об этом
[латекс] (- 2,4) [/ латекс] решение для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]
Прежде чем производить какие-либо вычисления, посмотрите на заданную точку и первое уравнение в системе. Можете ли вы предсказать ответ на вопрос, не занимаясь алгеброй?
Показать решениеПодставьте -2 вместо x и 4 вместо y в первое уравнение:
[латекс] \ begin {array} {l} y = 2x \\ 4 = 2 \ left (-2 \ right) \\ 4 = -4 \\\ text {FALSE} \ end {array} [/ latex]
Вы можете остановить тестирование, потому что точка, которая является решением системы, будет решением обоих уравнений в системе.
[латекс] (- 2,4) [/ латекс] НЕ является решением для системы
[латекс] \ begin {array} {r} y = 2x \\ 3x + 2y = 1 \ end {array} [/ latex]
Помните, что для решения системы уравнений значения точки должны быть решением обоих уравнений. Как только вы найдете одно уравнение, для которого точка неверна, вы определили, что оно не является решением системы.
Мы можем использовать тот же метод, чтобы определить, является ли точка решением системы линейных неравенств.
Определить, является ли упорядоченная пара решением системы линейных неравенств
На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными.
Напротив, точки M и A лежат за пределами области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система .В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]?
Показать решение Проверьте суть каждого неравенства. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] 2x + y <8. [/ Latex]
Поскольку (2, 1) является решением каждого неравенства, оно также является решением системы.
Ответ
Точка (2, 1) является решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex].
Вот график системы в примере выше. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия для двух неравенств.
Пример
Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]?
Показать решениеОтметьте точку с каждым неравенством. Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств?
[латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex]
(2, 1) — решение для [латекса] x + y> 1 [/ latex].
[латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex]
(2, 1) — это , а не как решение для [латекса] 3x + y <4 [/ latex].
Поскольку (2, 1) — это , а не как решение одного из неравенств, это не решение системы.
Ответ
Точка (2, 1) не является решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex].
Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область).
Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения общей для них области. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже:
- Изобразите каждое неравенство в виде линии и определите, будет ли оно сплошным или пунктирным.
- Определите, с какой стороны каждой граничной линии представлены решения неравенства, проверив точку на каждой стороне
- Заштрихуйте область, которая представляет решения для обоих неравенств
Пример
Закрасьте область графика, которая представляет решения для обоих неравенств.[латекс] x + y \ geq1 [/ латекс] и [латекс] y – x \ geq5 [/ латекс].
Показать решение Изобразите одно неравенство. Сначала нарисуйте граничную линию, используя таблицу значений, пересечений или любой другой метод, который вы предпочитаете. Граница для [латекса] x + y \ geq1 [/ latex] — это [латекс] x + y = 1 [/ latex] или [латекс] y = −x + 1 [/ latex]. Поскольку знак равенства стоит вместе со знаком «больше», граница будет сплошной.Найдите упорядоченную пару по обе стороны от ограничивающей линии. Вставьте значения x и y в неравенство [latex] x + y \ geq1 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение.
[латекс] \ begin {array} {r} \ text {Test} 1: \ left (−3,0 \ right) \\ x + y \ geq1 \\ — 3 + 0 \ geq1 \\ — 3 \ geq1 \\\ text {FALSE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ x + y \ geq1 \\ 4 + 1 \ geq1 \\ 5 \ geq1 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Поскольку (4, 1) приводит к истинному утверждению, область, которая включает (4, 1), должна быть заштрихована.
Проделайте то же самое со вторым неравенством. Постройте граничную линию, затем проверьте точки, чтобы определить, какая область является решением неравенства. В этом случае граница [латекс] y – x = 5 \ left (\ text {или} y = x + 5 \ right) [/ latex] сплошная.Контрольная точка (−3, 0) не является решением [latex] y – x \ geq5 [/ latex], а контрольная точка (0, 6) является решением.
Ответ
Фиолетовая область на этом графике показывает набор всех решений системы.
В этом разделе мы увидели, что решения систем линейных уравнений и неравенств могут быть упорядоченными парами. В следующем разделе мы будем работать с системами, у которых нет решений или есть бесконечно много решений.
Используйте график для классификации решений для систем
Напомним, что линейное уравнение отображается в виде линии, что означает, что все точки на линии являются решениями этого линейного уравнения.Есть бесконечное количество решений. Как мы видели в предыдущем разделе, если у вас есть система линейных уравнений, пересекающихся в одной точке, эта точка является решением системы. Что произойдет, если линии никогда не пересекаются, как в случае с параллельными линиями? Как бы вы описали решения для такой системы? В этом разделе мы исследуем три возможных результата решения системы линейных уравнений.
Три возможных исхода решений систем уравнений
Напомним, что решение системы уравнений — это значение или значения, которые верны для всех уравнений в системе.Есть три возможных исхода решений систем линейных уравнений. Графики уравнений внутри системы могут сказать вам, сколько решений существует для этой системы. Посмотрите на изображения ниже. На каждой показаны две линии, составляющие систему уравнений.
| Одно решение | Нет решений | Бесконечные решения |
|---|---|---|
| Если графики уравнений пересекаются, то существует одно решение, которое верно для обоих уравнений. | Если графики уравнений не пересекаются (например, если они параллельны), то для обоих уравнений нет истинных решений. | Если графики уравнений совпадают, то существует бесконечное количество решений, которые верны для обоих уравнений. |
- Одно решение: Когда система уравнений пересекается в упорядоченной паре, система имеет одно решение.
- Бесконечные решения: Иногда два уравнения отображаются в виде одной линии, и в этом случае у нас есть бесконечное количество решений.
- Нет Решение: Когда линии, составляющие систему, параллельны, решений нет, потому что эти две линии не имеют общих точек.
Пример
Используя график [latex] \ begin {array} {r} y = x \\ x + 2y = 6 \ end {array} [/ latex], показанный ниже, определите, сколько решений есть в системе.
Показать решение Линии пересекаются в одной точке. Таким образом, у этих двух линий есть только одна общая точка, есть только одно решение системы.Ответ
Есть одно решение этой системы.
Пример (расширенный)
Используя график [latex] \ begin {array} {r} y = 3,5x + 0,25 \\ 14x – 4y = -4,5 \ end {array} [/ latex], показанный ниже, определите, сколько решений имеет система. .
Показать решение Линии параллельны, то есть не пересекаются. Решения по системе нет.Ответ
Нет решений по системе.
Пример
Сколько решений имеет система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex]?
Показать решение Сначала изобразите оба уравнения на одних и тех же осях.Два уравнения изображены на одной линии. Таким образом, каждая точка на этой линии является решением системы уравнений.
Ответ
Система [latex] \ begin {array} {r} y = 2x + 1 \\ — 4x + 2y = 2 \ end {array} [/ latex] имеет бесконечное количество решений.
В следующем разделе мы изучим некоторые алгебраические методы нахождения решений систем уравнений. Напомним, что линейные уравнения с одной переменной могут иметь одно решение, без решения или много решений, и мы можем проверить это алгебраически.Мы будем использовать те же идеи для алгебраической классификации решений систем с двумя переменными.
Построение графиков линейных уравнений — MathBootCamps
Существует три способа построения графиков линейных уравнений: (1) вы можете найти две точки, (2) вы можете использовать точку пересечения по оси Y и наклон или (3) использовать точки пересечения по оси x и y. В следующем руководстве мы рассмотрим все три. Построение графиков линейных уравнений не должно быть трудным и даже интересным, если у вас есть эти методы!
объявление
Метод 1: использование двух точек для построения линейного уравнения
График любого линейного уравнения, такого как \ (y = 3x + 2 \) или \ (y = -x + 9 \), представляет собой линию, и для ее определения нужны только две точки.Идея этого метода состоит в том, чтобы найти две точки на линии, выбирая значения \ (x \).
Пример
Изобразите линейное уравнение:
\ (y = \ dfrac {1} {3} x — 2 \)
Решение
Чтобы найти две точки на линии, выберите любые два значения \ (x \), с которыми будет легко работать, а затем найдите соответствующее значение \ (y \). Двумя простыми значениями здесь будут 0 и 3 (поскольку 3 заменяется на 3 в дроби).
Пусть \ (x = 0 \):
\ (\ begin {align} y & = \ dfrac {1} {3} x — 2 \\ & = \ dfrac {1} {3} (0) — 2 \\ & = -2 \ end {align} \ )
Итак, одна точка на прямой равна \ ((x, y) = (0, –2) \).
Пусть \ (x = 3 \):
\ (\ begin {align} y & = \ dfrac {1} {3} x — 2 \\ & = \ dfrac {1} {3} (3) — 2 \\ & = 1 — 2 \\ & = — 1 \ end {align} \)
Итак, еще одна точка на прямой — это \ ((x, y) = (3, –1) \).
Когда у вас есть две точки, вы можете построить их, а затем нарисовать линию. Лучше всего использовать линейку или что-то подобное, чтобы убедиться, что вы нарисовали график как можно лучше.
СОВЕТ: Возможно, вам будет полезно найти три или четыре точки на графике, чтобы вы могли нарисовать его более точно.Для этого просто выберите больше значений x, чтобы найти точки!
Метод 2: Используйте наклон и точку пересечения оси Y
Линейное уравнение, записанное в форме \ (y = mx + b \), называется записанным в форме углового пересечения. Эта форма показывает наклон \ (m \) и точку пересечения оси y \ (b \) графика. Знание этих двух значений позволит вам быстро нарисовать график линейного уравнения, как вы можете видеть в примере ниже.
Пример
Изобразите линейное уравнение:
\ (y = \ dfrac {2} {3} x + 4 \)
Решение
Поскольку это уравнение имеет форму \ (y = mx + b \), вы знаете, что:
- Уклон:
\ (m = \ dfrac {2} {3} \) - Отсечка по оси Y:
\ (b = 4 \)
Давайте сначала посмотрим на точку пересечения по оси Y.
Пересечение оси y — это точка, в которой график пересекает ось y (вертикальная ось). Итак, вы можете изобразить эту точку как:
Теперь рассмотрим наклон. Наклон можно рассматривать как скорость изменения: он представляет изменение \ (y \) по сравнению с изменением \ (x \). Иногда это называется «подъем за пробегом».
\ (\ text {slope} = \ dfrac {\ text {rise}} {\ text {run}} = \ dfrac {\ text {изменение in} y} {\ text {изменение in} x} \)
Для этого примера:
\ (\ text {slope} = \ dfrac {2} {3} = \ dfrac {\ text {change in} y} {\ text {change in} x} \)
Это можно перевести на:
\ (\ dfrac {2} {3} = \ dfrac {\ text {до 2 единиц}} {\ text {на каждые 3 единицы справа}} \)
Следовательно, чтобы найти другую точку на линии, начните с точки пересечения оси Y и пройдите на 3 единицы вправо и на 2 единицы вверх.Сделайте это еще раз, и вы найдете другую точку. Фактически, вы можете продолжать делать это, чтобы найти столько точек, сколько, по вашему мнению, вам понадобится для построения хорошего графика.
Соедините точки, и у вас есть график вашей линейной функции!
Этот метод построения графиков линейных уравнений может применяться, даже если наклон отрицательный или если наклон не дробный, даже если это не так. Следующий пример покажет вам, как это работает!
Пример
Изобразите линейное уравнение:
\ (y = -2x + 1 \)
Решение
Отсечка по оси Y здесь равна 1, поэтому сначала постройте эту точку.
Наклон –2. Хотя это не дробь, ее можно рассматривать как единицу, если принять знаменатель равным 1.
\ (\ text {slope} = -2 = \ dfrac {-2} {1} \)
Другими словами:
\ (\ dfrac {-2} {1} = \ dfrac {\ text {на две единицы вниз}} {\ text {на каждую 1 единицу вправо}} \)
Теперь это можно применить для поиска точек на графике.
Наконец, соедините точки, чтобы нарисовать график линейного уравнения.
СОВЕТ: Если наклон представлен в десятичной форме, посмотрите, можно ли преобразовать его в дробь, чтобы применить этот метод.В противном случае лучше всего подойдет способ 1.
Метод 3. Использование пересечений по осям x и y
При построении графиков линейных уравнений, представленных в форме \ (y = mx + b \), проще всего применить метод 2. Но иногда линейные уравнения задаются в стандартной форме: \ (Ax + By = C \) , где \ (A \), \ (B \) и \ (C \) — положительные или отрицательные целые числа. В этом случае использование точки пересечения по осям x и y может быть самым быстрым подходом.
Пример
Изобразите линейное уравнение:
\ (- 3x + 2y = 6 \)
Решение
Чтобы найти точку пересечения с осью x, то есть точку, в которой график пересекает ось x, положим \ (y = 0 \) и решим относительно \ (x \):
\ (\ begin {align} -3x + 2y & = 6 \\ -3x + 2 (0) & = 6 \\ — 3x & = 6 \\ x & = -2 \ end {align} \)
Чтобы найти точку пересечения оси Y, то есть точку, в которой график пересекает ось Y, положим \ (x = 0 \) и решим относительно \ (y \):
\ (\ begin {align} -3 (0) + 2y & = 6 \\ 2y & = 6 \\ y & = 3 \ end {align} \)
Это дает вам две точки на линии, которые вы можете построить, а затем соединить, чтобы построить график линейного уравнения.
Чтобы узнать больше о x-перехватах и y-перехватах, ознакомьтесь со статьями Understanding x-intercepts и Understanding y-intercepts.
объявление
Сводка
Есть много возможных подходов к построению графиков линейных уравнений. Три распространенных подхода:
- Точки поиска:
выберите простые значения \ (x \) и найдите соответствующие значения \ (y \). Постройте эти точки и используйте их, чтобы построить линию. - Использование наклона и точки пересечения по оси Y:
использует концепцию «превышения высоты над пробегом» и точку пересечения по оси Y для поиска точек на графике. Этот метод особенно полезен, если линия имеет форму пересечения наклона. - Использование пересечений по осям x и y:
позвольте \ (x = 0 \) и \ (y = 0 \) найти точки пересечения графика. Затем используйте эти точки для построения линии. Этот метод полезен, когда линейное уравнение имеет стандартную форму.
Какой метод вы используете, зависит от формы имеющегося у вас линейного уравнения и от того, какой метод вам больше всего подходит.Несмотря ни на что, вы всегда можете найти очки, если застрянете.
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
СвязанныеУзнайте, как построить график правила функции, построить график входов (x) и выходов (y)
В этом видео мы узнаем, как построить график функции.Чтобы построить график функции, вы должны выбрать значения x и подставить их в уравнение. Как только вы подставите эти значения в уравнение, вы получите значение y . Ваши значения x и y составляют ваши координаты для одной точки. Продолжайте вводить значения x, чтобы получить координаты для построения большего количества точек на графике, и тогда вы увидите свою графическую функцию, как только точки будут соединены. Обязательно пометьте свой график. После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь.
Пример построения графика функции Правило
Эти координаты будут выглядеть так:
и
Стенограмма видеоурока
Пример 1
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Пример 2
Давайте выберем значения x, а затем решим соответствующие им значения y.
У нас есть значения x как.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
А теперь нарисуем координаты.
Давайте рассмотрим график функции-правила.
Например:
Давайте выберем значения, а затем решим соответствующие им значения.
У нас есть значения as.
Наша функция.
Итак, давайте заменим значения, чтобы получить значения.
Если
, затем
т.
Если
, затем
т.
Если
, затем
т.
Если
, затем
т.
Если
, затем
т.
Если
, затем
т.
И, наконец, если
, затем
т.
Так что давайте также напишем наши координаты и
Теперь давайте изобразим это.
После соединения точек важно поставить стрелки на обоих концах отрезка линии.
Потому что мы знаем, что эти точки являются точками функции. Но дело не только в этом.
Функция может перемещаться на обоих концах, обозначенных стрелками.
А затем пометьте график.
12.6: Квадрические поверхности — математика LibreTexts
Мы изучали векторы и векторные операции в трехмерном пространстве и разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями , для изучения множества других поверхностей, которые могут быть построены в трехмерной системе координат.
Идентификационные цилиндры
Первая поверхность, которую мы рассмотрим, — это цилиндр. Хотя большинство людей сразу же думают о полой трубке или соломке с газировкой, когда слышат слово «цилиндр», здесь мы используем широкое математическое значение этого термина. Как мы видели, цилиндрические поверхности не обязательно должны быть круглыми. Прямоугольный нагревательный канал представляет собой цилиндр, как и свернутый коврик для йоги, поперечное сечение которого имеет форму спирали. 2 = 9 \) описывает окружность с центром в начале координат и радиусом \ (3 \).2 = 9 \) представляет собой цилиндр радиуса \ (3 \) с центром на оси \ (z \). Это продолжается бесконечно в положительном и отрицательном направлениях.
Определение: цилиндры и линейки
Набор линий, параллельных заданной линии, проходящей через заданную кривую, известен как цилиндрическая поверхность или цилиндр . Параллельные линии называются постановлениями .
Из этого определения мы можем видеть, что у нас все еще есть цилиндр в трехмерном пространстве, даже если кривая не является окружностью.2 = 25 \) представляет собой цилиндр радиуса \ (5 \) с центром на оси \ (y \).
г. В этом случае уравнение содержит все три переменные — \ (x, y, \) и \ (z \) — поэтому ни одна из переменных не может изменяться произвольно. Самый простой способ визуализировать эту поверхность — использовать компьютерную утилиту для построения графиков (рис. \ (\ PageIndex {4} \)).
Рисунок \ (\ PageIndex {4} \)c. В этом уравнении переменная \ (z \) может принимать любое значение без ограничений. Следовательно, линии, составляющие эту поверхность, параллельны оси \ (z \).2 \).
- Подсказка
Переменная \ (x \) может принимать любое значение без ограничений.
- Ответ
При рисовании поверхностей мы увидели, что полезно рисовать пересечение поверхности с плоскостью, параллельной одной из координатных плоскостей. Эти кривые называются следами. Мы можем увидеть их на графике цилиндра на рисунке \ (\ PageIndex {6} \).
Определение: следы
Следы поверхности — это поперечные сечения, созданные, когда поверхность пересекает плоскость, параллельную одной из координатных плоскостей.
Трассы полезны при рисовании цилиндрических поверхностей. Однако для трехмерного цилиндра полезен только один набор следов. Обратите внимание на рис. \ (\ PageIndex {6} \), что след графика \ (z = \ sin x \) на плоскости xz полезен при построении графа. Однако след на плоскости xy представляет собой просто серию параллельных линий, а след на плоскости yz — это просто одна линия.
Рисунок \ (\ PageIndex {6} \): (a) Это один вид графика уравнения \ (z = \ sin x \). (b) Чтобы найти след графа на плоскости \ (xz \), положим \ (y = 0 \). След — это просто двумерная синусоида.Цилиндрические поверхности образованы набором параллельных линий. Однако не все поверхности в трех измерениях строятся так просто. Теперь мы исследуем более сложные поверхности, и следы являются важным инструментом в этом исследовании.
Квадрические поверхности
Мы узнали о трехмерных поверхностях, описываемых уравнениями первого порядка; это самолеты.2} = 1. \) Установите \ (x = 0 \), чтобы увидеть след эллипсоида на плоскости yz . Чтобы увидеть следы в плоскостях \ (xy \) — и \ (xz \) -, установите \ (z = 0 \) и \ (y = 0 \) соответственно. 2} = 1.2} = 1 \) в плоскости \ (xy \), когда мы положим \ (z = 0 \). (b) Когда мы устанавливаем \ (y = 0 \), мы получаем след эллипсоида в \ (xz \) — плоскости, который является эллипсом. (c) Когда мы устанавливаем \ (x = 0 \), мы получаем след эллипсоида в \ (yz \) — плоскости, который также является эллипсом.
Теперь, когда мы знаем, как выглядят следы этого твердого тела, мы можем нарисовать поверхность в трех измерениях (рис. \ (\ PageIndex {8} \)).
Рисунок \ (\ PageIndex {8} \): (a) Следы служат основой для поверхности. (б) Центр этого эллипсоида — начало координат.2} = 1 \) (см. Следующий рисунок).Гиперболоиды одного листа обладают удивительными свойствами. Например, они могут быть построены с использованием прямых линий, как в скульптуре на рисунке \ (\ PageIndex {1a} \). На самом деле градирни для атомных электростанций часто строят в форме гиперболоида. Строители могут использовать в конструкции прямые стальные балки, что делает башни очень прочными при использовании относительно небольшого количества материала (рис. 2} {100} = \ dfrac {z} {4}, \), где — фокус точка рефлектора?
Рисунок \ (\ PageIndex {12} \): энергия отражается от параболического отражателя и собирается в фокусной точке.2 + Dxy + Exz + Fyz + Gx + Hy + Jz + K = 0. \]На следующих рисунках приведены наиболее важные из них.
Рисунок \ (\ PageIndex {13} \): Характеристики общих квадратичных поверхностей: эллипсоид, гиперболоид одного листа, гиперболоид двух листов. Рисунок \ (\ PageIndex {14} \): Характеристики общих квадратичных поверхностей: эллиптический конус, эллиптический параболоид, гиперболический параболоид.Пример \ (\ PageIndex {5} \): определение уравнений квадратичных поверхностей
Определите поверхности, представленные данными уравнениями.2} {9} = 1. \ nonumber \]
Итак, это, на самом деле, эллипсоид с центром в начале координат.
г. Сначала заметим, что член \ (z \) возведен только в первую степень, так что это либо эллиптический параболоид, либо гиперболический параболоид. 2} {9} = z.2 + 2z − 10 = 0. \)
- Подсказка
Посмотрите на знаки и степени членов \ (x, y \) и \ (z \)
- Ответ
Гиперболоид из одного листа с центром в \ ((0,0,1) \).
Исчисление III — Функции нескольких переменных
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиПохоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-5: Функции нескольких переменных
В этом разделе мы хотим рассмотреть некоторые основные идеи о функциях более чем одной переменной.2} — 4 \).
Это эллиптический параболоид, являющийся примером квадратичной поверхности. Некоторые из них мы видели в предыдущем разделе. В дальнейшем в исчислении III мы будем довольно часто видеть квадратичные поверхности.
Другой распространенный график, который мы будем часто видеть в этом курсе, — это график плоскости. У нас есть соглашение для построения графиков плоскостей, которое упростит их построение и, надеюсь, визуализацию.
Напомним, что уравнение плоскости задается формулой
. \ [ax + by + cz = d \], или если мы решим это для \ (z \), мы можем записать его в терминах обозначения функций.Это дает,
\ [f \ left ({x, y} \ right) = Ax + By + D \]Для построения графика плоскости мы обычно находим точки пересечения с тремя осями, а затем строим треугольник, соединяющий эти три точки. Этот треугольник будет частью плоскости и даст нам довольно хорошее представление о том, как должна выглядеть сама плоскость. Например, давайте изобразим плоскость в виде
. \ [f \ left ({x, y} \ right) = 12 — 3x — 4y \]Для построения графика, вероятно, было бы проще записать это как
\ [z = 12 — 3x — 4y \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} \, \, \, \, \, 3x + 4y + z = 12 \]Теперь каждая из точек пересечения с тремя главными осями координат определяется тем фактом, что две из координат равны нулю. Например, пересечение с осью \ (z \) — определяется как \ (x = y = 0 \). Итак, три точки пересечения:
\ [\ begin {align *} & x — {\ mbox {axis:}} \ left ({4,0,0} \ right) \\ & y — {\ mbox {axis:}} \ left ({0 , 3,0} \ right) \\ & z — {\ mbox {axis:}} \ left ({0,0,12} \ right) \ hspace {0.25 дюймов} \ end {align *} \]Вот график самолета.
Теперь, если продолжить, графики функций вида \ (w = f \ left ({x, y, z} \ right) \) будут четырехмерными поверхностями. Конечно, мы не можем нанести их на график, но не помешает указать на это.
Далее мы хотим поговорить об областях функций более чем одной переменной. Напомним, что домены функций одной переменной \ (y = f \ left (x \ right) \) состояли из всех значений \ (x \), которые мы могли подключить к функции и получить обратно действительное число.Теперь, если мы подумаем об этом, это означает, что область определения функции одной переменной — это интервал (или интервалы) значений из числовой прямой или одномерного пространства.
Область функций двух переменных, \ (z = f \ left ({x, y} \ right) \), является областями из двухмерного пространства и состоит из всех пар координат, \ (\ left ({x, y} \ right) \), чтобы мы могли подключиться к функции и получить действительное число.
Пример 1 Определите домен каждого из следующих.2}} \ справа) \) Показать все решения Скрыть все решения a \ (f \ left ({x, y} \ right) = \ sqrt {x + y} \) Показать решениеВ данном случае мы знаем, что не можем извлечь квадратный корень из отрицательного числа, поэтому это означает, что мы должны требовать,
\ [х + у \ ge 0 \]Вот набросок графика этого региона.
b \ (f \ left ({x, y} \ right) = \ sqrt x + \ sqrt y \) Показать решение
Эта функция отличается от функции в предыдущей части.2}> 16 \]
Итак, область определения этой функции — это набор точек, полностью лежащих вне сферы радиуса 4 с центром в начале координат.
Следующая тема, которую мы должны рассмотреть, — это кривых уровня или контурных кривых . Кривые уровня функции \ (z = f \ left ({x, y} \ right) \) — это двумерные кривые, которые мы получаем, полагая \ (z = k \), где \ (k \) — любое число. Итак, уравнения линий уровня: \ (f \ left ({x, y} \ right) = k \).Обратите внимание, что иногда уравнение будет иметь вид \ (f \ left ({x, y, z} \ right) = 0 \), и в этих случаях уравнения кривых уровня имеют вид \ (f \ left ({x, y, k} \ right) = 0 \).
Вы, наверное, уже видели кривые уровня (или контурные кривые, как бы вы их ни называли) раньше. Если вы когда-нибудь видели карту высот для участка земли, это не что иное, как контурные кривые для функции, которая показывает высоту земли в этой области. Конечно, у нас, вероятно, нет функции, которая дает высоту, но мы можем, по крайней мере, изобразить контурные кривые.2}} \]
Вспомните из раздела «Квадрические поверхности», что это верхняя часть «конуса» (или поверхности в форме песочных часов).
Обратите внимание, что этого не требовалось для решения этой проблемы. Это было сделано для практики распознавания поверхности, и это может пригодиться в будущем.
А теперь перейдем к реальной проблеме. Кривые уровня (или контурные кривые) для этой поверхности задаются уравнением, которое находится путем замены \ (z = k \).2} \]
, где \ (k \) — любое число. Итак, в этом случае кривые уровня представляют собой окружности радиуса \ (k \) с центром в начале координат.
Мы можем построить график одним из двух способов. Мы можем либо изобразить их на самой поверхности, либо изобразить в двухмерной системе осей. Вот каждый график для некоторых значений \ (k \).
Обратите внимание, что мы можем думать о контурах в терминах пересечения поверхности, которая задается \ (z = f \ left ({x, y} \ right) \) и плоскостью \ (z = k \).Контур будет представлять собой пересечение поверхности и плоскости.
Для функций вида \ (f \ left ({x, y, z} \ right) \) мы время от времени будем смотреть на поверхностей уровня . Уравнения поверхностей уровня задаются формулой \ (f \ left ({x, y, z} \ right) = k \), где \ (k \) — любое число.
Последняя тема в этом разделе — трассировок . В чем-то они похожи на контуры. Как отмечалось выше, мы можем думать о контурах как о пересечении поверхности, задаваемой \ (z = f \ left ({x, y} \ right) \), и плоскости \ (z = k \). 2} \ hspace {0.2} \]
, а вот и эскизы кейса.
3D плоттер | Academo.org
Эта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности. График можно увеличивать, прокручивая мышью, и вращать, перетаскивая.Щелчок по графику покажет значения x, y и z в этой конкретной точке.
В таблице ниже перечислены функции, которые можно вводить в поле выражения.
| Выражение | Описание |
|---|---|
| sin (x) | Синус x в радианах |
| cos (x) | Косинус x в радианах |
| желто-коричневый (x) | Тангенс x в радианах |
| asin (x), acos (x), atan (x) | Обратная из трех тригонометрических функций, перечисленных выше |
| sqrt (x) | Квадратный корень из x (только для положительного x) |
| журнал (x) | Натуральный логарифм x |
| pow (x, y) | Степень x к y |
Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше \ (y \), и \ (x \) во всех областях, где x равен , а не больше y.
Ползунок разрешения можно использовать для увеличения количества точек данных, отображаемых на графике, что дает более плавный конечный результат, но поскольку для этого требуется больше вычислительной мощности, вы можете заметить небольшое снижение частоты кадров при взаимодействии с графиком.
Каждый раз, когда вы нажимаете кнопку «Рассчитать», URL-адрес обновляется с вашими текущими настройками, что означает, что вы можете поделиться ссылкой прямо на график по вашему выбору, не набирая значения в настройках.
Обратите внимание: если ваша поверхность содержит комплексные числа, будет отображена только действительная часть.
Пожалуйста, включите JavaScript, чтобы просматривать комментарии от Disqus. .