Калькулятор онлайн для расчетов процентов, дробей, степеней
Калькулятор давно и прочно вошел в нашу жизнь. Мы часто пользуемся им в повседневной жизни подбивая свои расходы за день, неделю, рассчитывая выплату коммунальных за месяц и т.д. С помощью онлайн калькулятора осуществляют простые арифметические расчеты студенты и школьники, продавцы в магазинах, торговцы на рынках, работники коммунальных служб, что позволяет сэкономить время, получить точные расчеты, избежать досадных ошибок.
| Клавиша | Символ | Операция |
|---|---|---|
| pi | pi | Постоянная pi |
| е | е | Число Эйлера |
| % | % | Процент |
| ( ) | ( ) | Открыть/Закрыть скобки |
| , | , | Запятая |
| sin | sin (α) | Синус угла |
| cos | cos (β) | Косинус |
| tan | tan (y) | Тангенс |
| sinh | sinh () | Гиперболический синус |
| cosh | cosh () | Гиперболический косинус |
| tanh | tanh () | Гиперболический тангенс |
| sin-1 | asin () | Обратный синус |
| cos-1 | acos () | Обратный косинус |
| tan-1 | atan () | Обратный тангенс |
| sinh-1 | asinh () | Обратный гиперболический синус |
| cosh-1 | acosh () | Обратный гиперболический косинус |
| tanh-1 | atanh () | Обратный гиперболический тангенс |
| x2 | ^2 | Возведение в квадрат |
| х3 | ^3 | Возведение в куб |
| xy | ^ | Возведение в степень |
| 10x | 10^() | Возведение в степень по основанию 10 |
| ex | exp () | Возведение в степень числа Эйлера |
| vx | sqrt (x) | Квадратный корень |
| 3vx | sqrt3 (x) | Корень 3-ей степени |
| yvx | sqrt (x,y) | Извлечение корня |
| log2x | log2 (x) | Двоичный логарифм |
| log | log (x) | Десятичный логарифм |
| ln | ln (x) | Натуральный логарифм |
| logyx | log (x,y) | Логарифм |
| I / II | Сворачивание/Вызов дополнительных функций | |
| Unit | Конвертер величин | |
| Matrix | Матрицы | |
| Solve | Уравнения и системы уравнений | |
| Построение графиков | ||
| Дополнительные функции (вызов клавишей II) | ||
| mod | mod | Деление с остатком |
| ! | ! | Факториал |
| i / j | i / j | Мнимая единица |
| Re | Re () | Выделение целой действительной части |
| Im | Im () | Исключение действительной части |
| |x| | abs () | Модуль числа |
| Arg | arg () | Аргумент функции |
| nCr | ncr () | Биноминальный коэффициент |
| gcd | gcd () | НОД |
| lcm | lcm () | НОК |
| sum | sum () | Суммарное значение всех решений |
| fac | factorize () | Разложение на простые множители |
| diff | diff () | Дифференцирование |
| Deg | Градусы | |
| Rad | Радианы | |
Виды калькуляторов
В зависимости от возможностей и сферы применения калькуляторы бывают простые, бухгалтерские, финансовые, инженерные.
- Бухгалтерскими калькуляторами пользуются бухгалтера и кассиры для арифметических расчетов с денежными суммами.
- Для финансовых расчетов пользуются финансовыми калькуляторами, у которых к стандартному набору математических функций добавлены операции со сложными процентами и функции, характерные для банковской сферы и финансовых приложений.
- Специализированные — это калькуляторы, применяемые для вычислений в конкретной сфере деятельности (строительные, ипотечные, статистические, медицинские).
- Печатающие — калькуляторы, которые с помощью печатающего устройства выводят полученные результаты, расчеты, графики и вычисления на бумажную ленту.
Отдельно выделяются:
- программируемые калькуляторы, используемые для выполнения сложных вычислений по заранее заложенной программе пользователя;
- графические, выполняющие построение и отображение графиков функций.

Простейший калькулятор предназначен выполнять ординарные арифметические расчеты (сложение, вычитание и т.п.), вычислять процент, извлекать квадратный корень, возводить число в степень. Помимо простых расчетов, строителям и архитекторам, инженерно-техническим и научным работникам, математикам и геодезистам, старшеклассникам и студентам технических специальностей очень часто приходится решать важнейшие инженерные задачи, осуществлять сложные математические расчеты.
Представленный на сайте тригонометрический калькулятор выполняет расчет:
- синусов;
- косинусов;
- тангенсов;
- котангенсов.
А также обратных тригонометрических функций:
- арксинусов;
- арккосинусов;
- арктангенсов;
- арккотангенсов.
Все тригонометрические расчеты с углами выполняются в радианах, градах и градусах.
На нашем сайте вы сможете пользоваться инженерным онлайн калькулятором, предназначенным для инженерных и научных расчетов разного уровня сложности.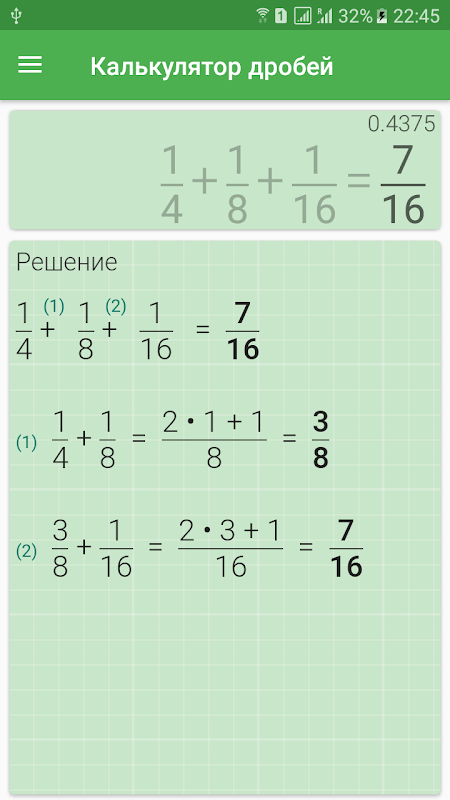
Инженерный калькулятор позволяет:
- производить сложные расчеты с дробями;
- возводить любое число в степень, извлекать корень из числа;
- рассчитать онлайн проценты, логарифмы, интегралы любой сложности;
- выполнять необходимые математические операции с одной или несколькими матрицами;
- находить производную онлайн как от элементарной, так и от сложной функции;
- решать алгебраические, линейные, логарифмические, тригонометрические и другие уравнения.
Онлайн калькулятор прост и понятен в обращении, применять его не составит труда тем, кто пользуется настольным инженерным калькулятором, принципы работы функций и программ аналогичны. По своему виду инженерный калькулятор онлайн имитирует настоящий калькулятор, поэтому для ознакомления с ним вам не понадобится много времени.
Калькулятор уравнений, интегралов, производных, пределов и пр.
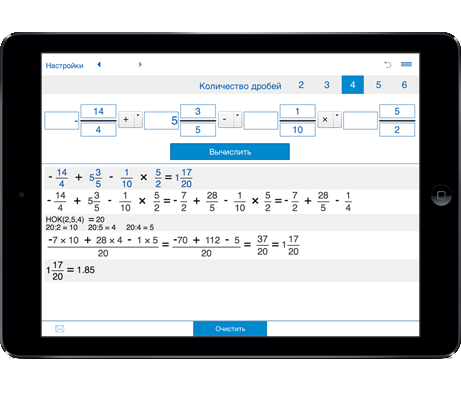
Онлайн-калькулятор позволяет решать математические выражения любой сложности с выводом подробного результата решения по шагам. Также универсальный калькулятор умеет решать уравнения, неравенства, системы уравнений/неравенств и выражения с логарифмами, вычислять пределы функций, определенные/неопределенные интегралы и производные любого порядка (дифференцирование), производить действия с комплексными числами, калькулятор дробей и пр.
Также универсальный калькулятор умеет решать уравнения, неравенства, системы уравнений/неравенств и выражения с логарифмами, вычислять пределы функций, определенные/неопределенные интегралы и производные любого порядка (дифференцирование), производить действия с комплексными числами, калькулятор дробей и пр.
Пояснения к калькулятору
- Для решения математического выражения необходимо набрать его в поле ввода с помощью предложенной виртуальной клавиатуры и нажать кнопку ↵.
- Управлять курсором можно кликами в нужное местоположение в поле ввода или с помощью клавиш со стрелками ← и →.
- ⌫ — удалить в поле ввода символ слева от курсора.
- C — очистить поле ввода.
- При использовании скобок ( ) в выражении в целях упрощения может производится автоматическое закрытие, ранее открытых скобок.
- Для того чтобы ввести смешанное число или дробь необходимо нажать кнопку ½, ввести сначала значение числителя, затем нажать кнопку со стрелкой вправо → и внести значение знаменателя дроби.
 2}(решить неравенство)
2}(решить неравенство)Решение систем уравнений и неравенств
Системы уравнений и неравенств также решаются с помощью онлайн калькулятора. Чтобы задать систему необходимо ввести уравнения/неравенства, разделяя их точкой с запятой с помощью кнопки ;.
Вычисление выражений с логарифмами
В калькуляторе кнопкой loge(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: loge(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$
$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)Вычисление пределов функций
Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim.

Решение интегралов
Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
∫ f(x) — для неопределенного интеграла;
ba∫ f(x) — для определенного интеграла.В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.
Вычисление производных
Математический калькулятор может дифференцировать функции (нахождение производной) произвольного порядка в точке «x». Ввод производной в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:
f'(x) — производная первого порядка;
f»(x) — производная второго порядка;
f»'(x) — производная третьего порядка.
fn(x) — производная любого n-о порядка.Действия над комплексными числами
Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.

как возвести число в дробную степень примеры
Как возвести число в дробную степень, если не представлять, как это работает, то можно, наверное, свихнуться! Но друзья мои! Я с вами и сегодня мы разберемся в такой непонятной
вещи, как число в дробной дроби!Видео: Как возвести число в дробную степень примеры
С самого начала выясним, что такое дробь, что я понимаю под этим – мы будем рассматривать дробь вида, например, как неудобная дробь 1/3, мы не будем сейчас обсуждать именно такую дробь и почему она очень неудобная в десятичном виде и десятичных степенях мы поговорим в другой раз!
И конечно же будем разбираться вместе с примерами и потом, мы уже… как раз сегодня доделали работу нашего калькулятора. Который мы научили работать с дробями!
Который мы научили работать с дробями!Как вообще считать числа в степени дроби!?
Если степень числа равна дроби, то это число можно представить, как корень в степени знаменателя из числа в степени числителя.
Мы как-то уже размещали картинку, когда разбирались с разными корнями и степенями: Если не совсем понятно! То давайте приведём пример, который для меня всегда остается эталоном и если я когда забываю, то сразу вспоминаю эту схему:
Чему равно число в степени одна третья!? Кубическом корню из этого числа! Единицу мы не видим, потому, что число в степени 1 будет число.Как возвести число в степень примеры
Для примера мы можем взять число 8 в степени одна третья и это будет равно кубическому корню из 8, что в свою очередь равно 2.81/3 = 3√8 =2
Какая скукотища – вы должны сказать! И вот мы подошли к самом интересному, из-за чего мы сделали данную страницу! «>Возвести число в дробную степень онлайн калькулятор. Мы уже писали, как возводить в любую степень, и сегодня же решили сделать возведение числа в дробь в нашем калькуляторе! Как мы видим. Что степень не активна, и она таковой останется до тех пор, пока вы не выберете то число, которое хотите возвести в степень дроби. 1.Не будем далеко ходить, возьмем то же число 8, как мы и делали сверху! Нажимаем кнопку 8. 2.Нажимаем кнопку степени – это кнопка «P»
Как видим, кнопка степени стала активна, и справа сверху табло, так же высветлялась буква P
3.После этого набираем нашу дробь… 1/3 и равно = 4.Видим результат возведения числа в степень дроби.Написать что-нибудь…
как возвести число в дробную степень , программа возводящая число в степень , возвести число в дробную степень онлайн , калькулятор возвести число в дробную степень , что значит возвести число в степень , возвести число в дробную степень онлайн калькулятор , как возвести число в степень в дробях , как возвести число в степень примеры , число в степени дроби , степень числа в виде дроби , число со степенью дробь , как возвести число в степень в дробях , возведение числа в степень дроби , число в степени дробь как решать , как считать числа в степени дроби , калькулятор чисел со степенями и дробями , возведение числа в степень десятичной дроби ,Отрицательная степень чисел и дробей
Что такое степень числа
В учебниках по математике можно встретить такое определение:
«Степенью n числа а является произведение множителей величиной а n-раз подряд»
где
a — основание степени
n — показатель степени
Соответственно, an= a · a · a · a.
 .. · a
.. · aЧитается такое выражение, как a в степени n
Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить данное число (основание степени) на само себя.
А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например число 2, то она решается довольно просто:
- 23 = 2 · 2 · 2, где
- 2 — основание степени
- 3 — показатель степени
Действия, конечно, можно выполнять и на калькуляторе. Их выбор велик, а доступность иногда на расстоянии одного клика в онлайн. Всё это безусловно можно использовать, но сейчас нам важно подробно разобрать принцип работы, чтобы не упасть в грязь лицом на контрольной по математике.
Таблица степеней
Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).
Число
Вторая степень
Третья степень
1
1
1
2
4
8
3
9
27
4
16
64
5
25
125
6
36
216
7
49
343
8
64
512
9
81
729
10
100
1000
Свойства степеней: когда складывать, а когда вычитать
Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления.
 Всего их пять штук — ниже мы их рассмотрим.
Всего их пять штук — ниже мы их рассмотрим.Свойство 1: произведение степеней
При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:
a — основание степени
m, n — показатели степени, любые натуральные числа.
Свойство 2: частное степеней
Когда мы делим степени с одинаковыми основаниями, то основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n
Свойство 3: возведение степени в квадрат
Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.
a — основание степени (не равное нулю)
m, n — показатели степени, натуральное число
Свойство 4: степень возведения
При возведении в степень произведения каждый из множителей возводится в степень.
 Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.a, b — основание степени (не равное нулю)
n — показатели степени, натуральное число
Свойство 5: степень частного
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
a, b — основание степени (не равное нулю), любые рациональные числа, b ≠ 0,
n — показатель степени, натуральное число
Степень с показателем 0
Любое целое a ≠ 0 в степени 0 равно 1.
Выражение 0 в степени 0 многие математики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0;0).
Степень с отрицательным показателем
Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:
К примеру, 4 в минус 2 степени — это 1/42, 2 в минус 3 степени — это 1/23, 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 (0,1).

Примеры
Степени с отрицательным показателям помогают компактно записывать крайне малые или постоянно уменьшающиеся величины. Например, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10-9). В школьной программе такие величины редкость: чаще всего используют 10 в минус 1 степени или 2 в минус 1 степени.
Чтобы разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с одинаковыми основаниями.
Деление степеней с разными основаниями, но одинаковыми показателями осуществляется по следующей формуле: показатели отнимаются, а основание остается неизменным.
Поэтому если степень делимого будет меньше степени делителя, то в результате получится число с отрицательной степенью:
a3 a6=a3 — 6 = a-3
Если записать деление в виде дроби, то при сокращении в числителе останется 1, а в знаменателе число будет иметь положительную степень:
Действия с отрицательными степенями
Умножение отрицательных степеней
При умножении отрицательных степеней с одинаковыми основаниями показатели степеней складываются:
am · an = am + n
Примеры
Деление отрицательных степеней
При делении отрицательных степеней с одинаковыми основаниями из показателя степени делимого вычитается показатель делителя:
Примеры
Возведение дроби в отрицательную степень
Чтобы возвести дробь в отрицательную степень, надо возвести в эту степень отдельно числитель и знаменатель:
Возведение произведения в отрицательную степень
Чтобы возвести произведение в отрицательную степень, необходимо возвести в эту степень каждый множитель произведения отдельно:
У нас есть отличная статья на тему — формулы сокращенного умножения, тебе стоит повторить ее!
Упростить выражение.
 Онлайн калькулятор с примерами
Онлайн калькулятор с примерамиЧто значит упростить выражение
Когда говорят упростить выражение, подразумевают конкретные математические действия с этим выражением, в результате чего оно примет иной вид.
Такими действиями могут быть раскрытие скобок, внесение и вынесение множителя за скобку, деление (сокращение), умножение, возведение в степень, приведение дробей к общему знаменателю и много других операций.
При этом часто используют формулы сокращенного умножения и теоремы, а в тригонометрии от простых формул приведения до самых сложных тригонометрических выражений.
Чем старше школьник, тем больше формул он знает и обладает богатым арсеналом математических действий.
В чем смысл таких действий
Задачи на упрощение выражений встречаются с самых младших классов. Дети сами того не осознавая, учатся шевелить мозгами в нужном направлении, чтобы преобразовать одно выражение в другое.
Разумеется, все задания составляются таким образом, что в любом случае они приводятся к более простому виду или подходящему для дальнейших операций.

Однако, при таком подходе теряется общий смысл поставленной задачи.
Когда ученик слышит, что надо что-то упростить, то машинально начинает перебирать всевозможные математические действия в голове, не задаваясь вопросом, а для чего упрощать?
Приведем наглядный пример
Допустим, сказано упростить выражение (a+b)2. В этом случае абсолютно каждый нормальный школьник раскроет скобки и будет доволен самим собой. Без сарказма это действительно так и это нормально.
Но вот другая постановка задачи: упростите выражение (a+b)2, затем подставьте следующие числовые значения a=⅔, b=⅓ и запишите получившееся число.
Кто теперь скажет, что раскрыть скобки, затем подставить a=⅔ и b=⅓, а затем вычислить ответ, это легче, чем сразу найти a+b=⅔+⅓=1? После этого возводи единицу хоть в сотую степень!
Заключение
Итак, главная цель задач на упрощение выражений в том, чтобы научить вас применять те или иные математические действия над выражениями.

Это обязательно нужно уметь делать. Но более важная проблема в том, чтобы научиться применять необходимые действия в нужный момент и воспользоваться результатом преобразования.
Благо есть онлайн калькуляторы упрощения выражений, например, такой как наш, с помощью которого можно проверить свои вычислительные результаты.
Желаем успехов!
Решение корней в онлайн калькуляторе
Решение корней — одна из многих функций, которой обладает бесплатный калькулятор, размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени калькулятор онлайн посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.
 д.
д.Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня.
 Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице кнопки калькулятора онлайн.
Извлечение квадратного корня
Нажатие этой кнопки вставит в строке ввода запись извлечения из квадратного корня: sqrt(x), вам нужно только внести подкоренное выражение и закрыть скобку.
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень.
 Она вставляет в строке ввода запись sqrt3(x).
Она вставляет в строке ввода запись sqrt3(x).Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n. В противном же случае расчет получится приблизительным, хотя и очень близким к идеалу, так как точность вычислений онлайн калькулятора достигает 14 знаков после запятой.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих.
 Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.Пример, как извлечь корень из корня:
Степень в корне
Выполняя извлечение корня степени, следует помнить, что по свойству корней степень самого корня и степень под корнем по возможности сокращаются на наибольший общий делитель (НОД). Кстати, функционал калькулятора включает также нахождение НОД, подробнее на странице дополнительные функции.
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени:
Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>
Действия с дробями
Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматься действия с обыкновенными дробями.
 Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой,
отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно
они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине
школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются
в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби
особых затруднений не вызывают. Итак, вперёд!
Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой,
отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно
они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине
школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются
в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби
особых затруднений не вызывают. Итак, вперёд!Две дроби и называются равными, если .
Например, , так как
Равными также являются дроби и (так как ), и (так как ).

Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
;
.
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь .
 Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
Числа 36 и 48 имеют наибольший общий делитель 12. Тогда.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробь называется несократимой.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
.
Решение. Для разложения числителя на множители, представив предварительно одночлен — 5xy в виде суммы — 2xy — 3xy, получим
Для разложения знаменателя на множители используем формулу разности квадратов:
.

В результате
.
Далее, изменяя знаки в числителе и знаменателе дроби, получим
Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим
.
Умножив числитель и знаменатель дроби на 5, получим
.
Итак, дроби приведены к общему знаменателю:
.
Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:
,
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и .
 Рассуждая, как в
предыдущем примере, получим
Рассуждая, как в
предыдущем примере, получим,
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.
Так как 120:4=5, то чтобы записать дробь со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным множителем. Значит .
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим .
Итак, данные дроби приведены к общему знаменателю.
Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.
Сложение дробей определяется следующим образом:
.
Например,
.
Если b = d, то
.
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,
.
Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,
.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Теперь рассмотрим пример сложения дробных выражений с переменными.

Пример 3. Преобразовать в одну дробь выражение
.
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:
1) ;
2) ;
3) .
Наименьший общий знаменатель:
Дополнительные множители, на которые умножаются числители дробей:
1) 6;
2) ;
3) .
Результат этого умножения:
.
Далее, раскрывая скобки и выполняя тождественные преобразования, получаем
.
Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей, т. е. .
Например,
.

При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого — на числитель делителя, т. е. .
Например,
.
1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .
2. Из пропорции вытекают следующие пропорции: , , , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно произведение крайних (средних) членов пропорции разделить на известный средний (крайний) член пропорции: и .
В высшей математике это действие с дробями чаще всего применяется при интегрировании рациональных функций. Поэтому оно подробно разобрано в уроке Интегрирование рациональных функций и метод неопределённых коэффициентов.

Другие темы в блоке «Школьная математика»
2-1Пример задачи Тираж Количество решаемых уравнений: 23456789 Пример задачи Решить Введите неравенство в график, например.  грамм. y
грамм. yПример задачи Тираж Количество решаемых неравенств: 23456789 Пример задачи Решить Наших пользователей:
Я никогда ничего подобного не видел! Постепенно я учу сложную алгебру вместе со своими детьми!
Лиза Шустер, Нью-ЙоркПока все отлично!
М. Б., Иллинойс
Б., Иллинойс Переезжать из города в город сложно, особенно когда нужно понимать, как преподает каждый учитель. С Алгебратором кажется, что есть только один учитель, и хороший тоже. Теперь мне не нужно беспокоиться о том, чтобы справиться с алгеброй. Я ищу помощи и в других областях.
Питер Гудман, TNСтуденты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2010-04-15:
- рабочий лист по математике для ks2
- лаплас для чайников
- прентис холл математика алгебра один
- общая викторина для второклассников
- Советы по алгебре для детей
- www.math trivia.com
- как вычесть десятичные дроби powerpoint
- Семерка — это неправильное число, как вы можете сделать это даже без сложения, вычитания, умножения или деления
- добавление 5 или 6 к числовому листу
- упрощающий калькулятор абсолютных значений
- пример перестановок начальная школа
- пример программы операций с квадратной формулой с использованием базового
- программное обеспечение
- учебники по компасу для курсов повышения квалификации по математике
- площадь без математических расчетов
- сравнение рабочих листов для упорядочивания целых чисел
- простой способ вычисления дробей
- делительный и умножающий радикал
- решение дробных показателей
- добавить отрицательные положительные целые числа для печати бесплатно
- клен решить комплексное уравнение
- решить нелинейное уравнение символьной Matlab
- Исчисление CLEP Бесплатное онлайн-руководство
- Калькулятор сложения и вычитания радикальных выражений
- комбинация упражнений по математике
- заданий по алгебре для 6 класса
- алгебраические уравнения для дробей
- алгебраические уравнения экспоненциальные
- решение квадратных уравнений с отрицательными показателями
- математика ответы читы
- загрузить visual ti 84
- как взять 2 цифры после десятичной точки + java
- преобразовать y перехватить javascript
- Интересные мелочи по математике
- математическая культура один в майя
- структура и метод алгебры и тригонометрии макдугала литтеля
- завершение упражнения на решение квадратных квадратичных листов
- бухгалтерская книга + pdf
- саксонская алгебра 1 ответы
- парабола, изображения
- как решить дифференциальное уравнение с помощью Matlab
- поиск в google / практический тест gre / перестановка
- бесплатные математические распечатки
- пример математических мелочей с ответами за 4 класс
- как упростить показатели с помощью переменных
- алгебра нахождение вершин по формуле корней
- рабочие листы положительное отрицательное сложение вычитание
- слово проблема-образец и решения
- деление квадратного корня на дробь
- учиться prealegbra онлайн бесплатно
- калькулятор трехчленов
- алгебра, используемая в сети
- Калькулятор квадратного уравнения
- рудок «глава 6», №7
- онлайн-эмулятор калькулятора ти-84
- бесплатные экзаменационные работы
- завершение математики квадратов
- дискретная математика
- рабочий лист «уравнения баланса» математика
- вопросов по практике квадратичных функций 10 класс
- книга по математике формула 1 C3 экзамен по графику
- что такое разложение знаменателя на простые множители
- квадратный корень с использованием множителей
- Завершение квадратной конструкции
- Показатели по математике в шестом классе Калькулятор делителей
- справка по распространенным ошибкам при сложении и вычитании радикальных выражений
- квадратные и квадратные корни, кубы и куберы
- онлайн-калькулятор с графиком гипербола
- Калькулятор квадратного корня из дроби
- ks3 запись формулы рабочего листа
- программное обеспечение для моделирования texas ti-83
- Упростить калькулятор квадратного корня
- решение уравнений 3-й степени
- преобразование десятичного числа в другое основание
- Урок элементарной алгебры
- Рабочие листы по алгебре KS2
- Порядок операций решения логарифмов
- изменение предмета n алгебраических формул бесплатные рабочие листы
- Калькулятор алгебры для продвинутых пользователей
- решить систему на TI 83
- Как понимать алгебру
- Печатные листы с координатами для 5-х классов
- математика мелочи с ответами математика
- упростить вычисление корня
- как решить квадратные уравнения, используя две точки
- однородный дифференциал
- вопросов по начальной математике «Экзамены»
- алгебра сложения пирамид
- вычислить наибольший общий делитель
- TI-83 ROM скачать
- алгебра powerpoint на пропорциях
- тесты по математике за седьмой год
- Упрощение алгебры деление на калькуляторе
- образец онлайн-экзамена
- понятия дробей и квадратных корней
- решение однородных уравнений
- год 8 учеников задачи по математике
Калькулятор дробной степени
Этот калькулятор дробной степени подскажет вам — сюрприз, сюрприз — дробные показатели степени.
 Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения.
Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения.Дробные показатели с числителем 1
Дробные показатели — это способ выражения степеней, а также корней в одной нотации .
Что именно это означает? Давайте сначала рассмотрим несколько простых примеров, где наш числитель равен 1 :
.- 64 (1/2) = √64
- 27 (1/3) = ³√27
Из приведенных выше уравнений мы можем вывести, что:
- Показатель степени 1/2 — это квадратный корень
- Показатель степени 1/3 — кубический корень
- Показатель степени 1/4 — корень четвертой степени
- …
- Показатель степени 1 / k является корнем k-й степени
Но почему это так? Постараемся это доказать:Давайте воспользуемся законом экспонент, который гласит, что мы можем складывать показатели при умножении двух степеней с одинаковым основанием:
x a + b = x a * x b
так, например, если n = 2
x² = x¹⁺¹ = x¹ * x¹ = x * x
Попробуйте это с любым числом, которое вам нравится, это всегда правда!
Затем давайте посмотрим на дробные показатели x:
x = x¹ = x (1/2 + 1/2) = x (1/2) * x (1/2)
Как позвонить по номеру, умножение которого само на себя дает другой номер? Конечно, это — квадратный корень из ! Итак, мы выяснили, что:
x (1/2) = √x
Если хотите, вы можете аналогичным образом проверить другие корни, например.
 грамм. кубический корень:
грамм. кубический корень:x = x (1/3 + 1/3 + 1/3) = x (1/3) * x (1/3) * x (1/3) = ³√x * ³√x * ³√x
т.
x (1/3) = ³√x
Теперь мы знаем, что x в степени одной трети равен кубическому корню из x.
Дробные показатели с числителем, отличным от 1 (любая дробь)
Итак, что произойдет, если наш числитель не равен 1 (n 1)?
Все, что вам нужно сделать, это возвести это число в степень n и взять корень d-й степени .Порядок не имеет значения, дробь n / d может быть разделена на две части:
- целое число (n)
- дробная часть (1 / d)
Давайте посмотрим на пример, где дробная экспонента = 3/2 и x = 16:
- 16 3/2 = 16 (3 * 1/2) = (16 3 ) 1/2 = √ (16³) = √4096 = 64
Или, как вариант, можно написать, что
- 16 3/2 = 16 (1/2) * 3 = (16 1/2 ) 3 = (√16) ³ = 4³ = 64
И результат действительно тот же.
 Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!
Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!Отрицательный и дробный показатель степени
Положительные показатели говорят нам, сколько раз мы используем число при умножении:
Но что произойдет, если наша экспонента будет отрицательным числом, вы можете догадаться? Да, он говорит вам, сколько раз вам нужно разделить на это число:
Кроме того, вы можете просто вычислить положительную экспоненту (например, x 4 ), а затем взять обратную величину (в нашем случае 1 / x 4 ).Конечно, аналогично, если у нас есть отрицательная И дробная экспонента.
Калькулятор степени дроби — как использовать
Мы считаем, что этот инструмент настолько интуитивно понятен и прост, что никаких дополнительных объяснений не требуется, но для записи мы быстро объясним, как вычислить дробные показатели:
- Введите базовое значение .
 Например, введите 7.
Например, введите 7. - Введите числитель и знаменатель дроби .Если вы хотите использовать этот калькулятор как простой инструмент экспоненты — с целым числом в качестве показателя вместо дроби — введите 1 в качестве знаменателя. Предположим, наша дробь равна -2/5. Введите -2 в числитель и 5 в поле знаменателя (также отметьте обратное действие).
- Наслаждайтесь результатом нашего калькулятора дробной степени! Это 0,4592 для нашей примерной задачи.
Надо ли говорить о гибкости нашего инструмента? Вам не нужно переходить калькулятор сверху вниз — вычислите любое неизвестное, какое захотите! Введите любые три значения, и четвертое появится в мгновение ока.
Еще одна полезная функция калькулятора — не только показатель степени может быть дробью, но и основание ! Например, если вы хотите вычислить (1/16) 1/2 , просто введите 1/16 в базовое поле. Отлично!
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т. Е. Для пятисотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.
Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью i.э., 1 2/3 (с таким же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .Десятичные числа (десятичные числа) вводятся с десятичной точкой .
 , и они автоматически конвертируются в дроби, то есть 1,45 .
, и они автоматически конвертируются в дроби, то есть 1,45 .Двоеточие : и косая черта / являются символом деления.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.Задачи с дробями:
следующие математические задачи »
Калькулятор дробей — базовые и расширенные вычисления с дробями
Используйте этот калькулятор дробей, чтобы легко выполнять вычисления с дробями. Складывайте, вычитайте, умножайте и делите дроби, а также возводите дробь в степень (дробь или нет). Поддерживает оценку смешанных дробей (например, «2 1/3») и отрицательных дробей (например, «2 1/3»).грамм. «-2/3»). Используйте «пи» или «π» вместо числа Пи. Мощный расширенный режим для вычисления целых выражений с дробями.

Использование калькулятора дробей
Калькулятор дробей предлагает два режима: основной и расширенный. Базовый режим поддерживает одну операцию (сложение, вычитание, умножение, деление, возведение в степень) только с двумя дробями, например 1/2 + 2 2/3 . В расширенном режиме вы можете оценивать очень сложные выражения, такие как ((2 x 2/5 / 13.1/2 .
Калькулятор поддерживает:
- Простые дроби: — например, 1/2, 3/4, 13/5 в обоих режимах.
- Смешанные фракции: — например, 1 1/2, 2 3/4, 10 3/5 в обоих режимах. Убедитесь, что вы оставили одно пространство между целой частью и дробной частью.
- Десятичные дроби: — например, 1.5, 3.45, 10.01 в обоих режимах. Вы также можете ввести такие вещи, как 1,5 / 2,5 . Убедитесь, что вы используете точку (.) В качестве десятичного разделителя.у).
- Группировки / круглые скобки: в расширенном режиме вы можете использовать круглые скобки для группировки элементов и принудительного порядка вычислений.
 В противном случае расчеты производятся в обычном порядке.
В противном случае расчеты производятся в обычном порядке. - Число Пи (π) : вы можете ввести «пи» или «π» в обоих режимах, например pi / 2 в базовом режиме, (pi + 5) / 2 в расширенном режиме. Он будет автоматически преобразован в правильное значение приблизительно 3,14159.
- Отрицательные дроби : оба режима поддерживают отрицательные дроби, десятичные дроби и числа.
В расширенном режиме порядок вычислений в инструменте следующий: круглые скобки, экспоненты, умножение, деление, сложение, вычитание (PEMDAS).
Результат представлен в виде десятичного числа (точность 12 позиций после десятичной точки) и в виде упрощенной смешанной дроби .
Как считать дроби
Принципы математики дробей одинаковы, независимо от того, кодируете ли вы их в калькуляторе или выполняете вычисления вручную.Во-первых, когда складывает или вычитает дроби , вам нужно начать с нахождения наименьшего общего знаменателя, также известного как наименьший общий знаменатель или наименьший общий знаменатель дробей, с которыми вам нужно работать.
 Это по определению наименьшее положительное целое число, которое делится на каждый знаменатель. ЖК-дисплей — это наименьшее общее кратное (НОК) знаменателей дробей. В этой операции нет необходимости при умножении, делении или возведении в степень.
Это по определению наименьшее положительное целое число, которое делится на каждый знаменатель. ЖК-дисплей — это наименьшее общее кратное (НОК) знаменателей дробей. В этой операции нет необходимости при умножении, делении или возведении в степень.Затем вам нужно преобразовать смешанные дроби в простые дроби, чтобы упростить работу.Чтобы найти числитель простой дроби, умножьте целую часть на знаменатель и прибавьте к ней числитель дробной части. Знаменатель останется прежним.
Наконец, выполните необходимые операции (сложение, вычитание, умножение, деление), работая с числителями. Затем вы получите результат расчета. Конечно, гораздо проще использовать мощный калькулятор дробей , как наш выше.
Если проиллюстрировать пошаговый процесс, то это:
- при сложении или вычитании дробей найдите наименьший общий знаменатель
- преобразовать смешанные дроби в простые дроби
- выполнять арифметические действия с числителями
Это не так сложно, но в определенных сценариях может быть сложно сделать вручную, что не является проблемой для онлайн-калькулятора.

Практические примеры
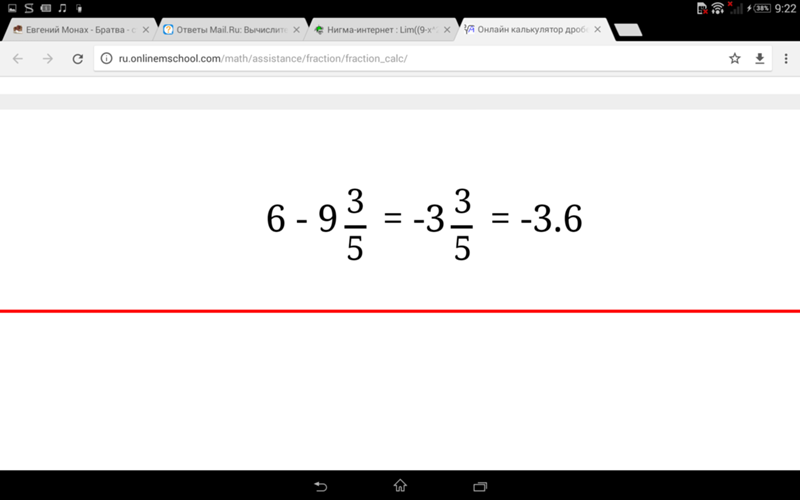
Пример задания № 1: сложить дроби 1/2 и 3/4.
Решение : Наименьший общий знаменатель 2 и 4 равен 4, поэтому 1/2 = 2/4, а 3/4 остается 3/4. Складываем 2 + 3 = 5, получаем 5/4. В виде смешанной дроби, равной 1 1/4, в десятичном виде: 1,25.
Пример задания № 2: вычесть дроби 1 1/5 и 2/3.
Решение : Сначала преобразуйте 1 1/5 в простую дробь по формуле (1 x 5 + 1) / 5 = 6/5. Наименьший общий знаменатель 5 и 3 равен 15, поэтому 6/5 = 18/15 и 2/3 = 10/15.Вычитая 10 из 18 = 8, получаем 8/15. Это не может быть далее упрощено. В десятичном виде это 0,53 (3). Вы можете проверить результат с помощью нашего инструмента.
Пример задания № 3: Умножение дробей 1/3 и 5/8
Решение : Чтобы вычислить это выражение, просто умножьте числители вместе, а затем знаменатели вместе. Умножив 1 на 5, мы получим 5, умножив 3 на 8, получим 24, поэтому ответ будет 5/24, или 0,2083 (3).
Математические онлайн-калькуляторы — SnapXam
Ознакомьтесь с полным списком математических калькуляторов онлайн.

- Абсолютная степень алгебраического выражения Калькулятор
- Сложение десятичных знаков Калькулятор
- Сложение целых чисел Калькулятор
- Сложение чисел Калькулятор
- Калькулятор расширенного дифференцирования
- Алгебраный калькулятор
- Алгебраические выражения Калькулятор Дробные выражения
Дробные выражения Калькулятор - Арифметический калькулятор
- По возрастанию и убыванию Калькулятор
- Формула изменения базы логарифмов Калькулятор
- Калькулятор основных правил дифференцирования
- Калькулятор биномиальных конъюгатов Калькулятор
- Биномиальный калькулятор теоремы Калькулятор цепного дифференцирования алгебраические выражения Калькулятор
- Объединение одинаковых терминов Калькулятор
- Калькулятор общего мономиального множителя
- Завершение вычисления квадрата
- Конденсация Калькулятор логарифмов
- Калькулятор константных правил
- Калькулятор циклического интегрирования по частям
- Калькулятор десятичных дробей
- Калькулятор определенных интегралов
- Определение производного калькулятора
- Производный калькулятор
- Производный калькулятор
- Гипер-калькулятор производных функций Производные функции Обратные тригонометрические функции Калькулятор
- Производные тригонометрических функций Калькулятор
- Калькулятор разности кубов
- Калькулятор дифференциальных уравнений
- Калькулятор десятичных дробей
- Деление целых чисел Калькулятор
- Деление чисел Калькулятор
- кубических уравнений Калькулятор Калькулятор
- Уравнения с квадратными корнями Калькулятор
- Эквивалентные выражения Калькулятор
- Вычислить логарифмы Калькулятор
- Развернуть Калькулятор логарифмов ding
- Калькулятор свойств экспоненты
- Калькулятор экспонент
- Калькулятор показателей и радикалов
- Выражение через синус и косинус Калькулятор
- Калькулятор метода FOIL
- Фактор на разность квадратов Калькулятор
- Дифференциал первого порядка
- Калькулятор уравнений
- Калькулятор перекрестного умножения дробей
- Калькулятор производных высшего порядка
- Калькулятор однородных и неоднородных значений
- Калькулятор неявного дифференцирования
- Калькулятор неправильных интегралов
- Калькулятор неопределенных интегралов
- 9067 Калькулятор интегралов 9067 Калькулятор интегралов в виде дробной части
- Калькулятор интегралов экспоненциальных функций
- Калькулятор интегралов рациональных функций
- Интегралы Калькулятор рациональных функций синуса и косинуса
- Интегралы от полиномиальных функций Калькулятор
- Калькулятор интегралов с радикалами
- Калькулятор методов интегрирования
- Интегрирование по частям Калькулятор
- Интегрирование с помощью подстановки Калькулятор
- Интегрирование по тригонометрической функции подстановки 9067 Калькулятор дифференцирования
- Калькулятор наименьшего общего кратного
- Как термины Калькулятор
- Калькулятор лимитов
- Лимиты по правилу L’Hôpital Калькулятор
- Лимиты путем прямой замены Калькулятор
- Лимиты с двойным рационализацией Калькулятор
- Лимиты на разложение
- Калькулятор лимитов
- Калькулятор рационализации
- Калькулятор пределов экспоненциальных функций
- Калькулятор пределов до бесконечности
- Буквальная часть члена Калькулятор
- Калькулятор логарифмических уравнений 90 672
- Калькулятор логарифмического дифференцирования
- Калькулятор матриц
- Умножение десятичных знаков Калькулятор
- Умножение целых чисел Калькулятор
- Умножение чисел Калькулятор
- Умножение степеней одного и того же основания Калькулятор
- Числовые коэффициенты Калькулятор числовое выражение
- Калькулятор линейных уравнений с одной переменной
- Калькулятор линейных неравенств с одной переменной
- Калькулятор операций с бесконечностью
- Калькулятор трехчлена точного квадрата
- Калькулятор полиномиального разложения
- Калькулятор полиномиального деления
- Полиномиальный калькулятор для производных правил Полиномиальные производные
- Калькулятор степеней
- Калькулятор степеней произведения
- Калькулятор степеней степеней
- Калькулятор предалгебры
- Калькулятор предвычисления
- Калькулятор разложения на простой коэффициент r
- Калькулятор правила дифференцирования продукта
- Произведение биномов с помощью калькулятора общего члена
- Калькулятор свойств логарифмов
- Калькулятор доказательства тригонометрических тождеств
- Калькулятор квадратных уравнений
- Калькулятор квадратичных формул
- Правило квантовых степеней
- Калькулятор дифференцирования
- Калькулятор радикальных уравнений и функций
- Калькулятор радикалов
- Калькулятор рациональных уравнений
- Калькулятор рационализации
- Калькулятор рациональных и иррациональных соотношений
- Калькулятор относительной степени алгебраических выражений Калькулятор
- Калькулятор математических выражений с разделением дифференциальных уравнений
- Упрощение алгебраических дробей Калькулятор
- Упрощение тригонометрических выражений Калькулятор
- Специальные продукты Калькулятор
- Spe Калькулятор частных частных
- Квадрат трехчлена Калькулятор
- Вычитание десятичных дробей Калькулятор
- Вычитание целых чисел Калькулятор
- Вычитание чисел Калькулятор
- Калькулятор правила суммирования дифференцирования
- Калькулятор синтетического деления таблиц Интегрирование7 Синтетическое деление полиномов Калькулятор уравнений
- Калькулятор тригонометрических тождеств
- Калькулятор тригонометрических интегралов
- Калькулятор тригонометрии
- Калькулятор линейных уравнений с двумя переменными
- Калькулятор линейных неравенств с двумя переменными
- Калькулятор подстановки Вейерштрасса Whoierstrass Substitution Calculator
- Whoierstrass Substitution Calculator
- Whoial Fraction Calculator
- Whoial Fraction Calculator Whoial
Визуальный калькулятор дробей
Добро пожаловать в калькулятор дробей
На этой странице находится калькулятор дробей, который может выполнять сложение, вычитание, умножение или деление двух дробей. Значения для расчета могут быть простыми или смешанными дробями или состоять только из целых чисел. Допускается ввод неправильных дробей. Введите значения прямо в соответствующие места в калькуляторе дробей, и ответ будет обновляться в режиме реального времени. Визуализация дробей операндов и дроби ответа отображается на панели внизу, где вводятся значения.
Значения для расчета могут быть простыми или смешанными дробями или состоять только из целых чисел. Допускается ввод неправильных дробей. Введите значения прямо в соответствующие места в калькуляторе дробей, и ответ будет обновляться в режиме реального времени. Визуализация дробей операндов и дроби ответа отображается на панели внизу, где вводятся значения.
Полные шаги для решения каждого типа операции с дробями будут перечислены в версии калькулятора дробей, которая выйдет в ближайшее время! Эта часть калькулятора дробей предназначена не только для иллюстрации ответов, но и для предоставления обучающего инструмента, чтобы вы могли увидеть, как были решены проблемы.
Если вы хотите сохранить калькулятор дробей, показывающий проблему, над которой вы работаете, ссылку «Поделиться этим вычислением» можно скопировать и вставить в электронное письмо, закладки браузера или на веб-страницу. Он вернется к калькулятору дробей и покажет проблему именно так, как вы ее видите.
Не используйте этот калькулятор дробей, чтобы быстро выполнять домашнее задание! Решайте проблемы самостоятельно и используйте калькулятор, чтобы проверить свою работу или посмотреть, как решить проблему, которую вы не понимаете. Этот калькулятор дробей — полезный инструмент, но он не заменяет мощный математический ум! Ничто не заменит выработку прочного набора концепций, и этот урок представляет собой интересное введение в дроби, если вы ищете другой подход.
Этот калькулятор дробей — полезный инструмент, но он не заменяет мощный математический ум! Ничто не заменит выработку прочного набора концепций, и этот урок представляет собой интересное введение в дроби, если вы ищете другой подход.
Изучая основные математические операции, мы начинаем с операций с целыми числами. Но мир полон частичного количества вещей … Полстакана сахара в рецепте, или шесть десятых амиле, или четверть доллара.Все они представляют собой часть целого, и именно это и есть дробь. Мы имеем дело с частичными суммами каждый день, поэтому эти идеи нам знакомы, даже если то, как мы должны работать с ними в математике, поначалу кажется немного пугающим. Не волнуйся! Мы сделаем это легко!
Использование калькулятора дробей в реальных условиях
Дробь — это способ математически представить меньшую часть целого чего-либо. Итак, в нашем примере с пиццей, если всю пиццу разрезать на восемь равных ломтиков, и вы съедите три ломтика, вы съедите три из восьми частей целого. Мы представляем это дробью как 3/8 и говорим «три восьмых», когда читаем это вслух.
Мы представляем это дробью как 3/8 и говорим «три восьмых», когда читаем это вслух.
Для чисел, составляющих дробь, используются особые термины. Число внизу называется знаменателем. Вот на сколько частей делится все целое. В нашем примере с пиццей все целое разделено на восемь частей, поэтому знаменатель этой дроби равен восьми. Знаменатель слова — это необычное слово, которое просто означает «то, что разделяет». Иногда вместо знаменателя можно встретить слово делитель, но это одно и то же.
Еще один способ подумать о знаменателе — это понять, насколько велика каждая дробная часть, поэтому, например, если наша пицца разрезана на восемь частей, вы можете приблизительно представить себе, насколько велика каждая из них. Если нашу пиццу нарезать на 20 кусочков, можно представить, что каждый кусочек будет намного меньше. Это может быть камнем преткновения … Чем больше знаменатель, тем меньше дробная часть целого. Это может сбивать с толку, когда вы впервые изучаете дроби, потому что мы привыкли к большим числам, соответствующим значению больших реальных значений, но в этом случае большее значение в делителе может фактически уменьшить значение всей дроби. Например, 1/8 — это на самом деле большее значение (больший кусок пиццы), чем 1/20.
Например, 1/8 — это на самом деле большее значение (больший кусок пиццы), чем 1/20.
Верхнее число дроби называется числителем, что является еще одной причудой, означающей «вещь, которая имеет значение». Это представляет собой фактическое значение с точки зрения того, сколько частей целого представлено дробью. В нашем примере с пиццей, когда вы действительно были голодны и съели три ломтика, мы представили это как дробь 3/8. В этом случае числитель равен трем и представляет три из восьми частей, составляющих целое.
Это действительно так сложно, как кажется. Простая дробь состоит всего из двух частей: числитель вверху и знаменатель внизу. Знаменатель говорит нам, на сколько частей делится целое, а числитель говорит нам, сколько из этих частей дробь должна представлять.
Если это все еще кажется нечетким, вот еще одно отличное описание концепций дроби с несколькими иллюстрациями.
Смешанные дроби и неправильные дроби с помощью калькулятора дробей
Смешанные дроби представляют собой некоторое количество целых, а также дробную часть. Три с половиной стакана сахара могут быть примером того, что вы представляете смешанной фракцией.
Три с половиной стакана сахара могут быть примером того, что вы представляете смешанной фракцией.
Иногда, работая с дробями на шагах, вы вычисляете числитель больше знаменателя. Это называется «неправильная дробь». Примером может быть что-то вроде 9/8, что означает 9 частей целого, где каждое целое делится на восемь частей. Если создатель говорит нам, что целое разделено на восемь частей, если у нас есть девять частей, у нас достаточно для полного целого с одной оставшейся частью.Это означает, что 9/8 — это одно целое плюс одна часть или смешанная дробь 1/8.
Когда вы используете калькулятор дробей на этой странице, вы можете вводить неправильные дроби или смешанные дроби, и он рассчитает результаты для вас соответствующим образом, но ответ всегда будет дан в виде правильной дроби.
Сокращение эквивалентных дробей с помощью калькулятора дробей
Если вы действительно думаете о работе с дробями, вы можете увидеть, что вы можете представить одну и ту же дробную величину разными дробями с разными знаменателями.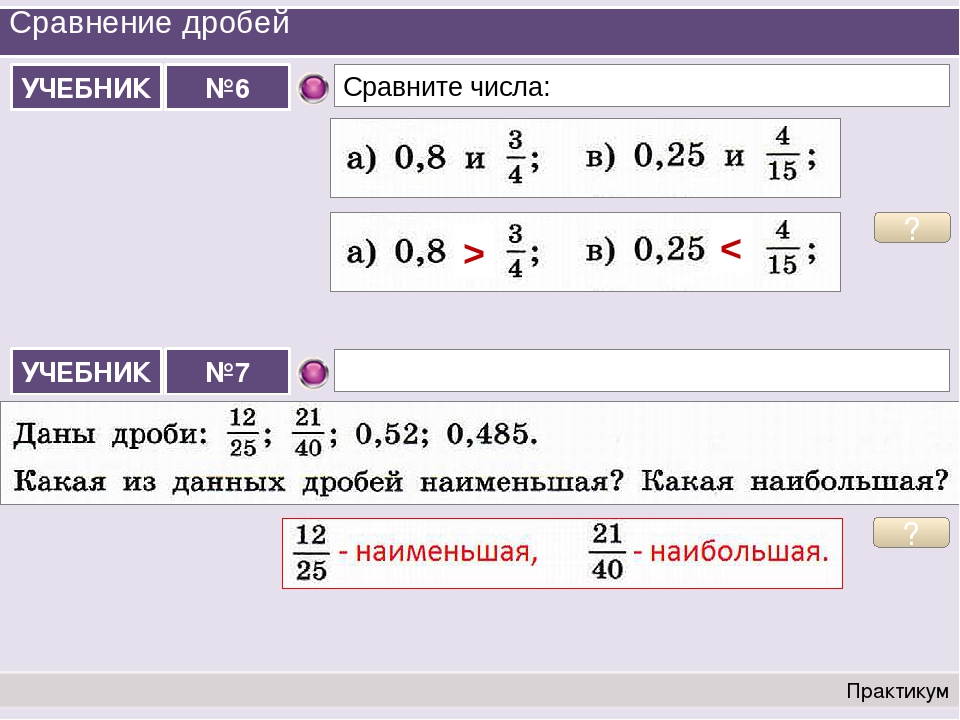 Если мы вернемся к визуализации нашей пиццы, если целое разделить на четыре части, половина будет двумя ломтиками. Однако если вместо этого целое разделить на восемь частей, половина пиццы будет состоять из четырех частей. В этих примерах 2/4 и 4/8 — это одинаковое количество целого. 2/4, 4/8 и 1/2 — все эквивалентные дроби, потому что представляют собой то же самое реальное количество целого значения.
Если мы вернемся к визуализации нашей пиццы, если целое разделить на четыре части, половина будет двумя ломтиками. Однако если вместо этого целое разделить на восемь частей, половина пиццы будет состоять из четырех частей. В этих примерах 2/4 и 4/8 — это одинаковое количество целого. 2/4, 4/8 и 1/2 — все эквивалентные дроби, потому что представляют собой то же самое реальное количество целого значения.
Конечно, самый простой способ представить любое из этих значений — просто сказать «половина», а дробь в простейшей форме, которая представляет это, очевидно, равна 1/2.Два в этом случае — это наименьший возможный делитель, представляющий дробь. Поиск наименьшего возможного разработчика называется «приведением дробей» к их простейшей форме. Этот калькулятор дробей автоматически сокращает дроби в ответах.
Сложение дробей с помощью калькулятора дробей
Процесс сложения дробей несложен, если знаменатели совпадают. Просто сложите числители, и полученная дробь будет иметь тот же знаменатель. Итак, один кусок пиццы (1/8) плюс другой (1/8) равняется двум кусочкам пиццы (2/8).Эта доля может быть уменьшена до 1/4, и это имеет смысл мысленно, потому что эти два фрагмента представляют собой четверть целого.
Итак, один кусок пиццы (1/8) плюс другой (1/8) равняется двум кусочкам пиццы (2/8).Эта доля может быть уменьшена до 1/4, и это имеет смысл мысленно, потому что эти два фрагмента представляют собой четверть целого.
Если вы начнете с двух дробей с разными знаменателями, вам нужно найти наименьший общий знаменатель. Это наименьший знаменатель, который поможет получить эквивалентные дроби для каждой из дробей, которые вы пытаетесь сложить. Например, если бы мы пытались сложить 3/16 и 1/8, мы могли бы превратить 1/8 в эквивалентную дробь 2/16. Теперь мы складываем 3/16 и 2/16, что равно 5/16.
Вы можете найти больше об общих знаменателях в целом на WikiPedia, но эта ссылка дает еще одно хорошее описание фактического поиска наименее общих знаменателей в Quick and Dirty Tips.
Несмотря на то, что 2/16 не является сокращенной дробью, для расчета ответа можно использовать несокращенные дроби или даже неправильные дроби. Мы просто хотим вернуть дроби в правильной сокращенной форме, когда дадим ответ в конце.
Опять же, этот калькулятор дробей делает все эти шаги за вас, поэтому, если вам нужно увидеть больше примеров, попробуйте решить задачу и посмотрите, как это работает! Обратите внимание, что когда вы добавляете дроби, предварительный просмотр в калькуляторе дробей показывает, как две исходные дроби могут объединиться, чтобы сформировать дробную часть ответа.
Вычитание дробей с помощью калькулятора дробей
Вычитание дробей работает так же, как и сложение дробей. Вам нужно убедиться, что дроби имеют общий знаменатель, а затем просто вычтите числители и уменьшите дробь ответа.
Как и при сложении, если вы начинаете со смешанной дроби, вам может потребоваться преобразовать дробь в неправильную форму, чтобы вычесть числители. Это процедура, обратная той, которую мы использовали для создания правильных дробей.Чтобы получить неправильную дробь, умножьте целые числа на знаменатель и прибавьте его к значению числителя. Итак, 1 и 1/8 — это одно целое плюс одна часть, или восемь частей плюс одна часть, или всего девять частей. Таким образом, правильная смешанная дробь 1 1/8 как неправильная дробь равна 9/8.
Таким образом, правильная смешанная дробь 1 1/8 как неправильная дробь равна 9/8.
При вычитании дробей, если вы отнимете большую дробь от меньшей дроби, у вас останется отрицательная величина. Вы покажете получившуюся дробь со знаком минус либо целиком, либо в числителе.Отрицательная дробь должна иметь только один отрицательный знак. Распространенная ошибка — думать, что нужно поставить и числитель, и знаменатель отрицательными, если вы получили отрицательный ответ. Не делай этого! Если ваш ответ отрицательный, вы должны увидеть только один отрицательный знак в полученной дроби.
Умножение дробей с помощью калькулятора дробей
Умножение дробей в некотором смысле проще, чем сложение или вычитание дробей, потому что вам не нужен общий знаменатель.Однако хороший первый шаг — посмотреть, можно ли уменьшить одну или обе умножаемые дроби. Это немного упростит расчеты.
Если какая-либо из фракций смешана, превратите их в неправильные фракции, как описано выше. Если вы умножаете дробь на целое значение, превратите целое в дробь со знаминателем, равным единице, так, например, целые 3 превращаются в дробь 3/1 для выполнения умножения.
Если вы умножаете дробь на целое значение, превратите целое в дробь со знаминателем, равным единице, так, например, целые 3 превращаются в дробь 3/1 для выполнения умножения.
Затем, чтобы получить числитель для ответа, умножьте два числителя дробей, с которой вы начинаете.Чтобы получить знаменатель, проделайте то же самое, умножьте два знаменателя и запишите результат как знаменатель в дробной части ответа.
Существует большая вероятность того, что полученная дробь неверна или может быть уменьшена. Вы всегда должны сокращать свой ответ и приводить его в надлежащей форме. Опять же, если вам нужна помощь с этим, попробуйте решить задачу умножения дробей, используя калькулятор дробей на этой странице, и он покажет вам пример. Этот калькулятор дробей всегда упрощает дроби в ответе.
Деление дробей с помощью калькулятора дробей
Процедура деления дробей аналогична умножению дробей с одним дополнительным шагом. Начните следовать инструкциям по умножению дробей. Как только у вас есть две дроби в неправильной форме и вы готовы перемножить числители и знаменатели, вы сначала делаете еще один шаг. Во второй дроби поменяйте местами числитель и знаменатель. Таким образом, старый знаменатель идет сверху и становится числителем, а старый числитель идет снизу и становится знаменателем.Затем завершите процедуру умножения дробей… Умножайте прямо поперек, уменьшайте и просто.
Как только у вас есть две дроби в неправильной форме и вы готовы перемножить числители и знаменатели, вы сначала делаете еще один шаг. Во второй дроби поменяйте местами числитель и знаменатель. Таким образом, старый знаменатель идет сверху и становится числителем, а старый числитель идет снизу и становится знаменателем.Затем завершите процедуру умножения дробей… Умножайте прямо поперек, уменьшайте и просто.
Когда вы меняете местами числитель и знаменатель дроби, получается нечто, называемое обратным. Эту процедуру иногда называют «инвертированием» или «взятием обратной» дроби. Обратная величина дроби имеет интересную особенность. Если вы умножите дробь на величину, обратную этой дроби, результат будет иметь такое же число в числителе и знаменателе, что означает, что он уменьшится до единицы.Попробуйте это в калькуляторе дробей, умножив 2/3 на 3/2, и увидите.
Калькулятор упрощенных дробей
Этот калькулятор дробей автоматически упростит результаты. Если вам нужно упростить дроби, этот калькулятор дробей может сделать эту работу за вас, введя обычную дробь, смешанную дробь или неправильную дробь, а затем умножив полученное значение на единицу. Калькулятор дробей просто ответит за вас. Например, если вы введете 4/32 x 1 в калькулятор дробей, упрощенное произведение будет 1/8.
Калькулятор дробей просто ответит за вас. Например, если вы введете 4/32 x 1 в калькулятор дробей, упрощенное произведение будет 1/8.
Калькулятор смешанных фракций
Этот калькулятор фракций обрабатывает смешанные дроби для всех операций и возвращает результат в простейшей форме. Когда калькулятор дробей имеет дело со смешанными дробями, процедура почти всегда упрощается, если целое число умножить на знаменатель и прибавить к числителю, чтобы получить неправильную дробь. Это преобразование смешанных чисел в неправильные дроби позволяет рассматривать проблемы с дробями так, как если бы целые числа не использовались.
Калькулятор дробей делает это внутренне для решения задач смешанных дробей.
Для сложения дробей или вычитания дробей калькулятор дробей должен определить общий знаменатель. Затем, после завершения операции, если результирующая дробь все еще неверна, калькулятор дробей преобразует ее обратно в смешанную дробь для использования в качестве ответа.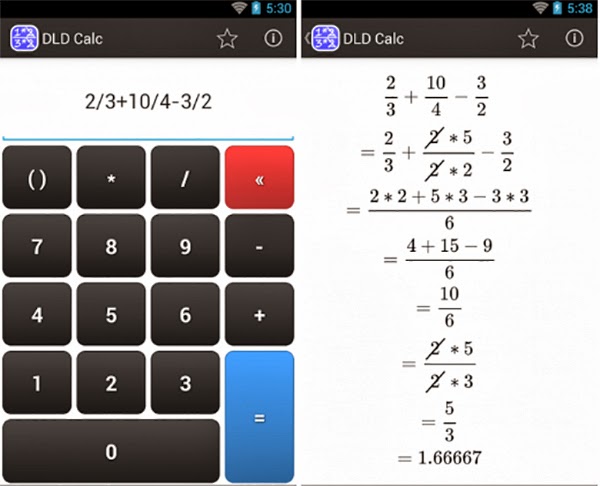
Даже после того, как калькулятор дробей вычитает целое число из неправильной дроби, полученная смешанная дробь может быть еще не в простейшей форме.Если дробь может быть уменьшена, калькулятор дробей найдет общий делитель числителя и знаменателя, а затем разделит оба компонента, чтобы упростить окончательную дробь.
Вы готовы к дробям с помощью нашего онлайн-калькулятора дробей
На этой странице дан очень краткий обзор дробей и дан ряд примеров, которые вы можете попробовать в калькуляторе дробей. Мы рассмотрели сложение дробей, вычитание дробей, умножение дробей и деление дробей, а также то, как создать правильную дробь из неправильной дроби (и наоборот), сокращение дробей, поиск наименьшего общего знаменателя, а также то, как получить обратную дробь.Вы видели, как использовать калькулятор дробей для упрощения неправильных дробей и как использовать калькулятор дробей для уменьшения дробей. Вы можете попробовать все эти концепции в калькуляторе дробей, изучить результаты, и вы сразу же обнаружите, что являетесь рок-звездой!
Когда вы будете готовы к большему, попробуйте на практике приведенные ниже таблицы дробей и поделитесь этим калькулятором дробей со своими друзьями!
Обновления калькулятора дробей
7 января 2018
Изменена загрузка файлов JavaScript, так что калькулятор дробей запускается раньше на странице, благодаря чему калькулятор появляется раньше во время загрузки страницы.
27 сентября 2016
Я получил выдающийся совет от моей подруги Марии Миллер по части предварительного просмотра калькулятора дробей. Предварительный просмотр для сложения и вычитания дробей теперь показывает небольшие смешанные дроби с целым компонентом в виде диаграмм, а не чисел. Для умножения дробей первое множимое отображается как числовая смешанная дробь, чтобы укрепить идею о том, что вторая дробь повторяется. Точно так же для деления дробей калькулятор дробей показывает, что делитель отображается в виде смешанной дроби, чтобы усилить идею о том, что дивиденд делится столько раз, чтобы получить частное.
9 октября 2016
Исправленный неверно сформированный HTML в инструкциях калькулятора дробей 4.
24 октября 2016
При умножении дробей калькулятор дробей неправильно отображал некоторые смешанные дроби.
Добавлены инструкции, как просто делить дроби с помощью калькулятора дробей путем умножения.
Калькулятор дробей | Математический калькулятор
Этот калькулятор преобразует десятичное число в дробь, как показано в следующем примере, чтобы преобразовать десятичное число в дробное.
Пр. 12,125
Шаг-1 подсчитайте количество десятичных разрядов
здесь в примере 3 десятичных разряда
Шаг 2 умножьте и разделите число на 10 десятичное число
| 10 3 | 12.125 * 1000 | ||
| 12,125 | = | ||
| 10 3 | 1000 |
Шаг-3 Найдите наибольший общий делитель (НОД) числителя и знаменателя и разделите числитель и знаменатель на НОД
.


 2}(решить неравенство)
2}(решить неравенство)

 Который мы научили работать с дробями!
Который мы научили работать с дробями! .. · a
.. · a Всего их пять штук — ниже мы их рассмотрим.
Всего их пять штук — ниже мы их рассмотрим. Затем полученные результаты перемножаются.
Затем полученные результаты перемножаются.

 д.
д. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени. Она вставляет в строке ввода запись sqrt3(x).
Она вставляет в строке ввода запись sqrt3(x). Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой,
отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно
они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине
школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются
в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби
особых затруднений не вызывают. Итак, вперёд!
Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой,
отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно
они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине
школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются
в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби
особых затруднений не вызывают. Итак, вперёд!
 Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
 Рассуждая, как в
предыдущем примере, получим
Рассуждая, как в
предыдущем примере, получим

 грамм. y
грамм. y Б., Иллинойс
Б., Иллинойс 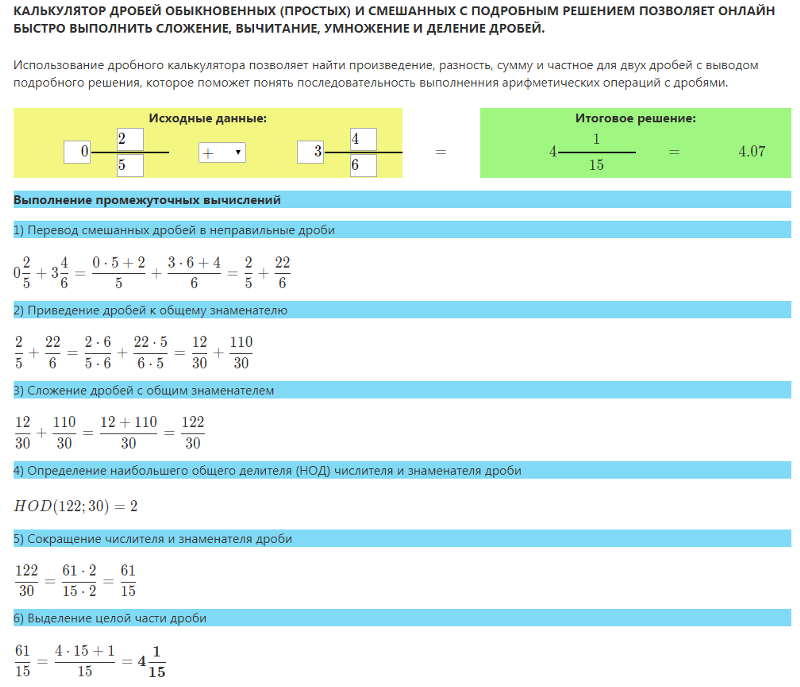 грамм. кубический корень:
грамм. кубический корень: Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!
Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени! Например, введите 7.
Например, введите 7. Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби.Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.

 В противном случае расчеты производятся в обычном порядке.
В противном случае расчеты производятся в обычном порядке. Это по определению наименьшее положительное целое число, которое делится на каждый знаменатель. ЖК-дисплей — это наименьшее общее кратное (НОК) знаменателей дробей. В этой операции нет необходимости при умножении, делении или возведении в степень.
Это по определению наименьшее положительное целое число, которое делится на каждый знаменатель. ЖК-дисплей — это наименьшее общее кратное (НОК) знаменателей дробей. В этой операции нет необходимости при умножении, делении или возведении в степень.