Квадратные уравнения с ответами 8 класс – 8 класс. Алгебра

Тренажёр по алгебре (8 класс) на тему: Неполные квадратные уравнения

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 1

Решить уравнения:

1. 3×2-12=0
2. 2х2+6х=0
3. 1,8х2=0
4. х2+25=0
5. х2-=0
6. х2=3х
7. х2+2х-3=2х+6
8. х2=3,6

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 2

Решить уравнения:

1. 2х2-18=0

2. 3х2-12х=0

3. 2,7х2=0

4. х2+16=0

5. х2-=0

6. х2=7х

7. х2-3х-5=11-3х

8. х2=2,5

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 3

Решить уравнения:

1. 3×2-1=0
2. 2х2-6х=0
3. 8х2=0
4. х2+81=0
5. х2-=0
6. х2=5х
7. х2+х-3=х+6
8. х2=8,1

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 4

Решить уравнения:

1. 2х2-32=0

2. 3х2-15х=0

3. 2,4х2=0

4. х2+49=0

5. х2-=0

6. х2=х

7. х2-7х-5=11-7х

8. х2=4,9

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 1

Решить уравнения:

9. 3×2-12=0
10. 2х2+6х=0
11. 1,8х2=0
12. х2+25=0
13. х2-=0
14. х2=3х
15. х2+2х-3=2х+6
16. х2=3,6

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 2

Решить уравнения:

1. 2х2-18=0

2. 3х2-12х=0

3. 2,7х2=0

4. х2+16=0

5. х2-=0

6. х2=7х

7. х2-3х-5=11-3х

8. х2=2,5

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 3

Решить уравнения:

9. 3×2-1=0
10. 2х2-6х=0
11. 8х2=0
12. х2+81=0
13. х2-=0
14. х2=5х
15. х2+х-3=х+6
16. х2=8,1

Самостоятельная работа по теме: «Неполные квадратные уравнения»

Вариант 4

Решить уравнения:

1. 2х2-32=0

2. 3х2-15х=0

3. 2,4х2=0

4. х2+49=0

5. х2-=0

6. х2=х

7. х2-7х-5=11-7х

8. х2=4,9

1		2		3		4
1	2;-2	1	3,-3	1	√1/3;-√1/3	1	4,-4
2	0;-3	2	0;4	2	0;3	2	0;5
3	0	3	0	3	0	3	0
4	Нет корней	4	Нет корней	4	Нет корней	4	Нет корней
5	√6;-√6	5	√5;-√5	5	√3;-√3	5	√5;-√5
6	0;3	6	0;7	6	0;5	6	0;1
7	√3;-√3	7	4;-4	7	3;-3	7	4;-4
8	0,6;-0,6	8	0,5;-0,5	8	0,9;-0,9	8	0,7;-0,7

nsportal.ru

Урок по теме «Решение квадратных уравнений». 8-й класс

Рассмотрим стандартные (изучаемые в школьном курсе математики) и нестандартные приёмы решения квадратных уравнений.

1. Разложение левой части квадратного уравнения на линейные множители.

Рассмотрим примеры:

3) х² + 10х – 24 = 0.

6(х² + х – х ) = 0 | : 6

х² + х – х – = 0;

х(х – ) + (х – ) = 0;

х(х – ) (х + ) = 0;

= ; – .

Ответ: ; – .

Для самостоятельной работы:

Решите квадратные уравнения, применяя метод разложения левой части квадратного уравнения на линейные множители.

а) х2 – х = 0; г) х2 – 81 = 0; ж) х2 + 6х + 9 = 0;

б) х2 + 2х = 0; д) 4х2 – = 0; з) х2 + 4х + 3 = 0;

в) 3х2 – 3х = 0; е) х2 – 4х + 4 = 0; и) х2 + 2х – 3 = 0.

Ответы:

а) 0; 1 г) ± 9 ж) – 3

б) -2; 0 д) з) -3; -1

в) 0; 1 е) 2 и) -3; -1

2. Метод выделения полного квадрата.

Рассмотрим примеры:

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод выделения полного квадрата.

3. Решение квадратных уравнений по формуле.

ах² + вх + с = 0, (а | · 4а

4а²х² + 4ав + 4ас = 0;

2ах + 2ах·2в + в

2 – в² + 4ас = 0;

² = в² – 4ас;

= ± ;

2ах = -в ±;

х_1,2 =.

Рассмотрим примеры.

Для самостоятельной работы.

Решите квадратные уравнения, применяя формулу х_1,2 =.

4. Решение квадратных уравнений с использованием теоремы Виета (прямой и обратной)

x² + px +q = 0 – приведённое квадратное уравнение

по теореме Виета.

Если то уравнение имеет два одинаковых корня по знаку и это зависит от коэффициента .

Если p, то .

Если p, то.

Например:

Если то уравнение имеет два различных по знаку корня, причём больший по модулю корень будет , если p и будет , если p.

Например:

Для самостоятельной работы.

Не решая квадратного уравнения, по обратной теореме Виета определите знаки его корней:

Ответы:

а, б, к, л – различные корни;

в, д, з – отрицательные;

г, е, ж, и, м – положительные;

5. Решение квадратных уравнений методом “переброски”.

Для самостоятельной работы.

Решите квадратные уравнения, применяя метод “переброски”.

6. Решение квадратных уравнений с применением свойств его коэффициентов.

I. ax² + bx + c = 0, где a ⁰

1) Если а + b + с = 0, то х₁ = 1; х₂ =

Доказательство:

ax² + bx + c = 0 |: а

х² + х + = 0.

По теореме Виета

По условию а + b + с = 0, тогда b = -а – с. Далее получим

Из этого следует, что х₁ =1; х₂ = . Что и требовалось доказать.

2) Если а – b + с = 0 (или b = а +с ) , то х₁ = – 1; х₂ = –

Доказательство:

По теореме Виета

По условию а – b + с = 0 , т.е. b = а +с . Далее получим:

Поэтому х₁ = – 1; х₂ = – .

Рассмотрим примеры.

1) 345 х² – 137 х – 208 = 0.

а + b + с = 345 – 137 – 208 = 0

х_{1 =} 1; х₂ = =

Ответ: 1;

2) 132 х² – 247 х + 115 = 0.

а + b + с = 132 -247 -115 = 0.

х_{1 =} 1; х₂ = =

Ответ: 1;

Для самостоятельной работы.

Применяя свойства коэффициентов квадратного уравнения, решите уравнения

II. ax² + bx + c = 0, где a ⁰

х_1,2 = . Пусть b = 2k, т.е. чётное. Тогда получим

х_1,2 = = = =

Рассмотрим пример:

3х^{2 –} 14х + 16 = 0 .

D₁ = (-7)² – 3·16 = 49 – 48 = 1

х_{1,2 = ;}

х₁ = = 2; х_{2 =}

Ответ: 2;

Для самостоятельной работы.

а) 4х^{2 –} 36х + 77 = 0

б) 15х^{2 –} 22х – 37 = 0

в) 4х² + 20х + 25 = 0

г) 9х^{2 –} 12х + 4 = 0

Ответы:

а) 3,5; 5,5

б) -1; 2

в) -2,5

г)

III. x² + px + q = 0

х_1,2 = – ± ²– q

Рассмотрим пример:

х² – 14х – 15 = 0

х_1,2 = 7 = 7

х₁ = -1_; х₂ = 15.

Ответ: -1; 15.

Для самостоятельной работы.

а) х² – 8х – 9 = 0

б) х² + 6х – 40 = 0

в) х² + 18х + 81 = 0

г) х² – 56х + 64 = 0

Ответы:

а) -1; 9

б) -10; 4

в) –9

г) 28 18

7. Решение квадратного уравнения с помощью графиков.

Примеры.

а) х² – 3х – 4 = 0

х² = 3х + 4

Ответ: -1; 4

б) х² – 2х + 1 = 0

х² = 3х + 4

Ответ: 1

в) х² – 2х + 5 = 0

х² = 2х -5

Ответ: нет решений

Для самостоятельной работы.

Решить квадратные уравнения графически:

8. Решение квадратных уравнений с помощью циркуля и линейки.

ax² + bx + c = 0,

х² + х + = 0.

х₁ и х₂ – корни.

Пусть А(0; 1), С(0;

По теореме о секущих:

ОВ· ОД = ОА · ОС.

Поэтому имеем:

х₁ · х₂ = 1 · ОС;

ОС = х₁ х₂

К(; 0), где = —

F(0; ) = (0; ) = )

S(-; )

Итак:

1) Построим точку S(-; ) – центр окружности и точку А(0;1).

2) Проведём окружность с радиусом R = SA/

3) Абсциссы точек пересечения этой окружности с осью ох являются корнями исходного квадратного уравнения.

Возможны 3 случая:

1) R > SK (или R > ).

Окружность пересекает ось ох в точке В(х₁; 0) и D(х₂; 0), где х₁ и х₂ – корни квадратного уравнения ax² + bx + c = 0.

2) R = SK (или R = ).

Окружность касается оси ох в тоске В₁(х₁; 0), где х₁ – корень квадратного уравнения

ax² + bx + c = 0.

3) R < SK (или R < ).

Окружность не имеет общих точек с осью ох, т.е. нет решений.

Примеры.

1) x² – 2x – 3 = 0.

Центр S(-; ),т.е.

х₀ = = – = 1,

у₀ = = = – 1.

(1; – 1) – центр окружности.

Проведём окружность (S; AS), где А(0; 1).

 

Ответ: х₁ = – 1; х₂ = 3.

2) x² – 5x + 4 = 0.

х₀ = = – = 2,5; у₀ = = = 2,5.

 

Ответ: х₁ = 1; х₂ = 4.

3) x² + 4x + 4 = 0.

х₀ = = – = – 2,

у₀ = = = 2,5

Ответ: х_{= -2.}

4) x² – 2x + 3 = 0.

х₀ = = – = 1,

у₀ = = = 2.

Ответ: нет решений.

Для самостоятельной работы.

Решить следующие квадратные уравнения с помощью циркуля и линейки:

9. Решение квадратных уравнений с помощью номограммы

Для решения используют Четырёхзначные математические таблицы В.М. Брадиса (таблица XXII, стр. 83).

Номограмма позволяет, не решая квадратного уравнения x² + px + q = 0, по его коэффициентам определить корни уравнения. Например:

5) z² + 4z + 3 = 0.

Оба корня отрицательные. Поэтому сделаем замену: z₁ = – t. Получим новое уравнение:

t² – 4t + 3 = 0.

t₁ = 1 ; t₂ = 3

z₁ = – 1 ; z₂ = – 3.

Ответ: – 3; – 1

6) Если коэффициенты p и q выходят за пределы шкалы, то выполняют подстановку z = k · t и решают с помощью номограммы уравнение: z²

+ pz + q = 0.

к² t² + p· kt + q = 0. |: к²

t² + t + = 0.

к берут с расчётом, чтобы имели место неравенства:

Для самостоятельной работы.

С помощью таблицы Брадиса решить следующие квадратные уравнения:

10. Геометрический метод решения квадратных уравнений

Рассмотрим примеры, которые решаются с помощью геометрии.

Пример 1. (из “Алгебры” ал-Хорезми)

х² + 10х = 39.

10 : 4 = 2 ; · 2 = 6 .

S_ABCD = х² + 4S_пр. + 4S_кв. = х² + 4·2х + 4 · 6 = х² + 10х + 25.

Заменим х² + 10х на 39.

S_ABCD = 39 + 25 = 64 = 8².

Значит сторона АВ = 8.

х= 8 – 2 – 2 =8 – 5 = 3.

х = 3

х_{1 +} х

2 = -10,

3 + х₂ = -10,

х₂ = -13.

Ответ: – 13

Пример 2. (решение уравнения древними греками)

у² + 6у – 16 = 0.

у² + 6у = 16, |+ 9

у² + 6у + 9 = 16 + 9

(у + 3)² = 25

у + 3 = ± 5,

у₁ = 2, у₂ = -8.

Ответ: -8; 2

Для самостоятельной работы.

Решите геометрически уравнение у^{2 –} 6у – 16 = 0.

Ответ: – 2; 8.

urok.1sept.ru

Решение квадратных уравнений 8 класс

ПЛАН-КОНСПЕКТ УРОКА по математике 8 класс
«Решение квадратных уравнений»

ФИО: Толстая Дарья Александровна

Место работы: МОУ «СОШ» с. Корткерос

Должность: учитель

Предмет: математика

Класс: 8 класс

Тема и номер урока в теме: «Формулы корней квадратных уравнений»

Учебник: Алгебра А.Г. Мордкович

8. Цель урока: Организация продуктивной деятельности учащихся, направленной на достижение ими:

1) личностных результатов:

• уметь слушать другого и понимать его речь;

• уметь хорошо говорить и легко выражать свои мысли;

• учиться применять свои знания и умения к решению новых проблем;.

• Умение формулировать для себя цели

2)метапредметных результатов:

познавательной

информационно-коммуникативной

• развитие умений анализировать, аргументировать сделанныйвыбор,

• умение вступать в речевое общение, участвовать в диалоге;

• приведение примеров, подбор аргументов, формулирование выводов;

• отражение в устной и письменной форме результатов своей деятельности

рефлексивной

• оценивание своих учебных достижений;

• владение навыками само- и взаимоконтроля;

• умение ставить личностные цели и оценивать степень их достижения.

3) предметных результатов:

• распознавать линейные и квадратные уравнения;

• решать квадратные уравнения;

• определять наличие корней квадратных уравнений по дискриминанту;

• закрепить знания учащихся по теме решения квадратных уравнений;

9.Оборудование.

1. УМК: Алгебра 8 класс (Мордкович)

2. Карточки для групповой работы.

10. Тип урока: урок обобщающего повторения

11. Формы работы учащихся: групповая, индивидуальная

12. Необходимое техническое оборудование: компьютер, проектор, экран.

13. Структура и ход урока

СТРУКТУРА И ХОД УРОКА

Ход урока

Деятельность учителя

Деятельность учеников

Виды формируемых УУД

Познавательная

Коммуникативная

Регулятивная

I. Организационно-мотивационный момент

Приветствует учащихся, проверяет готовность к уроку. Включает проектор, демонстрация презентации.

Приветствуют учителя, проверяют свою готовность к уроку .

2. Мотивация

Обратная связь на уроке осуществляется при помощи диалога учителя и ученика. Заполняем бланк ответов. За каждое верно выполненное задание или верный устный ответ на бланке, вы можете ставить 1 балл В конце урока при подведении итогов подсчитываем количество баллов и оцениваем свою работу на уроке. Учитель может добавить балл за оригинальную идею, либо другой способ решения».

Знакомятся с бланком ответов. Подписывают бланк.

3 . Постановка цели урока.

3. Актуализация знаний учащихся.

Устная работа.

Теоретическая разминка.

Продолжаем сегодня работать с квадратными уравнениями. И давайте сформулируем тему и цели нашего урока, а в этом нам поможет стихотворение.

Три ключевых слова в этом стихотворении: уравнения, решать, квадрат.

(Спрашивает несколько человек)

И так тема «решение квадратных уравнений» и цель: повторить и закрепить умение решать квадратные уравнения

В бланк ответов за каждый правильный ответ в раздел «Теоретическая разминка» ставим 1 балл.

1) из списка уравнений, убираем то, которое вы считаете лишним, ответ обоснуем

2)Закончить определение квадратного уравнения

3)Дать определение видам квадратных уравнений. И распределить уравнения по группам

4) От чего и как зависят корни уравнения?

5) Рассмотрим алгоритм решения квадратных уравнений. Формулу нахождения Д, формулы нахождения корней, в зависимости от Д

Читают стихотворение, обращают внимание на выделенные слова. Формируют тему и цель урока.

Открывают тетради, записывают число и тему урока

Работают устно. Отвечающий, ученик за каждый правильный ответ с объяснением, ставит в бланк по 1 баллу

1) из списка убирают линейное уравнение

2) ученик заканчивает определение

3) Ученик дает определения каждому виду квадратного уравнения и распределяют уравнения по колонкам

4) Рассказывает о дискриминанте

5) Рассматривают схематический алгоритм решения уравнений квадратных

Умение выделять существенную информацию из текста

Структурирование знаний;

Умение осуществлять анализ объектов с выделением существенных признаков ;

Умение осуществлять сравнение, сериацию и классификацию по заданным критериям

Осознанное построение речевого высказывания в устной форме;

Умение строить рассуждение в форме связи простых суждений об объекте, его строении, своиствах и связях

Умение формулировать личную цель

Умение формулировать собственное мнение;

Уметь строить понятные для партнера высказывания, учитывающие, что он знает и видит, а что нет;

Адекватно использовать речевые средства, строить монологическое высказывание, владеть диалоговой формой речи

Принимать и сохранять учебную задачу;

4. Решение задач

4.1. Найди ошибку

4.2. Историческая справка

1) в бланке, разделе «Найди ошибку» будем оценивать по трехбалльной системе

3- балла, если нашел ошибку и решил правильно уравнение

2- не нашел ошибку, но правильно нашел корни уравнения

1-балл, представил ответ у доски или помогал в вычислениях.

0- не участвовал в работе

У каждой группы есть карточки с решенными уравнениями. Вам необходимо проверить уравнения, если уравнение решено не верно найти ошибки и решить его

Работаем в группах. Каждой группе раздается по несколько уравнений. Решаем уравнения и на корни уравнении находим соответственную букву. В итоге у вас получается слово. После составления слова . На столе лежит информация о слове. Представитель с группы подходит и выбирает нужную информацию и представляет классу. За каждое решенное уравнение в раздел « Историческая справка» ставим по одному баллу.

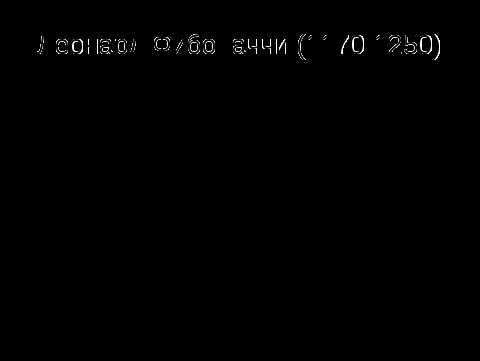
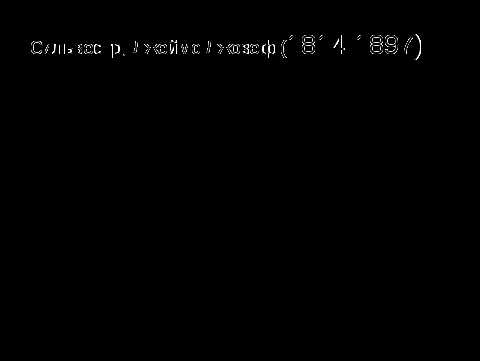
1) работают и обсуждают в группах. Находят ошибки, решают уравнения и представляют его у доски.

Оценивают друг друга в группе

Работают в группах. Уравнения распределяются между участниками групп. После составления слова выбирают информацию о слове и представляют ее классу

Использование знаково-символических средств, в том числе моделей и схем для решения задач;

Осознанное построение речевого высказывания в устной и письменной форме;

Понимать возможность различных позиций других людей;

Учитывать разные мнения;

Умение формулировать собственное мнение и позицию;

Умение договариваться и приходить к общему мнению;

Уметь контролировать действия партнера;

Адекватно использовать речевые средства, строить монологическое высказывание, владеть диалоговой формой речи

Взаимодействие

сотрудничество

Принимать и сохранять учебную задачу;

5. Подведение итогов

Каждый подсчитывает общее количество баллов и оценивает себя по следующим критериям

Каждый подсчитывает общее количество баллов и оценивает себя

V. Самостоятельная работа.

На отдельных листочках выполняются задание со слайда. После листочки сдаются.

Применение полученной информации самостоятельно.

VI.

Рефлексия

Дерево возможных вариантов.

На доске изображено дерево.

На партах у учащихся карточки трех цветов. Каждый ученик прикрепляет к дереву листок таким образом:

Зелененный – «Я усвоил тему»

Желтый – «Тему усвоил не до конца»

Красный – «Тема неусвоена полностью»

оценка процесса и результатов деятельности

контроль, коррекция своей работы

№

Этап урока

Название используемых ЭОР

(с указанием порядкового номера из Таблицы 2)

Деятельность учителя

(с указанием действий с ЭОР, например, демонстрация)

Деятельность ученика

Время

(в мин.)

1.

Организационно-мотивационный момент

Презентация (созданная учителем)

Приветствует учащихся, проверяет готовность к уроку. Включает проектор, демонстрация презентации.

Обратная связь на уроке осуществляется при помощи сигнальных карточек красного и зеленого цветов. Приготовьте свои сигнальные карточки. На каждый прозвучавший ответ вы поднимаете сигнальные карточки, показывая зелёным цветом своё согласие с ответом одноклассника. В случае расхождения мнений вы показываете красную карточку, идёт обсуждение, выявляется причина разногласия.

За каждое верно выполненное задание или верный устный ответ на полях своей тетради вы можете ставить знак «+». В конце урока при подведении итогов подсчитываем количество плюсов и оцениваем свою работу на уроке. Учитель может добавить «+» за оригинальную идею, либо другой способ решения».

Постановка личностной цели.

Ребята, а задумывался ли каждый из вас над тем, с какой целью он сегодня пришел в школу? Какая цель есть у каждого из вас? Я вам помогу вам сформулировать для себя цель. Предлагаю вам выбрать свою личную цель из списка на доске. Запишите ее номер в тетради на полях. Постарайтесь работать на эту цель в течение всего урока. В конце урока мы проанализируем, смогли ли Вы ее достичь и в какой мере.

Приветствуют учителя, проверяют свою готовность к уроку и выбирают себе цели из списка на экране.

2 мин.

2 . Постановка цели урока.

Презентация (созданная учителем)

Рассмотрите уравнения, записанные на доске, и постарайтесь разбить их на группы по одному или нескольким признакам и поясните, по какому признаку или каким признакам вы их разбили на группы.

5х – 20 = 10 + 2х,

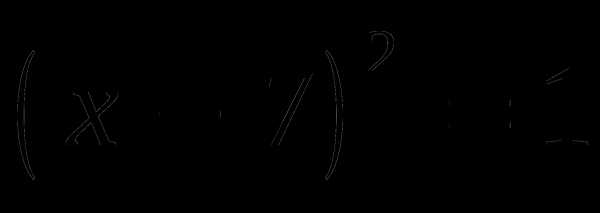
Учащиеся отвечают на вопросы и могут дать такие ответы:

данные уравнения можно разбить:

— на две группы: линейные и квадратные;

— на три группы: неизвестное в первой степени: неизвестное во второй степени и неизвестное и в первой, и во второй степени.)

3 мин.

А, как вы думаете, какая тема сегодняшнего урока? Что будет сегодня на уроке в роли «главного героя»?

(Могут быть ответы «Решение уравнений», или «Решение линейных и квадратных уравнений», или «Решение квадратных уравнений»)

Цель нашего урока:

научиться

• распознавать линейные и квадратные уравнения;

• решать квадратные уравнения, а также уравнения, сводящиеся к ним различными способами;

• определять наличие корней квадратных уравнений по дискриминанту и коэффициентам.

Правильно! Откройте тетради запишите дату, тема урока

3. Теоретическая разминка

Решение квадратного уравнения (N 138388),

ЭОР №1

А теперь устно решите следующие задачи. И  в каждой из них постарайтесь не пропустить ошибку.
Итак, в путь!

1.Сравните два утверждения «Квадратное уравнение ах² +х-2=0 имеет корни» и «Уравнение ах² +х-2=0 имеет корни», сделайте вывод: это одинаковые по смыслу утверждения или нет, поясните ответ.

Запускается ЭОР №1

Учащиеся отвечают на вопросы, аргументируя свое мнение.

5 мин.

Решение уравнения с квадратным корнем

(N 138298), ЭОР №2

2. Какие способы решения приведённого квадратного уравнения вы знаете?

Запускается ЭОР №2

Учащиеся отвечают на вопросы с аргументацией.

3. Всегда ли целесообразно применять формулы корней квадратного уравнения?

Учащиеся отвечают на вопрос, обосновывая свой ответ.

Формула (N 180658),

ЭОР №3

4. Назовите все возможные идеи решения уравнения:

1) 9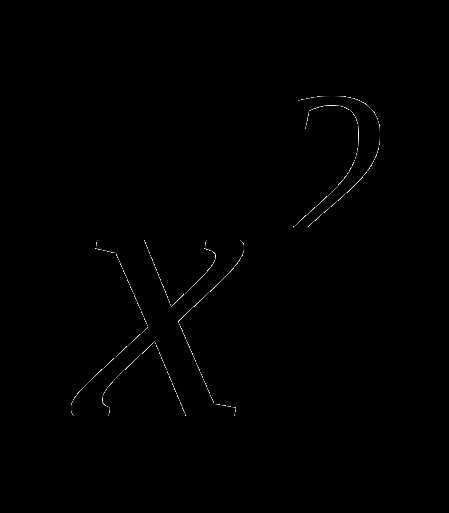 -6х+1=0

2) 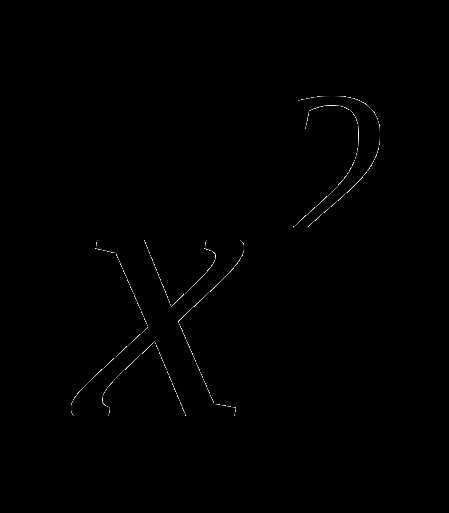-5х+4=0

3)3х + Зх — 6х -6х +х+1=0 (линейное уравнение, известные в одну сторону, неизвестные в другую).

Запускается ЭОР №3

Оцените результат своей деятельности на этом этапе урока и на полях поставьте знак + за каждый верный ответ

Учащиеся отвечают на вопрос

(Возможные ответы: метод выделения полного квадрата, формула корней квадратного уравнения)

(метод выделения полного квадрата; формула корней квадратного уравнения; теорема, обратная теореме Виета, по свойству коэффициентов).

(линейное уравнение, известные в одну сторону, неизвестные в другую).

4. Самостоятельная работа (работа в парах)

Закрепление умений решать неполные квадратные уравнения (N 191881), Запускается ЭОР №4

Запускается ЭОР №4

(Расположен на рабочем столе каждого компьютера, оценивает программа)

Закрепление умений решать неполные квадратные уравнения

Работа в парах.

10 мин

Определение квадратного уравнения. Неполные квадратные уравнения (N 191870), ЭОР №4

Определение квадратного уравнения. Неполные квадратные уравнения

Запускается ЭОР №5

(Расположен на рабочем столе каждого компьютера, оценивает программа)

Индивидуальная работа

5. ФИЗКУЛЬТМИНУТКА

Мы видим глазами наш удивительный мир, который пронизан светом ласкового солнца. Недаром говорят, что лучше один раз увидеть, чем сто раз услышать. Наши глаза помогают нам познавать окружающий мир, учиться, выполнять различную работу. Человеку с плохим зрением труднее будет учиться, работать. Наши глаза настолько драгоценны, что мы просто обязаны их беречь. И сейчас сделаем гимнастику для глаз. Дорогие гости присоединяйтесь к нам.

Упражнения для глаз (сидя на месте):

• Закрыть глаза, до лёгкого ощущения боли, сжать веки.

• Глядя на стену впереди, выполнить вращения глазами, мысленно рисуя знак бесконечности ∞

• Зажать правую руку в кулак так, чтобы большой палец был перпендикулярен потолку и вытянуть её перед собой. Двигая рукой влево, вправо, глазами смотреть на кончик большого пальца руки.

• Смотрим вверх, вниз, не двигая головой.

• Смотрим влево вправо, не двигая головой.

• Вытянули голову вверх, повернули ею влево, вправо, вверх, вниз.

• 7-8 раз.

Закончили упражнения.

Молодцы! Отдохнули, а теперь продолжаем.

Ребята выполняют упражнения

2 мин.

6. Самостоятельная работа

Решение квадратных уравнений по формуле. К1, ЭОР №6

Квадратные уравнения встречаются не только на уроках алгебры, но и на геометрии, физике. Эти уравнения занимают одно из главных мест в математике.Вы сами определяете, выбрав одно из двух заданий.

На работу вам 7 минут, а затем обсуждаем полученные решения.

10 мин

Запускается ЭОР №6

(Расположен на рабочем столе каждого компьютера, оценивает программа)

А) Решение квадратных уравнений по формуле

Работают индивидуально

Запускается ЭОР (дополнительно)

(Расположен на рабочем столе каждого компьютера, оценивает программа)

В) Тест по теме «Квадратные уравнения»

Работают индивидуально

С) Работа в рабочей тетради.

Взаимопроверка

Работают индивидуально в рабочей тетради.

Стр.43 № 217

7. Домашнее задание.

Откройте дневники, запишите задание на дом: 378(2а), 382(б). Творческое задание (по желанию) «Квадратные уравнения, полученные в данных задачах, решите несколькими способами».

Запись домашнего задания

1 мин.

8 . Интересная задача.

ЭОР №7

Запускается ЭОР №7

Как аль-Хорезми решал квадратные уравнения

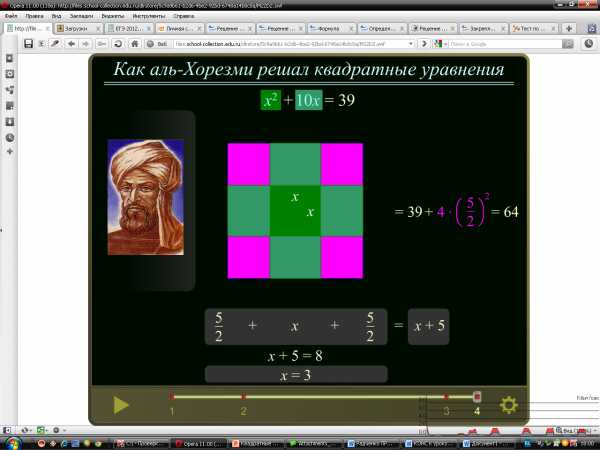
Слушают анимацию.

Записывают алгоритм.

2 мин.

9. Подведение итогов урока. Рефлексия

Анализ достижений предметных и метапредметных результатов

Вопросы к учащимся:

Что нового вы узнали сегодня на уроке? Чему научились?

Опыт использования каких «старых» знаний вам сегодня пригодился?

Что вызвало у вас удивление на уроке?Какой вид деятельности понравился вам больше всего и почему?

Как вы считаете, какой способ решения квадратных уравнений универсальный?

Молодцы! Всем вам, я думаю, хочется получить хорошую оценку

Оцените свою деятельность (в баллах и в словесной форме):

Критерии выставления отметок

«5» — 9-10 +,

«4» 7-8+,

«3»-5-6+.

Ребята подсчитывают количество «+» на полях и выставляют себе на полях в тетради отметку (положительные отметки будут выставлены в журнал).

Учащиеся отвечают на вопросы с аргументацией.

5 мин.

Анализ личностных результатов

А теперь посмотрим, достигли ли Вы своей личной цели, которую записывали в начале урока?

Покажите зеленую карточку, если вы достигли личную цель, и красную, если нет. (Ребята, может кто-то из вас открыто назовет свою цель и ответит на вопрос «достиг он ее и почему он так считает?)

Учащиеся отвечают на вопросы, аргументируя

Приложение к плану-конспекту урока

Решение квадратных уравнений

Таблица 2

ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР

№

Название ресурса

Тип, вид ресурса

Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)

Гиперссылка на ресурс, обеспечивающий доступ к ЭОР

1

Решение квадратного уравнения

(N 138388)

ЦОР, учебные и методические материалы (УММ),

инновационный учебный материал, информационный И

Презентация, теоретический слайд.

http://www.school-collection.edu.ru/catalog/res/50170cb2-c355-422b-bf7c-5cd58b27ee9f/?interface=pupil&subject=17

2

Решение уравнения с квадратным корнем (N 138298)

ЦОР, УММ,

инновационный учебный материал, И

Презентация, теоретический слайд

http://www.school-collection.edu.ru/catalog/res/213df871-b48c-41d0-94cf-cc2c99cf8437/

3

Формула (N 180658)

ЦОР, УММ,

инновационный учебный материал, И

Презентация. Алгоритм решения квадратного уравнения. Примеры

http://www.school-collection.edu.ru/catalog/res/aa8f5cca-dd62-49df-b476-edc728d688b1/?fullView=1&from=&interface=pupil&class=50&subject=17&rubric_id[]=108459&rubric_id[]=108460&rubric_id[]=108461&rubric_id[]=108462&rubric_id[]=108348

4

Закрепление умений решать неполные квадратные уравнения (N 191881

ЦОР, УММ,

Инновацион-ный учебный материал, П

Интерактивное задание. Ресурс содержит задания на закрепление умений решать неполные квадратные уравнения

http://school149.avers-telecom.ru/catalog/res/54467594-eccb-4d4e-8039-4a73b6f69ca6/?fullView=1&from=d356d90c-9bae-4d83-99a7-c6c3c51d765c&&rubric_id%5B%5D=112697

5

Определение квадратного уравнения. Неполные квадратные уравнения

(N 191870)

ЦОР, УММ, инновационный учебный материал, практический модуль (П)

Задание, интерактивная модель.

http://school-collection.edu.ru/catalog/res/54467594-eccb-4d4e-8039-4a73b6f69ca6/?from=253f44a5-bb2a-4221-ae16-5b990bb69526&interface=pupil&class=50&subject=17

6

Решение квадратных уравнений по формуле. К1

Открытая образовательная модульная мультимедийная система (ОМС), контрольный модуль (К)

5 заданий с параметризацией.

http://fcior.edu.ru/card/14481/reshenie-kvadratnyh-uravneniy-po-formule-k1.html

7

Как аль-Хорезми решал квадратные уравнения

ЦОР, УММ, коллекции, предметные коллекции, алгебра, инновационный учебный материал, И

Анимация из 3 сцен., демонстрация

http://files.school-collection.edu.ru/dlrstore/5c9a9b61-b2d6-4be2-92bd-6748a14b8c8a/M22D2.swf

Дополнительное задание

№

Название ресурса

Тип, вид ресурса

Форма предъявления информации (иллюстрация, презентация, видеофрагменты, тест, модель и т.д.)

Гиперссылка на ресурс, обеспечивающий доступ к ЭОР

1

Тест по теме «Квадратные уравнения»

ЦОР, учебные материалы для ученика, тест

Презентация содержит контрольные вопросы по теме

http://www.openclass.ru/node/242893

infourok.ru

Решение задач с помощью квадратных уравнений . Видеоурок. Алгебра 8 Класс

На этом уроке мы рассмотрим, как текстовые задачи решаются с помощью квадратных уравнений, и познакомимся с универсальным алгоритмом для решения любой текстовой задачи.

На этом уроке мы выясним, как решать текстовые задачи с помощью квадратных уравнений. Как вы уже знаете, при решении любой задачи необходимо сначала перевести её условие на математический язык, составить нужное уравнение (или не одно, а несколько уравнений – систему уравнений), а затем решить его. На этом уроке мы поговорим о таких задачах, в которых уравнения будут получаться не линейные, как это было раньше, а квадратные. Или сводящиеся к квадратным.

Рассмотрим такую геометрическую задачу.

Задача

Периметр прямоугольника равен  см, а его диагональ –  см (Рис. 1). Найти стороны прямоугольника.

Рис. 1. Иллюстрация к задаче

Решение

Пусть  см – одна сторона прямоугольника. Тогда другая –  см, так как удвоенная сумма сторон (периметр) равна  см. Теперь воспользуемся теоремой Пифагора для прямоугольного треугольника, который образован смежными сторонами прямоугольника и его диагональю, и составим уравнение.

По теореме Виета:

Это и есть длины сторон. Логично, что получилось два ответа: за  ведь можно было взять как меньшую сторону, так и большую.

Ответ:  см и  см.

Три основных типа текстовых задач в математике – на движение, на работу и на смеси. На смеси очень редко бывают задачи, сводящиеся к квадратным уравнениям, так что о них сейчас говорить не будем. Рассмотрим задачу на движение.

Задача

Катер прошел  км по течению реки и

interneturok.ru

Тест (алгебра, 8 класс) по теме: Тесты по теме «Квадратные уравнения»

Тема «Квадратные уравнения. Основные понятия».

Инструкция: В заданиях с 1 по 8 выберите один ответ из предложенных.

В заданиях 9 и 10 запишите решение и ответ.

                                                                   1 вариант.

1. Какое из уравнений является квадратным:

А)  1-12х=0           Б)  7х2-13х+5=0            В)  48х2+х3-9=0                Г)  = 0

2. В квадратном уравнении  -3х2+10х+5=0 укажите старший коэффициент:

А)  10                         Б)  5                      В)  -5                     Г)  -3

3. В уравнении -6х-5х2+9=0

А)  Старший коэффициент равен -6, второй коэффициент равен -5, свободный член равен 9.

Б)   Старший коэффициент равен 9, второй коэффициент равен -6, свободный член равен -5.

В)  Старший коэффициент равен -5, второй коэффициент равен -6, свободный член равен 9.

Г) Невозможно определить.

4. Какое из квадратных уравнений является приведённым:

А)  12-х2+3х=0      Б) х2-7х+16=0      В) -15х2+4х-2=0         Г) 4х2+х-1=0

5. Какое из квадратных уравнений является неполным:

А) 16х2-9=0         Б)  3-х2+х=0        В)  –х2-х-1=0         Г)  7-7х-7х2=0

6.  Какое из чисел является корнем квадратного уравнения 5х2=0

А)  5         Б)  0           В)  -5              Г)  25

7. Какое из чисел является корнем квадратного уравнения х2+6х+9=0:

А)  0         Б)  3           В)  1               Г)  -3

8. В каком из квадратных уравнений свободный член равен 0:

А)  5х2+2х=0        Б)  х2-9=0     В)  2-х-х2=0         Г)  4х2+5х-3=0

9. Составьте квадратное уравнение, у которого старший коэффициент равен 10, второй коэффициент равен  -, свободный член равен 0,6.

10. Являются ли числа 1 и -0,6 корнями квадратного уравнения 5х2-8х+3=0?  

Тема «Квадратные уравнения. Основные понятия».

Инструкция: В заданиях с 1 по 8 выберите один ответ из предложенных.

В заданиях 9 и 10 запишите решение и ответ.

2 вариант.

1. Какое из уравнений является квадратным:

А)  = 0         Б)  15х-3=0            В)  6х4+х2=0                Г)  4х2+3х-1=0

2). В квадратном уравнении  3х2+5х-9=0 укажите свободный член:

А)  9                         Б)  -9                      В)  3                     Г)  5

3. В уравнении 3+5х-7х2=0

А)  Старший коэффициент равен -7, второй коэффициент равен 5, свободный член равен 3.

Б)   Старший коэффициент равен 3, второй коэффициент равен 5, свободный член равен -7.

В)  Старший коэффициент равен 7, второй коэффициент равен 3, свободный член равен 5.

Г)  Невозможно определить.

4. Какое из квадратных уравнений является неприведённым:

А)  х2+3х-5=0      Б)  7х+16+х2=0      В)  12х2+4х-2=0         Г)  х2+х=0

5. Какое из квадратных уравнений является полным:

А)  16х2-9=0         Б)  3х2+х=0        В)  6х2-х-15=0         Г)  -7х2=0

6. Какое из чисел является корнем квадратного уравнения 8х2=0

А)  -8         Б)  8           В)  64              Г)  0

7. Какое из чисел является корнем квадратного уравнения х2-6х+9=0:

А)  0         Б)  3           В)  -3               Г)  1

8. В каком из квадратных уравнений второй коэффициент равен 0:

А)  х2-9=0         Б)  5х2+2х=0           В)  2-х-х2=0         Г)  4х2+5х-3=0

9. Составьте квадратное уравнение, у которого старший коэффициент равен 0,4, второй коэффициент равен , свободный член равен  — 13.

10. Являются ли числа -1 и -0,5 корнями квадратного уравнения 2х2+3х+1=0?  

Таблица верных ответов  

№ задания	1	2	3	4	5	6	7	8	9	10
1 вариант	Б	Г	В	Б	А	Б	Г	А	10х2-х+0,6=0	Да
2 вариант	Г	Б	А	В	В	Г	Б	А	0,4х2 +х – 13=0	Да

nsportal.ru

Квадратные уравнения. Алгебра, 8 класс: уроки, тесты, задания.

Вход на портал Вход на портал Регистрация Начало Поиск по сайту ТОПы Учебные заведения Предметы Проверочные работы Обновления Подписка Я+ Новости Переменка Отправить отзыв

• Предметы
• Алгебра
• 8 класс

1. Основные понятия

2. Формулы корней квадратного уравнения

3. Рациональные уравнения

4. Рациональные уравнения как математические модели реальных ситуаций

5. Ещё одна формула корней квадратного уравнения

6. Теорема Виета

7. Иррациональные уравнения

Отправить отзыв Нашёл ошибку? Сообщи нам! Copyright © 2019 ООО ЯКласс Контакты Пользовательское соглашение

www.yaklass.ru

«Решение квадратных уравнений» 8 класс.

Открытый урок по алгебре 8 класс по теме

«Решение квадратных уравнений по формуле»

План– конспект урока

1. 2. Организационный момент. Постановка целей и задач. Мотивация учебной деятельности

Эмоциональный настрой нашей совместной работы.

— Здравствуйте, ребята! Садитесь, пожалуйста. Сегодня у нас с вами урок изучения нового материала «Решение квадратных уравнений по формуле». Цель урока познакомиться с алгоритмом решения полного квадратного уравнения. Девизом урока будут слова: хочу, могу, умею, делаю. ( слайд 2)

МОГУ: ребята, на уроке можно ошибаться, сомневаться, консультироваться (задавать вопросы).

УМЕЮ: мы умеем решать неполные квадратные уравнения, полные квадратные уравнения выделением квадрата двучлена.

ХОЧУ: познакомиться с алгоритмом решения полного квадратного уравнения.

ДЕЛАЮ: делаем каждый себе установку «Понять и быть тем первым, который увидит правильный путь решения». Желаю всем удачи!

3. Актуализация знаний учащихся.

1. Фронтальная работа с классом (в это время 3 учащихся у доски работают по индивидуальным карточкам и целью контроля выполнения домашней работы (задания – аналогичны дом. заданию). Нам с вами ребята, необходимо вспомнить теоретический материал по изученной теме «Квадратные уравнения» (что же мы умеем):

— Что такое уравнение? Что такое корень уравнения? Что значит решить уравнение?

— Какие уравнения мы называем линейными? Какие уравнения мы называем квадратными? Приведите примеры

— Сколько корней может иметь линейное уравнение (квадратное) уравнение? Примеры.

— Какие виды неполных квадратных уравнений вам известны? Приведите примеры.

— Какой общий вид имеет полное квадратное уравнение? Приведите пример.

— Какие квадратные уравнения мы с Вами умеем решать? Приведите примеры

Индивидуальная карточка №1 Решите уравнения:

1. 2x² – 72 = 0

2. x² – 7x = 0

3. 4x(2x – 8) = 0

Индивидуальная карточка №2 Решите уравнение:

1. (2x – 4)(5x – 30) = 0

2. — 10x² = 0

3. 3x² – 18x = 0

Индивидуальная карточка №3 Решите уравнение:

1. — 5x² = 20

2. 4x² — 64 = 0

3. (5 – x)(x – 4) = 0

Проверка работы по индивидуальным карточкам. Комментарии учащихся класса (по цепочке) решенных уравнений у доски. Оценка работы учащихся у доски

2.Фронтальная работа. А теперь давайте проверим готовность двигаться дальше в решении квадратных уравнений. ( слайд 3)

Среди перечисленных уравнений укажите 1 ряд – квадратные уравнения;

2 ряд – линейные уравнения; 3 ряд – неполные квадратные уравнения

5x² – 12x + 7 = 0

x² = 1 = 0

— 4x + 16 = 20

5x – 45 = 8x – 13

— 7x² – 49x = 0

6x³ – 12x + 11 = 0

3x — 8 = 0

(x – 1) (x – 2) = 0

x(x – 4) = 0

5 (2x – 3) = 10

4. Первичное усвоения новых знаний

Из предыдущих уроков видно, что при решении квадратных уравнений приходилось выделять полный квадрат двучлена. Чтобы постоянно не выполнять таких преобразований, достаточно один раз выполнить эти преобразования для общего вида квадратного уравнения и получить формулу корней квадратного уравнения.

Вывести формулу корней квадратного уравнения (на доске)

Ввести понятие дискриминанта квадратного уравнения (Приложение 1, слайд 4)

Рассмотреть различные случаи решения квадратного уравнения в зависимости от значения дискриминанта (D) ( слайды 5-8)

Решение квадратных уравнений

ax² + bx + с = 0, где а ≠ 0

1. Найдем дискриминант (D) уравнения по формуле b² – 4ac

2. Определим количество корней уравнения в зависимости от значения дискриминанта D

D>0, уравнение имеет 2 корня; x₁ = , x₂ =

D= 0 уравнение имеет 1 корень ; x =

D<0, корней нет

3. Записать ответ

Запись в тетради алгоритма решения квадратного уравнения, формулу корней квадратного уравнения.

5. Физкультминутка ( слайд 9)

6. Первичная проверка понимания

Работа с готовыми решениями. Комментарии трех учащихся с места

Привести пример решения квадратноых уравнений (Приложение 1, слайды 10-12)

Приер 1.

5x² – 4x – 1 = 0

а = 5, b = — 4, с = -1

D = b² – 4ac = (-4)² – 4 ∙ 5 ∙ (-1) = 16 + 20 = 36, D>0уравнение имеет 2 корня

x₁ = = = 1

x₂ = = = — 0,2

Ответ: — 0,2; 1

Пример 2

4x² — 12x + 9 = 0

а = 4, b = — 12, с = 9

D = b² – 4ac = (-12)² – 4 ∙ 4 ∙ 9 = 144 — 144 = 0, D = 0, уравнение имеет 1 корень

x = = = 1,5

Ответ: 1,5

Пример 3

7x² + 3x + 5 = 0

а =7, b = 3, с = 5

D = b² – 4ac = (-3)² – 4 ∙ 7 ∙ 5 = 9 — 140 = 131, D < 0, уравнение корней не имеет

Ответ: нет корней

7. Первичное закрепление

Работа на уроке. Решение квадартных уравнений (работа в парах) (2 варианта)

На каждую парту 1 вариант. Сверка с образцом на доске (написано перед уроком на открывающихся досках).

Работа у доски по учебнику – по 2 учащихся № 25.1(а), 25.3(а), 25.5(а), 25.7(а)

8. Домашнее задание задачник Алгебра – 8, стр. 154, п. 25, № 25.1(в), 25.3(в), 25.5(в), 25.7(в)

9. Итог урокаю Рефлексия. Выставление оценок учащимся (слайд )

1. Напишите формулу нахождения дискриминанта квадратного уравнения.

2. Напишите формулу корней квадратного уравнения

3. Сколько корней может иметь квадратное уравнение? От чего это зависит?

Рефлексия ( слайд )

• На уроке я успел сделать…

• В результате я узнал и научился…

• Я не понял, у меня не получилось…

infourok.ru

No related posts.