Решить двойной интеграл онлайн: Решение двойных интегралов | Онлайн калькулятор

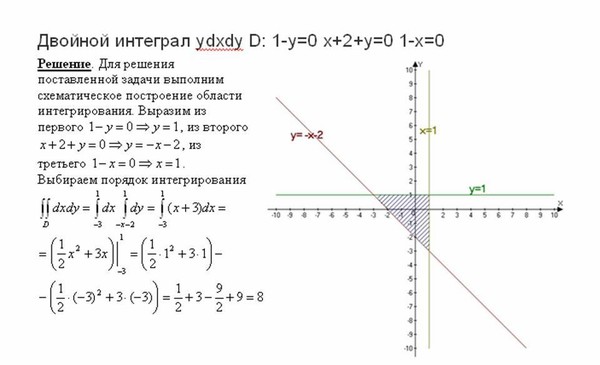
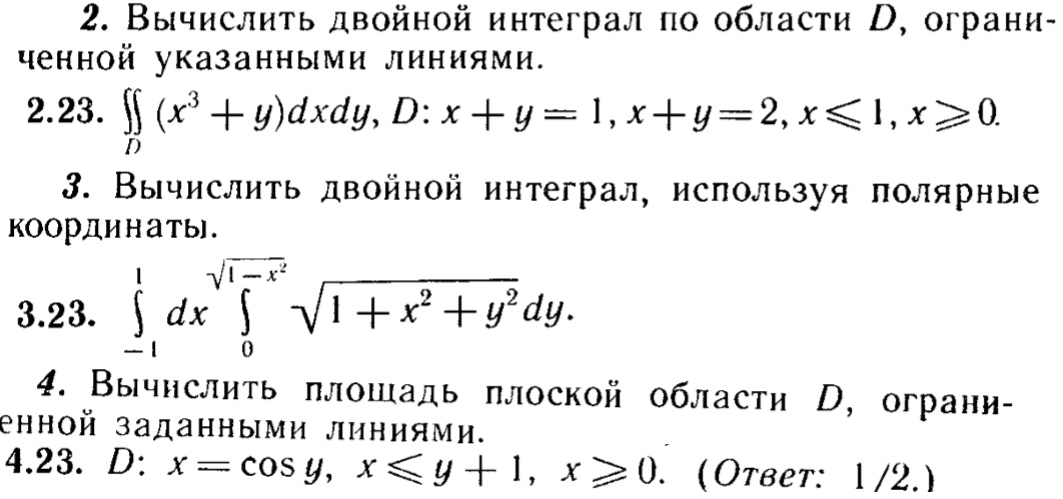Двойной интеграл — онлайн калькулятор.

Теория кратных интегралов представляет собой раздел математики, в котором методы интегрального исчисления обобщаются на вычисление интегралов по областям, расположенным на плоскости или в пространстве. Кратные, криволинейные и поверхностные интегралы, теория поля, числовые и функциональные ряды нашли широкое применение в различных разделах математики, включая теорию вероятностей, дифференциальные уравнения в частных производных, оптимальное управление, в теоретической физике и механике, механике сплошных сред, и многих других теоретических и прикладных науках. На нашем сервисе можно вычислить


двойной интеграл

Формулы для вычисления двойного интеграла

Пусть на плоскости Oxy задана ограниченная замкнутая область S с кусочно-гладкой границей L, и пусть на области S определена функция f ( x ,  y ). Тогда двойной интеграл

физически будет представлять собой массу области S плотностью p = f ( x ,  y ), отсеченную боковой поверхностью цилиндра с основанием на плоскости Oxy  и с образующими, параллельными оси Oz, исходящими из точек границы L. Геометрически такой интеграл представляет собой объем цилиндра,   который ограничен   снизу плоскостью Oxy, сверху поверхностью                z = f ( x ,  y ) , сбоку образующими, параллельными оси Oz, исходящими из точек границы L. Для того чтобы вычислять двойные интегралы, их необходимо преобразовать в повторный:

если S – правильная (простая) область, т.е. область S – область, ограниченная кривыми

или ограниченная кривыми

Рисунок 1 Пояснения к вычислению двойного интеграла

Если область S не правильная, то такую область разбивают на простые области так, чтобы у них не было общих внутренних точек, а интеграл будет представлять собой сумму интегралов по этим простым областям:

Изменение порядка интегрирования:

или наоборот. Если у вас возникли сложности с решением двойных интегралов, мы поможем с вычислением, на нашем сайте находится надежный онлайн калькулятор.

Примеры вычисления двойных интегралов

Вычислить:

Построить область интегрирования, поменять порядок интегрирования:

Построить область интегрирования, поменять порядок интегрирования:

Записать двойной интеграл в виде повторного, поменять пределы интегрирования: Область G – параллелограмм, ограниченный кривыми

Рисунок 2 Пояснения к замене переменных в двойном интеграле

Преобразовать двойной интеграл в повторный, поменять порядок интегрирования: Область G ограниченна кривыми

Рисунок 3 Пояснение к вычислению двойного интеграла в примере 5

 

На нашем портале вы так же можете ознакомиться с другими видами интегралов, и пробовать с помощью наших калькуляторов делать вычисления: ОПРЕДЕЛЕННЫХ ; ДВОЙНЫХ ; НЕОПРЕДЕЛЕННЫХ интегралов.

Posted in База знаний

вычисление двойного интеграла онлайн

Вы искали вычисление двойного интеграла онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление двойных интегралов онлайн, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «вычисление двойного интеграла онлайн».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как вычисление двойного интеграла онлайн,вычисление двойных интегралов онлайн,вычислить двойной интеграл онлайн,вычислить двойной интеграл онлайн по области d,вычислить двойной интеграл онлайн с подробным решением,вычислить двойной интеграл по области d онлайн,двойной интеграл в полярных координатах онлайн калькулятор,двойной интеграл калькулятор онлайн,двойной интеграл онлайн,двойной интеграл онлайн калькулятор,двойной интеграл онлайн калькулятор с подробным решением,двойной интеграл онлайн с подробным решением,двойной интеграл онлайн с подробным решением калькулятор,двойной интеграл решить онлайн,двойной интеграл с подробным решением онлайн,двойные интегралы онлайн,двойные интегралы онлайн калькулятор,двойные интегралы онлайн с подробным решением,калькулятор двойного интеграла,калькулятор двойных интегралов,калькулятор двойных интегралов онлайн,калькулятор двойных интегралов с решением,онлайн вычисление двойных интегралов,онлайн калькулятор двойного интеграла,онлайн калькулятор двойной интеграл,онлайн калькулятор двойной интеграл в полярных координатах,онлайн калькулятор двойные интегралы,онлайн калькулятор интегралов двойных,онлайн решение двойного интеграла,онлайн решение двойных интегралов,онлайн решение двойных интегралов с подробным решением,определенный двойной интеграл онлайн,повторный интеграл вычислить,представить двойной интеграл в виде повторного интеграла онлайн,расставить пределы интегрирования в двойном интеграле онлайн,решение двойного интеграла онлайн,решение двойных интегралов онлайн,решение двойных интегралов онлайн с подробным решением,решение онлайн двойного интеграла,решить двойной интеграл онлайн,решить двойной интеграл онлайн с решением,решить интеграл двойной онлайн,решить интеграл онлайн двойной,решить онлайн двойной интеграл.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и вычисление двойного интеграла онлайн. Просто введите задачу в окошко и нажмите «решить» здесь (например, вычислить двойной интеграл онлайн).

Решить задачу вычисление двойного интеграла онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор двойного интеграла — Калькулятор двойного интеграла онлайн

Калькулятор двойного интеграла вычисляет значение двойного интеграла. Площадь двумерной фигуры можно определить с помощью двойных интегралов. Двойное интегрирование представлено ‘∫∫’.

Что такое калькулятор двойных интегралов?

Калькулятор двойного интеграла — это онлайн-инструмент, который помогает интегрировать заданную функцию и получить значение двойного интеграла. Двойные интегралы можно использовать для нахождения объема под поверхностью и среднего значения функции с двумя переменными. Чтобы использовать Калькулятор двойных интегралов , введите значения в поля ввода.

Калькулятор двойных интегралов

Как пользоваться калькулятором двойных интегралов?

Чтобы найти значение двойного интеграла с помощью онлайн-калькулятора двойного интеграла, выполните шаги, указанные ниже:

• Шаг 1: Перейдите к онлайн-калькулятору двойного интеграла Cuemath.
• Шаг 2: Введите функцию и пределы в соответствующие поля ввода. Из выпадающего списка выберите, какая переменная будет интегрирована первой.
• Шаг 3: Нажмите кнопку «Вычислить» , чтобы найти значение двойного интеграла.
• Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.

Как работает калькулятор двойных интегралов?

Интегральное исчисление состоит из определенных типов интегрирований, таких как простое интегрирование, двойное интегрирование и тройное интегрирование. Когда мы имеем дело с функцией одной переменной, интегрирование применяется по интервалу (одномерному пространству). Таким образом, когда у нас есть функция, зависящая от двух переменных, мы по существу интегрируем ее по области (двухмерному пространству). 9{b}f(x,y)dxdy\), то мы используем следующие шаги, чтобы найти его значение.

• Сначала решим внутренний интеграл. Поскольку dx предшествует dy, мы сначала проинтегрируем функцию по x. Все члены, содержащие y, будут рассматриваться как константы.
• Применяются внутренние пределы определенного интеграла. Теперь наша функция будет только через y.
• Далее решаем внешний интеграл. Это означает, что мы интегрируем функцию по y. 9{2}]dxdy\)

☛ Статьи по теме:

• Интеграция
• Определенный интеграл
• Неопределенный интеграл

☛ Математические калькуляторы:

Нахождение среднего значения из двойного интеграла — Криста Кинг Математика

Формула для среднего значения с двойным интегралом

Мы можем оценить среднее значение области кривых уровня, используя формулу

???f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}???

где ???A(R)??? площадь прямоугольника определяется как ???R=[x_1,x_2]\times[y_1,y_2]???, и где двойной интеграл дает объем под поверхностью ???f(x,y)? ?? по области ???R???.

Привет! Я Криста.

Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.

Если уравнение не задано, мы можем использовать предоставленную диаграмму для оценки значения функции в средних точках.

Нахождение среднего значения по заданному региону с помощью двойного интеграла с функцией многих переменных

Пройти курс

Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂

Использование кривых уровня для оценки среднего значения по региону

Пример

Используйте набросок кривых уровня для оценки среднего значения региона, где ???m=n=2??? и???R=[0,2]\times[0,3]???.

Вопрос заключается в том, чтобы использовать эскиз кривых уровня, которые представляют нашу функцию, для оценки среднего значения области, изображенной и определенной ???R=[0,2]\times[0,3]??? .

Нам нужно будет использовать формулу для среднего значения:

???f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}???

Мы можем начать с вычисления ???A(R)??? общей площади региона ???R???.

???А(R)=(2)(3)???

???А(R)=6???

Далее мы можем найти ???\Delta{A}???, площадь одного из подпрямоугольников. Судя по полученной нами цифре, ширина каждого подпрямоугольника равна ???1??? а высота ???3/2???. Это означает, что площадь каждого подпрямоугольника равна

???\Delta{A}=(1)\left(\frac32\right)???

???\Delta{A}=\frac32???

Если уравнение не задано, мы можем использовать предоставленную диаграмму для оценки значения функции в средних точках.

Далее нам нужны середины каждого подпрямоугольника.

Использование ???R=[0,2]\times[0,3]???, ???m=n=2??? и на нашей диаграмме мы видим, что середины четырех меньших прямоугольников равны

???\left(\frac12,\frac34\right)???, ???\left(\frac32,\frac34\right) ???, ???\влево(\frac12,\frac94\вправо)??? и ???\влево(\frac32,\frac94\вправо)???

Поскольку у нас нет уравнения для нашей функции, мы можем использовать диаграмму ее кривых уровня для оценки значений функции в каждой средней точке.

При ???\left(\frac12,\frac34\right)??? функция приблизительно равна ???19???.

При ???\left(\frac32,\frac34\right)??? функция приблизительно равна ???35???.

При ???\left(\frac12,\frac94\right)??? функция приблизительно равна ???20???.

При ???\left(\frac32,\frac94\right)??? функция приблизительно равна ???26???.

Теперь у нас есть все необходимое, чтобы найти оценку среднего значения функции по региону. Мы будем использовать формулу

???f_{ave}=\frac{1}{A(R)}\int\int_Rf(x,y)\Delta{A}???

, но, поскольку у нас нет функции, мы будем использовать формулу правила средней точки вместо двойного интеграла, чтобы формула приняла вид

???f_{ave}=\frac{1}{A(R )}\left[\Delta{A}\left(f(x_1,y_1)+f(x_2,y_2)+f(x_3,y_3)+f(x_4,y_4)\right)\right]???

???f_{ave}=\frac{1}{6}\left[\frac32\left(19+35+20+26\right)\right]???

???f_{ave}=\frac{1}{6}\left[\frac32\left(100\right)\right]???

???f_{ave}=\frac{300}{12}???

???f_{ave}=25???

Используя правило средней точки, это наша оценка среднего значения функции по региону.