Определители третьего порядка с примерами | Математика
Пусть дана квадратная матрица третьего порядка
ОПРЕДЕЛЕНИЕ 1.8
Определителем третьего порядка, соответствующим данной квадратной матрице А, называется число
| (1.7) |
Помощь с решением задач
Определитель третьего порядка обозначается символом
| (1.8) |
где числа называются его элементами.
Индексы у элемента показывают номера строки и столбца, на пересечении которых записан этот элемент.
Например, элемент расположен на пересечении второй строки и третьего столбца .
Элементы образуют главную диагональ определителя, а элементы побочную диагональ.
Определение имеет сложный по форме вид, поэтому для нахождения определителя третьего порядка предложены более простые правила.
- вычислить с собственными знаками произведения элементов , лежащих на главной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны этой диагонали ;
- найти произведения элементов, лежащих на побочной диагонали и в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали, и взять их с противоположными знаками ;
- найти общую сумму всех произведений.
ПРИМЕР 1.1.7
Все свойства определителей второго порядка справедливы и для определителей третьего порядка. Доказательства этих свойств основаны на вычислении определителя третьего порядка по формуле (1.7).
Например, покажем, что определитель, у которого элементы двух его строк пропорциональны, равен нулю. Действительно,
Аналогично проверяется справедливость и других свойств.
Пусть дан определитель (1.8) третьего порядка.
ОПРЕДЕЛЕНИЕ 1.9: Минором элемента , где определителя третьего порядка, называется определитель второго порядка, полученный из данного вычеркиванием й строки и го столбца. Так, например, минор элемента есть определитель
Так, например, минор элемента есть определитель
а минор элемента есть
С помощью миноров определитель (7) можно записать в виде
| (1.9) |
ОПРЕДЕЛЕНИЕ 1.10: Алгебраическим дополнением элемента , где , называется минор этого элемента, взятый со знаком . По определению 4.3 имеем
| где / | (1.10) |
Например,
и т.д.
ТЕОРЕМА 1.1 Разложение определителя по элементам строки или столбца
Определитель третьего порядка равен сумме произведений элементов любой его строки (столбца) на их алгебраические дополнения. Иными словами, имеют место шесть равенств:
| (1.11) |
Проверим, например, справедливость равенства
Согласно определениям минора и алгебраического дополнения получим
ТЕОРЕМА 1. 2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
2 Сумма произведений элементов какой- либо строки (столбца) определителя на алгебраические дополнения элементов любой другой его строки (столбца) равна нулю.
Для определенности выберем элементы первой строки и алгебраические дополнения элементов второй строки определителя. Составим сумму произведений и покажем, что эта сумма равна нулю.
Действительно,
Аналогично проверяется равенство нулю и всех других подобных сумм.
В заключение рассмотрим схему использования свойств определителя и теоремы разложения при вычислении определителя.
ПРИМЕР 1.1.8
Вычислить определитель
Решение. Разложим определитель по элементам третьей строки.
ПРИМЕР 1.1.9
Вычислить определитель
Решение. Прибавляя ко второй строке первую, умноженную на — 8,
получим Раскладывая этот определитель по элементам второй его строки, найдем
- Определители n-го порядка с примерами
- Курс математики
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
Скачать рамки A4
Скачать миллиметровки
Скачать шрифты ГОСТ
Сохранить или поделиться с друзьями
Заказать решение
Поиск математических формул
Определители третьего порядка
Высшая математика / Практикум по аналитической геометрии
Выражение вида
называется определителем третьего порядка.
Определитель третьего порядка имеет девять элементов, три строки, три столбца, две диагонали — главную и побочную.
Рис.1
Формула (1) показывает, что в раскрытом виде определитель содержит шесть членов. Для их определения существуют простые способы. Рассмотрим два из них.
Способ I. Выписываем все элементы определителя в том же порядке, как они расположены в определителе, и приписываем справа первые два столбца определителя:
Способ II. Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента.
Возьмем со знаком плюс произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллельных к ней линиях, содержащих по три элемента.
Произведения же элементов, стоящих на побочной диагонали и на двух параллельных к ней линиях, содержащих по три элемента, возьмем со знаком минус.
Алгебраическая сумма этих шести произведений дает значение определителя третьего порядка.
Пример. Вычислить определитель:
Решение.
Способ III. Способ разложения определителя по элементам какой-либо строки или столбца.
Если в определителе третьего порядка вычеркнуть одну строку и один столбец, на пересечении которых стоит некоторый элемент, то оставшиеся элементы образуют определитель второго порядка, который называется минором определителя Δ, соответствующим этому элементу. Например, минором определителя
соответствующим элементу будет определитель второго порядка
Чтобы вычислить определитель третьего порядка, нужно каждый элемент строки или столбца, по которым разлагается определитель, умножить на его минор, взятый со знаком плюс или минус в зависимости от того, будет ли сумма номеров зачеркнутых строки и столбца четным или нечетным числом. Например,
Например,
— разложение определителя Δ по первому столбцу.
Пример. Вычислить определитель
Решение.
Основные свойства определителей третьего порядка.
Свойство 1. Величина определителя не изменится, если за¬писать столбцы вместо строк, а строки вместо столбцов.
Свойство 2. При перестановке двух столбцов или строк определитель меняет знак.
Свойство 3. Чтобы умножить определитель на какое-нибудь число, достаточно умножить на это число все элементы какой-нибудь одной строки или какого-нибудь одного столбца.
Свойство 4. Если в определителе имеются две одинаковых строки или два одинаковых столбца, то он равен нулю.
Свойство 5. Величина определителя не изменится, если к элементам некоторого ряда прибавить элементы параллельного ряда, предварительно умножив их на постоянный множитель.
— примеры, Калькулятор определителя онлайн
Калькулятор определителя— это онлайн-инструмент, который помогает найти определитель квадратной матрицы 3 x 3, используя формулу определителя. Найти определитель можно только квадратных матриц.
Что такое определительный калькулятор?
Калькулятор определителя помогает вычислить определитель квадратной матрицы 3 x 3. Когда мы находим сумму произведений элементов квадратной матрицы по какому-то заданному правилу, полученная таким образом величина называется определителем. Чтобы использовать Калькулятор определителя , введите значения в поля ввода.
Калькулятор определителя
ПРИМЕЧАНИЕ: Вводите значения не более 3 цифр.
Как пользоваться калькулятором определителя?
Выполните следующие действия, чтобы найти определитель матрицы 3 x 3 с помощью онлайн-калькулятора определителя.
- Шаг 1: Перейдите к онлайн-калькулятору определителя Cuemath.
- Шаг 2: Введите элементы матрицы в указанные поля ввода.
- Шаг 3: Нажмите кнопку «Вычислить» , чтобы найти определитель.
- Шаг 4: Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.
Как работает калькулятор определителя?
Определитель можно рассматривать как функцию, которая принимает элементы квадратной матрицы в качестве входных данных и выводит единственное значение. Детерминанты являются скалярными величинами. Определитель квадратной матрицы используется для нахождения обратной этой матрицы. Кроме того, нам потребуются определители, если мы решаем линейные уравнения, используя метод обращения матриц. Шаги для нахождения определителей матриц приведены ниже:
Шаги для нахождения определителей матриц приведены ниже:
1. Матрица 2 x 2
Пусть \(A_{2\times 2}\) = \(\begin{bmatrix} a & b\\ c & d \end{bmatrix}\)
Формула для вычислить определитель следующим образом:
\(\begin{vmatrix}A_{2\times 2} \end{vmatrix}\) = (a x d) — (b x c)
2. 3 x 3 Матрица
Пусть \ (A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix}\)
Шаг 1: Умножаем номера привязок с соответствующей квадратной подматрицей.
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a . \(\begin{vmatrix} e & f\\ h & i \end{vmatrix}\) — b . \(\begin{vmatrix} d & f\\ g & i \end{vmatrix}\) + c . \(\begin{vmatrix} d & e\\ g & h \end{vmatrix}\)
Шаг 2: Используя формулу определителя матрицы 2 x 2, мы решаем выражение на шаге 1, как указано ниже.
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei — fh) — b(di — fg) + c(dh — eg).
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры с определителями
Пример 1: Найти определитель следующей матрицы \(\begin{bmatrix} 3 & 4 & 5\\ 1& 2& 3\\ 2& 0 & 9 \ end{bmatrix}\) и проверьте его с помощью онлайн-калькулятора определителей.
Решение:
Дано: \(A_{3\times 3}\) = \(\begin{bmatrix} 3 & 4 & 5\\ 1& 2& 3\\ 2& 0 & 9 \end{bmatrix}\ )
По формуле
\(A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix} \)
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei — fh) — b(di — fg) + c(dh — eg)
Подставляя эти значений получаем
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = 3 (2 x 9- 0 x 3) — 4 (1 x 9 — 0 x 3) + 5 (1 x 0 — 2 x 2)
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = 22
Пример 2: Найдите определитель следующей матрицы \(\begin{bmatrix} -1 & 2 & -4\\ 7. 2& 6& 2.3\\ -5& 1.3 & 3 \end{bmatrix}\) и проверьте это с помощью онлайн-калькулятора определителя.
2& 6& 2.3\\ -5& 1.3 & 3 \end{bmatrix}\) и проверьте это с помощью онлайн-калькулятора определителя.
Решение:
Дано: \(A_{3\times 3}\) = \(\begin{bmatrix} -1 & 2 & -4\\ 7.2& 6& 2.3\\ -5& 1.3 & 3 \ конец{bmatrix}\)
По формуле
\(A_{3\times 3}\) = \(\begin{bmatrix} a & b & c\\ d& e& f\\ g& h & i \end{bmatrix}\ )
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = a(ei — fh) — b(di — fg) + c(dh — eg)
Подстановка этих значений получаем
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = -1 (6 x 3 — 2,3 x 1,3) — 2 (7,2 x 3 — 2,3 x (-5) ) — 4(7,2 x 1,3 — 6 x (-5))
\(\begin{vmatrix}A_{3\times 3} \end{vmatrix}\) = -238,65
Точно так же вы можете попробовать калькулятор определителей, чтобы найти определители для следующего:
- \(\begin{bmatrix} 3.2 & -2 & 3\\ 1& 0& 4\\ -1& -7 & 4.7 \end{ бматрица}\)
- \(\begin{bmatrix} 8.2 & -3 & 5\\ 1.9& 2.8& -3\\ 9& 1 & 1 \end{bmatrix}\)
☛ Математические калькуляторы:
Если все элементы на двух диагоналях определителя третьего порядка равны нулю, то каково значение определителя.

- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8 9
- Класс 7 024
- ИИТ ЕГЭ
- NCERT
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия0024
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ по биологии
- Образцы работ по физике
- Образцы работ по химии
- Экзаменационный уголок
- Онлайн-класс
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Блог
- О нас
- Карьера
- Скачать
- Получить приложение
- Toppers 4 Toppers 4
- Toppers 020
Вопрос
Обновлен: 06.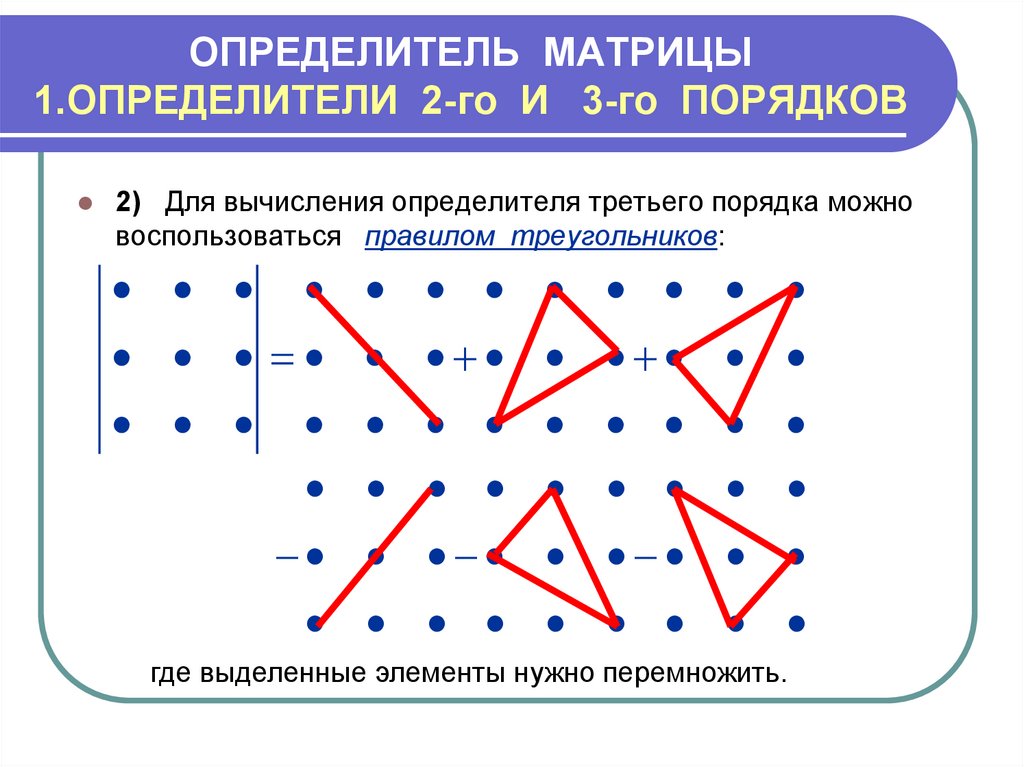 01.20210003 5 видео
01.20210003 5 видео
РЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Похожие видео
Если значение определителя третьего порядка равно 12, то найдите значение определителя, образованного заменой каждого элемента его сомножителем
14310
02:28
Если каждый элемент определитель второго порядка равен либо нулю, либо единице, какова вероятность того, что значение определителя неотрицательно?
26267
02:01
शून्य है, तो उसका मान …….. होगा |
234314030
01:37
Если каждый элемент строки выражается как сумма двух элементов, то проверьте для определителя третьего порядка, что определитель может быть выражен как сумма двух определителей.
254808671
06:02
Просмотреть все ्तम्भ के प्रत्येक अवयव को दो पदों के योग के रूप मम तीय स्तम्भ के प्रत्येक अवयव को तीन पदों के मो। क ं तथा तृतीय स्तम्भ के प्रत्येक अवयव को चार पदों के योग के रूप में लिखा गया है, तब इस सारणि। n न्न सारणिकों के योग के रूप में लिख सकते है, जहान न n №
618430242
04:35
Если значение определителя третьего порядка равно 12, то найти значение определителя, образованного заменой каждого элемента его сомножителем
642508098
9003 элемент определителя второго порядка равен нулю или единице, какова вероятность того, что значение определителя неотрицательно?
642566722
02:08
Если значение определителя третьего порядка равно 16, то значение определителя, образованного заменой каждого его элемента его кофактором, равно
642797320
02:05
Если значение определителя третьего порядка равно 12, то значение определителя, образованного заменой каждого элемента его сомножителем, будет равно 144
642912301
02:0052 2 Если каждый элемент определителя третьего порядка, имеющий значение 8, разделить на 2, то каково значение полученного определителя?643120610
02:55
Если каждый элемент определителя третьего порядка со значением 8 умножить на 2, то запишите значение нового определителя.
644177873
01:53

