Решить систему линейных уравнений и вычислить невязку: Решение систем линейных уравнений методом Гаусса

Содержание

Некоторые вычислительные особенности слау

Погрешности и невязки

Для оценки точности найденного решения СЛАУ существует две общеупотребительной меры погрешности:

вектор ошибок

где точное решение

-найденное решение

Мера абсолютно точная, только для того, чтобы ею пользоваться нужно

Чтобы избежать трудностей, вводят другую меру

вектор невязок

Невязка — количественная мера несоответствия между правыми и левыми частями системы уравнений при подстановки в них вычислительного решения.

Очевидно, что равенство нулю вектора ошибок влечет за собой равенство нулю вектора невязок.

Однако, в общем случае из малости величины невязок не следует малость ошибки. Т.е. несмотря на то, что найденное решение почти удовлетворяет уравнению, оно может совсем не подходить в качестве подлинного решения. Невязка полезна в том смысле, что с ее помощью можно осуществить контроль точности решения.

Т.к. использовать в качестве меры контроля вектор ошибок не представляется возможным в виду того, что неизвестно точное решение.

Пример. Рассмотрим систему

Предположим, что мы провели вычисления (неважно каким методом) и нашли решение

Если вычислить невязки, то невязки будут равны

Для погрешность 10^-2, но точное решение

В общем случае можно утверждать, что для оценки величины невязки и погрешности можно использовать следующие формулы:

Число называется числом обусловленности матрицы А и математически оно показывает, насколько матрица системы А близка к вырожденной или иными словами, числомера вырождения матрицы А, а именно, чем выше, тем ближе матрица к вырождению.

Обусловленность- это внутреннее свойство матрицы СЛАУ. Оно не связано с каким либо численным методом. В общем случае, можно утверждать, что матрица с большим числом обусловленности дает большие ошибки при решении СЛАУ.

Математически точно число обусловленности можно вычислить.

Введем число ;

Тогда число обусловленности представляет собой:

Тогда мы можем утверждать, что погрешность решения:

Вычислительная эффективность правила Крамера

Правило Крамера широко применяется для нахождения решения СЛУ

Если сосчитать количество операций, которых нам надо сделать

n	3	10	20
N	17	3.610*⁷	510*¹⁹
t

Численные методы решения СЛАУ

Все численные методы решения СЛАУ принято делить на два класса:

прямые
итерационные

Прямые методы используют некоторые формулы для вычисления неизвестных величин за конечное число шагов вычислительного процесса

Пример. Метод обратной матрицы

Существенным недостатком прямых методов является необходимость хранения в памяти компьютера всех n- квадратных элементов матрицы системы, т.е прямые методы никаким образом не учитывают разряженную структуру матрицы в системы.

Кроме этого применения прямых методов для решения СЛАУ с большим числом переменных приводит к значительному накоплению вычислительных погрешностей.

К широко известным методам относится метод Гаусса, метод прогонки.

Итерационные методы ( методы последовательных приближений)-это методы, в которых с помощью какого- либо алгоритма строится цепочка приближенных решений

Каждый цикл таких вычислений называется итерацией.

Итерационные алгоритмы сложнее прямых методов. Объем необходимых вычислений при их использовании заранее трудно определить, но они не требуеют при работе с разряженными матрицами хранение всех ее элементов. Более того, зачастую в них используются вычислительные формулы, задающие эти примеры.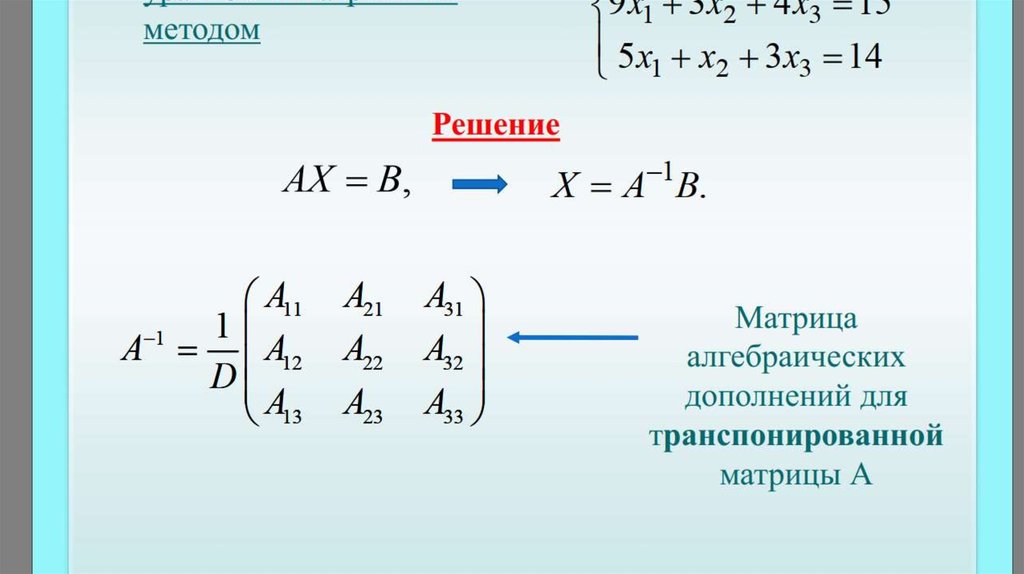 Итерационный процесс устроен таким образом, что вычислительные ошибки от итерации к итерации не накапливаются. Поэтому итерационный метод можно использовать как для решения хорошо обусловленных так и плохообусловленных СЛАУ.

Примеры: Метод простой итерации и метод Гаусса- Зейделя

Метод исключения Гаусса

Хорошо известно, что алгоритм метода Гаусса для решения СЛАУ состоит из двух основных шагов.

На прямом ходе путем последовательного исключения переменных из уравнений системы, матрицу системы приводят к треугольному виду.

решение методом исключения дает верхнетреугольную матрицу:

На обратном ходе вычисляется точное решение системы

подставляем в предыдущее уравнение и получаем:

Метод Гаусса применим эффективно лишь в том случае, когда матрица системы хорошо обусловлена, имеет низкое число обусловленности.

Точность вычисления значительно зависит от способа нахождения ведущего элемента, который мы используем, для исключения переменных на прямом ходе.

Пример.Рассмотрим систему:

Возьмем в качестве ведущего элемента

При решении получим:

если округлить, то примерно получим, что неправильно!

Теперь, возьмем в качестве ведущего элемента коэффициент перед из второго уравнения, т.е 1.

Тогда, если округлить, то получим правильное решение

Правила для выбора ведущего элемента:

выбор по столбцам

Рассматривается первый столбец. Предполагается, что мы хотим исключить . Находим в этом столбце максимальный элемент, т.е. Находим уравнение, где коэффициент присамый большой и переставляем это уравнение на первое место и используем коэффициент прив качестве ведущего элемента.

выбор по строке

Из первого уравнения находим переменную, которую будем исключать. Ищем и ищем соответственно, которое соответствует этому максимальному элементу. И ставимна первое место и исключаем его.

Эту методику можно обобщить на все элементы

по всей матрице

Сканируем столбцы и строчки и ищем . Находим, и ставим этот элемент на первое место .

Этот прием наиболее приемлем.

Метод прогонки

Метод прогонки является частным случаем метода Гаусса, который специально предназначен для решения систем уравнений с разряженной диагональной матрицей

Прямой ход состоит в том, что вычисляются коэффициенты

Сам процесс состоит в следующем.

Обратная прогонка соответствует вычислению переменных в обратном порядке, начиная с самого последнего x

зная , можно найти

Итерационные методы

В общем случае схема итерационных методов решения СЛАУ заключается в следующем:

каким- либо посторонним способом нужно установить, какое- либо начальное решение
вычисляем правую часть:
находим невязку:
находим решение системы уравнений: ,- вектор поправок
из 5. пункта идем во 2.

Важным вопросом является, когда нужно остановиться!

В качестве остановки используют какое- либо векторное неравенство, которое сравнивает решения, полученные на предыдущей и последующей итерации.

Введем норму:

Метод Гаусса

Определение метода Гаусса

Пусть дана система , ∆≠0. (1)
Метод Гаусса – это метод последовательного исключения неизвестных.

Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных. Рассмотрим одну из вычислительных схем. Эта схема называется схемой единственного деления. Итак, рассмотрим эту схему. Пусть a

11≠0 (ведущий элемент) разделим на a₁₁ первое уравнение. Получим
x₁+a⁽¹⁾₁₂·x₂+…+a⁽¹⁾_1n·x_n=b⁽¹⁾₁ (2)
Пользуясь уравнением (2), легко исключить неизвестные x₁ из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x₁), то есть на первом шаге получим
.

Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.

Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x₂ (шаг 2).
После n шагов вместо (1) получим равносильную систему
(3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x_n , x_n_-1, …, x₁.
Обозначим полученное решение за x₀. Тогда разность ε=b-A·x₀ называется невязкой.
Если ε=0, то найденное решение x₀ является верным.

Вычисления по методу Гаусса выполняются в два этапа:

Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.

Коэффициенты а₁₁, а₂₂, …, называют ведущими элементами.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.

Назначение метода Гаусса

Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.

Виды метода Гаусса

Классический метод Гаусса;
Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k-ом шаге ведущим элементом оказывался наибольший по модулю элемент k-го столбца.
Метод Жордано-Гаусса;

Отличие метода Жордано-Гаусса от классического метода Гаусса состоит в применении правила прямоугольника, когда направление поиска решения происходит по главной диагонали (преобразование к единичной матрице). В методе Гаусса направление поиска решения происходит по столбцам (преобразование к системе с треугольной матрицей).
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.

Пример решения методом Гаусса
Решим систему:

Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₃:
Из 2-ой строки выражаем x₂:
Из 3-ой строки выражаем x₁:

Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B
1 / 1 = 1	2 / 1 = 2	-2 / 1 = -2	1 / 1 = 1

Разрешающий элемент равен (3).

На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B

0 / 3 = 0	3 / 3 = 1	1 / 3 = 0.33	4 / 3 = 1.33

Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.

Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x₁	x₂	x₃	B


0 / -4 = 0	0 / -4 = 0	-4 / -4 = 1	-4 / -4 = 1

Ответ: x₁ = 1, x₂ = 1, x₃ = 1

Показатель	Метод Гаусса	Метод Жордано-Гаусса
Вид матрицы	Треугольная матрица	Единичная матрица
Время решения	0. 031	0.022
Объем используемой памяти, байт	5647	3277

Реализация метода Гаусса

Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi, а также имеется реализация метода Гаусса в онлайн режиме.

Использование метода Гаусса

Применение метода Гаусса в теории игр

В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.

Применение метода Гаусса при решении дифференциальных уравнений

Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.

Применение метода Жордано-Гаусса в линейном программировании

В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.

Примеры

Пример №1. Решить систему методом Гаусса:
x₁ +2x₂ — 3x₃ + x₄ = -2
x₁ +2x₂ — x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

Решение
Видео решение

Решение находим с помощью калькулятора.
Запишем систему в виде:

Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

Для удобства вычислений поменяем строки местами:

Умножим 1-ую строку на (0).

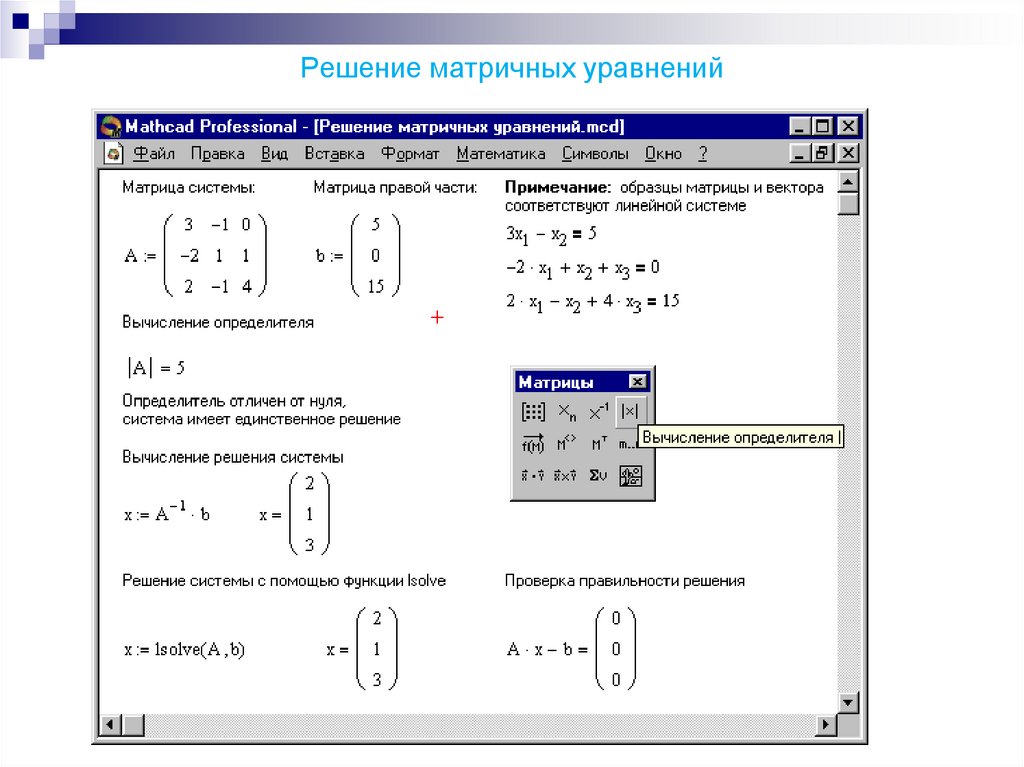Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₄

Из 2-ой строки выражаем x₃

Из 3-ой строки выражаем x₂

Из 4-ой строки выражаем x₁

Пример №3.

Решить СЛАУ методом Жордано-Гаусса. Запишем систему в виде:
5 -1 -1 3
1 2 3 6
4 3 2 9
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (5), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
1 -0.2 -0.2 0.6
0 2.2 3.2 5.4
0 3.8 2.8 6.6
Разрешающий элемент равен (2.2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 0 0.0909 1.09
0 1 1.45 2.45
0 0 -2.73 -2.73
Разрешающий элемент равен (-2.73). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
1 0 0 1
0 1 0 1
0 0 1 1
x₁ = 1. 00, x₂ = 1.00, x₃ = 1.00
Перейти к решению своей задачи

Example1
Систему линейных уравнений решить методом Гаусса
Пример
Посмотрите, как быстро можно определить, является ли система совместной
Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения: Решение
Example 4
Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
Решение:xls
Решить систему линейных уравнений тремя способами: а) методом Гаусса последовательных исключений неизвестных; б) по формуле x = A^-1b с вычислением обратной матрицы A^-1; в) по формулам Крамера.
Решение:xls
Решить методом Гаусса следующую вырожденную систему уравнений.
Скачать решение doc
Решите методом Гаусса систему линейных уравнений записанную в матричной форме:
7 8 -3 x 92
2 2 2 y = 30
-9 -10 5 z -114

Перейти к онлайн решению своего примера

Решение системы уравнений методом сложения

Решите 6x+5y=3, 3x+3y=4 систему уравнений методом сложения.
Решение.
6x+5y=3
3x+3y=4
Умножим второе уравнение на (-2).
6x+5y=3
-6x-6y=-8
============ (складываем)
-y=-5
Откуда y = 5
Находим x:
6x+5*5=3 или 6x=-22
Откуда x = -22/6 = -11/3

Пример №2. Решение СЛАУ в матричной форме означает, что исходную запись системы необходимо привести к матричной (так называемая расширенная матрица). Покажем это на примере.
Запишем систему в виде расширенной матрицы:

2	4	3
-2	5	4
3	0	1

Добавим 2-ую строку к 1-ой:

0	9	7
-2	5	4
3	0	1

Умножим 2-ую строку на (3).

Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:

0	9	7
0	15	14
3	0	1

Умножим 1-ую строку на (15). Умножим 2-ую строку на (-9). Добавим 2-ую строку к 1-ой:

0	0	-21
0	15	14
3	0	1

-21

Теперь исходную систему можно записать как:
x₃ = -21/(-21) = 1
x₂ = [29 — (14x₃)]/15
x₁ = [4 — (x₃)]/3
Из 2-ой строки выражаем x₂:
Из 3-ой строки выражаем x₁:

Пример №3. Решить систему методом Гаусса: x₁ +2x₂ — 3x₃ + x₄ = -2
x₁ +2x₂ — x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

Решение:
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

Для удобства вычислений поменяем строки местами:

Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₄

Из 2-ой строки выражаем x₃

Из 3-ой строки выражаем x₂

Из 4-ой строки выражаем x₁

Решение системы линейных алгебраических уравнений в параметрическом моделировании

Р.М.Ганеев, А.О.Максименко, А.В.Крючков

Система КОМПАС 3D предназначена для создания моделей (деталей и сборок) и графических документов. Параметрическое моделирование неотъемлемая часть КОМПАС 3D (как и всех современных CAD/CAM-систем), позволяющая быстро получать модели типовых изделий на основе прототипа.

Особенностью системы КОМПАС 3D является использование собственного математического ядра и параметрических технологий.

В этой статье рассматривается построение параметрического двумерного эскиза или чертежа. При этом параметрическая модель состоит из развитого набора геометрических и алгебраических ограничений, заданных на конечном множестве геометрических объектов и переменных. Наиболее распространены такие объекты, как точки, отрезки, окружности и дуги окружностей. А параметрические зависимости описываются с помощью таких геометрических ограничений, как параллельность, перпендикулярность, совпадение, касание, линейные и угловые размеры и прочие отношения. Задачей параметризации в таком случае является решение, благодаря которому все геометрические объекты эскиза (чертежа) приводятся в состояние, удовлетворяющее заданным ограничениям.

На рис. 1 представлен пример параметрического эскиза.

Рис. 1. Пример недоопределенной параметрической модели

Изображение на этом рисунке состоит из четырех прямых, шести точек, одной переменной и описывается системой из 20 ограничений:

где dispp (P1, P2, V) расстояние на величину V между точками P1 и P2, displ (P, L, V ) расстояние от точки P до прямой L, fix (P, c) фиксация координаты c у точки P, ang (L1, L2, V) угол V между прямыми L1, L2, fix (V,const) присвоение переменной V=const, hor (L) горизонтальность прямой.

Каждое из ограничений убирает одну степень свободы объекта. С учетом того, что степень свободы точки и прямой равна 2, а переменной равна 1, вся модель описывается 4*2 + 6*2 + 1 = 21 координатой степеней свобод. Таким образом, недостает ровно одного ограничения, чтобы полностью зафиксировать все объекты модели. Например, точки P2, P3, P4, Pc и прямая L2 имеют одну степень свободы перемещения, и в целом модель недоопределена.

Существуют различные подходы и методы решения задачи параметризации, и все они в основном подразделяются на методы, основанные на графах, на алгебраические и на численные:

• методы, основанные на графах, используют отвлеченную от геометрии эскиза информацию о структуре системы ограничений, например, для разбиения сложной в целом модели на более простые сепаратно решаемые подсистемы;

• алгебраические методы применяют к подсистемам, которые могут быть решены в аналитическом виде;

• численные методы хотя и проигрывают алгебраическим в эффективности, применяются в том случае, если ни один из альтернативных подходов не позволяет решить общую задачу.

Программное средство в составе CAD-системы, которое обеспечивает решение задач параметризации, как правило, применяет все описанные подходы в совокупности.

Для получения численного решения используют итерационные методы, которые, как известно, предполагают некоторое начальное приближение решения системы нелинейных уравнений. Оно уточняется на каждом шаге (итерации), пока не будет достигнута требуемая точность. Широко известный метод Ньютона-Рафсона на каждой итерации отыскивает решение системы линейных алгебраических уравнений (СЛАУ) согласно его итерационной формуле:

(1)

где k номер итерации, pk вектор решения на k-й итерации, Dp вектор направления поиска решения, F вектор значений функций, составляющих правую часть системы нелинейных уравнений, J матрица Якоби , состоящая из частных производных 1-го порядка.

Для привлечения метода Ньютона к решению параметрической модели последняя формулируется в виде системы нелинейных алгебраических уравнений F(p) = 0 из функций в (1) .

Особенность параметрического моделирования состоит в том, что в общем случае система уравнений недоопределена, то есть количество неизвестных превышает количество уравнений. Кроме того, матрица J на некоторой итерации, в том числе и при начальном приближении, может оказаться вырожденной или близкой к таковой, что создает дополнительные трудности применения метода Ньютона.

Согласно (1), на каждом шаге итерационного процесса мы сталкиваемся с решением СЛАУ

(2)

где A Rm,n, m количество строк матрицы (количество уравнений), n количество неизвестных, вектор правых частей c Rm , вектор неизвестных x R .

Вектор x определяет величину в (1). В общем случае rank(A) < m < n . Например, при решении системы нелинейных уравнений, получаемой из модели, показанной на рис. 1, при начальном приближении формируется прямоугольная матрица A R ^20,21. Как оказалось, матрица имеет неполный ранг (rank(A)=18) по причине того, что в СЛАУ присутствуют два уравнения, векторы-строки которых образуют линейную комбинацию с другими уравнениями. В итоге СЛАУ в этом примере имеет бесчисленное множество решений, удовлетворяющих условию минимума

Для обеспечения сходимости процесса (1) в этом множестве выбирают вектор минимальной длины (нормальное решение). Известные алгоритмы решения недоопределенных СЛАУ [1, 2] не учитывают разреженную структуру больших матриц и, как следствие, обладают малой скоростью.

Р.М.Ганеев для повышения скорости решения предложил строить нормальное решение на базе предварительного приведения СЛАУ к треугольной форме.

Пусть ранг матрицы СЛАУ (2) меньше количества неизвестных. Для приведения СЛАУ (2) к треугольной форме используются методы отражений Хаусхолдера или отражений/вращений Гивенса. В случае СЛАУ с разреженной матрицей более эффективны методы Гивенса.

Пусть после приведения к треугольной форме получена совместная СЛАУ:

Rx = b (3)

где R правая треугольная n*n -матрица. При этом считаем, что i -е уравнение отсутствует, то есть в матрице R в i-й строке находятся только нули, и в векторе правой части i-й элемент равен нулю. Таких уравнений может быть несколько.

Коэффициенты дополнительного i -го уравнения вычисляются по формулам:

(4)

Общий алгоритм решения СЛАУ (2) содержит следующие шаги:

1. Параметры СЛАУ (2) необходимо записать в расширенную матрицу: R = [ A Ю ].

Матрица R должна содержать не менее n строк. Если количество уравнений m меньше количества неизвестных (m < n) , то ниже массивов СЛАУ (2) нужно добавить (n-m) строк с нулями:

2. Преобразовать матрицу R к правой треугольной форме.

3. Попробовать решить СЛАУ:

3.1. Если R(n,n) = 0 , то произвести переход в 3.2.

3.1.1. Вычислить n-ю компоненту вектора решения:

x(n) = R(n,n+1) / R(n,n)

3. 1.2. Пересчитать правую часть с учетом вычисленного компонента вектора решения и перенести на место n-го столбца:

R(k,n) = R(k,n+1) – R(k,n)*x(n), k = 1,2,…,n–1.

3.1.3. Уменьшить счетчик количества неизвестных: n = n–1 .

3.1.4. Если n = 0 , то произвести переход в пункт 4.

3.1.5. Произвести переход в 3.1.

3.2. Построить недостающие уравнения. Возможны два варианта.

3.2.1. В R обязательно есть хотя бы одна строка, в которой элемент r_ii равен нулю, а остальные элементы этой строки не все равны нулю. Обнаружив такую строку с номером i (i = 1,2,3…) , нужно переместить ее в первую же свободную строку ниже (хотя бы одна свободная строка, благодаря пункту 3.1, обязательно есть) и на месте i-й строки построить дополнительное уравнение. Произвести переход в пункт 2.

Рис. 2. График сходимости итерационного процесса на примере модели из параметрического эскиза (рис. 1)

3.2.2. В R нулевые диагональные элементы расположены только в свободных строках. В этом случае построить все недостающие уравнения. Произвести переход в пункт 2.

4. Конец вычислений.

Для испытания предложенного метода был поставлен ряд вычислительных экспериментов с решением различных параметрических моделей. График на рис. 2 показывает сходимость итерационного процесса на примере модели, показанной на рис. 1. Характеристика снята в виде зависимости невязки || F(x_k) || на каждом шаге решения от номера итерации k . В этом примере отрабатывалось решение системы уравнений для изменения угла между L1 и L3 с 15° на 45°.

Из графика видно, что процесс решения по предлагаемому методу имеет устойчивую сходимость.

«САПР и графика» 6’2004

Объяснение урока: Решение систем линейных уравнений с помощью подстановки

В этом объяснителе мы научимся решать системы линейных уравнений с помощью подстановки.

Когда нас просят решить систему уравнений, это означает, что мы ищем набор значений переменных которые удовлетворяют каждому уравнению. Например, рассмотрим систему уравнений 𝑥+𝑦=3,𝑥−𝑦=−1.

Мы хотим найти значение для 𝑥 и значение для 𝑦 так, чтобы выполнялись оба уравнения истинный. Другими словами, мы ищем два значения, сумма которых равна 3, а разность -1. Мы мог сделать это методом проб и ошибок; однако это не будет работать для более сложных систем.

Вместо этого мы будем использовать тот факт, что мы можем решить любое линейное уравнение с одной переменной. Это означает, что если мы сможем найти линейное уравнение с любой переменной, мы можем решить для этого значения. Для этого заметим, что оба уравнения должны остаются верными, поэтому мы можем изменить одно уравнение, чтобы сделать одну переменную предметом. Например, мы можем переставить первое уравнение, вычитая 𝑥 с обеих сторон, чтобы получить 𝑦=3−𝑥.

Следовательно, если 𝑥 и 𝑦 являются решениями системы уравнений, они также должны удовлетворить этому уравнению. Так как теперь мы записали 𝑦 через 𝑥, и оба уравнения должно быть истинным, мы можем подставить это выражение в другое уравнение, чтобы получить 𝑥−𝑦=−1𝑥−(3−𝑥)=−1.

Распределение отрицательного числа по скобкам и упрощение выходов 𝑥−3+𝑥=−12𝑥−3=−12𝑥=2.

Разделение уравнения на 2 дает 𝑥=1.

Затем мы можем подставить это значение для 𝑥 в любое из этих уравнений, чтобы найти значение 𝑦. Подстановка 𝑥=1 в первое уравнение дает 1+𝑦=3𝑦=2.

Следовательно, 𝑥=1 и 𝑦=2 решают систему уравнений. Мы можем убедиться, что эти значения решают эту систему уравнений, подставляя значения в оба уравнения.

Подстановка 𝑥=1 и 𝑦=2 в левую часть первого уравнения дает 𝑥+𝑦=1+2=3, что равно правой части.

Подстановка 𝑥=1 и 𝑦=2 в левую часть второго уравнения дает 𝑥−𝑦=1−2=−1, что равно правой части. Поскольку оба уравнения верны, мы подтвердили, что это решение задачи. система уравнений.

Этот метод решения уравнений называется подстановкой, так как мы подставляем перестановку одного уравнения в другой. Стоит отметить, что наш выбор замены не имеет значения; мы могли бы переставить первый уравнение, чтобы сделать 𝑥 предметом или переставить второе уравнение для 𝑥 или 𝑦. Во всех этих случаях мы придем к одному и тому же решению.

Мы можем обобщить этот метод, чтобы попытаться решить любую систему из двух линейных уравнений с двумя неизвестными.

Как решить систему линейных уравнений с помощью замены

Чтобы решить систему линейных уравнений с помощью замены, мы используем следующий метод:

Переформулируйте одно из уравнений, чтобы сделать одно из неизвестных предметом.
Подставьте это в другое уравнение и решите полученное линейное уравнение с одним неизвестным.
Подставьте значение этого неизвестного в одно из уравнений и найдите оставшееся неизвестное.
Подтвердите ответ, проверив, что значения обоих неизвестных удовлетворяют другому уравнению.

Давайте рассмотрим пример применения этого процесса для решения системы двух линейных уравнений с двумя неизвестными.

Пример 1. Нахождение значения одной переменной в системе линейных уравнений

Найдите 𝑥 при условии 2𝑥−𝑦=5 и 𝑦=7𝑥.

Ответ

Нас просят найти значение 𝑥, которое решает два линейных уравнения с двумя неизвестными. Мы помните, мы можем сделать это путем замены. Обычно мы начинаем с перестановки уравнения, чтобы сделать переменную предмет; однако мы можем заметить, что второе уравнение, 𝑦=7𝑥, уже находится в этой форме. Теперь мы можем подставить это выражение для 𝑦 в первое уравнение, чтобы получить 2𝑥−(7𝑥)=5.

Упрощая, получаем −5𝑥=5.

Затем мы разделим уравнение на −5, чтобы получить 𝑥=−1.

В нашем следующем примере нам нужно будет решить систему двух линейных уравнений с двумя неизвестными, где мы должны сначала переставьте одно из уравнений, чтобы сделать переменную предметом.

Пример 2. Решение систем линейных уравнений с помощью подстановки

Решите следующую систему уравнений: 5𝑥−2𝑦=8,4𝑥+3𝑦=11.

Ответ

Нас просят решить систему двух линейных уравнений с двумя неизвестными и мы вспоминаем, что это можно сделать с помощью замена. Сначала нам нужно изменить одно из уравнений так, чтобы предметом была переменная. Мы можем отметить, что ни одно из уравнений уже не находится в этой форме, поэтому мы можем выбрать любое уравнение и переменную по желанию; мы будем переформулируйте второе уравнение для 𝑥.

Мы вычитаем 3𝑦 из обеих частей уравнения, чтобы получить 4𝑥=11−3𝑦.

Затем мы делим уравнение на 4, чтобы получить 𝑥=114−34𝑦.

Теперь мы можем подставить это выражение для 𝑥 в первое уравнение, чтобы построить уравнение полностью с точки зрения 𝑦. У нас есть 5114−34𝑦−2𝑦=8.

Теперь распределим 5 по скобкам, чтобы получить 554−154𝑦−2𝑦=8.

Упрощение дает −154−84𝑦=8−554−234𝑦=8−554−234𝑦=324−554−234𝑦=−234.

Деление уравнения на -234 дает 𝑦=1.

Теперь мы можем определить значение 𝑥, подставив 𝑦=1 в первый уравнение; мы получаем 5𝑥−2(1)=85𝑥−2=8.

Затем мы добавляем 2 к обеим частям уравнения, получая 5𝑥=10.

Наконец, мы делим уравнение на 5, чтобы получить 𝑥=2.

Итак, 𝑥=2 и 𝑦=1 является решением этой системы уравнений.

Мы можем проверить это решение, подставив оба значения в два уравнения, чтобы проверить, верны ли они.

Подстановка 𝑥=2 и 𝑦=1 в левую часть первого уравнения дает 5𝑥−2𝑦=5(2)−2(1)=10−2=8.

Это равно правой части уравнения, поэтому решение удовлетворяет первому уравнению.

Подстановка 𝑥=2 и 𝑦=1 в левую часть второго уравнения дает 4𝑥+3𝑦=4(2)+3(1)=8+3=11.

Это равно правой части уравнения, поэтому решение удовлетворяет второму уравнению.

Это подтверждает, что 𝑥=2, 𝑦=1 является решением этой системы уравнений.

Пример 3. Решение одновременных уравнений путем подстановки

Использование подстановки для решения одновременных уравнений 13𝑥+23=𝑦,6𝑥+35𝑦=645.

Ответ

Чтобы использовать подстановку для решения системы уравнений, нам сначала нужно изменить одно из уравнений, чтобы получить переменный предмет. В этом случае мы можем заметить, что первое уравнение уже имеет 𝑦 в качестве предмет, поэтому мы решаем систему уравнений, подставляя это выражение для 𝑦 в второе уравнение. Это дает 6𝑥+3513𝑥+23=645.

Распределение по скобкам дает нам 6𝑥+15𝑥+25=645.

Сбор одинаковых терминов и их перестановка дает 31𝑥5=625.

Затем мы можем разделить уравнение на 315, чтобы получить 𝑥=2.

Затем мы можем определить значение 𝑦, подставив 𝑥=2 в первое уравнение; мы получаем 13(2)+23=𝑦23+23=𝑦43=𝑦.

Мы можем проверить это решение, подставив 𝑥=2 во второе уравнение; мы получаем 6(2)+35𝑦=64512+35𝑦=645.

Вычитание 12 из обеих частей уравнения дает 35𝑦=45.

Деление обеих частей уравнения на 35 дает 𝑦=43.

Поскольку это согласуется с другим значением 𝑦, мы подтвердили, что это решение задачи система уравнений.

Следовательно, решение уравнений равно 𝑥=2 и 𝑦=43.

Пример 4. Написание и решение системы линейных уравнений с двумя неизвестными

Возраст мужчины в 9 раз больше возраста сына более чем в 2 раза. Учитывая, что сумма их возрастов равна 57, найти каждый из их возрастов.

Ответ

Начнем с преобразования полученной информации в уравнения. Назовем возраст человека 𝑚 и возраст его сына 𝑠. Нам говорят, что возраст мужчины на 9 больше, чем В 2 раза больше возраста его сына, поэтому, если мы удвоим возраст сына и добавим 9, мы должны получить возраст мужчины. Мы можно записать это как уравнение 2𝑠+9=𝑚.

Нам также говорят, что сумма их возрастов равна 57, поэтому 𝑠+𝑚=57.

Это система из двух линейных уравнений с двумя неизвестными, поэтому мы можем попытаться решить ее подстановкой. Мы будем заменить 𝑚=2𝑠+9во второе уравнение, чтобы получить 𝑠+(2𝑠+9)=57.

Затем мы можем упростить, чтобы получить 3𝑠+9=57.

Мы можем вычесть 9 из обеих частей уравнения, чтобы получить 3𝑠=57−9=48.

Наконец, мы делим на 3, что дает нам 𝑠=483=16.

Значит, сыну 16 лет. Мы можем определить возраст мужчины с помощью любого уравнения. Подставляем 𝑠=16 в первое уравнение и оцениваем получить 𝑚=2(16)+9=32+9=41.

Итак, их возраст 16 лет и 41 год.

До сих пор все наши системы уравнений имели единственное решение. Однако так будет не всегда. В на самом деле, есть еще две возможности для этих систем двух линейных уравнений с двумя неизвестными.

Во-первых, возможно, что система не будет иметь решений; когда это происходит, мы называем систему несовместимой. Чтобы увидеть пример этого, давайте рассмотрим систему уравнений 𝑥+𝑦=1𝑥+𝑦=2.

Мы можем сразу заметить, что в этой системе есть проблема, так как мы ищем два числа, которые складываются, чтобы дать 1 и добавить, чтобы получить 2, что невозможно. Однако давайте попробуем решить это путем замены, чтобы увидеть, что происходит.

Мы можем изменить первое уравнение, чтобы сделать 𝑦 субъектом: 𝑦=1−𝑥.

Затем мы можем подставить это выражение для 𝑦 во второе уравнение, чтобы получить 𝑥+(1−𝑥)=2.

Упрощение, затем выход 1=2.

Конечно, мы знаем, что 1 не равно 2. На самом деле это означает, что наше исходное предположение неверно: существуют нет значений 𝑥 и 𝑦, которые решают оба уравнения, так как мы не можем выбирать значения 𝑥 и 𝑦, чтобы сделать 1 равным 2.

Во-вторых, возможно, что система будет иметь бесконечное количество решений. Чтобы увидеть пример этого, рассмотрим систему уравнений 𝑥−𝑦=32𝑥−2𝑦=6.

Попробуем еще раз решить эту систему методом подстановки. Мы можем переставить первый уравнение, чтобы сделать 𝑥 предметом, добавив 𝑦 к обеим сторонам, что дает нам 𝑥=3+𝑦.

Затем мы можем подставить это выражение для 𝑥 во второе уравнение, чтобы получить 2(3+𝑦)−2𝑦=6.

Распределение коэффициента 2 по скобкам дает 6+2𝑦−2𝑦=6.

Это упрощает предоставление 6=6.

На первый взгляд видно, что это уравнение тривиально; мы знаем, что это верное утверждение. Однако мы также можем говорят, что это уравнение верно для любого значения 𝑦; это говорит нам, что любое значение 𝑦 может быть решением этой системы уравнений. Мы можем подтвердить это, выбрав несколько значений 𝑦.

Предположим, что 𝑦=0; у нас есть 𝑥−𝑦=3𝑥−0=3𝑥=3.

Итак, 𝑥=3 и 𝑦=0 — решение этой системы.

Также рассмотрим 𝑦=1; у нас есть 𝑥−𝑦=3𝑥−1=3𝑥=4.

Итак, 𝑥=4 и 𝑦=1 — решение этой системы.

Заметим, что любое решение уравнения 𝑥−𝑦=3 является решением всей системы уравнения. Мы можем показать, почему это так, уменьшив множитель 2 из второго уравнения: 2𝑥−2𝑦=62(𝑥−𝑦)=2×3𝑥−𝑦=3.

Другими словами, мы показали, что второе уравнение является скалярным множителем первого уравнения; мы называем системы в эта форма зависимых систем.

Давайте теперь рассмотрим пример, где нам нужно либо решить систему двух линейных уравнений с двумя неизвестными, либо показать, что решений нет.

Пример 5. Решение системы линейных уравнений с помощью подстановки, если решение существует

Если возможно, решите следующую систему уравнений: 𝑦=𝑥+1,𝑦=𝑥−9.

Ответ

Нас просят решить систему двух линейных уравнений с двумя неизвестными и мы вспоминаем, что можем попытаться сделать это с помощью замены. Сначала нам нужно изменить одно из уравнений так, чтобы предметом была переменная. Мы можем заметить, что оба уравнения уже в этой форме, так что мы можем просто приравнять два выражения для 𝑦; у нас есть 𝑥+1=𝑥−9.

Вычтем 𝑥 из обеих частей уравнения, чтобы получить 1=-9.

Нет значений 𝑥 или 𝑦, которые могут сделать это уравнение верным, поэтому мы можем сделать вывод об отсутствии решений этой системы уравнений.

В нашем следующем примере мы определим количество решений системы двух линейных уравнений с двумя неизвестными.

Пример 6. Нахождение количества решений системы уравнений

Найдите количество решений следующей системы уравнений: 𝑦+2𝑥=4,2𝑦+4𝑥=8.

Ответ

Нас просят решить систему двух линейных уравнений с двумя неизвестными и мы вспоминаем, что можем попытаться сделать это с помощью замены. Сначала нам нужно изменить одно из уравнений так, чтобы предметом была переменная. Поскольку коэффициент при 𝑦 в первом уравнении равен 1, мы изменим первое уравнение сделать 𝑦 предметом.

Вычтем 2𝑥 из обеих частей первого уравнения, чтобы получить 𝑦=4−2𝑥.

Затем мы можем подставить это выражение для 𝑦 во второе уравнение: 2(4−2𝑥)+4𝑥=8.

Распределение коэффициента 2 по скобкам дает 8−4𝑥+4𝑥=8.

Упрощение, затем выход 8=8.

Поскольку это уравнение верно для любого значения 𝑥, мы имеем, что любое значение 𝑥 дает решение этой системы уравнений.

Следовательно, у этой системы уравнений есть бесконечные решения.

Давайте закончим повторением некоторых важных моментов этого объяснения.

Ключевые моменты

Чтобы решить систему линейных уравнений с помощью замены, мы используем следующий метод:
Переставьте одно из уравнений так, чтобы одно из неизвестных стало предметом.
Подставьте это в другое уравнение и найдите неизвестное.
Подставьте значение этого неизвестного в одно из уравнений и решите для остальных неизвестных.
Убедитесь, что значения обоих неизвестных удовлетворяют другому уравнению.
Решение системы уравнений с помощью замены дает нам точные решения.
Мы можем проверить наши решения, подставив их обратно в систему уравнений чтобы убедиться, что уравнения выполняются.
Не все системы уравнений имеют решения. Если применить метод замены и придем к неверному уравнению, то система не имеет решений уравнений, и мы называем это противоречивой системой уравнений.
Системы из двух уравнений с двумя неизвестными также могут иметь бесконечное число решений. Если мы применим метод подстановки и получим уравнение, которое всегда верно, то существует бесконечное множество решений уравнения; они возникают, когда уравнения скалярно кратны друг другу. Мы называем эти зависимые системы уравнений.

О принципе невязки для итерационных и параметрических методов решения линейных некорректных уравнений

title={О принципе невязки итерационных и параметрических методов решения линейных некорректных уравнений }, автор={Роберт Платон}, журнал={Числовая математика}, год = {1996}, объем = {75}, страницы = {99-120} }
Р. Платон
Опубликовано 1 ноября 1996 г.
Математика
Numerische Mathematik
Резюме. Для численного решения (необязательно корректных) линейных уравнений в банаховых пространствах мы рассматриваем класс итерационных методов, который содержит хорошо известные методы, такие как итерация Ричардсона, если связанный оператор резольвенты удовлетворяет условию по отношению к сектору. Целью данной статьи является показать, что для заданной зашумленной правой части принцип невязки (являющийся правилом остановки для итерационных методов, принадлежащих указанному классу) определяет… 9{*}) — уровень шума для некорректных линейных интегральных уравнений в тихоновской регуляризации, что расширяет диапазон…
О задаче Коши: II. Завершение, регуляризация и приближение
М. Азаиз, Ф. Б. Бельгаком, H. El Fekih
Математика
2006
в Ben Belgacem и El Fekih (2005 на Cauche Обратные задачи 21 1915–36), вводится новая вариационная теория для пополнения данных Коши…
Нелинейные итерационные методы для линейных некорректных задач в банаховых пространствах
Ф. Шёпфер, А. Луис, Тал Шустер
Математика
2006
решение по норме операторного уравнения Ах = у в банаховых пространствах X, Y, где А — непрерывный линейный оператор из X в Y.…
Расширенная итерация типа Ньютона для нелинейных некорректных уравнений в банаховом пространстве
В этой статье мы изучаем нелинейные некорректные уравнения с m-аккретивными отображениями в банаховых пространствах. Мы создаем расширенную итеративную схему ньютоновского типа, которая кубически сходится к решению…
Оптимальные скорости для Лаврентьевской регуляризации с присоединенными исходными условиями
Р. Платон, П. Мате, Б. Хофманн
Математика
Матем. вычисл.
2018
Путем измерения оптимальности скоростей сходимости в терминах предельных порядков авторы демонстрируют свойства оптимальности скоростей сходимости для общих аккретивных операторов в условиях прямого и сопряженного источника, а также для подкласса неотрицательных самосопряженных операторов.
Методы MultiScale Collocation для неспособных интегральных уравнений с модифицированным выбором параметров задних сестер
Xingjun Luo, Chunmei Zeng, Suh-yuh Yang, Rongpei Zhang
Matematics
49949.shiest. решение некорректных интегральных уравнений Фредгольма первого рода в банаховых пространствах, если ассоциированный резольвентный интегральный оператор удовлетворяет условию…
Прямая регуляризация для системы интегро-алгебраических уравнений индекса-1
Фарахани М. С., Хадизаде М.
Математика
2018
Аннотация Известно, что связанная система, состоящая из интегральных уравнений Вольтерра первого и второго рода, относится к классу умеренно некорректных задач. В настоящей работе мы…
О регуляризующих свойствах метода GMRES
Показано, что когда ассоциированная безошибочная правая часть лежит в конечномерном подпространстве Крылова, метод GMRES является методом регуляризации .
Нелинейные методы обратной шкалы
M. Burger, Guy Gilboa, S. Osher, Jinjun Xu
Математика
2006
недавняя работа, к непрерывной во времени обратной масштабно-пространственной формулировке. Повторяющаяся процедура уточнения дает…
МНОГОПАРАМЕТРИЧЕСКАЯ РЕГУЛЯРИЗАЦИЯ ТИХОНОВА ДЛЯ ЛИНЕЙНЫХ НЕПРАВИЛЬНЫХ ОПЕРАТОРНЫХ УРАВНЕНИЙ
Zhong-ying, Chen, Yang
Математика
2008
Мы рассматриваем решение линейных некорректных операторных уравнений. На основе многомасштабной декомпозиции для пространства решений мы предлагаем многопараметрическую регуляризацию для решения уравнений. Мы устанавливаем…
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 15 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантность Наиболее влиятельные документыНедавность
Ускоренные итерации Ландвебера для решения некорректных уравнений
М. Ханке
Математика
1991
РезюмеВ данной статье рассматриваются возможности так называемых линейных полуитерационных методов для приближенного решения линейных некорректных задач и плохо обусловленных матричных уравнений. Несколько…
О некорректных задачах и методе сопряженных градиентов
Г. Брэкедж
Математика
1987
0029
H. Engl, Günther Hodina
Mathematics
1991
Optimal Estimation of Linear Operators in Hilbert Spaces from Inaccurate Data
A. Melkman, C. Micchelli
Mathematics
1979
Среди всех возможных методов оценки линейного оператора U по неточным данным сглаживание данных, за которыми следует U, является оптимальной процедурой. Этот результат, который мы формулируем и доказываем здесь в…
Конвергенция итераций для линейных уравнений
O. Nevanlinna
Математика
1993
1. Мотивация, проблема и заметка. для полиномиального ускорения.- 1.5 Минимальная ошибка и минимальная невязка.- 1.6…
О ФУНКЦИЯХ ПОЛОЖИТЕЛЬНОГО ОПЕРАТОРА
Е. И. Пустыльник
Математика
1984
Для функций , 0$ SRC=http://ej.iop.org/images/0025-5734/47/1/A02/tex_sm_2628_img2.gif/>, неубывающей и положительного оператора в банаховом пространстве operators and are constructed, their products…
Integral operators in spaces of summable functions
M. Krasnosel’skiǐ, P. P. Zabreyko, E. Pustylnik, P. E. Sobolevski
Mathematics
1975
Contents Preface xm Chapter 1. Линейные операторы в пространствах L a 1 1. Пространство L x 1 1.1. Описание помещений 1.2. Критерии компактности 1.3. Непрерывные линейные функционалы и слабая сходимость…
На минимальном равенстве для семинордов
Р. Д. Григорефф, Р. Платон
Математика
1995
ВЕСА.
Содержание: Введение — Обратные задачи, моделируемые интегральными уравнениями первого рода: причинно-следственная связь — оценка параметров в дифференциальных уравнениях: идентификация модели — математические основы…
Математика компьютерной томографии
Ф. Наттерер
Математика
1986
, выборка,…
Решение линейных систем с тремя переменными
3.4 Решение линейных систем с тремя переменными
Цели обучения
Проверить решения линейных систем с тремя переменными.
Решение линейных систем с тремя переменными методом исключения.
Выявление зависимых и несогласованных систем.
Решите задачи с тремя неизвестными.
Решения для линейных систем с тремя переменными
Реальные приложения часто моделируются с использованием более одной переменной и более одного уравнения. В этом разделе мы будем изучать линейные системы, состоящие из трех линейных уравнений с тремя переменными в каждом. Например,
{3x+2y− z=−7(1)6x− y+3z=−4(2)x+10y−2z=2(3)
Решением такой линейной системы является упорядоченная тройка Triples ( x , y , z ), которые определяют положение относительно начала координат в трехмерном пространстве. ( x , y , z ), который решает все уравнения. В этом случае (−2, 1, 3) — единственное решение. Чтобы убедиться, что упорядоченная тройка является решением, подставьте соответствующие x -, y — и z -values, а затем упростите, чтобы увидеть, получаете ли вы истинное утверждение из всех трех уравнений.
Поскольку упорядоченная тройка удовлетворяет всем трем уравнениям, мы заключаем, что это действительно решение.
Пример 1
Определите, является ли (1,4,43) решением следующей линейной системы:
{9x+y-6z=5-6x-3y+3z=-143x+2y-7z= 15 .
Решение:
Ответ: Точка не удовлетворяет всем уравнениям и, следовательно, не является решением.
Упорядоченная тройка, такая как (2,4,5), может быть изображена в трехмерном пространстве следующим образом:
Упорядоченная тройка указывает позицию относительно начала координат (0, 0, 0), в данном случае 2 единицы вдоль оси x , 4 единицы параллельно оси y и 5 единиц параллельно оси z . Линейное уравнение с тремя переменнымиУравнение, которое может быть записано в стандартной форме ax+by+cz=d где a , b , c и d — реальные числа. находится в стандартной форме, если топор+by+cz=d где a , b , c и d — действительные числа. Например, 6x+y+2z=26 в стандартной форме. Находя z , мы получаем z=-3x-12y+13 и можем рассматривать как x , так и y как независимые переменные. При построении графика в трехмерном пространстве его график будет образовывать прямую плоскую поверхность, называемую плоскостью. Любая плоская двумерная поверхность..
Следовательно, график системы трех линейных уравнений и трех неизвестных будет состоять из трех плоскостей в пространстве. Если существует одновременное решение, система непротиворечива, и решение соответствует точке пересечения трех плоскостей.
Построение плоскостей в трехмерном пространстве не входит в задачи данного учебника. Однако всегда важно понимать геометрическую интерпретацию.
Попробуйте! Определите, является ли (3, −1, 2) решением системы: { 2x−3y−z=73x+5y−3z=−24x−y+2z=17.
Ответ: Да, это решение.
(нажмите, чтобы посмотреть видео)
Решение линейных систем с тремя переменными методом исключения
В этом разделе метод исключения используется для решения систем трех линейных уравнений с тремя переменными. Идея состоит в том, чтобы исключить одну из переменных и преобразовать исходную систему в систему двух линейных уравнений, после чего мы можем решить ее как обычно. Шаги описаны в следующем примере.
Пример 2
Решение: {3x+2y -z = −7 (1) 6x -e+3z = −4 (2) .x+10y -2z = 2 (3)
Решение:
Все три уравнения имеют стандартный вид. Если бы это было не так, было бы лучше переписать уравнения в стандартной форме, прежде чем начинать этот процесс.
Шаг 1 : Выберите любые два уравнения и исключите переменную. В этом случае мы можем выстроить переменную z , чтобы исключить, если мы сгруппируем 3 раза первое уравнение со вторым уравнением.
Затем сложите уравнения.
9x+6y −3z=21+6x−y + 3z=−415x+5y=−25✓
Шаг 2 : Выберите любые два других уравнения и исключите ту же переменную. Мы можем выстроить 90 543 z 90 544, чтобы снова исключить, если мы сгруппируем -2 раза первое уравнение с третьим уравнением.
Затем добавьте
−6x−4y + 2z=14+x+10y−2z=2−5x+6y=16✓
Шаг 3 : Решите полученную систему двух уравнений с двумя неизвестными. Здесь решаем методом исключения. Умножьте второе уравнение на 3, чтобы выровнять переменную x исключить.
Затем сложите уравнения.
15x+5y=-25+-15x+18y=4823y=23y=1
Шаг 4 : Обратно заменить и определить все координаты. Чтобы найти x , используйте следующее:
15x+5y=−2515x+5(1)=−2515x=−30x=−2
Теперь выберите одно из исходных уравнений, чтобы найти z ,
3x+ 2y−z=−7 (1)3(−2)+2(1)−z=−7−6+2−z=−7−4−z=−7−z=−3z=3
Отсюда решение, представленное в виде упорядоченной тройки ( x , y , z ), равно (−2, 1, 3). Это та же самая система, которую мы проверяли в начале этого раздела.
Ответ: (−2, 1, 3)
Неважно, какую переменную мы изначально выбираем для исключения, если мы исключим ее дважды с помощью двух разных наборов уравнений.
Пример 3
Решите: {−6x−3y+3z=−149x+y−6z=53x+2y−7z=15.
Решение:
Поскольку y имеет коэффициент 1 во втором уравнении, эту переменную следует исключить. Используйте уравнения 1 и 2, чтобы исключить и .
Затем используйте уравнения 2 и 3, чтобы снова исключить y .
Остается система из двух уравнений с двумя переменными x и z ,
{21x−15z=1−15x+5z=5
Умножьте второе уравнение на 3 и исключите переменную z .
Теперь обратно подставляем найти z .
21x−15z=121(−23)−15z=1−14−15z=1−15z=15z=−1
Наконец, выберите одно из исходных уравнений, чтобы найти и .
−6x−3y+3z=−14−6(−23)−3y+3(−1)=−144−3y−3=−141−3y=−14−3y=−15y=5
Ответ : (−23,5,−1)
Пример 4
Решить: {2x+6y+7z=4−3x−4y+5z=125x+10y−3z=−13.
Решение:
В этом примере нет очевидного выбора исключаемой переменной. Мы решили исключить x .
(1)(2){2x+6y+7z=4−3x−4y+5z=12⇒×3⇒×2{6x+18y+21z=12−6x−8y+10z=24–10y+31z =36✓
Затем используйте уравнения 2 и 3, чтобы снова исключить x .
(2)(3){−3x−4y+5z=125x+10y−3z=−13⇒×5⇒×3{−15x−20y+25z=6015x+30y−9z=−39–10y+16z =21✓
Это оставляет систему двух уравнений с двумя переменными y и z ,
{10y+31z=3610y+16z=21
Умножьте первое уравнение на −1, чтобы исключить переменная и .
Теперь обратно подставьте найти y .
10y+31z=3610y+31(1)=3610y+31=3610y=5y=510y=12
Выберите любое из исходных уравнений, чтобы найти х .
2x+6y+7z=42x+6(12)+7(1)=42x+3+7=42x+10=42x=−6x=−3
Ответ: (−3,12,1)
Попробуйте! Решите: { 2x−3y−z=73x+5y−3z=−24x−y+2z=17.
Ответ: (3, −1, 2)
(нажмите, чтобы посмотреть видео)
Зависимые и противоречивые системы
Как и в случае с линейными системами с двумя переменными, не все линейные системы с тремя переменными имеют единственное решение. Иногда нет одновременных решений.
Пример 5
Решите систему: {4x-y+3z=521x-4y+18z=7-9x+y-9z=-8.
Решение:
В этом случае мы решили исключить переменную y .
(1)(3){4x−y+3z=5 −9x+y−9z=−8–−5x−6z=−3✓
Затем используйте уравнения 2 и 3, чтобы снова исключить y .
Остается система двух уравнений с двумя переменными x и z ,
{−5x− 6z=−3−15x−18z=−25
Умножьте первое уравнение на −3 и исключите переменную z .
Сложение полученных уравнений вместе приводит к ложному утверждению, которое указывает на несовместность системы. Одновременного решения нет.
Ответ: Ø
Система, не имеющая решений, является противоречивой системой. Учитывая три плоскости, не может быть одновременного решения несколькими способами.
Как и в случае с линейными системами с двумя переменными, некоторые линейные системы с тремя переменными имеют бесконечно много решений. Такие системы называются зависимыми системами.
Пример 6
Решите систему: {7x−4y+z=−153x+2y−z=−55x+12y−5z=−5.
Решение:
Исключить z , сложив первое и второе уравнения вместе.
(1) (2){7x−4y+z=−153x+2y−z=−5– 10x−2y=−20 ✓
Затем используйте уравнения 1 и 3, чтобы снова исключить z .
Это оставляет систему двух уравнений с двумя переменными x и y ,
{10x−2y=−2040x−8y=−80
Выстраивание переменной y исключить, разделив первое уравнение на 2, а второе уравнение на −8.
{10x−2y=−2040x−8y=−80⇒÷2⇒÷(−8) {5x−y=−10−5x+y=10–0=0 True
Верное утверждение указывает, что система зависим. Чтобы выразить бесконечное число решений (x, y, z) через одну переменную, мы решаем 90 543 y 90 544 и 90 543 z 90 544 через 90 543 x 90 544.
10x−2y=−20−2y=−10x−20−2y−2=−10x−20−2y=5x+10
Если у нас есть y в пересчете на x , мы можем решить для z с точки зрения x путем обратной подстановки в одно из исходных уравнений.
7x−4y+z=−157x−4(5x+10)+z=−157x−20x−40+z=−15−13x−40+z=−15z=13x+25
Ответ: (x ,5х+10,13х+25).
Непротиворечивая система с бесконечным числом решений является зависимой системой. Учитывая три плоскости, бесконечное количество одновременных решений может появиться разными способами.
Попробуйте! Решите: {7x+y-2z=-4-21x-7y+8z=47x+3y-3z=0.
Ответ: (x,73x+4,143x+4)
(нажмите, чтобы посмотреть видео)
Приложения, включающие три неизвестных
Многие реальные приложения включают более двух неизвестных. Когда приложению требуются три переменные, мы ищем отношения между переменными, которые позволяют нам написать три уравнения.
Пример 7
Общественный театр продал 63 билета на дневное представление на общую сумму 444 доллара. Взрослый билет стоит 8 долларов, детский — 4 доллара, а взрослый билет — 6 долларов. Если бы взрослым было продано в два раза больше билетов, чем детям и пенсионерам вместе взятым, сколько было бы продано каждого билета?
Решение:
Начните с определения трех переменных.
Пусть x представляет количество проданных билетов для взрослых.
Пусть y представляют количество проданных детских билетов.
Пусть z представляют количество проданных билетов для пенсионеров.
Первое уравнение получено из утверждения, что было продано 63 билета.
(1) x+y+z=63
Второе уравнение получается из общего объема продаж билетов.
(2) 8x+4y+6z=444
Третье уравнение основано на утверждении, что билетов для взрослых было продано в два раза больше, чем билетов для детей и взрослых вместе взятых.
x=2(y+z)x=2y+2z(3) x−2y−2z=0
Таким образом, задача моделируется следующей линейной системой.
{x+y+z=638x+4y+6z=444x−2y−2z=0
Решение этой системы остается в качестве упражнения. Решение (42,9,12).
Ответ: Театр продал 42 билета для взрослых, 9 билетов для детей и 12 билетов для пенсионеров.
Ключевые выводы
Одновременным решением линейной системы с тремя уравнениями и тремя переменными является упорядоченная тройка ( x , y , z ), которая удовлетворяет всем уравнениям. Если он не решает каждое уравнение, то это не решение.
Мы можем решить систему из трех линейных уравнений с тремя неизвестными методом исключения. Выберите любые два уравнения и исключите переменную. Затем выберите любые другие два уравнения и исключите ту же переменную. Это приведет к системе двух уравнений с двумя переменными, которую можно решить любым ранее изученным методом.
Если процесс решения системы приводит к ложному утверждению, то система несовместна и не имеет решения.
Если процесс решения системы приводит к истинному утверждению, то система зависима и имеет бесконечно много решений.
Для решения приложений, требующих трех переменных, ищите отношения между переменными, которые позволяют вам написать три линейных уравнения.
Упражнения по теме
Часть A: Линейные системы с тремя переменными
Определить, является ли данная упорядоченная тройка решением данной системы.
(3,-2,-1);
{х+у-г=22х-3у+2г=10х+2у+г=-3
(-8,-1,5);
{x+2y-z=-152x-6y+2z=03x-9y+4z=5
(1,−9,2);
{8x+y-z=-37x-2y-3z=19x-y+9z=28
(-4,1,-3);
{3x+2y-z=-7x-5y+2z=32x+y+3z=-16
(6,23,−12);
{х+6у-4г=12-х+3у-2г=-3х-9у+8г=-4
(14,-1,-34);
{2x-y-2z=34x+5y-8z=2x-2y-z=3
(3,−2,1);
{4x−5y=222y−z=8−5x+2z=−13
(1,52,−12);
{2y−6z=83x−4z=518z=−9
(12,−2,6);
{a−b+c=94a−2b+c=142a+b+12c=3
(-1,5,-7);
{3a+b+13c=-138a+2b+12c=-3225a+5b+c=-7
Часть B.
Решение линейных систем с тремя переменными
Решить.
{2x−3y+z=45x+2y+2z=2x+4y−3z=7
{5x−2y+z=−92x+y−3z=−57x+3y+2z=6
{х+5у-2г=153х-7у+4г=-72х+4у-3г=21
{х-4у+2г=32х+3у-3г=93х+2у+4г=-1
{5x+4y-2z=-54x-y+3z=146x+3y-5z=-12
{2x+3y-2z=-43x+5y+3z=172x+y-4z=-8
{х+у-4г=19х-3у+6г=2-6х+2у-4г=-2
{5x−8y+z=5−3x+5y−z=−3−11x+18y−3z=−5
{x−y+2z=32x−y+3z=2−x−3y+4z=1
{х+у+г=8х-у+4г=-7-х-у+2г=1
{4x-y+2z=36x+3y-4z=-13x-2y+3z=4
{х-4у+6г=-13х+8у-2г=25х+2у-3г=-5
{3x−4y−z=75x−8y+3z=112x+6y+z=9
{3x+y−4z=66x−5y+3z=19х+3у-4г=10
{7x−6y+z=8−x+2y−z=4x+2y−2z=14
{−9x+3y+z=312x−4y−z=2−6x+2y+z=8
{a−b+c=94a−2b+c=142a+b+12c=3
{3a+b+13c=-138a+2b+12c=-3225a+5b+c=-7
{3x−5y−4z=−54x−6y+3z=−226x+8y−5z=20
{7x+4y-2z=82x+2y+3z=-43x-6y-7z=8
{9x+7y+4z=84x-5y-6z=-11-5x+2y+3z=4
{3x+7y+2z=-75x+4y+3z=52x-3y+5z=-4
{4x−3y=12y−3z=23x+2z=3
{5y-3z=-283x+2y=84y-7z=-27
{2x+3y+z=16y+z=42z=-4
{х-3у-2г=52у+6г=-14г=-6
{2x=106x−5y=303x−4y−2z=3
{2x+7z=2−4y=68y+3z=0
{5x+7y+2z=412x+16y+4z=1510x+13y+3z=14
{8x+12y-8z=52x+3y-2z=24x-2y+5z=-1
{17x−4y−3z=−25x+12y−2z=−922x+5y−4z=−13
{3x−5y−12z=72x−y−12z=−123x−8y+z=11
{4a-2b+3c=93a+3b-5c=-610a-6b+5c=13
{6a-2b+5c=-24a+3b-3c=-13a+5b+6c=24
Часть C: Приложения
Составьте систему уравнений и решите с ее помощью следующее.
Сумма трех целых чисел равна 38. Меньшее целое число, умноженное на два меньше, чем в 4, равно сумме остальных. Сумма меньшего и большего целых чисел равна 2, что более чем в два раза больше, чем у другого. Найдите целые числа.
Сумма трех целых чисел равна 40. Меньшее число, умноженное на три, равно сумме остальных. Удвоенное большее равно на 8 больше, чем сумма остальных. Найдите целые числа.
Сумма углов A , B и C треугольника равна 180°. Больший угол C равен удвоенной сумме двух других. Четырежды наименьший угол A равен разности углов С и В . Найдите углы.
Сумма углов A , B и C треугольника равна 180°. Угол C равен сумме двух других углов. Пятикратный угол A равен сумме углов C и B . Найдите углы.
В общей сложности 12 000 долларов было инвестировано в три процентных счета. Процентные ставки составляли 2%, 4% и 5%. Если общая сумма простых процентов за один год составила 400 долларов, а сумма, вложенная под 2%, была равна сумме сумм на двух других счетах, то сколько было вложено на каждый счет?
Джо инвестировал свои бонусные 6000 долларов в три счета, заработав 412% годовых. Он вложил в этот счет вдвое больше, заработав 412%, чем в два других вместе взятых. Если общая сумма простых процентов за год составила 234 доллара, сколько Джо вложил в каждый счет?
Кувшин содержит пятицентовики, десять центов и четвертак. Есть 105 монет общей стоимостью 8,40 долларов. Если десятицентовиков в три раза больше, чем четвертаков, найдите, сколько монет каждой монеты находится в банке.
В бумажнике хранятся однодолларовые, пятидолларовые и десятидолларовые купюры, стоимость которых составляет 210 долларов. Всего имеется 50 банкнот, где количество однодолларовых банкнот на единицу меньше, чем удвоенное количество пятидолларовых банкнот. Сколько купюр каждой?
Медсестра хочет приготовить антисептический раствор для местного применения на 15 унций, содержащий 3% перекиси водорода. Для получения этой смеси к существующим продуктам с содержанием перекиси водорода 1,5% и 10% добавляется очищенная вода. Если доступно только 3 унции 10% раствора перекиси водорода, сколько потребуется 1,5% раствора перекиси водорода и воды?
Химик должен приготовить раствор на 32 унции, состоящий из 834% кислоты. У него есть три концентрата с 5%, 10% и 40% кислоты. Если он будет использовать в два раза больше 5% раствора кислоты, чем 10% раствора, то сколько унций 40% раствора ему понадобится?
Общественный театр продал 128 билетов на вечернее представление на общую сумму 1132 доллара. Взрослый билет стоит 10 долларов, детский — 5 долларов, взрослый билет — 6 долларов. Если бы взрослым было продано в три раза больше билетов, чем детям и пенсионерам, вместе взятым, сколько было бы продано каждого билета?
Джеймс продал 82 предмета на своп-встрече на общую сумму 504 доллара. Он продавал упаковки носков по 6 долларов, футболки с принтами по 12 долларов и шапки по 5 долларов. Если он продал в 5 раз больше головных уборов, чем футболок, сколько каждого предмета он продал?
Парабола проходит через три точки (−1,7), (1,−1) и (2,−2). Используйте эти точки и y=ax2+bx+c, чтобы построить систему трех линейных уравнений в терминах a , b и c , а затем решить систему.
Парабола проходит через три точки (−2,11), (−1,4) и (1,2). Используйте эти точки и y=ax2+bx+c для построения системы трех линейных уравнений относительно a , b и c и решите ее.
Часть D: Дискуссионная доска
Напишите на карточке шаги решения системы трех линейных уравнений с тремя переменными методом исключения. Используйте свои заметки, чтобы объяснить другу, как решить одно из упражнений в этом разделе.
Исследуйте и обсудите подгонку кривой. Почему подгонка кривой является важной темой?
Ответы
№
Да
Да
№
№
(2, −1, −3)
(4, 1, −3)
(1, −1, 3)
Ø
(5, −10, −6)
(12,−2,−12)
(3, 12, 0)
(х,32х-3,2х-10)
(1, −2, 6)
(-1, 2, -2)
(1,−3, 5)
(1, 1, 0)
(0, 1, −2)
(5, 0, 6)
Ø
(х,2х-1,3х+2)
(1, 2, 3)
8, 12, 18
A = 20°, B = 40° и C = 120°
Сумма, инвестированная по ставке 2%, составила 6000 долларов, сумма, инвестированная по ставке 4%, составила 2000 долларов, а сумма, инвестированная по ставке 5%, составила 4000 долларов.
No related posts.