Решить {l}{2x+5y=16}{4x-3y=6} | Microsoft Math Solver
x=3
y=2
Викторина
Simultaneous Equation
5 задач, подобных этой:
\left. \begin{array} { l } { 2 x + 5 y = 16 } \\ { 4 x — 3 y = 6 } \end{array} \right.
Подобные задачи из результатов поиска в Интернете
Поделиться
Скопировано в буфер обмена
2x+5y=16,4x-3y=6
Чтобы решить два уравнения методом подстановки, сначала решите одно из уравнений для одной из переменных. Затем подставьте результат для этой переменной в другое уравнение.
2x+5y=16
Выберите один из уравнений и решите его для x, изолируя x в левой части знака равенства.
2x=-5y+16
Вычтите 5y из обеих частей уравнения.
x=\frac{1}{2}\left(-5y+16\right)
Разделите обе части на 2.
x=-\frac{5}{2}y+8
Умножьте \frac{1}{2} на -5y+16.
4\left(-\frac{5}{2}y+8\right)-3y=6
Подставьте -\frac{5y}{2}+8 вместо x в другом уравнении 4x-3y=6.
-10y+32-3y=6
Умножьте 4 на -\frac{5y}{2}+8.
-13y+32=6
Прибавьте -10y к -3y.
-13y=-26
Вычтите 32 из обеих частей уравнения.
y=2
Разделите обе части на -13.
x=-\frac{5}{2}\times 2+8
Подставьте 2 вместо y в x=-\frac{5}{2}y+8. Так как получившееся уравнение содержит только одну переменную, вы можете напрямую найти решение для x.
x=-5+8
Умножьте -\frac{5}{2} на 2.
x=3
Прибавьте 8 к -5.
x=3,y=2
Система решена.
2x+5y=16,4x-3y=6
Приведите уравнения к стандартному виду, а затем решите систему уравнений с помощью матриц.
\left(\begin{matrix}2&5\\4&-3\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}16\\6\end{matrix}\right)
Запишите уравнения в матричном виде.
inverse(\left(\begin{matrix}2&5\\4&-3\end{matrix}\right))\left(\begin{matrix}2&5\\4&-3\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}2&5\\4&-3\end{matrix}\right))\left(\begin{matrix}16\\6\end{matrix}\right)
Левое произведение с матрицей, обратной \left(\begin{matrix}2&5\\4&-3\end{matrix}\right).
\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}2&5\\4&-3\end{matrix}\right))\left(\begin{matrix}16\\6\end{matrix}\right)
Произведение матрицы на обратную ей является единичной матрицей.
\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}2&5\\4&-3\end{matrix}\right))\left(\begin{matrix}16\\6\end{matrix}\right)
Перемножение матриц слева от знака равенства.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{-3}{2\left(-3\right)-5\times 4}&-\frac{5}{2\left(-3\right)-5\times 4}\\-\frac{4}{2\left(-3\right)-5\times 4}&\frac{2}{2\left(-3\right)-5\times 4}\end{matrix}\right)\left(\begin{matrix}16\\6\end{matrix}\right)
Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) с размерностью 2\times 2 обратная матрица имеет вид \left(\begin{matrix}\frac{d}{ad-bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матричное уравнение можно переписать в виде задачи умножения матриц.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{3}{26}&\frac{5}{26}\\\frac{2}{13}&-\frac{1}{13}\end{matrix}\right)\left(\begin{matrix}16\\6\end{matrix}\right)
Выполните арифметические операции.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{3}{26}\times 16+\frac{5}{26}\times 6\\\frac{2}{13}\times 16-\frac{1}{13}\times 6\end{matrix}\right)
Перемножьте матрицы.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}3\\2\end{matrix}\right)
Выполните арифметические операции.
x=3,y=2
Извлеките элементы матрицы x и y.
2x+5y=16,4x-3y=6
Для решения методом исключения коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сократилась при вычитании одного уравнения из другого.
4\times 2x+4\times 5y=4\times 16,2\times 4x+2\left(-3\right)y=2\times 6
Чтобы сделать 2x и 4x равными, умножьте все члены в обеих частях первого уравнения на 4 и все члены в обеих частях второго уравнения на 2.
{2}+2 x-3}
Решить {c}{4x+3y=1}{16x-5y=21} | Microsoft Math Solver.
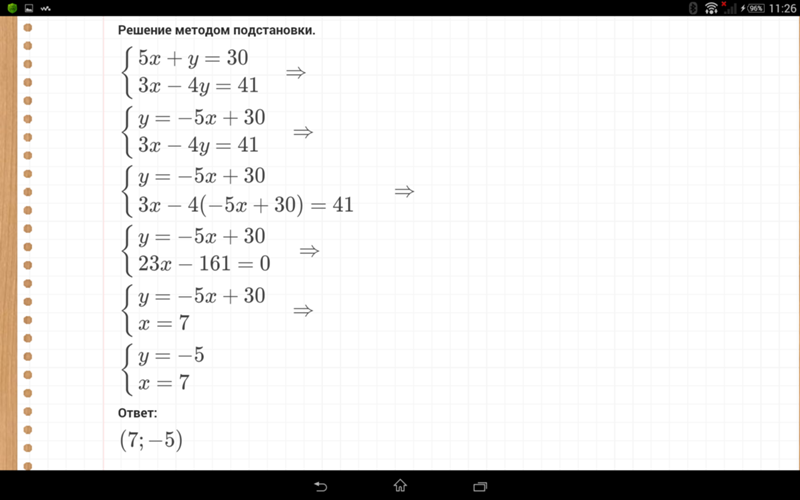\begin{array} { c } { 4 x + 3 y = 1 } \\ { 16 x — 5 y = 21 } \end{array} \right.Аналогичные задачи из веб-поиска
Поделиться
Скопировано в буфер обмена
4x+3y=1,16x-5y=21
Чтобы решить пару уравнений с помощью подстановки, сначала решите одно из уравнений для одной из переменных . Затем подставьте результат этой переменной в другое уравнение.
4x+3y=1
Выберите одно из уравнений и решите его относительно x, выделив x слева от знака равенства.
4x=-3y+1
Вычтите 3y из обеих частей уравнения.
x=\frac{1}{4}\left(-3y+1\right)
Разделить обе части на 4.
x=-\frac{3}{4}y+\frac{1}{ 4}
Умножьте \frac{1}{4} на -3y+1.
16\left(-\frac{3}{4}y+\frac{1}{4}\right)-5y=21
Подставьте \frac{-3y+1}{4} вместо x в другом уравнение, 16x-5y=21.
-12y+4-5y=21
Умножить 16 раз \frac{-3y+1}{4}.
-17 лет+4=21
Добавить от -12 лет до -5 лет.
-17y=17
Вычтите 4 из обеих частей уравнения.
y=-1
Разделите обе части на -17.
x=-\frac{3}{4}\left(-1\right)+\frac{1}{4}
Подставьте -1 вместо y в x=-\frac{3}{4}y+ \фракция{1}{4}. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую.
х=\фракция{3+1}{4}
Умножить -\frac{3}{4} на -1.
x=1
Добавьте \frac{1}{4} к \frac{3}{4}, найдя общий знаменатель и сложив числители. Затем уменьшите дробь до меньших членов, если это возможно.
x=1,y=-1
Теперь система решена.
4x+3y=1,16x-5y=21
Приведите уравнения к стандартной форме, а затем используйте матрицы для решения системы уравнений.
\left(\begin{matrix}4&3\\16&-5\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin {матрица}1\\21\конец{матрица}\справа)
Запишите уравнения в матричной форме.
обратная (\ левая (\ начало {матрица} 4 и 3 \\ 16 & — 5 \ конец {матрица} \ правая)) \ левая (\ начало {матрица} 4 и 3 \\ 16 & — 5 \ конец {матрица} \ правая) \ влево (\ начало {матрица} х \\ у \ конец {матрица} \ вправо) = обратное (\ влево (\ начало {матрица} 4 и 3 \\ 16 &-5 \ конец {матрица} \ вправо)) \ влево (\ начало {matrix}1\\21\end{matrix}\right)
Left умножьте уравнение на обратную матрицу \left(\begin{matrix}4&3\\16&-5\end{matrix}\right).
\left(\begin{matrix}1&0\\0&1\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin {матрица}4&3\\16&-5\конец{матрица}\справа))\слева(\начало{матрица}1\\21\конец{матрица}\справа)
Произведение матрицы и ее обратной является единичной матрицей.
\left(\begin{matrix}x\\y\end{matrix}\right)=inverse(\left(\begin{matrix}4&3\\16&-5\end{matrix}\right))\left (\begin{matrix}1\\21\end{matrix}\right)
Умножьте матрицы слева от знака равенства.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{-5}{4\left(-5\right)-3\ раз 16}&-\frac{3}{4\left(-5\right)-3\times 16}\\-\frac{16}{4\left(-5\right)-3\times 16} &\frac{4}{4\left(-5\right)-3\times 16}\end{matrix}\right)\left(\begin{matrix}1\\21\end{matrix}\right)
Для матрицы \left(\begin{matrix}a&b\\c&d\end{matrix}\right) 2\times 2, обратная матрица равна \left(\begin{matrix}\frac{d}{ad- bc}&\frac{-b}{ad-bc}\\\frac{-c}{ad-bc}&\frac{a}{ad-bc}\end{matrix}\right), поэтому матрица уравнение можно переписать как задачу умножения матриц.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{5}{68}&\frac{3}{68}\\ \frac{4}{17}&-\frac{1}{17}\end{matrix}\right)\left(\begin{matrix}1\\21\end{matrix}\right)
Подсчитайте.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}\frac{5}{68}+\frac{3}{68}\times 21\\\frac{4}{17}-\frac{1}{17}\times 21\end{matrix}\right)
Умножьте матрицы.
\left(\begin{matrix}x\\y\end{matrix}\right)=\left(\begin{matrix}1\\-1\end{matrix}\right)
Выполните арифметические действия.
x=1,y=-1
Извлечь элементы матрицы x и y.
4x+3y=1,16x-5y=21
Чтобы решить методом исключения, коэффициенты одной из переменных должны быть одинаковыми в обоих уравнениях, чтобы переменная сокращалась при вычитании одного уравнения из другого .
16\4x4x+16\times 3y=16,4\times 16x+4\left(-5\right)y=4\times 21
Чтобы сделать 4x и 16x равными, умножьте все члены на каждой стороне первое уравнение на 16, а все члены по обе стороны от второго на 4.
64x+48y=16,64x-20y=84
Упростить.
64x-64x+48y+20y=16-84
Вычтите 64x-20y=84 из 64x+48y=16, вычитая одинаковые члены по обе стороны от знака равенства.
48y+20y=16-84
Прибавьте 64x к -64x. Члены 64x и -64x сокращаются, оставляя уравнение только с одной переменной, которую можно решить.
68 лет = 16-84
Добавьте 48 лет к 20 годам.
68y=-68
Прибавьте 16 к -84.
y=-1
Разделите обе части на 68.
16x-5\left(-1\right)=21
Подставьте -1 вместо y в 16x-5y=21. Поскольку результирующее уравнение содержит только одну переменную, вы можете найти x напрямую.
16x+5=21
Умножьте -5 на -1.
16x=16
Вычтите 5 из обеих частей уравнения.
x=1
Разделите обе части на 16. 9{ 2 } — 4 x — 5 = 0
Тригонометрия
4 \sin \theta \cos \theta = 2 \sin \theta
Линейное уравнение
y = 3x + 4
Арифметика 909 07
699*533
Матрица
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin {array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]
Одновременное уравнение
\left.