Сюръекция инъекция: Дискретная математика, комбинаторика, теория чисел

Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения

Содержание:

1. Сюръекция, инъекция и биекция
2. Произведение множеств

 

По этой ссылке вы найдёте полный курс лекций по математике:

Решение задач по математике

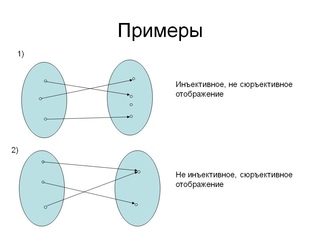
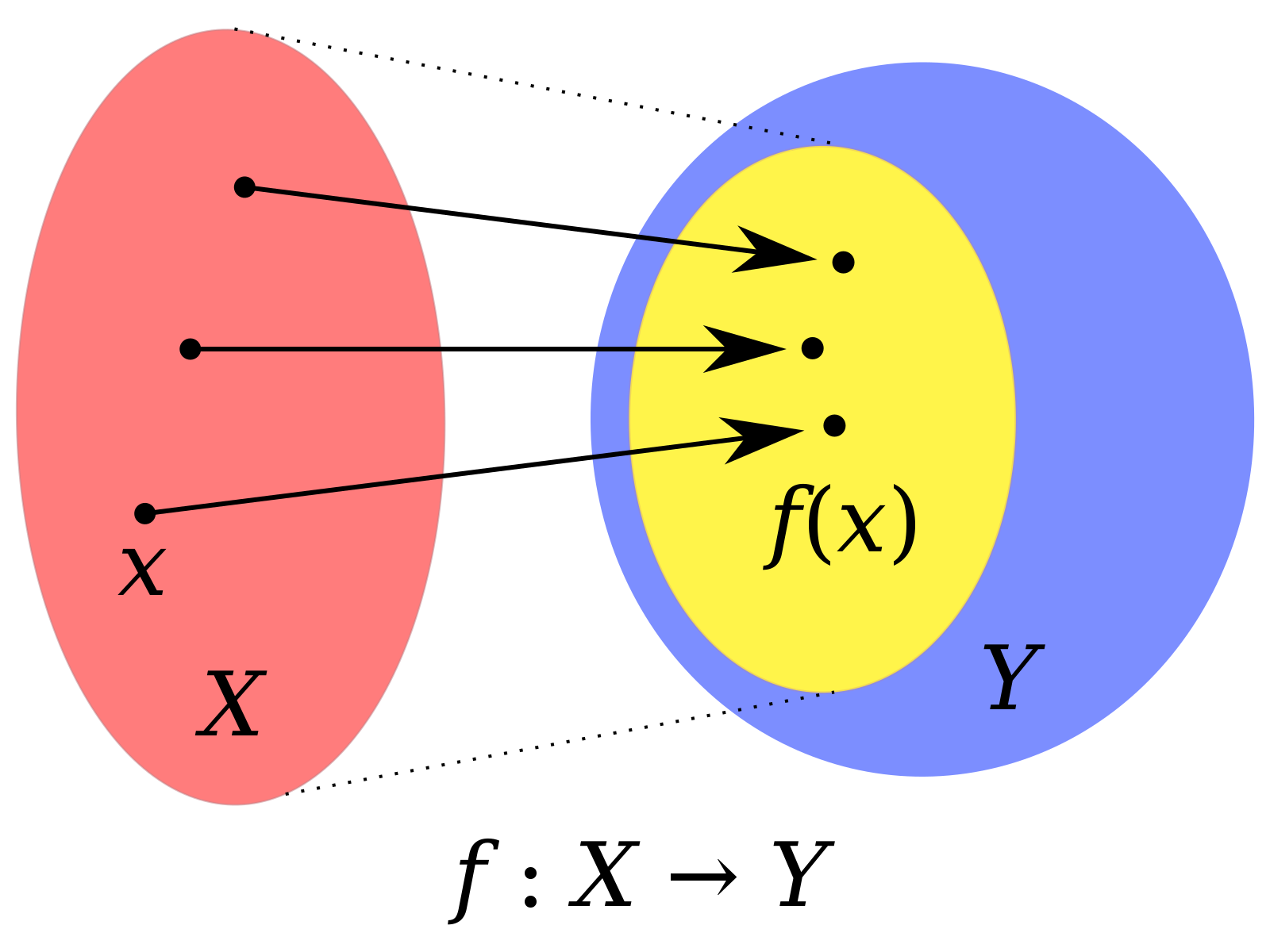
Правило, задающее отображение f: X (или функцию /), можно условно изобразить стрелками (рис. 2.1). Бели в множестве У есть хотя бы один элемент) на который не указывает ни одна из стрелок, то это свидетельствует о том, что область значений функции f не заполняет все множество У, т.е. f(X) С У. Если же область значений / совпадает с У, т.е. f{X) = У, то такую функцию называют сюръективной} или короче — сюръекцией, и говорят, что функция / отображает множество X на множество У (в отличие от общего случая отображения множества X в множество У согласно определению 2.

1). Итак, / : X есть сюръекция, если Vy 6 У Зх € X : /(х) = у. На рисунке в таком случае к каждому элементу множества У ведет хотя бы одна стрелка (рис. 2.2). При этом к некоторым элементам из У могут вести несколько стрелок. Если к любому элементу у € У ведет не более одной стрелки, то / называют инъективной функцией, или инъекцией. Эта функция не обязательно сюръективна, т.е. стрелки ведут не ко всем элементам множества У (рис. 2.3).

• Итак, функция /: X —У У представляет собой инъекцию, если два любых различных элемента из X имеют своими образами при отображении / два различных элемента из У, или Vy £ f{X) С У 3хеХ: f{x) = y. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Отображение /: X->У именуют биективным, или би-екцией, если каждый элемент у 6 У является образом некоторого и призом единственного элемента из X, т.е. Vy € f(X) = У Э!х € X : f(x) = у.

По сути, функция / в этом случае устанавливает взаимно однозначное соответствие между множествами X и У, и потому ее часто называют взаимно однозначной функцией.

Очевидно, что функция / биективна тогда и только тогда, когда она одновременно инъективна и сюръективна. В этом случае стрелки (рис. 2.4) соединяют попарно каждый элемент из X с каждым элементом из У.

При этом никакие два элемента из X не могут быть соединены стрелкой с одним и тем же элементом из У, ибо / инъективна, и никакие два элемента из У не могут быть соединены стрелками с одним и тем же элементом из X из-за требования единственности образа в определении 2.1 отображения.

Каждый элемент из X участвует в попарном соединении, поскольку X — область определения функции /. Наконец, каждый элемент из У тоже участвует в одной из пар, ибо / сюръективна. Роли X и У в этом случае как бы совершенно одинаковы, и если повернуть все стрелки вспять (рис. 2.5), то получим иное отображение или иную функцию д), которое тоже и инъективно, в сюръективно. Отображения (функции), допускающие такое обращение, будут играть большую роль в дальнейшем.

В частном случае множества X и У могут совпадать (X = У).

 

Тогда биективная функция будет осуществлять отображение множества X на себл. Биекцию множества на себя называют также пре-образов анием. 2.3. Обратное отображение Пусть /: X —? У — некоторая биекция и пусть у € У. Обозначим через /_1(у) единственный элемент х€Х, такой, что /(г) = у. Тем самым мы определим некоторое отображение 9 : Y Xу которое является снова биекцией. Ее называют обратным отображением, или обратной биекцией к /. Часто ее также называют просто обратной функцией и обозначают /»*. На рис. 2.5 функция д как раз и является обратной к /, т.е. д = f’1.

 

Возможно вам будут полезны данные страницы:

Концентрация растворенного вещества

Ионно-молекулярные уравнения реакции

Объемно-планировочное решение здания (ОПР) Расположение (компоновка) помещений

Круги Эйлера фигуры, условно изображающие множества

Функция /, определяемая формулой у = За — 2, я,у € R, является биекцией. комсество действительных чисел.

 

• Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. 2.4. Композиция отображений Если f:X-*Y и g:Y-*Zy то отображение (р:Х -+Z, заданное для каждого а: 6 А» формулой =, именуют композицией (суперпозицией) отображений (функций) / и д> или сложной функцией, и обозначают ро/ (рис. 2.6).
• Таким образом, сложная функция до f реализует правило: я Применяй сначала /, а затем ди, т.е. в композиции операций «до/ надо начинать с операции /, расположенной справа. Отметим, что композиция Рис. 2.6 отображений ассоциативна, т.е.если /: X -+Y , д: Y Z и h: Z-*H> то тогда (hog)of = = ho(gof)i что проще записывают в виде ho до /. Проверим это следующим образом: На любом wK«oaicecmee X определено отображение 1х -X X, называемое тождественным, обозначаемое часто также idx и задаваемое формулой Ix(x) = x Vx € А». Его -действие состоит в том, что оно оставляет все на своих местах.

Так, если является биекцией, обратной к биекции /: Х-+У, то /»1о/ = /х, а /о/-1 = /у, где и /у — тождественные отображения множеств X и У соответственно. Обратно, если отображения f: X ->Y и р : У Л» таковы, что gof = Ix и fog = /у, то функция / является биекцией, а у — ее обратной биекцией.

Очевидно, что если / — биекция Л» на У, а $ — биекция У на Z, то gof является биекцией X на Z, а будет по отношению к ней обратной биекцией. 2.5. Произведение множеств. График отображения Напомним, что две взаимно перпендикулярные координатные оси с масштабом, одинаковым для обеих осей, задают на плоскости прямоугольную декартову систему координат (рис. 2.7). Точку О пересечения координатных осей называют начало* координат. Каждой точке М можно поставить в соответствие пару (я, у) действительных чисел где х — координата точки Мх на ко-ординатной оси Ох, а у — координата точки Му на координатной оси Оу. Точки Мх и Му являются основаниями перпендикуляров, опущенных из точки М соответственно на оси Ох и Оу.

Числа х и у называют координатами точки М ( в выбранной системе координат), причем х называют абсциссой точки М, а у — ординатой этой точки.

Очевидно, что каждой паре (а, Ь) действительных чисел а, 6 6R соответствует на плоскости точка М, имеющая эти числа своими координатами. И обратно, каждой точке М плоскости соответствует пара (а, 6) действительных чисел а и 6. В общем случае пары (а, Ь) и (6, а) определяют разные точки, т.е. существенно, какое из двух чисел а и b стоит в обозначении пары на первом месте. Таким образом, речь идет об упорядоченной паре. В связи с этим пары (а, 6) и (6, а) считают равными между собой, и они определяют одну и ту же точку на плоскости, если только а = 6. Сюръекция, инъекция и биекция. Обратное отображение. Композиция отображений произведение множеств. График отображения. Множество всех пар действительных чисел, а также множество точек плоскости обозначают R2. Это обозначение связано с важным в теории множеств понятием прямого (или дек ар-това) произведения множеств (часто говорят просто о произведении множеств).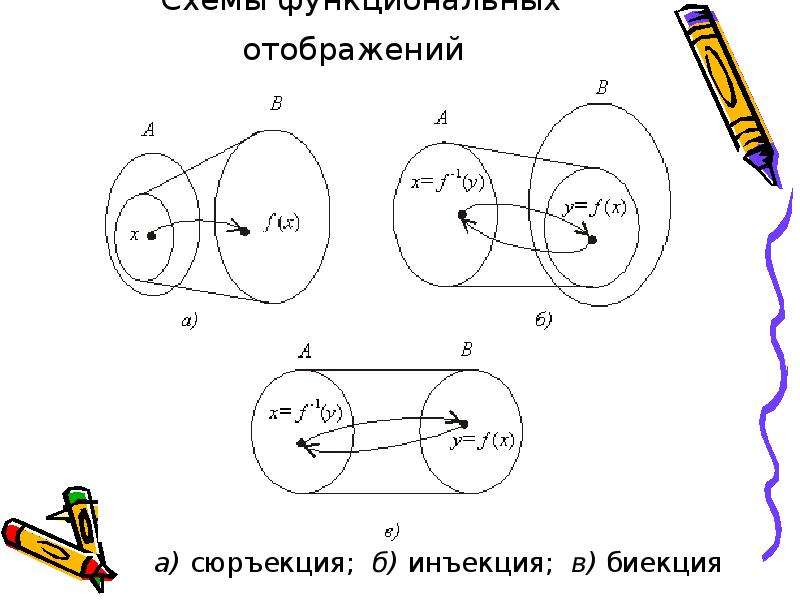

Определение 2.2.

Произведением множеств А и В называют множество Ах В возможных упорядоченных пар (ж, у), где первый элемент взят из А, а второй — из В, так что Равенство двух пар (х, у) и (&’, у’) определяют условиями х = х’ и у = у7. Пары (я, у) и (у, х) считают различными, если хфу. Это особенно важно иметь в виду, когда множества А и В совпадают. Поэтому в общем случае А х В ф В х Л, т.е. произведение произвольных множеств не коммутативно, но оно дистрибутивно по отношению к объединению, пересечению и разности множеств: где обозначает одну из трех названных операций.

Произведение множеств

Произведение множеств существенно отличается от указанных операций над двумя множествами. Результатом выполнения этих операций является множество, элементы которого (если оно не пустое) принадлежат одному или обоим исходным множествам. Элементы же произведения множеств принадлежат новому множеству и представляют собой объекты иного рода по сравнению с элементами исходных множеств.

Аналогично определению 2.2 можно ввести понятие произведения более чем двух множеств. Множества (А х В) х С и А*х (В х С) отождествляют и обозначают просто А х В х С, так что . Произведения Ах Ау Ах Ах А и т.д. обозначают, как правило, через А2 , А3 и т.д. Очевидно, плоскость R2 можно рассматривать как произведение R х R двух экземпляров множества действительных чисел (отсюда и происходит обозначение множества точек плоскости как произведения двух множеств точек числовой прямой). Множеству точек геометрического (трехмерного) пространства соответствует произведение R х R х R трех экземпляров множества точек числовой прямой, обозначаемое R3.

• Произведение п множеств действительных чисел обозначают Rn. Это множество представляет собой всевозможные наборы (xj, Х2, хп) из п действительных чисел Х2) хп £ R, а любая точка х* из Rn есть такой набор (xj, х, х*) действительных чисел хп € К*
• Произведение п произвольных множеств есть множество упорядоченных наборов из п (в общем случае разнородных) элементов. Для таких наборов употребляют названия кортеж или n-ка (произносят „энка»). Пример 2.3. Пусть А = { 1, 2} и В = {1, 2}. Тогда , и множество А х В можно отождествить с четырьмя точками плоскости R2, координаты которых указаны при перечислении элементов этого множества. Если С={ 1,2} и D={3,4}, то . Пример 2.4. Пусть Тогда Геометрическая интерпретация множеств Е х F и F х Е представлена на рис. 2.8. # Для отображения /: X можно составить множество упорядоченных пар (г, у), которое является подмножеством прямого произведения X х У.
• Такое множество называют графиком отображения f (или графиком функции я*»- Пример 2.5. В случае XCR и Y = К каждая упорядоченная пара задает координаты точки на плоскости R2. Если при этом X является промежутком числовой прямой R, то график функции может представлять некоторую линию (рис. 2.9). Пример 2.6. Ясно, что при XCR2 и У = R график функции есть некоторое множество точек в R3, которое может представлять некоторую поверхность (рис. 2.10).

Если же X С R, а У = R2, то график функции также есть множество точек в R3, которое может представлять некоторую линию, пересекаемую плоскостью х = const лишь в одной точке М с тремя координатами х} yi, у2 (рис. 2.11). # Все упомянутые примеры графиков функции являются важнейшими объектами математического анализа, и в дальнейшем они будут подробно рассмотрены.

Ответы по Matemat_logike2013

ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА

Федеральное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный университет водных коммуникаций»

Кафедра Комплексного обеспечения информационной безопасности

Дисциплина «Математическая логика и теория алгоритмов» ( ИЗ — I )

Специальность «090900.62 — Информационная безопасность» профиль «Безопасность автоматизированных систем»

Список вопросов

1. Свойства операций над множествами.

Свойства  операций над множествами.

Из определений объединения и пересечения множеств следует, что операции пересечения и объединения обладают следующими  свойствами :

1. Коммутативность.

A  B=B  A(объединение) A  B=B  A(Пересечение)

2. Ассоциативность.

(A  B)  C=A  (B  C) (A  B)  C= A  (B  C)

3. Дистрибутивность.

(A  B)  C = (A  C)  (B  C) (A  B)  C= (A  C)  (B  C)

4. A  A=A, A  A=A A  = A, A 

5. Законы де Моргана (законы двойственности).

1) A  B= A  B   2 ) A  B= A  B

Доказательство данных  свойств  проводится на основе определения равенства двух множеств.

Заметим, что закон ассоциативности при комбинировании операций объединения и вычитания, вообще говоря, не имеет места.

2. Отношения: инъекция, сюръекция, биекция, их свойства.

Определение 9 ( инъекция ,  сюръекция ,  биекция ).

Отображение называется  инъекцией , если для любых элементов x₁, x₂   X , для которых f(x₁) = f(x₂) следует, что x₁ =  x₂ . (рис. 7)

 Сюръекцией  (или отображением «на» ) называется отображение, при котором f(X) = Y (рис. 8).

 Биекция  – это одновременно и  сюръекция  и  инъекция  (рис. 9).

3. Отношение эквивалентности. Классы эквивалентности, их свойства.

Важным видом бинарного отношения является отношение эквивалентности.

Определение 5.1. Бинарное отношение  на множестве X называется отношением эквивалентности на X, если  рефлексивно, симметрично и транзитивно.

Отношение эквивалентности часто обозначают символами  ~,.

Примерами отношения эквивалентности служат:

• отношение тождества I_X = {(a, a)|aX} на непустом множестве X;

• отношение подобия на множестве фигур плоскости;

• отношение равносильности на множестве уравнений;

С отношением эквивалентности тесно связано разбиение множества на классы.

Определение 6.1. Система непустых подмножеств

{M₁, M₂, …}

множества M называется разбиением этого множества, если

M = M₁M₂  …

и при  ij

M_iM_j =O.

Сами множества M₁, M₂, … называются при этом классами данного разбиения.

Примерами разбиений служат:

• разложение всех многоугольников на группы по числу вершин — треугольники, четырехугольники, пятиугольники и т. д.;

• разбиение всех треугольников на классы подобных треугольников;

• разбиение множества всех учащихся данной школы по классам.

Классом эквивалентности, порождённым элементом х называется подмножество множества χ.

Теорема 6.1. Всякое разбиение  непустого множества M на классы определяет (индуцирует) на этом множестве отношение эквивалентности такое, что:

4. Отношения частичного и линейного порядка. Теорема об изоморфизме частично упорядоч. множеств.

Непустое множество X с заданным на этом множестве отношением частичного (линейного) порядка называется частично (линейно) упорядоченным множеством. Для отношения порядка на произвольном множестве часто используют символ <=, соответственно для строгого порядка можно использовать символ ≺

Два частично упорядоченных множества называются изоморф-

ными, если между ними существует изоморфизм, то есть взаимно

однозначное соответствие, сохраняющее порядок. (Естественно, что

в этом случае они равномощны как множества.) Можно сказать так:

биекция f : A → B называется изоморфизмом частично упорядочен-

ных множеств A и B, если

a1 6 a2 ⇔ f(a1) 6 f(a2)

для любых элементов a1, a2 ∈ A (слева знак 6 обозначает порядок в

множестве A, справа — в множестве B).

Очевидно, что отношение изоморфности рефлексивно (каждое

множество изоморфно самому себе), симметрично (если X изоморф-

но Y , то и наоборот) и транзитивно (два множества, изоморфные

третьему, изоморфны между собой). Таким образом, все частично

упорядоченные множества разбиваются на классы изоморфных, ко-

торые называют порядковыми типами.

5. Равносильность формул. Основные свойства.

6. Основные тавтологии.

7. Правильные рассуждения. Основные схемы.

Правильным называется рассуждение, в котором из конъюнкции посылок следует заключение, и оно является тавтологией. В этом случае, если посылки – истинны, заключение – истинно.

В этом случае, если посылки – истинны, заключение – истинно.

А⇒В ≡ (А⇒В) ∨ Л ≡ ¬(А⇒В) ⇒(С & ¬С) ≡ (А & ¬В) ⇒(С & ¬С).

А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ (С & ¬С) ≡¬ (¬А ∨ В) ⇒ (С & ¬С)

А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨¬А ≡¬ (¬А ∨ В) ⇒¬А ≡(А & ¬В) ⇒¬А

А⇒В ≡¬А ∨ В ≡ (¬А ∨ В) ∨ В ≡¬ (¬А ∨ В) ⇒ В≡ (А & ¬В) ⇒В

А⇒В≡ ¬А ∨ В ≡ В ∨ ¬А ≡ ¬В ⇒¬А – закон контрапозиции

8. Двойственные формулы. Лемма. Теорема – принцип двойственности.

НЕПОЛНЫЙ ОТВЕТ!!!!!!!!

Связки & и ∨ Называются двойственными.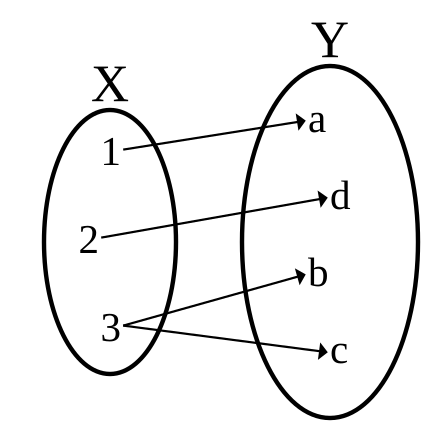

Формула F* называется двойственной формуле F, если она получена из F заменой символов функций на символы двойственных им функций.( & на ∨)(∨ на &). Для таких формул есть свойство:

F*(X1…Xn)= -F(-X1…-Xn)

9. Теорема о представлении булевой функции формулой логики высказываний.

Каждая булева функция порождается некой формулой, в которую кроме пропозиц.переменных входят только пропозиц.связки из множества(И, ИЛИ, НЕ)

Док-во.

Пусть F(X1-Xn) задана таблицей

1)Если она является тождественным нулём, то формула (А1 & ¬А1)∨ (А2 & ¬А2)∨…∨ (Аn & ¬Аn) является такой порождающей формулой.

2) Пусть среди значений функции есть хотя бы одна 1. Пусть это строка таблицы истинности с номером j.

Эта формула принимает значение Истина только на «своей» строистинности. На всех остальных она принимает значение Ложь

f=D1vD2v…vDn составленная по всем строкам со значением 1 является формулой порождающей исходную булеву функцию

10. Полные системы связок.

11. Дизъюнктивная нормальная форма. Совершенная ДНФ. Теорема о представлении в ДНФ.

12. Теоремы о приведении к СДНФ и об единственности СДНФ.

13. Конъюнктивная нормальная форма. Совершенная КНФ. Теорема о представлении в КНФ.

14. Теорема о представимости булевых функций многочленами Жегалкина.

15. Приложение логики высказываний: к синтезу логических схем вычисл. устройств, и др.

http://cs323524.vk.me/v323524284/7907/ilnj3Kv_tSs.jpg

http://cs309131.vk.me/v309131284/6914/enoGWqwlJ90.jpg

16. Простейшие свойства выводимых формул в аксиоматических теориях (1- 8).

17. Вывод в теории Черча: .

18. Вывод в теории Черча: если , то .

19. Вывод в теории Черча: .

20. Вывод в теории Черча: .

21. Вывод в теории Черча: и .

22. Теорема о дедукции.

23. Правило силлогизма.

24. Вывод формулы: .

25. Правило перевертывания.

26. Производное правило вывода: .

27. Производное правило вывода: .

28. Производное правило вывода: .

29. Производное правило вывода: и .

30. Производное правило вывода: если , то

31. Производное правило вывода: если , то .

32. Лемма к теореме о полноте (в широком смысле).

33. Теорема о корректности АТЧ.

Теорема. (о корректности АТЧ)

Любая теорема АТЧ является тавтологией.

Доказательство

Аксиомы А1, А2, А3 являются тавтологиями (см. стр. 8). Далее, единст-39

венное правило вывода MP, примененное к тавтологиям, снова приводит к

тавтологии (см. стр. 9). Поэтому каждая теорема является тавтологией. ■

34. Теорема о полноте (в широком смысле).

35. Теорема о непротиворечивости.

36. Теорема о абсолютной непротиворечивости. Теорема об альтернативности АТ.

37. Частично–рекурсивные и примитивно–рекурсивные функции: ; .

38. Машина Тьюринга для простейших функций.

39. Машина Тьюринга для копирования слов.

40. Машина Тьюринга для удвоения чисел.

41. Машина Тьюринга для сложения двух чисел

Терминология

— Инъекция против Суръекции: Мнемоника, чтобы запомнить, что есть что

$\begingroup$

Какие мнемоники помогут запомнить, что Инъекция = Один к одному, а Суръекция = На? Единственное, о чем я могу думать, это 1njection = 1-1.

• терминология
• мнемоника

$\endgroup$

8

$\begingroup$

Инъекция $A \to B$ отображает $A$ в $B$, т. е. позволяет найти копию $A$ внутри $B$.

A сюръекция $A \to B$ отображает $A$ на $B$ в том смысле, что образ покрывает все $B$. Слог «sur» имеет латинское происхождение и означает «над» или «выше», как, например, в слове «избыток» или «опрос».

$\endgroup$

2

$\begingroup$

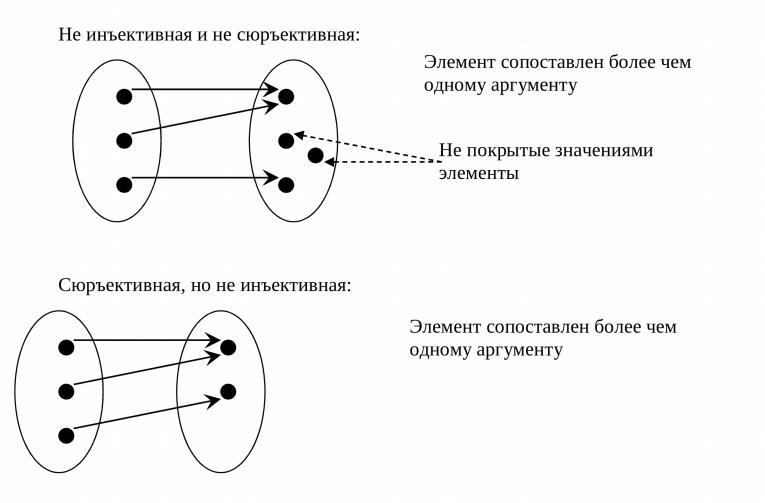
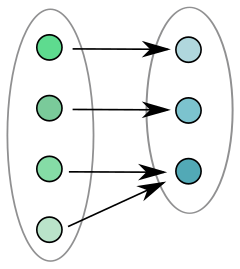
Взгляните на эту картинку (из Википедии):

Эта функция НЕ является инъекцией, потому что две стрелки указывают на одну точку на этой картинке.

А теперь представьте уколы у врача. Инъекции обычно болезненны, и вы, черт возьми, не хотели бы, чтобы кто-то несколько раз втыкал эту инъекцию в одну и ту же точку на вашем теле.

Вот почему инъективные функции не могут иметь несколько стрелок, указывающих на одну и ту же точку (значение)

🙂

$\endgroup$

$\begingroup$

Насколько я помню, когда делаешь прививку от гриппа, все твое тело не превращается в гигантский вирус гриппа, потому что игла меньше твоей руки.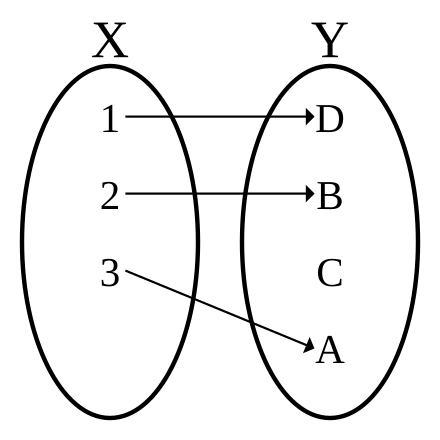 {-1}(f(x) = f( y)) \ подразумевает x = y$

Функция SURjective ОБЯЗАТЕЛЬНО поразит все элементы мишени.

Новый участник

Лейф П. — новый участник этого сайта. Будьте осторожны, запрашивая разъяснения, комментируя и отвечая. Ознакомьтесь с нашим Кодексом поведения.

$\endgroup$

$\begingroup$

Лучший способ запомнить — запомнить только одно, а затем путем исключения узнать другое.

Я предпочитаю запоминать инъекционное следующим образом:

Инъекции лечат вещи, и у вас есть одна инъекция на одно лекарство. т.е. один к одному.

$\endgroup$

2

Свойства проекций

Свойства проекций

Секции

Свойства сюръекций, инъекций и биекций

Некоторые свойства сюръекций, инъекций и биекций представлены здесь с доказательствами.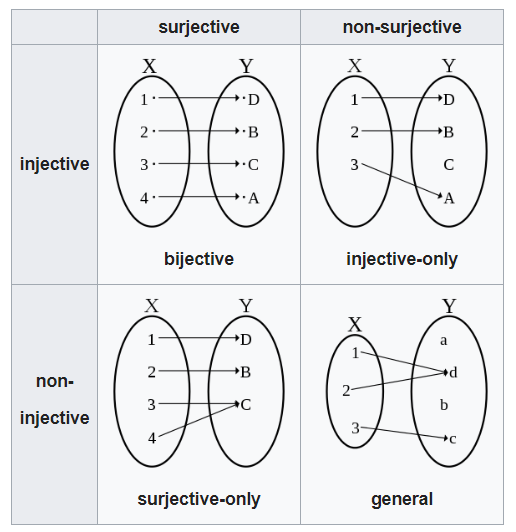
Ниже f находится функция из набора A в набор B , и g — функция из набора B в набор C .

Свойство 1: Если f и g — сюръекции, то fg — сюръекция.

Доказательство собственности 1 :

Пусть z — произвольный элемент в C .
Тогда, поскольку f является сюръекцией, существует элемент г в В так что z = f(y) .
Тогда, поскольку g является сюръекцией, в A есть элемент x так что y = g(x) .
Отсюда по определению составной функции z = f(g(x)) , то есть z = fg(x) .
Следовательно, fg является сюръекцией.
КЭД

Свойство 2: Если ф и г – инъекции, затем фг – инъекции.

Доказательство собственности 2 :

Пусть x ₁ и x ₂ — произвольные элементы в A .
Предположим, что f(g(x ₁ )) = f(g(x ₂ )) .
Тогда, поскольку f является впрыском, г(х ₁ ) = г(х ₂ ) .
Тогда с г — впрыск, х ₁ = х ₂ .
То есть для любой пары элементов x ₁ и x ₂ в A если f(g(x ₁ )) = f(g(x ₂ )) , то x ₁ = x ₂ .
Отсюда фг — инъекционный.
КЭД

Свойство 3: Если f и g — биекции, то fg — биекция.

Доказательство собственности 3 :
Очевидно, это следует из свойств 1 и 2.

Свойство 4: Если fg — сюръекция, то f — сюръекция.

Доказательство собственности 4 :

Пусть z — произвольный элемент в C .
Тогда, поскольку fg является сюръекцией, в A есть элемент x так что z = f(g(x)) .
По определению fg существует элемент y в B такой, что y = g(x) и z = f(y) .
Следовательно, для произвольного элемента z в C , существует элемент y в B такой, что z = f(y) .
Следовательно, f является сюръекцией.
КЭД

Свойство 5: Если фг — инъекция, затем г — инъекция.

Доказательство собственности 5 :

Доказательство оставлено в качестве упражнения.

Свойство 6: Если fg — биекция, то f — сюръекция и г для инъекций.

Доказательство собственности 6 :
Очевидно, это следует из свойств 4 и 5.

Ниже f — функция из набора А к комплекту В , S ⊆ A и T ⊆ B .

Свойство 7: Если f биекция, то f( S ∩ T ) = f(S) ∩ f(T)

Доказательство собственности 7 :

Поскольку f( S ∩ T ) ⊆ f(S) ∩ f(T) для функции f нам нужно доказать, что f(S) ∩ ф(Т) ⊆ f( S ∩ T ) для биекции f .

Пусть y — произвольный элемент множества f(S) ∩ f(T) .

Затем идет элемент x ₁ в S и элемент x ₂ в T так что y = f(x ₁ ) = f(x ₂ ) .

No related posts.