Решить слау методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса.

Решение системы линейных алгебраических уравнений методом Гаусса

Система линейных уравнений вида:

может быть решена методом Гаусса при помощи нашего калькулятора.

Система уравнений задается в виде расширенной матрицы, т. е. матрицы коэффициентов и свободных членов размерности [n : n+1] вида:

Описание метода Гаусса следует сразу за калькулятором.

Решение системы линейных уравнений методом Гаусса

8 3 4 5 31 14 4 33 23 17 15 4 23 7 22 4 11 17 1 51

СЛАУ в матричном виде

Точность вычисления

Знаков после запятой: 2

Количество решений

 

Вектор решения системы уравнений

 

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Загрузить close

content_copy Ссылка save Сохранить extension Виджет

Метод Гаусса

Метод был назван в честь гениального немецкого математика XIX века Карла Фридриха Гаусса. Сам Гаусс не был первооткрывателем метода (метод был известен и ранее (еще в I-II веке до н.

 э. метод упоминался в китайском труде «Математика в девяти книгах»).

Приведение матрицы к ступенчатому виду

На первом шаге решения системы уравнений методом Гаусса матрица коэффициентов и свободных членов приводится к ступенчатому виду:

Матрица превращается в ступенчатую форму путем элементарных преобразований — перемена строк местами, умножение строки на коэффициент, сложение строк.
В нашем калькуляторе для перехода к ступенчатому виду осуществляется последовательное вычитание из нижних строк матрицы, помноженных на , верхних строк , помноженных на коэффициент , где i — индекс текущей строки (индекс строки, которую вычитают из нижних строк).
При осуществлении этой операции требуется, чтобы коэффициент главной переменной был не нулевым. В случае нулевого коэффициента, строка меняется местами с любой другой нижней строкой, в которой в текущем столбце значение отлично от нуля.

Выражение базисных переменных

Получив ступенчатую матрицу, мы переходим к выражению базисных переменных, для этого сначала выполняется деление текущей строки на коэффициент , затем производится обратное вычитание из верхних строк , этой строки , помноженных на коэффициент , где j — индекс текущей строки (индекс строки, которую вычитают из верхних строк).

Операция повторяется с каждой строкой, начиная от n-й до 1-й.
В результате матрица приобретает диагональный вид:
,
далее, поделив строки матрицы на коэффициент , в столбце свободных членов получаем вектор решений системы уравнений.

Решение СЛАУ методом Гаусса — презентация онлайн

1. Решение СЛАУ методом Гаусса Тема урока

2. Иоганн Карл Фридрих Гаусс (30 апреля 1777, Брауншвейг — 23 февраля 1855, Гёттинген)

Имя Гаусса известно почти во всех областях
математики, а также в геодезии, астрономии,
механике. За глубину и оригинальность мысли, за
требовательность к себе и гениальность ученый и
получил звание «король математиков».
Метод решения системных уравнений, открытый
ученым, был назван методом Гаусса. Метод
состоит в последовательном исключении
переменных до приведения уравнения к
ступенчатому виду. Решение методом Гаусса
считается классическим и активно используется и
сейчас.
Память о Гауссе навсегда осталась в
математических и физических терминах (метод
Гаусса, дискриминанты Гаусса, прямая Гаусса,
Гаусс – единица измерения магнитной индукции
и др. ). Имя Гаусса носит лунный кратер, вулкан в
Антарктиде и малая планета.

3. Метод Гаусса

Метод Гаусса — классический метод решения системы
линейных алгебраических уравнений (СЛАУ).
Это метод последовательного исключения переменных,
когда с помощью элементарных преобразований система
уравнений приводится к равносильной системе
ступенчатого (или треугольного) вида, из которого
последовательно, начиная с последних (по номеру)
переменных, находятся все остальные переменные.

4. Пример. Решить СЛАУ методом Гаусса:

Запишем расширенную матрицу системы, составленную из
коэффициентов системы и свободных слагаемых.

5. С помощью элементарных преобразований сведем расширенную матрицу к подобной матрице ступенчатого вида:

6. Получаем систему линейных уравнений, эквивалентную исходной системе уравнений.

Ответ:

7. Ощутим свежее дыхание моря…

9. Самостоятельная работа

1 вариант
Решить СЛАУ
методом Гаусса:
2 вариант
Решить СЛАУ
методом Гаусса:

10.

Домашнее заданиеРешить СЛАУ:

11. Итоги урока

̶ анализ ответов;
̶ оценка результатов работы.

Матричный метод онлайн калькулятор с подробным решением. Матричный метод онлайн

Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, — так называемые системы крамеровского типа :

a 11 x 1 + a 12 x 2 +… + a 1n x n = b 1 ,

a 21 x 1 + a 22 x 2 +… + a 2n x n = b 2 , (5.3)

… … … … … …

a n1 x 1 + a n1 x 2 +… + a nn x n = b n .

Системы (5.3) решаются одним из следующих способов: 1) методом Гаусса, или методом исключения неизвестных; 2) по формулам Крамера; 3) матричным методом.

Пример 2.12 . Исследовать систему уравнений и решить ее, если она совместна:

5x 1 — x 2 + 2x 3 + x 4 = 7,

2x 1 + x 2 + 4x 3 — 2x 4 = 1,

x 1 — 3x 2 — 6x 3 + 5x 4 = 0.

Решение. Выписываем расширенную матрицу системы:

 .

Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу = 7  0; содержащие его миноры третьего порядка равны нулю:

Следовательно, ранг основной матрицы системы равен 2, т.е. r(A) = 2. Для вычисления ранга расширенной матрицы A рассмотрим окаймляющий минор

значит, ранг расширенной матрицы r(A) = 3. Поскольку r(A)  r(A), то система несовместна.

Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица — таблица элементов. О такой таблице, где m строк и n столбцов, говорят, что это матрица имеет размерность m на n .

Общий вид матрицы:

Для решения матриц необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:

• Главная диагональ, состоящая из элементов а 11 ,а 22 …..а mn .
• Побочная диагональ, состоящая из элементов а 1n ,а 2n-1 …. .а m1 .

Основные виды матриц:

• Квадратная — такая матрица, где число строк = числу столбцов (m=n ).
• Нулевая — где все элементы матрицы = 0.
• Транспонированная матрица — матрица В , которая была получена из исходной матрицы A путем замены строк на столбцы.
• Единичная — все элементы главной диагонали = 1, все остальные = 0.
• Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.

Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 , то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.

Методы решения матриц.

Почти все методы решения матрицы заключаются в нахождении ее определителя n -го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.

Нахождение определителей 2-го порядка.

Для вычисления определителя матрицы А 2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:

Методы нахождения определителей 3го порядка.

Ниже приведены правила для нахождения определителя 3го порядка.

Упрощенно правило треугольника, как одного из методов решения матриц , можно изобразить таким образом:

Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «+»; так же, для 2го определителя — соответствующие произведения берутся со знаком «-«, то есть по такой схеме:

При решении матриц правилом Саррюса , справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком «+»; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком «-«:

Разложение определителя по строке или столбцу при решении матриц.

Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.

Приведение определителя к треугольному виду при решении матриц.

При решении матриц методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.

Теорема Лапласа при решении матриц.

Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ — это определитель n -го порядка. Выбираем в нем любые k строк (либо столбцов), при условии k ≤ n — 1 . В таком случае сумма произведений всех миноров k -го порядка, содержащихся в выбранных k строках (столбцах), на их алгебраические дополнения будет равна определителю.

Решение обратной матрицы.

Последовательность действий для решения обратной матрицы :

1. Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
2. Вычисляем алгебраические дополнения.
3. Составляем союзную (взаимную, присоединённую) матрицу C .
4. Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
5. Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.

Решение систем матриц.

Для решения систем матриц наиболее часто используют метод Гаусса.

Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т. е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.

Метод Гаусса является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.

Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный — метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.

Матричный метод решения СЛАУ применяют к решению систем уравнений, у которых количество уравнений соответствует количеству неизвестных. Метод лучше применять для решения систем низкого порядка. Матричный метод решения систем линейных уравнений основывается на применении свойств умножения матриц.

Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.

Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:

Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):

Значит, её легко перевести в матричную форму:

AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.

Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A .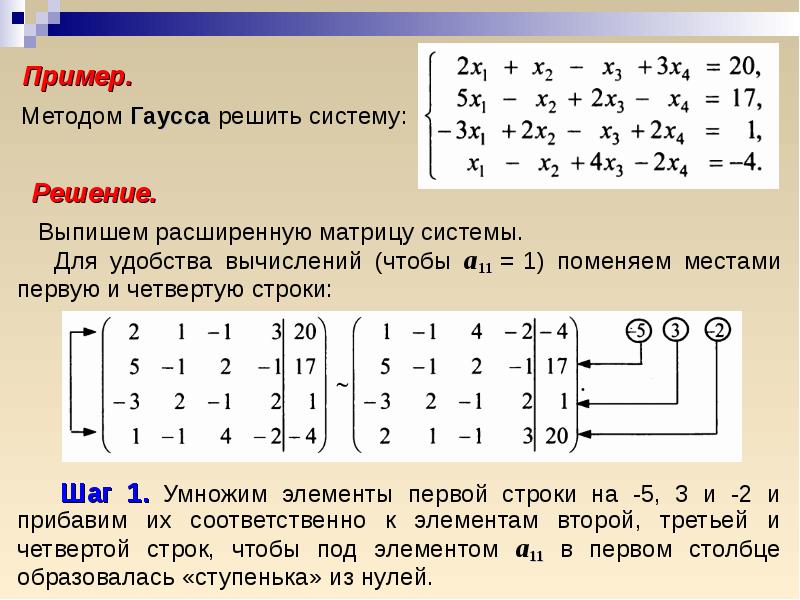 Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :

detA≠0.

Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т.е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.

Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы A −1 .

Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.

Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.

Пример решения неоднородной СЛАУ.

Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.

Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.

Подставляем переменные в формулу:

Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.

Итак, x=2; y=1; z=4.

При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :

НЕЛЬЗЯ записать как:

Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:

Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :

в матричной форме записываем так:

Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю. Когда в системе более 3-х уравнений, на нахождение обратной матрицы потребуется больше вычислительных усилий, поэтому, в этом случае целесообразно использовать для решения метод Гаусса.

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

×

Предупреждение

Очистить все ячейки?

Закрыть Очистить

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

Учитывая определение обратной матрицы, имеем A −1 A =E , где E — единичная матрица. Следовательно (4) можно записать так:

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b .

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

Матричный вид записи системы линейных уравнений: Ax=b , где

Вычислим все алгебраические дополнения матрицы A :

,

,

,

,

,

,

,

,

.

Обратная матрица вычисляется из следующего выражения.

Решение уравнений методом Гаусса | matematicus.ru

С помощью метода Гаусса можно решить любую систему линейных уравнений с различным числом уравнений и неизвестных переменных. И именно этим свойством этот метод превосходит матричный метод и метод Крамера.

Суть метода состоит в приведении системы линейных уравнений к ступенчатому (треугольному) виду за счет последовательного исключения неизвестных. Затем её решения с помощью обратной подстановки.

---

Допустимые преобразования матрицы:

1. Перестановка местами двух строк или двух столбцов;
2. Умножение строки на число, которое не равно 0;
3. Прибавление одной строки к другой.
4. Исключение или добавление нулевой строки

---

Допустим, дана система линейных алгебраических уравнений с четырьмя уравнениями и четырьмя неизвестными.

Составим расширенную матрицу СЛАУ:

Затем первое уравнение СЛАУ делим на a₁₁.  При этом a₁₁≠0, если равно нуля, то переставляем две строки или два столбца местами так, чтобы избавится от нуля. После полученное уравнение умножаем на a₂₁ и вычитаем из второго уравнения, дальше, умножаем на a₃₁ и вычитаем из третьего уравнения и т. д.

Также поступаем и с оставшемся уравнениями, т.е. со вторым, третьем и четвёртым. В итоге должна получится матрица ступенчатого или треугольного вида.

Система уравнений примет вид

Такую систему элементарно решить обратным ходом, т.е. последовательным решением уравнений от нижнего к верхнему.

Рассмотрим наиболее подробно метод Гаусса при решении СЛАУ на практике.

Пример 1

Решить методом Гаусса систему уравнений

Решение

Составим расширенную матрицу системы уравнений:

Первую строку разделим на a₁₁, но так как в этой строке a₁₁=0, то необходимо поменять строку у которой первый элемент не равен нулю. Выберем по модулю наибольшей элемент, это a₄₁=2 Поэтому поменяем первую и четвёртую строки местами.

Получаем:

Первую строку разделим на a₁₁=2. Получим матрицу:

Умножаем элементы первой строки на -1 и прибавляем к элементам второй строк. Получим матрицу:

Умножаем элементы первой строки на -1 и прибавляем к элементам третьей строки.

Четвёртую строку оставляем без изменений, так как её первый элемент равен нулю.

Теперь первый столбец не трогаем.

Начинаем повторять действия, которые применяли ранее.

Второе уравнение разделим на a₂₂=-1/2, тогда

Умножаем элементы второй строки на -1/2 и прибавляем к элементам третьей строки.

Умножаем элементы второй строки на -1 и прибавляем к элементам четвёртой строки.

Первый и второй столбец не трогаем.

Третьей столбец разделим на 2.

Умножаем элементы третьей строки на -1 и прибавляем к элементам четвёртой строки.

Получаем ступенчатую систему алгебраических уравнений:

Отсюда, решая систему снизу вверх, получаем корни системы уравнений

---

Приведём простой пример краткой записи решения СЛАУ методом Гаусса

Пример 2

Решить систему линейных уравнений с тремя неизвестными методом Гаусса.

Решение

Составим расширенную матрицу системы линейных уравнений .

Следовательно, искомая система может быть представлена в ступенчатом виде:

Решая последовательно уравнение, получаем:

Ответ: z = 3; y = 2; x = 1

Численные методы: решение систем линейных уравнений

В прикладных задачах часто возникает необходимость решать системы линейных уравнений.

Система линейных алгебраических уравнений с n неизвестными  —  это система уравнений вида

                                     (1)

Слово система означает, что все уравнения рассматриваются как одно целое.

В общем случае у нас имеется m — уравнений, n — количество неизвестных. x₁, x₂,…, x_n — неизвестные, которые следует определить.

В системе (1)  – фиксированные коэффициенты,  b₁, b₂, …, b_m — свободные члены — предполагаются известными.

Система (1) называется однородной, если все её свободные члены равны нулю (b₁ = b₂ = … = b_m = 0), иначе — неоднородной.

Система (1) называется квадратной, если число m уравнений равно числу n неизвестных.

Задача состоит в том, чтобы найти такие  которые удовлетворяют всем уравнениям (1).

В частном случае мы имеем одно линейное уравнение:

Конечно, такое уравнение легко решить, если предположить, что коэффициент  не равен 0, имеем:  = .

Очевидно, в общем случае имеются 3 варианта решений: система имеет ни одного решения, имеет одно решение, более одного решения.

Система (1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если нет ни одного решения.

Система линейных уравнений может быть представлена в матричной форме как:

или:

Ax = b

Здесь A — это матрица системы, x — столбец неизвестных, а b — столбец свободных членов.

Если к матрице A приписать справа столбец свободных членов, то получившаяся матрица называется расширенной.

Рассмотрим, например, систему вида и поймем, как найти ее решение:

                                      (2)

Предположим на минуту, что в первом уравнении y отсутствует, а во втором отсутствует x, тогда мы имели бы решение именно то решение, которое нам нужно.

Вопрос: как исходную систему привести к такому виду и можно ли это сделать.

Заметим, что с тождествами мы можем делать следующие вещи: домножать на одно и то же число, отличное от 0, складывать, вычитать и тд, это похоже с тем, что вы раскладываете монеты по своим карманам, не меняя общей суммы.

От этих операций тождество не меняется.

В системе (2) у нас два тождества, домножим второе тождество на 2 и вычтем из первого, получим:

                                      (3)

Формально у нас есть еще старое тождество , но оно нам не понадобится (подумайте, почему).

Система (3) точно такая же, как система (2).

Из второго уравнения системы (3) сразу получим:

 

Никто не мешает нам подставить это значение в первое уравнение:

Отсюда сразу находим, что

Итак, путем простых действий мы нашли, что система (2) может быть представлена в виде:

Именно такие естественные соображения приводят к общему методу решения систем линейных уравнений, известному как метод исключения или метод Гаусса.

Метод Гаусса является одним из самых распространенных прямых методов решения систем линейных уравнений Ax = b:

Опишем этот метод в общем случае.

Вначале исходная система приводится к верхнетреугольному виду.

Это достигается следующей последовательностью преобразований (прямой ход).

Будем считать для удобства, что элемент a_ij исходной матрицы и компоненты вектора b_i есть, соответственно, элементы a_ij ⁽¹⁾ первого шага преобразованной матрицы A₁ и преобразованного вектора b₁:A = A₁, b=b₁. 

Далее, на втором шаге прибавим к второй строке первую, умноженную на  

Аналогично поступим со всеми оставшимися строками, т.е. прибавим к каждой i-ой строке i=2,3,…,N, первую, умноженную на коэффициент  

При этом соответственно изменится и вектор b1.  

Таким образом, 2 шаг.

Имеем систему уравнений A₂x = b₂:

где

3 шаг.

Прибавим к новой третьей строке новую вторую, умноженную на  

То же самое сделаем с остальными строками 4,5,…,N, т.е. прибавим к i-ой строке вторую, умноженную на  

При этом получим систему A₃x = b₃:

(k+1)-ый шаг:

Здесь

Поступая так и далее, на шаге N-1 получаем верхнетреугольную систему:

При этом, мы также получили матрицу C переводных коэффициентов, имеющую вид:

Решение полученной треугольной системы  как легко видеть, имеет вид (обратный ход метода Гаусса):

Заметим, что при прямом ходе метода Гаусса может возникнуть ситуация, когда происходит деление на нуль, да и вообще, желательно не делить на малое число, чтобы не накапливалась ошибка.

Поэтому метод Гаусса обычно проводят с частичным выбором главного элемента, то есть после каждого шага (пусть это был k-й шаг) переставляют строки с номерами k,k+1,…,N таким образом, чтобы на месте kk оказался элемент  наибольший из всех в k-ом столбце при m>k (при этом, естественно, переставляются и компоненты вектора b).

Можно для максимальной точности переставлять также и столбцы преобразуемой матрицы, чтобы на месте kk оказался максимальный элемент из всех с индексами больше, либо равными k.

Эта процедура называется методом Гаусса с выбором главного элемента. Она несколько повышает точность по сравнению с частичным выбором главного элемента, но весьма неудобна, в том числе для программирования, поскольку при перестановке строк компоненты искомого вектора x переставлять не надо, тогда как при перестановке столбцов надо переставлять и соответствующие компоненты вектора x.

Опишем обратный ход метода Гаусса в несколько иной форме (треугольное разложение).

Введем матрицы M_k по правилу:

На каждом шаге метода Гаусса получается некоторая промежуточная матрица: 

 и вектор  

Нетрудно видеть, что

Вопрос. Почему

Если производить также выбор главных элементов, то необходимо использовать оператор P перестановки индексов l и m, матричные элементы которого равны:

При применении оператора перестановки индексов к матрице слева, меняются местами строки матрицы и компоненты свободного вектора (PAx = Pb), если же его применить справа к матрице, то меняются местами ее столбцы и компоненты решения

Существует большой класс так называемых итерационных методов решения систем уравнений, аналогичных итерационным методам нахождения корней нелинейных уравнений.

Итерационные методы последовательно уточняют решение, отправляясь от начального приближения.

При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций.

Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений.

Идея состоит в том, чтобы найти неподвижную точку матричного уравнения

                                     (5)

эквивалентного начальной системе линейных алгебраических уравнений.

При итерации  в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

.

Термин неподвижная точка становится ясен, если вы внимательно посмотрите на уравнение (5), по самому своему смыслу величина Х является неподвижной точкой.

Более подробное описание методов решения систем линейных уравнений можно найти в специальной литературе, наша задача дать обзор методов и основные идеи решения такого рода задач.

Обусловленность линейных систем, погрешность

При решении абстрактной задачи Ax = b, где A — оператор произвольной природы, важным моментом является корректность ее постановки.

Задача считается корректной, если решение существует и единственно и , кроме того, решение непрерывно зависит от данных (то есть, при  также стремится к нулю).

Однако и непрерывная зависимость от входных данных может иметь свои нюансы.

Чем меньшее (большее) изменение решения вызывает вариация входных данных, тем более хорошо (плохо) обусловленной считается задача.

Понятие обусловленности является тем более существенным для численных методов, поскольку на практике входные данные известны, как правило, с некоторой погрешностью.

Кроме того, существуют ошибки округления, возникающие при вычислениях.

Таким образом, формально корректная задача, являясь плохо обусловленной, может оказаться разрешимой столь неточно, что в этом будет отсутствовать практический смысл.

Чем можно охарактеризовать количественно обусловленность для линейных систем?

Пусть A — квадратная NxN — матрица.

Рассмотрим задачу Ax = b.

Пусть также  некоторая норма в пространстве R_N 

Норма оператора A определяется стандартно:

Обозначим y = Ax и введем число m по правилу:

Величина  называется числом обусловленности.

Очевидно:

2.      
3. если A — диагональная, то  (Для какой нормы, или для всех вышеприведенных?). Чем меньше число обусловленности C(A), тем лучше обусловлена система. Действительно, пусть  вариация правой части, а соответствующее изменение решения.

Тогда справедливо следующее неравенство:

 

Доказательство. Имеем:

Так как

то    

Аналогично, поскольку  

Объединяя два неравенства, окончательно получаем для оценки погрешности:

 

В начало

Содержание портала

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b - c = 6
a - b + c = 4
2*a - 3*b - 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

A=[4  1 -1; 1 -1  1; 2 -3 -3];   % коэффициенты
B=[6; 4; 4];

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

det(A)

Вывод: 30

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv.
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

x=inv(A)*B

Вывод:
2
-1
1

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1. Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) - левое деление.
При следующей записи:

x = A\B

Вывод:
2
-1
1

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

• разложение Холецкого
• LU разложение
• QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR — возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

[L, U] = lu(A);

Вывод:

L =
    1       0     0
    0.25    1     0
    0.5     2.8   1

U =
    4     1     -1
    0    -1.25   1.25
    0     0     -5

Затем:

y = L\B;
x = U\y

Вывод:

2
-1
1

QR разложение

И через QR разложение соответственно:

[Q, R] = qr(A);
x = R\(Q'*B)

Вывод:

2.0000
-1.0000
1.0000

Отметим, что апостроф (  '  ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve, с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

x = linsolve(A,B)

Вывод:

2
-1
1

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a - b - c = 0
a - 2*b + 3*d = 0
3*a - 4*b - 4*c = -1

A=[6 -1 -1; 1 -2 3; 3 -4 -4];
B=[0; 0; -1];

• Методом обратной матрицы:

x=inv(A)*B

Вывод:
    0.0476
    0.1810
    0.1048

Методом Гаусса:

x = A\B

Вывод:
    0.0476
    0.1810
    0.1048

LU разложение:

[L, U] = lu(A);
y = L\B;
x = U\y

Вывод:
    0. 0476
    0.1810
    0.1048

QR разложение:

[Q, R] = qr(A);
x = R\(Q'*B)

Вывод:
    0.0476
    0.1810
    0.1048

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Поделиться ссылкой:

Похожее

Решение уравнений в Excel методом итераций Крамера и Гаусса

В программе Excel имеется обширный инструментарий для решения различных видов уравнений разными методами.

Рассмотрим на примерах некоторые варианты решений.

Решение уравнений методом подбора параметров Excel

Инструмент «Подбор параметра» применяется в ситуации, когда известен результат, но неизвестны аргументы. Excel подбирает значения до тех пор, пока вычисление не даст нужный итог.

Путь к команде: «Данные» — «Работа с данными» — «Анализ «что-если»» — «Подбор параметра».

Рассмотрим на примере решение квадратного уравнения х² + 3х + 2 = 0. Порядок нахождения корня средствами Excel:

1. Введем в ячейку В2 формулу для нахождения значения функции. В качестве аргумента применим ссылку на ячейку В1.
2. Открываем меню инструмента «Подбор параметра». В графе «Установить в ячейку» — ссылка на ячейку В2, где находится формула. В поле «Значение» вводим 0. Это то значение, которое нужно получить. В графе «Изменяя значение ячейки» — В1. Здесь должен отобразиться отобранный параметр.
3. После нажатия ОК отобразится результат подбора. Если нужно его сохранить, вновь нажимаем ОК. В противном случае – «Отмена».

Для подбора параметра программа использует циклический процесс. Чтобы изменить число итераций и погрешность, нужно зайти в параметры Excel. На вкладке «Формулы» установить предельное количество итераций, относительную погрешность. Поставить галочку «включить итеративные вычисления».



Как решить систему уравнений матричным методом в Excel

Дана система уравнений:

1. Значения элементов введем в ячейки Excel в виде таблицы.
2. Найдем обратную матрицу. Выделим диапазон, куда впоследствии будут помещены элементы матрицы (ориентируемся на количество строк и столбцов в исходной матрице). Открываем список функций (fx). В категории «Математические» находим МОБР. Аргумент – массив ячеек с элементами исходной матрицы.
3. Нажимаем ОК – в левом верхнем углу диапазона появляется значение. Последовательно жмем кнопку F2 и сочетание клавиш Ctrl + Shift + Enter.
4. Умножим обратную матрицу Ах^-1х на матрицу В (именно в таком порядке следования множителей!). Выделяем диапазон, где впоследствии появятся элементы результирующей матрицы (ориентируемся на число строк и столбцов матрицы В). Открываем диалоговое окно математической функции МУМНОЖ. Первый диапазон – обратная матрица. Второй – матрица В.
5. Закрываем окно с аргументами функции нажатием кнопки ОК. Последовательно нажимаем кнопку F2 и комбинацию Ctrl + Shift + Enter.

Получены корни уравнений.

Решение системы уравнений методом Крамера в Excel

Возьмем систему уравнений из предыдущего примера:

Для их решения методом Крамера вычислим определители матриц, полученных заменой одного столбца в матрице А на столбец-матрицу В.

Для расчета определителей используем функцию МОПРЕД. Аргумент – диапазон с соответствующей матрицей.

Рассчитаем также определитель матрицы А (массив – диапазон матрицы А).

Определитель системы больше 0 – решение можно найти по формуле Крамера (D_x / |A|).

Для расчета Х₁: =U2/$U$1, где U2 – D1. Для расчета Х₂: =U3/$U$1. И т.д. Получим корни уравнений:

Решение систем уравнений методом Гаусса в Excel

Для примера возьмем простейшую систему уравнений:

3а + 2в – 5с = -1
2а – в – 3с = 13
а + 2в – с = 9

Коэффициенты запишем в матрицу А. Свободные члены – в матрицу В.

Для наглядности свободные члены выделим заливкой. Если в первой ячейке матрицы А оказался 0, нужно поменять местами строки, чтобы здесь оказалось отличное от 0 значение.

1. Приведем все коэффициенты при а к 0. Кроме первого уравнения. Скопируем значения в первой строке двух матриц в ячейки В6:Е6. В ячейку В7 введем формулу: =B3:Е3-$B$2:$Е$2*(B3/$B$2). Выделим диапазон В7:Е7. Нажмем F2 и сочетание клавиш Ctrl + Shift + Enter. Мы отняли от второй строки первую, умноженную на отношение первых элементов второго и первого уравнения.
2. Копируем введенную формулу на 8 и 9 строки. Так мы избавились от коэффициентов перед а. Сохранили только первое уравнение.
3. Приведем к 0 коэффициенты перед в в третьем и четвертом уравнении. Копируем строки 6 и 7 (только значения). Переносим их ниже, в строки 10 и 11. Эти данные должны остаться неизменными. В ячейку В12 вводим формулу массива.
4. Прямую прогонку по методу Гаусса сделали. В обратном порядке начнем прогонять с последней строки полученной матрицы. Все элементы данной строки нужно разделить на коэффициент при с. Введем в строку формулу массива: {=B12:E12/D12}.
5. В строке 15: отнимем от второй строки третью, умноженную на коэффициент при с второй строки ({=(B11:E11-B16:E16*D11)/C11}). В строке 14: от первой строки отнимаем вторую и третью, умноженные на соответствующие коэффициенты ({=(B10:E10-B15:E15*C10-B16:E16*D10)/B10}). В последнем столбце новой матрицы получаем корни уравнения.

Примеры решения уравнений методом итераций в Excel

Вычисления в книге должны быть настроены следующим образом:

Делается это на вкладке «Формулы» в «Параметрах Excel». Найдем корень уравнения х – х³ + 1 = 0 (а = 1, b = 2) методом итерации с применением циклических ссылок. Формула:

Х_n+1 = X_n– F (X_n) / M, n = 0, 1, 2, … .

M – максимальное значение производной по модулю. Чтобы найти М, произведем вычисления:

f’ (1) = -2 * f’ (2) = -11.

Полученное значение меньше 0. Поэтому функция будет с противоположным знаком: f (х) = -х + х³ – 1. М = 11.

В ячейку А3 введем значение: а = 1. Точность – три знака после запятой. Для расчета текущего значения х в соседнюю ячейку (В3) введем формулу: =ЕСЛИ(B3=0;A3;B3-(-B3+СТЕПЕНЬ(B3;3)-1/11)).

В ячейке С3 проконтролируем значение f (x): с помощью формулы =B3-СТЕПЕНЬ(B3;3)+1.

Корень уравнения – 1,179. Введем в ячейку А3 значение 2. Получим тот же результат:

Скачать решения уравнений в Excel

Корень на заданном промежутке один.

Калькулятор метода исключения Гаусса

— Онлайн-программа для сокращения строк

Поиск инструмента

Исключение по Гауссу

Инструмент для применения метода исключения Гаусса и получения формы сокращенного эшелона строки с шагами, деталями, обратной матрицей и векторным решением.

Результаты

Исключение Гаусса — dCode

Тег (и): Матрица, символьное вычисление

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Рекламные объявления

Калькулятор исключения по Гауссу

Преобразователь системы уравнений в матрицу

Ответы на вопросы (FAQ)

Что такое метод исключения Гаусса?

Алгоритм исключения Гаусса (также называемый методом Гаусса-Жордана или методом поворота) позволяет находить решения системы линейных уравнений и определять обратную матрицу.

Алгоритм работает со строками матрицы путем обмена или умножения строк между ними (с точностью до множителя).

На каждом шаге алгоритм стремится ввести в матрицу на элементах за пределами диагонали нулевые значения.

Как вычислить решения системы линейных уравнений с Гауссом?

Первым шагом из системы линейных уравнений является преобразование уравнений в матрицу.

Пример: $$ \ left \ {\ begin {array} {} x & — & y & + & 2z & = & 5 \\ 3x & + & 2y & + & z & = & 10 \\ 2x & — & 3y & — & 2z & = & — 10 \\\ end {массив} \ право.$$ можно записать в форме умножения «> матричного умножения: $$ \ left (\ begin {array} {ccc} 1 & -1 & 2 \\ 3 & 2 & 1 \\ 2 & -3 & 2 \ end { array} \ right). \ left (\ begin {array} {c} x \\ y \\ z \ end {array} \ right) = \ left (\ begin {array} {c} 5 \\ 10 \\ -10 \ end {array} \ right) $$, который соответствует (расширенной) матрице $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 3 & 2 & 1 & 10 \\ 2 & -3 & 2 & -10 \ end {array} \ right) $$

Затем для каждого элемента за пределами ненулевой диагонали выполните соответствующие вычисления, добавив или вычтя другие строки, чтобы элемент стал 0.

Пример: Вычтите 3 раза (строка 1) из (строка 2), например, элемент в строке 2, столбец 1 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 2 & -3 & -2 & -10 \ end {array} \ right) $$
Вычтите 2 раза (строка 1) до (строка 3) например, элемент в строке 3, столбец 1 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & -1 & -6 & -20 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из ​​(строка 3), например, элемент в строке 3, столбец 2 станет 0: $$ \ слева (\ begin {array} {ccc | c} 1 & -1 & 2 & 5 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 1/5 раз (строка 2) из ​​(строка 1), например, элемент в строке 1, столбец 2 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 1 & 4 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Отнимите 1/7 раз (строка 3) до (строка 1), например как элемент в строке 1, столбец 3 становится 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & -5 & -5 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$
Вычтите 5/7 раз (строка 3) из (строка 2), например, элемент в строке 2, столбец 3 станет 0: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 5 & 0 & 10 \\ 0 & 0 & -7 & -21 \ end {array} \ right) $$

Упростите каждую строку, разделив значение по диагонали.

Пример: $$ \ left (\ begin {array} {ccc | c} 1 & 0 & 0 & 1 \\ 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 3 \ end {array } \ right) $$

Результирующий вектор — это последний столбец.

Пример: $ {1,2,3} $, что соответствует $ {x, y, z} $, поэтому $ x = 1, y = 2, z = 3 $

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Исключение Гаусса». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любой алгоритм, апплет или фрагмент алгоритма исключения Гаусса (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой алгоритм исключения Гаусса ‘функция (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Исключения Гаусса» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

исключение, точка поворота, гаусс, иордания, матрица, система, уравнение

Ссылки

Источник: https: // www.dcode.fr/gaussian-elimination

© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.

Калькулятор исключения Гаусса

Как найти неизвестные переменные в уравнениях методом исключения Гаусса?

Исключение Гаусса или сокращение строки , это алгоритм решения системы линейных уравнений. Этот метод также называется исключением Гаусса-Жордана. Он представлен последовательностью операций, выполняемых над матрицей.Метод назван в честь Карла Фридриха Гаусса (1777-1855), хотя был известен китайским математикам. Метод решения системы линейных уравнений методом исключения Гаусса аналогичен методу решения матриц. Например, существует связь между системой трех линейных уравнений и ее матрицей коэффициентов. $$ \ begin {align} & a_1x + b_1y + c_1z = {d_1} \\ & a_2x + b_2y + c_2z = {d_2} \\ & a_3x + b_3y + c_3z = {d_3} \\ \ end {align} \ quad \ longmapsto \ left ( \ begin {array} {ccc} {a_1} & b_1 & c_1 \\ {a_2} & b_2 & c_2 \\ {a_3} & b_3 & c_3 \\ \ end {массив} \ right) $$ Есть три типа операций с элементарными строками:

• Замена двух рядов;
• Умножение строки на ненулевое число;
• Добавление числа, кратного одной строке, к другой строке.

Метод исключения Гаусса состоит из двух частей. Первая часть сводит данную систему к \ underline {форме эшелона строк}. Из формы эшелона строк мы можем сделать вывод, что у системы нет решений, единственное решение или бесконечно много решений. Вторая часть использует операции со строками, пока не будет найдено решение. Форма ступенчатого эшелона удовлетворяет следующим свойствам:

• Старший коэффициент каждой строки должен быть 1 $;
• Все элементы в столбце ниже $ 1 $ должны быть $ 0 $;
• Все строки, содержащие нули, находятся внизу матрицы.

Например, следующие матрицы представлены в виде эшелона строк $$ \ left ( \ begin {array} {cc} 1 и 5 \\ 0 и 1 \\ \ end {массив} \ справа), \ quad \ left ( \ begin {array} {cccc} 1 и 1 и 0 и 5 \\ 0 и 1, 3 и 4 \\ 0 & 0 & 1 & 2 \\ \ end {массив} \ вправо), \ квад \ влево ( \ begin {array} {cccc} 1 и 2 и 3 и 4 \\ 0 и 1, 3 и 4 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \\ \ end {массив} \ right) $$ Матрица находится в виде сокращенного эшелона строк , если, кроме того, в каждом столбце, содержащем ведущий коэффициент, все другие записи в этом столбце равны нулю.Например, матрицы, показанные ниже, являются примерами матриц в сокращенной форме эшелона строк. $$ \ left ( \ begin {array} {cc} 1 & 0 \\ 0 и 1 \\ \ end {массив} \ вправо), \ квад \ влево ( \ begin {array} {cccc} 1 & 0 & 0 & 7 \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ \ end {массив} \ вправо), \ квад \ влево ( \ begin {array} {cccc} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \\ \ end {массив} \ right) $$ Расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц.В случае решения системы нам необходимо увеличить матрицу коэффициентов и постоянную матрицу. Вертикальная линия показывает разделение между матрицей коэффициентов и постоянной матрицей. Итак, для системы трех уравнений $$ \ begin {align} & a_1x + b_1y + c_1z = {d_1} \\ & a_2x + b_2y + c_2z = {d_2} \\ & a_3x + b_3y + c_3z = {d_3} \\ \ end {align} $$ расширенная матрица $$ \ left ( \ begin {array} {ccc | c} a_1 & b_1 & c_1 & d_1 \\ a_2 & b_2 & c_2 & d_2 \\ a_3 & b_3 & c_3 & d_3 \\ \ end {массив} \ right) $$ Количество решений системы зависит только от ранга матрицы, представляющей систему, и ранга соответствующей расширенной матрицы.На основании теоремы Кронекера-Капелли любая система из трех линейных уравнений не имеет решений, если ранг расширенной матрицы больше ранга матрицы коэффициентов. Если ранги этих двух матриц равны, система должна иметь хотя бы одно решение. Решение уникально тогда и только тогда, когда ранг равен количеству переменных, в данном случае, если ранг равен 3 $. Например, решим решение системы методом исключения Гаусса $$ \ begin {align} & 4x + 5y + 3z = {10} \\ & 3x + 6y + 7z = {8} \\ & 2x + 3y + 0z = {8} \\ \ end {align} $$ Коэффициенты и постоянные члены системы дают матрицы $$ \ left ( \ begin {array} {ccc} 4 и 5 и 3 \\ 3 и 6 и 7 \\ 2 и 3 и 0 \\ \ end {массив} \ вправо), \ квад \ влево ( \ begin {array} {c} 10 \\ 8 \\ 8 \\ \ end {массив} \ right) $$ Расширенная матрица $$ \ left ( \ begin {array} {ccc | c} 4 и 5 и 3 и 10 \\ 3 и 6 и 7 и 8 \\ 2 и 3 и 0 и 8 \\ \ end {массив} \ right) $$ Чтобы решить систему, приведите расширенную матрицу к сокращенной форме эшелона строк следующим образом.

• Разделите строку $ 1 $ на $ 4 $ ($ R_1 = \ frac {R_1} 4) $, чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 3 и 6 и 7 и 8 \\ 2 и 3 и 0 и 8 \\ \ end {массив} \ right) $$
• Вычтите строку $ 1 $, умноженную на $ 3 $, из строки $ 2 $ ($ R_2 = R_2-3R_1 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 2 и 3 и 0 и 8 \\ \ end {массив} \ справа) $$
• Вычтите строку $ 1 $, умноженную на $ 2 $, из строки $ 3 $ ($ R_3 = R_3-2R_1 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & \ frac 94 & \ frac {19} 4 & \ frac 12 \\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ end {массив} \ справа) $$
• Умножьте строку $ 2 $ на $ \ frac 49 $ ($ R_2 = \ frac49 R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & \ frac 54 & \ frac 34 & \ frac {5} 2 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ end {массив} \ справа) $$
• Вычтите строку $ 2 $, умноженную на $ \ frac 54 $, из строки $ 1 $ ($ R_1 = R_1- \ frac54 R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & \ frac12 & — \ frac 32 & 3 \\ \ end {массив} \ справа) $$
• Вычтите строку $ 2 $, умноженную на $ \ frac 12 $, из строки $ 3 $ ($ R_3 = R_3- \ frac12R_2 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & — \ frac {23} 9 & \ frac {26} 9 \\ \ end {массив} \ right) $$
• Умножьте строку $ 3 $ на $ — \ frac9 {23} $ ($ R_3 = — \ frac9 {23} R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & — \ frac {17} 9 & \ frac {20} 9 \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ end {массив} \ справа) $$
• Добавьте строку $ 3 $, умноженную на $ \ frac {17} 9 $, в строку $ 1 $ ($ R_1 = R_1 + \ frac {17} 9R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & \ frac {19} 9 & \ frac 29 \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ end {массив} \ справа) $$
• Вычтите строку $ 3 $, умноженную на $ \ frac {19} 9 $, из строки $ 2 $ ($ R_2 = R_2- \ frac {19} 9R_3 $), чтобы получить $$ \ left ( \ begin {array} {ccc | c} 1 & 0 & 0 & \ frac2 {23} \\ 0 & 1 & 0 & \ frac {60} {23} \\ 0 & 0 & 1 & — \ frac {26} {23} \\ \ end {массив} \ right) $$ Итак, решение системы: $ (x, y, z) = (\ frac {2} {23}, \ frac {60} {23}, — \ frac {26} {23}) $.

Работа исключения Гаусса с шагами показывает полное пошаговое вычисление для поиска решения линейной системы трех уравнений с использованием метода исключения Гаусса. Для любой другой системы просто введите двенадцать действительных чисел в качестве коэффициентов линейных уравнений и нажмите кнопку «Создать работу». Учащиеся начальной школы используют этот Калькулятор исключения Гаусса для создания работы, проверки результатов решения систем линейных уравнений, выведенных вручную, или для эффективного выполнения домашних заданий.Во многих приложениях необходимо вычислить исключение матрицы, где этот онлайн-калькулятор исключения матрицы Гаусса может помочь легко упростить вычисления для соответствующих входных данных.

M.7 Устранение Гаусса-Джордана | STAT ONLINE

Исключение Гаусса-Жордана — это алгоритм, который можно использовать для решения систем линейных уравнений и поиска обратной матрицы для любой обратимой матрицы. Он основан на трех операциях с элементарной строкой , которые можно использовать с матрицей:

1. Поменять местами две строки
2. Умножьте одну из строк на ненулевой скаляр.
3. Добавить или вычесть скалярное кратное одной строки из другой строки.

В качестве примера операции с первой элементарной строкой поменяйте местами 1-ю и 3-ю строки.

\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 7 & 5 & 0 \\ 2 & -2 & 3 \\ 4 & 0 & -1 \ end {pmatrix} \]

Для примера операции со второй элементарной строкой умножьте вторую строку на 3.

\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 6 & -6 & 9 \\ 7 & 5 & 0 \ end {pmatrix} \]

В качестве примера операции с третьей элементарной строкой добавьте дважды первую строку ко второй строке.

\ [\ begin {pmatrix} 4 & 0 & -1 \\ 2 & -2 & 3 \\ 7 & 5 & 0 \ end {pmatrix} \ Rightarrow \ begin {pmatrix} 4 & 0 & -1 \\ 10 & -2 & 1 \\ 7 & 5 & 0 \ end {pmatrix} \]

---

Редукторный эшелон

Цель метода исключения Гаусса-Жордана состоит в том, чтобы использовать три операции с элементарными строками для преобразования матрицы в эшелонированную форму сокращенных строк.Матрица находится в форме сокращенного эшелона строки , также известной как каноническая форма строки , если выполняются следующие условия:

1. Все строки с нулевыми записями находятся внизу матрицы
2. Первая ненулевая запись в строке, называемая ведущей записью или поворотной точкой каждой ненулевой строки, находится справа от ведущей записи строки над ней.
3. Начальная запись, также известная как точка поворота, в любой ненулевой строке равна 1.
4. Все остальные записи в столбце, содержащем начальную единицу, являются нулями.

Например,

\ [A = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 3 \\ 0 & 0 & 0 \ end {pmatrix}, B = \ begin {pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix}, C = \ begin {pmatrix} 0 & 7 & 3 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \ end {pmatrix}, D = \ begin {pmatrix} 1 & 7 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {pmatrix} \]

Матрицы A, и B находятся в виде эшелона с уменьшенной строкой, а матрицы C и D — нет. C не находится в форме пониженного ряда, поскольку нарушает условия два и три. D не находится в форме пониженного ряда, поскольку нарушает четвертое условие. Кроме того, операции с элементарными строками могут использоваться для уменьшения матрицы D в матрицу B .

---

Шаги для исключения Гаусса-Джордана

Для выполнения исключения Гаусса-Джордана:

1. Поменяйте местами строки так, чтобы все строки со всеми нулевыми записями находились внизу
2. Поменяйте местами строки так, чтобы строка с самой большой левой ненулевой записью была наверху.
3. Умножьте верхнюю строку на скаляр так, чтобы ведущая запись верхней строки стала 1.
4. Сложить / вычесть кратные числа верхней строки из других строк, чтобы все остальные записи в столбце, содержащем ведущую запись верхней строки, были равны нулю.
5. Повторите шаги 2–4 для следующей самой левой ненулевой записи, пока все ведущие записи не станут 1.
6. Поменяйте местами строки так, чтобы ведущая запись каждой ненулевой строки находилась справа от ведущей записи строки над ней.

Выбранные примеры видео показаны ниже:

Чтобы получить инверсию матрицы n × n A :

1. Создайте разделенную матрицу \ ((A | I) \), где I — единичная матрица.{-1} = I \).

Матрицы по гусеничным формулам. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера

В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почвенного сложения системы уравнений. Всем, кто заходил на сайт через эту страницу, рекомендуется ознакомиться с первой частью. Возможно, некоторым посетителям материал покажется слишком простым, но в процессе решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.

А теперь разберем правило краулера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы представлены просто, подробно и понятно, практически все читатели смогут узнать, как решать системы вышеуказанными методами.

Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? — Ведь простейшую систему можно решить школьным методом, методом убивающего сложения!

Дело в том, что даже если и бывает, то такая задача встречается — решить систему двух линейных уравнений с двумя неизвестными по формулам краулера.Во-вторых, более простой пример поможет понять, как использовать правило краулера для более сложного случая — системы трех уравнений с тремя неизвестными.

Кроме того, существуют системы линейных уравнений с двумя переменными, которые желательно решать именно по правилу Крамера!

Рассмотрим систему уравнений

На первом этапе вычисляем определитель, он называется главным определителем системы .

Метод Гаусса.

Если, система имеет одно решение, и для нахождения корней мы должны вычислить еще два детерминанта:
и

.

На практике вышеуказанные детерминанты также могут обозначаться латинскими буквами.

Корни уравнений находятся по формулам:
,

Пример 7.

Решите систему линейных уравнений

Решение : Видим, что коэффициенты уравнения достаточно большие, в правой части стоят десятичные дроби с запятой.Запятая — довольно редкий гость в практических задачах по математике, я взял эту систему из эконометрической задачи.

Как решить такую ​​систему? Можно попробовать выразить одну переменную через другую, но в этом случае обязательно получатся ужасные штаны, с которыми крайне неудобно работать, а оформление раствора будет смотреться просто ужасно. Вы можете умножить второе уравнение на 6 и выполнить вычитание почвы, но также получатся те же дроби.

Что делать? В таких случаях на помощь приходит формула кратера.

;

;

Ответ :,

Оба корня имеют бесконечные хвосты и находятся приблизительно, что вполне приемлемо (и даже обыкновенно) для задач эконометрики.

Комментарии здесь не нужны, так как задача решается по готовым формулам, однако есть один нюанс. При использовании этого метода обязательный фрагмент дизайна задачи представляет собой следующий фрагмент: «Итак, система имеет единое решение» .В противном случае рецензент может наказать вас за неуважение к теореме Крамера.

Вовсе не будет лишним, что удобно проводить на калькуляторе: в левую часть каждого уравнения системы подставляем приблизительные значения. В итоге с небольшой ошибкой должны быть вывернуты числа, которые находятся в нужных частях.

Пример 8.

Ответ представить в обыкновенные неправильные дроби. Сделайте чек.

Это пример самостоятельного решения (пример чистого дизайна и ответа в конце урока).

Перейдем к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если, в системе бесконечно много решений или неприметных (не решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если система имеет единственное решение и для нахождения корней необходимо вычислить еще три определителя:
«

И, наконец, ответ рассчитывается по формулам:

Как видите, случай «три-три» принципиально не отличается от случая «два-два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.

Пример 9.

Решите систему в соответствии с формулами искателя.

Решение : Разрешение системы в соответствии с формулами поискового робота.

Итак, у системы есть единственное решение.

Ответ :.

Собственно, и здесь комментировать больше нечего, ввиду того, что решение проходит по готовым формулам.Но есть пара замечаний.

Бывает, что в результате вычислений получаются «плохие» неинтерпретируемые дроби, например:.
Рекомендую следующий алгоритм лечения. Если под рукой нет компьютера, сделайте так:

1) Допускается ошибка в расчетах. Как только вы столкнулись с «плохой» фракцией, сразу нужно проверить, правильно ли проводящий кондиционер . Если условие переписывается без ошибок, то нужно пересчитать детерминанты, используя разложение на другой строке (столбце).

2) Если проверка ошибок не обнаружена, вероятно, это опечатка в условии присвоения. В этом случае спокойно и осторожно доводим задачу до конца, а затем обязательно проверяем И делаем это на доводке после решения. Конечно, проверка дробного ответа неприятна, но это будет обезоруживающий аргумент для учителя, который очень любит ставить минус любому подобному бяке. Как работать с дробями подробно описано в ответе например 8.

Если под рукой есть компьютер, то воспользуйтесь автоматизированной программой, которую можно бесплатно скачать в самом начале урока.Кстати, выгоднее всего сразу использовать программу (еще до принятия решения), вы сразу увидите промежуточный шаг, на котором была допущена ошибка! Этот же калькулятор автоматически рассчитывает решение решения матричным методом.

Замечание Второе. Время от времени встречаются системы, в уравнениях которых отсутствуют переменные, например:

Здесь в первом уравнении нет переменной, во втором — переменной. В таких случаях очень важно правильно и внимательно записать основной идентификатор:
— На месте отсутствующих переменных стоят нули.
Кстати, определители с нулями рационально раскрыты по строке (столбцу), которая равна нулю, так как вычислений заметно меньше.

Пример 10.

Решите систему в соответствии с формулами искателя.

Это пример самостоятельного решения (образец чистого дизайна и ответ в конце урока).

Для случая системы из 4 уравнений с 4 неизвестными формула Крамера записывается по аналогичным принципам.Живой пример можно посмотреть на уроке свойств определителя. Уменьшение порядка определителя — пять определителей 4-го порядка полностью твердые. Хотя задание уже вполне напоминает сапог профессора на груди у удачливого ученика.

Решение системы с матрицей возврата

Метод обратной матрицы по существу является частным случаем матричного уравнения (см. Пример № 3 указанного урока).

Чтобы изучить этот раздел, вы должны уметь раскрыть детерминанты, найти обратную матрицу и выполнить матричное умножение. Соответствующие ссылки будут даны в ходе объяснения.

Пример 11.

Решите систему матричным методом

Решение : Запишите систему в матричной форме:
, где

Посмотрите, пожалуйста, на систему уравнений и матрицу. По какому принципу писать элементы в матрице, думаю всем понятно.Единственный комментарий: если бы в уравнениях не было переменных, то в соответствующих местах матрицы нужно было бы ставить нули.

Обратную матрицу находим по формуле:
где — транспонированная матрица алгебраических сложений к соответствующим элементам матрицы.

Сначала разберемся с определителем:

Здесь определитель раскрывается в первой строке.

Внимание! Если, то матрица возврата не существует, и решить систему матричным методом невозможно.В этом случае система решается путем исключения неизвестного (метод Гаусса).

Теперь вам нужно вычислить 9 несовершеннолетних и записать их в Mind Matrix

.

Ссылка: Полезно знать значение индексов двойной подстановки в линейной алгебре. Первая цифра — это номер строки, в которой находится этот элемент. Вторая цифра — это номер столбца, в котором находится этот элемент:

То есть индекс двойной подстановки указывает, что элемент находится в первой строке, третьем столбце и, например, элемент находится в 3 строках, 2 столбцах

Метод Крамера или так называемое правило краулера — это способ поиска неизвестных значений из систем уравнений.Его можно использовать только в том случае, если количество искомых значений эквивалентно количеству алгебраических уравнений в системе, то есть основная матрица, сформированная из системы, должна быть квадратной и не содержать нулевых строк, а также если ее определитель не должен быть нулевым.

Теорема 1.

Теорема Крамера Если главный определитель $ d $ основной матрицы, составленной на основе коэффициентов уравнений, не равен нулю, то система уравнений согласована, а решение имеет единственное.Решение такой системы вычисляется по так называемым формулам Крамера для решения линейных уравнений: $ x_i = \ FRAC (D_I) (D) $

Что такое метод Крамера

Суть метода Крамера заключается в следующим образом:

1. Чтобы найти решение системы методом Крамера, первым делом вычисляется главный определитель матрицы $ D $. Когда вычисленный определитель основной матрицы при вычислении метода Крамера оказался нулевым, то система не имеет единственного решения или имеет бесконечное количество решений.В этом случае рекомендуется применить метод Гаусса, чтобы найти общий или базовый отклик для системы.
2. Затем нужно заменить крайний столбец основной матрицы на столбец свободных элементов и вычислить идентификатор $ d_1 $.
3. Повторите то же самое для всех столбцов, получив определители от $ d_1 $ до $ d_n $, где $ n $ — номер крайнего правого столбца.
4. После того, как все определители найдены $ d_1 $ … $ d_n $, можно вычислить неизвестные переменные по формуле $ x_i = \ frac (d_i) (D) $.

Приемы вычисления определителя матрицы

Для вычисления определителя матрицы размерностью больше 2 к 2 можно использовать несколько способов:

• Правило треугольников, или правило Сарруса, напоминающее правило то же правило. Суть метода треугольника заключается в том, что при вычислении определителя произведение всех чисел, связанных на рисунке красной линии справа, записывается со знаком плюс, а все числа, соединенные таким же образом на рисунке на слева — со знаком минус.B, тогда другое правило подходит для матриц 3 x 3. 3. В случае правила Сарруски сначала соответствует сама матрица, а затем переписывается в свой первый и второй столбцы. Через матрицу и эти дополнительные столбцы по диагонали, элементы матрицы, лежащие на главной диагонали или параллельно ей, записываются со знаком плюс, а элементы, лежащие на боковой диагонали или параллельно ей — со знаком минус.

Рис. 1. Правило треугольника для вычисления определителя для метода Крамера

• Используя метод, известный как метод Гаусса, также иногда этот метод называют уменьшением порядка определителя.В этом случае матрица преобразуется и приводится к треугольной форме, а затем перемножаются все числа, стоящие на главной диагонали. Следует помнить, что при таком поиске определителя невозможно умножить или разделить строки или столбцы на числа, не сделав их как множитель или делитель. В случае поиска определителя возможно только вычесть и сложить струны и столбы между собой после предварительного скашивания вычтенной линии до ненулевого множителя.Также при каждой перестановке строк или столбцов матрицы местами следует помнить о необходимости изменения финального знака в матрице.
• При решении метода Крамера, Славы с 4 неизвестными лучше всего использовать именно метод Гаусса для поиска и нахождения идентификаторов или определять определитель через поиск минорных.

Решение систем уравнений по Крамеру

Применимый метод Крамера для системы двух уравнений и двух желаемых значений:

$ \ begin (Cases) a_1x_1 + a_2x_2 = b_1 \\\\ a_3x_1 + a_4x_2 = b_2 \\ End (Cases) $

Для удобства отобразить в развернутом виде:

$ A = \ begin (array) (CC | C) A_1 & A_2 & B_1 \\\\ A_3 & A_4 & B_1 \ \ END (Array) $

Найдем определитель основной матрицы, также называемый главным определителем системы:

$ D = \ begin (array) (| CC |) A_1 & A_2 \\\ \ A_3 & A_4 \\ END (Array) = A_1 \ CDOT A_4 — A_3 \ CDOT A_2 $

Если главный определитель не равен нулю, необходимо вычислить пару определителей из двух матриц с заменен столбец основной матрицы на строку свободных элементов для решения примера метода:

$ D_1 = \ begin (array) (| cc |) b_1 & a_2 \\\\ b_2 & a_4 \\\\ \ \ конец (массив) = b_1 \\ cdot a_4 — b_2 \\ cdot a_4 $

$ D_2 = \ begin (array) (| CC |) A_1 & B_1 \\\\ A_3 & B_2 \\\\ \\ END (Array) = A_1 \ CDOT B_2 — A_3 \ CDOT B_1 $

Теперь найдите неизвестные $ x_1 $ и $ x_2 $:

$ x_1 = \ FRAC (D_1) (D)

$

$ x_2 = \ FRAC (D_2) (D)

$

Пример 1.

Метод Крамера для решения уклона с основной матрицей 3 порядка (3 x 3) и три является искомым.

Решите систему уравнений:

$ \ begin (Дела) 3x_1 — 2x_2 + 4x_3 = 21 \ 3x_1 + 4x_2 + 2x_3 = 9 \ 2X_1 — X_2 — X_3 = 10 \ END (Дела)

$

Рассмотрим главный определитель матрицы, используя вышеупомянутое правило числа 1:

$ D = \ begin (array) (| CCC |) 3 & -2 & 4 \\\\ 3 & 4 & -2 \ ED (Array) = 3 \ CDOT 4 \ CDOT (- 1) + 2 \ Cdot (-2) \ CDOT 2 + 4 \ CDOT 3 \ CDOT (-1) — 4 \ CDOT 4 \ CDOT 2 — 3 \ CDOT (-2) \ CDOT (-1) — (- 1) \ CDOT 2 \ CDOT 3 = — 12-8-12-32-6 + 6 = — 64 $

А теперь еще три детерминанта:

$ D_1 = \ begin (массив) (| CCC |) 21 & 2 & 4 \\\\ 9 & 4 & 2 \\\\ 10 & 1 & 1 \ END (Array) = 21 \ CDOT 4 \ CDOT 1 + (- 2) \ CDOT 2 \ CDOT 10 + 9 \ CDOT (-1) \ CDOT 4-4 \ CDOT 4 \ CDOT 10-9 \ CDOT (-2 ) \ CDOT (-1) — (-1) \ CDOT 2 \ $ D_2 = \ begin (array) (| CCC |) 3 & 21 & 4 \\\\ 3 & 9 & 2 \\ ED (Массив) = 3 \ CDOT 9 \ CDOT (- 1) + 3 \ CDOT 10 \ CDOT 4 + 21 \ CDOT 2 \ CDOT 2-4 \ CDOT 9 \ CDOT 2-21 \ CDOT 3 \ CDOT (-1) — 2 \ CDOT 10 \ CDOT 3 = — 27 + 120 + 84-72 + 63-60 = 108 $

$ D_3 = \ begin (массив) (| CCC |) 3 & -2 & 21 \\\\ 3 & 4 & 9 \\\\ 2 & 1 & 10 \ END (массив) = 3 \ \ CDOT 4 \ CDOT 10 + 3 \ Cdot (-1) \ CDOT 21 + (-2) \ CDOT 9 \ CDOT 2-21 \ CDOT 4 \ CDOT 2 — (-2) \ CDOT 3 \ CDOT 10 — (-1) \ CDOT 9 \ CDOT 3 = 120 — 63 — 36 — 168 + 60 + 27 = — 60

$

Найдите нужные значения:

$ X_1 = \ FRAC (D_1) (D) = \ FRAC (- 296) (- 64) = 4 \ FRAC (5) (8)

$

$ X_2 = \ FRAC (D_1) (D) = \ FRAC (108) (-64) = — 1 \ FRAC (11) (16)

$

$ X_3 = \ FRAC (D_1) (D) = \ FRAC (-60) (-64) = \ FRAC (15) (16)

$

Методы

Cramer Gaussa и — Некоторые из самых популярных решений Slough .Кроме того, в некоторых случаях целесообразно использовать специальные методы. Сессия близка, и теперь пора повторить или освоить их с нуля. Сегодня мы разбираемся с решением по методу Крамера. Ведь решение системы линейных уравнений методом Крамера — очень полезный навык. Системы линейных алгебраических уравнений

Система линейных алгебраических уравнений — система уравнений вида:

Набор значений

X. , в котором уравнения системы обращаются к тождествам, называется решением решения, А. г. и — Реальные коэффициенты. Простую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме, либо выразив одну переменную через другую. Но переменных (ИС) в Славе может быть намного больше двух, и здесь этого мало для простых школьных манипуляций. Что делать? Например, решить Славу методом Крамера! Так пусть система состоит из

N. уравнения S. неизвестно. уравнения S. Такую систему можно переписать в матричном виде

Здесь

А. — основная матрица системы, Х. Б. и , соответственно, матрицы-столбцы неизвестных переменных и свободных членов. Раствор Славы по методу Крамера

Если определитель основной матрицы не равен нулю (матрица невырожденная), то система может быть решена по методу привода.

По методу Крамера решение по формулам:

дельта

А. — определитель основной матрицы, а Delta X. n-NO — определитель, полученный из определителя основной матрицы заменой столбца N-числа на столбец свободных элементов. {! LANG-cdef74b87d85d35b771d2e3275c6f3f7!}

В этом вся суть метода Крамера. Подстановка значений, найденных согласно приведенным выше формулам , в которых уравнения системы обращаются в тождества, называется решением решения, В желаемой системе убеждаемся в правильности (или наоборот) нашего решения.Чтобы вы быстро уловили суть, приведем пример подробного решения метода Славы кратера:

Даже если у вас не получится работать с первого раза, не волнуйтесь! Немного практики, и вы начнете щелкать Славу как орехи. Более того, теперь совершенно необязательно трезветь над блокнотом, решая громоздкие вычисления и записывая стержень. Вы легко можете решить метод Славы Крамера онлайн, только подставив коэффициенты в готовом виде.Попробуйте онлайн-калькулятор решений по методу Крамера, например, на этом сайте.

И если система оказалась упорной и не сдалась, всегда можно обратиться за помощью к нашим авторам, например, к. Будьте в системе хотя бы 100 неизвестных, мы обязательно решим ее верно и точно в срок!

Метод Крамера основан на использовании определителей при решении систем линейных уравнений. Это значительно ускоряет процесс принятия решения.

Кратерный метод можно использовать при решении системы стольких линейных уравнений, как в каждом уравнении неизвестного.Если определитель системы не равен нулю, в решении можно использовать метод Крамера, если он равен нулю, нельзя. Кроме того, метод Крамера можно использовать при решении систем линейных уравнений, имеющих единственное решение.

Определение . Определитель, составленный из коэффициентов при неизвестном, называется определителем системы и обозначается (дельта).

Deterpetes

получается заменой коэффициентов на соответствующие неизвестные для свободных участников:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, система линейных уравнений имеет одно единственное решение и неизвестное, равное отношению определителей. В знаменателе — определитель системы, а в числителе — определитель, полученный из определителя системы путем замены коэффициентов одновременно неизвестными свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решите систему линейных уравнений:

Согласно теореме крамера Имеем:

Итак, решение Решение (2):

Онлайн-калькулятор, решающий кратерный метод.

Три случая решения систем линейных уравнений

Как ясно теоремы Крамера При решении системы линейных уравнений может быть три случая:

Первый случай: система линейных уравнений имеет единственное решение

(совместно с системой)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместного и неопределенного)

**,

тех.Коэффициенты при неизвестных и свободных членах пропорциональны.

Третий случай: в системе линейных решений нет

(система непонятна)

Итак, система м. Линейные уравнения S. уравнений S. переменных называют без остановок, , если у нее нет решения, и стыковкой, , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется , определенное , более одного — неопределенное .

Примеры решения систем линейных уравнений по Крамеру

Пусть дано системе

.

На основе теоремы Крамера

………….
,

где
—

определение системы. Остальные определители получаем, заменяя столбец коэффициентами соответствующих переменных (неизвестных) свободных членов:

Пример 2.

.

Следовательно, система определена. Чтобы найти ее решения, вычислим определители

По формулам краулера находим:

Итак (1; 0; -1) — единственное решение системы.

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях нет переменных, то в определителе соответствующие им элементы равны нулю! Это следующий пример.

Пример 3. Решите систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Внимательно посмотрите на систему уравнений и определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система определена. Чтобы найти ее решения, мы вычисляем определители при неизвестном

.

По формулам краулера находим:

Итак, решение системы (2; -1; 1).

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

Начало страницы

Продолжаем решать систему по методу Крамера вместе

Как уже упоминалось, если определитель системы равен нулю, а определители при неизвестном не равны нулю, система непонятна, то есть решений не имеет. Проиллюстрируем следующий пример.

Пример 6. Решите систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо неполна и определена, либо противоречива, то есть не имеет решений. Для пояснения вычислим детерминанты при неизвестном

.

Определители при неизвестном не равны нулю, следовательно, система неполная, то есть не имеет решений.

Для проверки решений систем уравнений 3 x 3 и 4 x 4 вы можете использовать онлайн-калькулятор, решая метод Крамера.

В задачах по системе линейных уравнений встречаются и такие, где встречаются и другие буквы, обозначаемые переменными. Эти буквы обозначают какое-то число, чаще всего действительное. На практике такие уравнения и системы уравнений приводят к задачам поиска общих свойств любых явлений и объектов. То есть вы изобрели какой-то новый материал или устройство, и для описания его свойств, как правило, вне зависимости от размера или количества экземпляра, вам нужно решить систему линейных уравнений, где вместо некоторых коэффициентов с переменными — буквы.Например, ходить не обязательно.

Следующий пример представляет собой аналогичную задачу, только увеличивается количество уравнений, переменных и букв, обозначающих какое-либо допустимое число.