3. Однородные дифференциальные уравнения первого порядка
Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.
Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество
. | (3.1) |
Например, функция — однородная функция первого измерения, так как
;
— однородная функция третьего измерения , так как
;
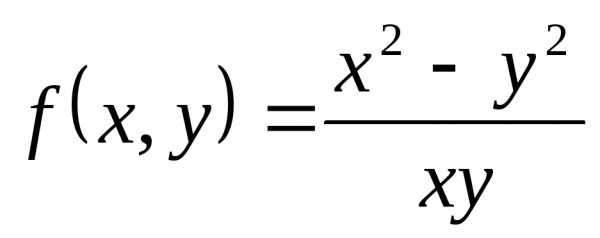 — однородная функция нулевого измерения,
так как
— однородная функция нулевого измерения,
так как
, т.е..
Определение 2.Дифференциальное уравнение первого порядкаy‘ = f(x,y) называется однородным, если функцияf(x,y) есть однородная функция нулевого измерения относительноx иy, или, как говорят,f(x,y) – однородная функция степени нуль.
Его можно представить в виде
P (x, y) dx + Q (x, y) dy = 0, | (3.2) |
где P(x,y) иQ(x,y) – однородные функции одинакового измерения: отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения (см. третий из приведенных выше примеров).
Возможна следующая форма записи уравнения (3.2):
| (3.3) |
что позволяет определить однородное уравнение как такое дифференциальное, которое можно преобразовать к виду (3.3).
Замена 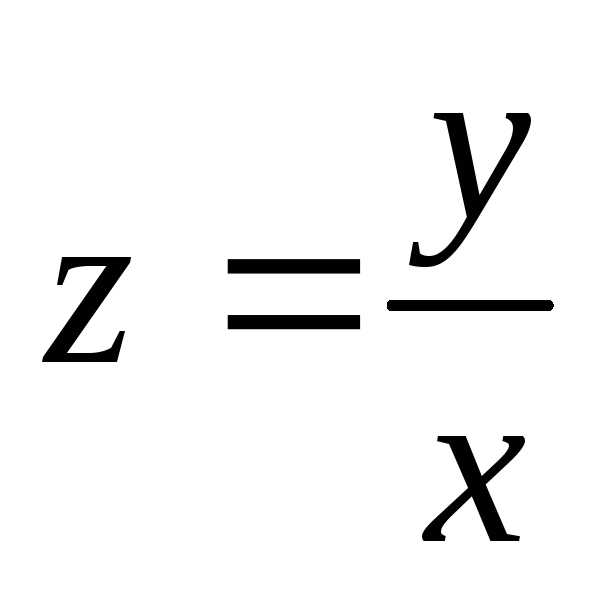 приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим
приводит однородное уравнение к
уравнению с разделяющимися переменными.
Действительно, после подстановкиу
= xzполучим ,
,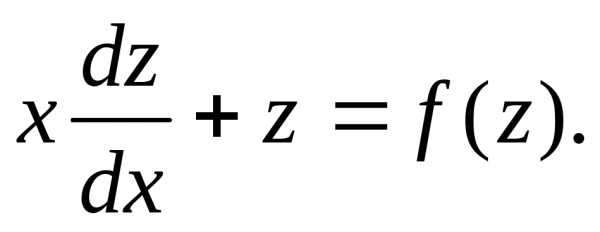 Разделяя переменные и интегрируя,
найдем:
Разделяя переменные и интегрируя,
найдем:
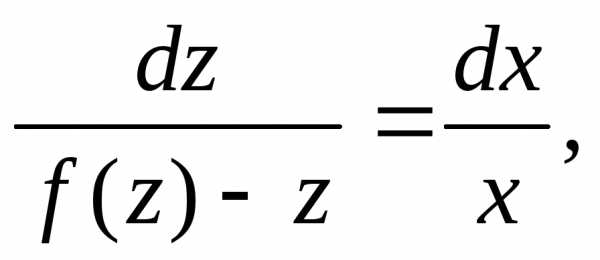 ,
,
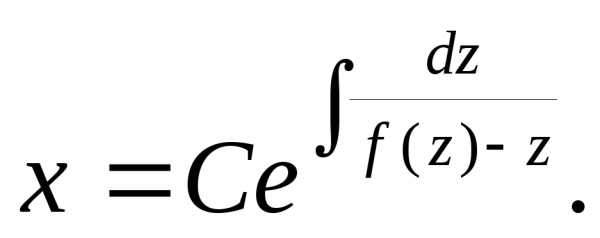
Пример 1.Решить уравнение .
Полагаем у = zx, 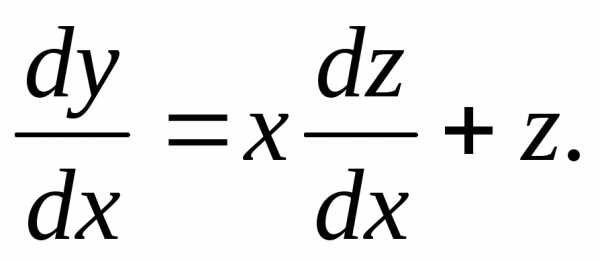 Подставляем
эти выраженияy иdyв данное уравнение:
Подставляем
эти выраженияy иdyв данное уравнение: или
или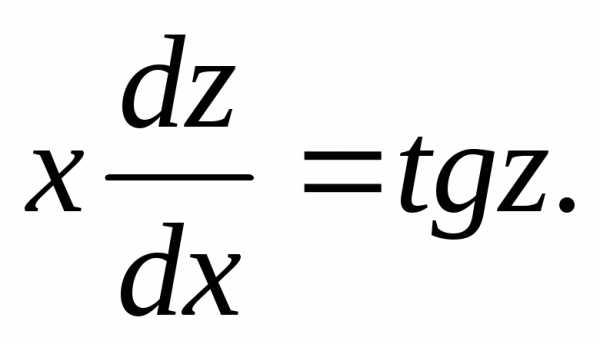 Разделяем переменные:
Разделяем переменные: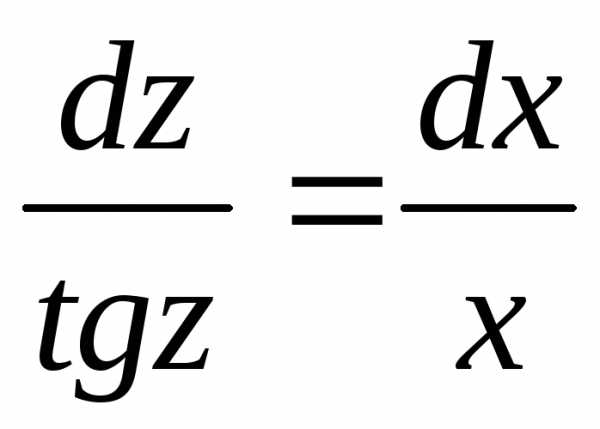 и интегрируем:
и интегрируем: ,
,
 ,
получим
,
получим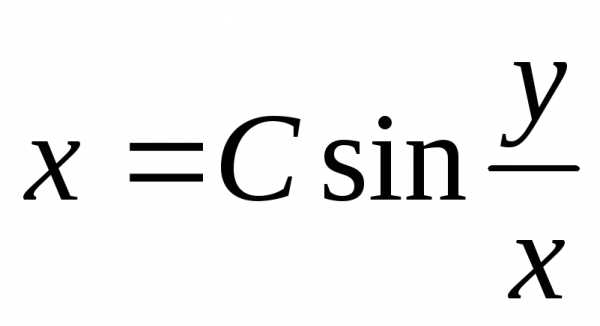 .
.Пример 2. Найти общее решение уравнения.
В данном уравнении P (x,y)
=x2-2y2,Q(x,y)
=2xy– однородные
функции второго измерения, следовательно,
данное уравнение является однородным.
Его можно представить в виде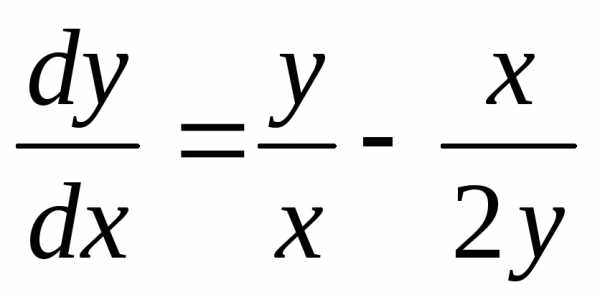 и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
и решать так же, как и представленное
выше. Но используем другую форму записи.
Положимy = zx,
откудаdy = zdx + xdz. Подставляя эти
выражения в исходное уравнение, будем
иметь
,
то есть

или
dx+2zxdz = 0.
Разделяем переменные, считая 
 .
.
Интегрируем почленно это уравнение
 ,
откуда
,
откуда
то есть 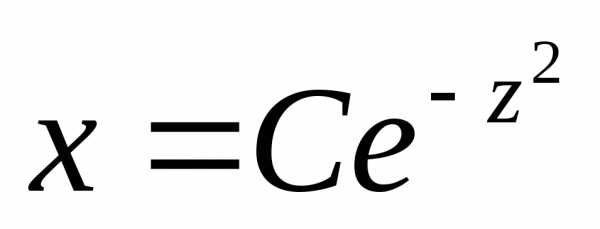 .
Возвращаясь к прежней функции
.
Возвращаясь к прежней функции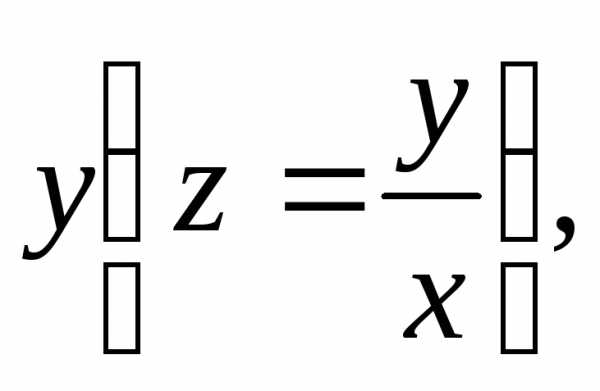
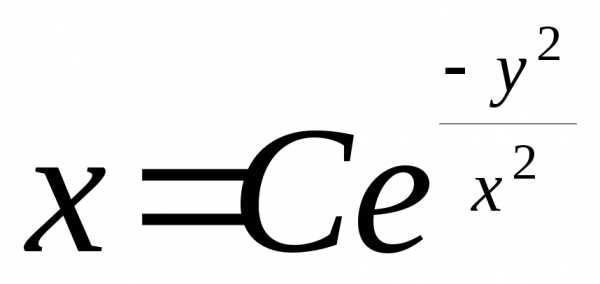
Пример 3. Найти общее
решение уравнения .
.
Цепочка преобразований:  ,y = zx,,
,y = zx,,  ,
, 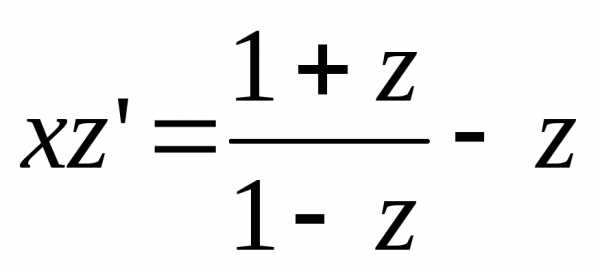 ,
,  ,
,  ,
,
, , ,
,
,
, , ,
Лекция 8.
4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид
, | (4.1) |
где  ,
, ,c(x) –
непрерывные функции.
,c(x) –
непрерывные функции.
Если ,
то уравнение (4.1) можно записать в
приведённом виде
,
то уравнение (4.1) можно записать в
приведённом виде
(4.1a) |
Здесь – свободный член, называемый также правой частью уравнения. В этом виде будем рассматривать линейное уравнение в дальнейшем.
Если  0,
то уравнение (4.1а) называется линейным
неоднородным. Если же
0,
то уравнение (4.1а) называется линейным
неоднородным. Если же 0, то уравнение принимает вид
0, то уравнение принимает вид
(4.2) |
и называется линейным однородным.
Название уравнения (4.1а) объясняется
тем, что неизвестная функция y и её производная входят в него линейно, т.е. в первой
степени.
входят в него линейно, т.е. в первой
степени.
В линейном однородном уравнении
переменные разделяются. Переписав его
в виде 
 и интегрируя, получаем:,т.е.
и интегрируя, получаем:,т.е. | (4.3) |
При делении на  теряем решение
теряем решение .
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
.
Однако оно может быть включено в найденное
семейство решений (4.3), если считать, чтоСможет принимать и значение 0.
Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций отх:
(4.4) |
Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).
Дифференцируя обе части равенства (4.4), находим .
Подставляя полученное выражение
производной  ,
а также значениеу в уравнение (4.1а), получаем,
или
,
а также значениеу в уравнение (4.1а), получаем,
или
. | (4.5) |
Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы
| (4.6) |
т.е. в качестве функции vвозьмём решение однородного линейного уравнения (4.6):
. | (4.3а) |
Ввиду произвольности в выборе v,мы можем не учитывать произвольную постояннуюС (точнее – можем приравнять её нулю). Подставляя найденное значениеv(x) в уравнение (4.5), получим, учитывая (4.6):
| (4.7) |
откуда
(4.8) |
(Здесь Cписать обязательно, иначе получится не общее, а частное решение).
Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).
Подставляя  иv(x) в
формулу (4.4), окончательно получаем
иv(x) в
формулу (4.4), окончательно получаем
,
или
. | (4.9) |
Пример 1.Найти общее решение
уравнения
Положим 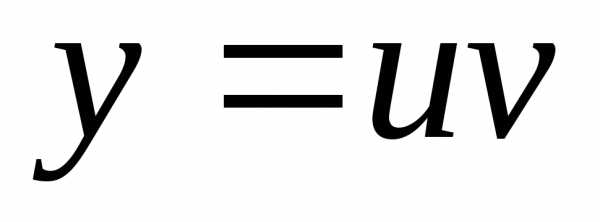 ,
тогда
,
тогда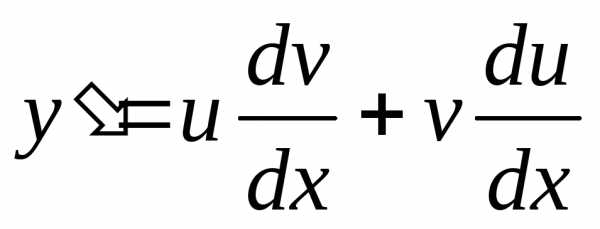 .
Подставляя выражения
.
Подставляя выражения и
и в
исходное уравнение, получимили(*)
в
исходное уравнение, получимили(*)
Приравняем нулю коэффициент при  :
: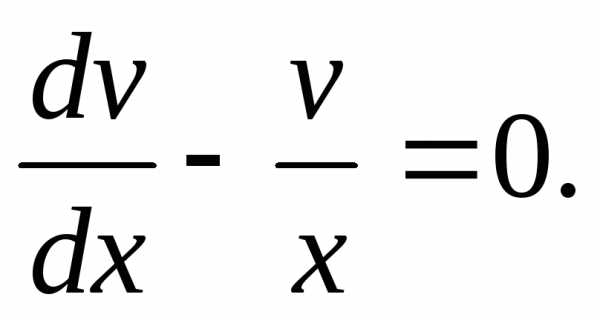
Разделяя переменные в полученном
уравнении, имеем 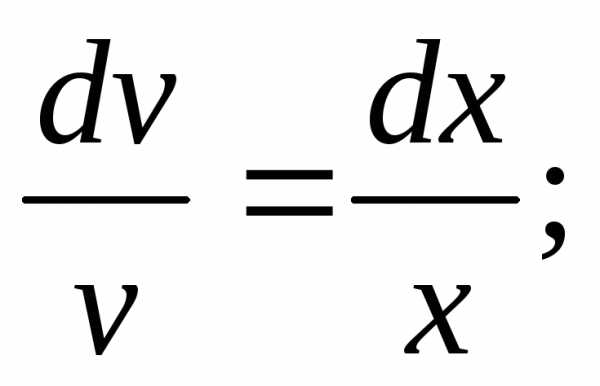

 (произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
(произвольную постояннуюC не пишем), отсюдаv=x.
Найденное значениеvподставляем в уравнение (*):
 ,,
,,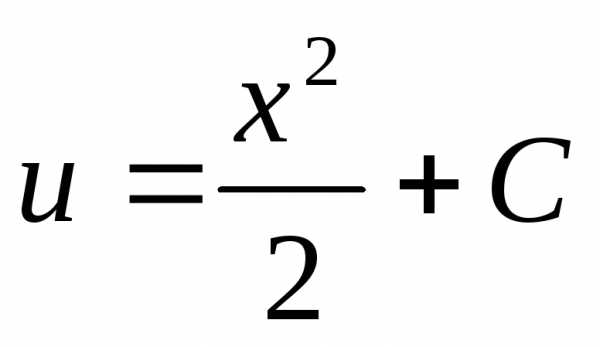 .
.
Следовательно, 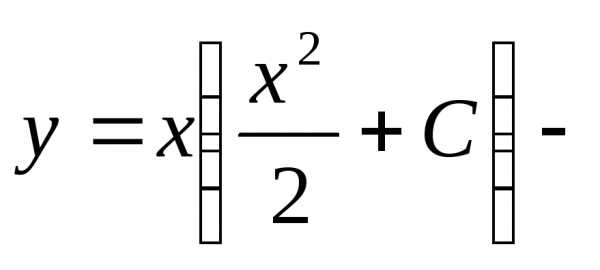 общее
решение исходного уравнения.
общее
решение исходного уравнения.
Отметим, что уравнение (*) можно было записать в эквивалентном виде:
.
Произвольно выбирая функцию u,
а неv, мы могли полагать .
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
.
Этот путь решения отличается от
рассмотренного только заменойvнаu(и, следовательно,uнаv),
так что окончательное значениеуоказывается тем же самым.
На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.
Приводим рассматриваемое уравнение к виду.
Используя подстановку
 ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.Группируем члены уравнения, выносим одну из функций uилиvза скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.
Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.
Записываем общее решение, подставив выражения для найденных функций u иvв равенство
 .
.Если требуется найти частное решение, то определяем Сиз начальных условий и подставляем в общее решение.
Отметим далее, что иногда уравнение первого порядка становится линейным, если усчитать независимой переменной, аx– зависимой, т.е. поменять ролиx иy. Это можно сделать при условии, чтоxиdxвходят в уравнение линейно.
Пример 2. Решить уравнение .
Однако если рассматривать xкак функцию оту, то, учитывая, что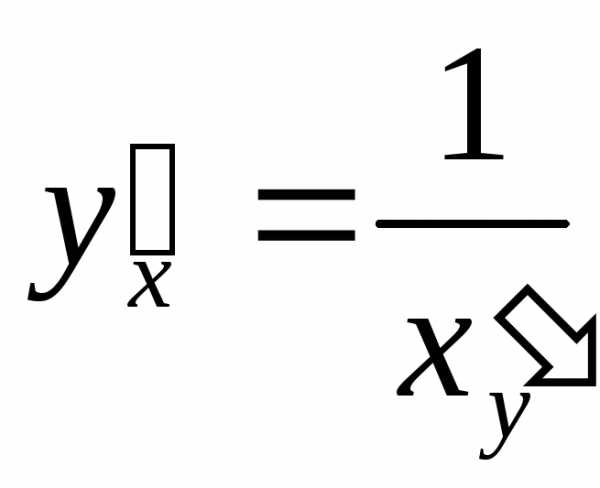 ,его
можно привести к виду
,его
можно привести к виду
| (4.1 б) |
Заменив  на
на ,получим
,получим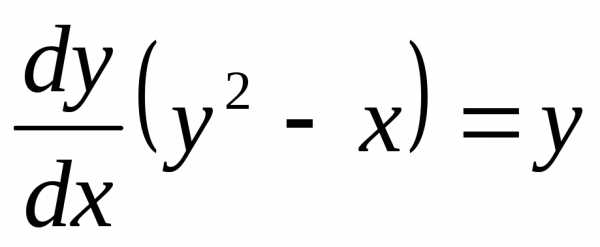 или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
или.
Разделив обе части последнего уравнения
на произведениеydy,
приведем его к виду
 , или
, или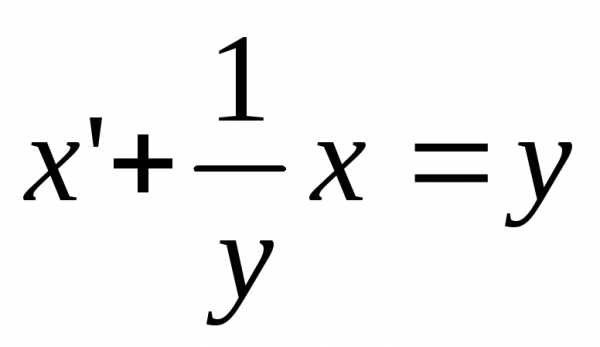 .
(**)
.
(**)
Здесь P(y)= ,
,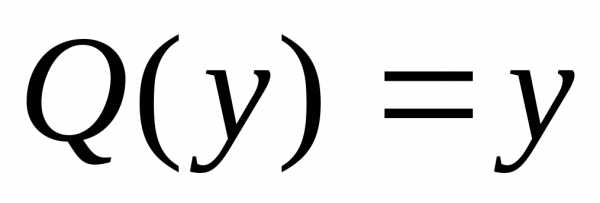 .
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
.
Это линейное уравнение относительноx. Полагаем,.
Подставляя эти выражения в (**), получаем
или.
Выберем vтак, чтобы ,
,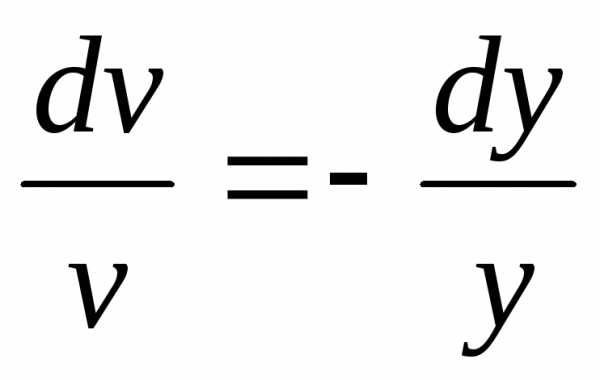 ,
откуда
,
откуда ;
;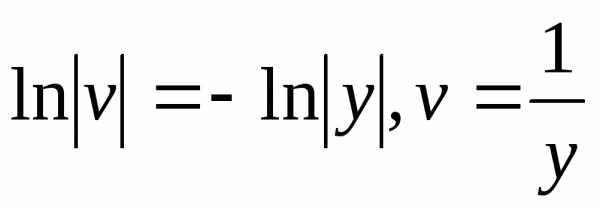 .
Далее имеем
.
Далее имеем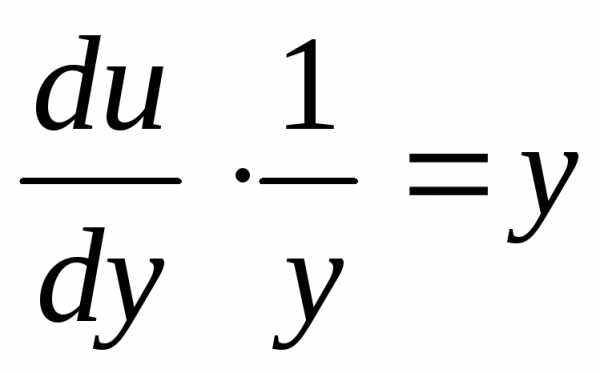 ,
, ,
,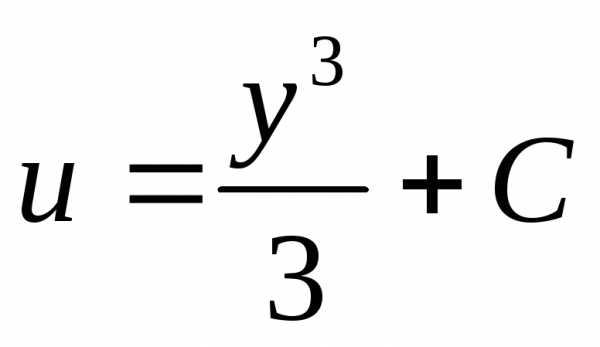 .
.
Т.к. , то приходим к общему решению данного уравнения в виде
 .
.
Отметим, что в уравнение (4.1а) P(x) иQ (x) могут входить не только в виде функций от x, но и констант:P=a,Q=b. Линейное уравнение
(4.10) |
можно решать и с помощью подстановки y=uv и разделением переменных:
 ;
; .
.
Отсюда  ;;;
где
;;;
где .
Освобождаясь от логарифма, получаем
общее решение уравнения
.
Освобождаясь от логарифма, получаем
общее решение уравнения
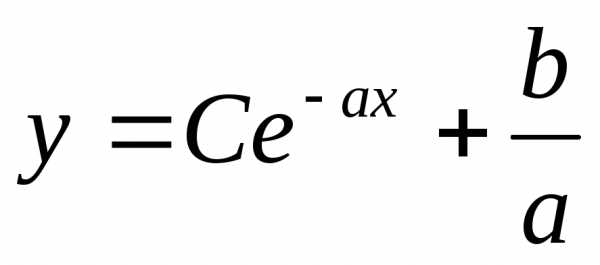 (здесь
(здесь ).
).
При b=0 приходим к решению уравнения
| (4.10а) |
в виде
| (4.11) |
(см. уравнение показательного роста
(2.4) при 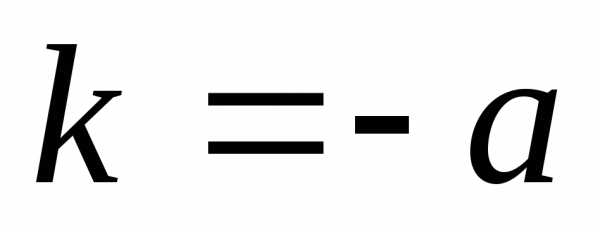 ).
).
Применим далее для интегрирования неоднородного линейного уравнения (4.1а) метод вариации произвольной постоянной (метод Лагранжа).
Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель Св (4.3) функцией отх, т.е. по существу делаем замену переменной
, | (4.3а) |
где C(x)-новая
неизвестная функцияx.
Подставляя производнуюв исходное неоднородное уравнение
(4.1а), получим: ,
или
,
или
, | (4.12) |
откуда, интегрируя, находим
dx+C1, | (4.13) |
где С1-постоянная. Следовательно,
. | (4.14) |
Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).
При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).
Применим метод Лагранжа к уравнению, рассмотренному в примере 1:
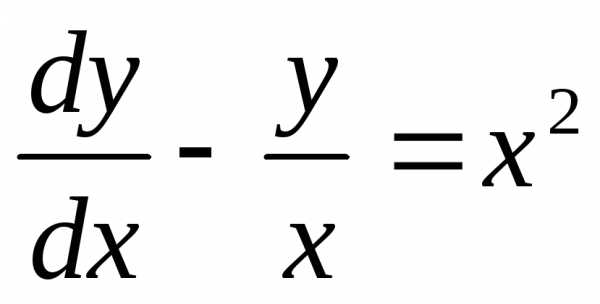 .
.
Интегрируем соответствующее однородное
уравнение  .
.
Разделяя переменные, получаем 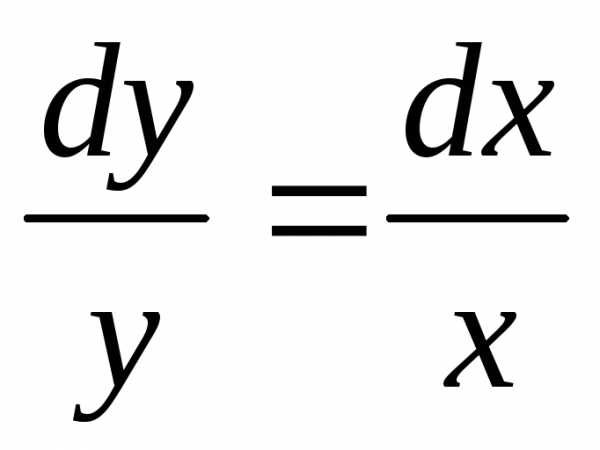 и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим;
и далее.
Решение выражения формулойy = Cx. Решение исходного
уравнения ищем в видеy = C(x)x.
Подставив это выражение в заданное
уравнение, получим;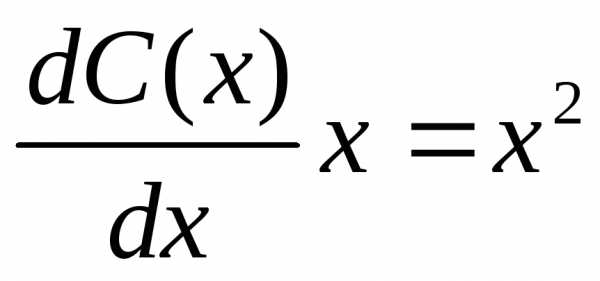 ;,
;, .
Общее решение исходного уравнения имеет
вид
.
Общее решение исходного уравнения имеет
вид
.
В заключение отметим, что к линейному уравнению приводится уравнение Бернулли
,
( | (4.15) |
которое можно записать в виде
. | (4.15а) |
Заменой  оно приводится к линейному уравнению:
оно приводится к линейному уравнению:
 ,
, ,.
,.
Уравнения Бернулли также решаются изложенными выше методами.
Пример 3. Найти общее решения уравнения.
Цепочка преобразований: 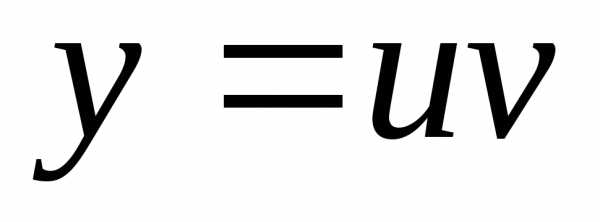 ,,,,
,,,, ,
, ,
,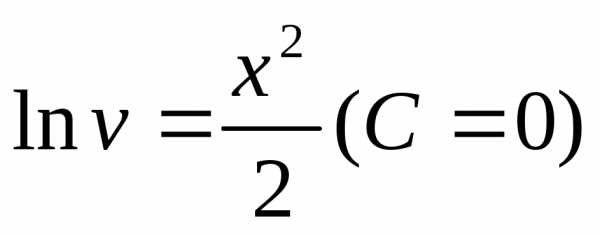 ,
, ,
, ,
, ,
,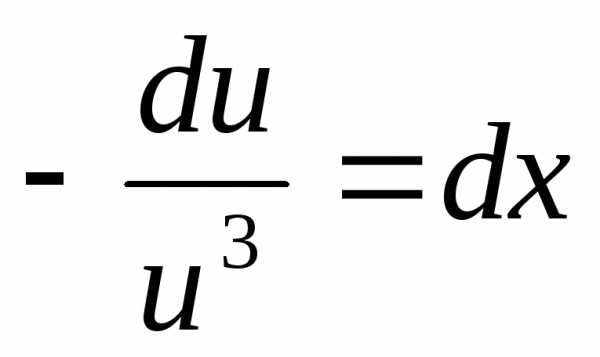 ,
, ,
,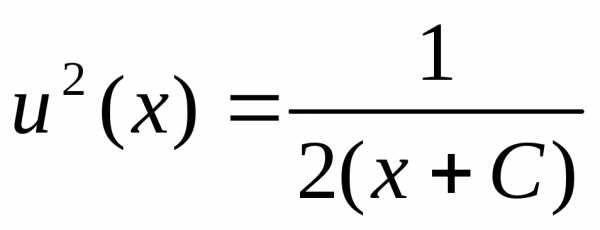 ,,
,,
studfiles.net
25. Д.У первого порядка, классификация ду
Уравнение
F(x, y, y ‘) = 0,
где y ‘= f(x,y) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.
Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ‘) = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y ‘(x)) ≡ 0 для всех x из (a,b) .
Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия. Чтобы найти частное решение, нужно воспользоваться задачей Коши
Уравнения с частными производными можно классифицировать по многим признакам.
Классификация уравнений важна потому, что для каждого класса существует своя общая теория и методы решения уравнений.
Можно выделить шесть методов классификации уравнений.
1.Порядок уравнения. Порядком уравнения называется наивысший порядок частных производных, входящих в уравнение.
2.Линейность .Дифференциальное уравнение вида
где a(x) и b(x) − непрерывные функции x, называется линейным неоднородным дифференциальным уравнением первого порядка.
26. Ур-я с разделяющимися переменными
Уравнение вида , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только оти только от, называетсяуравнением с разделяющимися переменными.
Путем деления на произведение оно приводится к уравнению с разделенными переменными:
Общий интеграл этого уравнения имеет вид
27.Однородные дифференциальные уравнения первого порядка
Однородные дифференциальные уравнения первого порядка – это уравнения вида
Как распознать однородное дифференциальное уравнение
Для того, чтобы распознать однородное дифференциальное уравнение, нужно ввести постоянную t и сделать замену y → ty, x → tx. Если, в результате такого преобразования, постоянная t сократится, то это однородное дифференциальное уравнение. Производная y′ при таком преобразовании не меняется:
28. Линейное дифференциальное уравнение первого порядка
Определение линейного дифференциального уравнения первого порядка. Рассмотрен способ решения линейных дифференциальных уравнений первого порядка методом интегрирующего множителя. Дан пример подробного решения линейного дифференциального уравнения.
Линейное дифференциальное уравнение первого порядка – это уравнение вида
Линейное однородное дифференциальное уравнение первого порядка – это уравнение вида
Линейное неоднородное дифференциальное уравнение первого порядка – это уравнение вида
Член q(x) называется неоднородной частью уравнения.
29. Интегрирование по частям в определенном интеграле
Осуществление определенных условий или действий для выявления рассматриваемого события носит название опыта или эксперимента.
Событие называется случайным, если в результате опыта оно может произойти или не произойти.
Событие называется достоверным, если оно обязательно появляется в результате данного опыта, и невозможным, если оно не может появиться в этом опыте.
Например, выпадение снега в Москве 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега на экваторе можно рассматривать как невозможное событие.
Одной из главных задач в теории вероятностей является задача определения количественной меры возможности появления события.
Каждый из равновозможных результатов испытаний (опытов) называется элементарным исходом. Их обычно обозначают буквами . Например, бросается игральная кость. Элементарных исходов всего может быть шесть по числу очков на гранях.
Из элементарных исходов можно составить более сложное событие. Так, событие выпадения четного числа очков определяется тремя исходами: 2, 4, 6.
Количественной мерой возможности появления рассматриваемого события является вероятность.
Наиболее широкое распространение получили два определения вероятности события: классическое и статистическое.
Классическое определение вероятности связано с понятием благоприятствующего исхода.
Исход называется благоприятствующим данному событию, если его появление влечет за собой наступление этого события.
В приведенном примере рассматриваемое событие — четное число очков на выпавшей грани, имеет три благоприятствующих исхода. В данном случае известно и общее количество возможных исходов. Значит, здесь можно использовать классическое определение вероятности события.
Классическое определение. Вероятность события равняется отношению числа благоприятствующих исходов к общему числу возможных исходов
(1.1)
где — вероятность события,— число благоприятствующих событиюисходов,— общее число возможных исходов.
В рассмотренном примере
Статистическое определение вероятности связано с понятием относительной частоты появления события в опытах.
Относительная частота появления события вычисляется по формуле
(1.2)
где — число появления события в серии изопытов (испытаний).
Статистическое определение. Вероятностью события называется число, относительно которого стабилизируется (устанавливается) относительная частотапри неограниченном увеличении числа опытов.
В практических задачах за вероятность события принимается относительная частотапри достаточно большом числе испытаний.
Из данных определений вероятности события видно, что всегда выполняется неравенство
Для определения вероятности события на основе формулы (1.1) часто используются формулы комбинаторики, по которым находится число благоприятствующих исходов и общее число возможных исходов.
Пример. Известно, что в поступившей партии из 30 швейных машинок 10 имеют внутренний дефект. Определить вероятность того, что из партии в 5 наудачу взятых машинок 3 окажутся бездефектными.
Решение. Для решения данной задачи введем обозначения. Пусть — общее число машинок,— число бездефектных машинок,— число отобранных в партию машинок,— число бездефектных машинок в отобранной партии.
Общее число комбинаций по машинок, т.е. общее число возможных исходов будет равно числу сочетаний изэлементов по, т.е.. Но в каждой отобранной комбинации должно содержаться по три бездефектные машинки. Число таких комбинаций равно числу сочетаний изэлементов по, т.е..
С каждой такой комбинацией в отобранной партии оставшиеся дефектные элементы тоже образуют множество комбинаций, число которых равно числу сочетаний из элементов по, т.е..
Это значит, что общее число благоприятствующих исходов определяется произведением . Откуда получаем
Подставим в эту формулу численные значения данного примера
studfiles.net
Примеры решения однородных линейных дифференциальных уравнений высших порядков
№ 1.
–характеристическое уравнение
Общее решение:
или
№ 2.
–характеристическое уравнение.
Общее решение: или.
№ 3.
Общее решение:
№ 4.
–характеристическое уравнение.
Положим 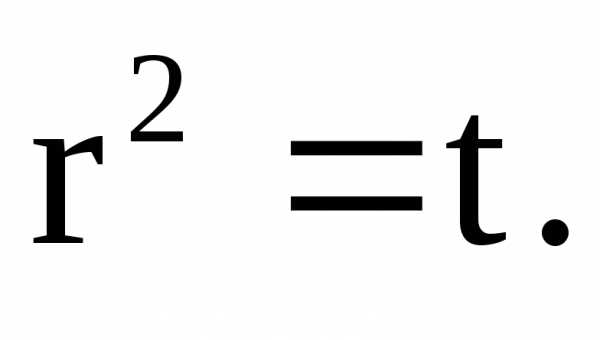
Общее решение уравнения:
Линейные неоднородные дифференциальные уравнения второго порядка
Линейное неоднородное уравнение отличается от однородного функцией в правой части. Линейное неоднородное уравнение имеет вид
а соответствующее ему линейное однородное уравнение –
которое, как известно, решается с помощью характеристического уравнения (16)
Сформулируем теорему о структуре общего решения неоднородного уравнения (13).
Теорема 2. Общее решение неоднородного линейного дифференциального уравнения равно сумме какого-либо частного решения этого уравнения и общего решения соответствующего однородного уравнения.
Пусть y – общее решение уравнения (13)
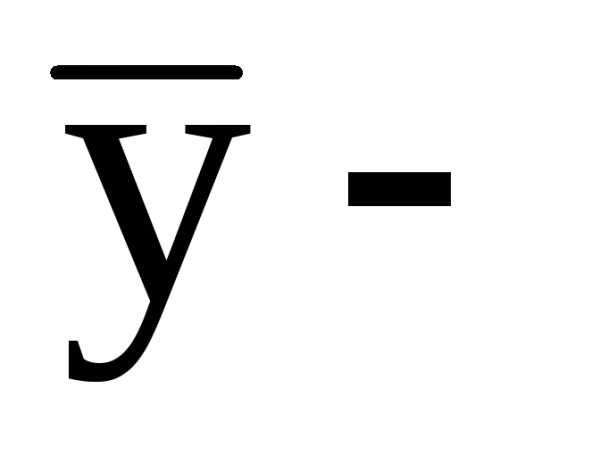 какое-либо
частное решение уравнения (13),
какое-либо
частное решение уравнения (13),
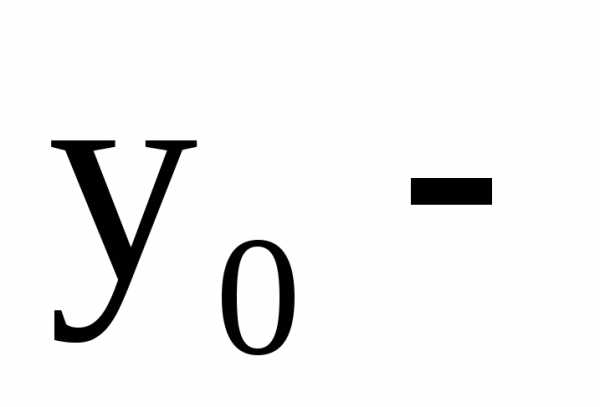 общее
решение соответствующего однородного
уравнения (14)
общее
решение соответствующего однородного
уравнения (14)
Тогда
Таким образом, основная задача при решении неоднородного линейного д.у. II состоит в нахождении какого-либо частного решения.
Укажем один из
методов нахождения частного решения
неоднородного уравнения , когда правая
часть уравнения  имеет специальный вид. К таким функциям
имеет специальный вид. К таким функциям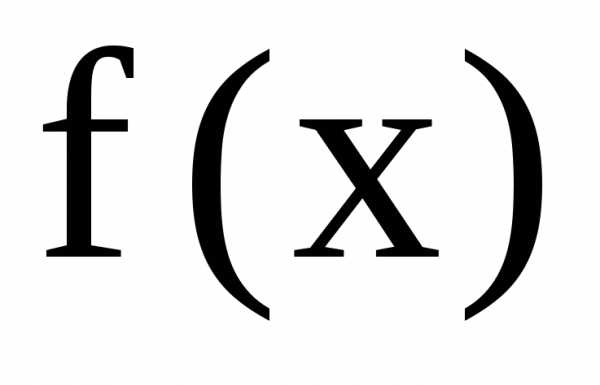 относятся следующие функции: экспонентамногочленыn-й
степени относительно переменной х
относятся следующие функции: экспонентамногочленыn-й
степени относительно переменной х 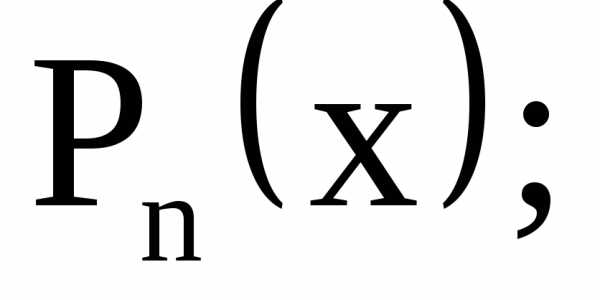 тригонометрические функцииа также их произведения.
тригонометрические функцииа также их произведения.
Метод неопределенных коэффициентов
Этот метод иначе
называется методом подбора частного
решения  уравне-ния (13) по виду правой части
уравне-ния (13) по виду правой части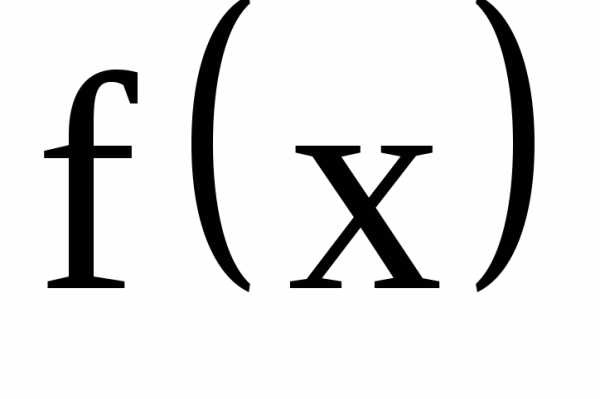 .
.
Пусть правая
часть  уравнения
уравнения
имеет вид т. е. представляет собой произведение экспоненты на многочлен, гдемногочленn-й относительно х. Тогда возможны следующие случаи.
Число не является корнем характеристического уравнения (16)
В этом случае частное решение нужно искать в виде
где 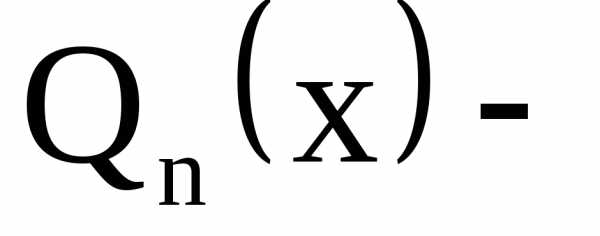 многочлен
той же степени, что и данный многочлен
многочлен
той же степени, что и данный многочлен ,
но с неопределенными коэффициентами.
,
но с неопределенными коэффициентами.
Число
 есть простой (однократный) корень
характеристического уравнения (т. е.
есть простой (однократный) корень
характеристического уравнения (т. е. совпадает с одним корнем характеристического
уравнения). В этом случае частное решение
нужноискать
в виде .
совпадает с одним корнем характеристического
уравнения). В этом случае частное решение
нужноискать
в виде .Число
 есть двукратный корень характеристического
уравнения (т. е.
есть двукратный корень характеристического
уравнения (т. е. совпадает с двумя равными корнями
характеристического уравнения). В этом
случае частное решение нужноискать
в виде Неизвестные (неопределенные) коэффициенты
многочлена
совпадает с двумя равными корнями
характеристического уравнения). В этом
случае частное решение нужноискать
в виде Неизвестные (неопределенные) коэффициенты
многочлена находим из условия, что функция
находим из условия, что функция является решением уравнения (13), т. е.
удовлетворяет этому уравнению.
является решением уравнения (13), т. е.
удовлетворяет этому уравнению.
Рассмотрим примеры, на которых покажем не только принцип применения метода, но и порядок оформления решения.
№ 1. Найти общее решение уравнения
1) Составим характеристическое уравнение и найдем его корни:
2) Запишем общее решение соответствующего однородного дифференциального уравнения:
3) Запишем формулу,
по которой следует искать частное
решение  данного уравнения. Для этого сравним
правую часть уравнения
данного уравнения. Для этого сравним
правую часть уравнения
с общим видом правой части:
–многочлен второй степени с коэффициентами 24; 16; –15.
В данном случае
показательная функция  ,
т. е.
,
т. е. Так как
Так как не совпадает ни с одним из корней
характеристического уравнения,
частное решение нужно искать в виде
не совпадает ни с одним из корней
характеристического уравнения,
частное решение нужно искать в виде
многочлен второй
степени  ,
неизвестные (неопределенные) коэффициенты
А,В,С
этого многочлена нужно найти, подставив
выражения
,
неизвестные (неопределенные) коэффициенты
А,В,С
этого многочлена нужно найти, подставив
выражения  в данное уравнение.
в данное уравнение.
4) Запишем  столбиком:
столбиком:


Слева указаны
коэффициенты 12, 7, 1, на которые следует
умножить  ,
чтобы получить левую часть уравненияВ левой части получим многочлен второй
степени с неопределенными коэффициентами,
который должен быть равен данному
многочлену второй степени в правой
части. Два многочлена будут равны тогда
и только тогда, когда равны коэффициенты
при одинаковых степенях х. Запишем
столбиком полученные уравнения:
,
чтобы получить левую часть уравненияВ левой части получим многочлен второй
степени с неопределенными коэффициентами,
который должен быть равен данному
многочлену второй степени в правой
части. Два многочлена будут равны тогда
и только тогда, когда равны коэффициенты
при одинаковых степенях х. Запишем
столбиком полученные уравнения:

 .
.
Получили систему трех уравнений с тремя неизвестными коэффициентами
А, В, С. Решив ее, найдем .
Частное решение:
5). Общее решение данного уравнения:
или
№ 2. Найти общее решение уравнения
1)
2)
3) Сравним
правую часть данного дифференциального
уравнения  с Отметим,
что
с Отметим,
что 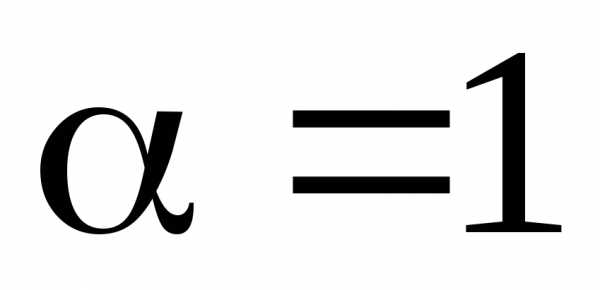 совпадает с одним корнем характеристического
уравнения; многочлен – число 3 – нулевой
степени, т. е.
совпадает с одним корнем характеристического
уравнения; многочлен – число 3 – нулевой
степени, т. е. .
Поэтому частное решение
.
Поэтому частное решение следует искать в виде
следует искать в виде
4) Запишем
Подставив выражения с указанными коэффициентами в данное дифференциальное уравнение, получим
или
откуда  Частное решение:
Частное решение:
5) Искомое общее решение данного уравнения:
№ 3.
3) Сравним правую часть данного уравнения с
Отмечаем, что 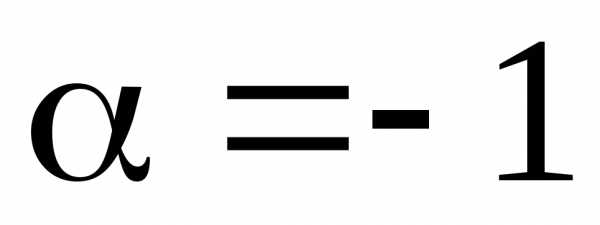 совпадает с одним корнем характеристического
уравнения и многочленх степени
совпадает с одним корнем характеристического
уравнения и многочленх степени 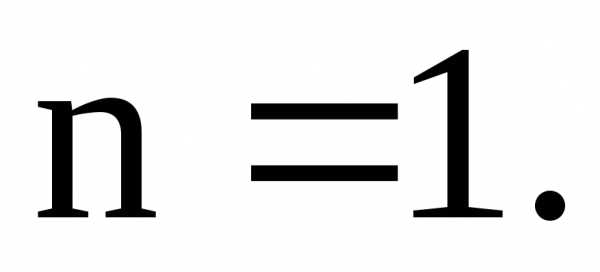 Поэтому частное решение следует искать
в виде
Поэтому частное решение следует искать
в виде
4) Так как
требуется найти
удобнее записать в виде
в виде
Запишем столбиком:
Подставим выражения  с указанными коэффициентами в данное
уравнение. Получим равенство
с указанными коэффициентами в данное
уравнение. Получим равенство
Разделим уравнение
на 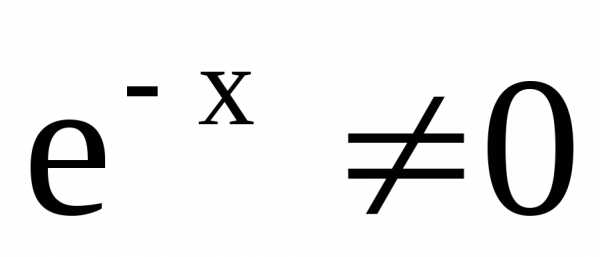 и упростим:
и упростим:



Частное решение:
Общее решение дифференциального уравнения:
Пусть правая
часть  уравнения (13)
уравнения (13)
имеет вид
где  – постоянные числа. Тогда вид частного
решения
– постоянные числа. Тогда вид частного
решения определяется следующим образом.
определяется следующим образом.
а) Если число  не есть корень характеристического
уравнения (16), то частное решение
не есть корень характеристического
уравнения (16), то частное решение имеет вид
имеет вид
где А и В – постоянные неопределенные коэффициенты.
б) Если число есть корень характеристического уравнения (16), то
Сделаем важное
замечание. Даже тогда, когда в правой
части уравнения стоит выражение,
содержащее только  или только
или только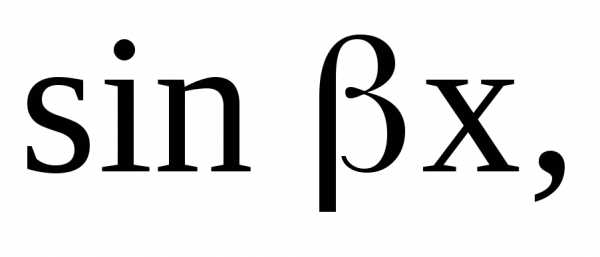 следует искать частное решение в том
виде, в каком оно было указано, т. е. с
синусом и косинусом. Иными словами, из
того, что правая часть не содержит
следует искать частное решение в том
виде, в каком оно было указано, т. е. с
синусом и косинусом. Иными словами, из
того, что правая часть не содержит или
или не следует, что частное решение уравнения
не содержит этих функций.
не следует, что частное решение уравнения
не содержит этих функций.
Пример № 1. Решить уравнение
1)
2)
3) Сравним правую часть уравнения с. ЗдесьТак как числане являются корнями характеристического уравнения, частное решение следует искать в виде
4) Найдем  и запишем столбиком
и запишем столбиком
Подставив эти выражения в данное дифференциальное уравнение, получим
или
Приравниваем коэффициенты при в левой и правой частях уравнения, получим систему уравнений:

Частное решение:
Общее решение данного дифференциального уравнения:
Пример № 2. Решить уравнение
1)
2)
3) Cравним правую часть уравнения с
Здесь Числане являются корнями характеристического уравнения. Частное решение следует искать в виде
4) Запишем

Подставив в уравнение, получим
или
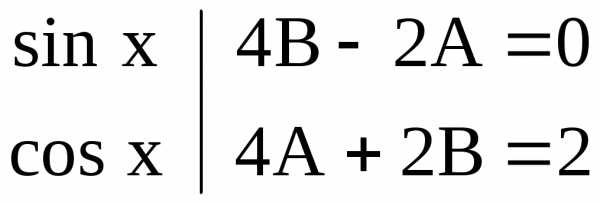
 .
.
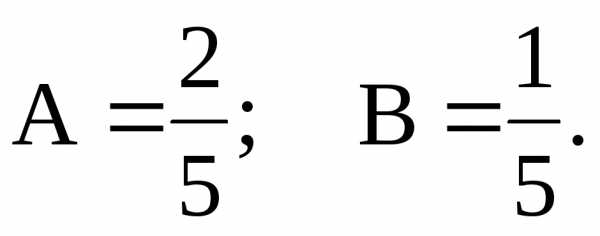
Частное решение:
5) Общее решение данного дифференциального уравнения:
Пусть правая
часть  неоднородного линейного д.у.II
представляет собой сумму функций
вида или
неоднородного линейного д.у.II
представляет собой сумму функций
вида или
Частное решение  этого уравнения следует искать в виде
суммычастных решений двух уравнений:
этого уравнения следует искать в виде
суммычастных решений двух уравнений:
и
№ 3. Решить уравнение
Здесь
1)
2)
3) При
 .
.


4) При



5) Общее решение данного дифференциального уравнения:
или
studfiles.net
Занятие №2. Решение однородных уравнений первого порядка
Цель занятия: знать и уметь решать типовые дифференциальные однородные уравнения первого порядка; воспитание навыков самостоятельной деятельности, организованности.
Учебные вопросы
1. Решение однородных уравнений первого порядка.
Ход занятия
Студенты должны знать ответ на следующие теоретические вопросы:
1. Определение однородного дифференциального уравнения первого порядка
2. Алгоритм решения дифференциального однородного уравнения первого порядка.
Основные рабочие формулы
Уравнение
| (*) |
однородное, если оно может быть приведено к виду: . При помощи подстановки , получим и уравнение (*) сведется к уравнению с разделяющимися переменными.
Задача 1. Проинтегрировать дифференциальное уравнение:
.
Решение. 1) Проверка однородности функции: Выразим т.е.
2) Сделаем подстановку или , тогда , подставим в 1):
или .
3) Разделяем переменные и интегрируем:
,
получим
4) Подставим :
.
Ответ:
Задача 2. Решить самостоятельно дифференциальное уравнение по образцу задачи 1: .
Задача 3. Найти общее и частное решение уравнения:
Решить уравнения:
Задача 4. .
Задача 5. .
Задача 6. .
Задача 7. .
Объяснить алгоритм решения одного из дифференциальных уравнений данного занятия.
Задание для самостоятельной работы
Решить уравнения:
Задача 8. .
Задача 9. .
Задача 10. ;
Задача 11. при ;
Задача 12. ;
Задача 13. ;
Задача 14. .
Занятие №3. Решение линейных дифференциальных уравнений первого порядка. Уравнение Бернулли
Цель занятия: уметь решать линейные дифференциальные уравнения первого порядка, знать подстановку, сводящую уравнение Бернулли к линейному уравнению; воспитание элементов самостоятельных навыков, целеустремленности.
Учебные вопросы
1. Решение линейных дифференциальных уравнений первого порядка.
2. Решение дифференциального уравнения Бернулли.
Ход занятия
Студенты должны предварительно подготовить теоретический материал лекции к данному практическому занятию по вопросам:
1. Определение линейного дифференциального уравнения первого порядка.
2. Алгоритм решения линейного уравнения первого порядка.
3. Вид уравнения Бернулли, алгоритм его решения.
Рабочие формулы
1) Вид линейного дифференциального уравнения I порядка:
| (1) |
Решение ищется в виде:
| (2) |
где
| (3) |
Подставляем (2) и (3) в (1):
| (4) |
Из уравнения (4) получим два уравнения с разделяющимися переменными:
| (5) | |
| (6) |
Решая уравнения (5) и (6), находим решение (2) уравнения (1).
2. Вид дифференциального уравнения Бернулли
| (7) |
Уравнение (7) разделим на , тогда
| (8) |
Вводится замена:
| (9) |
.
Подставляя (9) в (7) получим линейное уравнение первого порядка:
.
1. Решение линейных дифференциальных уравнений первого порядка
Задача 1. Решить линейное дифференциальное уравнение первого порядка:
| (*) |
Решение. 1) Полагаем, , тогда .
2) Подставляем в (*), получим:
;
.
3) Рассматриваем два уравнения:
| а) ; | (А) |
| б) | (В) |
4) Решаем уравнение с разделяющимися переменными:
(принимаем ).
5) Подставляем найденные значения в уравнение (Б):
;
.
6) Получим:
.
Ответ:
Решить самостоятельно уравнения по образцу задачи 1:
Задача 2. .
Задача 3. .
Задача 4. .
2. Решение дифференциального уравнения Бернулли
Задача 5. Решить дифференциальное уравнение Бернулли: .
Решение. 1) Делим обе части уравнения на
| (*) |
2) Сделаем замену , тогда .
3) Подставляем в уравнение (*): .
4) Решаем линейное уравнение .
5) Положим , тогда .
6) Решаем уравнение:
7) Подставляем значение v в уравнение:
8) Находим .
9) Найдем .
Ответ:
Задача 6. Решить самостоятельно уравнение Бернулли по образцу задачи 5:
.
Задание для самостоятельной работы
Задача 7. Решить линейное дифференциальное уравнение:
.
Задача 8. Решить линейное дифференциальное уравнение:
.
Задача 9. Решить уравнение Бернулли:
.
Решить уравнения:
Задача 10. ;
Задача 11. ;
Задача 12. ;
Задача 13. ;
Задача 14. ;
Задача 15. .
infopedia.su
Глава 87. Однородные дифференциальные уравнения первого порядка
Определение
Уравнения вида
, | (8.4.1) |
Называется Однородным, если и однородные функции степени .
Понятие однородного дифференциального уравнения связано с понятием однородной функции.
Определение
Функция называется Однородной функцией степени , если для произвольного числа выполняется равенство .
Пример
Выяснить, являются ли однородными следующие функции:
А) . Так как , то данная функция однородна степени 2.
Б) . . Функция однородна степени 0.
В) . . Данная функция неоднородная.
Дифференциальное уравнение вида (8.4.1) можно привести к виду
(8.4.2) |
И при помощи подстановки ( – неизвестная функция) преобразовать в уравнение с разделяющимися переменными. Поскольку , то Þ Þ Þ .После того, как общее решение последнего уравнения будет найдено, необходимо вернуться к старой функции .
Пример
Решить уравнение .
Решение
Разделим уравнение почленно на . Получим . Выполним замену . Следовательно, . Подстановка в исходное уравнение дает Þ – уравнение с разделяющимися переменными. Решая его, получим . Возвращаясь к функции , получим общее решение уравнения: .
Логарифмирование решения дает: .
Пример
Найти частное решение уравнения в точке .
Решение
Уравнение однородное нулевой степени – или . В результате подстановки (, ) получим уравнение с разделяющимися переменными относительно функции : . Интегрирование этого уравнения дает функцию: . Следовательно, общее решение исходного уравнения имеет вид: . Частное решение, соответствующее начальному условию, имеет вид: .
Определение
Дифференциальное уравнение вида
. | (8.4.3) |
Где и – непрерывные функции, называется Линейным дифференциальным уравнением первого порядка.
Неизвестная функция и ее производная входят в указанное уравнение линейно, что и объясняет название уравнения.
Если , то уравнение (8.4.3) называется Линейным однородным уравнением, если же , то уравнение (8.4.3) называется Линейным неоднородным уравнением.
Пусть линейное однородное уравнение.
(8.4.4) |
Соответствует уравнению (8.4.3). Мы рассмотрим так называемый метод вариации постоянной – метод решения неоднородного уравнения, основанный на предварительном решении однородного уравнения (8.4.4).
Уравнение (8.4.2) можно решить методом разделения переменных:
, откуда .
Потенцируя, получаем общее решение уравнения (8.4.4):
, | (8.4.5) |
Где .
Общее решение неоднородного уравнения (8.4.3) ищем в виде (8.4.5), полагая константу новой неизвестной функцией от аргумента.
. | (8.4.5а) |
Подставим решение (8.4.5а¢) в уравнение (8.4.3).
,
Откуда после приведения подобных получаем уравнение для :
. | (8.4.6) |
Интегрирование уравнения (8.4.4) дает выражение для : .
Подставляя выражение для в формулу общего решения, получаем окончательное выражение для решения неоднородного уравнения:
, | (8.4.7) |
Где – произвольная постоянная.
Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции . К таковым относится Уравнение Бернулли:
, | (8.4.8) |
Где и – непрерывные функции, а – некоторое постоянное число. При имеем линейное неоднородное уравнение, а при – линейное однородное уравнение .
Пусть и . Введем новую функцию . Тогда . Поделим обе части уравнения (8.4.8) на и умножим на : .
Выполняя замену, получим линейное неоднородное уравнение относительно новой функции : . Метод решения последнего нами уже изучен.
Пример
Решить уравнение .
Решение
Это линейное неоднородное уравнение первого порядка. Сначала решим соответствующее однородное уравнение . Разделяя переменные, получим Þ .
Полагая функцией от и подставляя найденное решение в исходное неоднородное уравнение, получаем после приведения подобных дифференциальное уравнение для : .
После интегрирования этого уравнения и подстановки в уже найденное решение однородного уравнения получим искомое общее решение исходного уравнения: .
Пример
Решить уравнение .
Решение
Опять начнем с однородного уравнения . После разделения переменных и интегрирования уравнения получаем общее решение однородного уравнения . Полагая, что , получаем после подстановки в неоднородное уравнение . Откуда . Стало быть, общее решение исходного уравнения имеет вид .
Пример
Решить уравнение .
Решение
Данное нелинейное уравнение представляет собой уравнение Бернулли при . Заменой искомой функции мы получим линейное неоднородное уравнение относительно : . По формуле (8.4.7) получаем общее решение этого уравнения . Теперь выполняя обратную замену , получаем решение исходного нелинейного уравнения:
Рассмотрим еще один из возможных способов решения линейного неоднородного уравнения (8.4.3) и уравнения Бернулли (8.4.8).
Решение этих уравнений ищем в виде произведения двух функций . Тогда линейное уравнение и уравнение Бернулли сводятся к двум уравнениям с разделяющимися переменными.
Так как , то линейное уравнение (8.4.3) преобразуется к виду .
Найдем сначала какое–нибудь частное решение уравнения . Тогда функция Решение уравнения .
Пример
Решить уравнение .
Решение
Исходное уравнение есть линейное неоднородное уравнение . Пусть , тогда . Следовательно, или . Положим . Проинтегрировав это уравнение, найдем какое–нибудь частное решение этого уравнения . Например, при получаем . Подставляя в уравнение Функцию , получим уравнение относительно функции : . Решением этого уравнения с разделяющимися переменными есть функция . Окончательное выражение для решения исходного уравнения имеет вид .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Лекция Однородные дифференциальные уравнения первого порядка
Скачать с Depositfiles
Лекция 2
Однородные дифференциальные уравнения первого порядка
Определение: Функция 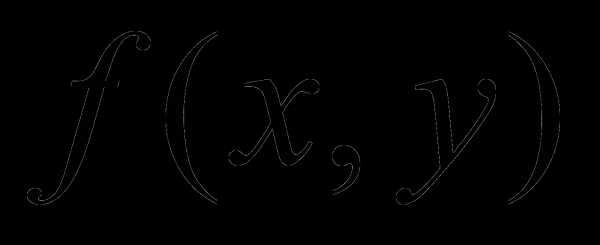 называется однородной функцией n-го измерения относительно переменных х и у, если при любом
называется однородной функцией n-го измерения относительно переменных х и у, если при любом  справедливо тождество
справедливо тождество
Примеры: — однородная функция первого измерения
— второго измерения
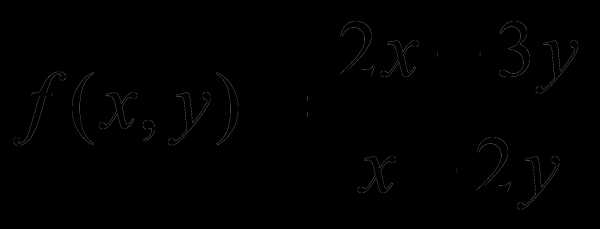 — нулевого измерения.
— нулевого измерения.
Определение. Дифференциальное уравнение первого порядка
 (1)
(1)
называется однородным относительно х и у, если функция  есть однородная функция нулевого измерения относительно х и у , т.е.
есть однородная функция нулевого измерения относительно х и у , т.е.
Решение однородного уравнения:
По условию: .
Полагая здесь  , получим:
, получим: 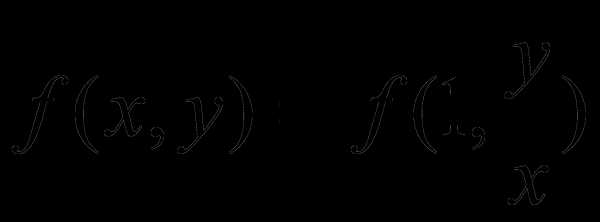 , и уравнение (1) запишем так:
, и уравнение (1) запишем так:
 (1’)
(1’)
Заметим, что перед делением на х следует проверить наличие частного решения  .
.
Сделаем подстановку  ;
;  ; .
; .
;
Подставляя сюда после интегрирования  , получим общий интеграл уравнения (1).
, получим общий интеграл уравнения (1).
Пример. Найти общий интеграл дифф. уравнения  .
.
Решение. Замена:  ; ;
; ;
 ;
; 
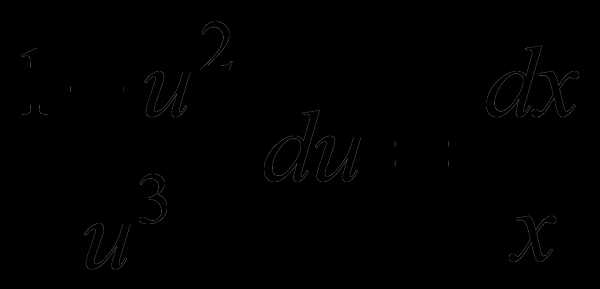

 — общий интеграл
— общий интеграл
Замечание: Уравнение вида будет однородным тогда и только тогда, когда  и
и 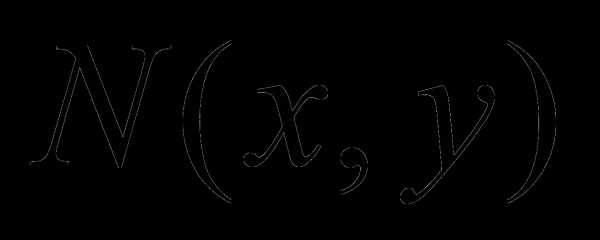 будут однородными функциями одного и того же измерения.
будут однородными функциями одного и того же измерения.
Пример. Найти общий интеграл уравнения: — однородное уравнение. Заметим, что оно допускает частное решение  .
.
Если 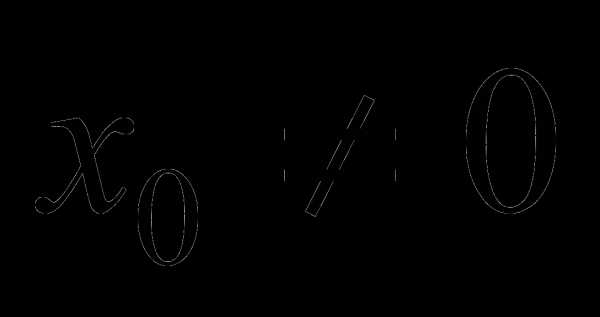 , то делаем замену
, то делаем замену  ; ; , ;
; ; , ;
 ; ;
; ; 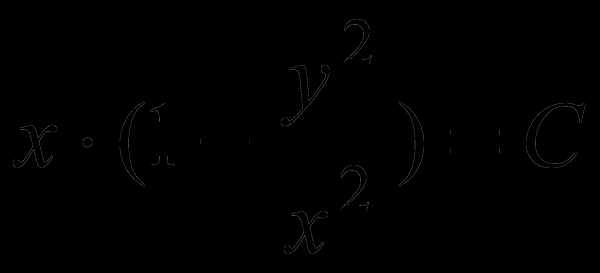 . – общий интеграл.
. – общий интеграл.
Определение:
Линейным ДУ первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной:
(1)
где  и
и 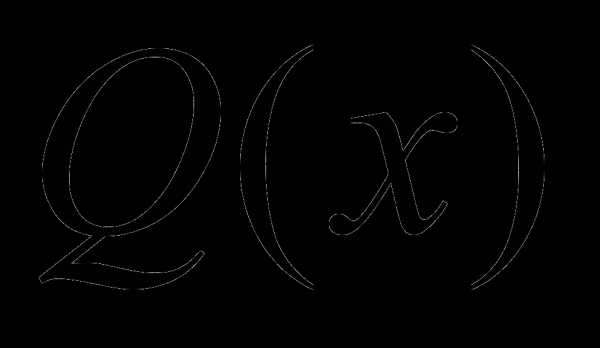 — непрерывные функции или константы.
— непрерывные функции или константы.
Решение уравнения (1) будем искать решение в виде произведения двух функций
(2)
Тогда
Тогда уравнение (1) можно записать в виде:
, или
(3)
Выберем  так, чтобы выполнялось равенство:
так, чтобы выполнялось равенство:
 (кроме
(кроме  ) (4)
) (4)
Тогда
Полагаем здесь  (нам нужно любое решение уравнения (4))
(нам нужно любое решение уравнения (4))
Окончательно получим общее решение в виде
Постоянную С можно найти из начальных условий: .
Пример: Решить задачу Коши

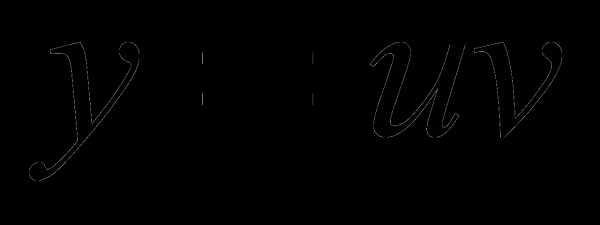 ;
;  ;
;
Уравнение Бернулли
Уравнения вида
(1)
где 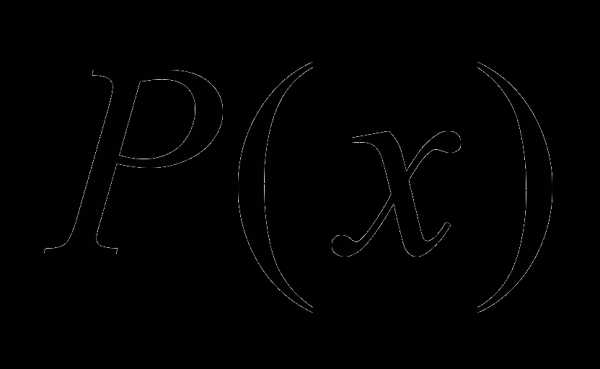 и
и  – непрерывные функции (или константы),
– непрерывные функции (или константы), 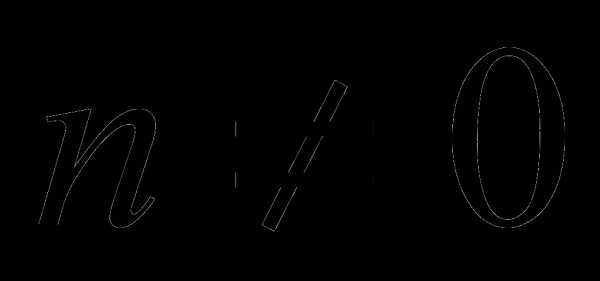 и
и  , называется уравнениями Бернулли. Заметим, что они допускают нулевое решение
, называется уравнениями Бернулли. Заметим, что они допускают нулевое решение  . Если
. Если , то они приводятся к линейным уравнениям заменой
, то они приводятся к линейным уравнениям заменой
(2)
Поделим обе части уравнения (1) на  , получим
, получим
(3)
(4)
-линейное д.у. Найдем его общее решение, сделаем в нем обратную замену  и получим общее решение уравнения (1).
и получим общее решение уравнения (1).
Пример. Найти общее решение уравнения
 (5)
(5)
Уравнение имеет нулевое решение . Найдем другие решения.
;  ;
; 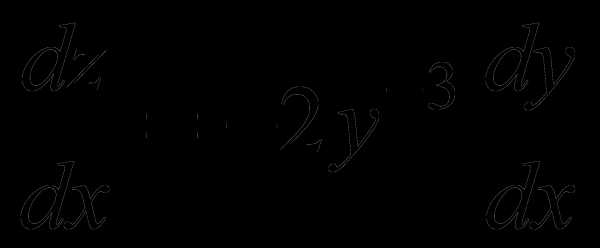 ;
;
 — линейное д.у.
— линейное д.у.
Практика
1. Уравнения с разделяющимися переменными.
1); 2);  ;
;
3); 4)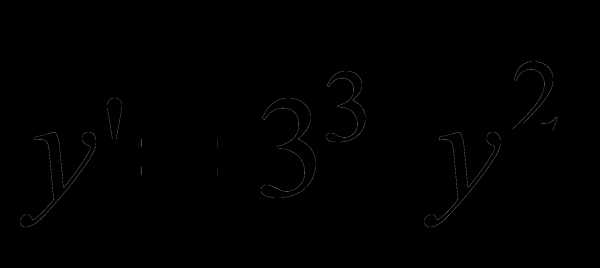 ;
; 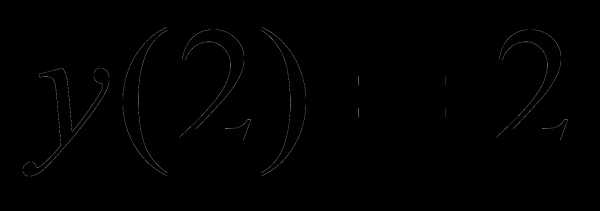 ;
;
2. Однородные
1); ;  ;
;
2); 3);
4); 5) ;
;
6) ;
3. Линейные первого порядка
1) ; 2);
3); 4).
4. Уравнения Бернулли
1); 2).
Скачать с Depositfiles
greleon.ru
Однородные дифференциальные уравнения первого порядка — Мегаобучалка
На данном уроке мы рассмотрим так называемые однородные дифференциальные уравнения первого порядка. Наряду с уравнениями с разделяющимися переменными и линейными неоднородными уравнениями этот тип ДУ встречается практически в любой контрольной работе по теме диффуров. Если Вы зашли на страничку с поисковика или не очень уверенно ориентируетесь в дифференциальных уравнениях, то сначала настоятельно рекомендую проработать вводный урок по теме – Дифференциальные уравнения первого порядка. Дело в том, что многие принципы решения однородных уравнений и используемые технические приемы будут точно такими же, как и для простейших уравнений с разделяющимися переменными.
В чём отличие однородных дифференциальных уравнений от других типов ДУ? Это проще всего сразу же пояснить на конкретном примере.
Пример 1
Решить дифференциальное уравнение
Решение:
Что в первую очередь следует проанализировать при решении любого дифференциального уравнения первого порядка? В первую очередь необходимо проверить, а нельзя ли сразу разделить переменные с помощью «школьных» действий? Обычно такой анализ проводят мысленно или пытаются разделить переменные на черновике.
В данном примере переменные разделить нельзя (можете попробовать поперекидывать слагаемые из части в часть, повыносить множители за скобки и т.д.). Кстати, в данном примере, тот факт, что переменные разделить нельзя, достаточно очевиден ввиду наличия множителя .
Возникает вопрос – как же решить этот диффур?
Нужно проверить, а не является ли данное уравнение однородным? Проверка несложная, и сам алгоритм проверки можно сформулировать так:
В исходное уравнение:
вместо подставляем , вместо подставляем , производную не трогаем:
Буква лямбда – это некоторый абстрактный числовой параметр, дело не в самих лямбдах, и не в их значениях, а дело вот в чём:
Если в результате преобразований удастся сократить ВСЕ «лямбды» (т.е. получить исходное уравнение), то данное дифференциальное уравнение является однородным.
Очевидно, что лямбды сразу сокращаются в показателе степени:
Теперь в правой части выносим лямбду за скобки:
Обе части уравнения можно сократить на эту самую лямбду:
В результате все лямбды исчезли как сон, как утренний туман, и мы получили исходное уравнение.
Вывод: Данное уравнение является однородным
Поначалу рекомендую проводить рассмотренную проверку на черновике, хотя очень скоро она будет получаться и мысленно.
megaobuchalka.ru

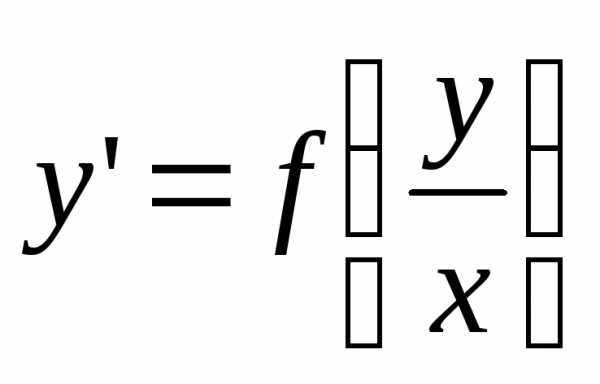 ,
,
 ,
, ,
, ,
находими
подставляем эти выражения в уравнение.
,
находими
подставляем эти выражения в уравнение.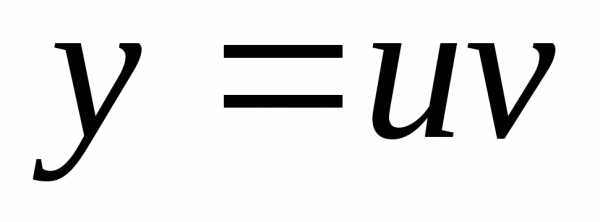 .
.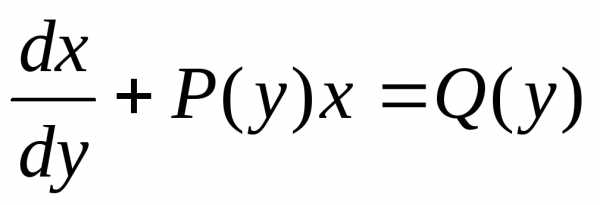

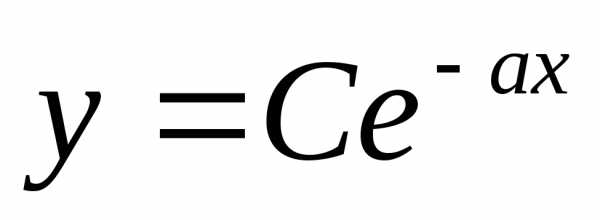
 )
) есть простой (однократный) корень
характеристического уравнения (т. е.
есть простой (однократный) корень
характеристического уравнения (т. е. совпадает с одним корнем характеристического
уравнения). В этом случае частное решение
нужноискать
в виде .
совпадает с одним корнем характеристического
уравнения). В этом случае частное решение
нужноискать
в виде . есть двукратный корень характеристического
уравнения (т. е.
есть двукратный корень характеристического
уравнения (т. е. совпадает с двумя равными корнями
характеристического уравнения). В этом
случае частное решение нужноискать
в виде Неизвестные (неопределенные) коэффициенты
многочлена
совпадает с двумя равными корнями
характеристического уравнения). В этом
случае частное решение нужноискать
в виде Неизвестные (неопределенные) коэффициенты
многочлена находим из условия, что функция
находим из условия, что функция является решением уравнения (13), т. е.
удовлетворяет этому уравнению.
является решением уравнения (13), т. е.
удовлетворяет этому уравнению.