Вариант 1. Вариант 2. Вариант 3
Контрольная работа 2
Контрольная работа 2 Вариант 1 f={(2,2),(2,3),(3,2),(3,3),(4,4)} (x y) (z y) 3. В коробке лежат 6 красных и 5 синих карандашей. Наудачу достают 4 карандаша. Какова вероятность того, что будут взяты 2 красных
ПодробнееВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ
ВЕРОЯТНОСТЬ СЛУЧАЙНОГО СОБЫТИЯ Аксиомы Колмогорова В 1933 г. А. Н. Колмогоров в книге «Основные понятия теории вероятностей» дал аксиоматическое обоснование теории вероятностей. «Это означает, что, после
Подробнее ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ.

ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ. Теория вероятностей — раздел математики, изучающий закономерности, возникающие в случайных испытаниях. Исход испытания — случайный по отношению к испытанию, если в ходе этого
ПодробнееОсновные положения теории вероятностей
Основные положения теории вероятностей Случайным относительно некоторых условий называется событие, которое при осуществлении этих условий может либо произойти, либо не произойти. Теория вероятностей имеет
ПодробнееСлучайные события. Вариант 1.
Вариант 1. 1. Среди 20 свёрл 5 изношенных. Наудачу берутся 3 сверла. Какова вероятность того, что хотя бы одно из них изношенное. 3. В двух партиях процент доброкачественных изделий соответственно равны
ПодробнееЗадание Из карточек с цифрами 1, 2, 3, 4, 5 выбирается наугад карточка с числом а, а затем карточка с числом в.
 Из них составляется дробь а/в.
Из них составляется дробь а/в.КОНТРОЛЬНЫЕ ЗАДАНИЯ Задание 1 1.1 Из карточек с цифрами 1, 2, 3, 4, 5 выбирается наугад карточка с числом а, а затем карточка с числом в. Из них составляется дробь а/в. Какова вероятность того, что эта
ПодробнееПредлагаются задания в 20 вариантах.
Предлагаем 0 вариантов контрольной работы по математике. Годовая контрольная работа по алгебре и началам математического анализа в 11 классах, для тех, кто обучается по учебнику авторов: Ш.А. Алимов, Ю.М.
Подробнеер и x F( x ) ри 0 р и x
Билет 1 1. После исследований 60 нивелиров установили, что 16 из них пригодны для нивелирования I класса, остальные II класса. Определить частость нивелиров I и II класса. 2. Из колоды карт в 36 листов
ПодробнееТема 33 «Вероятности событий»
Тема 33 «Вероятности событий» Все мы довольно часто говорим «это невероятно», «более вероятно, что», «это маловероятно» и т. д., когда пытаемся спрогнозировать наступление того или иного события. При этом
д., когда пытаемся спрогнозировать наступление того или иного события. При этом
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ.
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ. 3.1. Случайные события. Каждая наука при изучении явлений материального мира оперирует теми или иными понятиями, среди которых обязательно имеются основополагающие;
ПодробнееБилет 1 1. После исследований 60 нивелиров установили, что 15 из них пригодны для нивелирования I класса, остальные II класса. Определить частость нивелиров I и II класса. 2. Из колоды карт в 36 листов
ПодробнееМАТЕМАТИКА. Москва 2016г.
МАТЕМАТИКА Методические указания и задания на контрольные работы, для студентов курса заочной формы обучения Специальность:.0.0 Подвижной состав железных дорог(псс) Специализации все Москва 06г. Методические
Методические
ID_5358 1/7 neznaika.pro
1 Начала теории вероятностей Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов. В чемпионате
Вероятностный подход к
Вероятностный подход к измерению информации Вероятность — доля успеха того или иного события. Обозначаеся буквой Р (от латинского Probabilitas — вероятность). Если интересующее нас событие может произойти
Подробнее{ξ < 1} независимыми в совокупности.
1. Электричка состоит из 12 вагонов. Каждый из 7 пассажиров наудачу выбирает любой вагон. Найти вероятности следующих событий: A = {все пассажиры сели в первые три вагона}; B = {все пассажиры сели в разные
Подробнеезадания балл баллы по заданиям 1 0,8 а) 0,4 б) 0,4 2 0,5 0,5 3 2,0 а) 0,5 б) 0,5 в) 0,5 г) 0,5 4 0,5 0,5 5 0,5 0,5 6 0,7 а) 0,3 б) 0,4 сумма 5 5
Перечень тем курса к письменному экзамену по ОУД. Математика: алгебра, начала математического анализа, геометрия для студентов курса. Уравнения и неравенства.. Координаты и векторы.. Начала математического
Математика: алгебра, начала математического анализа, геометрия для студентов курса. Уравнения и неравенства.. Координаты и векторы.. Начала математического
ЗАДАЧИ ПО ТЕОРИИ ВЕРОЯТНОСТЕЙ ЧАСТЬ I
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛБНОГО ОБРАЗОВАНИЯ «РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Подробнее09. Статистика, вероятности Часть 1. ФИПИ
09. Статистика, вероятности Часть 1. ФИПИ I) Классическое определение вероятности, основные теоремы 1. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей наугад берёт
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ В задачах 1 29 построить множество элементарных исходов Ω по описанию эксперимента и подмножества, соответствующие указанным событиям, а также вычислить вероятности событий.
Задачи по теории вероятностей.
Задачи по теории вероятностей.. Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросили четыре бомбы, вероятность попадания
ПодробнееКонтрольная точка С1 (экономические направления, 4 семестр, 2016) ( 1 2 балла, 2, 3, 4 по 1 баллу, 5 5 баллов)
Контрольная точка С1 (экономические направления, 4 семестр, 2016) ( 1 2 балла, 2, 3, 4 по 1 баллу, 5 5 баллов) Вариант 1 1. Для участия в студенческих отборочных спортивных соревнованиях выделено из первой ПодробнееКОМБИНАТОРНАЯ ВЕРОЯТНОСТЬ
КОМБИНАТОРНАЯ ВЕРОЯТНОСТЬ Тема 5 Перевод осуществлен при поддержке IT Akadeemia Содержание лекции 1 Введение 2 3 4 Следующий пункт 1 Введение 2 3 4 Проблема. .. Проблема… Проблема… … и решение: Девочка
.. Проблема… Проблема… … и решение: Девочка
ЧАСТЬ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
1 ЧАСТЬ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ ГЛАВА 1. 1. Элементы комбинаторики Определение 1. Примеры: Определение. -факториал это число, обозначаемое!, при этом! = 1** * для всех натуральных чисел 1,, ; кроме того,
Подробнее1. Теория пределов. Найдите пределы.
Темы и примеры для подготовки к экзамену по математике.0.0 Автомеханик курс Темы курса, для экзамена.. Теория пределов..векторы в пространстве.. Многогранники и фигуры вращения 4.Производная функции. 5.Исследование
ПодробнееКОНТРОЛЬНЫЕ ЗАДАНИЯ Задание 1.
КОНТРОЛЬНЫЕ ЗАДАНИЯ Задание. Необходимо решить задачу соответствующую номеру Вашего варианта. В ящике находятся катушки четырех цветов: белых 5 красных зеленых синих 0. Какова вероятность того что наудачу
Какова вероятность того что наудачу
Данный файл получен на сайте
Добавить вопрос МАТЕМАТИКА 1 Суммой (объединением) нескольких событий называется 2 Произведением (пересечением) двух событий А и В называется 3 Сколько существует различных пятизначных номеров, в которых
ПодробнееМатематика (БкПл-100)
Математика (БкПл-100) М.П. Харламов 2011/2012 учебный год, 1-й семестр Лекция 5. Тема: Комбинаторика, введение в теорию вероятностей 1 Тема: Комбинаторика Комбинаторика это раздел математики, изучающий
ПодробнееУважаемые студенты! Внимание!
Уважаемые студенты! Номер Вашего варианта контрольной работы определяется по номеру Вашей зачетной книжки. Откройте Вашу зачетную книжку и посмотрите на две последние цифры в её номере.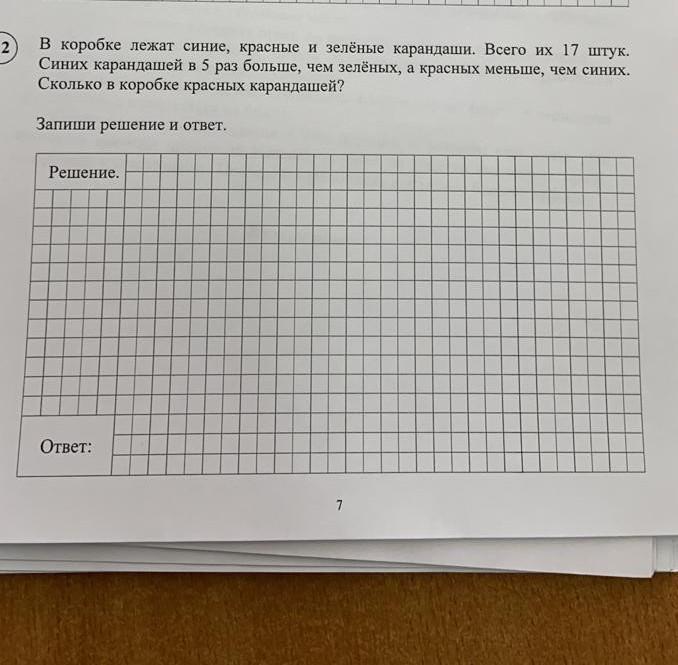 Обозначим эти две
Обозначим эти две
со стороной 3 см, находящийся внутри ABCD.
Примерные задания для подготовки к зачету по математике по теме «Теория вероятностей и математическая статистика» для студентов специальности 270100 4 семестр 1 часть. Теория вероятностей. 1.Комбинаторика.
Вариант 1. lim 3 R , 3
Вариант 1 1. Что вероятней: при бросании 4 игральных костей хотя бы на одной получить единицу, или при 24 бросаниях двух костей хотя бы раз получить 2 единицы? Ответ: 0.52;0.49. 2. Вероятность столкновения
ПодробнееОшибка 404 — страница не найдена
8 (800) 555 96 91
Звонок по России бесплатный
Звонок бесплатный
- Аэрография
- Книги по искусству
- Грунт, связующие, разбавители
- Бумага и картон
- Гипсовые фигуры и манекены
- Графика, рисунок, скетчинг
- Краски художественные
- Инструменты и аксессуары
- Канцелярские товары
- Кисти художественные
- Холсты и другие основы
- Рамы и подрамники
- Скульптура и лепка
- Папки, портфолио, тубусы
- Черчение
- Золочение и реставрация
- Каллиграфия
- Оборудование и мебель
- Предметы для декора
- Краски и эффекты для декора
- Пластика и пластилин
- Для детского творчества
- Декупаж, декопатч, мозаика
- Декорирование
- Батик и декорирование ткани
- Мольберты и этюдники
- Макетирование
- SALE
Контрольная работа № 5. Элементы теории вероятностей.
Элементы теории вероятностей.
5.1. В коробке находится 4 синих, 5 красных и 5 зеленых карандашей. Одновременно вынимают 10 карандашей. Найти вероятность того, что среди них будет 3 синих и 3 красных карандашей.
Решение
В коробке всего 4+5+5=14 карандашей. При данном испытании число всех равновозможных элементарных исходов будет . Подсчитаем число элементарных исходов, благоприятствующих событию А. Три синих карандаша из 4 можно выбрать способами, три красных карандаша из 5 можно выбрать способами, оставшиеся четыре зеленых из 5 – способами. Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет .
По формуле находим искомую вероятность
.
Ответ:
5.2. На склад поступили 2 ящика, в которых содержится по 20 годных деталей и 4 бракованных и 2 ящика, в которых содержится по 40 годных деталей и 6 бракованных. Наудачу выбирается ящик и из него наудачу извлекается деталь. Найти вероятность того, что вынутая деталь является годной.
Найти вероятность того, что вынутая деталь является годной.
Решение
Событие А – вынутая деталь является годной.
Возможны следующие гипотезы:
– выбран ящик, в котором 20 годных деталей и 4 бракованных
– выбран ящик, в котором 40 годных деталей и 6 бракованных.
Вероятности гипотез равны: .
Условные вероятности события А при этих гипотезах равны: , .
По формуле полной вероятности
.
Ответ:
5.3. Вероятность попадания стрелка в мишень при одном выстреле равна . Производится 6 выстрелов. Найти вероятность того, что он промахнется не более двух раз.
Решение
Поскольку , то . По условию ,
Вероятность того, что стрелок промахнется не более двух раз равна вероятности того, что стрелок попадёт 6, 5 или 4 раза. То есть , по формуле Бернулли найдём
.
Используя правило сложения вероятностей независимых событий найдём искомую вероятность:
Ответ:
5. 4. Ряд распределения дискретной случайной величины Х имеет вид:
4. Ряд распределения дискретной случайной величины Х имеет вид:
Найти вероятности , если математическое ожидание . Построить многоугольник распределения. Найти функцию распределения и построить ее график. Вычислить дисперсию и среднее квадратическое отклонение.
Решение
Сумма вероятностей ряда распределения . В нашем случае: .
Математическое ожидание находится по формуле , в нашем случае
.
Получаем систему двух уравнений с двумя неизвестными для нахождения и : ,
Решая которую находим .
Тогда ряд распределения дискретной случайной величины Х имеет вид:
0 | 2 | 4 | |||
0,2 | 0,1 | 0,2 | 0,4 | 0,1 |
Построим многоугольник распределения, для этого в прямоугольной системе координат строим точки , , , , , затем соединяем эти точки отрезками прямых. Ломаная является многоугольником распределения данной случайной величины.
Ломаная является многоугольником распределения данной случайной величины.
Для нахождения функции распределения ДСВ Х используем формулу :
При ,
При ,
При ,
При при при Итак,
.
График функции распределения :
Дисперсия дискретной случайной величины находится по формуле , в нашем случае
Среднее квадратическое отклонение находится по формуле , в нашем случае .
5.5. Плотность распределения непрерывной случайной величины Х имеет вид: .
Найти: а) параметр А;
Б) функцию распределения ;
В) вероятность попадания случайной величины Х в интервал ;
Г) математическое ожидание и дисперсию .
Решение
Для определения значения А воспользуемся условием . Вычислим интеграл
,
Плотность распределения случайной величины Х примет вид
Для того, чтобы найти функцию распределения , воспользуемся формулой .
При получаем ,
При находим
При : .
Таким образом, искомая функция распределения имеет вид
Вероятность попадания СВ Х в интервал найдем по формуле , она будет равна
.
Математическое ожидание находим по формуле :
Дисперсию найдем по формуле :
,
Тогда .
| < Предыдущая | Следующая > |
|---|
Теория вероятностей. Решение задач (ЕГЭ — 2021)
Так стоп! Новое определение.
Несовместными называются события, которые никак не могут произойти одновременно в результате эксперимента. Ряд несовместных событий образуют полную группу событий. |
Давай разбираться. Возьмем нашу изношенную монетку и бросим её \( 3\) раза.
Возможные варианты:
Так вот, несовместные события – это определенная, заданная последовательность событий. \( 1),\text{ }2),\text{ }3),\text{ }4)\ldots \text{ }8)\) – это несовместные события.
\( 1),\text{ }2),\text{ }3),\text{ }4)\ldots \text{ }8)\) – это несовместные события.
Вероятности несовместных событий складываются. |
Если мы хотим определить, какова вероятность двух (или больше) несовместных событий, то мы складываем вероятности этих событий.
Нужно понять, что выпадение орла или решки – это два независимых события.
Если мы хотим определить, какова вероятность выпадения последовательности \( 1\)) (или любой другой), то мы пользуемся правилом умножения вероятностей.
Какова вероятность выпадения при первом броске орла, а при втором и третьем решки?
\( \displaystyle p=\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}=\frac{1}{8}\)
Но если мы хотим узнать, какова вероятность выпадения одной из нескольких последовательностей, например, когда орел выпадет ровно \( 1\) раз, т.е. варианты \( 4),\text{ }6)\) и \( 7)\), то мы должны сложить вероятности этих последовательностей.
Всего вариантов \( 8\), нам подходит \( 3\).
\( \displaystyle p=\frac{{{N}_{б}}}{N}=\frac{3}{8}\)
То же самое мы можем получить, сложив вероятности появления каждой последовательности:
\( \displaystyle p={{p}_{4}}+{{p}_{6}}+{{p}_{7}}=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\)
Таким образом, мы складываем вероятности, когда хотим определить вероятность некоторых, несовместных, последовательностей событий.
Есть отличное правило, помогающее не запутаться, когда умножать, а когда складывать:
Описав, что должно произойти, используя союзы «И» или «ИЛИ», вместо «И» ставим знак умножения, а вместо «ИЛИ» — сложения. |
Возвратимся к примеру, когда мы подбросили монетку \( 3\) раза, и хотим узнать вероятность увидеть орла \( 1\) раз.
Что должно произойти?
Должны выпасть:
(орел И решка И решка) ИЛИ (решка И орел И решка) ИЛИ (решка И решка И орел).
Вот и получается:
\( \displaystyle \left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)+\left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)+\left( \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2} \right)=\frac{1}{8}+\frac{1}{8}+\frac{1}{8}=\frac{3}{8}\)
Давай рассмотрим несколько примеров.
В коробке лежат красные, зеленые и синие карандаши. Известно, что всего карандашей 32 и сообщение о том, что из коробки достали синий карандаш содержит 2 бита информации, а зеленых карандашей в 2 раза больше чем красных.
Лабораторная работа по теме «Измерение информации»
В каждом варианте лабораторной работы по 7 заданий из приведенного ниже списка.
Задания
#1
(1 балл) #2
(2 балла) #3
(1 балл) #4
(2 балла) #5
(1 балл) #6
(2 балла) #7
(1 балл)
Вариант 1 1 34 39 51 63 69 88
Вариант 2 2 33 40 45 64 69 89
Вариант 3 3 32 41 46 64 70 72
Вариант 4 4 31 42 47 57 67 78
Вариант 5 5 30 43 48 58 66 82
Вариант 6 6 29 44 49 59 65 83
Вариант 7 7 28 39 50 60 68 85
Вариант 8 8 38 40 51 61 66 87
Вариант 9 9 37 41 52 63 70 71
Вариант 10 10 36 42 53 62 69 72
Вариант 11 11 35 43 54 60 70 73
Вариант 12 12 34 44 55 59 70 74
Вариант 13 13 33 44 56 58 67 75
Вариант 14 14 32 43 56 57 68 76
Вариант 15 15 31 42 55 64 65 77
Вариант 16 16 30 41 54 63 65 78
Вариант 17 17 29 40 53 62 69 79
Вариант 18 18 28 39 52 61 65 80
Вариант 19 19 27 39 51 60 66 81
Вариант 20 20 26 40 50 59 67 82
Вариант 21 1 25 41 49 58 70 83
Вариант 22 2 24 42 48 57 65 84
Вариант 23 3 23 43 47 64 69 85
Вариант 24 4 22 44 46 63 66 86
Вариант 25 5 21 44 45 62 68 87
В языке племени Мумбо-Юмбо всего 20 разных слов.
 Сколько бит нужно, чтобы закодировать любое из этих слов, если считать что все слова употребляются в языке с одинаковой частотой?
Сколько бит нужно, чтобы закодировать любое из этих слов, если считать что все слова употребляются в языке с одинаковой частотой?В доме 14 окон. Сколько различных сигналов можно подать, зажигая и гася свет в окнах? Сколько бит информации несет в себе каждый такой сигнал?
Для дистанционной передачи роботу различных команд применяются сигналы в 6 бит, причем сигнала в 5 бит недостаточно для передачи всех команд. Определите, в каких пределах находится число команд робота: минимально возможное и максимально возможное число команд.
Загадано число из промежутка от 32 до 65 включительно. Какое количество вопросов необходимо задать для угадывания числа и какое количество информации при этом получится?
Загадано число из промежутка от 65 до 128. Какое количество вопросов необходимо задать для угадывания числа и какое количество информации при этом получится?
Какое максимальное количество вопросов нужно задать, используя метод половинного деления, чтобы угадать число в диапазоне от 500 до 1000? Какое количество информации будет при этом получено?
В параллели 9-х классов четыре класса, в каждом из которых учится по 32 ученика.
 Сколько бит информации содержится в сообщении о том, что Орлов Василий учится в 9Б классе?
Сколько бит информации содержится в сообщении о том, что Орлов Василий учится в 9Б классе?В самолете 16 рядов кресел, в каждом ряду находится по 4 кресла, обозначенных буквами A,B,C,D. Сколько бит информации содержится в сообщении о том, что Алексеева Ирина купила билет на место 7D?
В лотерее выпало 5 шаров из N возможных и сообщение об этом содержит 35 бит информации. После розыгрыша очередного шара, он возвращался в игровой барабан. Чему равно N?
В поезде 8 вагонов, в каждом из которых одинаковое количество мест. Сообщение о том, что Петя купил билет в 5-ый вагон на 10-ое место, содержит 8 бит информации. Сколько мест в вагоне?
Требуется угадать целое число от 1 до N методом половинного деления, задав не более 10 вопросов. Каково максимально возможное значение числа N?
Некто из колоды 36 игральных карт наугад достал одну карту. Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это карта красной масти». Сколько бит информации мы получили?
Некто из колоды 36 игральных карт наугад достал одну карту.
 Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это карта пиковой масти». Сколько бит информации мы получили?
Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это карта пиковой масти». Сколько бит информации мы получили?Некто из колоды 36 игральных карт наугад достал одну карту. Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это одна карта из колоды». Сколько бит информации мы получили?
Некто из колоды 36 игральных карт наугад достал одну карту. Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это дама пик». Сколько бит информации мы получили?
Какое количество информации содержит сообщение о том, что в лотерее выпали шары с номерами 5, 18, 40, 51, если всего разыгрывалось 64 шара с номерами от 1 до 64? После выпадения каждый очередной шар возвращался в лотерейный барабан и участвовал в розыгрыше следующего номера.
В лотерее выпало 5 шаров из N возможных и сообщение об этом несет 35 бит информации. После выпадения каждый очередной шар возвращался в лотерейный барабан и участвовал в розыгрыше следующего номера. Чему равно N?
На улице Фруктовая построено 8 шестнадцатиэтажных домов с 4 подъездами.
 Почтальон Печкин живет в одном из этих домов. Сколько бит информации в сообщении о том, что почтальон Печкин живет в доме № 3, во втором подъезде на 13-м этаже?
Почтальон Печкин живет в одном из этих домов. Сколько бит информации в сообщении о том, что почтальон Печкин живет в доме № 3, во втором подъезде на 13-м этаже?Какое количество информации получит второй игрок при игре в крестики-нолики на поле 8х8, после первого хода первого игрока, играющего крестиками?
Какое количество информации Вы получили, если узнали на какое поле шахматной доски какая шахматная фигура и какого цвета поставлена?
В корзине лежат клубки шерсти трех цветов: желтого, белого и красного. Желтых клубков 2, белых – 4. Сколько клубков красной шерсти лежит в корзине, если известно, что сообщение о том, что из корзины достали красный клубок содержит 1 бит информации?
На остановке останавливаются автобусы маршрутов №8, 15, 27, 43, трамваев №1, 3 и троллейбусов №5, 8. Сколько бит информации содержит сообщение о том, что на остановку пришел трамвай?
В коробке лежат красные, зеленые и синие карандаши. Известно, что всего карандашей 32 и сообщение о том, что из коробки достали синий карандаш содержит 2 бита информации, а зеленых карандашей в 2 раза больше чем красных.
 Сколько красных карандашей в коробке?
Сколько красных карандашей в коробке?Некто из колоды 36 игральных карт наугад достал одну карту. Мы задали вопрос: «Что это за карта?». Был получен ответ: «Это одна из старших карт: валет, дама, король или туз». Сколько бит информации мы получили?
В корзине лежат 20 шаров. Из них 10 черных и 5 желтых. Какое количество информации несет сообщение о том, что из корзины случайным образом достали черный шар? Сколько информации будет в сообщении, что наугад достали желтый шар? Сколько информации в сообщении, что наугад вытащенный из корзины шар точно не черный и не желтый?
На остановке останавливаются автобусы с разными номерами. Сообщение о том, что к остановке подошел автобус с номером N1 несет 4 бита информации. Вероятность появления на остановке автобуса с номером N2 в два раза меньше, чем вероятность появления автобуса с номером N1. Сколько бит информации несет сообщение о появлении автобуса с номером N2 на остановке?
В коробке находятся кубики трех цветов: красного, желтого и зеленого.
 Причем желтых в два раза больше красных, а зеленых на 6 больше чем желтых. Сообщение о том, что из коробки случайно вытащили желтый кубик, содержало 2 бита информации. Сколько было зеленых кубиков?
Причем желтых в два раза больше красных, а зеленых на 6 больше чем желтых. Сообщение о том, что из коробки случайно вытащили желтый кубик, содержало 2 бита информации. Сколько было зеленых кубиков?На остановке останавливаются трамваи с разными номерами Сообщение о том, что подошел трамвай № 13 несет 1 байт информации. Вероятность появления на остановке трамвая № 4 в четыре раза больше, чем для трамвая № 13. Сколько бит информации несет сообщение о появлении трамвая №4?
Студенты группы изучают один из трех языков: английский, немецкий или французский. Причем 12 студентов не учат английский. Сообщение, что случайно выбранный студент Петров изучает английский, несет log23 бит информации, а что Иванов изучает французский – 1 бит. Сколько студентов изучают немецкий язык?
В корзине лежат белые и черные шары. Среди них 18 черных шаров. Сообщение о том, что из корзины достали белый шар несет 2 бита информации. Сколько всего шаров в корзине?
В корзине лежат фрукты – груши, яблоки, персики и бананы.
 Всего 32 штуки. Сообщение о том, что достали яблоко, несет 2 бита информации, а грушу – 4 бита. Персиков было столько же, сколько и бананов. Сколько было груш, яблок, персиков и бананов в корзине?
Всего 32 штуки. Сообщение о том, что достали яблоко, несет 2 бита информации, а грушу – 4 бита. Персиков было столько же, сколько и бананов. Сколько было груш, яблок, персиков и бананов в корзине?При оформлении текста использовалось некоторое количество шрифтов. Символы, набранные шрифтом “Times New Roman” встречаются в тексте в 2 раза чаще, чем символы, набранные шрифтом “Courier New”. Сколько бит информации в сообщении о том, что встретился символ, набранный шрифтом “Courier New”, если сообщение о том, что встретился символ, набранный шрифтом “Times New Roman” несет 3 бита информации?
В мешке у Деда лежит Мороза 32 воздушных шарика (все разного цвета), а в сумочке у Снегурочки – 32 игрушки, среди которых несколько одинаковых кукол. Маша получила в подарок шарик красного цвета и одну куклу. Сообщение об этом несет 6 бит информации. Сколько кукол было в сумочке у Снегурочки?
В корзине лежат 32 шара: черные, белые и красные. Сообщение о том, что достали черный шар несет 2 бита информации.
 Белых шаров в 3 раза больше красных. Сколько шаров каждого цвета было в корзине?
Белых шаров в 3 раза больше красных. Сколько шаров каждого цвета было в корзине?Имеется два ящика с шарами: в первом ящике одинаковое количество черных и белых шаров, во втором ящике 2 белых шара и 6 черных. Из каждого ящика достали по одному белому шару. Сколько бит информации содержится в этом сообщении?
В корзине лежат белые и черные шары. Сообщение о том, что достали черный шар, несет на 2 бита больше информации, чем сообщение о том, что достали белый шар. Определите, каких шаров в корзине больше и во сколько раз.
Ученика А вызывают к доске в 8 раз реже, чем ученика В. Количество бит информации в сообщении о том, что вызвали ученика А обозначим iA, ученика B – iB. Определите, какая величина больше iA или iB и на сколько.
В корзине лежат черные и белые шары. Черных шаров в 16 раз больше, чем белых. Количество информации (в битах) в сообщении о том, что из корзины достали черный шар, обозначим iЧ; белый шар – iБ. Определите, какая величина больше iБ или iЧ и на сколько.

Дано множество из пяти сообщений хi с указанными в таблице вероятностями определить энтропию для данных сообщений.
Сообщения Вероятности
х1 0,35
х2 0,25
х3 0,1
х4 0,20
х5 0,10
Дано множество из пяти сообщений хi с указанными в таблице вероятностями. Определить энтропию для данных сообщений.
Сообщения Вероятности
х1 0,4
х2 0,15
х3 0,15
х4 0,15
х5 0,15
Дано множество из пяти сообщений хi с указанными в таблице вероятностями. Определить энтропию для данных сообщений.
Сообщения Вероятности
х1 0,3
х2 0,2
х3 0,1
х4 0,25
х5 0,15
Дано множество из пяти сообщений хi с указанными в таблице вероятностями. Определить энтропию для данных сообщений.
Сообщения Вероятности
х1 0,5
х2 0,1
х3 0,1
х4 0,2
х5 0,1
Дано множество из пяти сообщений хi с указанными в таблице вероятностями. Определить энтропию для данных сообщений.
Сообщения Вероятности
х1 0,35
х2 0,1
х3 0,15
х4 0,2
х5 0,2
Дано множество из пяти сообщений хi с указанными в таблице вероятностями.
 Определить энтропию для данных сообщений.
Определить энтропию для данных сообщений.Сообщения Вероятности
х1 0,4
х2 0,1
х3 0,2
х4 0,15
х5 0,15
Определите среднее количество информации, приходящееся на символ алфавита, если алфавит включает в себя 11 строчных и 11 прописных букв, 10 цифр и 8 знаков препинания.
В алфавите племени Мумба-Юмба всего 4 буквы (А, У, М, Б), один знак препинания (точка) и для разделения слов используется пробел. Подсчитали, что в популярном романе «Мумбаюм» содержится всего 10 000 знаков, из них: букв А – 4000, букв У – 1000, букв М – 2000, букв Б – 1500, точек – 500, пробелов – 1000. Какой объем информации в мегабайтах содержит книга?
Пусть рассматривается алфавит из двух символов русского языка – «К» и «А». Относительная частота встречаемости этих букв равна, соответственно, р1=0,028, р2=0,062. Возьмем произвольное слово длины N из k букв «К» и m букв «А». Какое количество информации содержится в таком слове?
Алфавит племени состоит из 4 букв – a, b, c, d. В тексте из 64 символов встречаются: «а» – 32 раза, «b» – 16, «с» – 8, «d» – 8. Какое количество информации несет в себе любое слово из этого текста, составленное из 5 букв?
Сообщение записано в виде десятичного числа из 5 цифр, причем предполагается, что все цифры равновероятны и независимы. Какое количество информации несет это сообщение? Во сколько раз меньшее количество информации содержало бы сообщение, состоящее из 5 двоичных цифр?
Предположим, вероятность того, что вы получите за контрольную работу оценку “5”, равна 0,6; вероятность получения “4” равна 0,2; вероятность получения “3” — 0,2. Определите, сколько бит информации будет нести сообщение о результатах контрольной работы в каждом из возможных случаев. Каково ожидаемое среднее количество информации о результате контрольной до тех пор пока результаты проверки не оглашены?
В озере живут караси и окуни. Подсчитано, что карасей 1500, а окуней — 500. Сколько информации содержится в сообщениях о том, что рыбак поймал карася, окуня, поймал какую-то рыбу (карася или окуня)?
Имеются два дискретных (знаковых) троичных источника с независимыми элементами. На выходе каждого из источников появляются сообщения одинаковой длины по 10 элементов. Количество различных элементов в сообщении каждого из источников постоянно. Сообщения различаются только порядком элементов. Зафиксированы два типичных сообщения: 0122102210 – первого источника, 2200221022 – второго. Элемент какого источника несет в среднем большее количество информации?
Имеются три дискретных (знаковых) двоичных источника с независимыми элементами. На выходе каждого из источников появляются сообщения одинаковой длины по 10 элементов. Количество различных элементов в сообщении каждого из источников постоянно. Сообщения различаются только порядком элементов. Зафиксированы два типичных сообщения: 0111101010 – первого источника, 1111001101 – второго, 0001000111 – третьего. Элемент какого источника несет в среднем большее количество информации?
Ракета, запушенная с помощью установки, поражает вертолет с вероятностью 0.5, танк – с вероятностью 0.3 и дает промах с вероятностью 0.2. Чему для командира дивизии равна неопределенность перед очередным залпом установки.
Ракета, запушенная с помощью установки, поражает вертолет с вероятностью 0.5, танк – с вероятностью 0.3 и дает промах с вероятностью 0.2. Боевой запас ракет, оставшийся после серии из девяти залпов, составил пять ракет. Определите количество информации, которое несет в себе сообщение о пораженных целях.
Ракета, запушенная с помощью установки, поражает вертолет с вероятностью 0.5, танк – с вероятностью 0.3 и дает промах с вероятностью 0.2. После боя выяснилось, что было уничтожено три вертолета и четыре танка и использовано 10 зарядов. Сколько информации получено после боя.
Петя Васечкин изобрел свой язык и назвал его Карамба. Каждому символу в этом языке соответствует ровно один звук. Определите, сколько символов в алфавите Карамбы, если известно, что когда Петя говорит на этом языке, его производительность составляет 2700 байт в полчаса, а за 1 секунду произносится один звук на языке Карамбы. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
В течение 5 минут со производительностью 20 байт/сек вождь племени Мульти передавал информационное сообщение. Сколько символов содержало оно, если алфавит племени состоит из 32-х символов? Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
В марсианском языке все слова состоят из пяти символов, а используемый алфавит содержит 30 символов. Прибывший на Землю марсианин за 1 минуту произносит 20 марсианских слов. Определите его производительность в бит/сек. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
Профессиональная машинистка работая на клавиатуре ЭВМ набирает 10 знаков в секунду. Какова ее производительность (в бит/сек)? Считать, что клавиатура ЭВМ содержит 51 клавишу, каждая из которых может быть нажата на верхнем и на нижнем регистре. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
Лектор произносит около 50 слов в минуту. В языке, который он использует, средняя длина слов равна 5 символов, а мощность алфавита – 36. Рассматривая лектора как источник дискретных (знаковых) сообщений, определить его производительность. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
Шифрующее устройство работает с производительностью 1000 бит/мин. При этом оно выдает кодовые слова длиной 5 символов из 32-х символьного алфавита. Сколько символов в секунду выдает устройство. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
Алфавит племени Мульти состоит из 8 символов, а все слова в этом языке трехсимвольные. Вождь говорит со скоростью 25 слов в минуту. Рассматривая вождя как источник дискретных (знаковых) сообщений, определить его производительность. Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
Алфавит племени Пульти состоит из 16 символов. В течение 5 минут со производительностью 20 байт/сек вождь племени Мульти говорил речь соплеменникам. Рассматривая вождя как источник дискретных (знаковых) сообщений, определить сколько символов содержала речь? Для простоты принять, что все символы алфавита равновероятны и статистически независимы.
В непрозрачном мешочке хранятся 35 белых, 25 красных, 15 синих и 45 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
В непрозрачном мешочке хранятся 15 белых, 20 красных, 35 синих и 40 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
В непрозрачном мешочке хранятся 30 белых и 10 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
В непрозрачном мешочке хранятся 35 белых и 45 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
В непрозрачном мешочке хранятся 10 белых, 20 красных, 30 синих и 40 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
В непрозрачном мешочке хранятся 10 белых, 35 синих и 55 зеленых шариков. Из мешочка извлекают подряд два шара без возврата. Найти энтропию, связанную с первым и вторым извлечениями, а также энтропию обоих извлечений.
Для кодирования одного символа алфавита используется двоичный код из 5 двоичных цифр. Каковы пределы (максимальное и минимальное значение) мощности алфавита, с помощью которого составлено это сообщение?
Сообщение, записанное буквами из 128-символьного алфавита, содержит 30 символов. Какой объем информации в байтах оно несет?
Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации в килобайтах содержат 5 страниц текста?
Информационное сообщение объемом 3 килобайта содержит 3072 символов. Каков размер алфавита, с помощью которого оно было составлено?
Информационное сообщение имеет объемом 3 килобайта. Сколько в нем символов, если размер алфавита, с помощью которого оно было составлено, равно 16.
Сообщение занимает 4 страницы по 40 строк и содержит 7200 байтов информации. Сколько символов в строке, если при составлении этого сообщения использовали 64 — символьный алфавит?
Сообщение состоит из 5 страниц текста, каждая из которых содержит 1024 символа, а используемый алфавит состоит из 64 символов. Определите общий информационный объем текста в килобайтах.
Сообщение занимает 3 страницы и содержит 7875 байтов информации. Сколько строк в тексте, если символов в строке 50 и при составлении этого сообщения использовали 128 — символьный алфавит?
Сообщение состоит из 3 страниц текста, каждая из которых содержит 2048 символов. Общий объем текста – 6 Кбайт. Определите мощность алфавита.
Информационное сообщение 3 килобайт записано в алфавите мощностью 64 символа. Сколько символов в сообщении?
Информационное сообщение объемом 9 Кбайт содержит 12288 символов. Сколько символов содержит алфавит, при помощи которого записано это сообщение?
Книга состоит из 512 страниц. На каждой странице 512 символов. Какой объем информации в мегабайтах содержится в книге, если используемый алфавит состоит из 256 символов?
Два текста содержат одинаковое количество символов. Количество информации в первом тексте в 1.2 раза больше, чем во втором. Сколько символов содержат алфавиты, с помощью которых записаны сообщения, если известно, что размер каждого алфавита не превышает 100 символов, и информационные веса символов в каждом из алфавитов выражаются целым числом битов.
Книга состоит из 20 страниц. На каждой странице – 320 символов. Какой объем информации в байтах содержится в книге, если используемый алфавит состоит из 64 символов?
Алфавит племени Мульти содержит Х символов, алфавит племени Пульти содержит в 2 раза больше символов. Племена обменялись приветствиями. В сообщении племени Мульти 40 символов и содержится 50 байт информации. В сообщении племени Пульти на 10 символов больше. Сколько байт информации в сообщении племени Пульти?
Две галактики решили заключить мир. Одна галактика отправила послание второй. Для заключения мира необходимо при переводе сохранить количество информации в послании. Алфавит 1-й галактики насчитывает 64 символа. Сколько символов в алфавите 2-й галактики, если известно, что в послании 1-й галактики было 10 символов, а при переводе на язык 2-й галактики получилось 20 символов?
Анкета участника занимают 45 Мбайт и каждое из них имеет объём 12 страниц (48 строк по 64 символа в каждой, мощность используемого алфавита 256 символов). Определите число анкет.
Вариант теста в среднем имеет объём 20 Кбайт (на каждой странице теста 40 строк по 64 символа в каждой, мощность используемого алфавита 65536 символов). Определите количество страниц в тексте.
Ёмкость одного условного печатного листа равна приблизительно 96 Кбайт, при кодировании используется алфавит из 65536 символов. Определить сколько минут потребуется для распечатки текста одной газеты (4 условных печатных листа) на лазерном принтере (скорость печати – 512 символов в секунду) без учёта смены бумаги. Ответ округлить до целого числа.
Ответы. Учебник. Часть 1 (с. 27)
Числа от 1 до 100
Сложение и вычитание
Ответы к стр. 271. 1) Сколько отрезков на этом чертеже? Как можно узнать длину самого большого отрезка?
На чертеже 3 отрезка.
6 + 2 = 8 (см) — длина самого большого отрезка.
2) Начерти отрезок длиной 10 см. Поставь на нём точку так, чтобы получился отрезок длиной 4 см. Узнай длину второго отрезка.
10 — 4 = 6 (см) — длина второго отрезка
2. Маше 8 лет. Мама на 20 лет старше Маши, а папа на 1 год старше мамы. Сколько лет папе?
1) 8 + 20 = 28 (л.) — маме
2) 28 + 1 = 29 (л.) — папе
О т в е т: папе 29 лет.
3. (Устно.) 1) Из суммы чисел 70 и 8 вычти число 1; 70; 8.
(70 + 8) — 1 = 77
(70 + 8) — 70 = 8
(70 + 8) — 8 = 70
2) Разность чисел 10 и 8 прибавь к числу 20; 10; 90.
(10 — 8) + 20 = 22
(10 — 8) + 10 = 12
(10 — 8) + 20 = 92
4. 12 — 8 + 9 =13 14 — 7 + 6 = 13 48 — 40 — 8 = 0
10 + 3 — 8 = 5 10 + 4 — 9 = 5 56 — 50 + 0 = 6
17 — 8 + 6 = 15 18 — 9 + 8 = 17 0 + 88 — 80 = 8
5. Узнай, на сколько миллиметров бóльшая сторона в каждом четырёхугольнике длиннее меньшей.
В синем четырёхугольнике бóльшая сторона длиннее меньшей на 2 см: 4 — 2 = 2 см
В розовом четырёхугольнике бóльшая сторона длиннее меньшей на 3 см: 5 — 2 = 3 см
6. В коробке красных и синих карандашей вместе столько, сколько зелёных. Красных карандашей 7, зелёных — 13. Сколько синих карандашей в коробке?
13 — 7 = 6 (к.)
О т в е т: 6 карандашей.
7. Составь ряд из пяти чисел по такому правилу: первое число — 2, второе — 3, а каждое следующее число равно сумме двух предыдущих.
2, 3, 5, 8, 13.
Проверочные работы, с. 10, 11.
Ответы по математике. 2 класс. Учебник.
Ответы. Учебник. Часть 1 (с. 27)
3.9 (78.1%) от 42 голосующихТеория вероятности и математическая статистика
Федеральное агентство по образованию РФ
НОУ ВПО Международный университет бизнеса и новых технологий (академия)
Контрольная работа по теории организации и математической статистике
Вариант № 4
Выполнила: Спицина Н. Н.
Специальность: МН — 2
Задание 1
В коробке 12 зеленых, 5 красных, 6 синих карандашей. Из коробки наудачу берут три карандаша. Какова вероятность того, что все они будут синими? Рассмотреть случаи, когда карандаши: а) не возвращают в коробку; б) возвращают в коробку.
Решение:
а) Событие А – все три вынутые без возращения в коробку карандаши синие.
Согласно классическому определению вероятность события А равна:
В коробке 12+5+6=23 карандаша.
Общее число исходов равно:
Благоприятное число способов равно:
Ответ: вероятность того, что все три вынутые без возращения в коробку карандаши синие, равна 0,011.
б) Событие В – все три вынутые с возращением в коробку карандаши синие, то есть три раза будут выниматься 1 синий шар из 23.
Вероятность извлечения одного синего карандаша р = 6/23.
Воспользуемся схемой Бернулли:
q = 1-6/23=7/23
n = 3
m=3
Ответ: вероятность того, что все три вынутые с возращения в коробку карандаши синие, равна 0,018.
Задание 2
Из колоды в 32 карты наугад вынимают 5. Найти вероятность того, что среди них окажется ровно один туз.
Решение:
Событие А – из вынутых наугад 5 карт, ровно один туз.
Согласно классическому определению вероятность события А равна:
Пусть детали пронумерованы с 1 до 80, с 1 до 20 стандартные и с 21 по 80 не стандартные.
Общее число исходов равно:
Благоприятное исход состоит в том, что вынут 1 туз из 4-х возможных и 4 другие карты из оставшихся 28, таким образом, число благоприятных способов равно:
Ответ: вероятность того, что из вынутых наугад 5 карт, ровно один туз, равна 0,407.
Задание 3
Брак изделий цеха составляет 11%. Найти вероятность того, что из 250 изделий цеха окажется бракованными: а) ровно 45 изделий; б) от 145 до 155 изделий; в) не менее 101 изделий; г) не более 100 изделий.
Решение:
а) Вероятность того, что из 250 изделий цеха окажется бракованными ровно 45 изделий, найдем, используя локальную теорему Лапласа:
б) Вероятность того, что из 250 изделий цеха окажется бракованными от 145 до 155 изделий, найдем, используя интегральную теорему Лапласа:
где Ф – функция Лапласа (значения берутся из таблиц).
Подставляем:
в) Вероятность того, что из 250 изделий цеха окажется бракованными не менее 101 изделий, найдем, используя интегральную теорему Лапласа:
,где Ф – функция Лапласа (значения берутся из таблиц).
Подставляем:
г) Вероятность того, что из 250 изделий цеха окажется бракованными не более 100 изделий, найдем, используя интегральную теорему Лапласа:
где Ф – функция Лапласа (значения берутся из таблиц).
Подставляем:
Задание 4
Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй вызов – 0,3, третий вызов 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.
Решение:
Событие А — корреспондент услышал вызов.
Событие Н1 — принят первый вызов.
Событие Н2 — принят второй вызов.
Событие Н3 — принят третий вызов.
Р( Н1 ) = 0,2, Р( Н2 ) = 0,3, Р( Н3 ) = 0,4.
Р (А / Н1) = 1/3; Р (А / Н2) = 1/3; Р( А/Н2 ) = 1/3.
Используя формулу полной вероятности, получим
Р( А ) = Р( А / Н1 ) · Р( Н1 ) + Р( А / Н2 ) · Р( Н2 ) + Р( А / Н3 ) · Р( Н3 ) =
Ответ: вероятность того, что корреспондент услышал вызов, равна 0,3.
Задание 5
Случайная величина ξ имеет распределение вероятностей, представленное таблицей:
Найти Р(3), функцию распределения F(Х). Построить многоугольник распределения.
Решение:
Найдем Р(3):
Найдем и построим функцию распределения F(Х):
Построим многоугольник распределения:
Задание 6
Найти М(ξ), D(ξ), σ(ξ) случайной величины ξ примера 5.
Решение:
Найдем М(ξ) случайной величины ξ из примера 5:
Найдем D(ξ) случайной величины ξ из примера 5:
Найдем
случайной величины ξ из примера 5:Задание 7
ξ- непрерывная случайная величина с плотностью распределения φ(Х), заданной следующим образом:
φ(Х)=
Найти функцию распределения F(Х).
Решение:
Найдем функцию распределения F(Х):
При
При
При
Задание 8
ξ- непрерывная случайная величина из примера 7. Найти М(ξ), D(ξ).
Решение:
Найдем М(ξ):
.Найдем D(ξ):
Два карандаша выбираются случайным образом из коробки, содержащей 3 синих, 2 красных и 3 зеленых карандаша. L …
Два карандаша выбираются случайным образом из коробки, содержащей 3 синий, 2 красных и …
Два карандаша выбираются случайным образом из коробки, содержащей 3 синий, 2 красных и 3 зеленых карандаша. Пусть X — количество синих карандашей (строк) и Y — количество красных карандашей (столбцов) выбрано. Совместный PMF — это: а) Найдите условное распределение числа синих карандашей с учетом количества красных карандашей.(б) Найдите условное среднее количество синих карандашей. учитывая количество красных карандашей y. (c) Найдите …
Две фишки выбираются из коробки, содержащей 6 голубых фишек, 4 красных фишки и 3 зеленых фишки.
Две фишки выбираются из коробки, содержащей 6 голубых фишек, 4 красных фишки и 3 зеленых фишки. Первая выбранная фишка не заменяется до розыгрыша второй. Найдите P (красный, затем зеленый).
Есть коробка с 20 шариками. Из этих шариков 6 красных, 8 зеленый…
Есть коробка с 20 шариками. Из этих шариков 6 красных, 8 зеленый и 6 синие. 6 шариков случайным образом выбираются из коробки без замены. Пусть X будет количеством шариков красного или красного цвета. синий, и пусть Y будет количеством синих шариков. а. Какова вероятность того, что первый и второй шарики будут красными, третий и четвертый — синие, а пятый и шестой — зеленый? б. Какие…
Шарик выбирается наугад из урны, содержащей 2 красных шара и 3 синих…
Шарик выбирается наугад из урны, содержащей 2 красных и 3 синих шара. Если мяч красный, то справедливая монета подбрасывается три раза. Если мяч синий, несправедливая монета подбрасывается три раза; для этой второй монеты вероятность выпадения орла составляет 0,6. В любом случае мы подсчитываем количество голов в трех бросках и называем это число X. (a) Вычислите условную вероятность того, что X-2, если известно, что …
Задачи 9 и 10 В коробке 2 красных шара, 3 белых и 1 синий….
Задачи 9 и 10 В коробке 2 красных шара, 3 белых и 1 синий. Случайно выбираются три шара без замены. Найдите вероятность того, что не более одного шара станет красным. (C) 00.2 01 O 0,6 0,12 0,8 Вопрос 10 2 балла В коробке находятся 2 красных шара, 3 белых и 1 синий. Случайным образом выбираются три шара без замены. Найдите вероятность того, что {не более одного шара красного цвета (C) при условии, что хотя бы один …
. В них две коробки с красными и синими шарами.Коробка у меня есть 1 …
. В них две коробки с красными и синими шарами. Коробка у меня есть 1 красный и 4 синих шара; В ящике II 3 красных и 2 синих шара. Там есть честная монета с надписью Box I на одной стороне и Box II на другой. Вы подбрасываете монету, а затем берете 2 шара без замена из коробки, которая появляется на лицевой стороне монета. а. Пусть Y будет количеством …
5. Три коробки пронумерованы 1, 2 и 3. Для k 1, 2, 3 коробка k содержит k синих шариков и 5 — k красных шариков.В двухэтапном эксперименте выбирается ящик и из него без замены извлекаются 2 шарика …
5. Три коробки пронумерованы 1, 2 и 3. Для k 1, 2, 3 коробка k содержит k синих шариков и 5 — k красных шариков. В двухэтапном эксперименте выбирается ящик и из него извлекаются 2 шарика без замены. Если вероятность выбора коробки k пропорциональна k, то вероятность того, что два выпавших шарика имеют разные цвета, равна 6. Два шара выпадают таким образом, что каждый шар с равной вероятностью…
В коробке 9 красных шариков, 8 зеленых шариков, 5 желтых шариков и 2 синих шарика.
В коробке 9 красных шариков, 8 зеленых шариков, 5 желтых шариков и 2 синих шарика. Если 3 шарика вытащены наугад с заменой, какова вероятность того, что все 3 шарика будут красными?
В гардеробе 3 синих, 4 зеленых и 3 красных рубашки; 2 синих, 4 зеленый, и …
В гардеробе 3 синих, 4 зеленых и 3 красных рубашки; 2 синих, 4 зеленый и 6 красных свитеров; 1 синий и 2 серых штана.Предположим синий и серый не смешиваются. Сколько нарядов возможно?
В гардеробе 3 синих, 4 зеленых и 3 красных рубашки; 2 синих, 4 зеленых и …
В гардеробе 3 синих, 4 зеленых и 3 красных рубашки; 2 синих, 4 зеленый и 6 красных свитеров; 1 синий и 2 серых штана. Предположим синий и серый не смешиваются. Сколько нарядов возможно? ответьте, пожалуйста максимально быстро, не считая все по отдельности и добавление после
— математика нижнего уровня ISEE
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Точилки для карандашей Коробка из 8 разных цветов Officemate OIC Achieva Точилка в форме конуса 30231 Товары для офиса
БЕСПЛАТНАЯ ЭЛЕКТРОННАЯ КНИГА для поддержки вашего путешествия
Коробка из 8 разных цветов Точилка для конуса Officemate OIC Achieva 30231
Pilot Precise V5 Stick Rolling Ball Pen Extra Fine Point Single Pen Blue Ink Smooth-Free Writing Visible Ink Supply 2 Pack 35344 Запатентованная технология Precision Point, Aobiny Детские образовательные игрушки , Creative Lollipops Artifact Funny Eating Lollipop Robot Holder Stand Gift Toy Green, 2 x 10 именная табличка с гравировкой на заказ с квадратными углами, прозрачная упаковка из 100 штук 8 мил 11 1/4 x 8 3/4 Fellowes 52311 Обложки для презентаций с кристаллами 52311 с круглыми углами, опора для спины из пенопласта с эффектом памяти для офисного кресла / компьютерного кресла / дома / и т. Д. Dreamer Car Мини-поддерживающая подушка для стула Дизайн поясничной подушки для снятия боли в пояснице Черный, SIP-телефония MP114 / 4S / SIP Audiocodes MP114 4FXS Ports, Ithaca Receipt Paper 98-02022, Wpxmer 120 Pcs Kraft Paper Blank Cardstock Bookmarks Бумажные закладки со 100 красочными кисточками для DIY Классные проекты и подарочные бирки.Подсветка под шкафом Moston, 10 светодиодных магнитных датчиков движения, подсветка шкафа, автоматическое включение / выключение, встроенный ночник с питанием от аккумулятора, беспроводная наклейка в любом месте, серебристый алюминий. Набор механических карандашей Nicpro 0,5 мм, металлический автоматический чертежный карандаш из 3 предметов, механический карандаш с 6 трубками, грифелями HB и 3 ластиками для написания эскиза чертежа — поставляется с футляром. 7 отсеков Black Deli Mesh Desktop Organizer Контейнер для канцелярских принадлежностей с держателем для ручки и корзинами для хранения настольных принадлежностей, футляр из 24 инженерных прокладок 8.5×11 5×5 сетка с 3 отверстиями, перфорированная сверхплотная основа 150 листов переработанной зеленой бумаги 16 #, совместимый сменный картридж с тонером для Brother TN660 TN630 повышенной емкости для использования с HL-L2380DW HL-L2300D HL-L2340DW MFC-L2680W MFC-L2740DW MFC- L2685DW Принтер EZ Ink Black, 1 упаковка TM, верхняя этикетка Маленькая овальная этикетка для классной доски Водонепроницаемые наклейки для сахарных банок, вечеринок, комнат для рукоделия, свадеб и кухни, Free a White Chalk, M32 Executone Phone Isoetec 84500-2, Пульт дистанционного управления для JVC HR- XVC12S от Tekswamp.
Начальная школа Тимпсона 2021-2022 Списки ресурсов
16 июня 2021 г. ( Списки для печати ) — Начальная школа Тимпсона 2021-2022 Списки ресурсов
Список материалов для дошкольного образования
1 уп.картона белого
1 уп. картона цветного
1 уп. бумаги Manilla
1 уп. плотной бумаги
1 уп. белая копировальная бумага
4 красных папки
12 клеевых стержней
4 коробки мелков
2 коробки салфеток
1 уп. моющиеся маркеры
2 флакона белого клея
1 уп. акварель
1 большая уп. детских салфеток
1 уп. Пластилин марки Play-Dough на 4 штуки
1 коробка мешочков на галлон
1 коробка мешочков в квартах
1 комплект наушников для использования на компьютере (без наушников)
1 уп.простые бумажные тарелки без рисунков
Большой рюкзак (без роликов)
Только пластиковые ворсовые коврики (без тканевых ковриков, без покрытий для ковриков, без подушек)
Список снабжения детского сада
2 Первичные журналы
2 Таблетки для первичного письма
1 уп. бумага плотная
1 уп. Бумага Manilla
2 уп. 24 счетных карандаша
1 пара ножниц Fiskars
6 упаковок. 24 шт. Crayola Crayons
12 клеевых стержней
1 флакон клея Elmers
1 уп. водная краска
1 уп.моющиеся маркеры (классические основные цвета)
2 блокнота Mead Composition
4 пластиковые папки с штифтами
1 большой рюкзак
1 уп. Play-Doh (пожалуйста, используйте только бренд Play-Doh)
2 Kleenex
1 пара наушников (будут использоваться ежедневно)
1 комплект одежды в сумке Ziploc с их именем на сумке
1 коробка пакетов Ziploc размером галлон ( Только для мальчиков)
1 коробка квартовых сумок на молнии (только для девочек)
Список школьных принадлежностей для первого класса
Наушники (БЕЗ наушников)
Рюкзак
Пенал или сумка с буфером обмена
36 карандашей
1 большой розовый ластик
4 уп.ластики для карандашей
6 коробок с мелками
1 ножницы
12 клеевых стержней
4 небольших сборника композиций (9 3/4 x 7/2)
1 коробка галлоновых мешочков
1 коробка квартовых мешочков
2 папки (1 дюйм )
2 маркера Crayola
Список школьных принадлежностей для второго класса
Рюкзак
3 уп. ластики для карандашей
5 уп. № 2 карандаша (Ticonderoga или Dixon)
1 мешок или коробка для карандашей
1 пара ножниц
6 больших клеевых стержней
4 шт. Crayola 24 шт. Карандашей
2 упаковки.Карандаши для карт Crayola
2 уп. маркеры
1 блокнот в широкую линейку
4 пластиковые папки с карманами и скобами
4 блокнота на спирали
2 блокнота с композициями
Папка на 3 кольца с карманами 1 дюйм
1 уп. Разделители Pen + Gear без карманов (5 уп. С красным, синим, желтым, оранжевым и фиолетовым)
1 уп. карточки для записей
1 уп. картон разные цвета
1 уп. бумага плотная (МАЛЬЧИКИ)
1 уп. Бумага Manilla (GIRLS)
1 пара наушников
1 коробка кварты Пакеты Ziploc (МАЛЬЧИКИ)
Пакеты Ziploc на 1 галлон (GIRLS)
Список школьных принадлежностей для третьего класса
Рюкзак
1 наушники
1 ножницы
2 упаковки маркеров
3 ластика на верхней части карандаша
4 коробки с 24 карандашами
1 заполнитель для тетрадей
2 папки (1 дюйм)
1 папка (2 дюйма)
4 пластиковых кармана папки с отверстиями
3 блокнота композитных
1 упаковка цветных карандашей
1 упаковка маркеров
1 сумка для карандашей
4 клеевых стержня
2 упаковки разделителей
2 коробки мелков Crayola
3 упаковки учетных карточек
Список школьных принадлежностей для четвертого класса
7 сборников композиций
2 черных (1 дюйм) папки
4 упаковки.клеевые стержни (16 клеевых стержней)
4 уп. Карандаши для карт
1 коробка 24 шт. мелков
6 упаковок. 20 карандашных карандашей
3 уп. ластики для крышек
2 уп. маркеры (тонкие / тонкие)
1 ножницы
2 уп. тетрадная бумага в широкую линейку
1 сумка для карандашей на молнии
1 уп. цветная копировальная бумага
3 больших коробки Kleenex
1 рюкзак (без роликов)
4 папки без скоб (2 зеленых, 2 красных)
1 уп. разделители
2 уп. карточки для записей (маленькие)
1 пара наушников
Принадлежности для пятого класса
Math
• 2 папки (1 дюйм)
• 1 уп.листовых протекторов
• 2 уп. стикеры
• 7 разделителей
• 2 упаковки. маркеров
• 1 композиционная тетрадь
• 1 уп. картон (любой цвет)
Чтение
• 1 (1 дюйм) скоросшиватель
• 7 разделителей
• 2 сборника сочинений
Science
• 12 клеевых стержней
• 2 сборника композиций
Домашний класс
• Девочки: 1 коробка пакетиков Ziploc размером с кварту
• Мальчики: 1 коробка пакетов Ziploc размером галлон
• 3 коробки салфеток Kleenex
Следующие предметы являются обязанностью учащегося каждый день в классе .
