Распределение Стьюдента — Helpstat
Форма распределения Стьюдента зависит от числа степеней свободы. Например, критическое значение, соответствующее вероятности 0.05 t-распределения с 6 степенями свободы, находится на пересечении столбца 0.05 и строки 6: t(.05,6) = 1.943180.
dfp | 0.40 | 0.25 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.0005 |
1 | 0.324920 | 1.000000 | 3.077684 | 6.313752 | 12.70620 | 31.82052 | 63.65674 | 636.6192 |
2 | 0.288675 | 0.816497 | 1.885618 | 2.919986 | 4.30265 | 6.96456 | 9.92484 | 31.5991 |
3 | 0.276671 | 0.764892 | 1.637744 | 2.353363 | 3.18245 | 4.54070 | 5.84091 | 12.9240 |
4 | 0.270722 | 0.740697 | 1.533206 | 2.131847 | 2.77645 | 3.74695 | 4.60409 | 8.6103 |
5 | 0.267181 | 0.726687 | 1.475884 | 2.015048 | 2.57058 | 3.36493 | 4.03214 | 6.8688 |
6 | 0.264835 | 0.717558 | 1.439756 | 1.943180 | 2.44691 | 3.14267 | 3.70743 | 5.9588 |
7 | 0.263167 | 0.711142 | 1.414924 | 1.894579 | 2.36462 | 2.99795 | 3.49948 | 5.4079 |
8 | 0.261921 | 0.706387 | 1.396815 | 1.859548 | 2.30600 | 2.89646 | 3.35539 | 5.0413 |
9 | 0.260955 | 0.702722 | 1.383029 | 1.833113 | 2.26216 | 2.82144 | 3.24984 | 4.7809 |
10 | 0.260185 | 0.699812 | 1.372184 | 1.812461 | 2.22814 | 2.76377 | 3.16927 | 4.5869 |
11 | 0.259556 | 0.697445 | 1.363430 | 1.795885 | 2.20099 | 2.71808 | 3.10581 | 4.4370 |
12 | 0.259033 | 0.695483 | 1.356217 | 2.17881 | 2.68100 | 3.05454 | 4.3178 | |
13 | 0.258591 | 0.693829 | 1.350171 | 1.770933 | 2.16037 | 2.65031 | 3.01228 | 4.2208 |
14 | 0.258213 | 0.692417 | 1.345030 | 1.761310 | 2.14479 | 2.62449 | 2.97684 | 4.1405 |
15 | 0.257885 | 0.691197 | 1.340606 | 1.753050 | 2.13145 | 2.60248 | 2.94671 | 4.0728 |
16 | 0.257599 | 0.690132 | 1.336757 | 1.745884 | 2.11991 | 2.58349 | 2.92078 | 4.0150 |
17 | 0.257347 | 0.689195 | 1.333379 | 1.739607 | 2.10982 | 2.56693 | 2.89823 | 3.9651 |
18 | 0.257123 | 0.688364 | 1.330391 | 1.734064 | 2.10092 | 2.55238 | 2.87844 | 3.9216 |
19 | 0.256923 | 0.687621 | 1.327728 | 1.729133 | 2.09302 | 2.53948 | 2.86093 | 3.8834 |
20 | 0.256743 | 0.686954 | 1.325341 | 1.724718 | 2.08596 | 2.52798 | 2.84534 | 3.8495 |
21 | 0.256580 | 0.686352 | 1.323188 | 1.720743 | 2.07961 | 2.51765 | 2.83136 | 3.8193 |
22 | 0.256432 | 0.685805 | 1.321237 | 1.717144 | 2.07387 | 2.50832 | 2.81876 | 3.7921 |
23 | 0.256297 | 0.685306 | 1.319460 | 1.713872 | 2.06866 | 2.49987 | 2.80734 | 3.7676 |
24 | 0.256173 | 0.684850 | 1.317836 | 1.710882 | 2.06390 | 2.49216 | 2.79694 | 3.7454 |
25 | 0.256060 | 0.684430 | 1.316345 | 1.708141 | 2.05954 | 2.48511 | 2.78744 | 3.7251 |
26 | 0.255955 | 0.684043 | 1.314972 | 1.705618 | 2.05553 | 2.47863 | 2.77871 | 3.7066 |
27 | 0.255858 | 0.683685 | 1.313703 | 1.703288 | 2.05183 | 2.47266 | 2.77068 | 3.6896 |
28 | 0.255768 | 0.683353 | 1.312527 | 1.701131 | 2.04841 | 2.46714 | 2.76326 | 3.6739 |
29 | 0.255684 | 0.683044 | 1.311434 | 1.699127 | 2.04523 | 2.46202 | 2.75639 | 3.6594 |
30 | 0.255605 | 0.682756 | 1.310415 | 1.697261 | 2.04227 | 2.45726 | 2.75000 | 3.6460 |
inf | 0.253347 | 0.674490 | 1.281552 | 1.644854 | 1.95996 | 2.32635 | 2.57583 | 3.2905 |
Критические точки распределения Стьюдента
(двусторонняя критическая область)
| Число степеней свободы k | Уровень значимости a | |||||
| 0.10 | 0.05 | 0.02 | 0.01 | 0.002 | 0.001 | |
| 1 | 6.31 | 12.7 | 31.82 | 63.7 | 318.3 | 637.0 |
| 2 | 2.92 | 4.30 | 6.97 | 9.92 | 22.33 | 31.6 |
| 3 | 2.35 | 3.18 | 4.54 | 5.84 | 10.22 | 12.9 |
| 4 | 2.13 | 2.78 | 3.75 | 4.60 | 7.17 | 8.61 |
| 5 | 2.01 | 2.57 | 3.37 | 4.03 | 5.89 | 6.86 |
| 6 | 1.94 | 2.45 | 3.14 | 3.71 | 5.21 | 5.96 |
| 7 | 1.89 | 2.36 | 3.00 | 3.50 | 4.79 | 5.40 |
| 8 | 1.86 | 2.31 | 2.90 | 3.36 | 4.50 | 5.04 |
| 9 | 1.83 | 2.26 | 2.82 | 3.25 | 4.30 | 4.78 |
| 10 | 1.81 | 2.23 | 2.76 | 3.17 | 4.14 | 4.59 |
| 11 | 1.80 | 2.20 | 2.72 | 3.11 | 4.03 | 4.44 |
| 12 | 1.78 | 2.18 | 2.68 | 3.05 | 3.93 | 4.32 |
| 13 | 1.77 | 2.16 | 2.65 | 3.01 | 3.85 | 4.22 |
| 14 | 1.76 | 2.14 | 2.62 | 2.98 | 3.79 | 4.14 |
| 15 | 1.75 | 2.13 | 2.60 | 2.95 | 3.73 | 4.07 |
| 16 | 1.75 | 2.12 | 2.58 | 2.92 | 3.69 | 4.01 |
| 17 | 1.74 | 2.11 | 2.57 | 2.90 | 3.65 | 3.95 |
| 18 | 1.73 | 2.10 | 2.55 | 2.88 | 3.61 | 3.92 |
| 19 | 1.73 | 2.09 | 2.54 | 2.86 | 3.58 | 3.88 |
| 20 | 1.73 | 2.09 | 2.53 | 2.85 | 3.55 | 3.85 |
| 21 | 1.72 | 2.08 | 2.52 | 2.83 | 3.53 | 3.82 |
| 22 | 1.72 | 2.07 | 2.51 | 2.82 | 3.51 | 3.79 |
| 23 | 1.71 | 2.07 | 2.50 | 2.81 | 3.59 | 3.77 |
| 24 | 1.71 | 2.06 | 2.49 | 2.80 | 3.47 | 3.74 |
| 25 | 1.71 | 2.06 | 2.49 | 2.79 | 3.45 | 3.72 |
| 26 | 1.71 | 2.06 | 2.48 | 2.78 | 3.44 | 3.71 |
| 27 | 1.71 | 2.05 | 2.47 | 2.77 | 3.42 | 3.69 |
| 28 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 29 | 1.70 | 2.05 | 2.46 | 2.76 | 3.40 | 3.66 |
| 30 | 1.70 | 2.04 | 2.46 | 2.75 | 3.39 | 3.65 |
| 40 | 1.68 | 2.02 | 2.42 | 2.70 | 3.31 | 3.55 |
| 60 | 1.67 | 2.00 | 2.39 | 2.66 | 3.23 | 3.46 |
| 120 | 1.66 | 1.98 | 2.36 | 2.62 | 3.17 | 3.37 |
| ¥ | 1.64 | 1.96 | 2.33 | 2.58 | 3.09 | 3.29 |
| 0.05 | 0.025 | 0.01 | 0.005 | 0.001 | 0.0005 | |
| Уровень значимости a (односторонняя критическая область) | ||||||
Вернуться Статистические таблицы
Расчет критерия Стьюдента в Excel

Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.
Определение термина
Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.
Расчет показателя в Excel
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.
Способ 1: Мастер функций
Проще всего производить вычисления данного показателя через Мастер функций.
- Строим таблицу с двумя рядами переменных.
- Кликаем по любой пустой ячейке. Жмем на кнопку «Вставить функцию» для вызова Мастера функций.
- После того, как Мастер функций открылся. Ищем в списке значение ТТЕСТ или СТЬЮДЕНТ.ТЕСТ. Выделяем его и жмем на кнопку «OK».
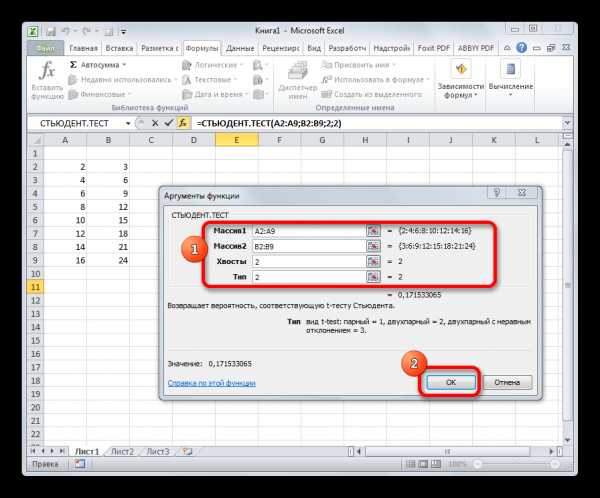
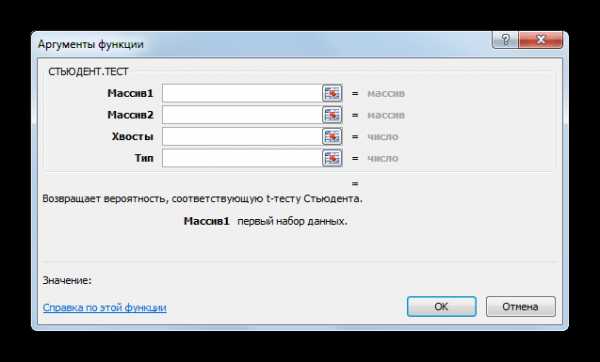
- Открывается окно аргументов. В полях «Массив1» и «Массив2» вводим координаты соответствующих двух рядов переменных. Это можно сделать, просто выделив курсором нужные ячейки.
В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.
В поле «Тип» вводятся следующие значения:
- 1 – выборка состоит из зависимых величин;
- 2 – выборка состоит из независимых величин;
- 3 – выборка состоит из независимых величин с неравным отклонением.
Когда все данные заполнены, жмем на кнопку «OK».

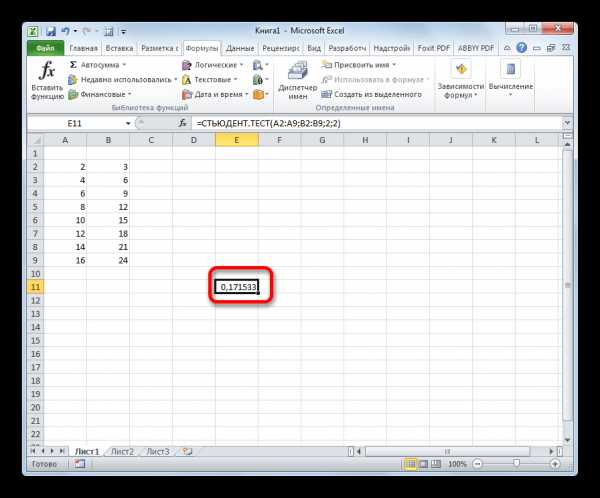
Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.
Способ 2: работа со вкладкой «Формулы»
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.
- Выделяем ячейку для вывода результата на лист. Выполняем переход во вкладку «Формулы».
- Делаем клик по кнопке «Другие функции», расположенной на ленте в блоке инструментов «Библиотека функций». В раскрывшемся списке переходим в раздел «Статистические». Из представленных вариантов выбираем «СТЬЮДЕНТ.ТЕСТ».
- Открывается окно аргументов, которые мы подробно изучили при описании предыдущего способа. Все дальнейшие действия точно такие же, как и в нём.
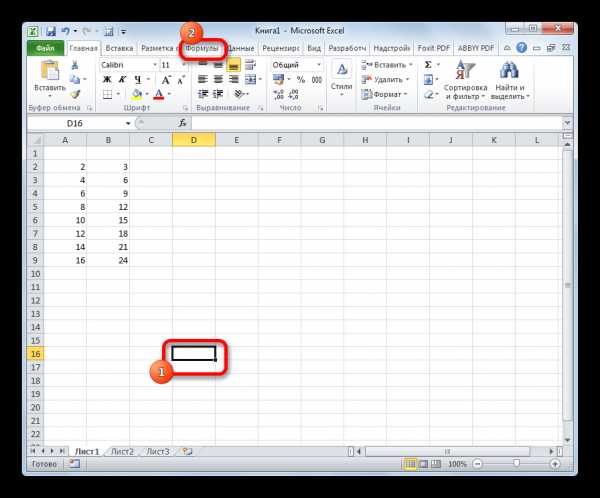

Способ 3: ручной ввод
Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:
= СТЬЮДЕНТ.ТЕСТ(Массив1;Массив2;Хвосты;Тип)
Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.
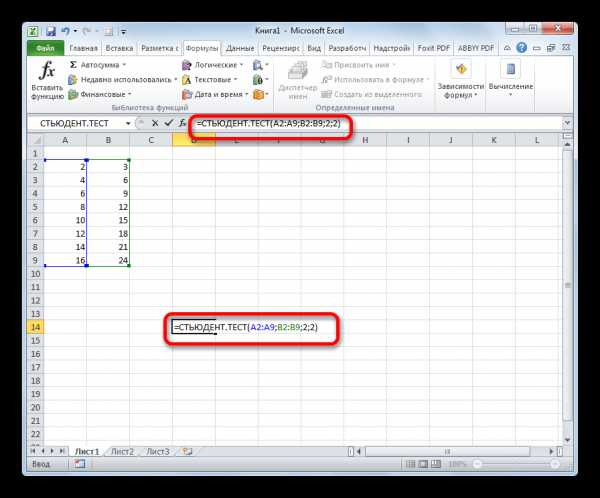
После того, как данные введены, жмем кнопку Enter для вывода результата на экран.
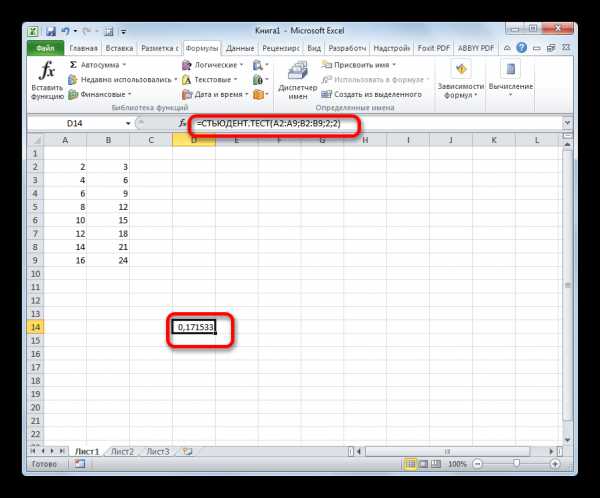
Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.
Мы рады, что смогли помочь Вам в решении проблемы.Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТlumpics.ru
Критерий Т-Стьюдента
В этом обучающем видео представлен пошаговый алгоритм расчета критерия Т-Стьюдента для независимых выборок в программе SPSS.
Читать далее [Видео] Алгоритм расчета критерия Т-Стьюдента для независимых выборок в SPSS
В этом обучающем видео представлен пошаговый алгоритм расчета критерия Т-Стьюдента для зависимых выборок в программе SPSS.
Читать далее [Видео] Алгоритм расчета критерия Т-Стьюдента для зависимых выборок в SPSS
В этом обучающем видео представлена интерпретация результатов расчета критерия Т-Стьюдента для независимых выборок в программе SPSS.
Читать далее [Видео] Интерпретация результатов расчета критерия Т-Стьюдента для независимых выборок в SPSS
В этом обучающем видео представлена интерпретация результатов расчета критерия Т — Стьюдента для независимых выборок в программе SPSS.
Читать далее [Видео] Интерпретация результатов расчета критерия Т-Стьюдента для зависимых выборок в SPSS
Предположим, что необходимо сравнить между собой результаты выполнения логических задач до и после курса обучения. Чтобы узнать различаются ли результаты до курса обучения и после необходимо вычислить t-критерий Стьюдента для зависимых выборок.
Читать далее Пример расчета t-критерия Стьюдента для зависимых выборок
Предположим, что надо сравнить между собой результаты выполнения тестов на внимание в двух группах. Чтобы узнать различаются ли группы между собой необходимо вычислить t-критерий Стьюдента для независимых выборок.
Читать далее Пример расчета t-критерия Стьюдента для независимых выборок
В таблице критических значений t-критерия Стьюдента находятся теоретические значения критерия.
Читать далее Таблица критических значений t-критерия Стьюдента
Предположим нам необходимы вычислить отличается ли от нормального интеллект детей обучающихся по специальной программе. Для этого используем статистический критерий t-Стьюдента.
Читать далее Пример расчета t-критерия Стьюдента для одной выборки
Для того, чтобы рассчитать t-критерий Стьюдента для зависимых выборок используя статистически пакет SPSS необходимо сделать следующий шаги:
Читать далее Расчет t-критерия Стьюдента для зависимых выборок в SPSS
Для того, чтобы рассчитать t-критерий Стьюдента для независимых выборок используя статистически пакет SPSS необходимо сделать следующий шаги:
Читать далее Расчет t-критерия Стьюдента для независиымх выборок в SPSS
Для того, чтобы рассчитать t-критерий Стьюдента для одной выборки используя статистический пакет SPSS необходимо сделать следующий шаги:
Читать далее Расчет t-критерия Стьюдента для одной выборки в SPSS
t-критерий Стьюдента для зависимых выборок применяется для сравнения средних значений двух зависимых между собой выборок.
Читать далее t-критерий Стьюдента для зависимых выборок
t-критерий Стьюдента для независимых выборок применяется для сравнения средних значений двух независимых между собой выборок.
Читать далее t-критерий Стьюдента для независимых выборок
t -критерий Стьюдента для одной выборки используется для сравнения дисперсии изучаемой выборки с некоторой известной заранее величиной.
Читать далее t-критерий Стьюдента для одной выборки
Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок) в Excell необходимо сделать следующие шаги:
Читать далее Расчет критерия Стьюдента в Excell
statpsy.ru
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | 10,13 7,71 6,61 5,99 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45 4,41 4,38 4,35 4,32 4,30 4,28 4,26 4,24 4,22 4,21 | 34,12 21,20 16,26 13,74 12,25 11,26 10,56 10,04 9,65 9,33 9,07 8,86 8,68 8,53 8,40 8,28 8,18 8,10 8,02 7,94 7,88 7,82 7,77 7,72 7,68 | 167,5 74,1 47,0 35,5 29,2 25,4 22,9 21,0 19,7 18,6 17,8 17,1 16,6 16,1 15,7 15,4 15,1 14,8 14,6 14,4 14,2 14,0 13,9 13,7 13,6 | 28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 80 100 125 150 200 400 1000 ¥ | 4,20 4,18 4,17 4,15 4,13 4,11 4,10 4,08 4,07 4,06 4,05 4,04 4,03 4,02 4,00 3,99 3,98 3,96 3,94 3,92 3,91 3,89 3,86 3,85 3,84 | 7,64 7,60 7,56 7,50 7,44 7,39 7,35 7,31 7,27 7,24 7,21 7,19 7,17 7,12 7,08 7,04 7,01 6,96 6,90 6,84 6,81 6,76 6,70 6,66 6,64 | 13,5 13,4 13,3 13,2 13,1 13,0 12,9 12,8 12,7 12,5 12,4 12,3 12,2 12,1 12,0 11,9 11,6 11,6 11,5 11,4 11,3 11,2 11,0 10,9 10,8 |
studfiles.net
T-критерий Стьюдента — это… Что такое T-критерий Стьюдента?
t-критерий Стьюдента
t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
История
Данный критерий был разработан Уильямом Госсеттом для оценки качества пива в компании Гиннесс. В связи с обязательствами перед компанией по неразглашению коммерческой тайны (руководство Гиннесса считало таковой использование статистического аппарата в своей работе), статья Госсета вышла в 1908 году в журнале «Биометрика» под псевдонимом «Student» (Студент).
Требования к данным
Для применения данного критерия необходимо, чтобы исходные данные имели нормальное распределение. В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства дисперсий. Существуют, однако, альтернативы критерию Стьюдента для ситуации с неравными дисперсиями.
Двухвыборочный t-критерий для независимых выборок
В случае с незначительно отличающимся размером выборки применяется упрощённая формула приближенных расчётов:
В случае, если размер выборки отличается значительно, применяется более сложная и точная формула:
Где M1,M2 — средние арифметические, σ1,σ2 — стандартные отклонения, а N1,N2 — размеры выборок.
Количество степеней свободы рассчитывается как
Двухвыборочный t-критерий для зависимых выборок
Для вычисления эмпирического значения t-критерия в ситуации проверки гипотезы о различиях между двумя зависимыми выборками (например, двумя пробами одного и того же теста с временным интервалом) применяется следующая формула:
где Md — средняя разность значений, а σd — стандартное отклонение разностей.
Количество степеней свободы рассчитывается как
Одновыборочный t-критерий
Применяется для проверки гипотезы об отличии среднего значения от некоторого известного значения :
Количество степеней свободы рассчитывается как
Непараметрические аналоги
Аналогом двухвыборочного критерия для независимых выборок является U-критерий Манна-Уитни. Для ситуации с зависимыми выборками аналогами являются критерий знаков и T-критерий Вилкоксона
Автоматический расчет t-критерия Стьюдента
dic.academic.ru
