Теорема Виета
Тема «Теорема Виета»
Тест по алгебре для 8 класса к учебнику Ю.Н. Макарычева.
Комментарий по выполнению заданий и их оценке
Вопросы и задания теста разделены на три уровня сложности (А, В, С).
Уровень А базовый. Он содержит 5 вопросов, каждый из которых имеет 4 варианта ответа (правильный только один).
Уровень В является более сложным, состоит из 2 заданий с краткими ответами.
Уровень С включает одно задание повышенного уровня сложности, на которое учащиеся должны дать полное решение и ответ.
Время выполнения 15-20 минут.
Критерии оценки ответов. За каждое верно выполненное задание в части А ставится 0,5 баллов, в части В – 1 балл, в части С – 2 балла.
Соответствие количества баллов и оценки:
Баллы | Оценка |
2,5 — 3 | «3» |
3,5 – 4,5 | «4» |
5 – 6,5 | «5» |
Вариант 1
А1. Найдите подбором корни уравнения x2 – 5x + 6 = 0.
Найдите подбором корни уравнения x2 – 5x + 6 = 0.
A2. Найдите один из корней квадратного уравнения x2 + 17x – 38 = 0.
А3. Найдите q, если уравнение x2 + px + q = 0 имеет корни -3; 5.
А4. Найдите среднее арифметическое корней уравнения y2 – 14y + 40 = 0.
А5. Один из коней уравнения x2 + kx – 16 = 0 равен -2. Найдите коэффициент k и второй корень уравнения.
- k = -6, x2 = 8
- k = -6, x2 = -8
- k = 6, x2 = -8
- k = 6, x2 = 8
B1. Пусть x1 и x2 – корни уравнения x2 + 7x – 11 = 0. Не решая уравнения, найдите значение выражения .
B2. Пусть x1 и x2 – корни уравнения x2 – 4x – 8 = 0. Не решая уравнения, найдите значение выражения + .
C1. Пусть x1 и x2 – корни уравнения x2 + 10x + 9 = 0. Запишите квадратное уравнение, корнями которого были бы числа .
Вариант 2
А1. Найдите подбором корни уравнения x2 – 4x + 3 = 0.
A2. Найдите один из корней квадратного уравнения x2 – 21x + 54 = 0.
А3. Найдите p, если уравнение x2 + px + q = 0 имеет корни -5; 6.
А4. Найдите среднее арифметическое корней уравнения y2 + 6 y — 27 = 0.
А5. Один из коней уравнения x2 + kx + 18 = 0 равен -3. Найдите коэффициент k и второй корень уравнения.
- k = -9, x2 = 6
- k = -9, x2 = -6
- k = 9, x2 = -6
- k = 9, x2 = 6
B1. Пусть x1 и x2 – корни уравнения x2 – 9x – 17 = 0. Не решая уравнения, найдите значение выражения .
B2. Пусть x1 и x2 – корни уравнения x2 + 3x – 9 = 0. Не решая уравнения, найдите значение выражения + .
C1. Пусть x1 и x2 – корни уравнения x2 – 11x + 18 = 0. Запишите квадратное уравнение, корнями которого были бы числа .
Ключи к тесту
вариант | А1 | А2 | А3 | А4 | А5 | В1 | В2 | С1 |
1 | 1 | 4 | 2 | 3 | 1 | 32 | 9x2 + 10x + 1 = 0 | |
2 | 1 | 2 | 3 | 2 | 3 | 85 | 18x2 – 11x + 1 = 0 |
Самостоятельная работа по теме «Уравнения»
ВАРИАНТ 1
1. Решите уравнение x2 = 5x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решите уравнение x2 = 5x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения 3x+3 = 5x.
3. Найдите корень уравнения 8+7x = 9x+4.
4. Найдите корень уравнения 10(x−9) = 7.
5. Решите уравнение x2 +3x=10. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6. Решите уравнение x2 +6 = 5x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
7. Найдите корень уравнения x – x/7 = 6.
8. Найдите корень уравнения 7/(x+8) = − 1.
9. Решите уравнение (− 5x+3) (− x+6) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 7x
11. Решите уравнение 5x2 +4x−1=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
12. Решите уравнение x2 −144=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 2
1. Решите уравнение 2x2 = 8x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения 6x+1 = − 4x.
3. Найдите корень уравнения − 5+9x = 10x+4.
4. Найдите корень уравнения 4(x−6) = 5.
5. Решите уравнение x2 +7x = 18. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6. Решите уравнение x2 +4 = 5x. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
7. Найдите корень уравнения x + x/11 = 24/11.
8. Найдите корень уравнения 1/(x+6) = 2.
9. Решите уравнение (− 2x+1) (− 2x−7) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 3x2 +12x = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
11. Решите уравнение 5x2 +8x+3=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
12. Решите уравнение x2 −36=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 3
1. Решите уравнение 3x2 = 9x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения x+3 = − 9x.
3. Найдите корень уравнения − 4+7x = 8x+1.
4. Найдите корень уравнения 5(x−6) = 2.
5. Решите уравнение x2 +2x=15. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
6. Решите уравнение x2 −x = 12. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
7. Найдите корень уравнения x + x/5 = − 12/5.
8. Найдите корень уравнения 4/(x−4) = − 5.
9. Решите уравнение (− x−4) (3x+3) = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
10. Решите уравнение 5x2 +20x = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
11. Решите уравнение 5x2 +9x+4=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
12. Решите уравнение x2 −64=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 4
1. Решите уравнение 4x2 = 20x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения x−2 = − 3x.
3. Найдите корень уравнения 7+8x = − 2x−5.
4. Найдите корень уравнения 4(x+10) = − 1.
5. Решите уравнение x2 −6x = 16. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
6. Решите уравнение x2 +4x=5. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
7. Найдите корень уравнения x + x/9 = − 10/3.
8. Найдите корень уравнения 4/(x+3) = 5.
9. Решите уравнение (x−6) (4x−6) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 4x2 −20x = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
11. Решите уравнение 6x2 −9x+3=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −4=0. Если уравнение имеет более одного корня, в ответ запишите больший
из корней.
ВАРИАНТ 5
1. Решите уравнение 5x2 = 35x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − 2x−4 = 3x.
3. Найдите корень уравнения 9+8x = 6x−2.
4. Найдите корень уравнения 4(x+1) = 9.
5. Решите уравнение x2 −3x=18. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6.Решите уравнение x2 +7=8x. Если уравнение имеет более одного корня, в ответ запишите меньший
из корней.
7. Найдите корень уравнения x + x/2=− 9.
8. Найдите корень уравнения 7/(x−5) = 2.
9. Решите уравнение (− 5x−3) (2x−1) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 6x2 +24x = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
11. Решите уравнение 8x2 −10x+2=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −81=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 6
1. Решите уравнение 6x2 = 36x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − x−7 = x.
3. Найдите корень уравнения − 1−3x = 2x+1.
4. Найдите корень уравнения 10(x+2) = − 7.
5. Решите уравнение x2 −18=7x. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6. Решите уравнение x2 +18 = 9x.Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
7. Найдите корень уравнения x + x/4 = − 5.
8. Найдите корень уравнения 11/(x−9) = − 10.
9. Решите уравнение (5x−2) (− x+3) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 3x2 +18x = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
11. Решите уравнение 8x2 −12x+4=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −49=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 7
1. Решите уравнение 7x2 = 42x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − 3x−9 = 2x.
3. Найдите корень уравнения − 4−6x = 4x−3.
4. Найдите корень уравнения 4(x−2) = − 1.
5. Решите уравнение x2 +4x = 21. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
6.Решите уравнение x2 −7x = 8. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
7. Найдите корень уравнения x + x/2 = -9.
8. Найдите корень уравнения 6/(x+5) = − 5.
9. Решите уравнение (6x−3) (− x+3) = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
10. Решите уравнение 5x2 +15x = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
11. Решите уравнение 5x2 −9x+4=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −25=0.Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 8
1. Решите уравнение 8x2 = 72x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − 4x−9 = 6x.
3. Найдите корень уравнения 1−10x = 5x+10.
4. Найдите корень уравнения 5(x+9) = − 8.
5. Решите уравнение x2 −21=4x. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6. Решите уравнение x2 +10 = 7x. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
7. Найдите корень уравнения x + x/7=− 8.
8. Найдите корень уравнения 11/(x+3) = 10.
9. Решите уравнение (x−6) (− 5x−9) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 4x2 −16x = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
11. Решите уравнение 5x2 −12x+7=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
12. Решите уравнение x2 −16=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 9
1. Решите уравнение 9x2 = 54x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − 2x−7 = − 4x.
3. Найдите корень уравнения 2+3x = − 7x−5.
4. Найдите корень уравнения 5(x+4) = − 9.
5. Решите уравнение x2 −15=2x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
6. Решите уравнение x2 −20 = x. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
7. Найдите корень уравнения x − x/12 = 11/3.
8. Найдите корень уравнения 6/(x+8) = − 3/4.
9. Решите уравнение (5x+2) (− x−4) = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
10. Решите уравнение 5x2 −10x = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
11. Решите уравнение 2x2 +5x−7=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −121=0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
ВАРИАНТ 10
1. Решите уравнение 10x2 = 80x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
2. Найдите корень уравнения − 8x−3 = − 6x.
3. Найдите корень уравнения − 5+2x = − 2x−3.
4. Найдите корень уравнения 4(x−8) = − 5.
5. Решите уравнение x2 −5x = 14. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
6. Решите уравнение x2 −35 = 2x. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
7. Найдите корень уравнения x − x/12 = 55/12.
8. Найдите корень уравнения 12/(x+5) = − 12/5.
9. Решите уравнение (x−2) (− 2x−3) = 0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
10. Решите уравнение 3x2 −9x = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.
11. Решите уравнение 2x2 −3x+1=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
12. Решите уравнение x2 −9=0. Если уравнение имеет более одного корня, в ответ запишите больший
из корней.
Теорема Виета. Примеры и решение
Теорема Виета:
Сумма корней приведённого квадратного уравнения
x2 + px + q = 0
равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену
x1 + x2 = -p, x1 · x2 = q.
Доказательство:
Если приведённое квадратное уравнение имеет вид
x2 + px + q = 0,
то его корни равны:
,
где D = p2 — 4q. Чтобы доказать теорему, сначала найдём сумму корней:
Чтобы доказать теорему, сначала найдём сумму корней:
,
а теперь найдём их произведение:
Равенства, показывающие зависимость между корнями и коэффициентами квадратного уравнения:
x1 + x2 = —p,
x1 · x2 = q
называются формулами Виета.
Примечание: если дискриминант равен нулю (D = 0), то подразумевается, что уравнение имеет не один корень, а два равных корня.
Обратная теорема
Теорема:
Если сумма двух чисел равна -p, а их произведение равно q, то эти числа являются корнями приведённого квадратного уравнения:
x2 + px + q = 0.
Доказательство:
Пусть дано x1 + x2 = —p, значит, x2 = —p — x1. Подставим это выражение в равенство x1 · x2 = q, получим:
Подставим это выражение в равенство x1 · x2 = q, получим:
x1(-p — x1) = q;
—px1 — x12 = q;
x12 + px1 + q = 0.
Это доказывает, что число x1 является корнем уравнения x2 + px + q = 0. Точно так же можно доказать, что и число x2 является корнем для этого уравнения.
Решение примеров
Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.
Пример 1. Найти корни уравнения:
x2 — 3x + 2 = 0.
Решение: Так как
x1 + x2 = -(-3) = 3;
x1 · x2 = 2;
очевидно, что корни равны 1 и 2:
1 + 2 = 3;
1 · 2 = 2.
Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:
12 — 3 · 1 + 2 = 0
и
22 — 3 · 2 + 2 = 0.
Ответ: 1, 2.
Пример 2. Найти корни уравнения:
x2 + 8x + 15 = 0.
Решение:
x1 + x2 = -8;
x1 · x2 = 15.
Методом подбора находим, что корни равны -3 и -5:
-3 + -5 = -8;
-3 · -5 = 15.
Ответ: -3, -5.
С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.
Пример 1. Составить квадратное уравнение по его корням:
x1 = -3, x2 = 6.
Решение: Так как x1 = -3, x2 = 6 корни уравнения x2 + px + q = 0, то по теореме, обратной теореме Виета, составим уравнения:
p = -(x1 + x2) = -(-3 + 6) = -3;
q = x1 · x2 = -3 · 6 = -18.
Следовательно, искомое уравнение:
x2 — 3x — 18 = 0.
Ответ: x2 — 3x — 18 = 0.
Пример 2. Записать приведённое квадратное уравнение, имеющее корни:
x1 = 2, x2 = 3.
Решение:
p = -(x1 + x2) = -(2 + 3) = -5;
q = x1 · x2 = 2 · 3 = 6.
Ответ: x2 — 5x + 6 = 0.
Теорема Виета
Предварительные навыкиЧто называют теоремой?
Если человек обнаружил в математике какую-нибудь закономерность, позволяющую быстро решить ту или иную задачу, то ему не следует говорить о том, что он сделал открытие. Потому что может случиться так, что эта закономерность работает только для определённых случаев, а для других не работает или вовсе решает задачу неправильно.
Чтобы поделиться своим открытием с другими людьми, найденную закономерность следует сформулировать в виде утверждения, а затем доказать это утверждение, приводя неоспоримые факты.
Сформулированное утверждение называют теоремой. А доказательство теоремы состоит из фактов, логических рассуждений и вычислений, которые не оспариваются.
Например, теоремой можно назвать следующее утверждение:
«Если числитель и знаменатель обыкновенной дроби умнóжить на какое-нибудь число, то значение данной дроби не измéнится».
А затем привести такое доказательство:
Пусть, имеется дробь . Умнóжим числитель и знаменатель этой дроби на число с. Тогда полýчится дробь . Докáжем, что дроби и равны. То есть докажем, что равенство является верным.
Для доказательства этого равенства воспользуемся основным свойством пропорции:
От перестановки мест сомножителей произведение не меняется. Поэтому в получившемся равенстве можно упорядочить правую часть по алфавиту:
Поскольку равенство является пропорцией, а пропорция это равенство двух отношений, то дроби и равны. Теорема доказана.
Теорема доказана.
Теорема Виета
Французский математик Франсуа Виет выявил интересную взаимосвязь между коэффициентами приведённого квадратного уравнения и корнями этого же уравнения. Эта взаимосвязь представлена в виде теоремы и формулируется так:
Сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком, а произведение корней равно свободному члену.
То есть, если имеется приведённое квадратное уравнение x2 + bx + c = 0, а его корнями являются числа x1 и x2, то справедливы следующие два равенства:
Знак системы (фигурная скобка) говорит о том, что значения x1 и x2 удовлетворяют обоим равенствам.
Покажем теорему Виета на примере приведённого квадратного уравнения x2 + 4x + 3 = 0.
Мы пока не знаем какие корни имеет уравнение x2 + 4x + 3 = 0. Но по теореме Виета можно записать, что сумма этих корней равна второму коэффициенту 4, взятому с противоположным знáком. Если коэффициент 4 взять с противоположным знáком, то получим −4. Тогда:
А произведение корней по теореме Виета будет равно свободному члену. В уравнении x2 + 4x + 3 = 0 свободным членом является 3. Тогда:
Теперь проверим действительно ли сумма корней равна −4, и равно ли произведение 3. Для этого найдём корни уравнения x2 + 4x + 3 = 0. А для удобства воспользуемся формулами для чётного второго коэффициента:
Корнями уравнения являются числа −1 и −3. По теореме Виета их сумма должна была равняться второму коэффициенту уравнения x2 + 4x + 3 = 0, взятому с противоположным знаком. Действительно, так оно и есть. Вторым коэффициентов в уравнении x2 + 4x + 3 = 0 является 4. Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
Если взять его с противоположным знаком и приравнять сумму корней x1 + x2 к этому коэффициенту, то получается верное равенство:
А произведение корней −1 и −3 по теореме Виета должно было равняться свободному члену уравнения x2 + 4x + 3 = 0, то есть числу 3. Видим, что это условие тоже выполняется:
Значит выражение является справедливым.
Рассмотрим квадратное уравнение x2 − 8x + 15 = 0. По теореме Виета сумма корней этого уравнения равна второму коэффициенту, взятому с противоположным знаком. Второй коэффициент равен −8. Если взять его с противоположным знаком, то получим 8. Тогда:
А произведение корней равно свободному члену. В уравнении x2 − 8x + 15 = 0 свободным членом является 15. Тогда:
Теперь проверим действительно ли сумма корней равна 8, и равно ли произведение 15. Для этого найдём корни данного уравнения. А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
А для удобства воспользуемся формулами для чётного второго коэффициента. В этот раз пропустим нéкоторые подробные записи:
Видим, что корнями уравнения x2 − 8x + 15 = 0 являются числа 5 и 3. Их сумма равна 8. То есть сумма корней равна второму коэффициенту уравнения x2 − 8x + 15 = 0, взятому с противоположным знаком.
А произведение чисел 5 и 3 равно 15. То есть равно свободному члену уравнения x2 − 8x + 15 = 0.
Значит выражение является справедливым.
Замечание. Чтобы теорема Виета выполнялась, квадратное уравнение обязательно должно быть приведённым и иметь корни.
Например, рассмотрим квадратное уравнение x2 − 2x + 4 = 0. Напишем сумму и произведение корней этого уравнения:
Но уравнение x2 − 2x + 4 = 0 не имеет корней, сумма которых равна 2, а произведение которых равно 4.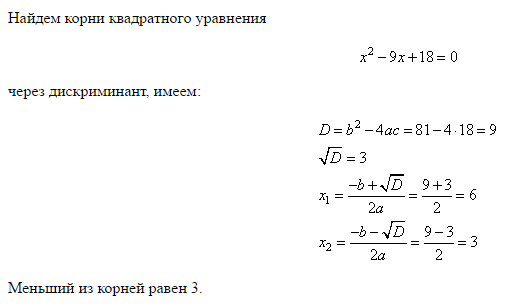 Убедиться в этом можно, вычислив дискриминант:
Убедиться в этом можно, вычислив дискриминант:
D1 = k2 − ac = (−1)2 − 1 × 4 = −3
А значит записывать выражение не имеет смысла.
Теорема Виета полезна тем, что позволяет до начала решения узнать знаки корней уравнения.
Например, запишем для уравнения x2 − 5x + 6 = 0 сумму и произведение его корней. Сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Посмотрев на эти два равенства можно сразу понять, что оба корня должны быть положительными. Потому что произведение x1 × x2 = 6 будет выполняться только в двух случаях: если значения x1 и x2 положительны либо они оба отрицательны. Если эти значения будут отрицательными, то не будет выполняться равенство x1 + x2 = 5, поскольку его правая часть равна положительному числу. А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5, так и равенству x1 × x2 = 6.
А значения x1 и x2 должны удовлетворять как равенству x1 + x2 = 5, так и равенству x1 × x2 = 6.
Ещё одна польза от теоремы Виета в том, что корни можно найти методом подбора. В данном примере корни должны быть такими, чтобы они удовлетворяли как равенству x1 + x2 = 5 так и равенству x1 × x2 = 6. Очевидно, что таковыми являются корни 3 и 2
Значит, x1 = 3, x2 = 2
Доказательство теоремы Виета
Пусть дано приведённое квадратное уравнение x2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену:
Докажем, что равенства x1 + x2 = −b и x1 × x2 = c имеют место быть.
Вспомним формулы корней квадратного уравнения:
Найдём сумму корней x1 и x2. Для этого подставим в выражение x1 + x2 вместо x1 и x2 соответствующие выражения из правой части формул корней квадратного уравнения. Не забываем, что в приведённом квадратном уравнении x2 + bx + c = 0 старший коэффициент a равен единице. Тогда в процессе подстановки знаменатель станет равен просто 2
Запишем правую часть в виде дроби с одним знаменателем:
Раскроем скобки в числителе и приведём подобные члены:
Сократим дробь на 2, тогда получим −b
Значит x1 + x2 действительно равно −b
x1 + x2 = −b
Теперь аналогично докажем, что произведение x1 × x2 равно свободному члену c.
Подставим вместо x1 и x2 соответствующие выражения из формул корней квадратного уравнения. Не забываем, что коэффициент a всё ещё равен единице:
Чтобы перемнóжить дроби, нужно перемнóжить их числители и знаменатели:
В числителе теперь содержится произведение суммы двух выражений и разности этих же выражений. Воспользуемся тождеством (a + b)(a − b) = a2 − b2. Тогда в числителе полýчится А знаменатель будет равен 4
Теперь в числителе выражение (−b)2 станет равно b2, а выражение станет равно просто D
Но D равно b2 − 4ac. Подстáвим это выражение вместо D, не забывая что a = 1. То есть вместо b2 − 4ac надо подставить b2 − 4c
В получившемся выражении раскроем скобки в числителе и приведём подобные члены:
Сократим получившуюся дробь на 4
Значит x1 × x2 действительно равно c.
x1 × x2 = c
Таким образом, сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту, взятому с противоположным знáком (x1 + x2 = −b), а произведение корней равно свободному члену (x1 × x2 = c). Теорема доказана.
Теорема, обратная теореме Виета
Когда записана сумма и произведение корней приведённого квадратного уравнения, обычно начинается подбор подходящих корней к этому уравнению. В этот момент в работу включается так называемая теорема, обратная теореме Виета. Она формулируется так:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел x1 и x2 равно свободному члену уравнения x2 + bx + c = 0, то числа x1 и x2 являются корнями уравнения x2 + bx + c = 0.
Обратные теоремы бывают поставлены так, что их утверждением является заключение первой теоремы.
Так, доказывая теорему Виета мы пришли к заключению, что сумма x1 и x2 равна −b, а произведение x1 и x2 равно c. В обратной же теореме это заключение служит утверждением.
Ранее мы решили уравнение x2 − 5x + 6 = 0 и написали для него такую сумму и произведение корней:
А затем подобрали корни 3 и 2. По сути мы применили теорему, обратную теореме Виета. Числа 3 и 2 таковы, что их сумма равна второму коэффициенту уравнения x2 − 5x + 6 = 0, взятому с противоположным знаком (числу 5), а произведение чисел 3 и 2 равно свободному члену (числу 6). Значит числа 3 и 2 являются корнями уравнения x2 − 5x + 6 = 0.
Пример 2. Решить квадратное уравнение x2 − 6x + 8 = 0 по теореме, обратной теореме Виета.
В данном уравнении a = 1. Значит квадратное уравнение является приведённым. Его можно решить по теореме, обратной теореме Виета.
Сначала запишем сумму и произведение корней уравнения. Сумма корней будет равна 6, поскольку второй коэффициент исходного уравнения равен −6. А произведение корней будет равно 8
Теперь имея эти два равенства можно подобрать подходящие корни. Они должны удовлетворять как равенству x1 + x2 = 6, так и равенству x1 × x2 = 8
Подбор корней удобнее выполнять с помощью их произведения. Используя равенство x1 × x2 = 8 нужно найти такие x1 и x2, произведение которых равно 8.
Число 8 можно получить если перемножить числа 4 и 2 либо 1 и 8.
4 × 2 = 8
1 × 8 = 8
Но значения x1 и x2 надо подбирать так, чтобы они удовлетворяли не только равенству x1 × x2 = 8, но и равенству x1 + x2 = 6.
Сразу делаем вывод, что значения 1 и 8 не годятся, поскольку они хоть и удовлетворяют равенству x1 × x2 = 8, но не удовлетворяют равенству x1 + x2 = 6.
Зато значения 4 и 2 подходят как равенству x1 × x2 = 8, так и равенству x1 + x2 = 6, поскольку эти значения удовлетворяют обоим равенствам:
Значит корнями уравнения x2 − 6x + 8 = 0 являются числа 4 и 2.
Обратная теорема, как и любая теорема нуждается в доказательстве. Докажем теорему, обратную теореме Виета. Для удобства корни x1 и x2 обозначим как m и n. Тогда утверждение теоремы, обратной теореме Виета примет следующий вид:
Если числа m и n таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знáком, а произведение чисел m и n равно свободному члену уравнения x2 + bx + c = 0, то числа m и n являются корнями уравнения x2 + bx + c = 0
Для начала запишем, что сумма m и n равна −b, а произведение mn равно c
Чтобы доказать, что числа m и n являются корнями уравнения x2 + bx + c = 0, нужно поочередно подстáвить буквы m и n в это уравнение вместо x, затем выполнить возможные тождественные преобразования. Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.
Если в результате преобразований левая часть станет равна нулю, то это будет означать, что числа m и n являются корнями уравнения x2 + bx + c = 0.
Помимо букв m и n нам нужно знать чему равен параметр b. Выразим его из равенства m + n = −b. Легче всего это сделать, умножив обе части этого равенства на −1
Теперь всё готово для подстановок. Подстáвим m в уравнение x2 + bx + c = 0 вместо x, а выражение −m − n подставим вместо b
Видим, что при x = m получается верное равенство. Значит число m является корнем уравнения x2 + bx + c = 0.
Аналогично докажем, что число n является корнем уравнения x2 + bx + c = 0. Подставим вместо x букву n, а вместо c подставим mn, поскольку c = mn.
Видим, что при x = n тоже получается верное равенство. Значит число n является корнем уравнения.
Следовательно, числа m и n являются корнями уравнения x2 + bx + c = 0.
Примеры решения уравнений по теореме, обратной теореме Виета
Пример 1. Решить квадратное уравнение x2 − 4x + 4 = 0 по теореме, обратной теореме Виета.
Запишем сумму корней x1 и x2 и приравняем её к второму коэффициенту, взятому с противоположным знаком. Также запишем произведение корней x1 и x2 и приравняем его к свободному члену:
В данном примере очевидно, что корнями являются числа 2 и 2. Потому что их сумма равна 4 и произведение равно 4
Значение x1 совпадает с x2. Это тот случай, когда квадратное уравнение имеет только один корень. Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Если мы попробуем решить данное уравнение с помощью формул корней квадратного уравнения, то обнаружим что дискриминант равен нулю, и корень вычисляется по формуле
Данный пример показывает, что теорема обратная теореме Виета, работает и для уравнений, имеющих только один корень. Признаком того, что квадратное уравнение имеет только один корень является то, что значения x1 и x2 совпадают.
Пример 2. Решить уравнение x2 + 3x + 2 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Теперь подберём значения x1 и x2. Здесь начинается самое интересное. Произведение корней равно 2. Число 2 можно получить перемножив 1 и 2. Но сумма корней x1 + x2 равна отрицательному числу −3. Значит значения 1 и 2 не подходят.
Сумма бывает отрицательной если оба слагаемых отрицательны либо отрицательным является одно слагаемое, модуль которого больше.
Если подберём корни с разными знаками, то не будет выполняться равенство x1 × x2 = 2.
Если подберем положительные корни, то будет выполняться равенство x1 × x2 = 2, но не будет выполняться равенство x1 + x2 = −3.
Очевидно, что корнями являются два отрицательных числа. Произведение отрицательных чисел есть положительное число. А сумма отрицательных чисел есть отрицательное число.
Тогда равенствам будут удовлетворять числа −1 и −2.
Итак, корнями являются числа −1 и −2
Пример 3. Решить уравнение x2 + 16x + 15 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Как и в прошлом примере сумма корней равна отрицательному числу, а произведение корней — положительному числу.
Произведение бывает положительным если оба сомножителя положительны либо оба сомножителя отрицательны. Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Первый вариант отпадает сразу, поскольку сумма корней равна отрицательному числу. Тогда получается, что оба корня будут отрицательными. Попробуем подобрать их.
Число 15 можно получить, если перемножить числа −1 и −15 или (−3) и (−5). В данном случае подходит первый вариант, поскольку сумма чисел −1 и −15 равна −16, а их произведение равно 15. Значит корнями уравнения x2 + 16x + 15 = 0 являются числа −1 и −15
Пример 4. Решить уравнение x2 − 10x − 39 = 0 по теореме, обратной теореме Виета.
Запишем сумму и произведение корней данного уравнения:
Произведение корней равно отрицательному числу. Значит один из корней является отрицательным. Число −39 можно получить если перемножить числа −3 и 13 либо −13 и 3. Из этих комбинаций больше годится комбинация −3 и 13, поскольку при перемножении этих чисел получается −39, а при сложении 10
Значит корнями уравнения x2 − 10x − 39 = 0 являются числа −3 и 13
Пример 5. Первый корень уравнения x2 + bx + 45 = 0 равен 15. Найти второй корень этого уравнения, а также значение коэффициента b.
Первый корень уравнения x2 + bx + 45 = 0 равен 15. Найти второй корень этого уравнения, а также значение коэффициента b.
По теореме Виета произведение корней приведённого квадратного уравнения равно свободному члену. В данном случае это произведение равно 45
x1 × x2 = 45
При этом один из корней уже известен — это корень 15.
15 × x2 = 45
Тогда второй корень будет равен 3, потому что число 45 получается, если 15 умножить на 3
15 × 3 = 45
Значит x2 = 3
Этот второй корень также можно было бы получить, выразив из равенства 15 × x2 = 45 переменную x2
Теперь определим значение коэффициента b. Для этого напишем сумму корней уравнения:
15 + 3 = 18
По теореме Виета сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
Если сумма корней равна 18, а 18 это положительное число, то в самóм уравнении этот коэффициент будет отрицательным:
x2 − 18x + 45 = 0
Значит b = −18.
Обычно решение к такой задаче записывают так. Сначала записывают основную теорему Виета в виде суммы и произведения корней:
Затем в это выражение подставляют имеющиеся известные значения. В нашем случае известно, что первый корень равен 15, а свободный член уравнения x2 + bx + 45 = 0 равен 45
Из этой системы следует найти x2 и b. Выразим эти параметры:
Из этой системы мы видим, что x2 равно 3. Подставим его в первое равенство:
Теперь из первого равенства мы видим, что −b равно 18
Но нас интересует b, а не −b. Следует помнить, что −b это −1b. Чтобы найти b нужно 18 разделить на −1. Тогда b станет равно −18
Тогда b станет равно −18
Этот же результат можно получить если в выражении умножить первое равенство на −1
Теперь возвращаемся к исходному уравнению x2 + bx + 45 = 0 и подставляем найденное значение b
Выполним умножение −18 на x. Получим −18x
Раскроем скобки:
Пример 6. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа 2 и 8.
В этом задании корни уже известны. То есть x1 = 2, x2 = 8. По ним надо составить квадратное уравнение вида x2 + bx + c = 0.
Запишем сумму и произведение корней:
По теореме Виета сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком. Если сумма корней 2 и 8 равна 10, то в самóм уравнении число 10 должно быть с противоположным знаком. Значит b = −10.
Значит b = −10.
Произведение корней по теореме Виета равно свободному члену. У нас это произведение равно 16.
Значит b = −10, c = 16. Отсюда:
x2 − 10x + 16 = 0
Пример 7. Используя теорему Виета, написать приведённое квадратное уравнение, корнями которых являются числа и .
Запишем сумму и произведение корней:
Сумма корней равна 2. Тогда в уравнении второй коэффициент будет равен −2. А произведение корней равно −1. Значит свободный член будет равен −1. Тогда:
x2 − 2x − 1 = 0
Когда квадратное уравнение неприведённое
Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым.
Если квадратное уравнение не является приведённым, но всё равно возникла необходимость применить теорему Виета, то обе части неприведённого квадратного уравнения следует разделить на коэффициент, который располагается перед x2.
Если к примеру в квадратном уравнении ax2 + bx + c = 0 коэффициент a не равен единице, то данное уравнение является неприведённым. Чтобы сделать его приведённым, надо разделить обе его части на коэффициент, который располагается перед x2, то есть на a
Получилось уравнение , которое является приведённым. В нём второй коэффициент равен , а свободный член равен . Тогда сумма и произведение корней будут выглядеть так:
Например, решим квадратное уравнение 4x2 + 5x + 1 = 0. Это уравнение не является приведённым. Приведённым оно станет, если разделить обе его части на коэффициент, который располагается перед x2, то есть на 4
Получили приведённое квадратное уравнение. В нём второй коэффициент равен , а свободный член . Тогда по теореме Виета имеем:
Отсюда методом подбора находим корни −1 и
Возможно этот метод вы редко будете использовать при решении квадратных уравнений. Но знать о нём не помешает.
Но знать о нём не помешает.
Пример 2. Решить квадратное уравнение 3x2 − 7x + 2 = 0
Данное уравнение не является приведённым, а значит его пока нельзя решить по теореме, обратной теореме Виета.
Сделаем данное уравнение приведенным. Разделим обе части на коэффициент, который располагается перед x2
Получили уравнение . Запишем сумму и произведение корней этого уравнения:
Отсюда методом подбора находим корни 2 и
Пример 3. Решить квадратное уравнение 2x2 − 3x − 2 = 0
Это неприведённое квадратное уравнение. Чтобы сделать его приведённым, нужно разделить обе его части на 2. Сделать это можно в уме. Если 2x2 разделить на 2, то полýчится x2
Далее если −3x разделить на 2, то полýчится . Чтобы видеть где коэффициент, а где переменная, такое выражение записывают в виде
Далее если −2 разделить на 2, то полýчится −1
Прирáвниваем получившееся выражение к нулю:
Теперь применяем теорему Виета. Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Сумма корней будет равна второму коэффициенту, взятому с противоположным знáком, а произведение корней свободному члену:
Отсюда методом подбора находим корни 2 и
Задания для самостоятельного решения
Задание 1. Написать сумму и произведение корней для квадратного уравнения:
Решение:
Задание 2. Написать сумму и произведение корней для квадратного уравнения:
Решение:
Задание 3. Написать сумму и произведение корней для квадратного уравнения:
Решение:
Задание 4. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Задание 5. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Задание 6. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Задание 7. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Задание 8. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Задание 9. Решить квадратное уравнение по теореме, обратной теореме Виета:
Решить квадратное уравнение по теореме, обратной теореме Виета:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
«Теорема Виета в решении квадратных уравнений». 8-й класс
Цели урока:
Образовательные: повторить ранее изученные методы решения квадратных уравнений, продолжить формирование умения решать квадратные уравнения, познакомить учащихся с теоремой Виета и обратной теоремой Виета.
Развивающие: развивать навыки
познавательной, мыслительной деятельности,
логическое мышление, вырабатывать умение
анализировать, развитие умений выделять главное
при работе,развитие речи, внимания; формирование
самостоятельности в мышлении.
Воспитательные: развивать интерес к математике, привитие аккуратности и трудолюбия, навыков самостоятельной работы и самооценки.
Оборудование: интерактивная доска, компьютер, карточки с дифференцированными заданиями.
Ход урока
I. Организационный момент
II. Актуализация опорных знаний
— Мы начнем сегодняшний урок с высказывания математика Джорджа Пойа “Лучший способ изучить что-либо — это открыть самому”. (Слайд 1. Презентация).Это высказывание я выбрала не случайно, так как сегодня на уроке вам предстоит самим сформулировать теорему, которая играет важнейшую роль для дальнейшего изучения математики.
— Для начала давайте вспомним, какую тему мы с вами изучаем?
— Составьте, пожалуйста, синквейн по данной теме. (Слайд 2)
Заслушиваем несколько учащихся.
— Какое уравнение называется квадратным? (Слайд 3)
— Является ли квадратным уравнение:
а) 5x2-7x3+13=0;
б) 8x-5x2+4=0;
в)
Возьмите приложение 1 и выполните задания. Соедините каждое уравнение, стоящее в левом
столбце, с соответствующими ему коэффициентами
а, b, с из правого столбца (Слайд 4):
Соедините каждое уравнение, стоящее в левом
столбце, с соответствующими ему коэффициентами
а, b, с из правого столбца (Слайд 4):
| -х2 + 6х – 8 = 0 | а = 8; b = — 6; с = 1 |
| -6x+ 8х2 + 1 = 0 | а = -8; b = 0; с = 6 |
| -8 – х + 6х2 = 0 | а = -1; b = 6; с = — 8 |
| -8х2 + 6= 0 | а = 1; b = 8; с = — 1 |
| -1 + x2 + 8x=0 | а = 6; b = -1; с = — 8 |
Соедините каждое утверждение, стоящее в левом
столбце, с соответствующим ему словом из правого
столбца. (Слайд 5)
(Слайд 5)
| Квадратное уравнение спервым коэффициентомравным 1 | неполное |
| Подкоренное выражениев формуле корней квадратного уравнения | коэффициенты |
| Один из видов квадратного уравнения | приведенное |
| a,b, с в квадратном уравнении. | дискриминант |
-
Что называют дискриминантом квадратного
уравнения? (Слайд 6)
- Как с помощью дискриминанта можно определить, сколько корней имеет квадратное уравнение?
- Назовите формулы корней квадратных уравнений.

Вы научились решать неполные квадратные уравнения по специальным алгоритмам, а полные квадратные уравнения – по формулам. Решение по формулам громоздко, поэтому давайте с вами найдем другой более простой способ нахождения корней квадратного уравнения. Для этого проведем небольшую исследовательскую работу в парах. Возьмите приложение 2 и выполните задания, напечатанные в нем.
1. Решите приведенные квадратные уравнения
х2 – 7х – 18=0;
х2 — 10х + 21=0;
х2 + 13х — 30=0
2. Заполните таблицу (Слайд 7).
| Уравнение | а | b | c | Найдите значение D | x1 | x2 | x1+x2 | x1*x2 | |
| х2 – 7х – 18=0 | |||||||||
| х2 — 10х + 21=0 | |||||||||
| х2 + 13х — 30=0 |
Проверка полученных результатов учащихся с
помощью заполненной таблицы (Слайд 8).
III. Изучение нового материала.
3. Установить связь между корнями приведенного квадратного уравнения и его коэффициентами.
4. Запишите в тетради приведенное квадратное уравнение в общем виде, в котором второй коэффициент обозначим буквой p, а свободный член буквой q: х2 + px + q = 0.
5. Запишите общую формулу корней приведенного квадратного уравнения.
6. Найдите сумму корней приведенного квадратного уравнения (x1 + x2 = — p)
7. Найдите произведение корней приведенного квадратного уравнения (x1 * x2 = q).
8. Сформулируйте полученный результат. (Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).
Данное утверждение носит название теоремы
Виета по имени французского математика Франсуа
Виета. В 1591 году Виет ввел буквенные обозначения
не только для неизвестных величин, но и для
коэффициентов уравнений; благодаря этому стало
впервые возможным выражение свойств уравнений и
их корней формулами.
В 1591 году Виет ввел буквенные обозначения
не только для неизвестных величин, но и для
коэффициентов уравнений; благодаря этому стало
впервые возможным выражение свойств уравнений и
их корней формулами.
Запишите, пожалуйста, в тетради тему сегодняшнего урока: «Применение теоремы Виета к решению квадратных уравнений» (Слайд 9).
Откройте учебники и запишите теорему Виета (Слайд 10).
Можно ли использовать теорему Виета для решения неприведенных квадратных уравнений вида ax2 + bx + c= 0?
Для уравнений вида ax2+bx+c=0 сумма корней равна ,
а произведение (Слайд 11).
Как вы думаете для чего нам нужна теорема Виета? Используя теорему Виета, можно выразить сумму и произведение корней произвольного квадратного уравнения через его коэффициенты.
Справедливо утверждение, обратное теореме Виета:
Если m и n таковы, что их сумма равна — p, а
произведение равно q, то эти числа являются
корнями уравнения х2 + px + q = 0. Запишите
данную теорему в тетради (слайд 12).
Запишите
данную теорему в тетради (слайд 12).
По теореме, обратной теореме Виета, можно проверять, правильно ли найдены корни квадратного уравнения.
Если выполняется равенство и , то числа х1 и х2 являются корнями квадратного уравнения ах2 + bх + с = 0.
IV. Физминутка (Слайд 13).
V. Закрепление изученного материала.
Трое учащихся с помощью учителя по очереди решают у доски 3 примера, а остальные учащиеся записывают эти решения в тетради.
Пример 1
Найдем сумму и произведение корней уравнения 3x2-5x+2=0.
Дискриминант D=1 — положительное число. Значит, уравнение имеет корни. Эти же корни имеет приведенное квадратное уравнение . Значит, сумма корней равна , а произведение равно .
Пример 2
Решим уравнение x2+3x-40=0 и выполним
проверку по теореме, обратной теореме Виета.
Найдем дискриминант: D=169.
По формуле корней квадратного уравнения получаем: x1 = — 8, x2 = 5.
Покажем, что корни уравнения найдены правильно.
В уравнении x2+3x-40=0 коэффициент p = 3, а свободный член q= — 40. Сумма найденных чисел -8 и 5 равна -3, а их произведение равно -40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения x2+3x-40=0.
Пример 3
Найдем подбором корни уравнения x2-x-12=0.
Найдем дискриминант: D=49-положительное число. Пусть x1 и x2— корни уравнения. Тогда
Если x1и x2 — целые числа, то они являются делителями числа -12.
Учитывая также, что сумма этих чисел равна 1, нетрудно догадаться, что x1= — 3 и x2 = 4.
Учащимся предлагается выполнить номера из
учебника.
Задание 1. Найдите сумму и произведение корней уравнений № 580 а,д,в,г.
Задание 2. Решите уравнение и выполните проверку по теореме, обратной теореме Виета. № 581 ав.
Задание 3. Методом подбора найдите корни уравнений. № 583 ав.
Учащимся быстрее других, справившихся с данными номерами, предлагается решить следующее дополнительное задание:
Один из корней данного квадратного уравнения равен – 2.
Найдите коэффициент k и второй корень уравнения: 3х2 + kх + 10 = 0 (к = 11, ).
VI. Самостоятельная работа на 10-15 минут. (Слайд 14)
Возьмите приложение 3 и выполните самостоятельную работу.
| Номер задания | Количество баллов | Задание |
| Обязательная часть | ||
| 1 | 1 | Чему равно произведение корней уравнения квадратного уравнения х2 + 3х — 1=0? |
| 2 | 1 | Чему равна сумма корней уравнения квадратного уравнения х2 – 6х +8=0? |
| 3 | 1 | Составьте приведенное
квадратное уравнение, корнями которого являются
числа – 3; 7.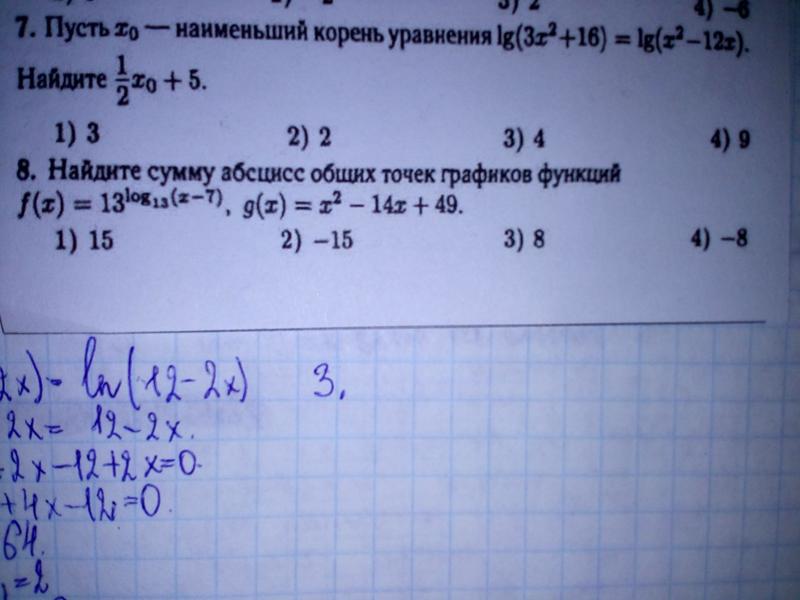 |
| 4 | 2 | Чему равно произведение корней уравнения квадратного уравнения 2х2 + 9х — 6=0? |
| 5 | 2 | Один из корней данного квадратного уравнения равен –3. Найдите коэффициент k и второй корень уравнения: х2 +4х + k = 0 |
| Дополнительная часть | ||
| 6 | 3 | Составьте приведенное квадратное уравнение, корнями которого являются числа . |
| 7 | 3 | Не вычисляя корней уравнения х2
– 4 х – 5 = 0, найдите , где х1 и х2 — корни
данного уравнения. |
| Оценка | Количество, набранных баллов |
| 2 | 0-6 |
| 3 | 7-8 |
| 4 | 9-10 |
| 5 | 11-13 |
VII. Подведение итогов урока.
— Что нового вы сегодня узнали на уроке?
— Сформулируйте теорему Виета и теорему обратную теореме Виета.
— Всегда ли можно применять теорему Виета? (Нет,
только когда D?0).
— Для чего нам нужна теорема Виета?
— Как можно решить уравнение: х2 + 2х – 3 = 0.
Ответ: С помощью формул, с помощью теоремы Виета.
— Какие же корни? (-3 и 1).
— А еще это уравнение можно решить графически и этот способ решения мы изучим с вами на следующем уроке.
— Надеюсь, этот материал вы не забудете. Помните слова французского инженера-физика Лауэ: “Образование есть то, что остается, когда все выученное уже забыто”. (Слайд 15)
VIII. Домашнее задание (слайд 16).
1. Пункт 24, № 580 бежз, 581 г, 583 б.
2. Решить уравнение: х2+ 2013х – 2014=0.
IX. Рефлексия. (Слайд 17).
Лист самооценки
Оцените степень сложности урока.
Вам было на уроке:
- легко;
- обычно;
- трудно.
Оцените степень вашего усвоения материала:
- усвоил полностью, могу применить;
- усвоил полностью, но затрудняюсь в применении;
- усвоил частично;
- не усвоил.

Приложение 1
Приложение 2
Приложение 3
Приложение 4
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Теорема Виетта 8 класс онлайн-подготовка на Ростелеком Лицей
Теорема Виета
Приведенное квадратное уравнение x2-7х+10 = 0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Докажем, что таким свойством обладает любое приведенное квадратное уравнение, которое имеет корни.
Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Докажем, что таким свойством обладает любое приведенное квадратное уравнение, которое имеет корни.
Рассмотрим приведенное квадратное уравнение. Обозначим второй коэффициент буквой p, а свободный член буквой q:
x2+px+q=0
D=p2-4q
x1=-p-D2
x2=-p+D2
Найдем сумму корней:
x1+x2=-p-D2+-p+D2=-2p2=-p
Найдем произведение корней:
x1·x2=-p-D2·-p+D2=(-p-D)(-p+D)4=p2-D4
В числителе применили формулу разности квадратов. Теперь подставим вместо дискриминанта выражение для него:
p2-D4=p2-p2+4q4=4q4=q
Мы доказали теорему Виета, названную по имени знаменитого французского математика Франсуа Виета:
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Ее можно записать и короче:
В уравнении вида x2+px+q=0 выполняется
x1+x2=-px1·x2=q
Справедливо утверждение и обратное теореме Виета: если числа m и n таковы, что их сумма равна –р, а произведение равно q, то эти числа являются корнями уравнения х2+px+q = 0.
Рассмотрим применение теоремы Виета.
Зависимость между корнями и коэффициентами квадратного уравнения позволяет в некоторых случаях находить корни уравнения устно, не используя формулу корней.
Пример 1. Найти корни уравнения x2-3x+2 = 0.
Так как сумма корней равна 3, а произведение равно 2, очевидно, что корни равны 1 и 2:
1+2 = 3
1·2 = 2
Подставив числа 1 и 2 в уравнение, убедимся, что корни найдены правильно:
12-3·1+2 = 0
и
22-3·2+2 = 0
Ответ: 1; 2.
Пример 2. Найти корни уравнения x2+8x+15 = 0
Решение:
x1+x2 = -8
x1·x2 = 15
Методом подбора находим что корни равны -3 и -5:
(-3)+(-5) = -8
(-3)·(-5) = 15
Ответ: -3; -5.
С помощью теоремы, обратной теореме Виета, можно составлять квадратное уравнение по его корням.
Пример 3. Составить квадратное уравнение по его корням x1 = -3, x2 = 6.
Составить квадратное уравнение по его корням x1 = -3, x2 = 6.
Решение: так как x1 = -3, x2 = 6 – корни уравнения x2+px+q = 0, то по теореме, обратной теореме Виета, составим уравнения:
p = -(x1+x2) = -(-3+6) = -3
q = x1·x2 = -3·6 = -18
Следовательно, искомое уравнение:
x2-3x-18 = 0
Ответ: x2 — 3x — 18 = 0.
2-4 (1) (- 18)————————————— —————
2 (1)
-3 плюс или минус квадратный корень из «9 + 72»
————— ——————————
2
-3 плюс или минус квадратный корень из «81»
—- ————————————-
2
-3 плюс-минус «9»
———————
2
два уравнения, которые у вас есть:
-3 + 9-3-9
—- ——
2 2
6-12
— —-
2 2
3-6
x = {3, -6}
Решено: используйте квадратичную формулу, чтобы найти корни.
 ..
..- математика
- алгебра
- вопросы и ответы по алгебре
- Используйте квадратичную формулу, чтобы найти корни уравнения, X2 + 3x — 18 = 0 Выберите один ответ. …
Показать транскрибированный текст изображения
Лучший ответ
100% (1 оценка) Предыдущий вопрос Следующий вопрос Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения, x2 + 3x — 18 = 0 Выберите один ответ. а. {-6, 3} б. {-2, 9} с. {- 3, 6} д.{-9, 2} Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения. 2X2 — 28x + 98 = 0 Выберите один ответ. а. {-7, 7} б. {7} в. {-2,49} д. нет решения в виде действительного числа Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения. При необходимости округлите до десятых, x2 + x + 10 = 0 Выберите один ответ. а. {3.2} б. {-5,5, -2} с. {-3.2, 3.2} d. нет решения в виде действительного числа Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения. При необходимости округлите до десятых, x2 — 6x + 2 = 0 Выберите один ответ. а. {0.4, 5.6} б. {0,5, 4,8} в. {1.4, 2.4} d. нет решения в виде действительного числа Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения. При необходимости округлите до десятых. 3X2 — 4x — 8 = 0 Выберите один ответ. а. {-1,7, 2,8} б. {-2,8, 2} в. {-1,1, 2,4} d. нет реального решения Используйте формулу корней квадратного уравнения, чтобы найти нули функции. y = 16X2 + 40x + 25 Выберите один ответ. а. {-1,25, 1,25} б. {-1.25} c. {- 4,5} d. {-0.8} Используйте формулу корней квадратного уравнения, чтобы найти нули функции. При необходимости округлите до десятых.y = 17X2 — 21 Выберите один ответ. а. {-1.1, 1.1} б. {1.1} в. {-4.1, 4.6} d. нет реального решения Используйте формулу корней квадратного уравнения, чтобы найти нули функции. При необходимости округлите до десятых. y = 3×2 + 5x Выберите один ответ. а. {-2.23, 1.7} б. {-1,7, 0} c. {-2,8, 1,7} d. нет реального решения Бейсболист отбивает бейсбольный мяч за пределы поля.
При необходимости округлите до десятых, x2 — 6x + 2 = 0 Выберите один ответ. а. {0.4, 5.6} б. {0,5, 4,8} в. {1.4, 2.4} d. нет решения в виде действительного числа Используйте формулу корней квадратного уравнения, чтобы найти корни уравнения. При необходимости округлите до десятых. 3X2 — 4x — 8 = 0 Выберите один ответ. а. {-1,7, 2,8} б. {-2,8, 2} в. {-1,1, 2,4} d. нет реального решения Используйте формулу корней квадратного уравнения, чтобы найти нули функции. y = 16X2 + 40x + 25 Выберите один ответ. а. {-1,25, 1,25} б. {-1.25} c. {- 4,5} d. {-0.8} Используйте формулу корней квадратного уравнения, чтобы найти нули функции. При необходимости округлите до десятых.y = 17X2 — 21 Выберите один ответ. а. {-1.1, 1.1} б. {1.1} в. {-4.1, 4.6} d. нет реального решения Используйте формулу корней квадратного уравнения, чтобы найти нули функции. При необходимости округлите до десятых. y = 3×2 + 5x Выберите один ответ. а. {-2.23, 1.7} б. {-1,7, 0} c. {-2,8, 1,7} d. нет реального решения Бейсболист отбивает бейсбольный мяч за пределы поля. Следующее уравнение моделирует траекторию мяча. Если его не поймают, когда приземлится бейсбол? Округлите до ближайшей десятой секунды. h = -16t2 + 50t + 4 Выберите один ответ.а. 3,0 секунды б. 3,2 секунды c. 3,4 секунды d. 3,6 секунды Баланс благотворительного фонда моделируется следующим образом: y = -4,1×2 + 7,1x + 145, где y — это баланс, а x — годы после 1996 года. Если в фонд не добавляются деньги, через сколько лет фонд будет иметь нулевой баланс? С округлением до ближайшего года. Выберите один ответ. а. 6 лет б. 7 лет c. 8 лет d. 9 лет
Следующее уравнение моделирует траекторию мяча. Если его не поймают, когда приземлится бейсбол? Округлите до ближайшей десятой секунды. h = -16t2 + 50t + 4 Выберите один ответ.а. 3,0 секунды б. 3,2 секунды c. 3,4 секунды d. 3,6 секунды Баланс благотворительного фонда моделируется следующим образом: y = -4,1×2 + 7,1x + 145, где y — это баланс, а x — годы после 1996 года. Если в фонд не добавляются деньги, через сколько лет фонд будет иметь нулевой баланс? С округлением до ближайшего года. Выберите один ответ. а. 6 лет б. 7 лет c. 8 лет d. 9 лет
Как найти решение квадратного уравнения
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Решение квадратного уравнения множителем
Решение квадратного уравнения множителем Поскольку, 3x 2 — 5x + 2 — квадратичный многочлен;
3x 2 — 5x + 2 = 0 — квадратное уравнение.
Также
3x 2 — 5x + 2 = 3x 2 — 3x — 2x + 2 [Факторизация]
= 3x (x — 1) — 2 (x — 1)
= (x — 1) (3x — 2)
Таким же образом:
3x 2 — 5x + 2 = 0 ⇒ 3x 2 — 3x — 2x + 2 = 0 [Факторизация LHS]
⇒ (x — 1) (3x — 2) = 0
то есть, x — 1 = 0 или 3x — 2 = 0
⇒ x = 1 или x = 2/3
, что является решением данного квадратного уравнения.
Чтобы решить данное квадратное уравнение:
1.Очистите дроби и квадратные скобки, если они указаны.
2. Перенося каждый член в левую часть; Выразите данное уравнение в виде
ax 2 + bx + c = 0 или a + bx + cx 2 = 0
3. Факторизуйте левую часть полученного уравнения (правая часть равна нулю).
4. Положив каждый множитель равным нулю; Найди решение.
Пример 1: Решите (i) x 2 + 3x — 18 = 0 (ii) (x — 4) (5x + 2) = 0
(iii) 2x 2 + ax — a2 = 0; где «а» — действительное число.
Сол. (i) x 2 + 3x — 18 = 0
⇒ x 2 + 6x — 3x — 18 = 0
⇒ x (x + 6) — 3 (x + 6) = 0
, т. е. (x + 6) (x — 3) = 0
⇒ x + 6 = 0 или x — 3 = 0
⇒ x = — 6 or x = 3
Корни данного уравнения — 6 и 3
(ii) (x — 4) (5x + 2) = 0
⇒ x — 4 = 0 или 5x + 2 = 0
x = 4 или x = — 2/5
(iii) 2x 2 + ax — a 2 = 0
⇒ 2x 2 + 2ax — ax — a 2 = 0
⇒ 2x (x + a) — a (x + a) = 0
i.е., (x + a) (2x — a) = 0
⇒ x + a = 0 или 2x — a = 0
⇒ x = — a или x = a / 2
Пример 2: Решите следующие квадратные уравнения
(i) x 2 + 5x = 0 (ii) x 2 = 3x (iii) x 2 = 4
Sol. (i) x 2 + 5x = 0 ⇒ x (x + 5) = 0
⇒ x = 0 или x + 5 = 0
⇒ x = 0 или x = — 5
(ii) x 2 = 3x
⇒ x 2 — 3x = 0
⇒ x (x — 3) = 0
⇒ x = 0 или x = 3
(iii) x 2 = 4
⇒ x = ± 2
Пример 3: Решите следующие квадратные уравнения
(i) 7x 2 = 8 — 10x (ii) 3 (x 2 — 4) = 5x (iii) x (x + 1) + (x + 2) (x + 3) = 42
Сол. (i) 7x 2 = 8 — 10x
(i) 7x 2 = 8 — 10x
⇒ 7x 2 + 10x — 8 = 0
⇒ 7x 2 + 14x — 4x — 8 = 0
⇒ 7x (x + 2) — 4 (x + 2) = 0
⇒ (x + 2) (7x — 4) = 0
⇒ x + 2 = 0 или 7x — 4 = 0
⇒ x = — 2 или x = 4/7
(ii) 3 (x 2 — 4) = 5x
⇒ 3x 2 — 5x — 12 = 0
⇒ 3x 2 — 9x + 4x –¬ 12 = 0
⇒ 3x (x — 3) + 4 (x — 3) = 0
⇒ (x — 3) (3x + 4) = 0
⇒ x — 3 = 0 или 3x + 4 = 0
⇒ x = 3 или x = –4/3
(iii) x (x + 1) + (x + 2) (x + 3) = 42
⇒ x 2 + x + x 2 + 3x + 2x + 6-42 = 0
⇒ 2x 2 + 6x — 36 = 0
⇒ x 2 + 3x — 18 = 0
⇒ x 2 + 6x — 3x — 18 = 0
⇒ x (x + 6) — 3 (x + 6) = 0
⇒ ( x + 6) (x — 3) = 0
⇒ x = — 6 или x = 3
Пример 4: Решите для x: 12abx 2 — (9a 2 — 8b 2 ) x — 6ab = 0
Данное уравнение имеет вид 12abx 2 — (9a 2 — 8b 2 ) x — 6ab = 0
⇒ 3ax (4bx — 3a) + 2b (4bx — 3a) = 0
⇒ (4bx — 3a) (3ax + 2b) = 0
⇒ 4bx — 3a = 0 или 3ax + 2b = 0
⇒ x = 3a / 4b или x = — 2b / 3a
неравенств calprep3
неравенств calprep3НЕРАВЕНСТВА
| ОСНОВНОЕ ПРАВИЛО НЕРАВЕНСТВА Деление или умножение на минус, ПЕРЕВОЗКА НЕРАВЕНСТВА. |
Итак, если — 3 x > — 18, то x <6.
1) ЛИНЕЙНЫЕ НЕРАВЕНСТВА :
Решайте как линейные уравнения, но следуйте основному правилу.
например: 3 x — 2 <5 x + 10 становится — 2 x <12 становится x > — 6
2) КВАДРАТИЧЕСКИЕ НЕРАВЕНСТВА :
Найдите нули факторизацией или квадратной формулой,
затем используйте числовую линию или график, чтобы найти интервалы, удовлетворяющие неравенству.
Пример: x 2 > — 3 x +10 становится x 2 + 3 x — 10> 0 становится ( x + 5) ( x -2)> 0
нули — 5 и +2
Это парабола, открывающаяся вверх, изменяющаяся от> 0 до <0 при –5 и +2.
, поскольку мы хотим x 2 + 3 x — 10> 0, нам нужны x , которые делают y положительным.
Это означает, что кривая должна быть выше оси x ,
.
поэтому решение будет x <- 5 и x > 2.
.
3) ДРОБНЫЕ НЕРАВЕНСТВА (постоянные знаменатели):
Умножьте хотя на 1см знаменателя и решите, как линейное неравенство. Большинство студентов называют это перекрестное умножение , потому что оно выглядит так. На самом деле, мы умножаем все уравнение на пк и знаменателей.
пример: lcm здесь 6.
4) ДРОБНЫЕ НЕРАВЕНСТВА (переменные в знаменателях)
Относится к нулю !! Найдите общий знаменатель и объедините в одну дробь. Затем используйте числовую линию, как в квадратных неравенствах. Отметьте нули, затем проверьте знак функции в каждом из интервалов, определяемых этими нулями, чтобы увидеть, является ли он положительным или отрицательным.
пример: решить для x :
Мы отмечаем эти значения на числовой строке, чтобы определить интервалы, в которых значения функции
y не равны нулю,
где они либо положительны (> 0), либо отрицательны (<0).
У нас есть четыре интервала для проверки:
| x < — 3 , | — 3 < x <1/5 , | 1/5 < x <5 , | x > 5 . |
Устанавливаем x = — 4, x = 0, x = 2, и x = 6 .
Мы находим, что дробь положительна (> 0), когда — 3 < x <1/5 и когда x > 5 .
5) НЕРАВЕНСТВА АБСОЛЮТНОЙ СТОИМОСТИ :
a) менее неравенство по абсолютной величине:
| 2 x — 3 | <5 означает, что 2 x — 3 — это , зажатый между между — 5 и + 5 , начиная с
этот интервал включает все числа с абсолютным значением меньше 5.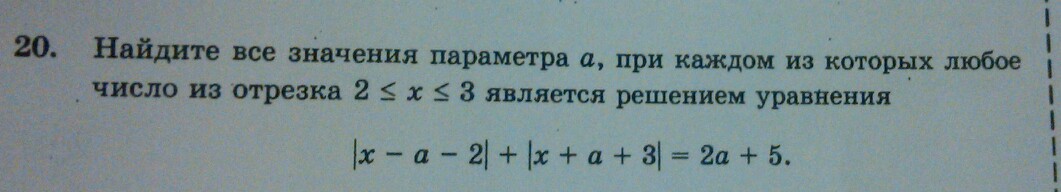
Следовательно, мы решаем абсолютное значение , отношение « меньше » на , помещая выражение между отрицательными и положительными значениями константы.
| Если | вещь | <а , затем — <вещь <а. |
Завершим приведенный выше пример:
| 2 x — 3 | <5 становится — 5 <2 x — 3 <5 становится — 2 <2 x <8
так — 1 < x <4 ,
решение представляет собой интервал , обозначенный ( — 1, 4) или ] — 1, 4 [
б) больше чем неравенство по абсолютной величине:
Мы устанавливаем выражение либо меньше отрицательного значения константы (левый хвост),
или больше положительного значения константы (правый хвост ).
Пример: | 2 x — 3 | > 5 .
Здесь 2 x — 3 должно быть на меньше — 5 или больше 5 , как показано.
Так | 2 x — 3 | > 5 мы разбиваем на два отдельных неравенства следующим образом:
| 2 x — 3 | > 5 становится 2x — 3 < — 5 или 2 x — 3> 5
- так, 2 x < — 2 становится x < — 1 или 2 x > 8 становится x > 4
Примечание: решение — это два отдельных интервала , x ‘s меньше чем — 1 , или x больше 4 .
| Если | вещь | > , затем вещь <- или вещь> |
Менее : сэндвич вещь между — а и а. Решение — один интервал.
Больше, чем : поместите вещь в хвосты , решите 2 неравенства. Решение — 2 отдельных интервала.
.
Теперь возьмите карандаш, ластик и записную книжку, скопируйте вопросы,
выполните практические упражнения, а затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем попробуйте еще раз.
УПРАЖНЕНИЕ
Решите эти неравенства:
.
РЕШЕНИЯ
| 1) — 7 <2 x — 3 <7 так — 2 < x <5 | 2) 3 x + 6 <- 9 или 3 x + 6> 9 x <- 5, или x > 1 | 3) — 3 <5 - 2 x <3 — 8 <- 2 x <- 2 1 < x <4 |
| 4) 4 — x <- 5 или 4 - x > 5 — x <- 9 или - x > 1 x > 9, или x <- 1 | 5) x 2 — 3 x — 18> 0 ( x + 3) ( x — 6)> 0 x <- 3 или x > 6 | 6) нули в — 5/2, 2 и 4 нам нужно> 0 x <- 5/2, или 2 < x <4 |
| 7) умножить на 12, 8 x + 24 <3 x — 12 нам нужно <0 x <- (36/5) | 8) нули в — 5, — 2 и 4 нам нужно <0 — 5 < x <- 2, или x > 4 | 9) примечание 2 x + 6 = 2 (x + 3) нам нужно> 0 x > — 3 |
| 10) нули в точках — 5, 0, 4 и 7 x <- 5, или 0 < x <4, или x > 7 |
.
Индексная страница Cal-Prep
(все содержание уроков MathRoom © Tammy the Tutor; 2004 -).
Алгебраическое решение уравнений
Алгебраическое решение уравненийСодержание: Эта страница соответствует § 2.4 (с. 200) текста.
Предлагаемые проблемы из текста:
с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97
Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения
Квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0.
Факторинг
Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.
Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2 или x = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt (k).
Пример 2.
x 2 — 9 = 0.
x 2 = 9.
x = 3 или x = -3.
Пример 3.
Пример 4.
x 2 + 7 = 0.
х 2 = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.
Завершение квадрата
Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.
Пример 5.
x 2 + 6x — 1 = 0.
x 2 + 6x = 1.
x 2 + 6x + 9 = 1 + 9.
9, прибавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Поэтому эта процедура называется — завершение квадрата .[Заинтересованный читатель может видеть, что это истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 .
Чтобы получить «а» нужно всего лишь разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
(x + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня, а затем решить относительно x.
x = -3 ± sqrt (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент при x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x 2 + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) 2 = 9/4.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x 2 + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.
Пример 7.
x 2 = 16.
x 2 — 16 = 0.
(x + 4) (x — 4) = 0.
x = -4 или x = 4.
В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.
Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению
топор 2 + bx + c = 0.
Результатом завершения квадрата в этом общем уравнении является формула для решений уравнения называется квадратной формулой.
Квадратичная формула
Решение уравнения ax 2 + bx + c = 0:
Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.
Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!
Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как
сделай это!
Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x 2 + 6x — 5.
Пример 9.
4x 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует отметить два момента.
- Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
- Решение упрощено, так что квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом. (Все квадратные уравнения могут быть решены путем факторизации! Я имею в виду, что это могло быть решено легко факторингом.)
4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0.
х = -1/2.
Пример 10.
х 2 + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов. функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2 + x + 1 не имеет пересечений по x.
Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.
1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.
Примечания к проверке решений
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко сделать невнимательные ошибки.
Алгебраический метод, который заключается в подстановке числа обратно в уравнение и проверке того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.
Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) 2 +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту для построения графика y = 2x 2 + 6x — 5 и проследите график, чтобы приблизительно определить, где х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и сразу перешли к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, значит, вы, наверное, правы!
Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3x 2 -5x — 2 = 0. Ответ
(b) (x + 1) 2 = 3. Ответ
(c) x 2 = 3x + 2. Ответ
Вернуться к содержанию
Уравнения с участием радикалов
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал
является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.
д. Эта операция может вводить посторонние корни, поэтому все решения
необходимо проверить.
Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы радикальный член сам по себе на одной стороне уравнения.
Пример 11.
Теперь, когда мы изолировали радикальный член в правой части, возводим обе стороны в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является координата x точки пересечения графиков y = x и у = sqrt (х + 1) +1.
Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал срок.
Это хуже того, с чего мы начали!
Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем уменьшить количество радикальных членов на , возведя в степень.
Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.
Пример 12.
Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат снова обе стороны.
Чек:
Подставляя x = 5/4 в исходное уравнение, получаем
sqrt (9/4) + sqrt (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание по проверке решений:
В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение — координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).
Упражнение 2:
Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью
Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее. Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой.
Когда мы встречаемся
такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать
решения с графической утилитой.
Нулевая постоянная
Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.
Пример 13.
2x 3 + 3x 2 -5x = 0.
x (2x 2 + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x 2 + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный фактор во втором уравнении, мы могли бы прибегнуть к к использованию квадратичной формулы.[Убедитесь, что вы получаете те же результаты, что и ниже.
]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x 3 + 3x 2 -5x.
Фактор по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0.
Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа слагает один и два, а также три и четыре.
x 2 (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x 2 — 9) = 0.
Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.
x — 2 = 0 или x 2 — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся из пересечений графика f (x) = x 3 -2x 2 -9x +18.
Квадратичная форма
Пример 15.
x 4 — x 2 — 12 = 0.
Этот многочлен неквадратичный, у него четвертая степень. Однако его можно рассматривать как квадратичный по x 2 .
(x 2 ) 2 — (x 2 ) — 12 = 0.
Это может помочь вам фактически заменить z на x 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на x 2 и решите полученные уравнения.
x 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i , или x = — i.
Итак, есть четыре решения: два реальных и два комплексных.
Примечание: Эти решения находятся на пересечении графика f (x) = x 4 — х 2 — 12.
График f (x) = x 4 — x 2 -12 и масштабирование, показывающее его локальное экстремумы.
Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения, содержащие дробные выражения или абсолютные значения
Пример 16.
Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).
Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Корпус 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (х — 1) = х + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что кажется, что мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение принимает вид
.-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по оси x, или вы можете найти решение как координаты x точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).
Упражнение 4:
(a) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ
Вернуться к содержанию
7.
 Найдите корни уравнения x2 + 3x
Найдите корни уравнения x2 + 3xMath, 28.10.2019 19:29
► действие 9: насколько я понял, ответьте на следующий вопрос.1. как вы описываете квадратичные неравенства? 2. приведите не менее трех примеров квадратичных неравенств. 3. как найти множество решений квадратного неравенства с одной переменной? vкак насчет квадратичных неравенств двух переменных? 4. как бы вы описали множество решений каждого из следующих квадратичных неравенств? а. у <х2 + 9х + 14с. у <2x2 + 11x + 5b. у> х2 — 3х — 18d. y 23×2 + 10x — 85. Согласны ли вы, что наборы решений y  Предположим, что коробка вмещает не более 140 кубиков. каковы возможные размеры коробки? 8. Компания решила увеличить размер коробки для упаковки консервированных сардин. Длина оригинальной упаковочной коробки была на 40 см больше ее ширины, высота — 12 см, а объем — не более 4800 см.а. как бы вы изобразили ширину оригинальной упаковочной коробки? как насчет длины коробки? б. Каким выражением будет обозначен объем оригинальной упаковочной коробки? как насчет математического предложения, отражающего его объем? определить используемые переменные. c. какие могут быть максимально возможные размеры коробки, если каждое измерение выражено в целых сантиметрах? объясните, как вы пришли к своему ответу. d. Предположим, что длина новой упаковочной коробки все еще на 40 см больше ее ширины, а высота составляет 12 см.какое математическое предложение будет обозначать объем новой упаковочной коробки? определить используемые переменные. e. какие могут быть размеры коробки? укажите возможные размеры как минимум трех разных коробок
Предположим, что коробка вмещает не более 140 кубиков. каковы возможные размеры коробки? 8. Компания решила увеличить размер коробки для упаковки консервированных сардин. Длина оригинальной упаковочной коробки была на 40 см больше ее ширины, высота — 12 см, а объем — не более 4800 см.а. как бы вы изобразили ширину оригинальной упаковочной коробки? как насчет длины коробки? б. Каким выражением будет обозначен объем оригинальной упаковочной коробки? как насчет математического предложения, отражающего его объем? определить используемые переменные. c. какие могут быть максимально возможные размеры коробки, если каждое измерение выражено в целых сантиметрах? объясните, как вы пришли к своему ответу. d. Предположим, что длина новой упаковочной коробки все еще на 40 см больше ее ширины, а высота составляет 12 см.какое математическое предложение будет обозначать объем новой упаковочной коробки? определить используемые переменные. e. какие могут быть размеры коробки? укажите возможные размеры как минимум трех разных коробок
Ответы: 2
.





 Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .] Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.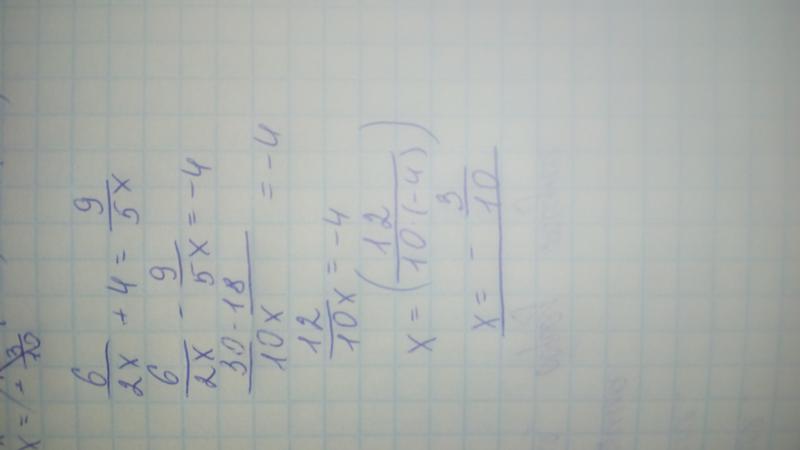


 Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение.
Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно
те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно
не точное решение.

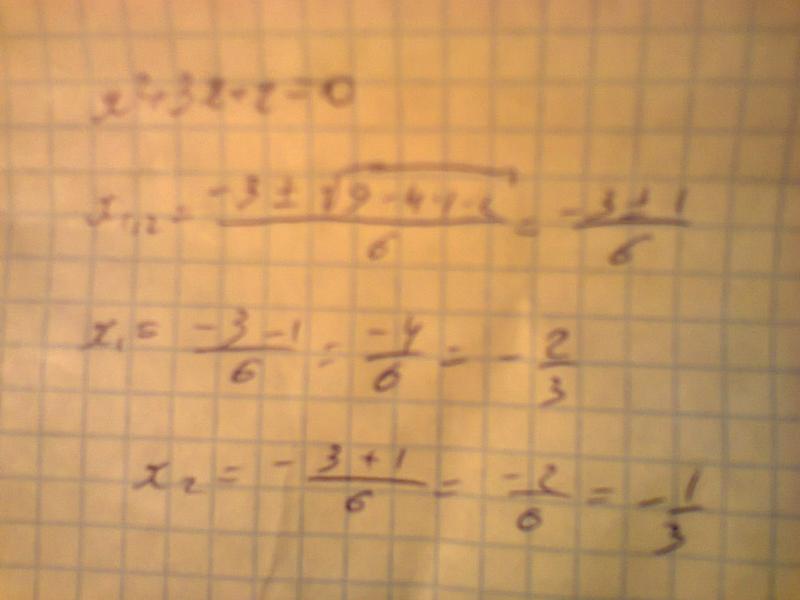 ]
]


