Метод потенциалов онлайн
Примеры решенийМетод Гомори Симплекс-метод Метод Фогеля Транспортная задачаЗадача о назначениях Распределительный методМетод потенциаловЗадача коммивояжера Открытые и закрытые задачи
dij = сij* — сij,
где сij — затраты (истинные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения; сij* — расчётные затраты (косвенные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения, определяемые для тех клеток опорного плана, ресурсы в которые не распределены (для незаполненных клеток).
- Шаг №1
- Шаг №2
- Видеоинструкция
Инструкция. Необходимо выбрать вид исходных данных.
Вид исходных данных: Таблица
Размерность таблицы: x
Решать как транспортную задачу
Полученное решение сохраняется в файле MS Word. см. также метод потенциалов для ориентированного графа.
 Для каждой заполненной клетки, т. е. для каждой базисной переменной строится соотношение:
Для каждой заполненной клетки, т. е. для каждой базисной переменной строится соотношение:
ui+vj=cij
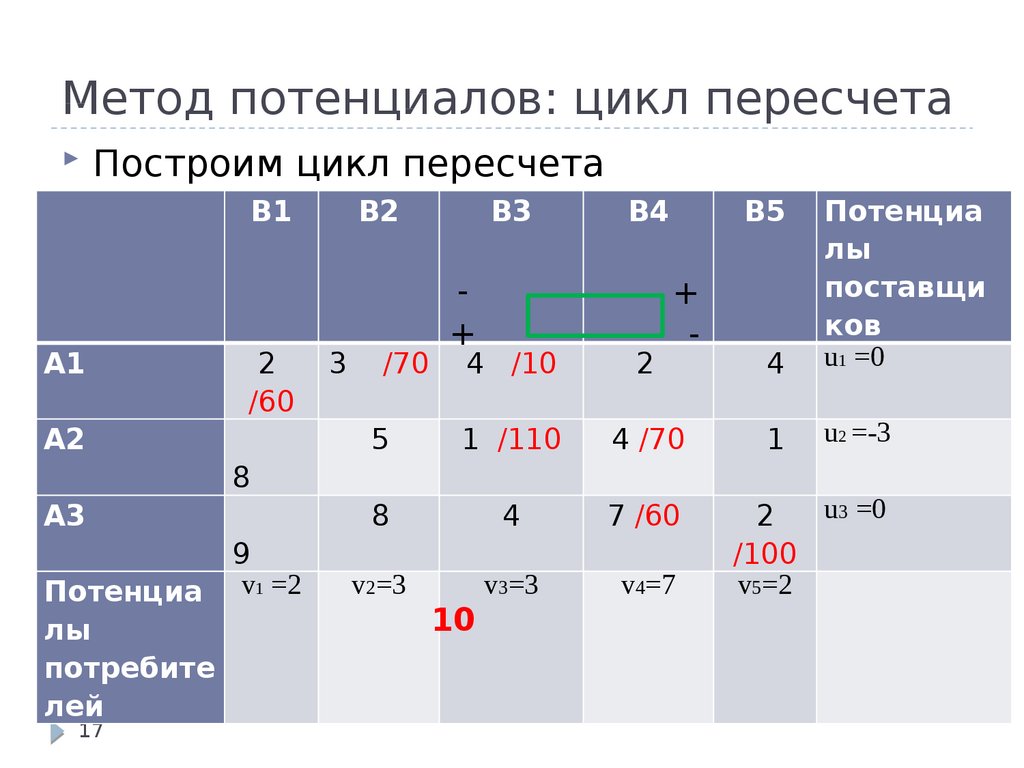
Получаем систему с числом уравнений, равным количеству базисных переменных. Из этой системы определяем неизвестные потенциалы ui и vj, полагая ui=0. Для каждой незаполненной клетки, т. е. для каждой небазисной переменной, рассчитываются косвенные тарифы cij* по формуле: cij* = ui+vj. Затем полученный план проверяют на оптимальность по критерию оптимальности dij. Если для каждой незаполненной клетки выполняется условие: dДля правильного перемещения перевозок, чтобы не нарушить ограничения задачи, строят так называемый цикл, т.
 е. замкнутый многоугольник, соединяющий выбранную клетку с ней же самой и проходящий через заполненные клетки.
е. замкнутый многоугольник, соединяющий выбранную клетку с ней же самой и проходящий через заполненные клетки.
Цикл строится следующим образом: вычёркиваются (мысленно) все строки и столбцы, содержащие ровно одну заполненную клетку, при этом считается, что выбранная клетка без поставки является заполненной; все оставшиеся после вычеркивания клетки составляют цикл и лежат в его углах, они соединяются ломаной линией.
В каждую клетку цикла, начиная с незаполненной, поочередно вписывают знаки “+” и “-“. В клетках с отрицательными знаками выбирается минимальная величина поставки, обозначаемая как D. В те вершины, которые имеют знак “+” прибавляется поставка D, а в вершинах со знаком “-“ поставки уменьшаются на величину D. При этом суммы поставок по строкам и столбцам не изменяются. В результате клетка, для которой строился цикл, станет занятой, а в одной из бывших занятых клеток окажется нулевая поставка и её надо объявить свободной. Общее количество заполненных клеток не изменится, следовательно, новый план перевозок является невырожденным.

Если в результате пересчета одновременно в нескольких ранее занятых клетках цикла поставки примут нулевые значения, то свободной объявляется лишь одна из них. Остальные считаются условно занятыми с нулевыми поставками.
Значения переменных, включенных в цикл, после пересчета переносятся в новую таблицу без изменений. Полученный новый план проверяется на оптимальность.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Как решить транспортную задачу. Руководство
Примеры решенийМетод Гомори Симплекс-метод Метод Фогеля Транспортная задачаЗадача о назначениях Распределительный методМетод потенциаловЗадача коммивояжера Открытые и закрытые задачи
Транспортные задачивключает пять онлайн-калькуляторов:
- Классическая транспортная задача (задача Хитчкока-Купманса).
 Вариант транспортной задачи с ограничениями на пропускную способность.
Вариант транспортной задачи с ограничениями на пропускную способность.
- Универсальная транспортная задача.
- Решение ТЗ методом дифференциальных рент.
- Задача коммивояжера.
- Задача о назначениях.
- Сетевое планирование.
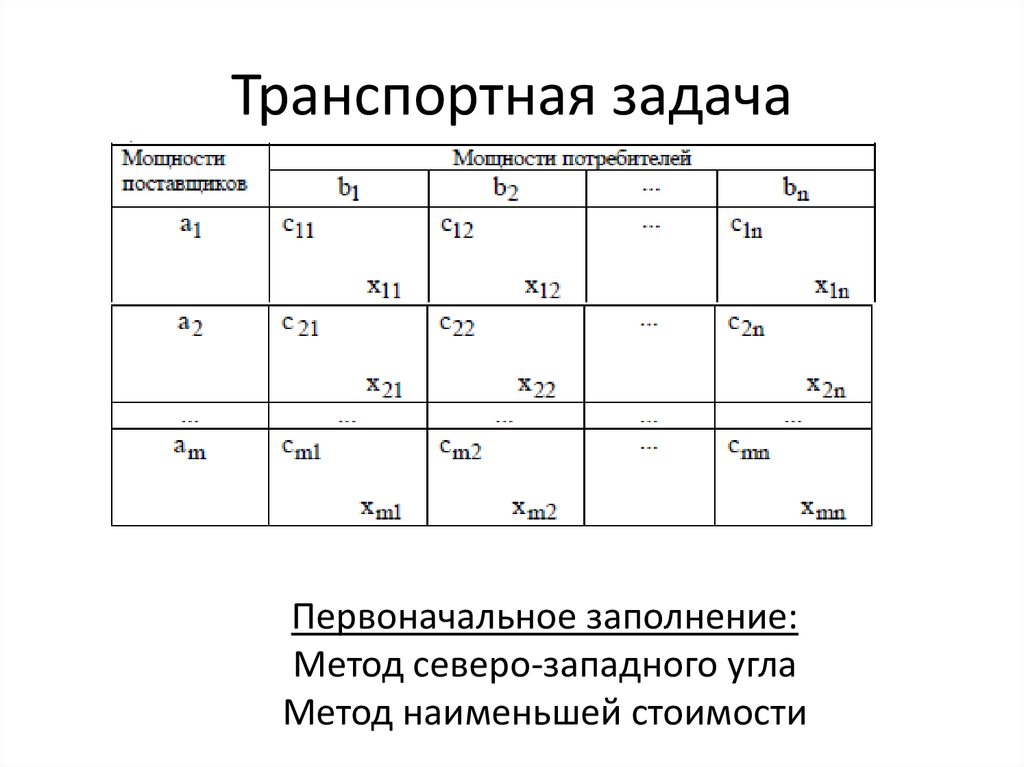
После этого необходимо будет заполнить матрицу тарифов, запасы поставщиков и потребности магазинов.
- Минимального элемента;
- Северо-западного угла;
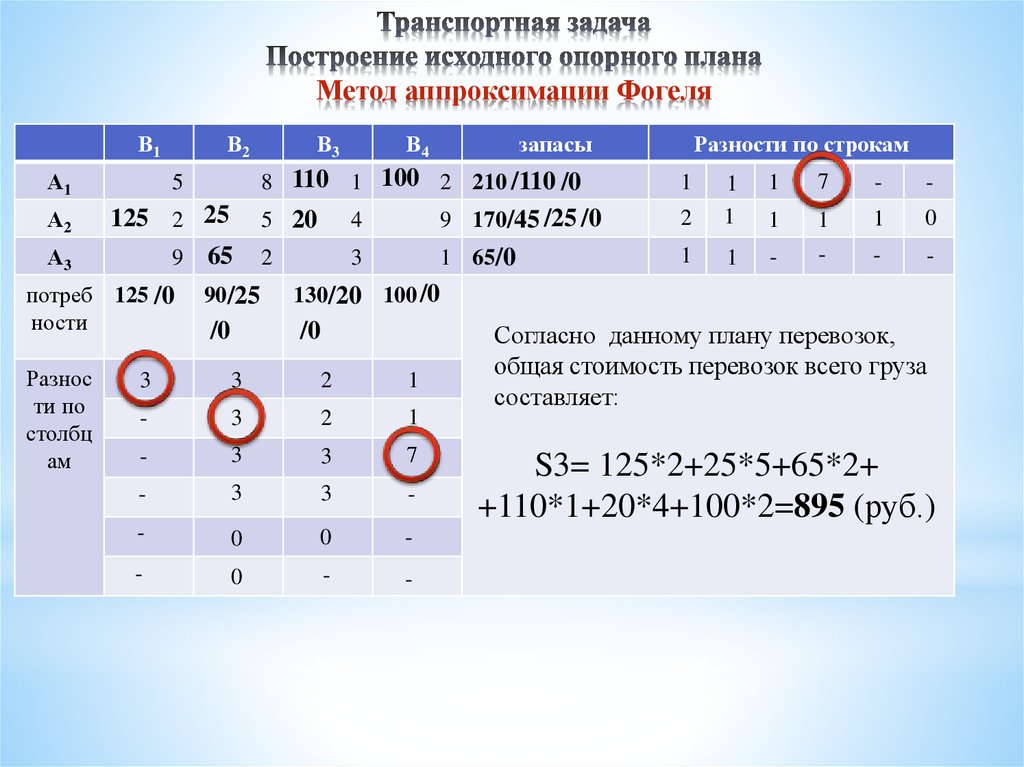
- Аппроксимация Фогеля;
- Двойного предпочтения.
Далее выбирается метод улучшения опорного плана: Метод потенциалов или Распределительный метод.

Для большинства транспортных задач требуется найти минимальные затраты на перевозки, поэтому в качестве целевой функции выбираем Минимальные затраты.
Если потребуется найти максимальное значение целевой функции (получение максимальной прибыли, получение максимального урожая и т.п.), то выбираем Максимальная прибыль.
После решения создается сетевая модель транспортной задачи в виде графа для наглядного отображения оптимального плана перевозок.
Рекомендуется сразу проверять решение в Excel (см. ссылку для скачивания шаблона после решения).
Кроме решения транспортной задачи существуют так называемая универсальная транспортная задача, в условиях которой необходимо найти максимальное значение функции при заданных матрице тарифов и матрице доходов. Для решения данного типа задач можно воспользоваться сервисом Максимизация удельного показателя перевозок.
Пример. Задание. Решить транспортную задачу в эксель.
Решить транспортную задачу в эксель.
Помимо этого решить в ручную эту же транспортную задачу методом-северо западного угла, методом Фогеля, методом минимального тарифа. Используя результат полученный методом северо-западного угла улучить план методом потенциалов.
Помимо этого решить задачу на запрет поставки из Аi в Bi (в Excel):
- Запретим поставку груза от 1-го поставщика к 3-му потребителю. Для этого увеличим соответствующую стоимость перевозки до большого числа. Зафиксировать насколько изменится целевая функция.
- 2-й поставщик может поставить 3-му потребителю только половину товара. Зафиксировать изменение целевой функции;
- 3-й поставщик может поставить 3-му потребителю не менее половины товара. зафиксировать изменение целевой функции.
Перейти к онлайн решению своей задачи
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
оптимизировать Транспортная проблема | Towards Data Science
Транспортная задача (TP) с примером (правило N-W Corner, метод наименьших затрат, VAM, сбалансированный TP, несбалансированный TP)
Фото Зейна Ли на UnsplashВ этом быстро меняющемся мире потребность в товар растет день ото дня. Соответственно, важность транспорта играет большую роль в жизни общества. Прибыль и состояние компаний, перемещающих товары из одного уголка страны в другой, определяются транспортом. Это особенно верно, когда транспортные расходы и время транспортировки превышают производственные затраты и время производства. Что, если транспортировка во всех областях осуществляется профессионально и если соответствующие затраты сделаны оптимальными, производительность страны повысится, даже если не будет затронут ни один другой фактор!
Изучение оптимальной транспортировки и распределения ресурсов; Теория транспорта или теория транспорта. Французский математик Гаспар Монж формализовал эту проблему в 1781 году. Значительные успехи в этой области были достигнуты во время Второй мировой войны советским математиком и экономистом Леонидом Канторовичем, поэтому известная как транспортная задача Монжа-Канторовича .
Французский математик Гаспар Монж формализовал эту проблему в 1781 году. Значительные успехи в этой области были достигнуты во время Второй мировой войны советским математиком и экономистом Леонидом Канторовичем, поэтому известная как транспортная задача Монжа-Канторовича .
Важный тип транспортной проблемы, который решается линейным программированием (ЛП), находится в области физического распределения товаров и услуг из нескольких центров снабжения в центры спроса. Другими словами, транспортные проблемы связаны с перемещением товаров из разных источников в разные пункты назначения с общей целью минимизации транспортных расходов. Такая формулировка транспортной задачи с помощью линейного программирования также известна как транспортная задача Хичкока – Купманса.
Применения транспортной модели используются в авиационной отрасли, исследованиях и разработках, коммивояжерах, перевалочных перевозках и т. д. количество источников.

ПРЕДПОЛОЖЕНИЯ
Перед использованием любого метода транспортировки делаются следующие основные предположения:
- Общее количество, доступное во всех источниках, равно общему количеству, необходимому в пунктах назначения. Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные адресаты.
- Удельная стоимость перевозки из одного пункта отправления в пункт назначения известна и определена.
- Стоимость единицы товара не зависит от количества перевозимых товаров.
- Цель состоит в том, чтобы минимизировать общую стоимость транспортировки.
- Хотя транспортные задачи могут быть сформулированы как LPP, для их решения разработаны другие более простые алгоритмы.

В основном существует 3 основных шага
1. Формулировка транспортной модели в LPP
2. Поиск базового допустимого решения (BFS)
3. Проверка оптимальности ТРАНСПОРТИРОВОЧНОЙ МОДЕЛИ в LPP
При решении задачи исследования операций ключевой момент заключался в формулировании модели путем расшифровки задачи. Для транспортной задачи обычно задача задается в табличной форме или в матричной форме, называемой транспортной таблицей или матрицей эффективности затрат.
Давайте проверим пример ниже.
Пример транспортной задачи с источником = {A, B, C} с общим предложением = 70 и пунктами назначения = {1,2,3} с общим спросом = 70 [изображение автора]Здесь,
Источник = {A, B, C}
Они представляют источники с мощностью предложения 10,35,25 единиц товаров соответственно (выделены оранжевым цветом)
Следовательно, общее предложение=10+35+25=70
Направления= {1,2,3}
Представляют направления, требующие 20,25,25 единиц товаров соответственно (обозначены зеленым цветом).
Следовательно, общий спрос = 20+25+25=70
Элементы, представленные в матрице (выделены белым цветом), называются затратами. т. е. стоимость единицы товара, связанная с перемещением единицы товара из одного пункта отправления в другой пункт назначения.
Например,
Затраты на перемещение 1 единицы товара из источника A в пункт назначения 1= 2 ₹/-
Затраты на перемещение 1 единицы товара из источника A в пункт назначения 1= 2 ₹/- (здесь мы смотрим на сечение источника A и места назначения 1 ) [изображение автора]Аналогично,
Затраты на перемещение одной единицы товара из источника B в место назначения 2 = ₹ 4/-
и так далее. [Здесь мы рассматриваем пересечение источника и назначения]
ВИДЫ ТРАНСПОРТНЫХ ЗАДАЧ
Прежде чем идти дальше, давайте рассмотрим различные типы транспортных задач.
Существуют в основном 2 типа транспортных задач:
1. Сбалансированная транспортная задача
2. Несбалансированная транспортная задача
Несбалансированная транспортная задача
Давайте заглянем в него.
1. Сбалансированная транспортная задача
общее доступное количество = общее требуемое количество
т. е. общее предложение = общий спрос
Давайте проверим пример ниже.
Пример сбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 75 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]Здесь,
Общее предложение =75
Общий спрос=75
Следовательно, общий объем предложения= общий спрос
2. Несбалансированная транспортная задача
общее доступное количество ≠ общее требуемое количество
т. е. общее предложение ≠ общий спрос
Общее количество, доступное во всех источниках, равно общему количеству, необходимому в пунктах назначения.
Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные пункты назначения, чтобы сделать это стандартной транспортной задачей.
Есть 2 ситуации, приводящие к такому дисбалансу
(и). Общее предложение> Общий спрос
(ii). Общий объем предложения< Общий спрос
(i). Общее предложение> Общий спрос
То есть, общее доступное количество > общее необходимое количество
Давайте проверим пример ниже.
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 60 [изображение автора]Здесь,
Общее предложение = 65
Общий спрос = 60
Следовательно, Общее предложение> Общий спрос
В таких случаях мы добавляем фиктивный пункт назначения, дающий фиктивный спрос с каждой стоимостью, равной нулю (0) но фиктивный спрос для фиктивного пункта назначения как общий спрос-предложение.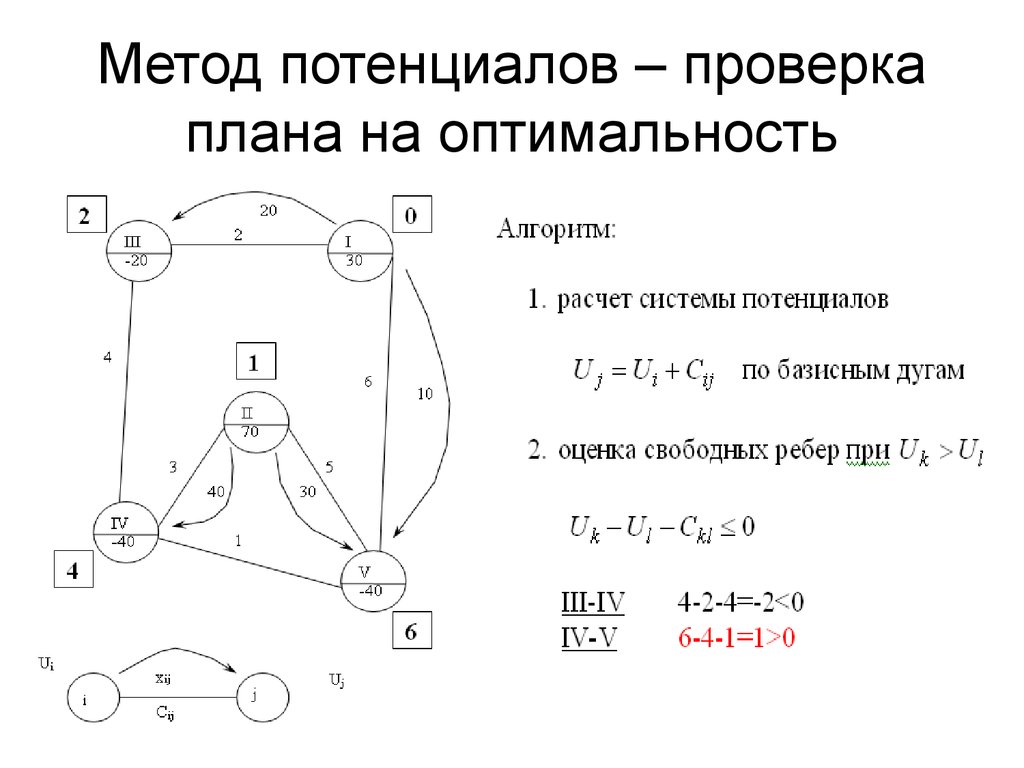
В этом примере фиктивный спрос = 65–60 = 5
Таким образом, общий объем предложения = общий спрос
(ii). Общее предложение < Общее потребление
То есть, общее доступное количество <общее необходимое количество
Давайте проверим пример ниже.
Пример несбалансированной транспортной задачи с источником = {A, B, C} с общим предложением = 65 и пунктами назначения = {1,2,3} с общим спросом = 75 [изображение автора]Здесь
Общее предложение =65
Общий спрос = 75
Следовательно, общий запас < общий спрос
В таких случаях мы добавляем фиктивный источник, дающий фиктивный источник с каждой стоимостью, равной нулю (0), но фиктивный запас для фиктивного пункта назначения как общий спрос-общий объем поставок .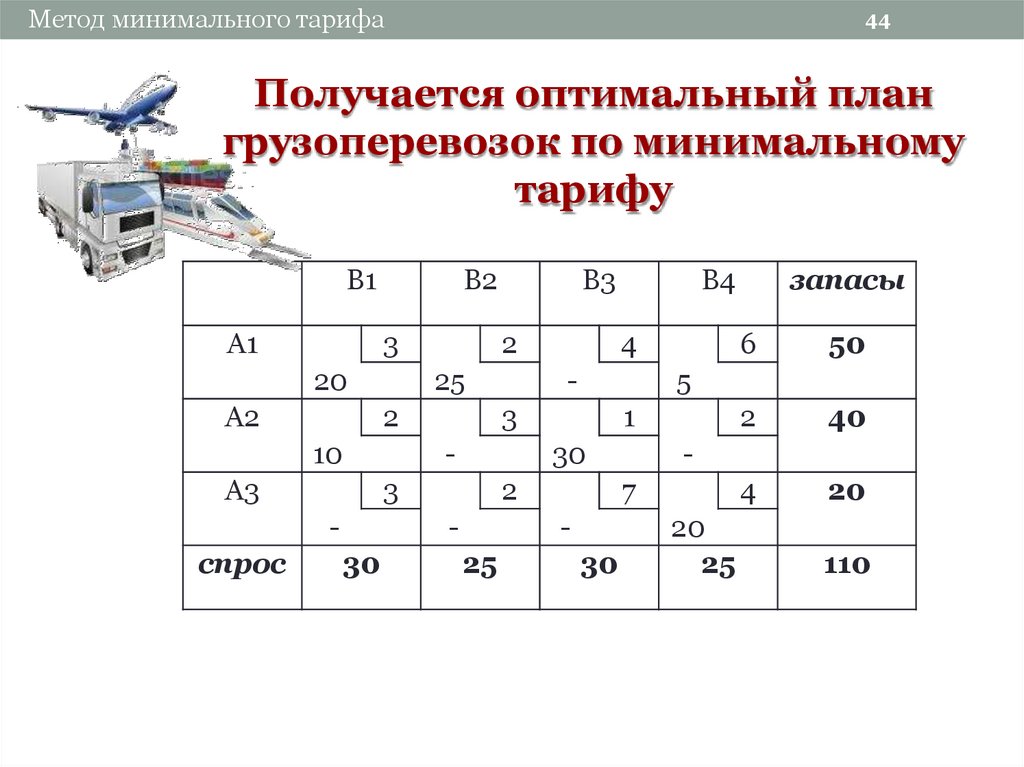
In в этом примере фиктивное предложение = 75–65 = 10.
Таким образом, общее предложение = общий спрос
Решение, которое ищет каждая проблема в транспортировке, состоит в том, чтобы количество из каждого источника должно направляться в какой пункт назначения, чтобы все потребности и в то же время затраты были сведены к минимуму.
Для этого мы должны преобразовать каждую задачу в стандартную задачу, чтобы идти дальше.
2. ОСНОВНОЕ ДОПУСТИМОЕ РЕШЕНИЕ (BFS)Существуют различные методы получения начального основного допустимого решения. Их:
(1). Северо-Западный (СЗ) Угловой Правило
(2). Метод наименьших затрат (или метод матричного минимума)
(3). Метод приближения Фогеля [VAM] (или метод штрафа)
Метод приближения Фогеля [VAM] (или метод штрафа)
Давайте углубимся в каждый метод.
Для этого рассмотрим пример задачи для лучшего понимания.
Вопрос приведен ниже.
[изображение автора]Первый шаг — сделать это стандартной транспортной задачей.
Для этого проверьте, является ли это сбалансированной или несбалансированной транспортной задачей.
[изображение автора]Данная задача является сбалансированной транспортной задачей. Итак, продолжим.
Теперь нам нужно найти базовое допустимое решение. Для того же у нас есть 3 разных метода. Давайте проверим один за другим с помощью этой задачи.
(1). Северо-западное (СЗ) угловое правило
Северо-западное направление [изображение автора]Выберите ячейку Северо-западный угол. т. е. стоимость пересечения 1-й строки и 1-го столбца. [Здесь 5 (выделено синим цветом)]
Сравните спрос и предложение этой ячейки. [Здесь 65 и 70 (выделено красным)]
[изображение автора]Выделить ячейку с наименьшим значением [Здесь 65 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 70–65=5]
т. е. выделенное значение ячейки. [Здесь 70–65=5]
Удалите столбец или строку соответственно, вычеркнув их. [Здесь столбец с пунктом назначения 1 (отмечен красной линией)]
Всегда общий спрос и предложение будут оставаться одинаковыми. (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 42+43+65=150 (общая потребность) и 5+30+50+65=150 (общая поставка)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите ячейку North-West(N-W) и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора] Здесь и спрос, и предложение будут одинаковыми, которые в дальнейшем будут распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один способ проверить, были ли все вышеперечисленные шаги правильными или нет.)
[Здесь, 43] (Это еще один способ проверить, были ли все вышеперечисленные шаги правильными или нет.)
Методы проверки правильности процесса:
Суммарный спрос и предложение останутся неизменными на всех этапах.
На последнем этапе одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Решение о том, какой из них выбрать, остается исключительно за пользователем. 👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает начальное допустимое решение методом N-W Corner.
[изображение автора]Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(65×5) +(5×7) +(30×4) +(7×7) +(43×7)
=325+35+120+49+301
=830
Теперь давайте разберемся, что мы выяснили.
₹830 — это общие затраты, связанные с перемещением товаров.
Пройденный путь представлен красными стрелками, как мы нашли с помощью метода N-W Corner.
[изображение автора]Представим то же самое в виде таблицы
таблица окончательного решения [изображение автора]Это может представлять или не представлять оптимальное решение этой задачи, т.е. могут существовать другие способы распределение, которое может дать лучшее решение с более низкой общей стоимостью.
Необходимо провести проверку оптимальности, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
(2). Метод наименьшей стоимости (или метод минимума матрицы)
Давайте обсудим на том же примере.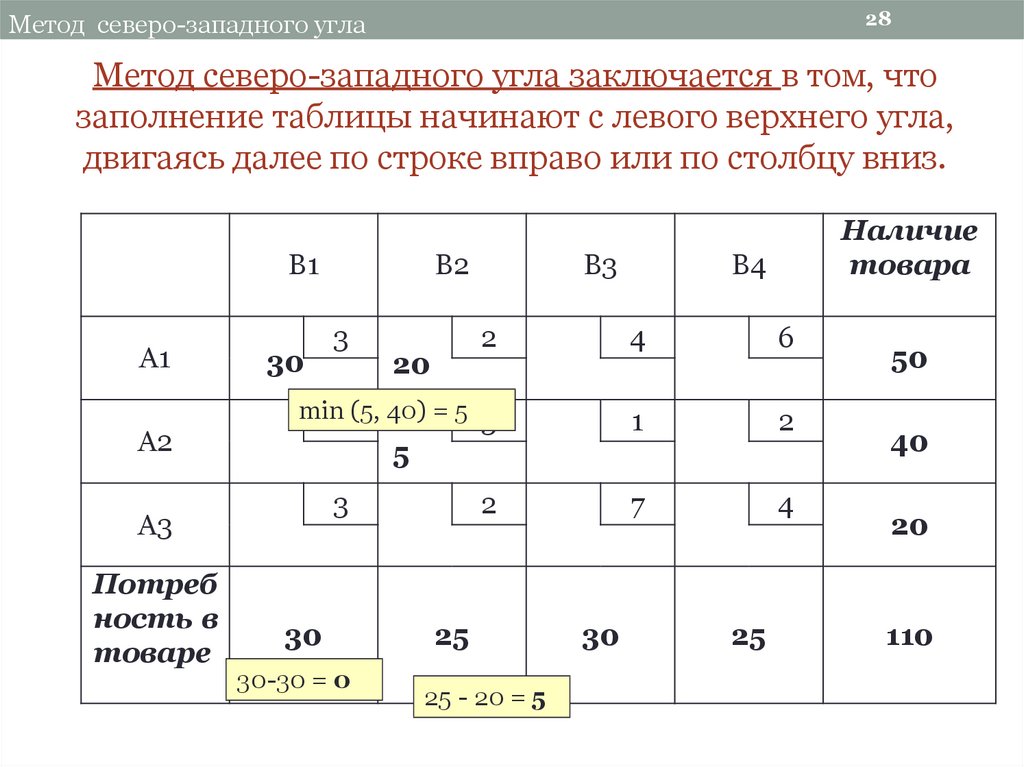
Выберите наименьшее значение среди всех затрат (выделены белым цветом). то есть минимальная стоимость. [Здесь, 4 (выделены синим цветом)]
Здесь есть две ячейки с наименьшей стоимостью. Это исключительно выбор пользователя, чтобы решить, какой из них выбрать.
[изображение автора]Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, среди них можно выбрать любой. (Это исключительно выбор пользователя, чтобы решить, какой из них выбрать.👍)
Сравните спрос и предложение этой ячейки. [Здесь 30 и 65 (выделено красным)] Выделить ячейку с наименьшим значением [Здесь 30 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 65–30=35]
Исключите столбец или строку, соответственно, вычеркнув их. [Здесь строка с источником B (отмечена красной линией)]
Суммарный спрос и предложение всегда остаются неизменными.
(Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 35+42+43+30=150 (общая потребность) и 70+50+30=150 (общая поставка)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите ячейку с наименьшей стоимостью и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]Здесь и спрос, и предложение будут одинаковыми, которые в дальнейшем будут распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один метод проверки правильности всех вышеперечисленных шагов.)
Методы проверки правильности процесса:
Общий спрос и предложение останутся неизменными через шаги.
На последнем этапе одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Это чисто выбор пользователя, чтобы решить, какой из них выбрать.👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает изначально допустимое решение методом наименьших затрат.
[изображение автора]Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(35х5) +(30х4) +(35х7) +(7х7) +(43х7)
=175+120+245+49+301
=890
Теперь разберемся, что мы обнаружили
₹890 — представляет собой общую стоимость, связанную с перемещением товаров.
Путь, по которому мы шли, перепечатывается красными стрелками, как мы нашли методом наименьших затрат.
[изображение автора]Представим то же самое в виде таблицы.
таблица окончательного решения [изображение автора]Это может представлять или не представлять оптимальное решение этой проблемы, т. е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью
Тест на оптимальность необходимо провести, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
( 3). Метод приближения Фогеля [VAM] (или метод штрафа)
Давайте обсудим на том же примере.
[изображение автора] Выбор ячейки затрат для распределения не так прост в VAM, как если бы мы обсуждали метод N-W Corner и метод ячейки наименьшей стоимости. (Расслабься, чувак, 😎 это не так сложно.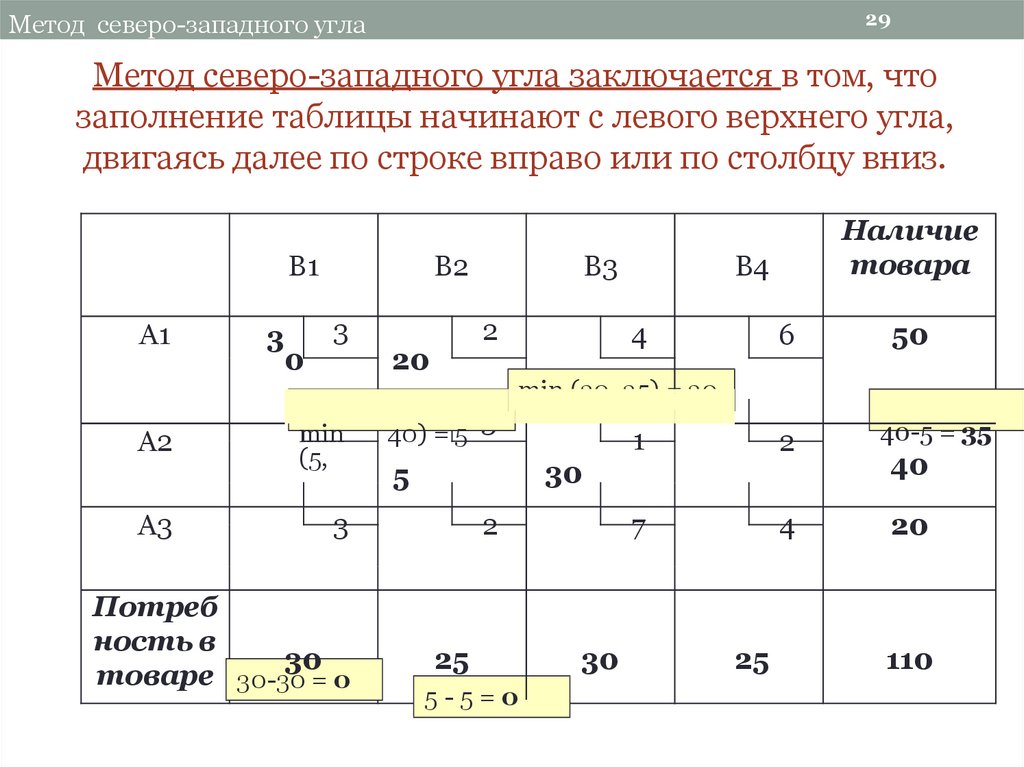 😇 Но процесс немного дольше, чем раньше. 😅)
😇 Но процесс немного дольше, чем раньше. 😅)
В VAM мы должны сначала определить разницу между двумя самыми низкими затратами в каждой строке и столбце. Они известны как штрафы/дополнительные расходы.
[изображение автора]Учитывается разница между двумя наименьшими значениями.
[Здесь штрафы = {2,0,1,1,3,1}]
Теперь найдите максимальное значение среди штрафов независимо от строки или столбца.
[Здесь макс. (Пенальти)=3 (выделены розовым цветом)]
[изображение автора]Если ничья, выберите любого. (Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)
Теперь просмотрите соответствующую строку или столбец соответственно.
[Здесь столбец (выделен розовым цветом)]
Выберите наименьшее значение среди всех затрат (выделено розовым цветом). то есть минимальная стоимость. [Здесь, 4 (обозначены синим цветом на рисунке ниже)]
[изображение автора]Если имеется более 1 ячейки с одинаковой наименьшей стоимостью; галстук, среди них можно выбрать любой.
(Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)
Сравните спрос и предложение этой ячейки [Здесь, 30 и 42 (выделено красным)]
[изображение автора]Выделить ячейку с наименьшим значением [Здесь 30 (выделено желтым цветом)]
Вычесть исключенную ячейку с наименьшим значением. т. е. выделенное значение ячейки. [Здесь 42–30=12]
Удалите столбец или строку, соответственно, вычеркнув их. [Здесь столбец с источником B (отмечен красной линией)]
Всегда общий спрос и предложение будут оставаться одинаковыми. (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
[т.е. здесь 65+12+43+30=150 (общая потребность) и 70+50+30=150 (общая поставка)]
Теперь продолжите процесс с оставшимися ячейками.
Снова найдите штраф и выполните те же действия, что и выше.
Давайте посмотрим то же самое в этом примере.
[изображение автора] [изображение автора] [изображение автора] [изображение автора]Здесь и спрос, и предложение будут одинаковыми, которые в дальнейшем будут распределяться в оставшихся одиночных клетка. [Здесь, 43] (Это еще один способ проверить, были ли все вышеперечисленные шаги правильными или нет.)
Методы проверки правильности процесса:
Суммарный спрос и предложение останутся неизменными на всех этапах.
На последнем шаге одной ячейке будет присвоено значение либо со спросом, либо с предложением, так как оба будут иметь одинаковые значения.
Если спрос и предложение имеют одинаковые значения; галстук, вы можете выбрать любой из них, чтобы выделить ячейку, обнулив другое значение. (Решение о том, какой из них выбрать, остается исключительно за пользователем.
👍)
Итоговая таблица со всеми выделенными ячейками будет такой.
Это дает начальное допустимое решение с помощью VAM.
[изображение автора]Теперь давайте рассчитаем стоимость, связанную с этими распределениями.
Чтобы найти то же самое, сложите все произведения всех выделенных значений ячеек (отмечены желтым цветом) и стоимость соответствующей ячейки (отмечены синим цветом).
т.е. общая стоимость=(65×5) +(5×7) +(30×4) +(7×7) +(43×7)
=325+35+120+49+301
= 830
Теперь давайте разберемся, что мы выяснили.
₹830 — это общие затраты на перемещение товаров.
Путь обозначен красными стрелками, как мы нашли VAM.
[изображение автора]Представим то же самое в виде таблицы.
таблица окончательного решения [изображение автора]Это может представлять или не представлять оптимальное решение этой проблемы, т.е. могут существовать другие способы распределения, которые могут дать лучшее решение с более низкой общей стоимостью.

Необходимо провести проверку оптимальности, чтобы проверить, является ли полученный ответ оптимальным. Если нет, тест на оптимальность приводит нас к вероятному улучшению.
3. Тест на ОПТИМАЛЬНОСТЬ
Хотя базовое допустимое решение может учитывать все ограничения по источникам и местоположению, оно не обязательно должно давать решение с наименьшими затратами. Может быть несколько основных возможных решений, но оптимальным считается то, которое минимизирует общие транспортные расходы. После того, как базовое допустимое решение было определено любым из перечисленных выше методов, решение должно быть дополнительно проверено на предмет оптимальности. Тесты на оптимальность проверят, является ли данное решение лучшим, а если нет, то оно приведет нас к лучшему или оптимальному решению (I предпочел бы плохой вариант худшему.😉)
(Об этом мы поговорим подробно в другой статье, так как она сама мне кажется длинной.😂)
[1]Dr. K. P. Phaneesh, Operations Research (2009), Sudha Publications
До сих пор мы обсуждали поиск простого возможного решения. Мы можем сделать вывод о выборе правильного пути только после теста на оптимальность, о котором будет рассказано в другой статье.
Мы можем сделать вывод о выборе правильного пути только после теста на оптимальность, о котором будет рассказано в другой статье.
Объяснение транспортной проблемы | Что такое Транспортная проблема?
Содержание
- Транспортная проблема
- Сбалансированная задача
- Несбалансированная проблема
- Пример
- Заключение
Предоставил: Патрик
ВведениеИсследование операций (ОИ) — это современный подход, используемый для решения проблем и принятия решений. ИЛИ помогает любой организации достичь наилучшей производительности при заданных ограничениях или обстоятельствах. Известные методы OR:
- Линейное программирование
- Целевое программирование
- Целочисленное программирование
- Динамическое программирование
- Сетевое программирование
Одной из проблем, с которыми сталкиваются организации, является транспортная проблема. Первоначально это означает проблему транспортировки / доставки товаров из отрасли в пункты назначения с наименьшими возможными затратами при удовлетворении ограничений спроса и предложения. Это особый класс методов линейного программирования, разработанный для моделей с линейными целевыми функциями и функциями ограничений. Их применение может быть распространено на другие области деятельности, включая
Первоначально это означает проблему транспортировки / доставки товаров из отрасли в пункты назначения с наименьшими возможными затратами при удовлетворении ограничений спроса и предложения. Это особый класс методов линейного программирования, разработанный для моделей с линейными целевыми функциями и функциями ограничений. Их применение может быть распространено на другие области деятельности, включая
- Планирование и тайм-менеджмент
- Оптимизация сети
- Управление запасами
- Планирование ресурсов предприятия
- Планирование процессов
- Оптимизация маршрутизации
Обозначения представления:
m источников и n пунктов назначения
(i , j) соединение источника (i) и пункта назначения (j)
c ij 🡪 транспортные расходы на единицу
x ij 🡪 количество отправлено
a i 🡪 объем предложения в источнике (i)
b j 🡪 объем спроса в пункте назначения (j)
Транспортная задача работает таким образом, чтобы минимизировать функцию затрат. Здесь функция затрат представляет собой сумму денег, потраченную поставщиком логистических услуг на транспортировку товаров от места производства или поставщика до места спроса. На стоимость перевозки влияет множество факторов. Он включает в себя расстояние между двумя точками, пройденный путь, вид транспорта, количество перевозимых единиц, скорость транспортировки и т. д. Таким образом, основное внимание здесь уделяется перевозке товаров с минимальными затратами на транспортировку без каких-либо компромиссов в спрос и предложение. Транспортная задача является расширением метода линейного программирования, поскольку транспортные расходы формулируются как линейная функция от объема предложения и спроса. Ознакомьтесь с курсом по транспортной аналитике.
Здесь функция затрат представляет собой сумму денег, потраченную поставщиком логистических услуг на транспортировку товаров от места производства или поставщика до места спроса. На стоимость перевозки влияет множество факторов. Он включает в себя расстояние между двумя точками, пройденный путь, вид транспорта, количество перевозимых единиц, скорость транспортировки и т. д. Таким образом, основное внимание здесь уделяется перевозке товаров с минимальными затратами на транспортировку без каких-либо компромиссов в спрос и предложение. Транспортная задача является расширением метода линейного программирования, поскольку транспортные расходы формулируются как линейная функция от объема предложения и спроса. Ознакомьтесь с курсом по транспортной аналитике.
Транспортная проблема существует в двух формах.
- Сбалансированный
- Несбалансированный
Это случай, когда общее предложение равно общему спросу.
Это случай, когда либо спрос превышает предложение, либо наоборот.
В большинстве случаев проблемы принимают сбалансированную форму. Это потому, что обычно производственные подразделения работают, принимая во внимание запасы и спрос. Перепроизводство увеличивает стоимость запасов, в то время как недостаточное производство оспаривается спросом. Следовательно, компромисс должен быть тщательно изучен. Принимая во внимание, что несбалансированная форма существует в ситуации, когда наблюдается беспрецедентный рост или снижение спроса.
Давайте разберемся с этим гораздо проще, на простом примере.
Пример Предположим, что существует ведущая мировая компания-поставщик автомобилей под названием JIM. JIM имеет свои производственные предприятия во многих странах и поставляет продукцию всем ведущим производителям автомобилей в мире. Например, предположим, что в Индии есть три завода в точках M, N и O.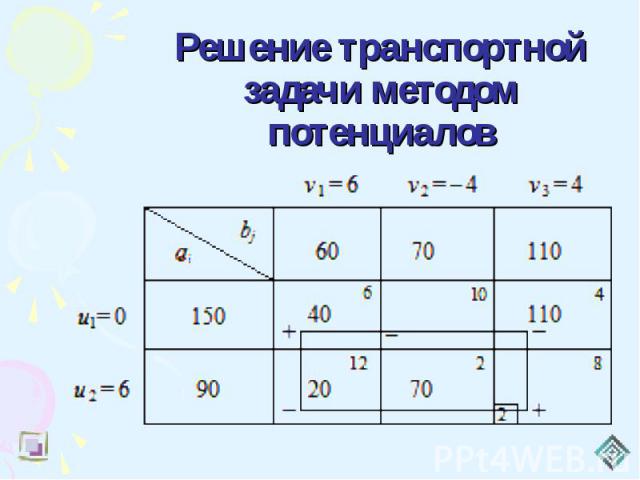 Мощность заводов 700, 300, 550 в сутки. Завод поставляет четырем клиентам A, B, C и D, потребность которых составляет 650, 200, 450, 250 в день. Стоимость перевозки за единицу на километр в индийских рупиях и расстояние между каждым пунктом отправления и пунктом назначения в километрах приведены в таблицах ниже.
Мощность заводов 700, 300, 550 в сутки. Завод поставляет четырем клиентам A, B, C и D, потребность которых составляет 650, 200, 450, 250 в день. Стоимость перевозки за единицу на километр в индийских рупиях и расстояние между каждым пунктом отправления и пунктом назначения в километрах приведены в таблицах ниже.
Здесь цель состоит в том, чтобы определить неизвестное, соблюдая все ограничения спроса и предложения. Стоимость доставки от источника до места назначения прямо пропорциональна количеству отправленных единиц.
РешениеМногие сложные языки программирования эволюционировали, чтобы решать задачи OR гораздо проще и легче. Но значение Microsoft Excel не может быть скомпрометировано и обесценено в любое время. Это также дает нам лучшее понимание проблемы, чем другие. Поэтому мы будем использовать Excel для решения проблемы.
Всегда лучше сформулировать рабочую процедуру пошагово, чтобы она помогала лучшему пониманию и не допускала ошибок.
Шаги, которые необходимо выполнить для решения проблемы:
- Создать транспортную матрицу (определить переменные решения)
- Определить целевую функцию
- Сформулировать ограничения
- Решить методом LP
Создание транспортной матрицы:
Транспортная матрица — это способ понять максимальные возможности, которые могут быть осуществлены при отправке. Это также известно как переменные решения, потому что это представляющие интерес переменные, которые мы будем изменять для достижения цели, то есть минимизации функции затрат.
| Откуда/до | А | В | С 9017 9017| 30 8 | Снабжение | | |
| M | x мА | x
| x md | 700 | ||
| Н | x нет | x 6 7 9 18 | x НЗ | x nd | 300 | |
| 8 O8 7 x oa | x об | x ок | x од | 550 | 6 | 7 | 650 | 9Ступень 02 Определите целевую функцию: Целевая функция — это наша целевая переменная. Целевой функцией является общая стоимость. Она получается путем произведения суммы затрат на единицу на километр и переменных решения (выделены красным), поскольку общая стоимость прямо пропорциональна сумме произведения количества отгруженных единиц и стоимости транспортировки на единицу в расчете на один километр. км. Столбец «Всего отгружено» представляет собой сумму столбцов A, B, C и D для соответствующих строк, а строка «Общая потребность» представляет собой сумму строк M, N и O для соответствующих столбцов. Эти два столбца вводятся для удовлетворения ограничений количества спроса и предложения при решении функции затрат. Шаг 3Сформулируйте ограничения: Ограничения сформулированы относительно спроса и предложения для соответствующих строк и столбцов. Например, четвертое ограничение, x ma + x na + x oa = 650, используется для обеспечения того, чтобы количество единиц, поступающих с заводов M, N и O потребителю A, не было меньше или выше спроса, который есть у А. Аналогично первое ограничение x ma + x mb + x mc + x md = 700 гарантирует, что мощность установки M не будет ниже или выше заданной мощности, следовательно, установка может быть использована в полной мере без компрометация инвентаря. Шаг 4Решение методом LP: Самый простой и эффективный метод решения — использование решателя. Входные параметры подаются, как указано ниже, и приступают к решению. Это наилучшая оптимизированная функция стоимости, и нет никакой возможности получить меньшую стоимость, чем эта, при тех же ограничениях. Из решенного решения видно, что завод M отгружает 100 единиц покупателю A, 350 единиц C и 250 единиц D. Но почему клиенту B ничего не отгружается? Аналогичная тенденция наблюдается и для других растений. Что может быть причиной этого? Да, вы правильно угадали! Это связано с тем, что некоторые другие заводы отгружают клиенту по более выгодной цене, чем другие, и в результате вы можете найти несколько заводов, поставляющих ноль единиц определенным клиентам. Итак, когда же эти поставщики нулевой единицы станут прибыльными и смогут поставлять этим клиентам? Ждать! Не паникуйте. Excel тоже сошёл с рук. После перехода к решению появится диалоговое окно, в котором выберите отчет о чувствительности и нажмите ОК. Вы получите замечательный отчет о конфиденциальности, в котором подробно описаны альтернативные издержки или ценность ресурса. Основное объяснение переменных отчета, Ячейка: Идентификатор ячейки в Excel Имя: Соединение поставщика с клиентом Окончательное значение: Количество отгруженных единиц (после решения) Сниженная стоимость: Насколько должны быть снижены транспортные расходы на единицу продукции на километр, чтобы сделать завод нулевым поставщиком рентабельно и начать поставки Объективный коэффициент: Текущая стоимость перевозки на единицу в км для каждой пары клиентов-поставщиков Допустимое увеличение: Он говорит нам, что максимальная стоимость текущей стоимости перевозки на единицу в км может быть увеличена, что не не вносить никаких изменений в решение Допустимое снижение: Указывает, насколько может быть снижена текущая стоимость перевозки на единицу на километр, что не вносит никаких изменений в решение. Здесь посмотрите на первую строку отчета о чувствительности. Завод М поставляет покупателю А. Здесь стоимость транспортировки за единицу на км составляет 14 фунтов стерлингов, и 100 единиц отгружаются покупателю А. В этом случае стоимость транспортировки может увеличиться максимум на 6 фунтов стерлингов и может снизиться максимум до ₹1. Для любого значения в этом диапазоне окончательное решение не изменится. А теперь кое-что интересное. Посмотрите на второй ряд. Между MB нет ни одной единицы, поставляемой покупателю B с завода M. Текущая стоимость доставки составляет 22 фунта стерлингов, и чтобы сделать эту пару прибыльной и начать бизнес, стоимость должна снизиться на 6 фунтов стерлингов за единицу на км. При этом нет возможности увеличить стоимость даже на рупию. Если стоимость доставки для этой пары снизится до 16 фунтов стерлингов, мы можем ожидать, что между ними начнется бизнес, и окончательное решение изменится соответственно. Приведенный выше пример представляет собой задачу сбалансированного типа, в которой предложение равно спросу. |

 Вариант транспортной задачи с ограничениями на пропускную способность.
Вариант транспортной задачи с ограничениями на пропускную способность.

 Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные пункты назначения, чтобы сделать это стандартной транспортной задачей.
Если они не соответствуют друг другу, добавляются фиктивные источники или фиктивные пункты назначения, чтобы сделать это стандартной транспортной задачей.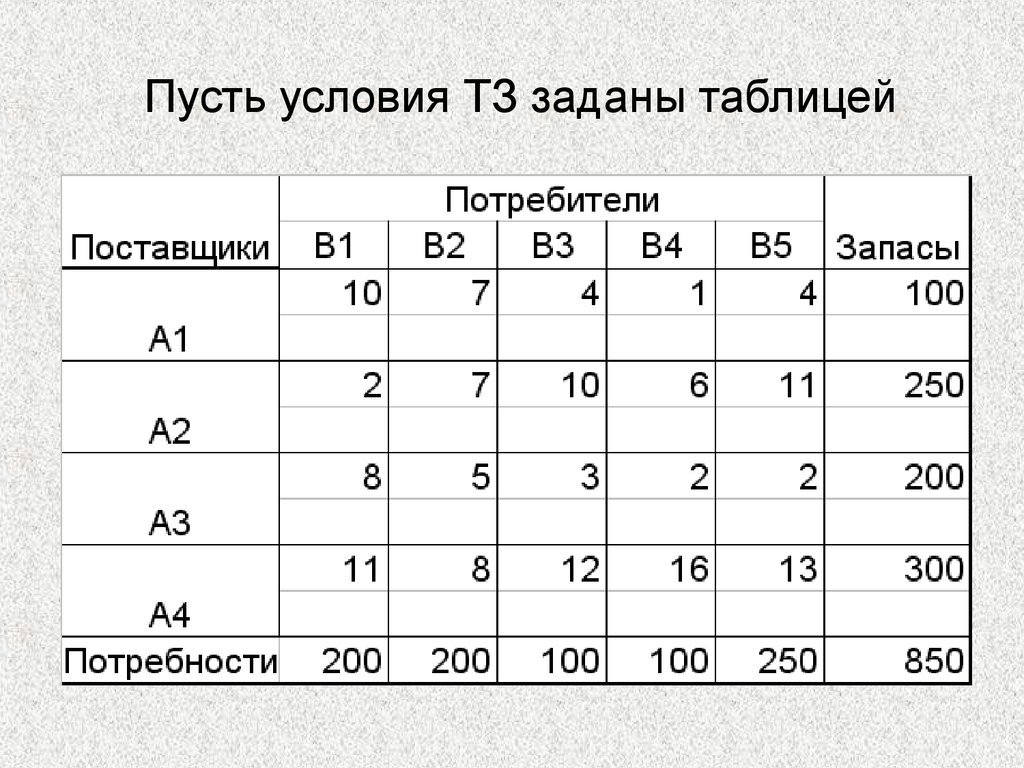 (Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
(Вы можете рассмотреть этот метод, чтобы проверить, идете ли вы по правильному пути или нет.) Потому что мы выделяем ячейки с новыми значениями таким образом, что общий спрос и предложение останутся прежними.
 (Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)
(Решение о том, какой из них выбрать, остается исключительно за пользователем.👍)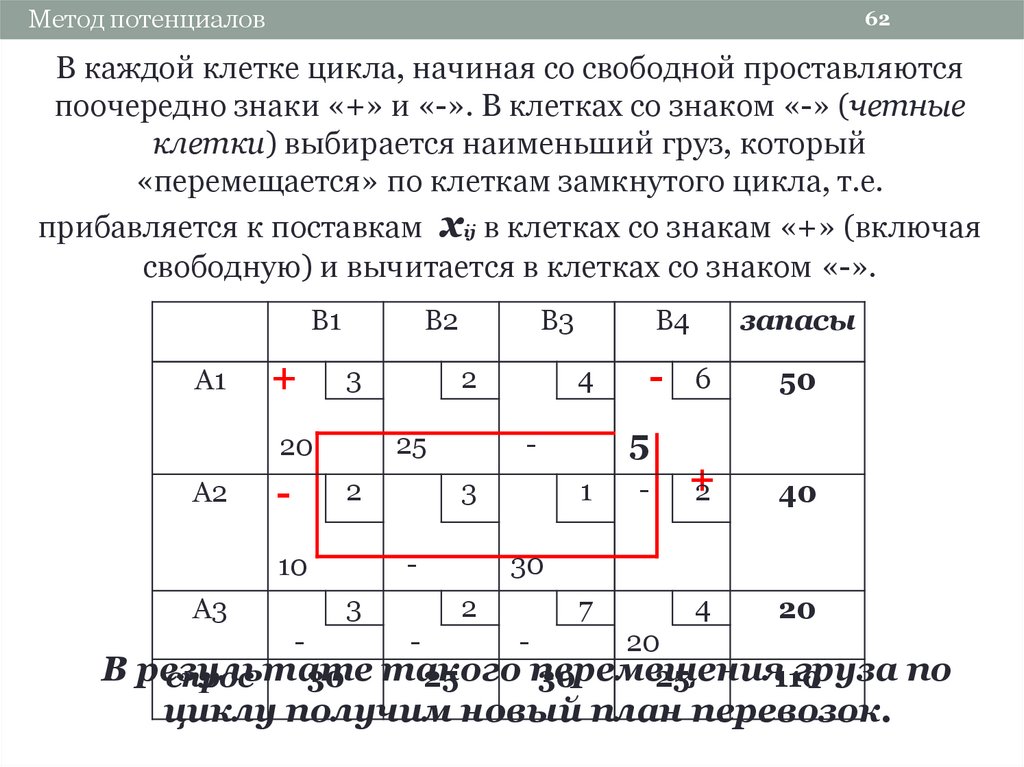 👍)
👍)
 Это функция затрат, то есть общие затраты на транспортировку. Она известна как целевая функция, потому что здесь мы заинтересованы в минимизации транспортных расходов при соблюдении всех ограничений спроса и предложения.
Это функция затрат, то есть общие затраты на транспортировку. Она известна как целевая функция, потому что здесь мы заинтересованы в минимизации транспортных расходов при соблюдении всех ограничений спроса и предложения. Важность этих ограничений заключается в обеспечении того, чтобы они удовлетворяли всем ограничениям спроса и предложения.
Важность этих ограничений заключается в обеспечении того, чтобы они удовлетворяли всем ограничениям спроса и предложения.