Тест с ответами: “Решение квадратных неравенств”
1. Решите неравенство: -2х2+5х-2≤0:
а) (0,5;2) +
б) [0,5;2]
в) (-∞;0,5)∪(2;+∞)
2. Решите неравенство: х2-11х+30<0:
а) (-∞;5)∪(6;+∞)
б) (5;6) +
в) (-∞;5]∪[6;+∞)
3. Решите неравенство: х2-64<0:
а) [-8;8]
б) (-∞;-8)∪(8;+∞)
в) (-8;8) +
4. Решением, какого неравенства является множество всех действительных чисел:
а) 12х2+12х+3≥0 +
б) х2 +8х>0
в) -х2+8х<0
5. Укажите неравенство, которое не имеет решений:
а) х2+50>0
б) х2-50>0
в) х2+50<0 +
6. Один из методов решения квадратных неравенств:
а) графический +
б) практический
в) стандартный
7. Неравенство называют квадратным, если старшая (наибольшая) степень неизвестного «x» равна:
а) одному
б) трем
в) двум +
8. Один из методов решения квадратных неравенств:
а) метод промежутков
б) метод интервалов +
в) метод провалов
9. Укажите тип неравенства x − 7 < 0:
а) квадратное
б) зависит от условия задачи
в) линейное +
10.
Один из методов решения квадратных неравенств:
а) через выделение квадрата двучлена в левой части +
б) через выделение квадрата двучлена в правой части
в) не имеет значения
11. Укажите тип неравенства 2x − 7 > 5:
а) линейное +
б) квадратное
в) зависит от условия задачи
12. Укажите тип неравенства x2 + 5x ≥ 0:
а) квадратное +
б) линейное
в) зависит от условия задачи
13. Решить квадратное неравенство с одной переменной можно методом:
а) сложения
б) интервалов +
в) умножения
14. Укажите тип неравенства x2 + x − 12 ≤ 0:
а) квадратное +
б) линейное
в) зависит от условия задачи
15. К квадратным неравенствам с помощью равносильных преобразований можно прийти от:
а) неравенств только одного вида
б) неравенств других видов +
в) зависит от условия задачи
16. Решать квадратное неравенство таким же образом как и линейное:
а) можно
б) нельзя +
в) можно, в редких случаях
17.
Является универсальным методом решения неравенств:
а) метод пробелов
б) метод квадратов
в) метод интервалов +
18. Для решения квадратного неравенства используется специальный способ, который называется методом:
а) подставления
б) интервалов +
в) промежутков
19. При решении квадратных неравенств можно ограничиться:
а) графическим методом
б) схематическим рисунком
в) оба варианта верны +
20. Чтобы решить квадратное неравенство методом интервалов нужно:
а) перенести все члены неравенства в левую часть, так чтобы в правой осталась только единица
б) перенести все члены неравенства в левую часть, так чтобы в правой остался только ноль +
в) перенести все члены неравенства в левую часть, так чтобы в правой осталась только двойка
21. Чтобы решить квадратное неравенство методом интервалов нужно:
а) сделать так, чтобы при неизвестном «x2» стоял отрицательный коэффициент
б) сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент +
в) не имеет значения
22.
Чтобы решить квадратное неравенство методом интервалов нужно:
а) приравнять левую часть неравенства к единице и решить полученное квадратное уравнение
б) приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение +
в) приравнять левую часть неравенства к двойке и решить полученное квадратное уравнение
23. Чтобы решить квадратное неравенство методом интервалов нужно:
а) полученные корни уравнения разместить на числовой оси в порядке убывания
б) полученные корни уравнения разместить на числовой оси в порядке возрастания +
в) не имеет значения
24. Чтобы решить квадратное неравенство методом интервалов нужно:
а) нарисовать «арки» для интервалов, слева направо, начиная с «+», проставить чередуя знаки «+» и «−»
б) нарисовать «арки» для интервалов, слева направо, начиная с «−», проставить чередуя знаки «+» и «−»
в) нарисовать «арки» для интервалов. Справа налево, начиная с «+», проставить чередуя знаки «+» и «−»
25.
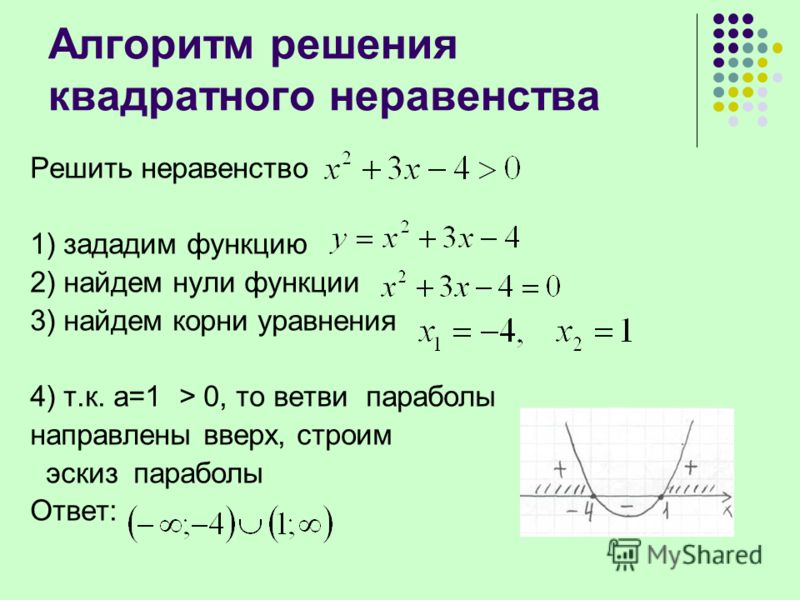Чтобы решить квадратное неравенство методом интервалов нужно:
а) выбрать необходимые интервалы и умножить на два
б) выбрать необходимые интервалы и записать их в ответ +
в) выбрать необходимые интервалы и разделить на два
26. При решении квадратного неравенства необходимо найти … соответствующего квадратного уравнения:
а) значение двойки
б) корни +
в) равенство
27. Квадратное неравенство – это неравенство, состоящее из … квадратичной(ых) функции(й):
а) одной +
б) двух
в) трех
28. Если перед нами неравенство вида ax2+bx+c>0, то фактически задача сводится к тому, чтобы определить числовой промежуток значений x, при котором парабола лежит выше оси:
а) b
б) а
в) x +
29. Если перед нами неравенство вида ax2+bx+c<0, то фактически задача сводится к тому, чтобы определить числовой промежуток значений x, при котором парабола лежит ниже оси:
а) x +
б) b
в) a
30. Вторым названием квадратных уравнений является название:
а) неравенства третьей степени
б) неравенства второй степени +
в) неравенства первой степени
Тест по теме «Квадратные неравенства»
Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 87»
г.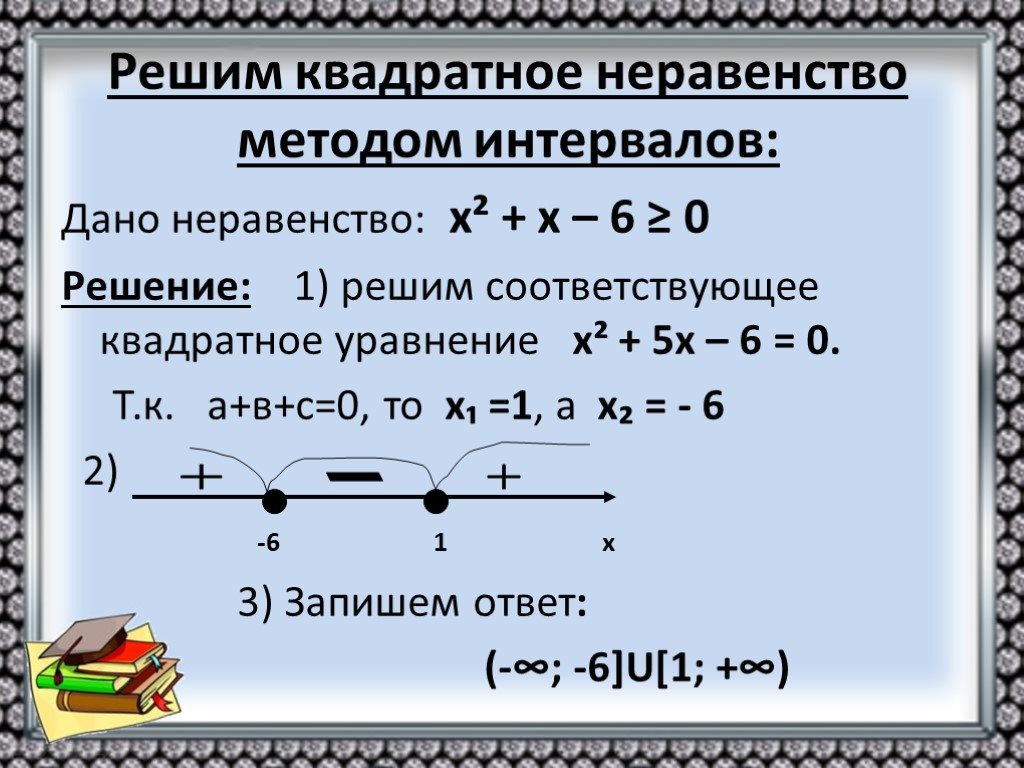
Северск, Томской области
Методическая разработка урока
по алгебре
«Квадратные неравенства »
для учащихся 9 классов
тип урока тест
Автор разработки
учитель математики
Цыгер Ольга Викторовна
Северск
Анкета
1. Цыгер Ольга Викторовна.
2. МБОУ «СОШ № 87», г. Северск, Томской области, учитель математики.
3. Предмет: математика.
4. Тип урока: тест.
5.
комплектация
работы: данный файл.
Аннотация
Данный тест составлен по теме «Квадратные неравенства» и предназначен для учащихся 9 классов. Он может быть использован на уроках промежуточного и обобщающего контроля по данной теме, и при подготовке к ГИА.
Пояснительная записка
Данный тест
позволяет систематизировать знания учащихся по теме «Квадратные неравенства», своевременно
выявить пробелы в изученном материале. Принцип построения теста — «от простого
к сложному» — позволяет использовать его в классах с разной математической
подготовкой. Используемые здесь задания построены таким образом, чтобы учащиеся
смогли оценить как существенные, так и несущественны для данной задачи
свойства квадратичной функции. Отрабатываются два способа решения неравенств
второй степени: аналитический и графический. В тесте представлены все типы
квадратных неравенств имеющие два корня, один или ни одного. Также
представлены задания более сложные, которые сводятся к решению неравенств
второй степени и требуют нестандартного подхода.
Задание 1
Вариант 1
Куда направлены ветви параболы у= aх2 +
- вниз
- вверх
Вариант 2
Куда направлены ветви параболы у= aх2 +bх +с при решении неравенства: 2х — 5х2 + 8 ≥0 ?
- вниз
- вверх
Вариант 3
Куда направлены ветви параболы у= aх2 +bх +с при решении неравенства: 7 — 6х — 9х2≤0 ?
- вниз
- вверх
Вариант 4
Куда направлены ветви параболы у= aх2 +bх +с при решении неравенства: 9 — 8х — 3х2≤0 ?
- вниз
- вверх
Задание 2
Вариант 1
Верно ли, что следующие неравенства 5х2 — 6х — 7> 0 и 6х – 5х2 + 7 > 0 равносильны?
- нет
- да
Вариант 2
Верно ли, что следующие неравенства 3х2 — 5х – 8 < 0 и 5х – 3х2 + 8 < 0 равносильны?
- нет
- да
Вариант 3
Верно ли, что следующие неравенства 5х2 — 4х +21 > 0 и 4х – 5х2 — 21 > 0 равносильны?
- нет
- да
Вариант 4
Верно ли, что следующие неравенства 4х2 — 2х + 13 < 0 и 2х – 4х2 — 13 < 0 равносильны?
- нет
- да
Задание 3
Вариант 1
Верно ли, что следующие неравенства -3х2+ 6х ≥
1.
да
2. нет
Вариант 2
Верно ли, что следующие неравенства -3х2 — 36х ≤0 и х2 +12х ≥ 0 равносильны?
1. да
2. нет
Вариант 3
Верно ли, что следующие неравенства -4х2+ 12х ≥0 и х2 – 3х ≤ 0 равносильны?
1. да
2. нет
Вариант 4
Верно ли, что следующие неравенства -6х2 — 30х ≤0 и х2 +5х ≥ 0 равносильны?
1. да
2. нет
Задание 4
Вариант 1
На рисунке изображен схематически график функции у= g(
x).Используя график, решите неравенство g(x) ≥0.
- (-∞; — 3] U [1; +∞)
- [- 3;1]
- (-∞; — 3) U (1; +∞)
- (- 3;1)
Вариант 2
На рисунке изображен схематически график функции у= g(x).
Используя график,
решите неравенство g(x) ≥0.
- (-∞; 0] U [3; +∞)
- [0;3]
- (-∞; 0) U (3; +∞)
- (0;3)
Вариант 3
На рисунке изображен схематически график функции у= g(x). Используя график, решите неравенство g(x) ≥0.
- (-∞; — 3] U [0; +∞)
- [- 3;0]
- (-∞; — 3) U (0; +∞)
- (- 3;0)
Вариант 4
На рисунке изображен схематически график функции у= g(x). Используя график, решите неравенство g(x) ≥0.
1. (-∞; -1] U [3; +∞)
2. [-1;3]
3.
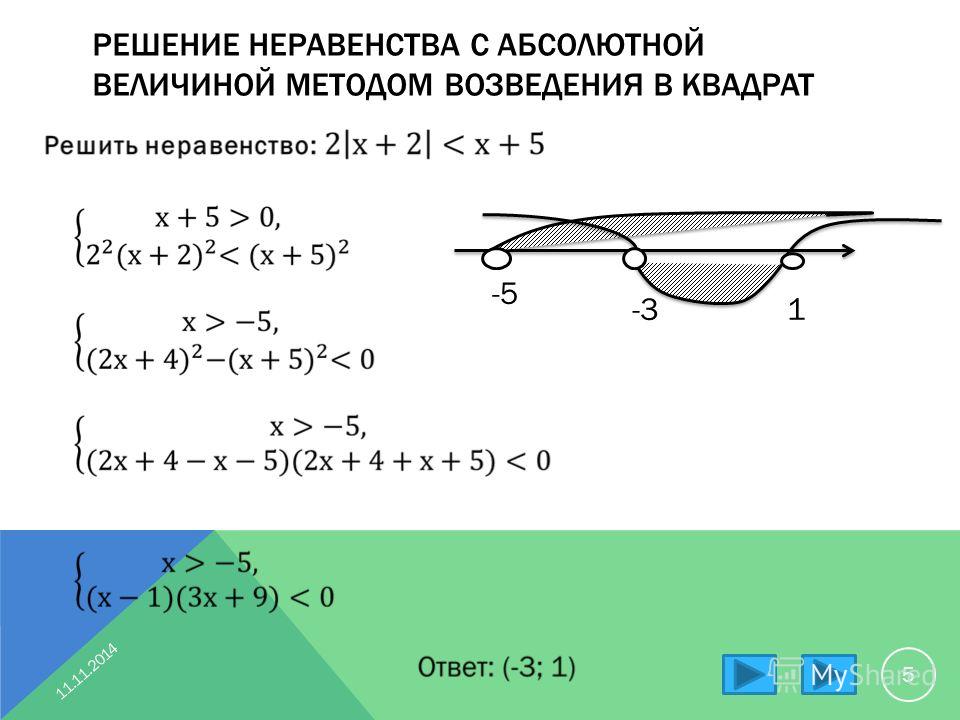(-∞; -1) U (3; +∞)
4. (-1;3)
Задание 5
Вариант 1
Решите неравенство х2 – 2х – 8 ≤ 0.
- [-2; 4]
- (-∞; — 2] U [4; +∞)
- (-2; 4)
- (-∞; — 2) U (4; +∞)
Вариант 2
Решите неравенство х2 – 8х + 15 ≤ 0.
- [3; 5]
- (-∞; 3] U [5; +∞)
- (3; 5)
- (-∞; 3) U (5; +∞)
Вариант 3
Решите неравенство х2 – 10х +21 ≤ 0.
- [3; 7]
- (-∞; 3] U [7; +∞)
- (3; 7)
- (-∞; 3) U (7; +∞)
Вариант 4
Решите неравенство х2 – 7х + 10 ≤ 0.
- [2; 5]
- (-∞; 2] U [5; +∞)
- (2; 5)
- (-∞; 2) U (5; +∞)
Задание 6
Вариант 1
Решите неравенство х2 – 4х ≥ — 3.
1.(-∞; 1] U [3; +∞)
2.[1;3]
3.(-∞; — 3] U [- 1; +∞)
4.(-∞; 1) U (3; +∞)
5.(1;3)
Вариант 2
Решите неравенство х2 +2х ≥ 3.
- (-∞; — 3] U [1; +∞)
- [- 3;1]
- (-∞; — 3) U (1; +∞)
- (-∞; — 1] U [3; +∞)
- (- 3;1)
Вариант 3
Решите неравенство х2 – 7х ≥ 18.
- (-∞; -2] U [9; +∞)
- [- 2; 9]
- (-2; 9)
- (-∞; -2) U (9; +∞)
- [- 9; 2]
Вариант 4
Решите неравенство х2 – 8х ≥ -7.
- (-∞; 1] U [7; +∞)
- [1; 7]
- (-∞; -7] U [1; +∞)
- (-7; 1)
- (-∞; 1) U (7; +∞)
Задание 7
Вариант 1
Решите неравенство 11х + 4 > 3х2 .
- (-1/3; 4)
- (-∞; -4] U [1/3; +∞)
- (- 4; 1/3)
- (-∞; -1/3) U (4; +∞)
- [-4; 1/3]
Вариант 2
Решите неравенство 4х + 15 >3х2 .
- (-5/3; 3)
- (-∞; -3] U [5/3; +∞)
- (- 3; 5/3)
- (-∞; -5/3) U (3; +∞)
- [-3; 5/3]
Вариант 3
Решите неравенство 2х + 11 >9х2 .
- (- 1; 11/9)
- (-∞; -1] U [11/9; +∞)
- (- 11/9; 1)
- (-∞; -11/9) U (1; +∞)
- [-1; 11/9]
Вариант 4
Решите неравенство — х + 22 >6х2 .
- (- 2; 11/6)
- (-∞; -2) U (11/6; +∞)
- (- 11/6; 2)
- (-∞; -11/6) U (2; +∞)
- [-2; 11/6]
Задание 8
Вариант 1
На рисунке
изображен схематически график функции у= x2-3x.
Используя график, решите неравенство x2-3x>0.
1. (- ∞; -3) U (-3; +∞)
2. (- ∞; +∞)
3. решений нет
4. (0; +∞)
Вариант 2
На рисунке изображен схематически график функции у= g(x).
Используя график, решите неравенство g(x)<0.
1. решений нет
2. (- ∞; -3) U (-3; +∞)
3. (- ∞; -3)
4. (- ∞; +∞)
Вариант 3
На рисунке изображен схематически график функции у= g(x).
Используя график, решите неравенство g(x)>0.
- (- ∞; 3) U (3; +∞)
- (- ∞; +∞)
- (0; +∞)
- решений нет
Вариант 4
На рисунке
изображен схематически график функции у= g(x).
Используя график, решите неравенство g(x)<0.
1. решений нет
2. (- ∞; 3) U (3; +∞)
3. (- ∞; 3)
4. (- ∞; +∞)
Задание 9
Вариант 1
Решите неравенство х2≤ 4 .
- [- 2; 2]
- (-∞; -2] U [2; +∞)
- (- 2; 2)
- (-∞; — 2) U (2; +∞)
Вариант 2
Решите неравенство х2≤ 1 .
- [- 1; 1]
- (-∞; -1] U [1; +∞)
- (- 1; 1)
- (-∞; — 1) U (1; +∞)
Вариант 3
Решите неравенство х2≤ 9 .
- [- 3; 3]
- (-∞; -3] U [3; +∞)
- (- 3; 3)
- (-∞; — 3) U (3; +∞)
Вариант 4
Решите неравенство х2≤ 16 .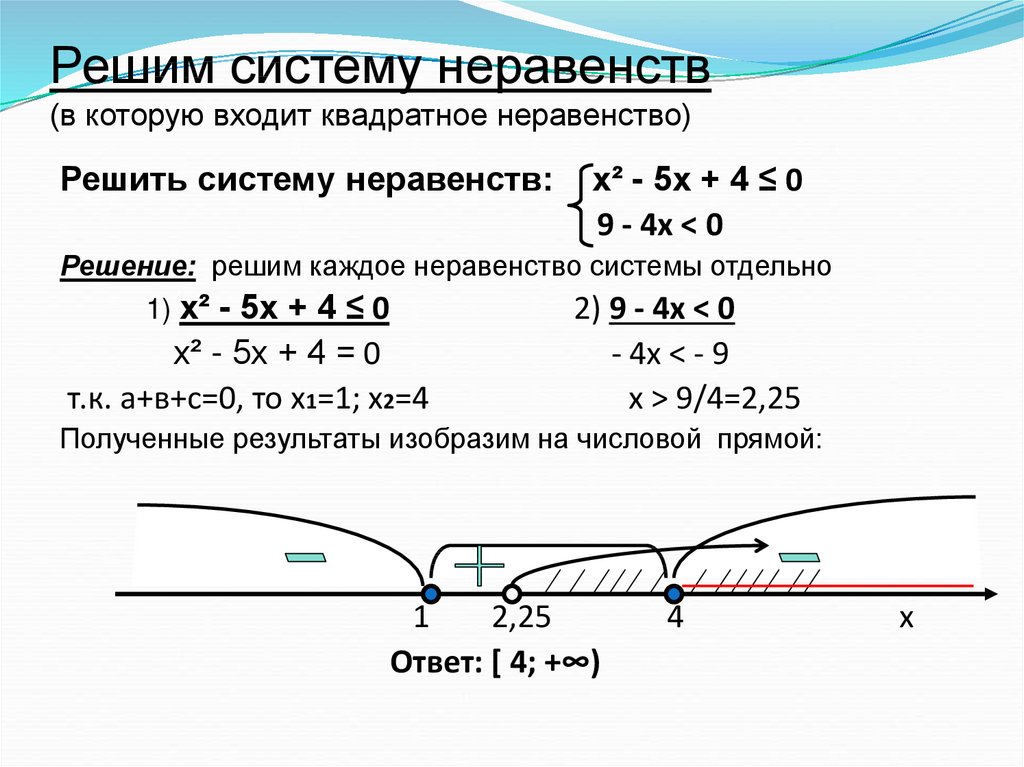
- [- 4; 4]
- (-∞; -4] U [4; +∞)
- (- 4; 4)
- (-∞; — 4) U (4; +∞)
Задание 10
Вариант 1
Сопоставьте неравенства и множества их решений.
Неравенства | Множества решений |
А) х2 +х – 6 ≥ 0 Б) (х – 2)(х +3) > 0 В) х2+х ≤ 6 | 1) [- 3; 2] 2) (-∞; -3] U [2; +∞) 3) (- 3; 2) 4) (-∞; — 3) U (2; +∞) |
1. А — 2; Б – 4; В -1
2. А — 1; Б – 3; В -1
3. А — 1; Б – 4; В -2
Вариант 2
Сопоставьте неравенства и множества их решений.
Неравенства | Множества решений |
А) х2 — х + 6 ≥ 0 Б) (х + 2)(х — 3) > 0 В) х2+6 ≤ х | 1) [- 2; 3] 2) (-∞; -2] U [3; +∞) 3) (- 2; 3) 4) (-∞; — 2) U (3; +∞) |
1.
А — 2; Б –
4; В -1
2. А — 1; Б – 3; В -1
3. А — 1; Б – 4; В -2
Вариант 3
Сопоставьте неравенства и множества их решений.
Неравенства | Множества решений |
А) х2 — 6х — 16 ≥ 0 Б) (х + 2)(х — 8) > 0 В) х2— 6х ≤ 16 | 1) [- 2; 8] 2) (-∞; -2] U [8; +∞) 3) (- 2; 8) 4) (-∞; — 2) U (8; +∞) |
1. А — 2; Б – 4; В -1
2. А — 1; Б – 3; В -1
3. А — 1; Б – 4; В -2
Вариант 4
Сопоставьте неравенства и множества их решений.
Неравенства | Множества решений |
А) х2 + 6х — 16 ≥ 0 Б) (х -2)(х +8) > 0 В) х2+ 6х ≤ 16 | 1) [- 8; 2] 2) (-∞; -8] U [2; +∞) 3) (- 8; 2) 4) (-∞; — 8) U (2; +∞) |
1.
А — 2; Б –
4; В -1
2. А — 1; Б – 3; В -1
3. А — 1; Б – 4; В -2
Задание 11
Вариант 1
Какие из неравенств справедливы при любых значениях переменной?
1) 2х2-5х+16 >0;
2) 3х2— 6х+1 <0;
3) 2х2-4х + 2 >0;
4) — 6х2+ 2х- 9<0;
5) 3х2— х >0;
6) 5х2+ 9 >0;
1. 1; 4; 6
2. 2; 3; 5
3. 1; 3; 4
4. 1; 6
Вариант 2
Какие из неравенств справедливы при любых значениях переменной?
1) 3х2-6х+32 >0;
2) 2х2+ 5х-7 <0;
3) 4х2-12х + 9 >0;
4) 5х2 – х >0;
5) 3х2+5 >0;
6) -7х2+ 9х- 6< 0;
1. 1; 5; 6
2. 2; 3; 5
3. 1; 3; 4
4. 1; 6
Вариант 3
Какие из неравенств справедливы при любых значениях переменной?
1) х2+12х+80 >0;
2) 5х2+3х- 8 <0;
3) х2-8х + 16 >0;
4) 7х2— х >0;
5) 4х2+ 10 >0;
6) 5х — 9х2— 6<0.
1. 1; 5; 6
2. 2; 3; 5
3. 1; 3; 4
4. 1; 6
Вариант 4
Какие из неравенств справедливы при любых значениях переменной?
1) 4х2-2х+13 >0;
2) 2х2-13х +6 <0;
3) 9х2-12х + 4 >0;
4) 9х2— х >0;
5) х — 12х2— 35<0;
6) 3х2+ 12 >0.
1. 1; 5; 6
2. 2; 3; 5
3. 1; 3; 4
4. 1; 6
Задание 12
Вариант 1
Решите неравенство, используя метод интервалов < 0
1. (-7;5)
2. (-∞; -7) U (5; +∞)
3. (-5; 7)
- (-∞; -5) U (7; +∞)
Вариант 2
Решите неравенство, используя метод интервалов < 0
1. (-8;3)
2. (-∞; -8) U (3; +∞)
3. (-3; 8)
- (-∞; -3) U (8; +∞)
Вариант 3
Решите неравенство, используя метод интервалов < 0
1.
(-6;3)
2. (-∞; -6) U (3; +∞)
3. (-3; 6)
- (-∞; -3) U (6; +∞)
Вариант 4
Решите неравенство, используя метод интервалов < 0
1. (-10;5)
2. (-∞; -10) U (5; +∞)
3. (-5; 10)
- (-∞; -5) U (10; +∞)
Задание 13
Вариант 1 ______
Найдите область определения функции у = √3х – 2х2
- D(y) = [0; 1,5]
- D(y) = (-∞; 0] U [1,5; +∞)
- D(y) = (0; 1,5)
- D(y) = (-∞; 0) U (1,5; +∞)
Вариант 2 ______
Найдите область определения функции у = √5х – 2х2
- D(y) = [0; 2,5]
- D(y) = (-∞; 0] U [2,5; +∞)
- D(y) = (0; 2,5)
- D(y) = (-∞; 0) U (2,5; +∞)
Вариант 3 ______
Найдите область определения функции у = √2х – х2
- D(y) = [0; 2]
- D(y) = (-∞; 0] U [2; +∞)
- D(y) = (0; 2)
- D(y) = (-∞; 0) U (2; +∞)
Вариант 4 ______
Найдите область определения функции у = √7х – 2х2
- D(y) = [0; 3,5]
- D(y) = (-∞; 0] U [3,5; +∞)
- D(y) = (0; 3,5)
- D(y) = (-∞; 0) U (3,5; +∞)
Задание 14
Вариант 1
Решите неравенство ≤ 0
- [0; 2,5)
- (-∞; 0] U [2,5; +∞)
- [0; 2,5]
- (-∞; 0) U (2,5; +∞)
- (0; 2,5)
Вариант 2
Решите неравенство ≤ 0
- [0; 2)
- (-∞; 0] U [2; +∞)
- [0; 2]
- (-∞; 0) U (2; +∞)
- (0; 2)
Вариант 3
Решите неравенство ≤ 0
- [0; 1,5)
- (-∞; 0] U [1,5; +∞)
- [0; 1,5]
- (-∞; 0) U (1,5; +∞)
- (0; 1,5)
Вариант 4
Решите неравенство ≤ 0
- [0; 0,4)
- (-∞; 0] U [0,4;
- [0; 0,4]
- (-∞; 0) U (0,4; +∞)
- (0; 0,4)
Задание 15
Вариант 1
При каких значениях х имеет смысл выражение значение :
1.
(-∞; 2) U (2; +∞)
2. (-∞; -2) U (2; +∞)
- (-2; 2)
4. (-∞; 0) U (0; +∞)
Вариант 2
При каких значениях х имеет смысл выражение значение :
1. (-∞; 3) U (3; +∞)
2. (-∞; -3) U (3; +∞)
- (-3; 3)
4. (-∞; 0) U (0; +∞)
Вариант 3
При каких значениях х имеет смысл выражение значение :
1. (-∞; 4) U (4; +∞)
2. (-∞; -4) U (4; +∞)
- (-4; 4)
4. (-∞; 0) U (0; +∞)
Вариант 4
При каких значениях х имеет смысл выражение значение :
1. (-∞; 5) U (5; +∞)
2. (-∞; -5) U (5; +∞)
- (-5; 5)
4. (-∞; 0) U (0; +∞)
Самоанализ
Разрабатывая данный методический продукт, я ставила следующие задачи:
1.
Подобрать
различные типы заданий по теме «Квадратные неравенства», соответствующие
программе по математике 9 класса;
2. Включить задания разного уровня сложности, включая нестандартные;
3. Возможность использовать данный тест учителю для закрепления и контроля знаний учащихся;
4. Возможность использовать данный тест для самостоятельной работы учеников и подготовке к экзамену.
Поставленные задачи выполнены.
Литература
1. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова «Алгебра 9 класс»
М., «Просвещение», 2010 г
2. М.Б. Миндюк,
Н.Г. Миндюк «Разноуровневые дидактические материалы по алгебре.
9 класс» М.,
Издательский Дом «Генжер», 1997 г
3. С.П. Ковалева «Алгебра 9 класс. Поурочные планы по учебнику Ю.Н. Макарычева и др.»; Волгоград; «Учитель»; 2005 г
4. Ю. А. Глазков, И.К. Варшавский, М.Я. Гаиашвили «Тесты по алгебре. 9 класс. К учебнику Ю.Н. Макарычева и др.»., М: Издательство «Экзамен», 2011г
5. Э. Г. Гельфман, Л.Н.Демидова, В.И. Слободской «Развитие логического мышления учащихся в процессе преподавания тем «Квадратные уравнения», « Квадратичная функция», « Неравенства второй степени», Томск: Издательство Томского пединститута, 1984г.
6. ЕГЭ: 3000 задач с ответами по математике. Все задания группы B/ Под редакцией А. Л. Семенова, И. В. Ященко. – М.: Издательство “Экзамен”, 2014 г.
7. В.И. Жохов, Л.Б. Крайнева «Уроки алгебры в 9 классе». Пособие для учителей. – М.: Вертум –М, 2000 г
Интернет –источники:
http://uztest.ru
Квадратичные неравенства. Предварительное исчисление
Все ресурсы для предварительного исчисления
12 Диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
Precalculus Help » Неравенства и линейное программирование » Квадратные неравенства
Решите следующее неравенство
Возможные ответы:
Все действительные числа
Нет решения
Правильный ответ:
Пояснение:
Начнем с переноса всех наших членов в левую часть неравенства.
Затем факторизуем.
Это означает, что наша левая часть будет равна 0, когда . Однако мы также хотим знать значения, когда левая часть меньше нуля. Мы можем сделать это, используя тестовые области. Мы начинаем с рисования числовой линии с нашими двумя числами, помеченными.
Мы замечаем, что наши два числа делят нашу линию на три области. Нам просто нужно попробовать тестовое значение в каждом регионе. Мы начинаем с нашего крайнего левого региона, выбирая число меньше . Затем мы подставляем это значение в левую часть нашего неравенства, чтобы увидеть, будет ли результат положительным или отрицательным. Любое значение (например, ) даст нам положительное значение.
Затем мы повторяем этот процесс с центральной областью, выбирая значение между двумя нашими числами. Любое значение (например, ) приведет к отрицательному результату.
Наконец, мы завершаем процесс с самой правой областью, выбрав значение больше . Любое значение (например, ) приведет к положительному значению.
Затем мы соответствующим образом помечаем наши регионы.
Поскольку мы хотим, чтобы результат был меньше нуля, нам нужны значения между двумя нашими числами. Однако, поскольку наша левая часть может быть меньше или равна нулю, мы также можем включить сами два числа. Мы можем выразить это как
Сообщить об ошибке
Решите квадратное неравенство.
Возможные ответы:
Правильный ответ:
Пояснение:
Начнем с решения уравнения для его нулей. Это делается путем замены знака на знак .
Поскольку мы знаем нули уравнения, мы можем затем проверить площади вокруг нулей, поскольку мы естественным образом разделили реальную линию на три части:
Сначала проверяем
Следовательно, первый интервал можно включить в наш ответ.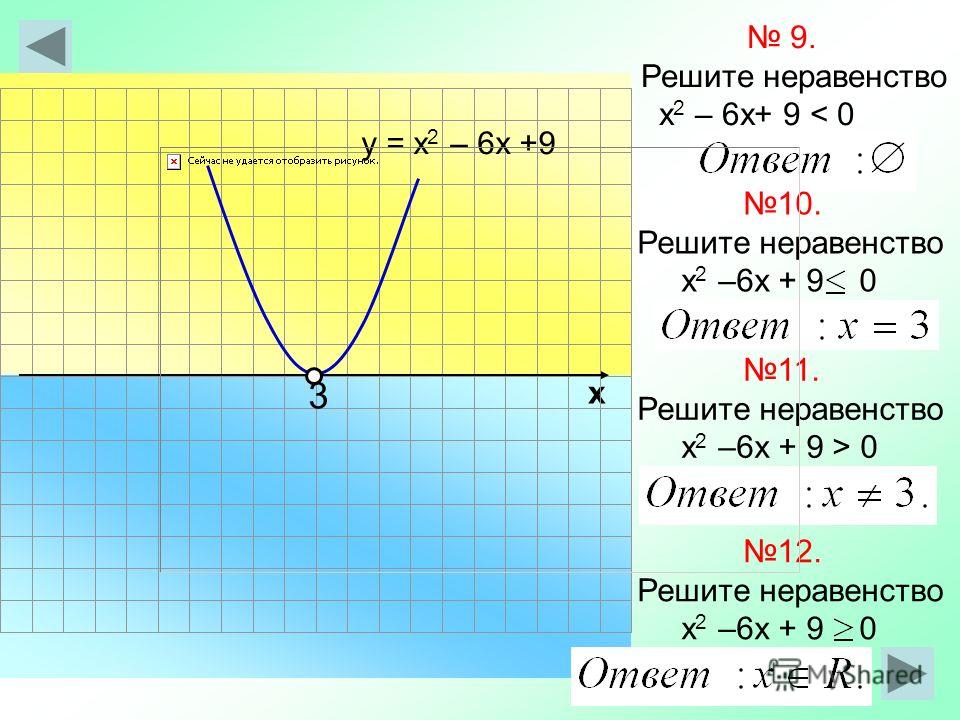
Кроме того, мы знаем, что удовлетворяет уравнению, поэтому мы можем с уверенностью сказать, что интервал является частью ответа.
Далее проверяем что-то во втором интервале. Пусть , тогда
Следовательно, второй интервал не может быть включен в ответ.
Наконец, мы проверяем третий интервал. Пусть , тогда
Что действительно удовлетворяет исходному уравнению. Поэтому в ответ можно включить и третий интервал. Поскольку мы знаем, что это также удовлетворяет уравнению, мы можем включить его в интервал следующим образом:
Следовательно,
Сообщить об ошибке
Решить:
3 Возможные ответы:44
Объяснение:
Метод 1:
1) Умножьте левую часть, затем перепишите неравенство в виде уравнения:
2) Теперь переписывайте квадратичное уравнение и решайте уравнение:
3) Следующие интервалы настройки с использованием решений и проверьте первоначальное неравенство, чтобы увидеть, где он держит истину, используя значения.
для на каждом интервале.
4) Интервал между и верен для исходного неравенства.
5) Решение:
Метод 2:
С помощью графического калькулятора найдите график. Функция находится ниже оси x (меньше ) для значений x . Используя обозначение интервала для , .
Способ 3:
Для неравенства выражение переменной в терминах меньше , а неравенство имеет диапазон значений, из которых состоит решение. Это означает, что каждое из значений решения для находится строго между двумя решениями . «Между» — для случая «меньше», «За пределами» — для случая «больше».
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы Precalculus
12 Диагностические тесты 380 практических тестов Вопрос дня Карточки Учитесь по концепции
Как решать квадратные неравенства на уровне GCSE по математике
В сентябре 2015 года учебная программа GCSE по математике была обновлена, чтобы включить в нее новые темы, в том числе векторы, итерационные методы и способы решения квадратных неравенств.
Британское правительство хотело привести выпускные экзамены по математике в Великобритании в соответствие с международными стандартами и требованиями меняющегося рынка труда. Это побудило их ввести новые концепции и больше сосредоточиться на развитии навыков рассуждения, а не только на счете 9.0005
Давайте взглянем на ожидания от новой учебной программы GCSE по математике, исследуя недавно введенную тему, с которой ученики часто сталкиваются: квадратные неравенства .
Что такое квадратные неравенства?
Квадратные уравнения описывают параболическое движение: симметричную плоскую кривую, которую можно изобразить в форме буквы U. Парабола часто используется в реальных задачах экономики, физики и техники.
Квадратное неравенство — это уравнение второй степени, в котором вместо знака равенства используется знак неравенства.
Решение вопроса квадратного неравенства GCSE по математике
В этой статье я решаю девятнадцатый вопрос из июньского 2017 года статьи 3 (более высокий уровень).
Экзаменационной комиссией является Pearson Edexcel.
Это непростая задача. Это требует понимания квадратичной формулы, а также понимания подстановки и умения рисовать графики. К сожалению, здесь нет двух вариантов: ученики не любят рисовать графики.
Сам вопрос простой и краткий.
Решите 2
x 2 + 3 x – 2 > 0Здесь я объясню решение этого квадратного неравенства в несколько логических шагов.
1) Во-первых, нам нужно решить квадратное уравнение, используя квадратную формулу. Мы могли бы попытаться разложить на множители или использовать другие методы, но лучше избегать этих методов во время экзаменов.
Наша цель – начертить график параболы – кривой с определенными свойствами, чтобы получить математическое решение из нашего графика.
2) is the quadrantic formula
3) At this point we need to remember that a quadratic equation has the form y = ax 2 + b x + C
В нашем случае, A = 2 , B = 3 , C = — 2 .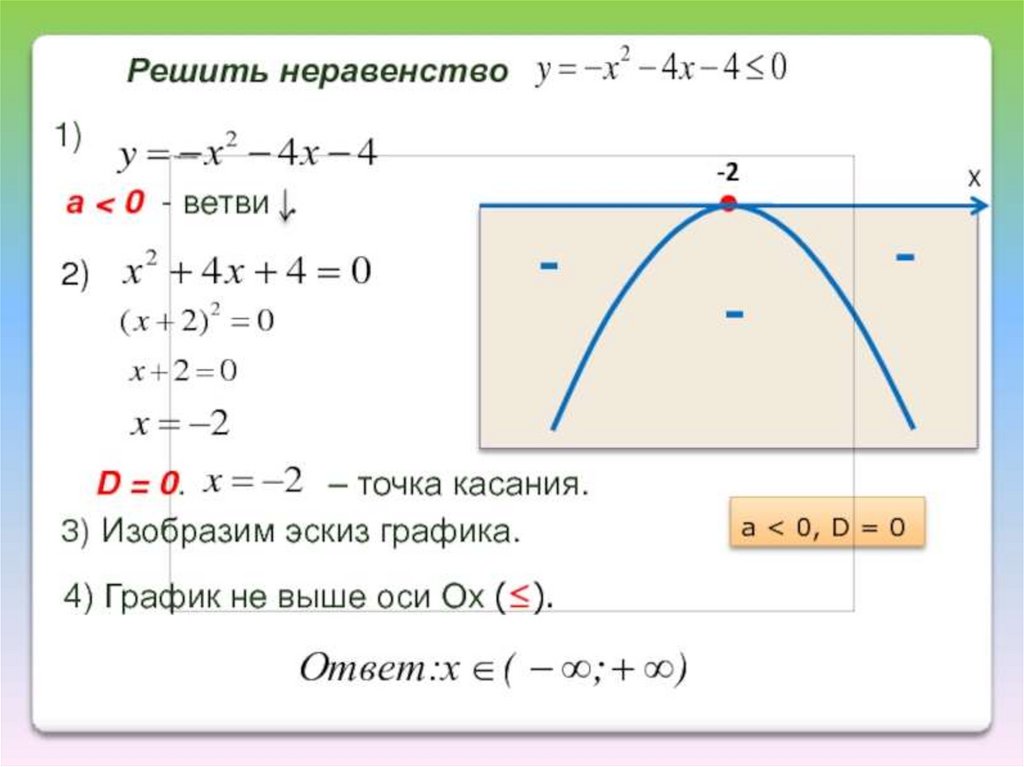
Подставляя в квадратную формулу, получаем:
4) Решая два уравнения, мы получаем две точки, в которых график пересекает горизонтальную ось (оси x ). Их называют корнями.
5) Теперь все становится немного сложнее, поскольку нам нужно помнить, что ориентация параболы задается знаком члена a .
Если a > 0 , то парабола имеет форму ∪. Если a < 0 парабола имеет форму ∩ . В нашем случае знак a положительный ( a = 2 ), поэтому наша кривая имеет форму ∪.
6) Теперь все становится еще сложнее, так как нам нужно нарисовать график. Здесь я использую компьютерную программу, но я буду излагать основные мысли по мере продвижения.
Первое, что нам нужно сделать, это начертить ось и определить горизонтальную ось ( x оси) положение точек x 1 и x 2 .