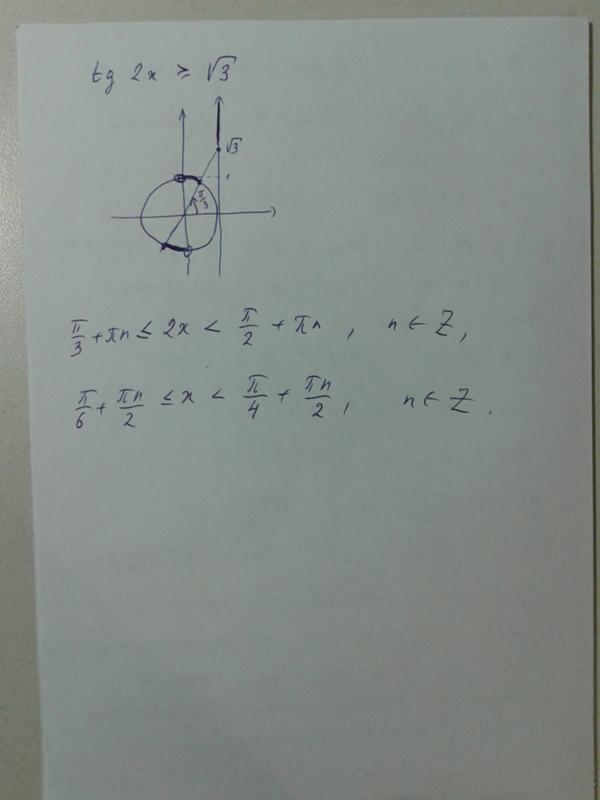Тест по «Алгебре и начала анализа»-Решение тригонометрических уравнений.(10-11 класс)
ТЕСТ ПО ТЕМЕ
«Решение тригонометрических уравнений»
11 класс Алгебра и начала математического анализа
Выполнила: учитель математики
МАОУ Улу-Юльской СОШ, Первомайского района,
Томской области
Олей В.И.
Инструкция по выполнению работы
Работа состоит из трёх частей и содержит 25 заданий.
Часть I содержит 9 заданий. Задания вида: продолжите утверждения и с выбором верного
ответа. Задания части I считаются выполненными, если учащийся продолжил утверждение и
Часть II содержит 5 заданий с выбором верного ответа, соответствующих базовому уровню и
уровню возможностей. При их выполнении надо записать полное решение и ответ (цифру
Часть III содержит 5 заданий, соответствующих уровню возможностей и доступных
учащимся, хорошо успевающим по математике.
При их выполнении надо записать полное
На выполнение тестовой работы даётся 80 мин.
Проводится работа в два этапа. При этом реализуется основной принцип итоговой
аттестации: успешное выполнение заданий II или III частей работы не компенсирует
отсутствие результата выполнения заданий первой части. Оценивание осуществляется
На первом этапе в первый день в течение 40 мин учащиеся выполняют первую и вторую
часть работы. В оставшееся время урока после сдачи учащимися работ проводится проверка
ответов и устанавливается, кто из школьников не преодолел «порог», позволяющий
получить положительную отметку. Проводится анализ возможных причин затруднений
На втором этапе во второй день в течение 40 минут учащиеся, не прошедшие «порог» в
первый день, вновь пытаются это сделать, решая задания первой и второй частей (другой
вариант). Остальные учащиеся выполняют задания III части работы. При этом некоторые из
них могут попытаться улучшить результат, выполнения заданий второй части.
Советуем учащимся для экономии времени пропускать задание, которое не удаётся
выполнить сразу, и переходить к следующему. К выполнению пропущенных заданий можно
вернуться, если у вас останется время.
* С данной инструкцией необходимо ознакомить школьников до проведения тестовой
работы. Инструкция и текст работы выдаются каждому школьнику.
Для оценивания результатов выполнения работы применяются отметки «2», «3», «4», или
«5». Полное правильное выполнение всей работы – 11 +9+13=33
Отметка «3» выставляется, если набрано от 5 до 7 баллов из части I и от 4 до 6 из части
Отметка «4» выставляется, если набрано от 8 до 10 баллов из части I и от 7 до 8 из части
Для получения отметки «5» необходимо набрать 11 баллов из части I и 9 баллов части II,
и от 10 до 13 баллов III части.
ТЕСТ ПО ТЕМЕ «Решение тригонометрических уравнений» | |||
Часть 1 | |||
№ | Задание | балл | |
1 | Продолжите утверждение: Тригонометрическим уравнением называется уравнение, содержащее …. | 1 | |
2 | Продолжите утверждение: Уравнения cos х=a и sin х=a имеют решения, если a … | 1 | |
3 | Все корни уравнения sin х=a, если a … можно найти по формуле … | 2 | |
4 | Укажите формулу, по которой можно найти все корни уравнения cos х=а , где|а|≤ 1: 1) х=(−1 )n arccos a+πn ,nϵZ ; 2) х=arccos a+2 πn , nϵZ ; 3) х=−arccos a+πn , nϵ Z ; 4) х=± arccos a+2 πn , nϵ Z . | 1 | |
5 | Из данных уравнений выберите те, которые являются тригонометрическими (в ответ запишите набор цифр без запятых): 1) sin x=1 ; 2) 72−х = 5 х; 3) tgx=2; 4) х + 5х = 0; 5) cos (3 x−1)=0, 2 | 1 | |
6 | Какие из тригонометрических уравнений не имеют корней (в ответ запишите набор цифр без запятых): 1) cos x=1,1 ; 2) sin x=−2 ; 3) tg x=7; 4) cos x=π ; 5) sin x = −1,09. | 2 | |
7 | Установите соответствие между уравнением и формулой, по которой можно найти все корни уравнения (каждой букве поставьте в соответствие цифру): а) cos x=−1; б) sinx=0; в) sinx=1; г) cos x = 0; д) sinx=−1. | 1 | |
x=−π1) +2 п n , nϵ Z 2 ; 2) x = пn, nϵZ; π 3) x= +nn , nϵZ2 ; 4) x = п + 2 пn, nϵZ; 5) x= π +2 п n , nϵZ . | |||
8 | Укажите уравнение, которому соответствует решение х = (-1)n arcsin a + пn, n ϵ Z (в графе напротив буквы поставьте знак «+»): 1) cos x=a ; 2) sin x=a; 3) tg x=a; 4) ctg x=a; 5) sin x=−a. | 1 | |
9 | Установите соответствие между уравнением и формулой, по которой можно найти все корни уравнения (каждой букве поставьте в соответствие цифру): а) tgx = — a; б) sinx = — a; в) ctg x = — a; г) cos x = — a . 1) х = (-1)n+1 arcsin a + пn, n ϵ Z; 2) х=±( п — arc cos x) +2πn ;3)= — arctg a+ πn, n ϵ Z; 4) х = п — arcсtg a+ πn, n ϵ Z. | 1 | |
Итого: | 11 | ||
Часть 2 | |||
1 | Решите уравнение sin х= 0.5 | 1 | |
2 | Решите уравнение cos2x = 0 | 1 | |
3 | Решите уравнение -3sinx =1. | 2 | |
4 | Укажите наибольший отрицательный корень уравнения 2 sin х+1=0. Ответ запишите в градусах. 1) — 600; 2) -300; 3) – 450; 4) – 900 | 2 | |
5 | Найдите корни уравнения cos ( +2 х)=1 на интервале [0; п] 1) ; 2) ; 3) ; 4) ; | 3 | |
Итого | 9 | ||
Часть 3 | |||
1 | Решите уравнение: 3 −5sin х−2=0. | 2 | |
2 | Решите уравнение: 3 +2 t gх — 1 = 0 | 2 | |
3 | Решите уравнение: −3 cos х+sin х=0. | 3 | |
4 | Решите уравнение: 5 + 6 sin х — 6 = 0 | 3 | |
5 | Решите уравнение: +√3sin х cos х=0 | 3 | |
Итого | 13 | ||
Пояснения
Тест «предназначен для выявления степени усвоения учащимися 10 класса материала
по теме: «Решение тригонометрических уравнений».
Материал может быть использован в 11 классе на уроках итогового повторения при
Часть I направлена на проверку достижения уровня обязательной подготовки и
содержит 9 заданий, соответствующих минимуму содержания курса тригонометрии.
Максимальное число баллов за одно задание – 2 балла.
Часть II проверяет уровень владения программным материалом и умение применять
базовые знания, и состоят из заданий открытого банка заданий ЕГЭ по математике.
Максимальное число баллов за одно задание – 3балла.
Часть III включает в себя тригонометрические уравнения, которые необходимо
решить с использованием формул тригонометрии и записать ответ. Задания с отбором
корней. Задание считается выполненным верно, если учащийся решил уравнение и
обоснованно указал корни уравнения, принадлежащие заданному отрезку.
Подведение итогов: проводится на следующем уроке. Необходимо разобрать решение тех
задач, которые вызвали затруднения у большинства учащихся.
алгоритмов — Решение tanx = x?
$\begingroup$
Как найти решения tanx = x с точностью до любого числа десятичных знаков?
(Конечно, есть графический метод, но он только помогает найти приблизительное значение.
..)
- алгоритмы
$\endgroup$
1
$\begingroup$
Кроме решения $x=0$ для каждого $n>0$ существуют два решения $\pm x_n$ с $x_n={(2n-1)\pi\over2}-\tau_n$, где $\tau_n >0$ равно $O({1\over n})$. Легко видеть, что $\tau_n$ удовлетворяет уравнению $$\tau=\arctan{1\over (2n-1)\pi/2 — \tau}=:f(\tau).$$ Поскольку $|f'(\tau)|\ll1$ в окрестности $\tau=0$, мы можем получить $\tau_n$ численно, перебирая $f$, начиная с $\tau=0$.
$\begingroup$
Вы знаете, что существует решение $x_k$ в окрестности $2 \pi k$ для каждого целого числа $k$.
И уравнение можно также записать как
$x_k = \arctan(x_k) + 2 k \pi$
где арктангенс возвращает главное значение.
Затем вы можете повторить:
$x_k[0] = 2 k \pi$
$x_k[n] = \arctan(x_k[n-1]) + 2 k \pi$
Сходится очень быстро — эмпирически — доказательство оставлено в качестве упражнения 🙂
Если у вас есть приблизительное начальное значение, вы выбираете $k$, округляя $x_0/(2 \pi)$
$\endgroup$
1
$\begingroup$
Решение Ньютона-Рафсона для нулей $f(x) = tan x — x$
$\endgroup$
2$\begingroup$
Сегодня был вопрос о корнях $tan(x)=2x$
Не могу найти.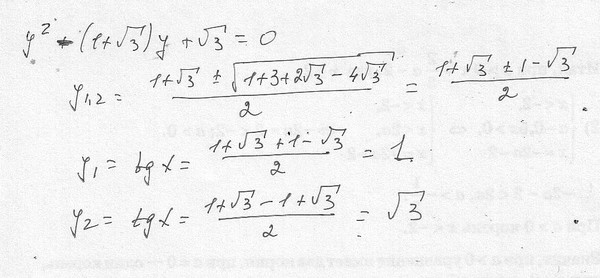
Может этот вопрос отложили?
Тем не менее, я обнаружил, что этот вопрос связан с $tan(x)=x$ . Итак, мой ответ будет обоим.
Конечно, корни — это трансцендентные числа, которые не могут быть выражены через конечное число элементарных функций. Но их можно выразить в виде ряда:
$\endgroup$
2
$\begingroup$
(Это должен быть комментарий к ответу Леонблоя)
Правильное выражение для итерации с фиксированной точкой для $n$-го ненулевого решения $x=\tan\;x$ равно $x_{k+1}= \arctan(x_k)+n\pi$. Фактически, для более общего трансцендентного уравнения $\tan\;x=\lambda x$ итерация с фиксированной точкой $x_{k+1}=\arctan(\lambda x_k)+n\pi$ работает хорошо; можно использовать фиксированную точку, начинающуюся с $x_0=n\pi$, для первых нескольких итераций, а затем переключиться на Ньютона-Рафсона, как только итерация с фиксированной точкой начнет сходиться.