Древняя информатика: Давайте создадим преобразователь римских цифр с нуля 🏺📜
Сегодня мы отправимся в путешествие во времени! Вернемся к году CCXVII, то есть к 217, вплоть до железного века: Римская империя.
Но сегодня мы не будем исследовать Колизей или Пантеон, не будем разговаривать с легионерами или ходить по Cursus publicus. Вместо этого мы узнаем о концепции, которая позволила создать большую часть римской экономики, а также некоторые из самых великолепных архитектурных шедевров. Сегодняшняя тема — римские цифры.
Подождите, как же CCXVII переводится как 217?
Очень хороший вопрос! Давайте проанализируем.
(Короткая интерлюдия: Если вы не знали, цифры, к которым мы привыкли (0-9), называются «арабскими цифрами», так как они возникли в западной части Аравии и Северной Африке. А знаете ли вы, что фраза, которую я там нацарапал, даже не соответствует действительности? Как @youngdad33
Как отмечалось в комментариях, хорошо известные цифры с основанием 10 произошли из Индии, попали в арабскую часть мира, затем были обнаружены европейцами во время крестовых походов и, следовательно, ошибочно названы «арабскими цифрами».
Прежде всего, что означают C, X, V и I?
В этой таблице представлен обзор римских цифр и их значений:
| Римская цифра | Значение |
|---|---|
я | 1 |
В | 5 |
Х | 10 |
Л | 50 |
С | 100 |
Д | 500 |
М | 1000 |
Точно так же, как числа с основанием 10, римские числа состоят из цифр. Цифры, однако, не совсем соответствуют разным значениям в разных местах (например, 217 будет 2 * 100, 1 * 10 и 7 * 1), но вместо этого они складываются в большее число. Количество одинаковых цифр соответствует значению. Поэтому мы могли бы переписать CCXVII от до C + C + X + V + I + I . В приведенной выше таблице это переводится как
В приведенной выше таблице это переводится как 100 + 100 + 10 + 5 + 1 + 1 = 217 .
Так, например, число 4 можно записать как IIII , верно? Почти! Хотя это могло быть интуитивным ответом, изобретатели решили, что это не тот путь. Вместо этого все, что нельзя записать сложением максимум трех одинаковых цифр, записывается как вычитание из следующего большего числа. Итак, вместо того, чтобы писать 1 + 1 + 1 + 1 = 4 , запишем 5 - 1 = 4 , римскими цифрами V - I или просто IV .
Таким образом, это означает, что если цифра A ( осталось от цифры B) меньше цифры B, она вычитается, в противном случае добавляется. Для иллюстрации:
IV --> I < V --> V - I Но: VI --> V > I --> V + IВойти в полноэкранный режимВыйти из полноэкранного режима
Это работает для любого номера:
CDXLIV --> (D - C) + (L - X) + (V - I) = (500 - 100) + (50 - 10) + (5 - 1) = 444 ХС = (100 - 10) = 90Войти в полноэкранный режимВыйти из полноэкранного режима
Однако 99 записывается не как 100 - 1 , а как (100 - 10) + (10 - 1) .
Таким образом, это правила преобразования однозначного числа с основанием 10 N в римские цифры:
- Если N <= 3, повторить
Iот 1 до 3 раз - Если N === 4, это 5 — 1, поэтому
VI - Если N === 5, это
В - Если N < 9, это 5 + повтор
Iот 1 до 3 раз - Если N === 9, это 10 — 1, поэтому
IX
Если мы посмотрим на приведенную выше таблицу, то заметим, что для каждой степени от 10 до 1000 (1, 10, 100, 1000) есть одиночные (1, 10 и т. д.) и пятерки (5, 50, 500) — поэтому мы можем повторить описанные выше шаги для каждой степени 10 и соответствующим образом изменить набор цифр, которые мы используем.
Кодирование от base10 до Roman
Сначала мы переводим обычные числа с основанием 10 в римские цифры.
Нам нужна простая схема преобразования римских цифр в числа:
const romanNumerals = {
1: «Я»,
5: «В»,
10: «Х»,
50: 'Л',
100: 'С',
500: 'Д',
1000: «М»
}
Войти в полноэкранный режимВыйти из полноэкранного режима Далее нам нужно реализовать правила преобразования одиночных цифр.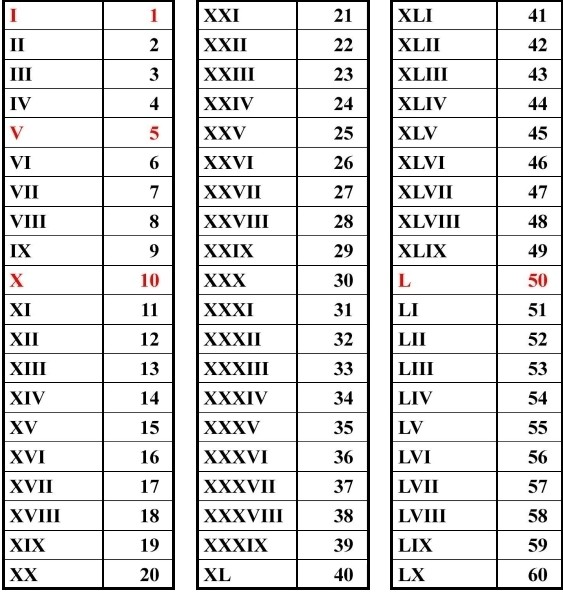 Приведенные выше правила можно перевести в набор из
Приведенные выше правила можно перевести в набор из if утверждений напрямую, нам нужно знать только степень числа 10, поэтому мы выбрали правильные римские цифры:
const romanNumerals = {
1: «Я»,
5: «В»,
10: «Х»,
50: 'Л',
100: 'С',
500: 'Д',
1000: «М»
}
/**
* Переводит одну цифру в степени 10 в римскую цифру.
* @параметр п
* @параметр powerOf10
* @returns {*|строка}
*/
const numDigitToRomDigits = (n, powerOf10) => {
if (n <= 3) { // I, II, III, X, X, XXX, C, CC, CCC
return romanNumerals[powerOf10].repeat(n)
}
if (n === 4) { // IV, XL, CD
вернуть римские цифры[powerOf10]
+ римские цифры [powerOf10 * 5]
}
if (n === 5) { // V, L, D
вернуть римские цифры [powerOf10 * 5]
}
если (n < 9) { // VI, VII, VIII и т. д.
вернуть римские цифры [powerOf10 * 5]
+ римскиеЧисла[powerOf10].repeat(n - 5)
}
// МС, ХС, IX
вернуть римские цифры[powerOf10]
+ римские цифры [powerOf10 * 10]
}
Войти в полноэкранный режимВыйти из полноэкранного режима Давайте попробуем это:
numDigitToRomDigits(7, 10) // "70", дает `LXX` numDigitToRomDigits(5, 100) // "500", возвращает `D` numDigitToRomDigits(3, 1) // "3", дает `III` numDigitToRomDigits(4, 10) // "40", дает `XL`Войти в полноэкранный режимВыйти из полноэкранного режима
Выглядит хорошо! Теперь мы можем использовать эту функцию для преобразования больших чисел:
/** * Переводит целое число в римские цифры.* @параметр х * @возвращает {строка} */ константа num2rom = x => { // Разбить число на цифры и наоборот, // так вычислить степень числа 10 проще. константные цифры = x.toString() .расколоть('') .map(n => parseInt(n)) .задний ход() // Большие числа не работают, пишется 5000 // как V с дефисом сверху, у нас этого нет // персонаж... если (х > 3999) { выдать новую ошибку( «Числа больше 3999 не могут быть преобразованы» ) } // Перебираем все цифры, каждую преобразуем пусть romanNum = '' for (пусть i = 0; i < digits.length; i++) { РоманЧисло = numDigitToRomDigits (цифры [i], 10 ** i) + romanNum // Прикрепляем к началу уже сконвертированного } вернуть romanNum }
Попробуем так:
num2rom(3724) // выдает `MMMDCCXXIV` - работает!Войти в полноэкранный режимВыйти из полноэкранного режима
От римских цифр снова к основанию 10
Другой способ будет немного сложнее - нам нужно разобрать римские цифры и снова преобразовать их обратно в основание 10.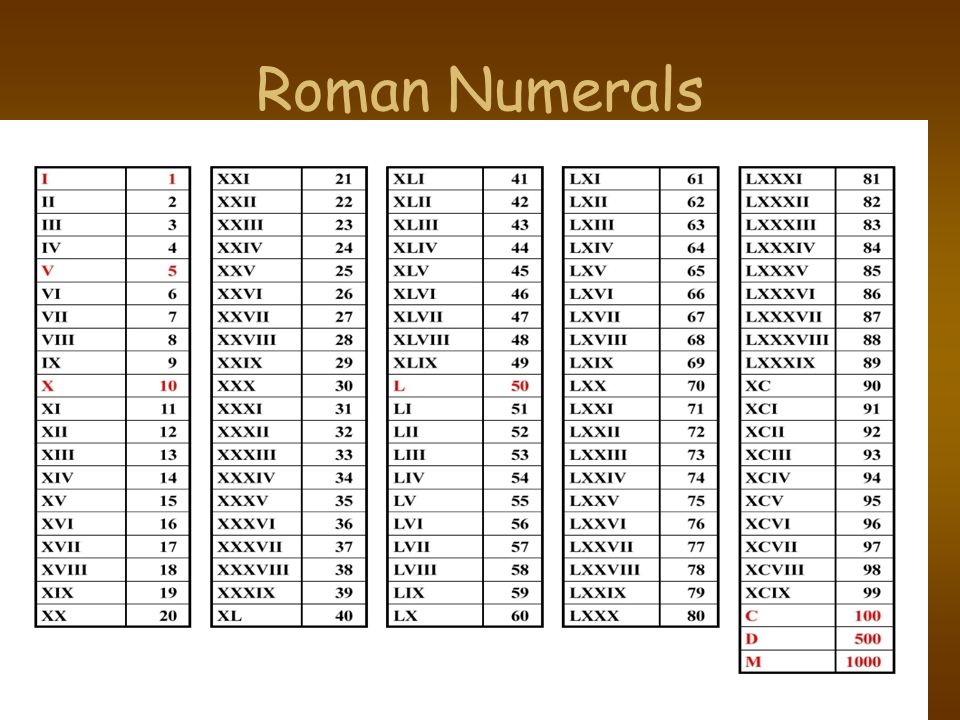 Во-первых, мы переворачиваем карту ранее. Stackoverflow рассказывает нам, как это сделать.
Во-первых, мы переворачиваем карту ранее. Stackoverflow рассказывает нам, как это сделать.
const flipObject = obj => Object.entries(obj)
.reduce((акк, [ключ, значение]) => (акк[значение] = ключ, соотв), {})
const base10Numerals = flipObject(romanNumerals)
/* дает
{
С: "100"
Д: "500"
Я: "1"
Л: "50"
М: "1000"
В: "5"
Х: "10"
}
*/
Войти в полноэкранный режимВыйти из полноэкранного режима Сейчас мы реализуем метод вычитания/сложения. Мы знаем, что добавляются большие числа слева от других чисел. Если число слева меньше, оно вычитается. Итак, в основном: VI = V + I , но IV = V - I . Поскольку не существует такой вещи, как IIV , мы можем проверить следующее число, чтобы определить, добавляем ли мы текущее число или вычитаем его. Итак, примерно так:
Слева направо, Если следующее число справа больше: Вычесть текущую цифру Еще Добавить текущую цифруВойти в полноэкранный режимВыйти из полноэкранного режима
В коде это будет выглядеть так:
/** * Преобразует римское число в base10.Войти в полноэкранный режимВыйти из полноэкранного режима* @параметр х * @ возвращает {число} */ константа rom2num = х => { // Разделить число и присвоить base10 // значение для каждой цифры. // parseInt необходим, потому что // флип дает строки. константные цифры = x.split('') .map (d => parseInt (base10Numerals [d])) пусть сумма = 0 // Перебираем каждую цифру for (пусть i = 0; i < digits.length; i++) { // Если число справа больше, чем // текущий номер если (цифры [i + 1] > цифры [i]) { сумма -= цифры[i] } еще { сумма += цифры[i] } } возвращаемая сумма }
Давайте посмотрим, работает ли это, переведя все числа от 1 до 3999 туда и обратно:
let result = true
для (пусть я = 0; я < 3999; я ++) {
результат = результат && rom2num(num2rom(i)) === i
}
console.log(результат) // верно, работает!
Войти в полноэкранный режимВыйти из полноэкранного режимаРезультат
Теперь нам нужны поля ввода и кнопки, и вуаля:
Уф, хватит пока древних времен, вернемся в 21 век.
Надеюсь, вам понравилось читать эту статью так же, как мне понравилось ее писать! Если да, то оставьте ❤️ или 🦄 ! Я пишу технические статьи в свободное время и время от времени люблю выпить кофе.
Если вы хотите поддержать мои усилия, вы можете предложить мне кофе ☕ или подпишитесь на меня в Твиттере 🐦 ! Вы также можете поддержать меня напрямую через Paypal!
Римские цифры для KS2 — образование
Балджит Догра 22 декабря 2020 г. математика, Номера
Балджит Догра
22 декабря 2020 г. математика, Цифры
Содержание
- 1 Что такое римские цифры?
- 2 Формирование чисел – Правила
- 2.
 1 Правило 1
1 Правило 1 - 2.2 Правило 2
- 2.3 Правило 3
- 2.4 Правило 4
- 2.5 Правило 5
- 2.
- 3 Цель познакомить с римскими цифрами на ключевом этапе 2
- 4 Римские цифры в наше время
- 5 Загрузить практические пакеты
- 6 Дополнительная литература
Что такое римские цифры?
Как следует из названия, римские цифры были созданы и использовались римлянами в качестве системы нумерации для связи и торговли до средних веков. В этой системе алфавиты используются для обозначения чисел и их комбинаций для создания больших чисел. Современное использование использует семь основных символов, и каждый из них соответствует фиксированному значению. Символы I, V, X, L, C, D и M представляют 1, 5, 10, 50, 100, 500 и 1000 соответственно.
Вы можете помочь своему ребенку научиться пользоваться римскими цифрами и чувствовать себя более комфортно, регулярно практикуясь. Первоначально используйте три символа за раз, и если ваш ребенок сталкивается с проблемами, запоминая, какой символ представляет какое значение, используйте мнемонические приемы. Мы упомянули некоторые из них ниже. Предложите ребенку искать римские цифры на часах, телепередачах, книгах и т. д. Попросите ребенка перевести различные числа и даты в римские цифры, используя приведенную выше таблицу.
Мы упомянули некоторые из них ниже. Предложите ребенку искать римские цифры на часах, телепередачах, книгах и т. д. Попросите ребенка перевести различные числа и даты в римские цифры, используя приведенную выше таблицу.
Составление чисел – правила
Чтобы понять, как работают римские цифры и как мы можем создавать большие числа с помощью этих символов, нам необходимо понять некоторые основные правила.
Правило 1Римские цифры I, X и C могут повторяться три раза, чтобы образовать числа.
Например:
1.) I = 1, I + I = 2, I + I + I = 3
2.) X = 10, X + X = 20, X + X + X = 30
3 .) C = 100, C + C = 200, C + C + C = 300
Это правило не действует для цифр V, L и D; эти цифры не должны повторяться для образования больших чисел.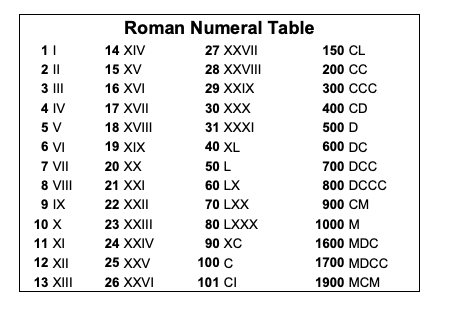
Когда меньшая цифра помещается справа от старшей цифры значения, все значения складываются.
Примеры:
1. VI = 5 + 1 = 6
2. XXIII = 10 + 10 + 1 + 1 + 1 = 23
3. LXXXV = 50 + 10 + 10 + 10 + 5 = 85
Применяется это правило к значению подобных цифр, как показано в правиле 1
Когда младшая цифра помещается слева от цифры большего значения, меньшее значение вычитается из цифры большего значения.
Например:
1. IV = 5 – 1 = 4
2. XCIV = 100-10-1+5 = 94
3. CLIX = 100 + 50 + (10 – 1) = 159
Чтобы преобразовать числа больше 10, мы должны сначала записать число 10 или группу из 10, а затем меньшие числа 1 или 5 по мере необходимости.
Например:
1. 13 = 10 + 3 = 1 0 + 1 + 1 + 1 = XIII
2. 37 = 10 + 10 + 10 + 5 + 1 + 1 = XXXVII
3. 59 = 100 + 50 + (10 – 1) = CLIX
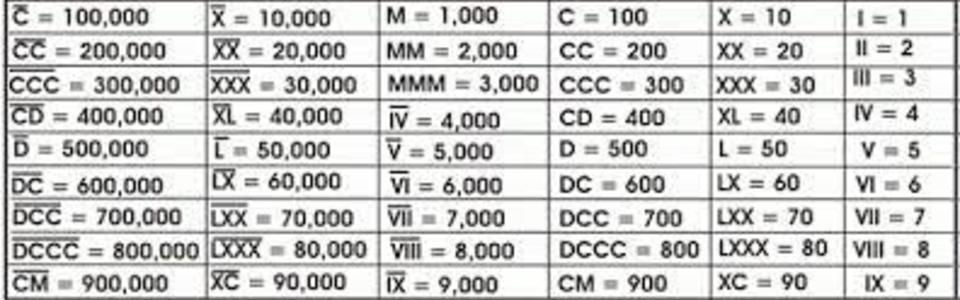
Значение цифр увеличивается в 1000 раз, когда над римскими цифрами проводится горизонтальная линия.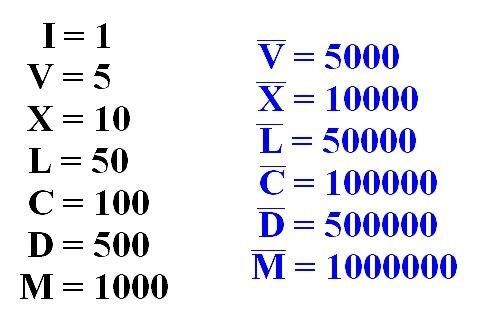

 * @параметр х
* @возвращает {строка}
*/
константа num2rom = x => {
// Разбить число на цифры и наоборот,
// так вычислить степень числа 10 проще.
константные цифры = x.toString()
.расколоть('')
.map(n => parseInt(n))
.задний ход()
// Большие числа не работают, пишется 5000
// как V с дефисом сверху, у нас этого нет
// персонаж...
если (х > 3999) {
выдать новую ошибку(
«Числа больше 3999 не могут быть преобразованы»
)
}
// Перебираем все цифры, каждую преобразуем
пусть romanNum = ''
for (пусть i = 0; i < digits.length; i++) {
РоманЧисло =
numDigitToRomDigits (цифры [i], 10 ** i)
+ romanNum // Прикрепляем к началу уже сконвертированного
}
вернуть romanNum
}
* @параметр х
* @возвращает {строка}
*/
константа num2rom = x => {
// Разбить число на цифры и наоборот,
// так вычислить степень числа 10 проще.
константные цифры = x.toString()
.расколоть('')
.map(n => parseInt(n))
.задний ход()
// Большие числа не работают, пишется 5000
// как V с дефисом сверху, у нас этого нет
// персонаж...
если (х > 3999) {
выдать новую ошибку(
«Числа больше 3999 не могут быть преобразованы»
)
}
// Перебираем все цифры, каждую преобразуем
пусть romanNum = ''
for (пусть i = 0; i < digits.length; i++) {
РоманЧисло =
numDigitToRomDigits (цифры [i], 10 ** i)
+ romanNum // Прикрепляем к началу уже сконвертированного
}
вернуть romanNum
}

 1 Правило 1
1 Правило 1