С искусственным базисом симплекс метод: Метод искусственного базиса. Решение задач и контрольных работ по линейному программированию онлайн

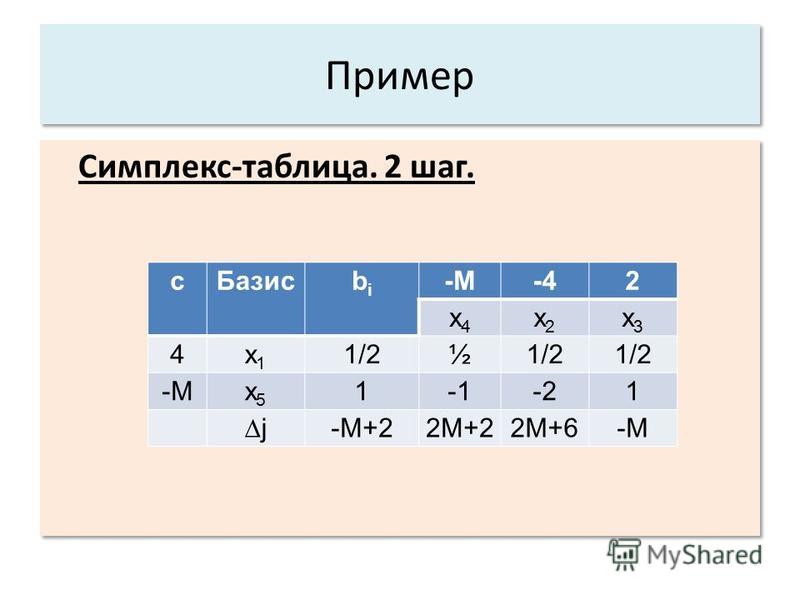
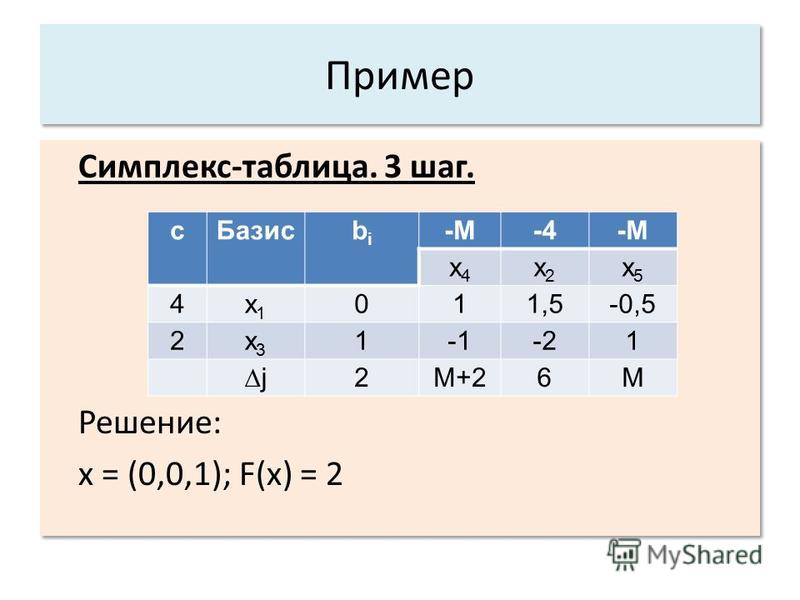
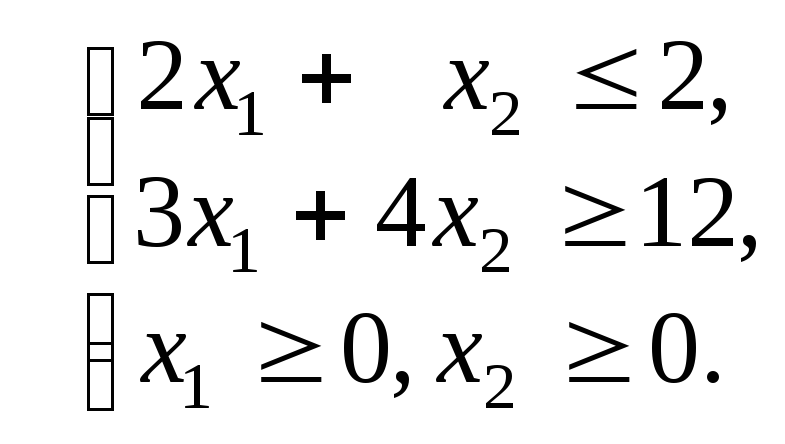15. Симплекс-метод с искусственным базисом.

Метод искусственного базиса применяется, когда задача не имеет начального опорного решения, т.е. отсутствуют базисные переменные в системе ограничений.

Согласно данному методу для решаемой задачи составляется расширенная задача, которую решают симплекс-методом и на основе полученного решения либо находят для исходной задачи оптимальное решение, либо устанавливается причина его отсутствия.

Чтобы составить расширенную задачу в исходную задачу вводят искусственные переменные. Искусственными переменными называют неотрицательные переменные, которые вводят в ограничение неравенства для получения начального опорного решения с базисом. Каждая искусственная переменная вводится в левую часть с коэффициентом _1 и в целевую функцию в задаче на максимум с коэффициентом –М и коэффициентом +М в задаче на минимум, где число М сколь угодно большое по сравнению с 1.

В общем случае расширенная задача на максимум имеет вид:

Z(x)=C₁x₁+C₂x₂+…+C_nx_n-Mx_n+1-Mx_n+2-…-Mx_n—m→ max

Ограничение:

x_j≥0; j=

Теорема 1.

Любому допустимому решению исходной задачи Х^/=(x₁^/, x₂^/, …, x_n^/) соответствует допустимое решение расширенной задачи X^/=(x₁^/, x₂^/, …, x_n^/, 0, 0, …, 0).

Теорема 2.

Значение целевой функции расширенной задачи на максимум (минимум) на любом допустимом решении X^/=(x₁^/, x₂^/, …, x_n^/, 0, 0, …, 0), у которого все искусственные переменные равны 0 больше (меньше) значения целевой функции на любом допустимом решении, у которого хотя бы одна искусственная переменная отлична от 0.

Теорема 3.

Если расширенная задача имеет оптимальное решение X^*=(x₁^*, x₂^*, …, x_n^*, 0, 0, …, 0), у которого все искусственные переменные равны 0, то исходная задача будет иметь оптимальное решение X^*=(x₁^*, x₂^*, …, x_n^*).

Теорема 4.

Если расширенная задача имеет оптимальное решение, в котором хотя бы 1 искусственная переменная отлична от 0, то исходная задача не имеет решения в виду несовместности системы ограничений.

Теорема 5.

Если расширенная задача не имеет решения в виду неограниченности целевой функции, то исходная задача также не имеет решения по той же причине.

Особенности метода:

1)В виду того, что начальное опорное решение расширенной задачи содержит переменные, входящие в целевую функцию в задаче на максимум с коэффициентом –М, в задаче на минимум с коэффициентом –М оценки разложений k состоят из двух слагаемых, одно из которых не зависит от М, а другое – зависит. Так как М сколь угодно велико по сравнению с 1, то на первом этапе расчёта последнюю оценочную строку делят на две части.

2)Векторы, соответствующие искусственным переменным, которые выводятся из базиса, в дальнейшем исключаются из рассмотрения.

3)После того, как все искусственные переменные исключатся из базиса, расчёты продолжаются обычным симплекс-методом.

Любой задаче линейного программирования можно поставить в соответствие другую задачу, которую называют двойственной или сопряжённой.

Например, составить двойственную задачу к задаче использования ресурсов.

Имеется m видов сырья в количестве b₁, b₂, …, b_m, которые используют для изготовления n видов продукции. Известно, что на единицу каждого вида продукции расходуется a_ij количество сырья, где i=, j=. Пусть C_j – прибыль при реализации j-того вида продукции.

Математическая модель данной задачи имеет вид:

Z(x)=C₁x₁+C₂x₂+…+C_nx_n → max

x_j≥0; j=

Предположим, что второй производитель хочет перекупить сырьё.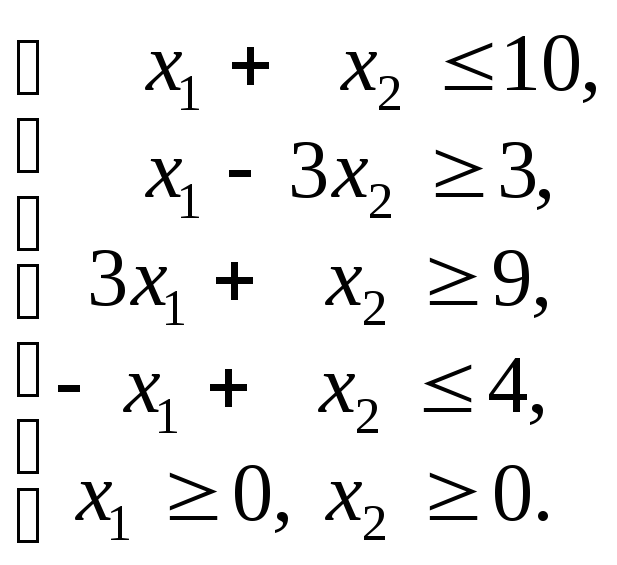

Составим двойственную задачу, решение которой позволит определить условие продажи сырья. Введём цены видов сырья: I=y₁, II=y₂, …, N=y_m. Затраты на приобретение i-того вида сырья в количестве b_i=b_iy_i. Второму производителю выгодно минимизировать суммарные затраты на приобретение всех видов сырья. По этому целевая функция задачи имеет вид: F(y)=b₁y₁+b₂y₂+…+b_my_m→ min

Первому производителю не выгодно продать сырьё, если суммарная стоимость всех видов сырья, расходуемых на каждое изделие j-той продукции a_1jy₁+a_2jy₂+…+a_mjy_m≤C_j.

Тогда система ограничений задачи имеет вид.

y_j≥0; j=

Связь исходной и двойственной задач состоит в том, что коэффициенты C_jисходной задачи являются свободными членами системы ограничений двойственной задачи. А свободные члены системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи. Матрица коэффициентов системы ограничений двойственной задачи является транспонированной матрицей коэффициентов системы ограничений исходной задачи.

Двойственные задачи бывают симметричными и несимметричными.

Симметричные пары:

1)если Z(x) → max, Ах≤А₀, х≥0, то F(y) =YA₀→ min, YA≥С, y≥0;

2)если Z(x) → min, Ах≥А₀, х≥0, то F(y) =YA₀→ max, y≥0.

Общие правила составления двойственных задач:

1)Во всех ограничения исходной задачи свободные члены должны находится в правой части, а члены с независимыми – в левой.

2)Ограничения неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.

3)Если знаки неравенств в исходной задаче ≤, то целевая функция должна стремится к максимуму, если знаки ≥, то должна стремится к минимуму.

4)Целевая функция двойственной задачи F(y)=с₀+b1y1+b₂y₂+…+b_my_n→ min, где с₀ – свободный член целевой функции Z(x).

5)Целевая функция F(y) должна оптимизироваться противоположным, по сравнению с Z(x), образом.

6)Каждому неизвестному x_jисходной задачи соответствует ограничение в двойственной задаче.

Подробный разбор симплекс-метода / Хабр

Пролог

Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему.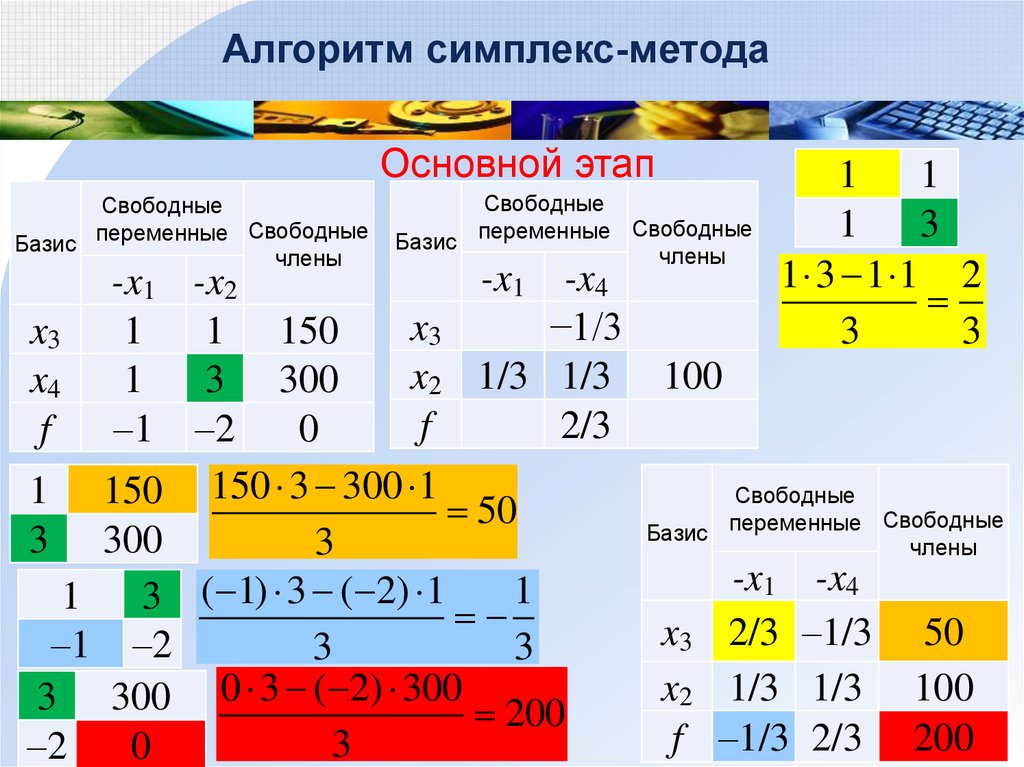 Об этом, собственно, и поговорим.

Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.

§1. Постановка задачи линейного программирования

Определение:

Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.

Общая задача линейного программирования (далее – ЛП) имеет вид:

§2. Каноническая форма задачи ЛП

Каноническая форма задачи ЛП:

Замечание: Любая задача ЛП сводится к канонической.

Алгоритм перехода от произвольной задачи ЛП к канонической форме:

1. Неравенства с отрицательными умножаем на (-1).
2. Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
3. Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
4. Делаем замену переменных:

• Если , то
• Если — любой, то , где

Замечание:

Будем нумеровать по номеру неравенства, в которое мы его добавили.

Замечание: ≥0.

§3. Угловые точки. Базисные/свободные переменные. Базисные решения

Определение:

Точка называется угловой точкой, если представление возможно только при .

Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).

Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.

Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.

§4. Симплекс-метод

Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции. Это возможно только в том случае, если возрастание какой-то переменной приведет к увеличению значения функционала.

Необходимые условия для применения симплекс-метода:

1. Задача должна иметь каноническую форму.
2. У задачи должен быть явно выделенный базис.

Определение:

Явно выделенным базисом будем называть вектора вида:, т.е. только одна координата вектора ненулевая и равна 1.

Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.

Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:

• В первой строке указывают «наименование» всех переменных.
• В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
• В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
• Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
• Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.

Замечание:

Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.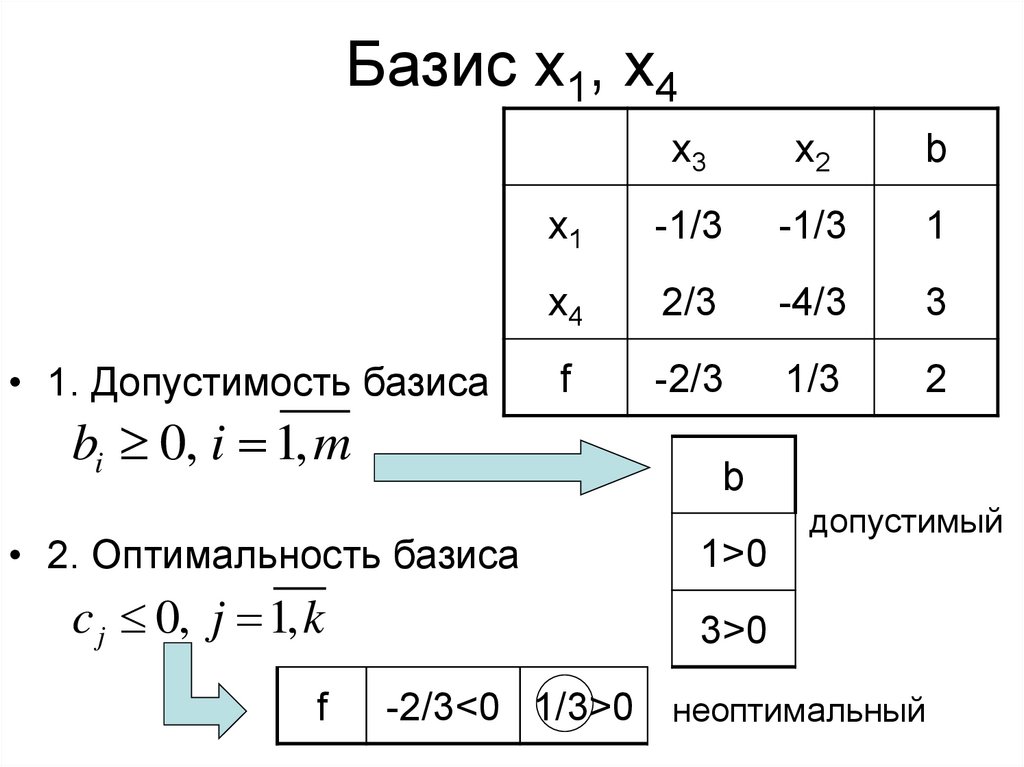

Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.

Замечание: Коэффициенты в строке функционала берутся со знаком “-”.

Алгоритм симплекс-метода:

1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:

• Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
• Если задача на максимум – выбираем минимальный отрицательный.

Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.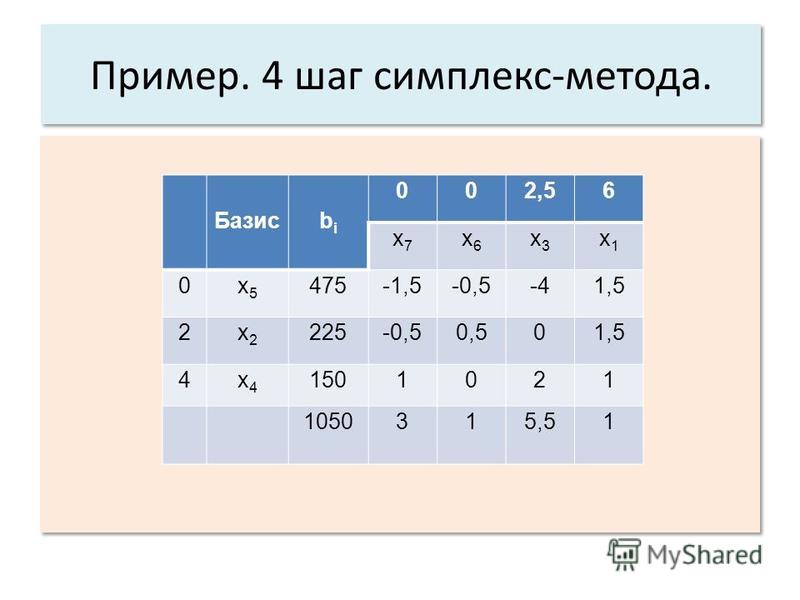

Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.

Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется ведущим столбцом.

2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:

• Вектор правых частей почленно делится на ведущий столбец
• Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)

Определение:

Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.

Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.

3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.

Определение: Такой элемент называется ведущим элементом.

4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.

5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.

• Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
• Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка

Замечание:

Преобразование такого вида направлено на введение выбранной переменной в базис, т.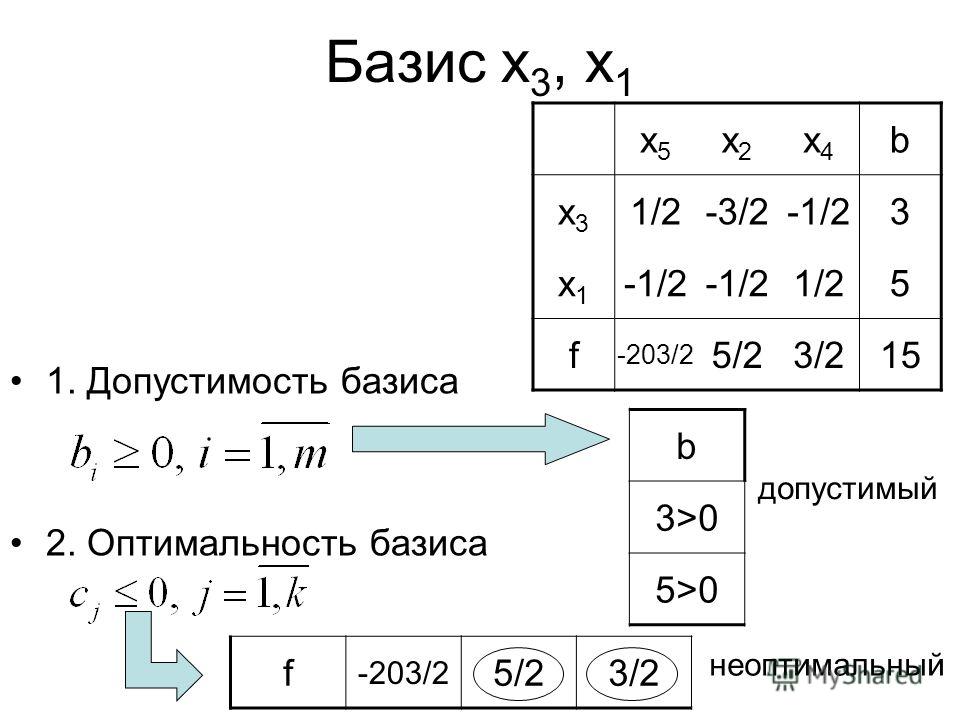 е. представление ведущего столбца в виде базисного вектора.

6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.

§5. Интерпретация результата работы симплекс-метода

1. Оптимальность

Условие оптимальности полученного решения:

• Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
• Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).

2. Неограниченность функционала

Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:

При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.

Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.

3. Альтернативные решения

При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).

Алгебраический признак существования альтернативы:

После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.

Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.

Эпилог

Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори. Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.

Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.

Спасибо за внимание!

P.S.

Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.

Big M и двухфазный метод

Когда Джордж Данциг первоначально предложил симплекс-метод, он был ограничен только задачами LP, имеющими известное допустимое решение, обычно называемое начальным базисным допустимым решением. Когда традиционный симплекс-метод применяется к более крупным задачам LP, количество переменных и количество итераций значительно увеличивается, а вместе с этим и сложность.

Поскольку симплекс-метод, возможно, является лучшим и наиболее универсально применяемым сводным алгоритмом для решения задач LP, стало важно разработать более общие методы для решения задач LP, где может быть произвольное начальное базовое решение (которое не обязательно является допустимым решением). используется для начала процесса поворота.

Содержание

• 1 Метод искусственных переменных
  • 1.1 Метод больших М (метод штрафа/метод Чарнса)
  • 1.2 Двухфазный метод

Данциг (1955) и Вагнер (1956) подчеркнули, что для LP без начального базового допустимого решения почти все современные варианты симплекс-метода применимы в два этапа. На этапе I базовое допустимое решение генерируется путем добавления переменных, известных как искусственные переменные, к задаче со специально созданной вспомогательной целью, направленной на минимизацию суммы всех искусственных переменных при сохранении выполнимости.

Когда все искусственные переменные достигают нулевого значения, это означает, что все недопустимости устранены, и мы можем продолжить работу с обычным симплекс-методом на этапе II. Если нет, то задача не имеет допустимого решения. Искусственные переменные также используются в другом симплексном методе, который предшествует двухфазному методу и известен как метод Big M.

Метод Big M позволяет применять симплекс-алгоритм к задачам, содержащим ограничения типа «больше чем», путем введения большой отрицательной константы M, которая не будет частью окончательного оптимального решения, если таковое имеется.

В этой статье читатели получат представление об искусственных переменных и двух методах, использующих их для расширения симплекс-метода для решения задач LP.

Техника искусственных переменных

В предыдущей статье вы изучали задачи, в которых резервные и избыточные переменные легко обеспечивали начальное базовое допустимое решение. Этим переменным в целевой функции присваивается нулевая стоимость.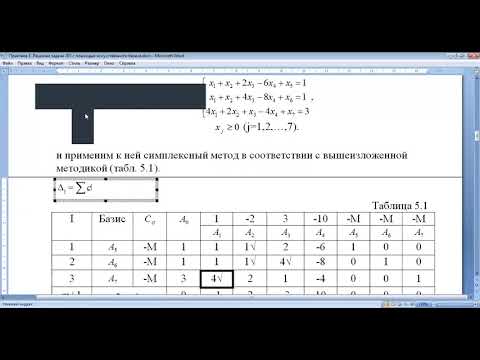 Проблема может возникнуть, когда резервные переменные не обеспечивают начального базового допустимого решения, и становится трудно начать и продолжить работу с исходной симплексной таблицей. Это происходит, когда переменные резерва имеют отрицательные значения. Например, рассмотрим ограничение:

x + 3y ≥ 175

Чтобы заменить это неравенство уравнением, вам нужно вычесть резервную переменную, чтобы получить:

x + 3y – S = 175

Теперь, если x и y не являются базовыми переменных в задаче, то в качестве исходной базовой переменной принимается S. Но это означает, что значение S = –175, что недопустимо. Вы не можете продолжать итерации симплекс-метода с недопустимым базовым решением. Чтобы сгенерировать начальное решение, вам нужно использовать метод искусственных переменных, чтобы вы могли использовать симплекс-метод, пока не будет достигнуто оптимальное решение.

Искусственные переменные добавляются к ограничениям со знаком больше или равно для создания начального решения задачи LP.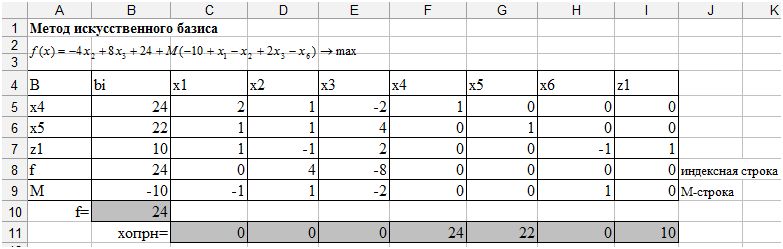 В физическом смысле искусственные переменные не имеют смысла, они являются чисто средством получения начального решения задачи ЛП и впоследствии отсеиваются.

---

Метод Big M (метод штрафа/метод Чарнса)

В некоторых задачах LP переменные запаса не могут дать начальное базовое допустимое решение. В этих типах задач LP минимум одно ограничение относится к типу ≥. Поскольку базисная матрица не может быть получена как единичная матрица в исходной симплексной таблице, вы используете новый тип переменной, называемой искусственной переменной, для создания исходного базового решения.

Вы можете расширить симплекс-метод для решения таких задач ЛП с искусственными переменными, используя любой из двух методов:

• Метод большой М (также известный как метод штрафа или метод Чарнса)
• Двухфазный симплекс-метод

Алгоритм Big M

Шаг 1: Выразите задачу LP в стандартной форме, добавив резерв и/или избыточные переменные.

Шаг 2: Введите неотрицательные искусственные переменные в левую часть всех уравнений с ограничениями типа > или =. Помните, что добавление этих искусственных переменных приводит к нарушению соответствующих ограничений. Следовательно, мы должны исключить эти переменные и не можем допустить их появления в окончательном решении. Чтобы сделать это, мы должны назначить очень большой штраф (-M для максимизации и + M для минимизации) в целевой функции.

Шаг 3: Использовать симплекс-метод для решения модифицированной задачи ЛП, пока на итерации не возникнет один из трех случаев: выполняются, то говорят, что текущее решение является оптимальным базовым допустимым решением.

Если есть хотя бы один вектор, соответствующий искусственной переменной на нулевом уровне в базисе, и выполнены условия оптимальности, то текущее базовое решение является оптимальным, хотя и вырожденным решением.

Если имеется хотя бы один вектор, соответствующий искусственной переменной на положительном уровне в базисе, и выполняются условия оптимальности, то допустимого решения исходной задачи нет. Штраф в этом случае очень велик, а решение, удовлетворяющее ограничениям, не оптимизирует целевую функцию.

Вставка переменных резерва, излишка и искусственных переменных в метод Big M

Переменная резерва добавляется к типам ограничений меньше или равно, чтобы преобразовать их в равенства. Переменная избытка добавляется к типам ограничений больше или равно, чтобы преобразовать их в равенства.

Для связывающего ограничения соответствующий резерв или избыточное значение будет равно нулю. В модель ЛП вводится искусственная переменная для получения начального базового допустимого решения. Он используется для ограничений равенства и для ограничений типа больше или равно неравенству.

Сравнение различных типов переменных

Недостаток Переменная	Излишек Переменная	Искусственная переменная
Используется с типом ограничения ≤	Используется с типом ограничения ≥	Используется с типом ограничения ≥ или = значение должно быть удалено для получения BFS	Не имеют физической ценности. Они используются для создания BFS
Имеют коэффициент уравнения +1	Имеют коэффициент уравнения –1	Иметь коэффициент уравнения +1
Иметь целевой коэффициент 0	Иметь целевой коэффициент 0	Иметь целевой коэффициент –M для задачи максимизации и +M для задачи минимизации

Давайте теперь посмотрим, где переменные вставлены в метод Big M:

На шаге 1 метода Big M ограничения данной задачи LP выражаются в форме уравнения путем включения резервных переменных для ограничения типа ≤ или избыточные переменные для ограничения типа ≥.

Теперь можно определить базовое решение задачи, недопустимое, так как базовая переменная отрицательна для ограничений типа ≥.

На шаге 2 метода Big M неотрицательные искусственные переменные добавляются в левую часть каждого из уравнений, соответствующих ограничениям типов > и =, чтобы сгенерировать начальное базовое допустимое решение.

Двухфазный метод

Двухфазный метод назван так потому, что задача ЛП решается в два этапа. Симплекс-метод применяется к специально построенной вспомогательной задаче ЛП на этапе I, и проблема решается путем применения симплекс-метода, который помогает генерировать базовое допустимое решение исходной задачи.

Процесс исключения искусственных переменных выполняется на этапе I решения, а этап II используется для получения оптимального решения с использованием симплекса.

На этапе I искусственные переменные вводятся для того, чтобы сделать переменные исходной задачи небазисными и обнулить их, даже если это может быть невозможно для исходной задачи. Полученные в результате недопустимости берутся за искусственные переменные, и они являются базовыми в начале фазы I.

Теперь рассмотрим шаги двухэтапного метода:

ФАЗА 1

Шаг 1: Выразите заданную задачу ЛП в стандартной форме и проверьте, существует ли исходное базисное допустимое решение задачи. Может возникнуть один из двух случаев:

• Существует готовое начальное базовое допустимое решение, и в этом случае мы можем перейти к Фазе II.
• Для проблемы не существует начального базового допустимого решения, и в этом случае вы переходите к следующему шагу этапа I.

Шаг 2: Добавьте искусственную переменную в левую часть каждого уравнения, которое не имеет требуемых начальных базовых переменных. Постройте вспомогательную целевую функцию, целью которой является минимизация суммы всех искусственных переменных.

Следовательно,

Минимизировать Z= A1 + A2 + A3 + ………. +

становится

Максимизация Z* = – A1 – A2 – A3 – ………. – An

, где Ai (i = 1,2,3…m) – неотрицательные искусственные переменные.

Шаг 3: Примените симплекс-алгоритм к специально построенной вспомогательной задаче ЛП. На последней итерации может иметь место один из следующих трех случаев:

• Max Z* < 0 и в базисе присутствует хотя бы одна положительная искусственная переменная, и в этом случае для исходной ЛП не существует допустимого решения проблема.
• Max Z* = 0 с хотя бы одной искусственной переменной, имеющей нулевое значение в базисе, и в этом случае для исходной задачи ЛП существует допустимое решение. Чтобы получить основное допустимое решение, мы можем либо перейти непосредственно к Фазе II, либо исключить искусственную базовую переменную и затем перейти к Фазе II.
• Max Z* = 0 и в базисе нет искусственной переменной, и в этом случае вы получили базовое допустимое решение исходной задачи ЛП, и мы можем перейти к Фазе II.

ЭТАП 2

Оптимальное базисно допустимое решение фазы I используется в качестве начального базисно допустимого решения исходной задачи ЛП. Присвойте фактические коэффициенты переменным в целевой функции и нулевое значение искусственным переменным, которые показывают нулевое значение в окончательной симплекс-таблице фазы I. Используйте обычный симплекс-алгоритм на модифицированной симплекс-таблице, чтобы получить оптимальное решение исходной задачи.

---

Сравнение симплекс-метода Big M и двухфазного симплекс-метода

Симплекс-метода Big M	Двухфазного симплекс-метода
В M раз умножьте сумму искусственных переменных и решите задачу, используя исходную цель.	При двухэтапном подходе вы сначала решаете специально построенную вспомогательную задачу на первом этапе, затем переходите ко второму этапу, чтобы получить допустимое решение исходной задачи.
Метод Big M решает проблему в один этап.	Двухфазный метод решает ее в два этапа.
Преимущество использования метода Big M заключается в том, что для него требуется только одна целевая функция, а исходная цель используется на протяжении всего процесса решения.	В двухэтапном методе на этапе I рассматривается только вспомогательная задача, поэтому вы можете не знать, есть ли у нас решение исходной задачи, пока не завершите этап I.
Метод Big M предполагает большой штраф M, а также увеличивает сложность вычислений.

недостаток метода большого M связан с тем, как мы выбираем штраф M. Если M слишком мало, окончательное решение исходной задачи может быть даже неосуществимым, не говоря уже об оптимальном, поскольку штраф за невыполнимость была недостаточно велика.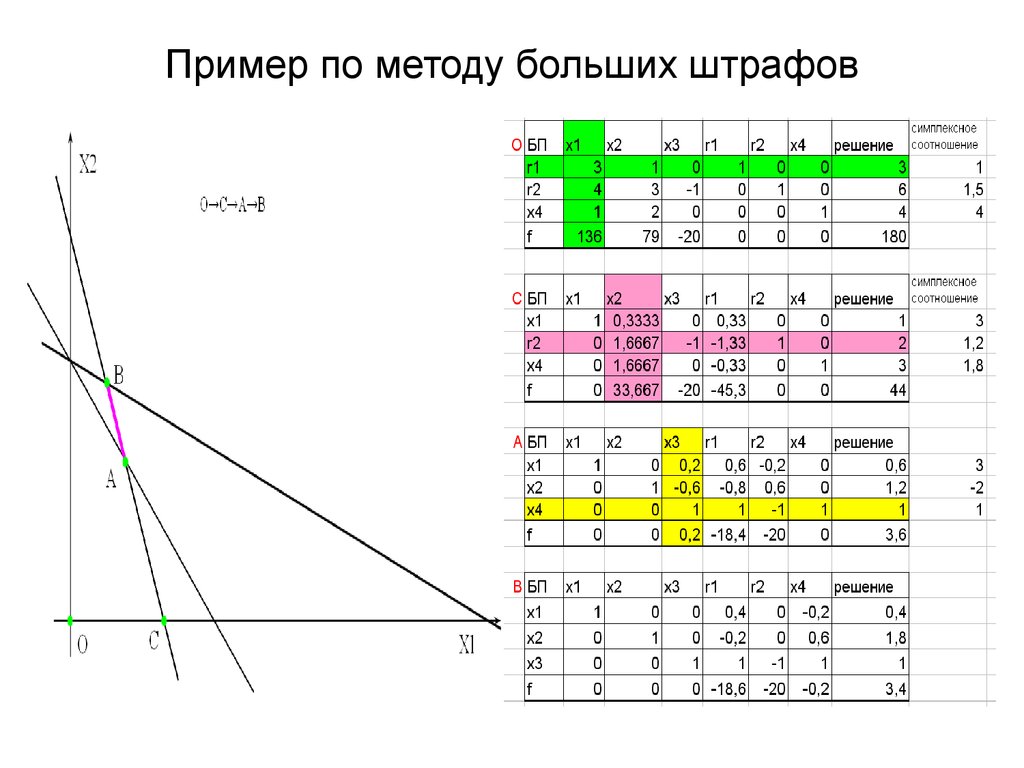

С другой стороны, если M очень велико, у исходной задачи могут быть проблемы с числовыми параметрами, и окончательное решение может оказаться неоптимальным. Иногда не существует значения M, которое могло бы предотвратить обе эти проблемы. Еще одно ограничение метода большого М по сравнению с двухфазным методом заключается в том, что в первом случае выполнимость неизвестна до тех пор, пока не будет достигнута оптимальность.

сообщить об этом объявлении

оптимизация — почему в Фазе I симплекс-метода, если искусственная переменная становится небазовой, она никогда не становится базовой? 9Т х \\ & А х = б \\ & х \geq 0 \конец{массив} Они предполагают, что $b\geq 0$; если это не так, инвертируйте соответствующие строки, чтобы сделать это так. (Для простоты предположим, что $b$ имеет хотя бы одно ненулевое значение.) Соответствующая задача фазы I выглядит следующим образом: \begin{массив}{ll} \text{свернуть} & \textstyle\sum_i y_i \\ & А х + у = б \\ & х \geq 0, у \geq 0 \конец{массив} Теперь вы понимаете, почему значение $b\geq 0$ важно: $(x,y)=(0,b)$ представляет собой тривиальное допустимое решение, так что это ваша отправная точка для метода Фазы I с начальной целью $\ сумма_i b_i>0$.

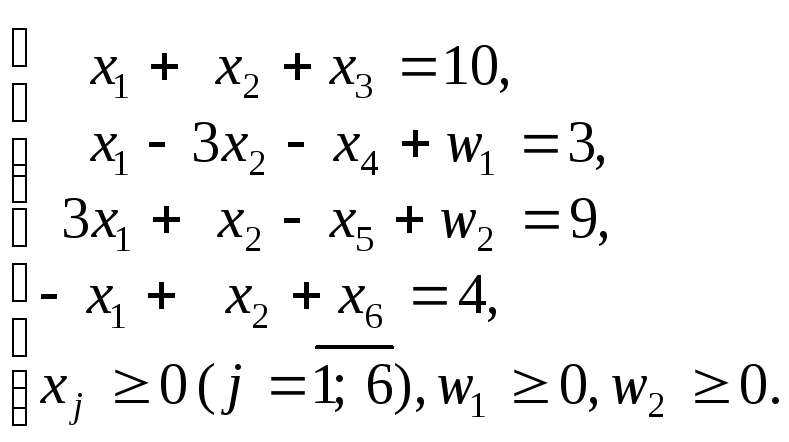Если оптимальное значение этой модели Фазы I равно нулю, то исходная модель реализуема; в противном случае исходная модель невозможна.

Важно внимательно прочитать заявление. Это , а не , утверждающий, что искусственная переменная никогда не войдет в базис, если вы оставите ее в таблице. На самом деле, может. Если у вас есть книга, посмотрите пример 3.8. На одном из шагов одна из неосновных искусственных переменных имеет отрицательную приведенную стоимость, что делает ее 90 253 полностью действительным 90 254 кандидатом для выбора, в зависимости от используемого вами сводного правила. (Однако в примере выбрана другая точка опоры.)

Таким образом, утверждение не в том, что никогда не повторно войдет в базу. Скорее, утверждение говорит о том, что не нуждается в для повторного входа в базу. Мы хотим показать, что удаление одной из этих переменных из таблицы не препятствует правильному завершению симплекс-метода.

Чтобы понять, почему это так, рассмотрим этот «перезапуск» подхода к решению модели Фазы I:

1. Инициализация: base $\mathcal{B}=(y_1,y_2,\dots,y_n)$, $( х, у) = (\vec{0},\vec{1})$.
2. Начать симплексный алгоритм с текущим базисом $\mathcal{B}$ и текущими $(x,y)$.
3. Если алгоритм завершится до того, как будет устранена искусственная переменная:
   • Если стоимость равна нулю, СТОП. Задача разрешима, но необходимо предпринять дополнительные шаги, чтобы вытеснить из базиса оставшиеся искусственные переменные. Подробности см. в разделе 3.5.
   • Если стоимость положительна, СТОП. проблема неразрешима.
4. Как только из базиса будет удалена искусственная переменная, остановить симплекс-метод и получить текущий базис $\mathcal{B}$ и текущую точку $(x,y)$. (В первый раз это произойдет при самом первом развороте. В последующих итерациях это может занять больше времени.)
5. Удалите из задачи новую неосновную искусственную переменную. Если не осталось базовых искусственных переменных, СТОП. Ваша проблема выполнима, и у вас есть базовое возможное решение.
6. Повторить шаги 2-6.

Ключом к успеху этого подхода является то, что после удаления неосновной искусственной переменной на шаге 5 у вас все еще остается действующая модель псевдофазы I и достижимая точка для этой модели.